Energy Consumption Analysis of Helicopter Traction Device: A Modeling Method Considering Both Dynamic and Energy Consumption Characteristics of Mechanical Systems
Abstract
1. Introduction
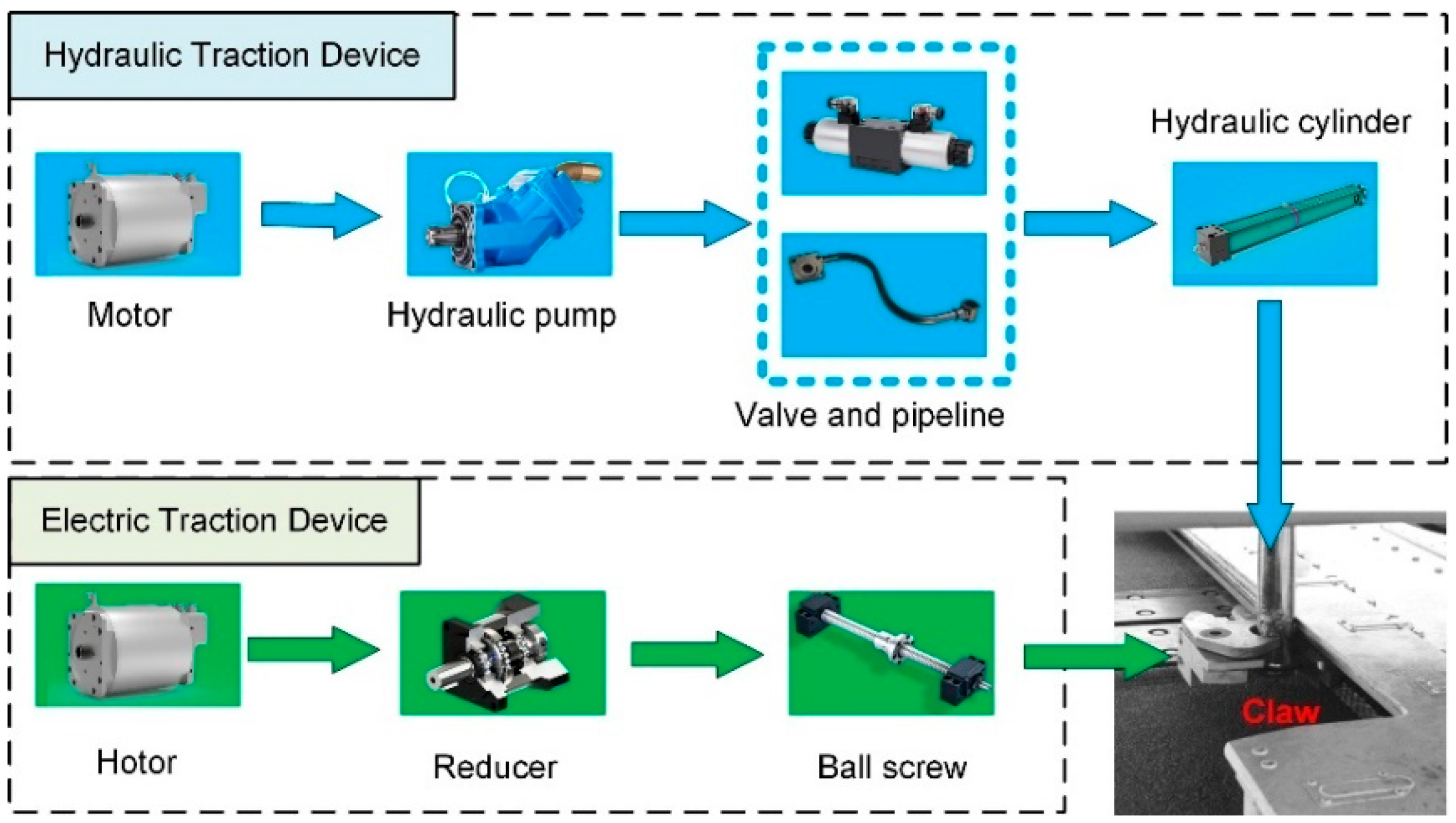
2. Principles of Helicopter Traction Devices
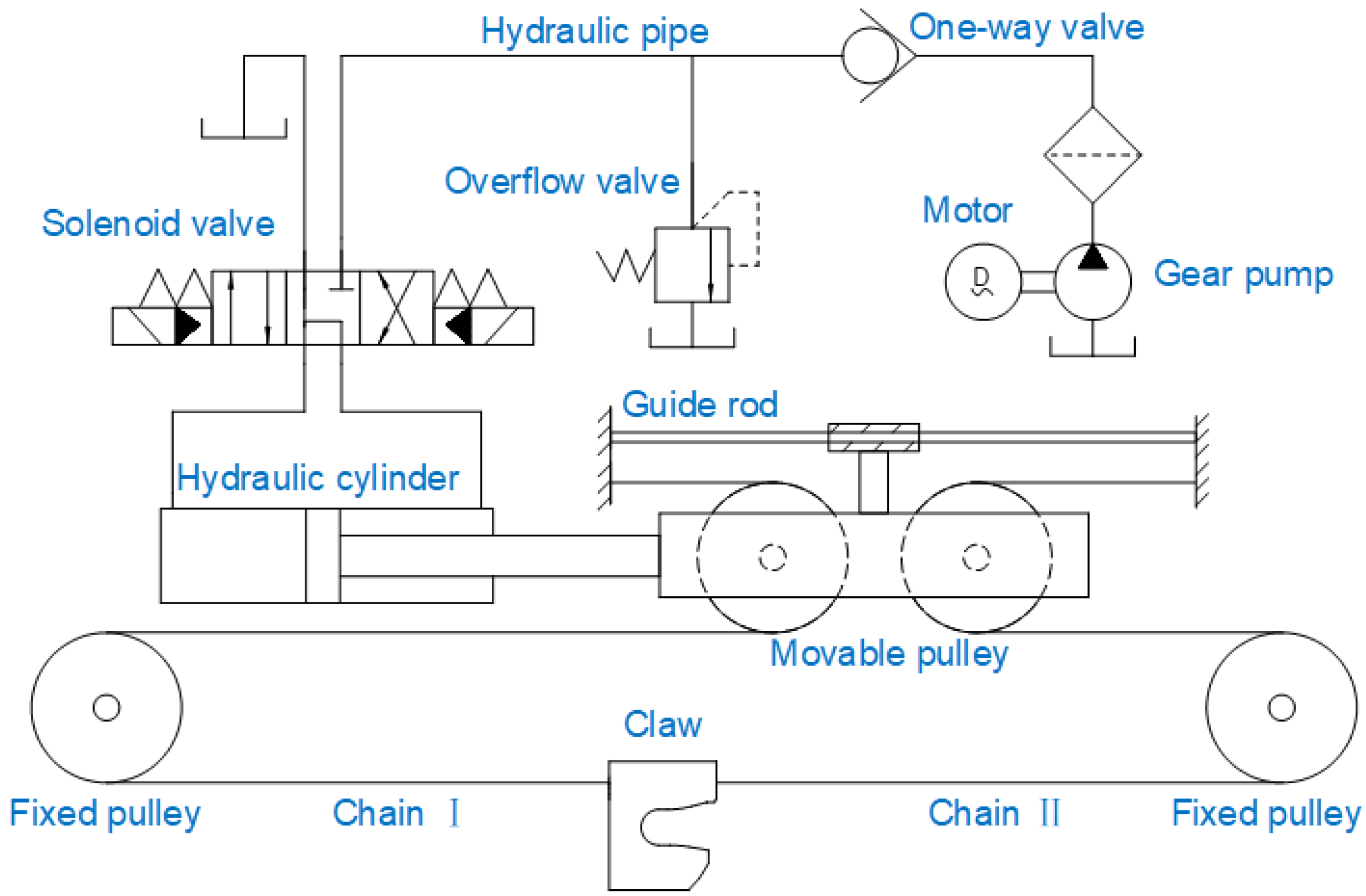
2.1. Transmission Principle of HTD
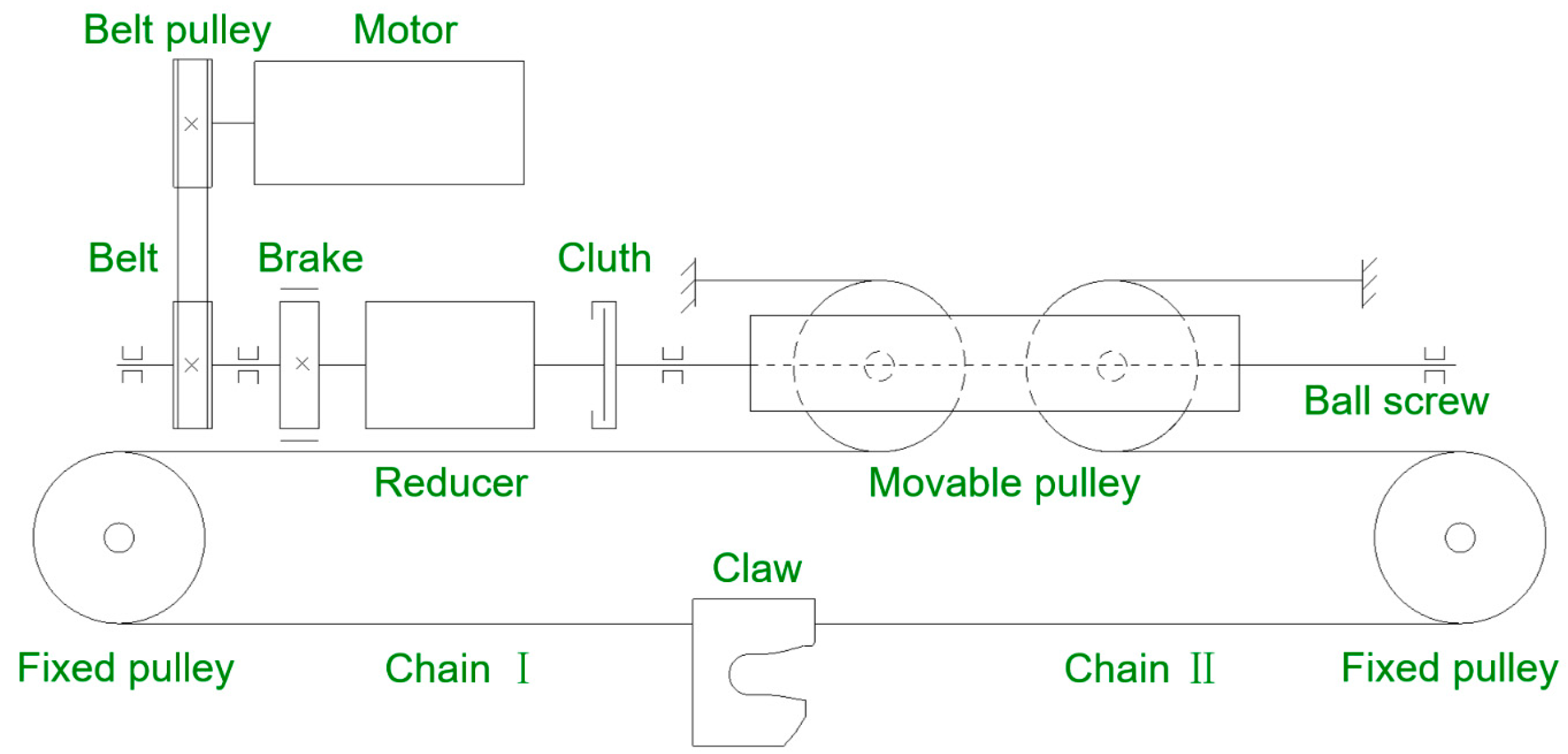
2.2. Transmission Principle of the ETD
3. System Dynamics Model
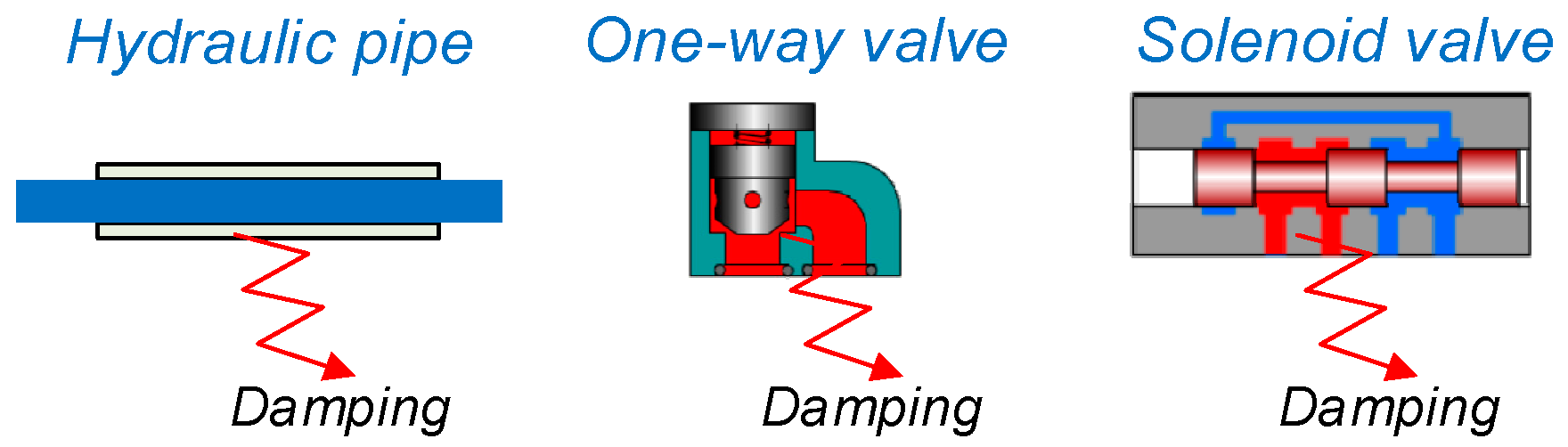
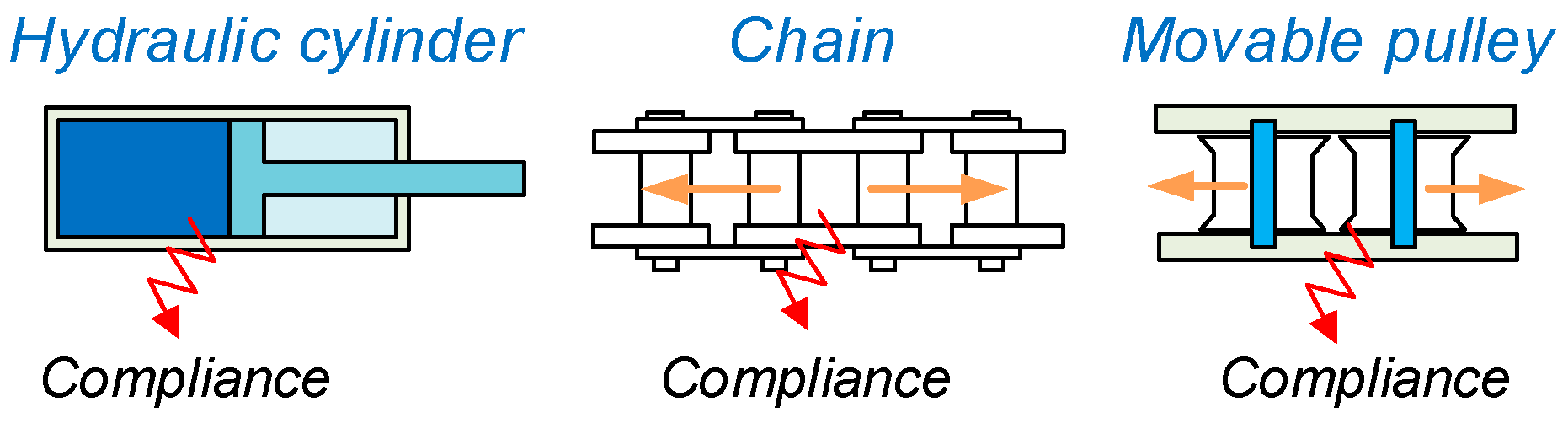
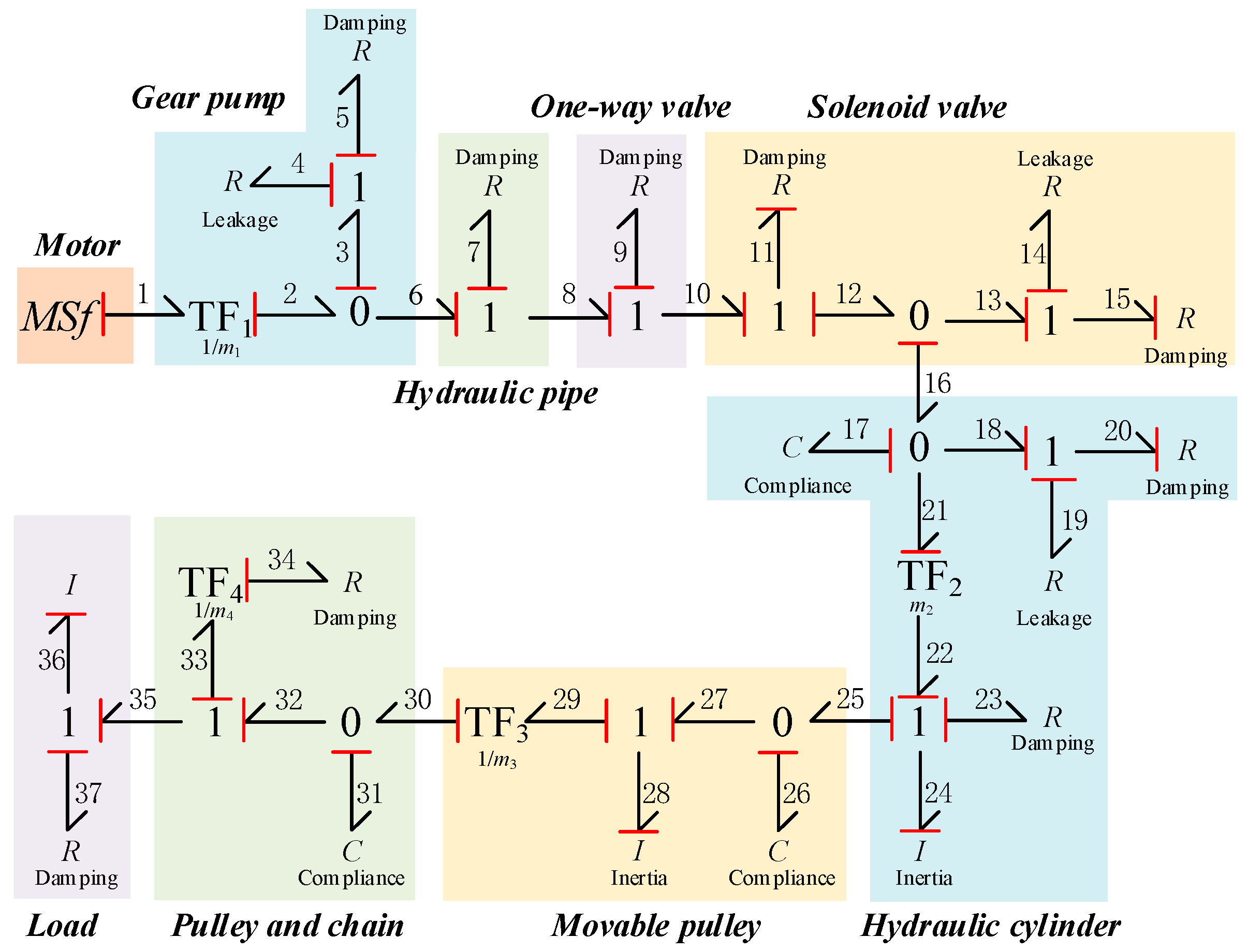
3.1. Energy Consumption Analysis of HTD
- Motion damping
- 2.
- Flow damping
- 3.
- Leakage loss
- 4.
- Energy storage loss
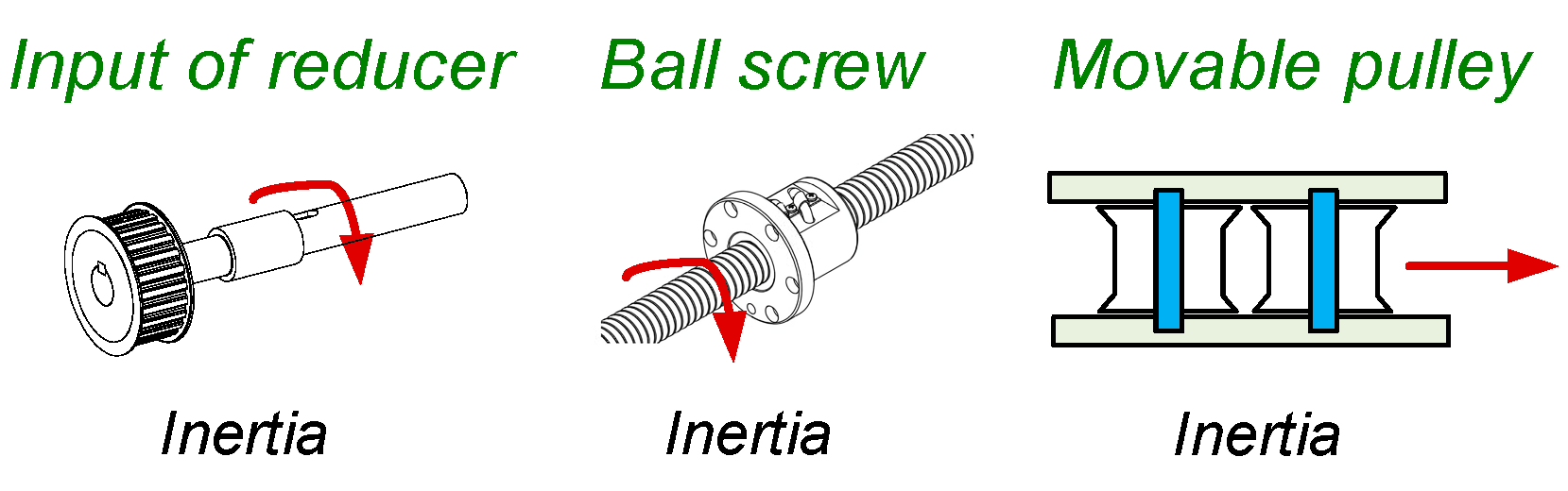
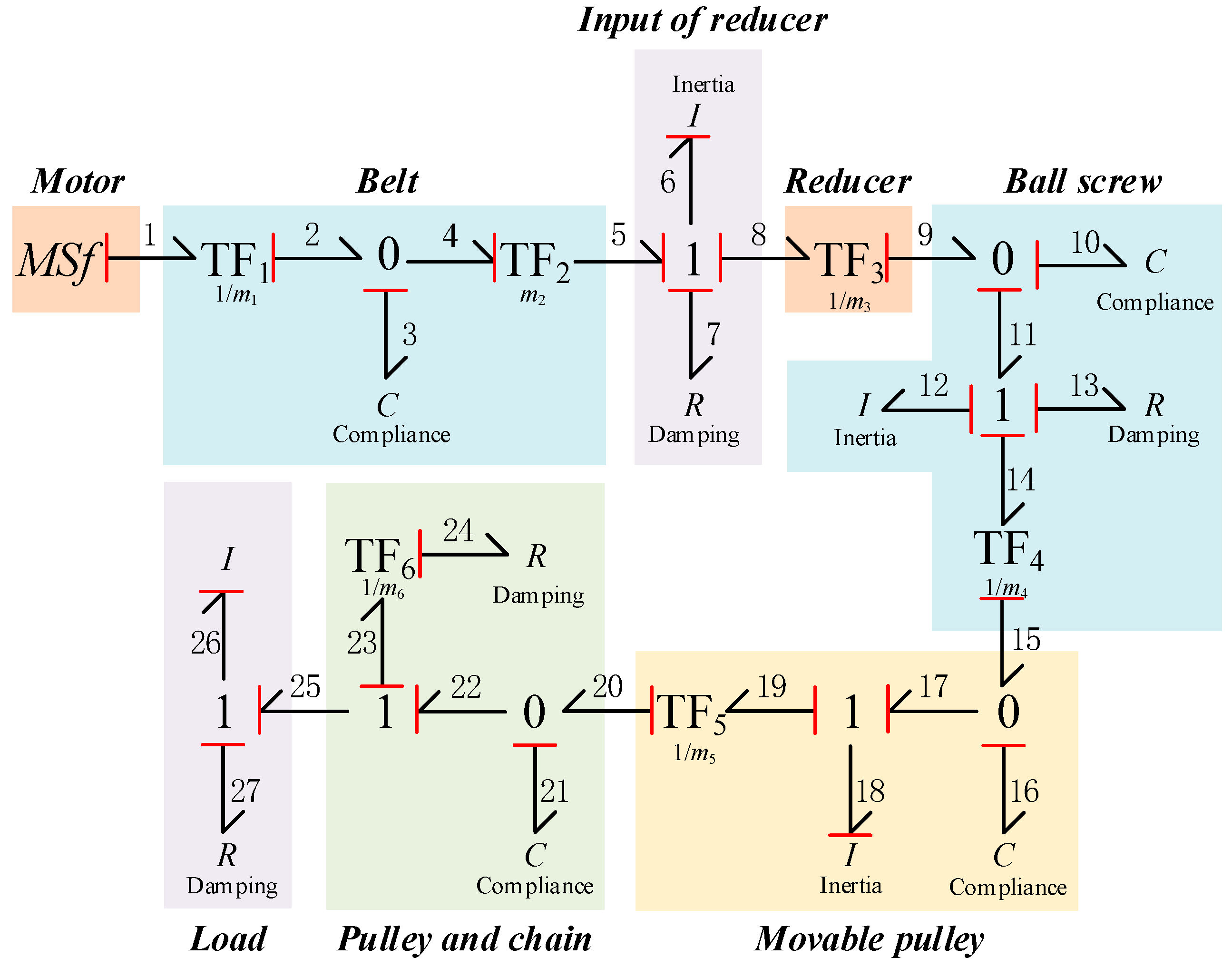
3.2. Energy Consumption Analysis of the ETD
- Motion damping
- 2.
- Energy storage loss
3.3. System Dynamics Model
- Resistance element
- 2.
- Compliance element
- 3.
- Inertance element
- 4.
- Auxiliary element
4. Simulation Tests
4.1. The Simulation Conditions
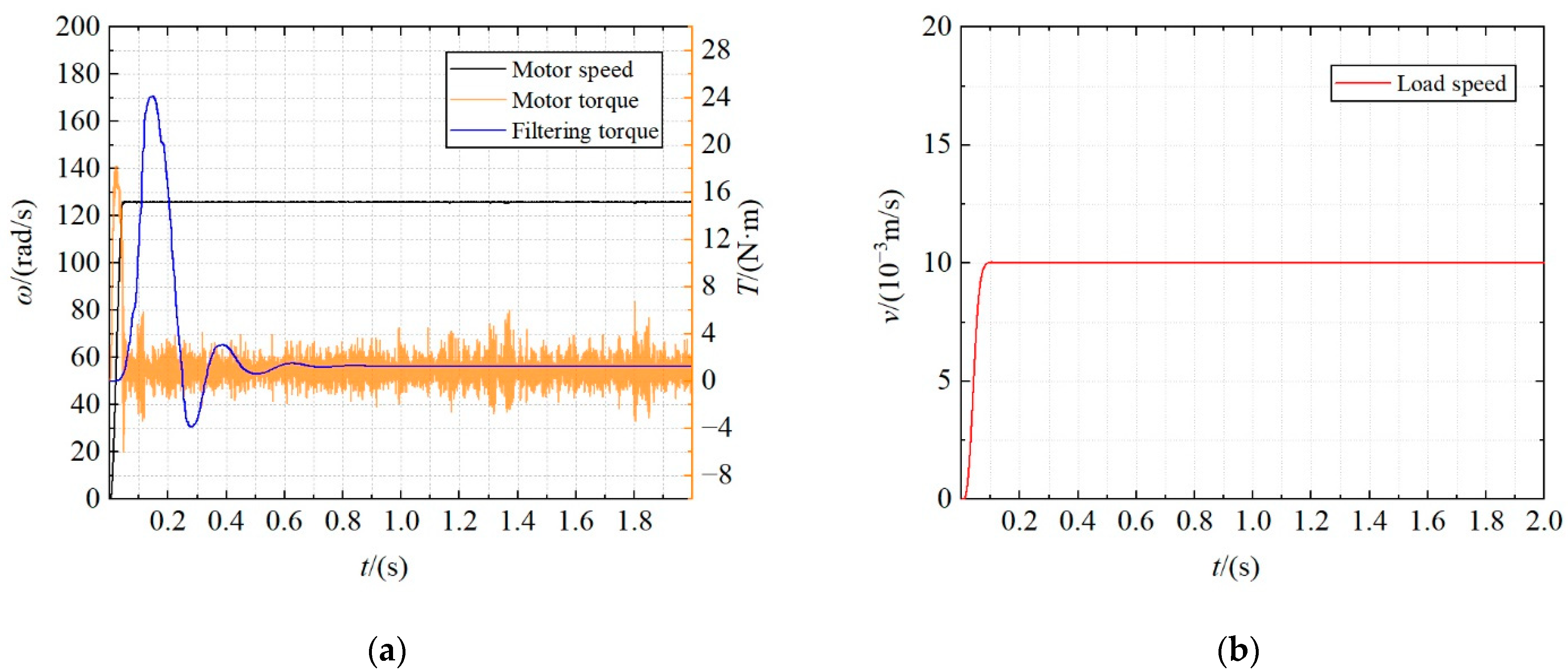
4.2. Dynamic Characteristics and Energy Consumption Characteristics of HTD
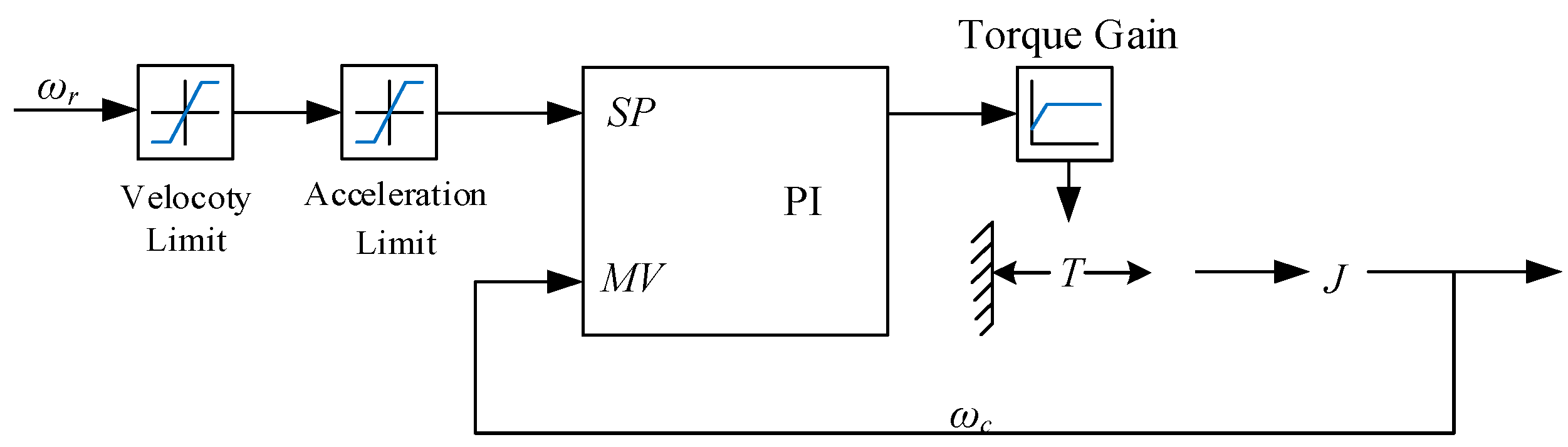
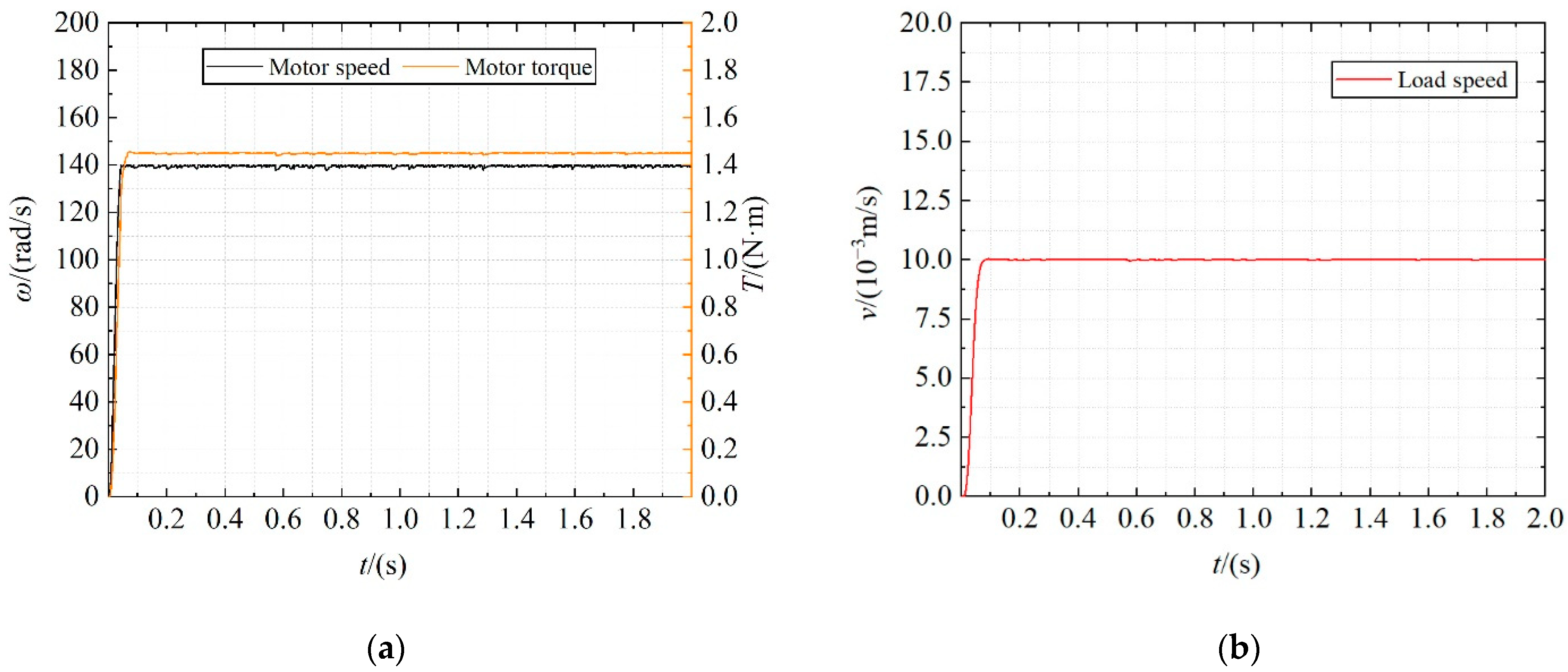
4.3. Dynamic Characteristics and Energy Consumption Characteristics of the ETD
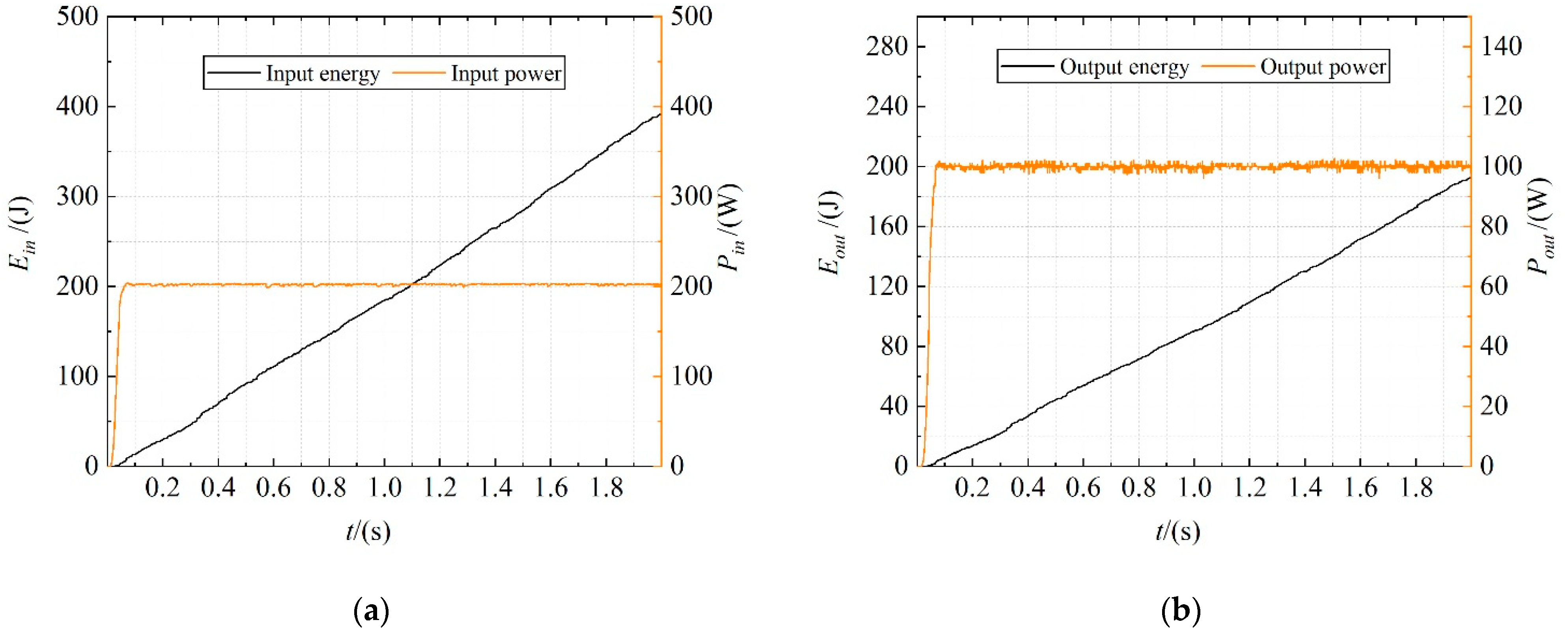
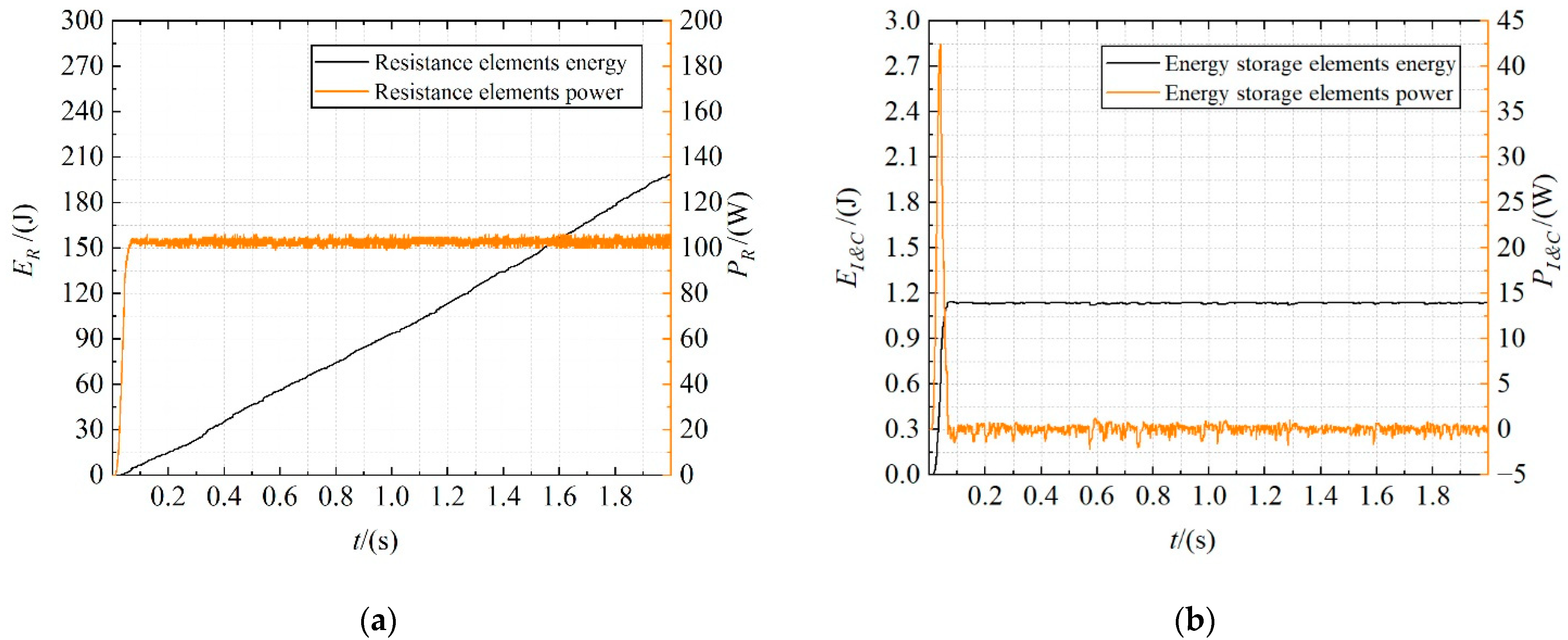
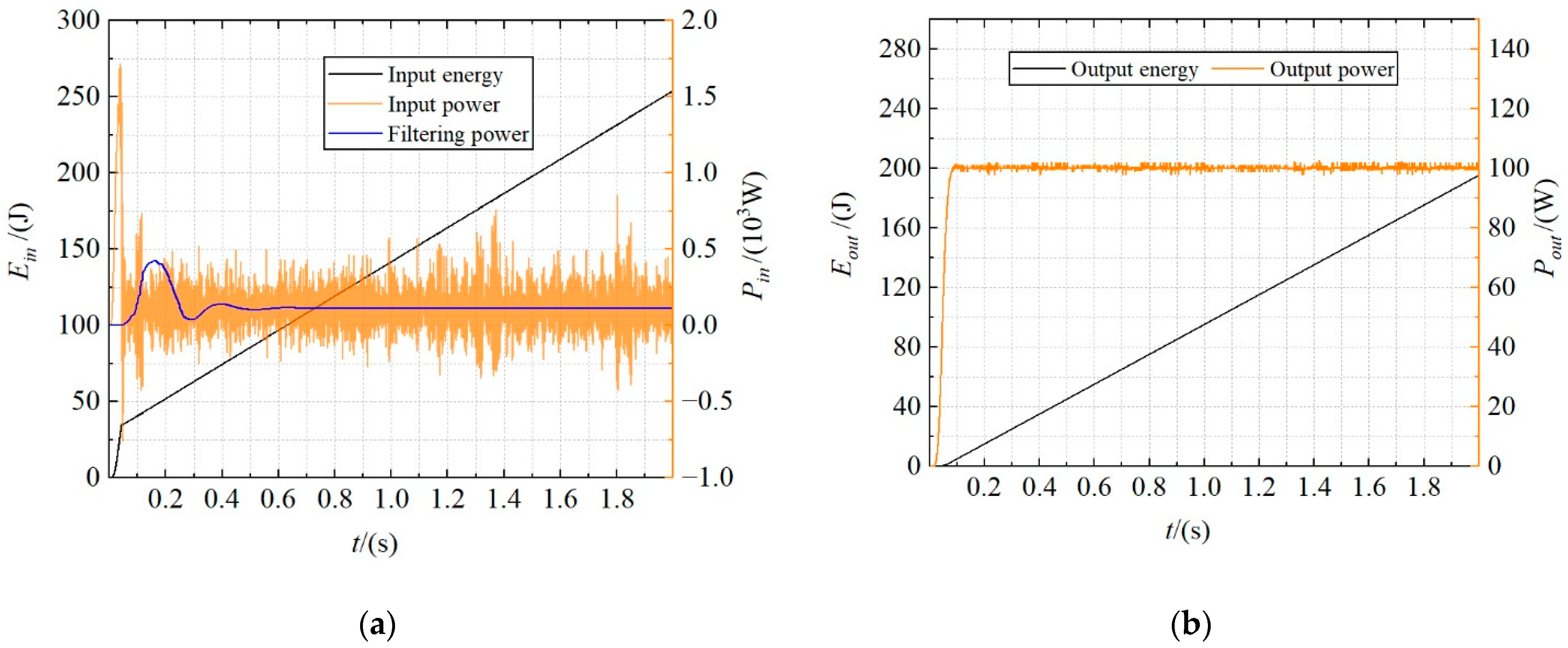
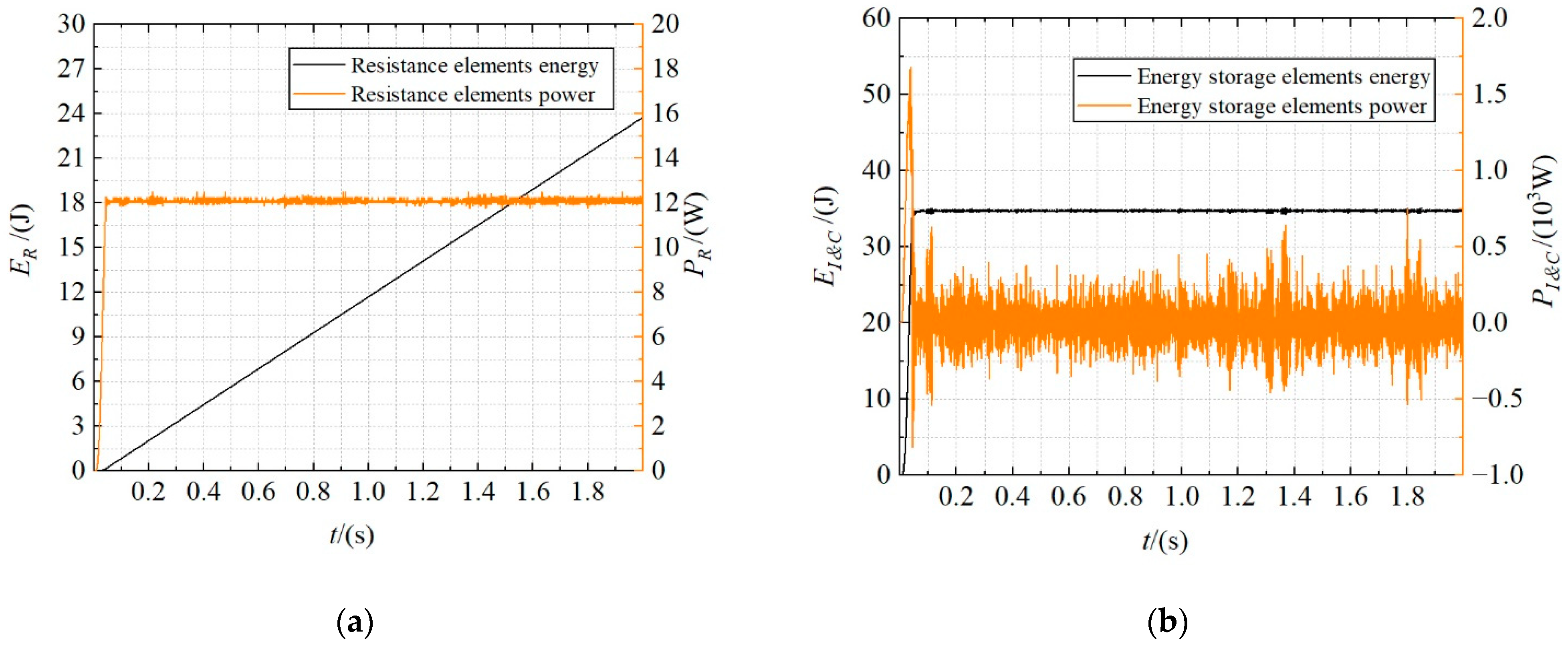
4.4. Analysis of Energy Consumption
5. Conclusions
- The proposed modeling method can better reflect the dynamic characteristics of the system and accurately describe the energy consumption trend in each link of the system. This modeling method is mainly used for energy consumption analysis and the optimization design of shipborne equipment. It also has essential reference significance for the modeling and analysis of other complex mechanical systems.
- Compared with the HTD, the ETD has a higher energy utilization rate and more stable system operation in the steady state. Therefore, in shipborne equipment, it is of great significance to popularize the application of electric drive equipment to improve the capability of ocean voyages and long-term combat.
- The energy consumption of the HTD is mainly concentrated on the resistance elements, accounting for 50.87% of the total energy consumption. The energy consumption of the ETD is mainly concentrated in the inertance elements, accounting for 13.39% of the total energy consumption. This conclusion is helpful for designers to optimize the energy consumption of the system and improve its efficiency.
Author Contributions
Funding
Conflicts of Interest
References
- Beecher, J.D. The FFG7 guided missle frigate program model for the future. Nav. Eng. J. 1978, 90, 93–105. [Google Scholar] [CrossRef]
- Hu, Z.; Jin, Y.; Hu, Q.; Sen, S.; Zhou, T.; Osman, M.T. Prediction of Fuel Consumption for Enroute Ship Based on Machine Learning. IEEE Access 2019, 7, 119497–119505. [Google Scholar] [CrossRef]
- Yu, H.; Fang, Z.; Fu, X.; Liu, J.; Chen, J. Literature review on emission control-based ship voyage optimization. Transp. Res. Part D Transp. Environ. 2021, 93, 102768. [Google Scholar] [CrossRef]
- Man, Y.; Sturm, T.; Lundh, M.; MacKinnon, S.N. From Ethnographic Research to Big Data Analytics—A Case of Maritime Energy-Efficiency Optimization. Appl. Sci. 2020, 10, 2134. [Google Scholar] [CrossRef]
- Balsamo, F.; De Falco, P.; Mottola, F.; Pagano, M. Power Flow Approach for Modeling Shipboard Power System in Presence of Energy Storage and Energy Management Systems. IEEE Trans. Energy Convers. 2020, 35, 1944–1953. [Google Scholar] [CrossRef]
- Nuchturee, C.; Li, T.; Xia, H. Energy efficiency of integrated electric propulsion for ships—A review. Renew. Sustain. Energy Rev. 2020, 134, 110145. [Google Scholar] [CrossRef]
- Taymourtash, N.; Zagaglia, D.; Zanotti, A.; Muscarello, V.; Gibertini, G.; Quaranta, G. Experimental study of a helicopter model in shipboard operations. Aerosp. Sci. Technol. 2021, 115, 106774. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Zhao, D.; Wang, L.; Yang, P. Research on Shipborne Helicopter Electric Rapid Secure Device: System Design, Modeling, and Simulation. Sensors 2022, 22, 1514. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Zhao, D.; Wang, L.; Jia, T. Electrical Aircraft Ship Integrated Secure and Traverse System Design and Key Characteristics Analysis. Appl. Sci. 2022, 12, 2603. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, D.X.; Wei, H.L.; Zhao, Y. Study of the Landing Dynamics of Carrier Based Helicopter Under Complex Sea Conditions. J. Northeast. Univ. (Nat. Sci.) 2017, 38, 1595. [Google Scholar]
- Zhao, D.X.; Wang, Q.; Zhang, Z.X. Extenics theory for reliability assessment of carrier helicopter based on analytic hierarchy process. J. Jilin Univ. (Eng. Technol. Ed.) 2016, 46, 1528–1531. [Google Scholar]
- Su, D.; Xu, G.; Huang, S.; Shi, Y. Numerical investigation of rotor loads of a shipborne coaxial-rotor helicopter during a vertical landing based on moving overset mesh method. Eng. Appl. Comput. Fluid Mech. 2019, 13, 309–326. [Google Scholar] [CrossRef]
- Linn, D.R.; Langlois, R.G. Development and experimental validation of a shipboard helicopter on-deck maneuvering simulation. J. Aircr. 2006, 43, 895–906. [Google Scholar] [CrossRef]
- Feldman, A.R.; Langlois, R.G. Autonomous straightening and traversing of shipboard helicopters. J. Field Robot. 2006, 23, 123–139. [Google Scholar] [CrossRef]
- Karpenko, M.; Prentkovskis, O.; Šukevičius, Š. Research on high-pressure hose with repairing fitting and influence on energy parameter of the hydraulic drive. Eksploatacja Niezawodność 2022, 24, 25–32. [Google Scholar] [CrossRef]
- Karpenko, M.; Bogdevičius, M. Investigation into the hydrodynamic processes of fitting connections for determining pressure losses of transport hydraulic drive. Transport 2020, 35, 108–120. [Google Scholar] [CrossRef]
- Liu, W.; Li, L.; Cai, W.; Li, C.; Li, L.; Chen, X.; Sutherland, J.W. Dynamic characteristics and energy consumption modelling of machine tools based on bond graph theory. Energy 2020, 212, 118767. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, Q.; Guo, Q.; Gong, Y. Dynamic Modeling and Experimental Validation of a Water Hydraulic Soft Manipulator Based on an Improved Newton—Euler Iterative Method. Micromachines 2022, 13, 130. [Google Scholar] [CrossRef]
- Zhang, F.; Yuan, Z. The Study of Coupling Dynamics Modeling and Characteristic Analysis for Flexible Robots with Nonlinear and Frictional Joints. Arab. J. Sci. Eng. 2022, 1–17. [Google Scholar] [CrossRef]
- Ungureanu, L.M.; Petrescu, F.I.T. Dynamics of Mechanisms with Superior Couplings. Appl. Sci. 2021, 11, 8207. [Google Scholar] [CrossRef]
- Burghardt, A.; Skwarek, W. Modeling the Dynamics of Two Cooperating Robots. Appl. Sci. 2021, 11, 6019. [Google Scholar] [CrossRef]
- Burghardt, A.; Gierlak, P.; Skwarek, W. Modeling of dynamics of cooperating wheeled mobile robots. J. Theor. Appl. Mech. 2021, 59, 649–659. [Google Scholar] [CrossRef]
- Tu, T.W. Dynamic modelling of a railway wheelset based on Kane’s method. Int. J. Heavy Veh. Syst. 2020, 27, 202–226. [Google Scholar] [CrossRef]
- Qi, F.; Chen, B.; Gao, S.; She, S. Dynamic model and control for a cable-driven continuum manipulator used for minimally invasive surgery. Int. J. Med. Robot. Comput. Assist. Surg. 2021, 17, e2234. [Google Scholar] [CrossRef]
- Somu, N.; M R, G.R.; Ramamritham, K. A hybrid model for building energy consumption forecasting using long short term memory networks. Appl. Energy 2020, 261, 114131. [Google Scholar] [CrossRef]
- Wang, G.; Ding, L.; Gao, H.; Deng, Z.; Liu, Z.; Yu, H. Minimizing the Energy Consumption for a Hexapod Robot Based on Optimal Force Distribution. IEEE Access 2019, 8, 5393–5406. [Google Scholar] [CrossRef]
- Liu, E.; Lv, L.; Yi, Y.; Xie, P. Research on the Steady Operation Optimization Model of Natural Gas Pipeline Considering the Combined Operation of Air Coolers and Compressors. IEEE Access 2019, 7, 83251–83265. [Google Scholar] [CrossRef]
- Saeedi, M.; Moradi, M.; Hosseini, M.; Emamifar, A.; Ghadimi, N. Robust optimization based optimal chiller loading under cooling demand uncertainty. Appl. Therm. Eng. 2018, 148, 1081–1091. [Google Scholar] [CrossRef]
- Su, S.; Wang, X.; Cao, Y.; Yin, J. An Energy-Efficient Train Operation Approach by Integrating the Metro Timetabling and Eco-Driving. IEEE Trans. Intell. Transp. Syst. 2019, 21, 4252–4268. [Google Scholar] [CrossRef]
- Fu, Y.; Tian, G.; Fathollahi-Fard, A.M.; Ahmadi, A.; Zhang, C. Stochastic multi-objective modelling and optimization of an energy-conscious distributed permutation flow shop scheduling problem with the total tardiness constraint. J. Clean. Prod. 2019, 226, 515–525. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, D.; Wang, L.; Zhang, Z.; Wang, L.; Hu, Y. Dynamic simulation and analysis of the elevating mechanism of a forklift based on a power bond graph. J. Mech. Sci. Technol. 2016, 30, 4043–4048. [Google Scholar] [CrossRef]
- Deam, K. Understanding Automobile Roll Dynamics and Lateral Load Transfer Through Bond Graphs. Trans. Korean Soc. Automot. Eng. 1998, 6, 34–44. [Google Scholar]
- Couenne, F.; Jallut, C.; Maschke, B.; Tayakout, M.; Breedveld, P. Structured modeling for processes: A thermodynamical network theory. Comput. Chem. Eng. 2008, 32, 1120–1134. [Google Scholar] [CrossRef]
- Borutzky, W.; Barnard, B.; Thoma, J.U. Describing bond graph models of hydraulic components in Modelica. Math. Comput. Simul. 2000, 53, 381–387. [Google Scholar] [CrossRef]
- Fu, J.; Maré, J.-C.; Fu, Y. Incremental Modeling and Simulation of Mechanical Power Transmission for More Electric Aircraft Flight Control Electromechanical Actuation System Application. In Proceedings of the ASME 2016 International Mechanical Engineering Congress and Exposition, Phoenix, AZ, USA, 11–17 November 2016; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 50510, p. V001T03A040. [Google Scholar]
- Badoud, A.E.; Merahi, F.; Bouamama, B.O.; Mekhilef, S. Bond graph modeling, design and experimental validation of a photovoltaic/fuel cell/electrolyzer/battery hybrid power system. Int. J. Hydrogen Energy 2021, 46, 24011–24027. [Google Scholar] [CrossRef]
- Song, K.; Wang, Y.; An, C.; Xu, H.; Ding, Y. Design and Validation of Energy Management Strategy for Extended-Range Fuel Cell Electric Vehicle Using Bond Graph Method. Energies 2021, 14, 380. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, B. Double Vectors Model Predictive Torque Control Without Weighting Factor Based on Voltage Tracking Error. IEEE Trans. Power Electron. 2017, 33, 2368–2380. [Google Scholar] [CrossRef]
- Faiz, J.; Heidari, M.; Sharafi, H. Torque ripple and switching frequency reduction of interior permanent magnet brushless direct current motors using a novel control technique. IET Power Electron. 2019, 12, 3852–3858. [Google Scholar] [CrossRef]









| Driving Part | Translational Motion | Rotation Motion | Liquid Flow | |||
|---|---|---|---|---|---|---|
| Value | Unit | Value | Unit | Value | Unit | |
| Potential variable | Force | N | Torque | N·m | Pressure | N/m2 |
| Flow variable | Velocity | m/s | Angular velocity | rad/s | Flow | m3/s |
| Generalized momentum | Momentum | N·s | Angular momentum | N·m·s | Pressure momentum | (N·s)/m2 |
| Generalized displacement | Displacement | m | Angular displacement | rad | Volume | m3 |
| Driving Part | Symbol | Value | Unit |
|---|---|---|---|
| Gear pump | TF1 | 3.14 × 106 | rad/m3 |
| R4 | 3.21 × 10−12 | m3/(s·pa) | |
| R5 | 4.72 × 105 | pa·s/m3 | |
| Hydraulic pipe | R7 | 1.81 × 108 | pa·s/m3 |
| One-way valve | R9 | 8.76 × 109 | pa·s/m3 |
| Solenoid valve | R11 | 1.03 × 1010 | pa·s/m3 |
| R14 | 3.3 × 10−13 | m3/(s·pa) | |
| R15 | 1.32 × 104 | pa·s/m3 | |
| Hydraulic cylinder | C17 | 2.51 × 10−14 | m3/pa |
| R19 | 1.04 × 10−12 | m3/(s·pa) | |
| R20 | 6.37 × 106 | pa·s/m3 | |
| TF2 | 5.02 × 10−3 | m2/s | |
| I24 | 46.32 | kg | |
| R23 | 60.0 | N | |
| Movable pulley | I28 | 35.75 | kg |
| TF3 | 0.5 | ||
| C26 | 4.3 × 10−9 | m/N | |
| Pulley and chain | C31 | 1.49 × 10−8 | m/N |
| R34 | 7.6 × 10−2 | N·m·s | |
| TF4 | 56.25 × 10−3 | m/rad | |
| Load | R37 | 1 × 104 | N |
| I36 | 6.04 × 103 | kg |
| Driving part | Symbol | Value | Unit |
|---|---|---|---|
| Belt | TF1 | 20.61 | rad/m |
| C3 | 1.92 × 10−7 | m/N | |
| TF2 | 48.52 × 10−3 | m/rad | |
| Input of reducer | I6 | 4.25 × 10−3 | kg·m2 |
| R7 | 7.6 × 10−4 | N·m·s | |
| Reducer | TF3 | 40 | -- |
| Ball screw | C10 | 7.8 × 10−6 | rad/(N·m) |
| I12 | 22.95 × 10−3 | kg·m2 | |
| R13 | 7.3 × 10−4 | N·m·s | |
| TF4 | 628.93 | Rad/m | |
| Movable pulley | I18 | 35.75 | kg |
| TF5 | 0.5 | ||
| C16 | 4.3 × 10−9 | m/N | |
| Pulley and chain | C21 | 1.49 × 10−9 | m/N |
| R24 | 7.6 × 10−2 | N·m·s | |
| TF6 | 56.25 × 10−3 | m/rad | |
| Load | R27 | 1 × 104 | N |
| I26 | 6.04 × 103 | kg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Zhang, Z.; Jia, T.; Wang, L.; Zhao, D. Energy Consumption Analysis of Helicopter Traction Device: A Modeling Method Considering Both Dynamic and Energy Consumption Characteristics of Mechanical Systems. Energies 2022, 15, 7772. https://doi.org/10.3390/en15207772
Liu Q, Zhang Z, Jia T, Wang L, Zhao D. Energy Consumption Analysis of Helicopter Traction Device: A Modeling Method Considering Both Dynamic and Energy Consumption Characteristics of Mechanical Systems. Energies. 2022; 15(20):7772. https://doi.org/10.3390/en15207772
Chicago/Turabian StyleLiu, Qian, Zhuxin Zhang, Tuo Jia, Lixin Wang, and Dingxuan Zhao. 2022. "Energy Consumption Analysis of Helicopter Traction Device: A Modeling Method Considering Both Dynamic and Energy Consumption Characteristics of Mechanical Systems" Energies 15, no. 20: 7772. https://doi.org/10.3390/en15207772
APA StyleLiu, Q., Zhang, Z., Jia, T., Wang, L., & Zhao, D. (2022). Energy Consumption Analysis of Helicopter Traction Device: A Modeling Method Considering Both Dynamic and Energy Consumption Characteristics of Mechanical Systems. Energies, 15(20), 7772. https://doi.org/10.3390/en15207772






