Impact of Temperature and Nanoparticle Concentration on Turbulent Forced Convective Heat Transfer of Nanofluids

Cieśliński, Janusz T.; Lubocki, Dawid; Smolen, Slawomir

doi:10.3390/en15207742

Open AccessArticle

Impact of Temperature and Nanoparticle Concentration on Turbulent Forced Convective Heat Transfer of Nanofluids

by

Janusz T. Cieśliński

^1,*

,

Dawid Lubocki

¹ and

Slawomir Smolen

²

¹

Faculty of Mechanical Engineering and Ship Technology, Institute of Energy, Gdańsk University of Technology, Narutowicza 11/12, 80233 Gdańsk, Poland

²

Faculty of Nature and Engineering, J.R. Mayer–Institute for Energy Engineering, City University of Applied Sciences Bremen, Neustadtswall 30, 28199 Bremen, Germany

^*

Author to whom correspondence should be addressed.

Energies 2022, 15(20), 7742; https://doi.org/10.3390/en15207742

Submission received: 19 September 2022 / Revised: 13 October 2022 / Accepted: 17 October 2022 / Published: 19 October 2022

(This article belongs to the Section D3: Nanoenergy)

Download

Browse Figures

Versions Notes

Abstract

:

Theoretical analysis of the influence of nanoparticles and temperature on the average Nusselt (Nu) number and the average heat transfer coefficient (HTC) during the turbulent flow of nanofluid in a horizontal, round tube was carried out. The Nu number is a function of the Reynolds (Re) number and the Prandtl (Pr) number, which in turn are functions of the thermophysical properties of the liquid and the flow conditions. On the other hand, the thermophysical properties of nanoliquids are primarily a function of nanoparticle concentration (NPC) and temperature. Hence, the correct determination of the value of the Nu number, and then the HTC, which is needed for engineering calculations, depends on the accuracy of determining the thermophysical properties of nanofluids. In most cases, the thermophysical properties of the nanofluids are calculated as functions of the corresponding thermophysical properties of the base liquid. Therefore, the accuracy of the calculations of the thermophysical properties of nanofluids is equally determined by the reliable correlations for the base liquids. Therefore, new correlations for the calculation of the thermophysical properties of water have been developed. The results of calculations of the thermophysical properties of the base liquid (water) and the water-Al₂O₃ nanofluids by use of carefully selected correlations is presented. It was established that even for small concentrations of nanoparticles, a significant intensification of heat transfer using nanofluids as compared to the base liquid is obtained for the tested temperature range.

Keywords:

nanofluids; thermophysical properties; forced convective heat transfer; horizontal tube

1. Introduction

Constant technological progress means that the heat fluxes that occur in devices are increasing. This presents a real challenge for heat transfer engineers and researchers. Two directions of intensification of heat transfer are being developed. The first is related to the modification of the heat exchange surface, e.g., [1,2,3]. The second is related to the search for new thermal fluids that are characterized by better thermophysical properties, such as thermal conductivity or contact angle. Among the new thermal fluids, the greatest hope is raised by a mixture of a base liquid and nanoparticles with a size below 100 nm, referred to as a nanofluid [4]. The use of nanofluids in a great number of areas is considered, such as single-phase systems, e.g., [5,6], two-phase systems, e.g., [7,8], magnetic nanofluids, e.g., [9,10], non-Newtonian nanofluids, e.g., [11,12], viscoelastic nanofluids, e.g., [13,14], chemical reaction systems, e.g., [15,16], bio-nanofluids, e.g., [17,18], nanofuels, e.g., [19,20], and others [21].

The single-phase convective heat transfer of nanofluids is of particular interest due to potential applications in many cooling/heating systems, e.g., heat exchangers, electronics, nuclear reactors, car radiators, solar devices, e.g., [22,23,24,25], medical applications, e.g., [26,27], thermal energy storage, e.g., [28,29], or even rocketry applications [30]. Although different aspects, e.g., flow regimes—laminar or turbulent, boundary conditions, nanoparticle type and concentration, of single-phase forced convection of nanofluids in tubes were studied both experimentally [31,32,33,34] and numerically [35,36,37,38,39,40,41,42] there is still controversy about the influence of nanoparticles on heat transfer efficiency and flow resistance. Experimental works show that the addition of nanoparticles can both intensify and deteriorate heat transfer. In turn, numerical works most often show the intensification of heat transfer as a result of adding nanoparticles. A similar controversy concerns flow resistance. Intensive work is still underway to determine the thermophysical properties of nanofluids and their stability [43,44].

The nanofluid, which is inherently a two-phase mixture of liquid and solid particles, can be modeled as a single-phase continuum (single phase fluid) with the thermophysical properties which take into account the effect of the presence of nanoparticles. The results of numerical simulations obtained with the single-phase approach and the two-phase model [45,46], did not differ significantly. The condition for the accuracy of the single-phase approach is the correct selection of the correlation on the thermophysical properties of nanofluids.

In the present study, a theoretical analysis of the influence of temperature and NPC during forced convection of nanofluids inside a horizontal circular tube is presented. It was assumed that the analyzed nanofluid can be treated as a homogeneous, single-phase liquid. The Nu number and average HTC were parameters of the intensity of the convective heat transfer. For forced convection, the Nu number is a function of the Re number and Pr number. The Re number and Pr number are functions of the thermophysical properties of nanofluids. The thermophysical properties of nanofluids varied first of all with temperature and NPC. Therefore, an analysis was conducted to evaluate the effects on the performance of nanofluids due to variations of thermal conductivity, viscosity, density, and specific heat, which are functions of NPC and temperature. Water-based nanofluids with dispersed alumina (Al₂O₃) nanoparticles at mass concentrations of 0.1%, 1%, and 5% within the temperature range 20–70 °C are considered. Water-Al₂O₃ nanofluids were selected because frequent application in both numerical and experimental studies. Moreover, thermophysical properties of water-Al₂O₃ nanofluids are comprehensively and thoroughly investigated [47].

2. Materials and Methods

2.1. Tested Nanofluids

In this study alumina (Al₂O₃) nanoparticles were selected while distilled, deionized water was tested as base fluid. Alumina nanoparticles were tested at the concentration of 0.1%, 1%, and 5% by weight. It was assumed that nanoparticles have a spherical form with mean diameter of d_p = 47 nm.

The properties of alumina (Al₂O₃) nanoparticles are shown in Table 1.

2.2. Correlations for Forced Convection Heat Transfer inside Horizontal Tubes

Recognized correlation equations used for the determination of an average Nu number for forced convection inside horizontal cylinders in base fluids are collected in Table 2. The Nu number for water is a benchmark to the values calculated for the analyzed nanofluids. Hence, the selection of the correct correlation is important when comparing the results for the base fluid and nanofluids.

Figure 1 shows the dependence of the Nu number on the Re number on the basis of the correlations shown in Table 1. The calculations were performed for the Pr = 5. The values of the correction coefficients were assumed to be equal to one. Noteworthy is the fact that the values of the Nu number are significantly higher from the Notter and Sleicher correlation [55] compared to the other correlations. Note, however, that the Notter and Sleicher correlations (Equations (6) and (7)) are suitable for fluids with a very low Pr number. Figure 1 shows that the correlations proposed by Dittus and Boelter, Kraußold, Sieder and Tate, Mikhejew, Hausen, and Gnieliński give similar values of the Nu number, although the difference between the Kraußold correlation and Hausen correlation for Re = 10⁵ is as much as 45%.

In Table 3 are collected experimental and numerical correlation equations used for determination of an average Nu number for forced convection inside horizontal cylinders in nanofluids.

Figure 2 shows the dependence of the Nu number on the Re number for nanofluids and correlations shown in Table 3. The calculations were performed for the Pr = 5, w = 1 m/s, φ_v = 1% and d_p = 40 nm.

As seen in Figure 2, except Equation (17), the correlations show pretty good consistency. The numerically developed correlation equation proposed by Saha and Paul, Equation (18), was selected for the analysis, as it fits the experimental data for water-Al₂O₃ nanofluids very well and contains parameters that characterize both nanoparticles and molecules of the base fluid.

2.3. Correlations for Thermophysical Properties of Nanofluids

A large number of correlations devoted to calculate viscosity of nanofluids are published in the literature, e.g., [67,68]. In Table 4 are shown correlations proposed for water-Al₂O₃ nanofluids.

The correlation proposed by Corcione, Equation (26), was selected for the analysis, as it fits the experimental data of the viscosity of water-Al₂O₃ nanofluids very well.

Equally important as reliable correlations for nanofluids are the formulas for calculating the properties of base liquids. Tested correlations for calculation viscosity of water are shown in Table 5.

Figure 3 shows the viscosity of water against temperature calculated from correlations presented in Table 5. As seen in Figure 3, predictions realized with Equation (27) deviate by about 20% for minimum temperature 20 °C. Higher temperature difference between predictions is negligible.

Figure 4 shows influence of NPC on the viscosity of the tested nanofluids against temperature, calculated by the use of Equation (26) in combination with Equation (31).

As seen in Figure 4, viscosity of the tested nanofluids decreases sharply with a temperature increase and slightly increases with NPC increase. The slight influence of nanoparticles on the viscosity of the tested nanofluids is due to the very small used NPC.

Similarly to viscosity several correlations devoted to thermal conductivity of nanofluids are published in literature, e.g., [79,80]. In Table 6 are collected correlations proposed for water-Al₂O₃ nanofluids.

The correlation proposed by Corcione, Equation (33), was selected for the analysis, as it fits the experimental data of the thermal conductivity of water-Al₂O₃ nanofluids very well, as it takes into account the influence of Brownian motion on the thermal conductivity of nanofluids.

Correlations for calculation thermal conductivity of water are shown in Table 7.

Figure 5 shows thermal conductivity of water against temperature calculated from correlations presented in Table 7.

Figure 6 shows influence of NPC on the thermal conductivity of the tested nanofluids against temperature calculated by use of Equation (33) in combination with Equation (41).

As seen in Figure 6 thermal conductivity of the tested nanofluids increases moderately with temperature increase and for given temperature increases with NPC increase.

The density of nanofluids is generally calculated by the use of the mixture model (Table 8).

The correlation proposed by Pak and Cho, Equation (43), was selected for the analysis, as it fits the experimental data of the density of water-Al₂O₃ nanofluids very well and is based on the general mixture theory.

Density of pure water can be estimated by use of correlations given in Table 9.

Figure 7 shows the density of water against temperature calculated from correlations presented in Table 9. The maximum difference between the predictions is equal to 0.4%.

Figure 8 illustrates influence of the NPC on density of the tested nanofluids as a function of temperature by use of Equations (43) and (49).

As seen in Figure 8, the density of the analysed nanofluids decreases with temperature increase and increases with NPC increase because the density of the nanoparticle material (Table 1) is higher than density of water.

Several investigators have been involved in the physics of the specific heat of nanofluids [87,88,89]. In Table 10 are collected correlations proposed for water-Al₂O₃ nanofluids.

The correlation proposed by Williams et al. [90] was selected for the analysis. As shown in [49] Equation (52) much better fits the experimental data of the specific heat of water-Al₂O₃ nanofluids than Equation (51) based on the mixture theory. The better accuracy of Equation (52) results from the assumption of thermal equilibrium between the particles and the liquid, which does not have to be present due to the Brownian motion of nanoparticles and different thermophysical properties of the nanoparticle material and the base liquid.

The specific heat of water can be estimated by use of correlations given in Table 11.

Figure 9 shows the specific heat of water against temperature calculated from correlations presented in Table 11. The difference between the individual correlations seems large, but for 70 °C it does not exceed 3.4%.

Figure 10 illustrates influence of NPC on the specific heat of the tested nanofluids as a function of temperature calculated by the use of Equation (52) in combination with Equation (60).

As seen in Figure 10, the specific heat of water-Al₂O₃ nanofluids decreases with temperature increases, and for the given temperature decreases with NPC increases because the specific heat of the nanoparticle material (Table 1) is lower than the specific heat of water. It is worthy to note the non-monotonic course of specific heat for water-based nanofluids against the temperature that results from the data for water (Figure 9).

Figure 11 illustrates the influence of NPC on thermal diffusivity of the tested nanofluids as a function of temperature. The thermal diffusivity of water was calculated by the use of present correlations, i.e., Equations (41), (49) and (60), while thermal diffusivity of nanofluids was determined by use of Equations (33), (43) and (52). As seen in Figure 11, the thermal diffusivity of water and nanofluids increases with temperature increase, however the growth rate is higher for nanofluids. Moreover, thermal diffusivity increases with NPC increase.

As seen in Figure 12, the thermal diffusivity of the tested nanofluids increases slightly with NPC, although the rate of growth increases with temperature increase.

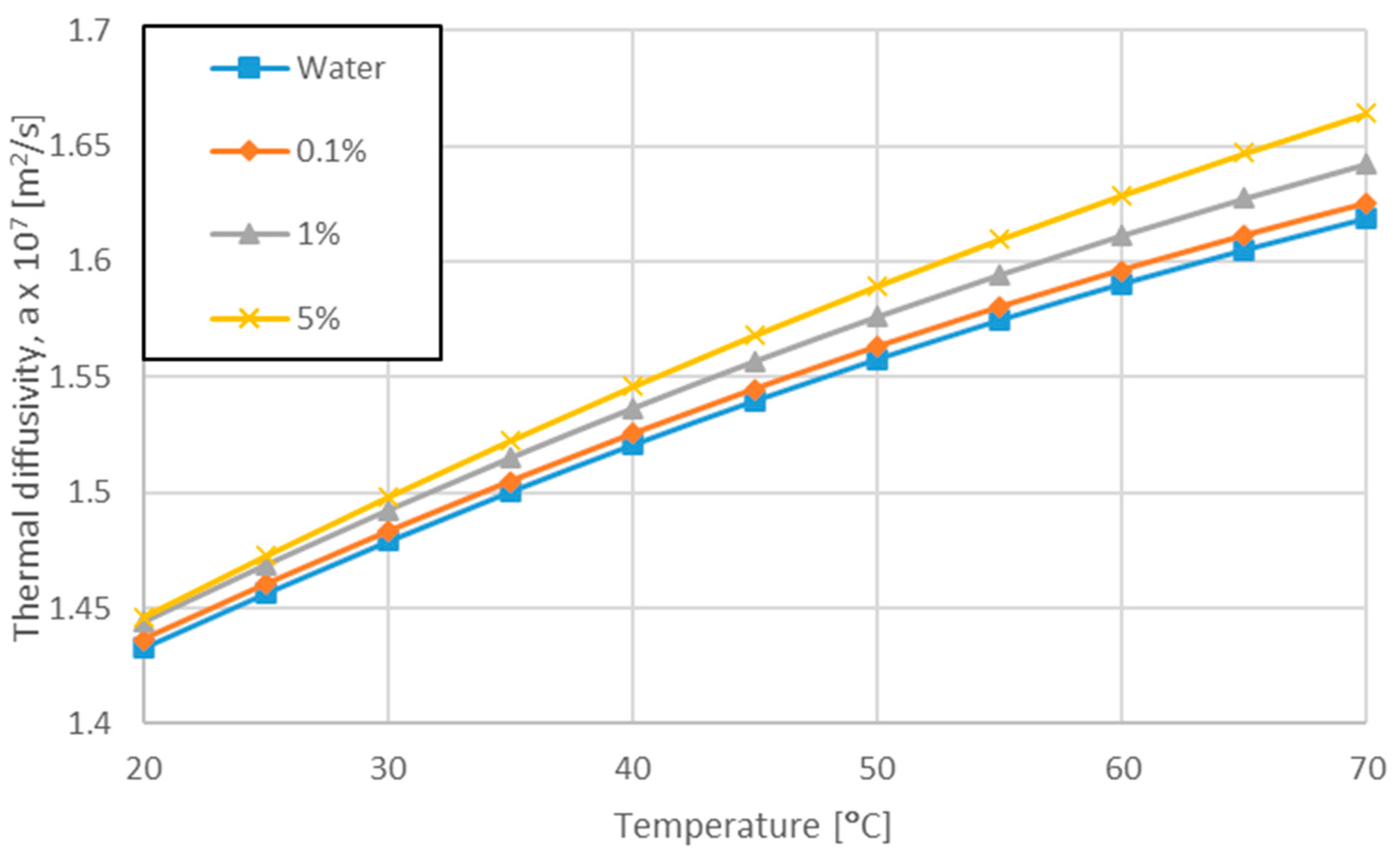
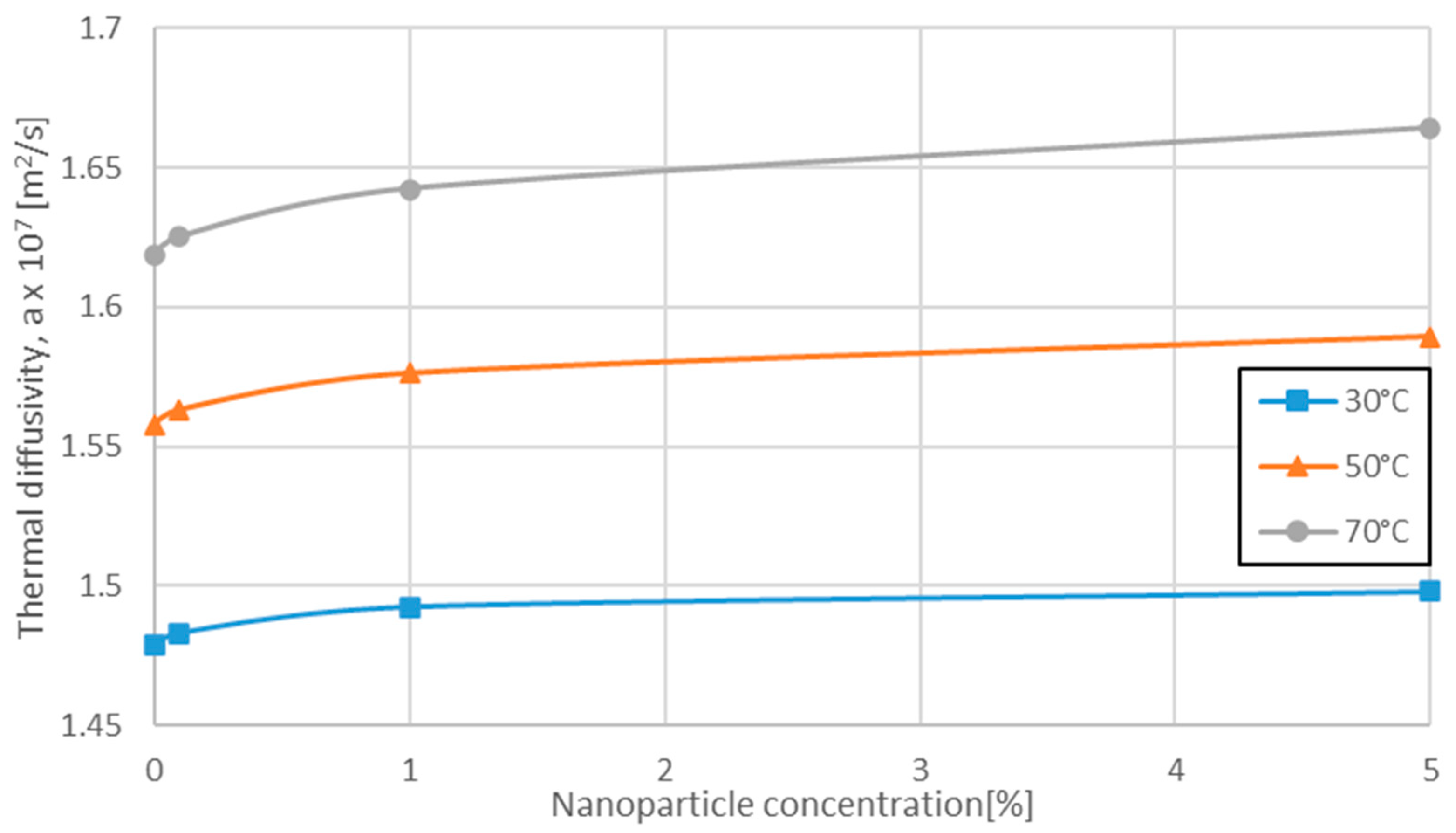
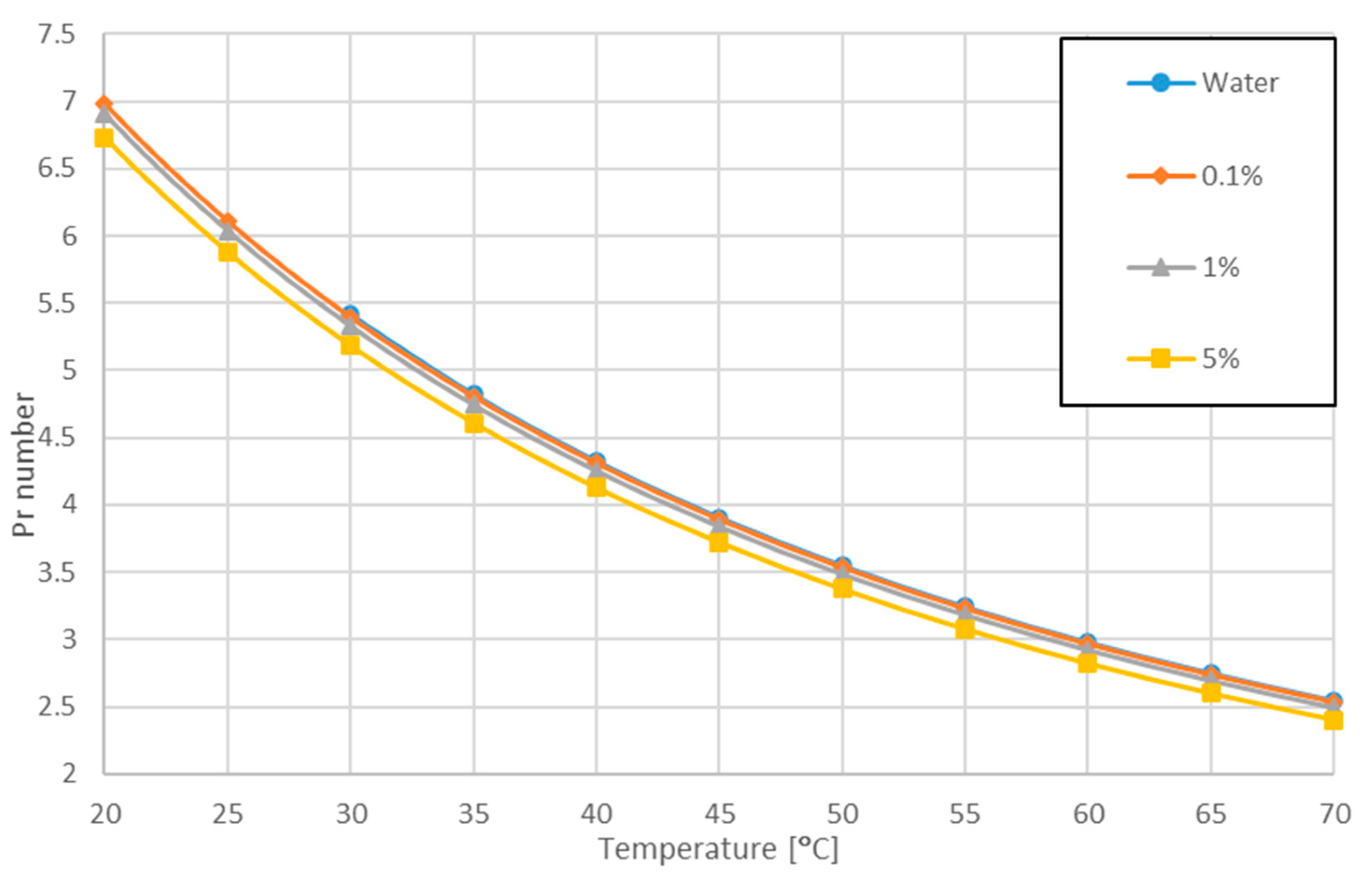
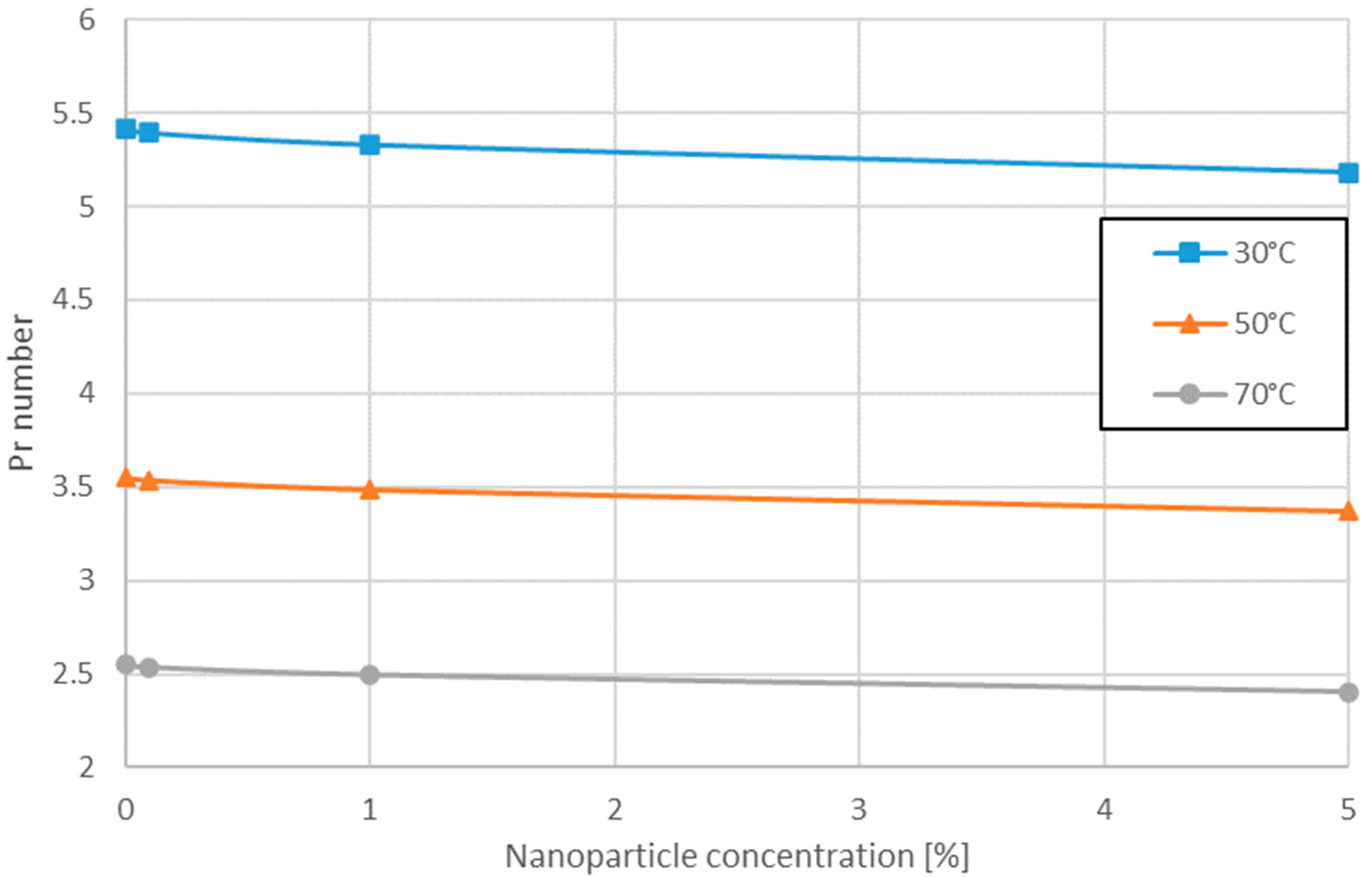
3. Results and Discussion

3.1. Variation of Pr Number

Figure 13 shows a comparison of Pr numbers of the water-Al₂O₃ nanofluids as a function of temperature. The Pr number for water was calculated by use of present correlations, i.e., Equations (31), (41), (49) and (60), while the Pr number of nanofluids was determined by use of Equations (26), (33), (43) and (52). For the tested nanofluids, the Pr number decreases with an increase in temperature, predominantly due to the decrease in viscosity (Figure 4).

Figure 14 illustrates the influence of NPC on Pr number of the tested nanofluids at three temperatures, namely 30 °C, 50 °C, and 70 °C. As seen in Figure 12, the Pr number for water-Al₂O₃ decreases slightly with the NPC increase. Regardless of the temperature, the decrease in Pr number with the increase in NPC does not exceed 3%.

As shown in Figure 13 and Figure 14, the Pr number decreases with both temperature increase and NPC increase. However, the decrease due to the increase in NPC for a given temperature is small, and the decrease due to the increase in temperature is very large for a given NPC. The Pr number of the nanofluid for the tested range of temperature and NPC is determined by the temperature, not by the NPC. As it results from the correlations presented in Table 2, the Nu number is a function of

P r^{m}

, hence the higher the value of the Pr number, the higher the value of the Nu number.

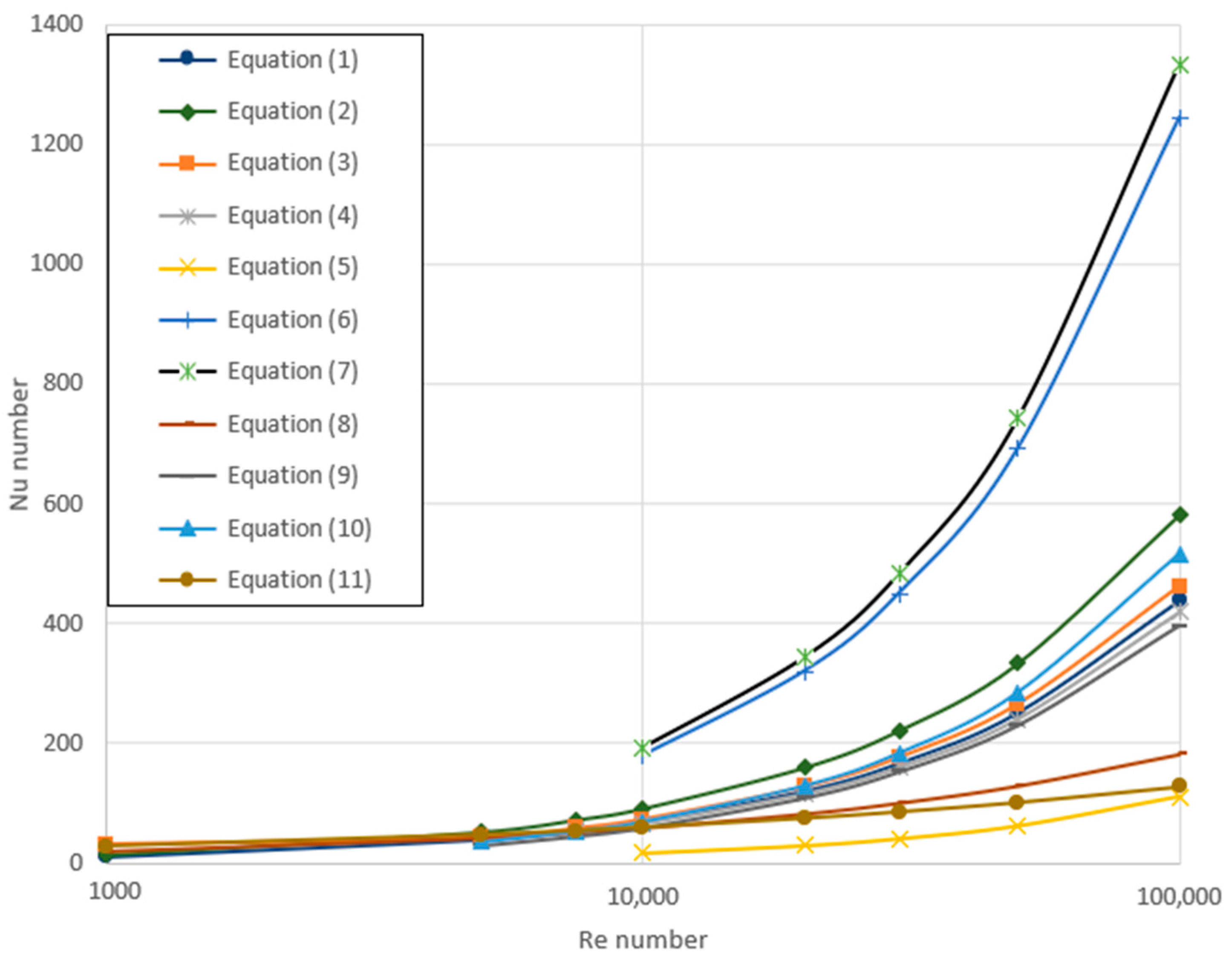
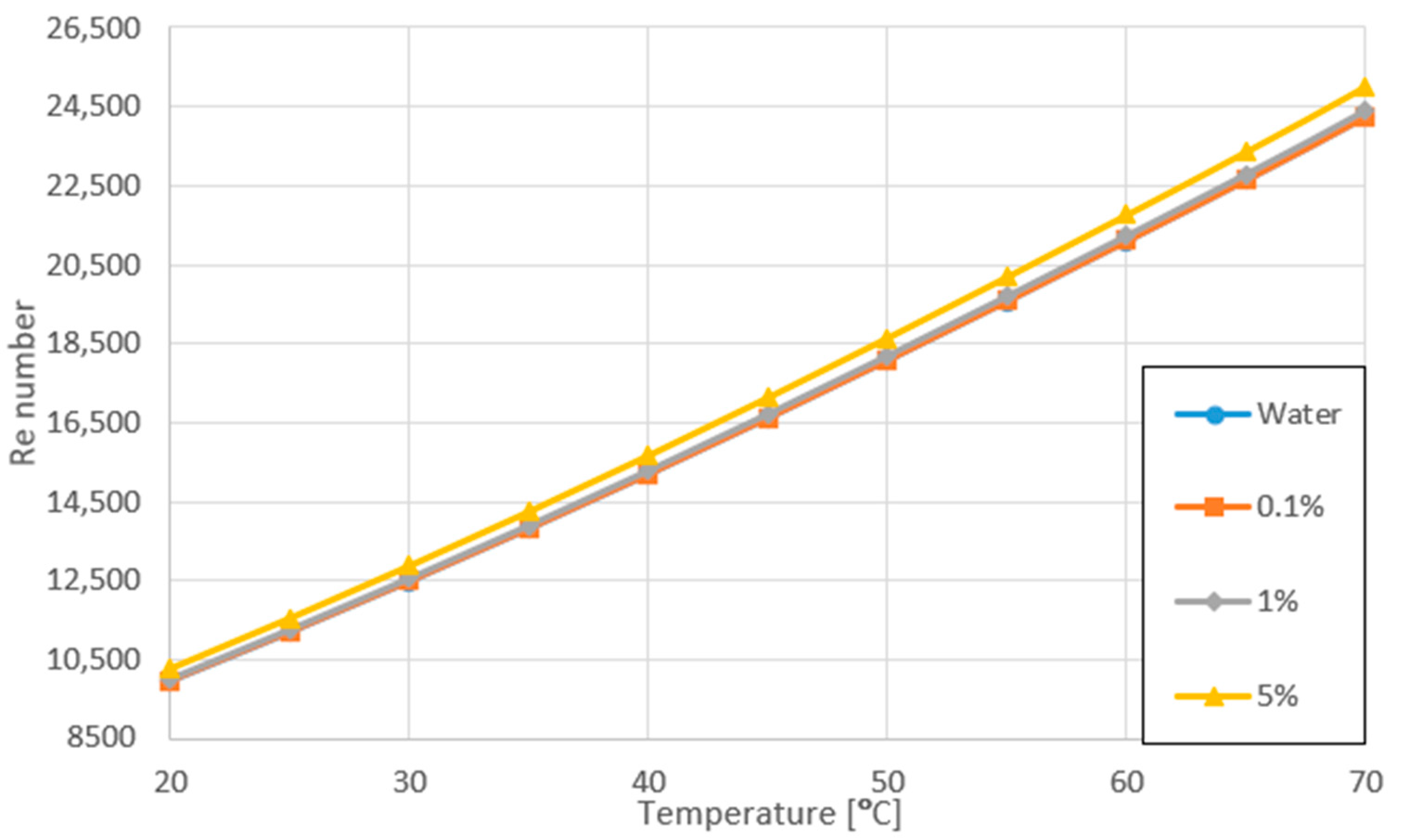
3.2. Variation of Re Number

Figure 15 illustrates the change of Re number versus temperature for the tested nanofluids. In this case the average velocity and the diameter of the horizontal tube are held constant at the values taken from the experiment presented in [93], i.e., w = 1 m/s, D = 10 mm. The Re number for water was calculated by use of present correlations, i.e., Equations (31) and (49), while the Re number of nanofluids was determined by use of Equations (26) and (43).

As seen in Figure 15 Re number definitively increases with temperature increase, which also results in increase of the Nu number.

Figure 16 shows the change of Re number against NPC for selected temperatures. It is observed that an increase in NPC results in a gradual increase of Re number for all tested temperatures.

As shown in Figure 15 and Figure 16, Re number increases with both temperature increase and NPC increase. However, the increase due to the increase in NPC for a given temperature is small, and the increase due to the increase in temperature is substantial. It follows that the value of the Re number in the studied temperature and NPC range is primarily determined by temperature, and the influence of NPC is modest.

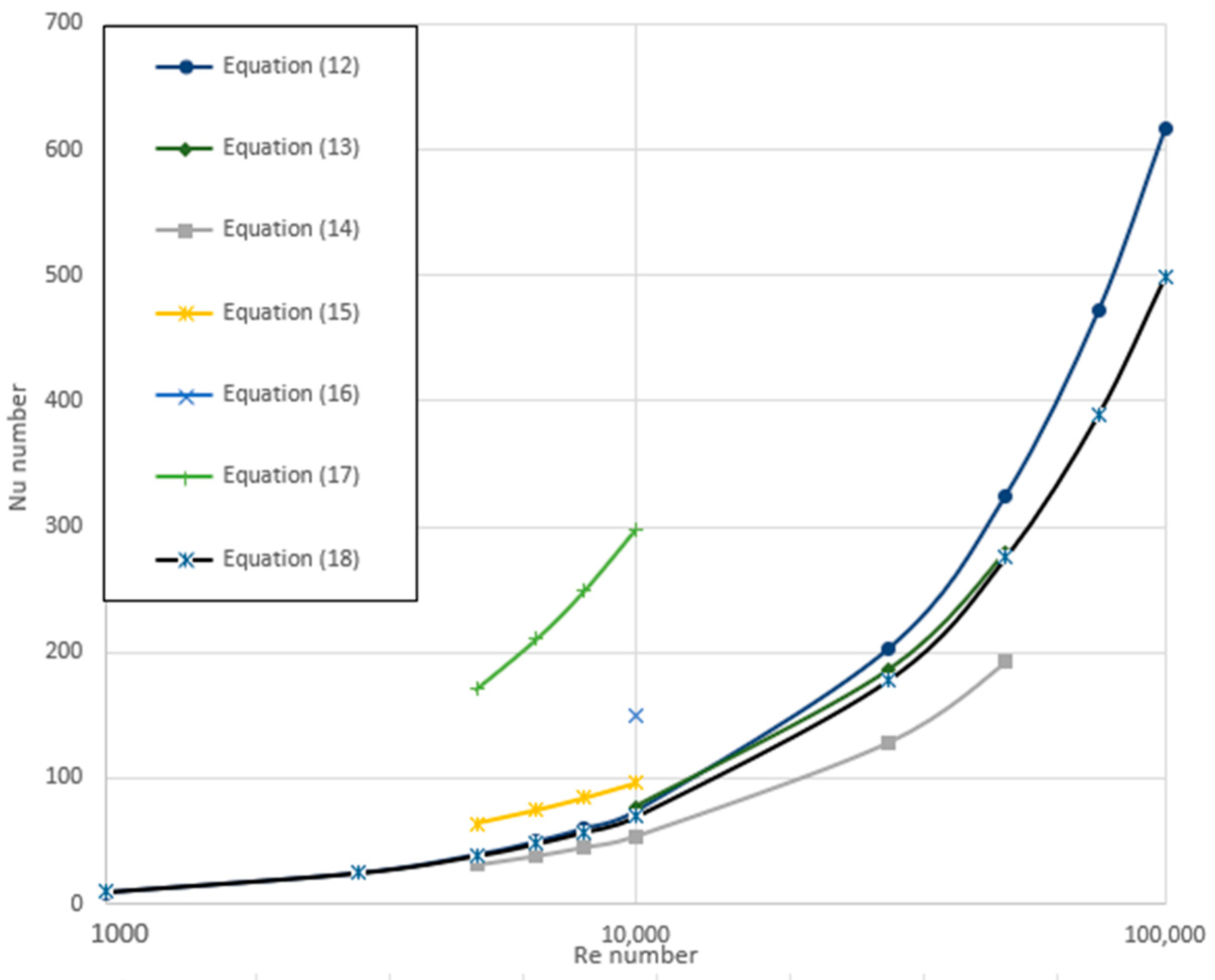
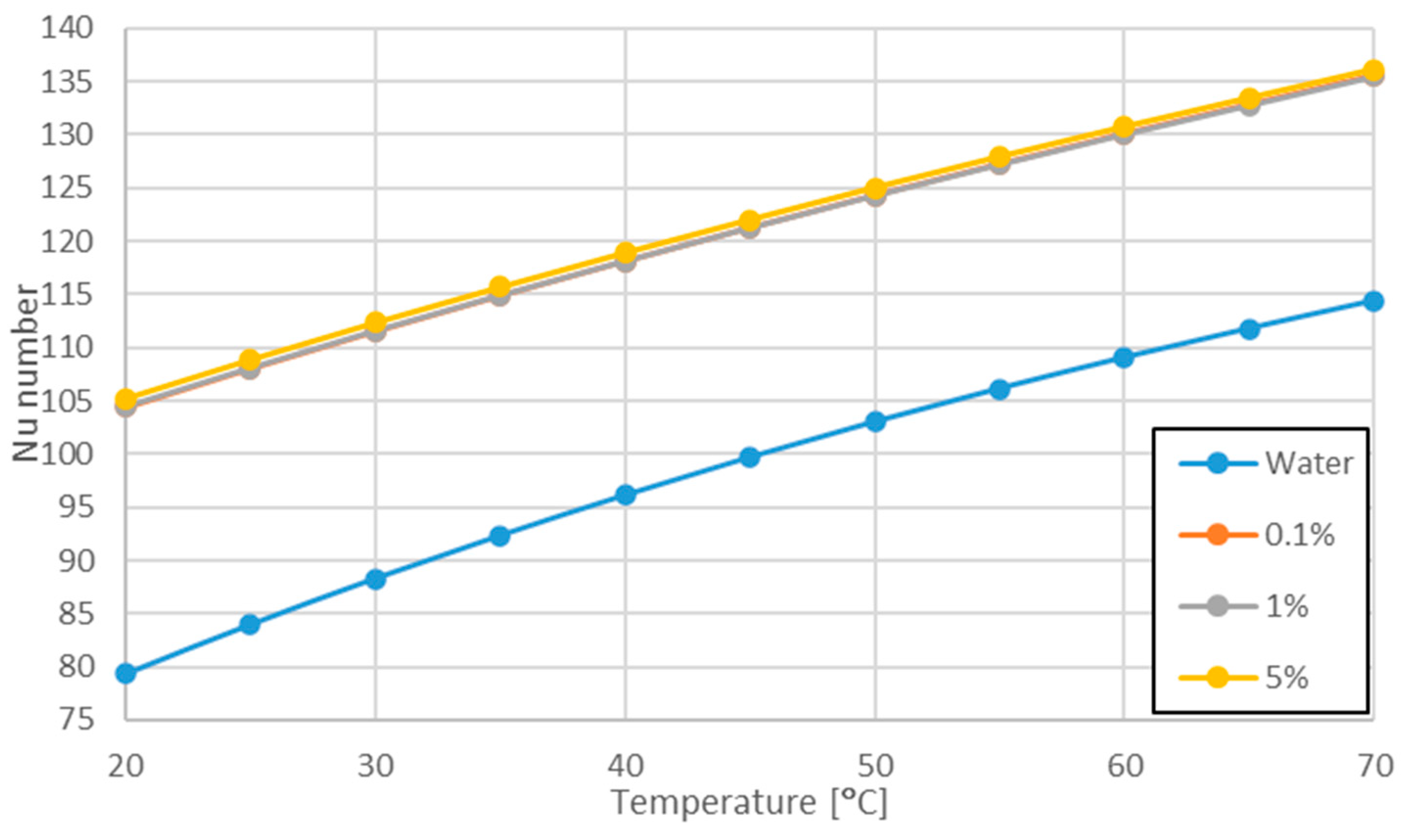
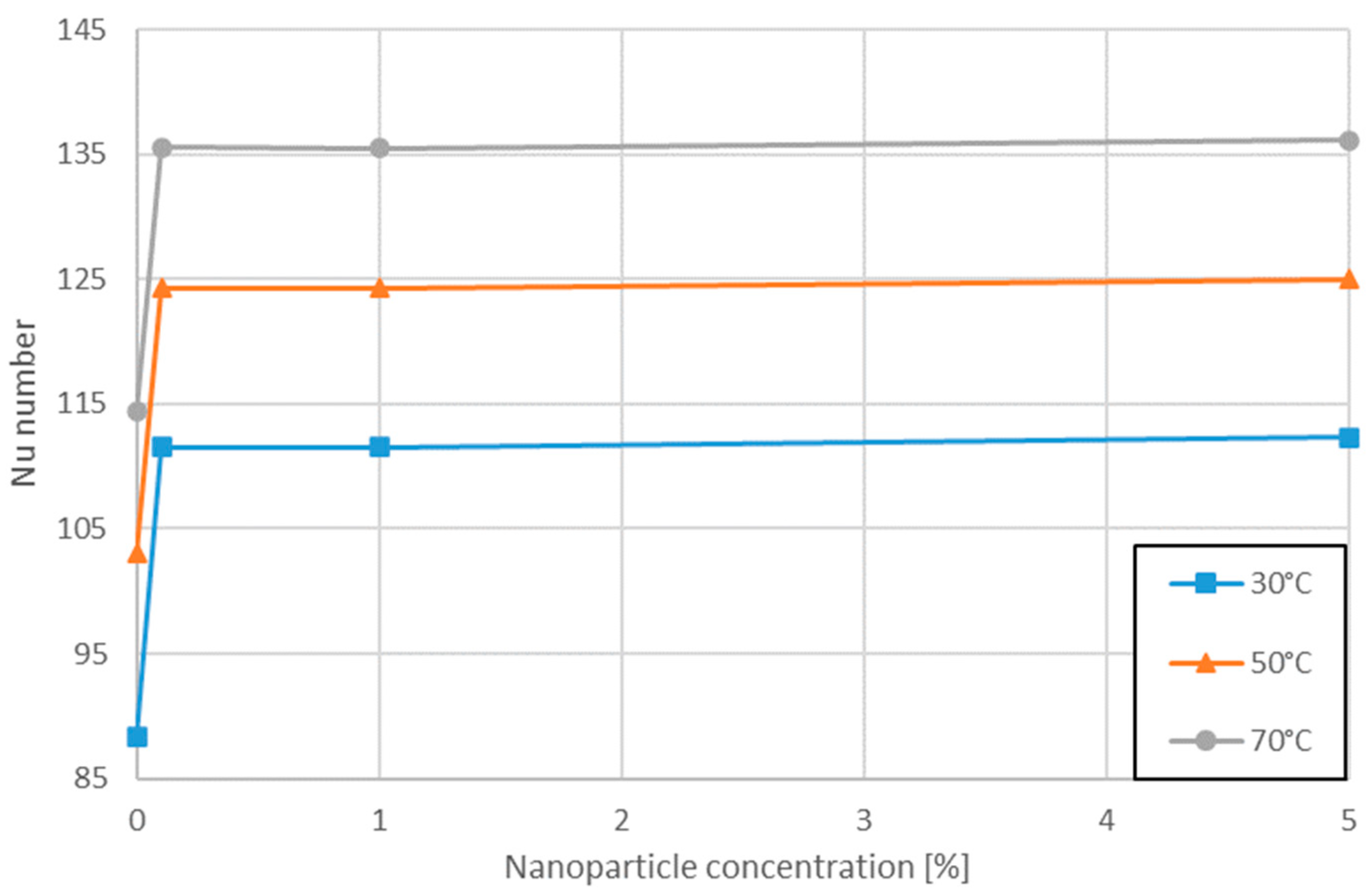
3.3. Variation of Nu Number

Figure 17 shows the variation of Nu number against temperature for water-Al₂O₃ nanofluids predicted from the Saha and Paul correlation, Equation (18). Results are compared to the predictions for water from the commonly accepted Gnieliński correlation, Equation (10). Calculations for water were conducted by the use of present correlations for thermophysical properties of water. As seen in Figure 17, Nu number increases with temperature increase. For the tested NPC range 0.1% ≤ φ_m ≤ 5% Nu number for nanofluids is higher than for pure water. It means that the addition of Al₂O₃ nanoparticles to water results in substantial heat transfer improvement.

The influence of nanoparticles on the Nu number is clearer in Figure 18. Figure 18 shows the variation of the Nu number against NPC for water-Al₂O₃ nanofluids and three selected temperatures, namely 30 °C, 50 °C, and 70 °C. As seen in Figure 18, the addition of even the smallest amount of nanoparticles (

φ_{m} = 0.001

) causes a sharp increase in the Nu number. However, the Nu number increase for

φ_{m} > 0.001

is negligible, and the increase in the Nu number is practically due to the increase in temperature.

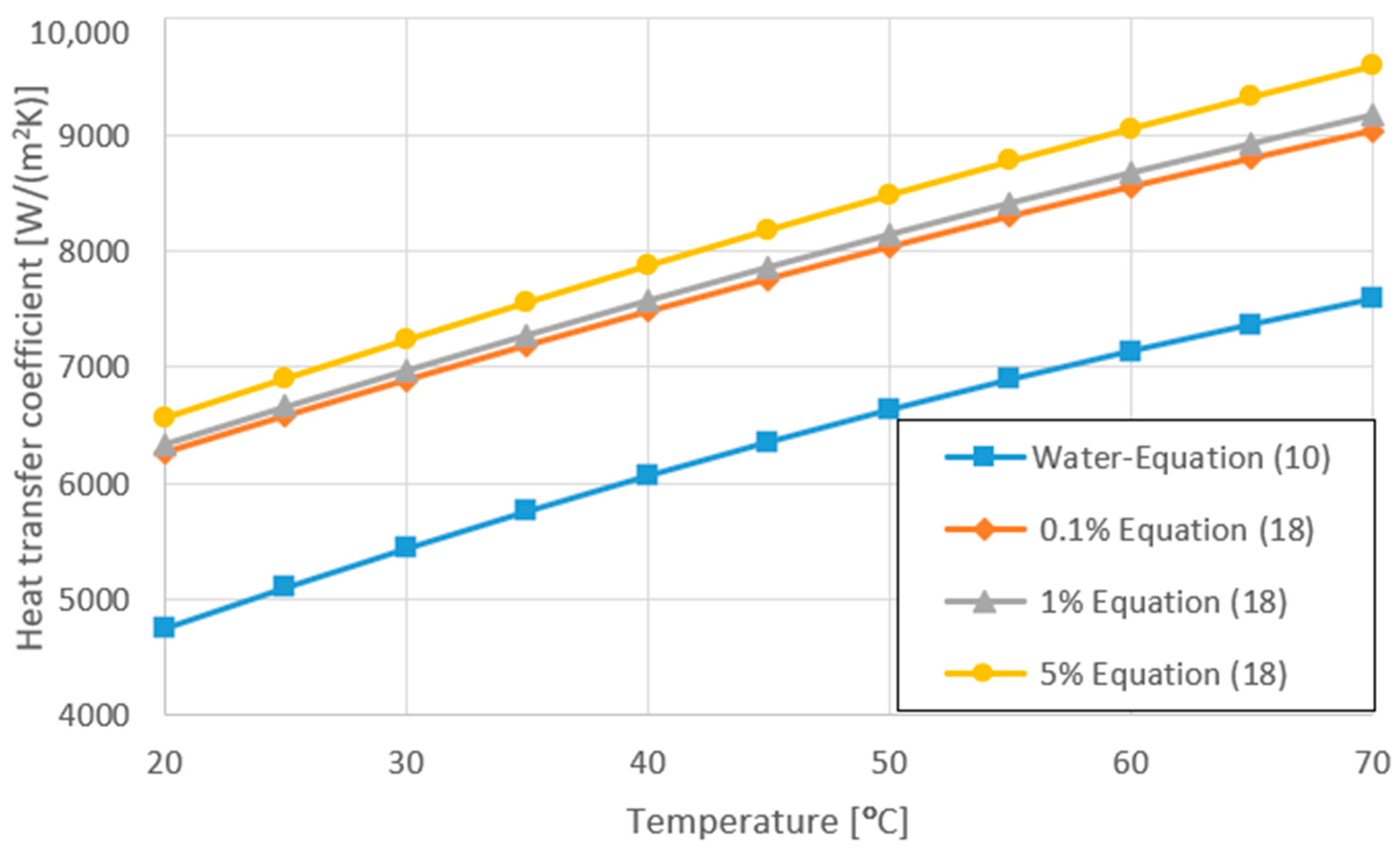
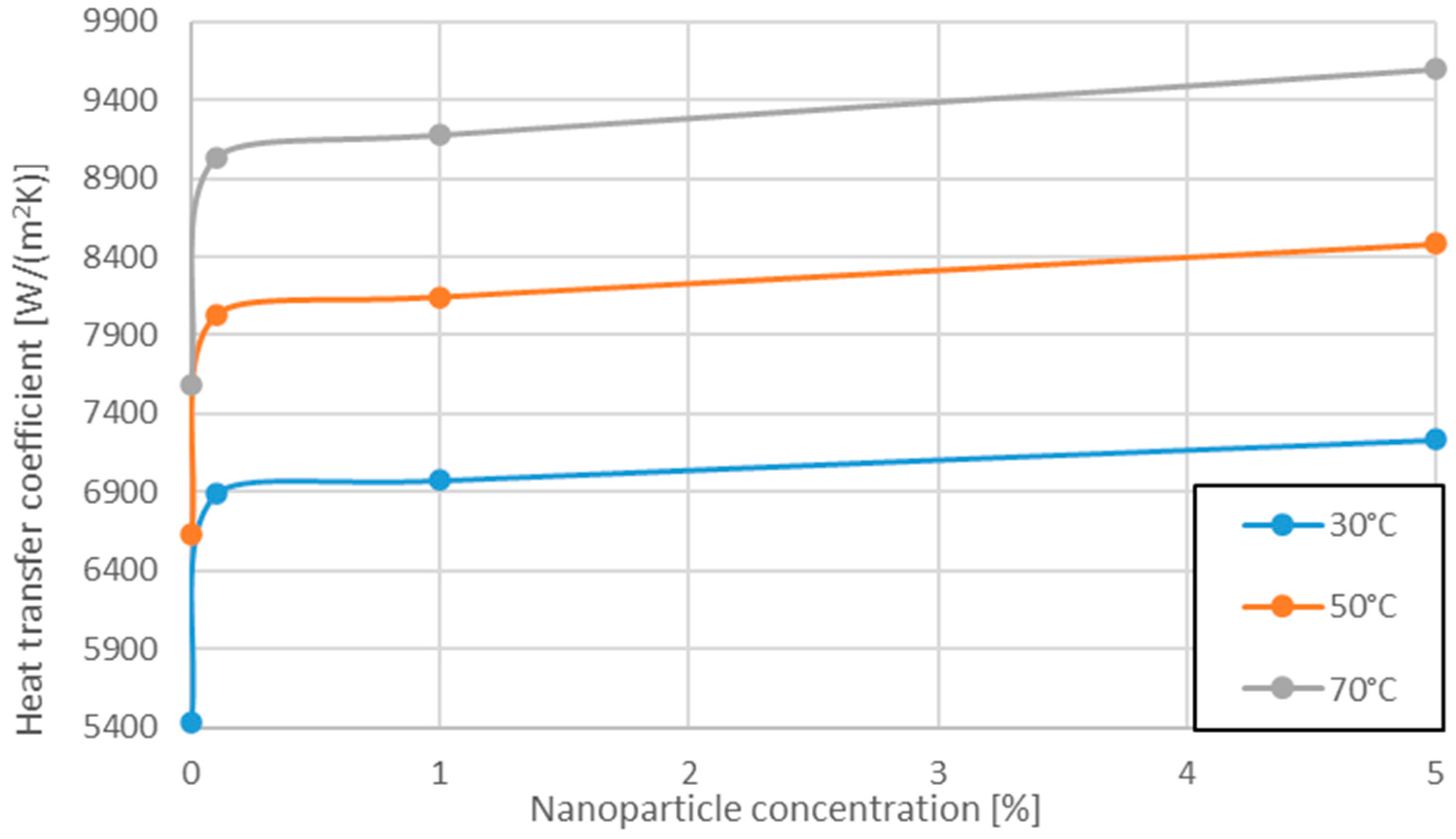
3.4. Variation of Heat Transfer Coefficient

Figure 19 shows the variation of heat transfer coefficient against temperature for water-Al₂O₃ nanofluids predicted from the Saha and Paul correlation (Equation (18)). The results are compared to the predictions from the Gnieliński correlation (Equation (10)) for water. As seen in Figure 19, heat transfer coefficient increases with temperature. For the tested mass concentration range 0.1% ≤ φ_m ≤ 5% heat transfer coefficient for nanofluids is higher than for water. It means that addition of Al₂O₃ nanoparticles to water results in substantial heat transfer improvement. In the literature, several mechanisms of heat transfer improvement in nanofluids have been discussed, e.g., [44,94]. According to Buongiorno [95], two mechanisms are responsible for heat transfer improvement in nanofluids, namely Brownian motion and thermophoresis.

Figure 20 shows variation of heat transfer coefficient against NPC for water-Al₂O₃ nanofluids and three selected temperatures, namely 30 °C, 50 °C and 70 °C. As seen in Figure 20, the influence of NPC on HTC for the tested mass concentration range 0.1%

< φ_{m} \leq 5 %

is negligible for the given temperature.

As shown in Figure 19 and Figure 20, HTC increases with both temperature increase and NPC increase. However, the increase due to the increase in NPC for a given temperature is small, and the increase due to the increase in temperature is significant. It is worth noting that maximum HTC increase is higher than Nu number increase and equals 38%, while for the Nu number it is 31%.

4. Conclusions

The analysis showed that the addition of Al₂O₃ nanoparticles with a mass concentration of 0.1% ≤ φ_m ≤ 5% within the temperature range of 20–70 °C to water as a base liquid causes the intensification of heat transfer under conditions of turbulent forced convection in round tubes.

The slight influence of the studied concentration of nanoparticles on the thermophysical properties of nanofluids indicates that the intensification of heat transfer results from the transport mechanisms, and not from the improvement of the thermophysical properties of nanofluids.

Author Contributions

Conceptualization, J.T.C.; methodology, J.T.C. and S.S.; software, D.L.; validation, J.T.C.; formal analysis J.T.C. and S.S.; investigation, D.L.; data curation, D.L.; writing—original draft preparation, J.T.C.; writing—review and editing, J.T.C. and S.S.; funding acquisition, S.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors thank Paweł Dąbrowski (Gdańsk University of Technology) for developing present correlations for thermal properties of water.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

a	Thermal diffusivity	(m²/s)
c_p	Specific heat	(J/(kgK))
$d_{f}$	Base fluid molecule diameter	(m)
$d_{p}$	Particle diameter	(m)
D	Inside diameter of tube	(m)
f	Friction factor	(-)
h	Local heat transfer coefficient	(W/(m² K))
$\bar{h}$	Average heat transfer coefficient	(W/(m² K))
k	Thermal conductivity	(W/(m K))
L	Length	(m)
$N u = \frac{h D}{k}$	Local Nusselt number	(-)
$\bar{N u} = \frac{\bar{h} D}{k}$	Average Nusselt number	(-)
$P e = R e P r$	Peclet number	(-)
$P e_{p} = \frac{w d_{p}}{a_{n f}}$	Peclet number related to d_p	(-)
$P r = \frac{ν}{a}$	Prandtl number	(-)
$q$	Heat flux	(W/m²)
$R e = \frac{w D}{ν}$	Reynolds number	(-)
$t$	Temperature	[°C]
$T$	Temperature	[K]
w	Velocity	(m/s)
x	Axial coordinate	(m)
Greek symbols
µ	Dynamic viscosity	(Pas)
$ν$	Kinematic viscosity	(m²/s)
ρ	Density	(kg/m³)
$φ$	Nanoparticle concentration	(-)
Subscripts
bf	Base fluid
f	Fluid
m	Mass
nf	Nanofluid
nl	Nanolayer
p	Particle
v	Volume
w	Wall
Abbreviations
HTC	Heat transfer coefficient
NPC	Nanoparticle concentration

References

Webb, R.L. Principles of Enhanced Heat Transfer; John Wiley & Sons, Inc.: New York, NY, USA, 1994. [Google Scholar]
Xie, S.; Beni, M.S.; Cai, J.; Zhao, J. Review of critical-heat-flux enhancement methods. Int. J. Heat Mass Transf. 2018, 122, 275–289. [Google Scholar] [CrossRef]
Mousa, M.H.; Miljkovic, N.; Nawaz, K. Review of heat transfer enhancement techniques for single phase flows. Renew. Sustain. Energy Rev. 2021, 137, 110566. [Google Scholar] [CrossRef]
Choi, S. Enhancing thermal conductivity of fluids with nanoparticles. In Developments and Applications of Non-Newtonian Flows; ASME: New York, NY, USA, 1995; Volume 231/MD, pp. 99–105. [Google Scholar]
Liang, G.; Mudawar, I. Review of single-phase and two-phase nanofluid heat transfer in macro-channels and micro-channels. Int. J. Heat Mass Transf. 2019, 136, 324–354. [Google Scholar] [CrossRef]
Lodhi, M.S.; Sheorey, T.; Dutta, G. Single-phase fluid flow and heat transfer characteristics of nanofluid in a circular microchannel: Development of flow and heat transfer correlations. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2020, 234, 3689–3708. [Google Scholar] [CrossRef]
Cheng, L.; Filho, E.P.B.; Thome, J.R. Nanofluid Two-Phase Flow and Thermal Physics: A New Research Frontier of Nanotechnology and Its Challenges. J. Nanosci. Nanotechnol. 2008, 8, 3315–3332. [Google Scholar] [CrossRef] [PubMed]
Dey, D.; Sahu, D.S. Nanofluid in the multiphase flow field and heat transfer: A review. Heat Transf. 2021, 50, 3722–3775. [Google Scholar] [CrossRef]
Nkurikiyimfura, I.; Wang, Y.; Pan, Z. Heat transfer enhancement by magnetic nanofluids—A review. Renew. Sustain. Energy Rev. 2013, 21, 548–561. [Google Scholar] [CrossRef]
Shaw, S.; Mabood, F.; Muhammad, T.; Nayak, M.K.; Alghamdi, M. Numerical simulation for entropy optimized nonlinear radiative flow of GO-Al₂O₃ magneto nanomaterials with auto catalysis chemical reaction. Numer. Methods Partial Differ. Equ. 2022, 38, 329–358. [Google Scholar]
Sivaraj, R.; Banerjee, S. Transport properties of non-Newtonian nanofluids and applications. Eur. Phys. J. Special Top. 2021, 230, 1167–1171. [Google Scholar] [CrossRef]
Shamshuddin, M.D.; Ghaffari, A.; Usman. Radiative heat energy exploration on Casson-type nanoliquid induced by a convectively heated porous plate in conjunction with thermophoresis and Brownian movements. Int. J. Ambient Energy 2022. [Google Scholar] [CrossRef]
Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. Model and Comparative Study for Flow of Viscoelastic Nanofluids with Cattaneo-Christov Double Diffusion. PLoS ONE 2017, 12, e0168824. [Google Scholar] [CrossRef] [PubMed]
Li, Y.M.; Al-Khaled, K.; Gouadria, S.; El-Zahar, E.R.; Usman; Khan, S.U.; Khan, M.I.; Malik, M.Y. Numerical simulations for three-dimensional rotating porous disk flow of viscoelastic nanomaterial with activation energy, heat generation and Nield boundary conditions. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
Mahato, R.; Das, M.; Sen, S.S.S.; Shaw, S. Entropy generation on unsteady stagnation-point Casson nanofluid flow past a stretching sheet in a porous medium under the influence of an inclined magnetic field with homogeneous and heterogeneous reactions. Heat Transf. 2022, 51, 5723–5747. [Google Scholar] [CrossRef]
Khan, S.U.; Usman; Al-Khaled, K.; Hussain, S.M.; Ghaffari, A.; Khan, M.I.; Ahmed, M.W. Implication of Arrhenius Activation Energy and Temperature-Dependent Viscosity on Non-Newtonian Nanomaterial Bio-Convective Flow with Partial Slip. Arab. J. Sci. Eng. 2022, 47, 7559–7570. [Google Scholar] [CrossRef]
Zapata, K.; Rodríguez, Y.; Lopera, S.H.; Cortes, F.B.; Franco, C.A. Development of Bio-Nanofluids Based on the Effect of Nanoparticles’ Chemical Nature and Novel Solanum torvum Extract for Chemical Enhanced Oil Recovery (CEOR) Processes. Nanomatererials 2022, 12, 3214. [Google Scholar] [CrossRef]
Mandal, S.; Shit, G.C.; Shaw, S.; Makinde, O.D. Entropy analysis of thermo-solutal stratification of nanofluid flow containing gyrotactic microorganisms over an inclined radiative stretching cylinder. Therm. Sci. Eng. Prog. 2022, 34, 101379. [Google Scholar] [CrossRef]
Mehta, R.N.; Chakraborty, M.; Parikh, P.A. Nanofuels: Combustion, engine performance and emissions. Fuel 2014, 120, 91–97. [Google Scholar] [CrossRef]
Cieśliński, J.T.; Krzyżak, J.; Kropiwnicki, J.; Kneba, Z. Experiments on compression ignition engine powered by nano-fuels. Combust. Engines 2022, 188, 55–59. [Google Scholar] [CrossRef]
Taylor, R.; Coulombe, S.; Otanicar, T.; Phelan, P.; Gunawan, A.; Lv, W.; Rosengarten, G.; Prasher, R.; Tyagi, H. Small particles, big impacts: A review of the diverse applications of nanofluids. J. Appl. Phys. 2013, 113, 011301. [Google Scholar] [CrossRef]
Huminic, G.; Huminic, A. Application of nanofluids in heat exchangers: A review. Renew. Sustain. Energ. Rev. 2012, 16, 5625–5638. [Google Scholar] [CrossRef]
Sajid, M.U.; Ali, H.M. Recent advances in application of nanofluids in heat transfer devices: A critical review. Renew. Sustain. Energy Rev. 2019, 103, 556–592. [Google Scholar] [CrossRef]
Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Taylor, R.A.; Abu-Nada, E.; Rashidi, S.; et al. Recent advances in modeling and simulation of nanofluid flows-Part II: Applications. Phys. Rep. 2019, 791, 1–59. [Google Scholar] [CrossRef]
Cieśliński, J.T. Application of Nanofluids in Thermal Technologies; Contemporary Issues of Heat and Mass Transfer; Publishing House of the Koszalin University of Technology: Koszalin, Poland, 2019; Tom 1, No. 360; pp. 33–48. [Google Scholar]
Patil, M.; Mehta, D.S.; Guvva, S. Future impact of nanotechnology on medicine and dentistry. J. Indian Soc. Periodontol. 2008, 12, 34–40. [Google Scholar]
Shaw, S.; Shit, G.C.; Tripathi, D. Impact of drug carrier shape, size, porosity and blood rheology on magnetic nanoparticle-based drug delivery in a microvessel. Colloids Surf. A Physicochem. Eng. Asp. 2022, 639, 128370. [Google Scholar] [CrossRef]
Kalbande, V.P.; Walke, P.V.; Kriplani, C.V.M. Advancements in Thermal Energy Storage System by Applications of Nanofluid Based Solar Collector: A Review. Environ. Clim. Technol. 2020, 24, 310–340. [Google Scholar] [CrossRef]
Li, Z.; Cui, L.; Li, B.; Du, X. Mechanism exploration of the enhancement of thermal energy storage in molten salt nanofluid. Phys. Chem. Chem. Phys. 2021, 23, 13181. [Google Scholar] [CrossRef] [PubMed]
Sundararaj, A.J.; Pillai, B.C.; Asirvatham, L.G. Convective heat transfer analysis of refined kerosene with alumina particles for rocketry application. J. Mech. Sci. Technol. 2018, 32, 1685–1691. [Google Scholar] [CrossRef]
Kakaç, S.; Pramuanjaroenki, J.A. Single-phase and two-phase treatments of convective heat transfer enhancement with nanofluids—A state-of-the-art review. Int. J. Therm. Sci. 2016, 100, 75–97. [Google Scholar] [CrossRef]
Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmad, H.; et al. Recent advances in modeling and simulation of nanofluid flows—Part I: Fundamentals and theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
Solangi, K.H.; Sharif, S.; Sadiq, I.O.; Hisam, M.J. Experimental and numerical investigations on heat transfer and friction loss of functionalized GNP nanofluids. Int. J. Mech. Eng. Technol. 2019, 10, 61–77. [Google Scholar]
Singh, P.; Oberoi, A.S.; Nijhawan, P. Experimental heat transfer analysis of copper oxide nanofluids through a straight tube. IJATCSE 2019, 8, 495–500. [Google Scholar] [CrossRef]
Karabulut, K.; Buyruk, E.; Kilinc, F. Experimental and numerical investigation of convection heat transfer in a circular copper tube using graphene oxide nanofluid. J. Braz. Soc. Mech. Sci. 2020, 42, 230. [Google Scholar] [CrossRef]
Kong, M.; Lee, S. Performance evaluation of Al₂O₃ nanofluid as an enhanced heat transfer fluid. Adv. Mech. Eng. 2020, 12, 1–13. [Google Scholar] [CrossRef]
Boertz, H.; Baars, A.J.; Cieśliński, J.T.; Smolen, S. Numerical Study of Turbulent Flow and Heat Transfer of Nanofluids in Pipes. Heat Transf. Eng. 2018, 39, 241–251. [Google Scholar] [CrossRef]
Minea, A.A.; Buonomo, B.; Burggraf, J.; Ercole, D.; Karpaiya, K.R.; Pasqua, A.D.; Sekrani, G.; Steffens, J.; Tibaut, J.; Wichmann, N.; et al. NanoRound: A benchmark study on the numerical approach in nanofluids’ simulation. Int. Commun. Heat Mass Transf. 2019, 108, 104292. [Google Scholar] [CrossRef]
Onyiriuka, E.J.; Ikponmwoba, E.A. A numerical investigation of mango leaves-water nanofluid under laminar flow regime. Niger. J. Technol. 2019, 38, 348–354. [Google Scholar] [CrossRef]
Jamali, M.; Toghraie, D. Investigation of heat transfer characteristics in the developing and the developed flow of nanofluid inside a tube with different entrances in the transition regime. J. Therm. Anal. Calorim. 2020, 139, 685–699. [Google Scholar] [CrossRef]
Fadodun, O.G.; Amosun, A.A.; Salau, A.O.; Olaloye, D.O.; Ogundeji, J.A.; Ibitoye, F.I.; Balogun, F.A. Numerical investigation and sensitivity analysis of turbulent heat transfer and pressure drop of Al₂O₃/H₂O nanofluid in straight pipe using response surface methodology. Arch. Thermodyn. 2020, 41, 3–30. [Google Scholar]
Uribe, S.; Zouli, N.; Cordero, M.E.; Al-Dahhan, M. Development and validation of a mathematical model to predict the thermal behaviour of nanofluids. Heat Mass Transf. 2021, 57, 93–110. [Google Scholar] [CrossRef]
Angayarkanni, S.A.; Philip, J. Review on thermal properties of nanofluids: Recent developments. Adv. Colloid Interface Sci. 2015, 225, 146–176. [Google Scholar] [CrossRef]
Ilyas, S.U.; Pendyala, R.; Marneni, N. Stability of Nanofluids. Topics in Mining, Metallurgy and Materials Engineering. In Engineering Applications of Nanotechnology. From Energy to Drug Delivery; Korada, V.S., Hamid, N.H.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
Akbari, M.; Galanis, N.; Behzadmehr, A. Comparative assessment of single and two-phase models for numerical studies of nanofluid turbulent forced convection. Int. J. Heat Fluid Flow 2012, 37, 136–146. [Google Scholar] [CrossRef]
Moraveji, M.K.; Esmaeili, E. Comparison between Single-Phase and Two-Phases CFD Modeling of Laminar Forced Convection Flow of Nanofluids in Circular Tube under Constant Heat Flux. Int. Commun. Heat Mass Transf. 2012, 39, 1297–1302. [Google Scholar] [CrossRef]
Duan, F. Thermal Property Measurement of Al₂O₃-Water Nanofluids. Smart Nanoparticles Technology; Abbass, H., Ed.; InTech: London, UK, 2012; ISBN 978-953-51-0500-8. [Google Scholar]
Buongiorno, J.; Venerus, D.C.; Prabhat, N.; McKrell, T.; Townsend, J.; Chrisianson, R.; Tolmachev, Y.V.; Keblinski, P.; Hu, L.-w.; Alvarado, J.L.; et al. A benchmark study on the thermal conductivity of nanofluids. J. Appl. Phys. 2009, 106, 094312. [Google Scholar] [CrossRef] [Green Version]
Vajjha, R.S.; Das, D.K. Specific heat measurement of three nanofluids and development of new correlations. ASME J. Heat Transf. 2009, 131, 071601–071607. [Google Scholar] [CrossRef]
Dittus, F.W.; Boelter, L.M.K. Heat transfer in automobile radiators of the tubular type. Univ. Calif. Publ. Eng. 1930, 2, 443–461. [Google Scholar] [CrossRef]
Kraußold, H. Die Wärmeübertragung an Flüssigkeiten in Rohren bei turbulenter Strömung. Forschung auf dem Gebiet des Ingenieurwesens; Springer: Berlin/Heidelberg, Germany, 1933; Band 1; pp. 39–44. [Google Scholar]
Sieder, E.N.; Tate, G.E. Heat transfer and pressure drop of liquids in tubes. Ind. Eng. Chem. Res. 1936, 28, 1429–1435. [Google Scholar] [CrossRef]
Mikhejev, M.A.; Mikhejeva, I.M. Teplootdacza pri Turbulentom Dwiżenji w Trubach; Osnovy teploperedczi, Energija: Moscow, Russia, 1973. (In Russian) [Google Scholar]
Petukhov, B.S. Heat Transfer and Friction in Turbulent Pipe Flow with Variable Physical Properties. Adv. Heat Transf. 1970, 503–564. [Google Scholar]
Notter, R.H.; Sleicher, C.A. A solution to the turbulent Graetz problem—III fully developed and entry region heat transfer rates. Chem. Eng. Sci. 1972, 27, 2073–2093. [Google Scholar] [CrossRef]
Churchill, S.W.; Ozoe, H. Correlations for laminar forced convection in flow over an flat plate and in developing and fully developed flow in a tube. J. Heat Trans-T ASME 1973, 95, 78–84. [Google Scholar] [CrossRef]
Hausen, H. Erweiterte Gleichung für den Wärmeübergang in Rohren bei turbulenter Strömung. Wärme Stoffübertragung 1974, 7, 222–225. [Google Scholar] [CrossRef]
Gnieliński, V. Neue Gleichungen für den Wärme—und den Stoffübergang in turbulent durchströmten Rohren und Kanälen. In Forschung in Ingenieurwesen; Springer: Berlin/Heidelberg, Germany, 1975; Band 41; pp. 8–16. [Google Scholar]
Kutateladze, S.S. Osnovy teorii Teploobmena; Atomizdat: Moscow, Russia, 1979. (In Russian) [Google Scholar]
Xuan, Y.; Li, Q. Investigation on Convective Heat Transfer and Flow Features of Nanofluids. J. Heat Trans-T ASME. 2003, 125, 151–155. [Google Scholar] [CrossRef] [Green Version]
Vasu, V.; Krishna, K.R.; Kumar, A.C.S. Analytical prediction of forced convective heat transfer of fluids embedded with nanostructured materials (nanofluids). PRAMANA J. Phys. 2007, 69, 411–421. [Google Scholar] [CrossRef]
Hussein, A.M.; Sharma, K.V.; Bakar, R.A.; Kadirgama, K. The Effect of Nanofluid Volume Concentration on Heat Transfer and Friction Factor inside a Horizontal Tube. J. Nanomater. 2013, 2013, 1–12. [Google Scholar] [CrossRef] [Green Version]
Sahin, B.; Gültekin, G.G.; Manay, E.; Karagoz, S. Experimental investigation of heat transfer and pressure drop characteristics of Al₂O₃-water nanofluid. Exp. Therm. Fluid Sci. 2013, 50, 21–28. [Google Scholar] [CrossRef]
Chavan, D.; Pise, A.T. Experimental investigation of convective heat transfer augmentation using Al₂O₃/water nanofluid in circular pipe. Heat Mass Transf. 2015, 51, 1237–1246. [Google Scholar] [CrossRef]
Durga Prasad, P.V.; Gupta, A. Experimental investigation on enhancement of heat transfer using Al₂O₃/water nanofluid in a u-tube with twisted tape inserts. Int. Commun. Heat Mass Transf. 2016, 75, 154–161. [Google Scholar] [CrossRef]
Saha, G.; Paul, M.C. Heat transfer and entropy generation of turbulent forced convection flow of nanofluids in a heated pipe. Int. Commun. Heat Mass Transf. 2015, 61, 26–36. [Google Scholar] [CrossRef] [Green Version]
Meyer, J.P.; Adio, S.A.; Sharifpur, M.; Nwosu, P.N. The Viscosity of Nanofluids: A Review of the Theoretical, Empirical, and Numerical Models. Heat Transf. Eng. 2016, 37, 387–421. [Google Scholar] [CrossRef]
Bashirnezhad, K.; Bazri, S.; Safaei, M.R.; Goodarzi, M.; Dahari, M.; Mahian, O.; Dalkılıça, A.S.; Wongwises, S. Viscosity of nanofluids: A review of recent experimental studies. Int. Commun. Heat Mass Transf. 2016, 73, 114–123. [Google Scholar] [CrossRef]
Krieger, I.M.; Dougherty, T.J. A mechanism for non-newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheology. 1959, 3, 137–152. [Google Scholar] [CrossRef]
Palm, S.J.; Roy, G.; Nguyen, C.T. Heat transfer enhancement with the use of nanofluids in radial flow cooling systems considering temperature dependent properties. Appl. Therm. Eng. 2006, 26, 2209–2218. [Google Scholar] [CrossRef]
Nguyen, C.T.; Desgranges, F.; Roy, G.; Galanis, N.; Mare, T.; Boucher, S.; Mintsa, A. Temperature and particle-size dependent viscosity data for water-based nanofluids—Hysteresis phenomenon. Int. J. Heat Fluid Flow 2007, 28, 1492–1506. [Google Scholar] [CrossRef]
Khanafer, K.; Vafai, K. A critical synthesis of thermophysical characteristics of nanofluids. Int. J. Heat Mass Transf. 2011, 54, 4410–4428. [Google Scholar] [CrossRef]
Pastoriza-Gallego, M.J.; Lugo, L.; Legido, J.L.; Piñeiro, M.M. Thermal conductivity and viscosity measurements of ethylene glycol-based Al₂O₃ nanofluids. Nanoscale Res. Lett. 2011, 6, 221. [Google Scholar] [CrossRef] [Green Version]
Corcione, M. Empirical correlating equations for predicting the effective thermal conductivity and dynamic viscosity of nanofluids. Energy Convers. Manag. 2011, 52, 789–793. [Google Scholar]
Chon, C.H.; Kihm, K.D. Empirical correlation finding the role of temperature and particle size for nanofluid (Al₂O₃) thermal conductivity enhancement. Appl. Phys. Lett. 2005, 87, 153107. [Google Scholar] [CrossRef]
Purohit, N.; Purohit, V.A.; Purohit, K. Assessment of nanofluids for laminar convective heat transfer: A numerical study. Eng. Sci. Technol. Int. J. 2016, 19, 574–586. [Google Scholar] [CrossRef] [Green Version]
Saeed, F.R.; Al-Dulaimi, M.A. Numerical investigation for convective heat transfer of nanofluid laminar flow inside a circular pipe by applying various models. Arch. Thermodyn. 2021, 42, 71–95. [Google Scholar]
Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23, Reference Fluid Thermodynamic and Transport Properties (REFPROP), Version 9.0; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
Kleinstreuer, C.; Feng, Y. Experimental and theoretical studies of nanofluid thermal conductivity enhancement: A review. Nanoscale Res. Lett. 2011, 6, 229. [Google Scholar] [CrossRef] [Green Version]
Aybar, H.Ş.; Sharifpur, M.; Azizian, M.R.; Mehrabi, M.; Meyer, J.P. A Review of Thermal Conductivity Models for Nanofluids. Heat Transf. Eng. 2015, 36, 1085–1110. [Google Scholar] [CrossRef] [Green Version]
Chen, G. Nonlocal and nonequilibrium heat conduction in the vicinity of nanoparticles. J. Heat Trans-T ASME 1996, 118, 539–545. [Google Scholar] [CrossRef]
Hassani, S.; Saidur, R.; Mekhilef, S.; Hepbasli, A. A new correlation for predicting the thermal conductivity of nanofluids; using dimensional analysis. Int. J. Heat Mass Transfer. 2015, 90, 121–130. [Google Scholar] [CrossRef]
Sawicka, D.; Cieśliński, J.T.; Smolen, S.A. Comparison of Empirical Correlations of Viscosity and Thermal Conductivity of Water-Ethylene Glycol-Al₂O₃ Nanofluids. Nanomaterials 2020, 10, 1487. [Google Scholar] [CrossRef] [PubMed]
Pak, B.C.; Cho, Y.I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp. Heat Transf. 1998, 11, 151–170. [Google Scholar] [CrossRef]
Sharifpur, M.; Yousefi, S.; Meyer, J.P. A new model for density of nanofluids including nanolayer. Int. Commun. Heat Mass Transf. 2016, 78, 168–174. [Google Scholar] [CrossRef] [Green Version]
Saha, G.; Paul, M.C. Numerical analysis of the heat transfer behaviour of water based Al₂O₃ and TiO₂ nanofluids in a circular pipe under the turbulent flow condition. Int. Commun. Heat Mass Transf. 2014, 56, 96–108. [Google Scholar] [CrossRef] [Green Version]
Shahrul, I.M.; Mahbubul, I.M.; Khaleduzzaman, S.S.; Saidur, R.; Sabri, M.F.M. A comparative review on the specific heat of nanofluids for energy perspective. Renew. Sustain. Energy Rev. 2014, 38, 88–98. [Google Scholar] [CrossRef]
Riazi, H.; Murphy, T.; Webber, G.B.; Atkin, R.; Tehrani, S.S.M.; Taylor, R.A. Specific heat control of nanofluids: A critical review. Int. J. Therm. Sci. 2016, 107, 25–38. [Google Scholar] [CrossRef]
Hentschke, R. On the specific heat capacity enhancement in nanofluids. Nanoscale Res. Lett. 2016, 11, 88. [Google Scholar] [CrossRef] [Green Version]
Williams, W.; Buongiorno, J.; Hu, L.W. Experimental investigation of turbulent convective heat transfer and pressure loss of alumina/water and zirconia/water nanoparticle colloids (nanofluids) in horizontal tubes. J. Heat Trans-T ASME 2008, 130, 042412. [Google Scholar] [CrossRef]
Corcione, M.; Cianfrini, M.; Quintino, A. Heat transfer of nanofluids in turbulent pipe flow. Int. J. Therm. Sci. 2012, 56, 58–69. [Google Scholar] [CrossRef]
Sekhar, Y.R.; Sharma, K.V. Study of viscosity and specific heat capacity characteristics of water-based Al₂O₃ nanofluids at low particle concentrations. J. Exp. Nanosci. 2012, 56, 58–69. [Google Scholar]
Cieśliński, J.T.; Kozak, P. Experimental investigation of forced convection of water-Al₂O₃ nanofluids inside horizontal tubes. In Proceedings of the XVI International Symposium Heat Transfer and Renewable Sources of Energy, Szczecin-Międzyzdroje, Poland, 10–13 September 2016. [Google Scholar]
Godson, L.; Raja, B.; Lal, D.M.; Wongwises, S. Enhancement of heat transfer using nanofluids—An overview. Renew. Sust. Energy Rev. 2010, 14, 629–641. [Google Scholar] [CrossRef]
Buongiorno, J. Convective Transport in Nanofluids. J. Heat Transfer 2006, 128, 240–250. [Google Scholar] [CrossRef]

Figure 1. Nu-Re relationships for water.

Figure 2. Nu-Re relationships for water-Al₂O₃ nanofluids.

Figure 3. Viscosity of water.

Figure 4. Viscosity of water-Al₂O₃ nanofluids.

Figure 5. Thermal conductivity of water.

Figure 6. Thermal conductivity of water-Al₂O₃ nanofluids.

Figure 7. Density of water.

Figure 8. Density of water-Al₂O₃ nanofluids.

Figure 9. Specific heat of water.

Figure 10. Specific heat of water-Al₂O₃ nanofluids.

Figure 11. Thermal diffusivity of water-Al₂O₃ nanofluids.

Figure 12. Thermal diffusivity of water-Al₂O₃ nanofluids.

Figure 13. Prandtl number for water-Al₂O₃ nanofluids.

Figure 14. Variation of Pr number for water-Al₂O₃ nanofluids.

Figure 15. Variation of Re number for water-Al₂O₃ nanofluids.

Figure 16. Variation of Re number for water-Al₂O₃ nanofluids.

Figure 17. Variation of Nu number for water-Al₂O₃ nanofluids.

Figure 18. Variation of Nu number for water-Al₂O₃ nanofluids.

Figure 19. Variation of heat transfer coefficient for water-Al₂O₃ nanofluids.

Figure 20. Variation of heat transfer coefficient for water-Al₂O₃ nanofluids.

Table 1. Properties of Al₂O₃ nanoparticles.

Thermal Conductivity k_p [W/(mK)]	Density ρ_p [kg/m³]	Specific Heat c_p,p [J/(kg K)]
35 *	3600 **	765 **

*—[48]; **—[49].

Table 2. Correlation equations for turbulent flow of base fluid.

Authors	Correlation	Range	Remarks	Equation
Dittus and Boelter [50]	$\bar{N u} = 0.23 R e^{0.8} P r^{n}$	Re > 10⁴ 0.7 < Pr < 100	n = 0.4—heating n = 0.3—cooling	Equation (1)
Krauβold [51]	$\bar{N u} = 0.032 R e^{0.8} P r^{n} {(\frac{L}{D})}^{- 0.054}$	Re > 10⁴	n = 0.37—heating n = 0.3—cooling	Equation (2)
Sieder and Tate [52]	$\bar{N u} = 0.027 R e^{4 / 5} P r^{1 / 3} {(\frac{μ_{f}}{μ_{w}})}^{0.14}$	Re > 10⁴ 0.7 < Pr < 16,700	T_w = const.	Equation (3)
Mikhejev [53]	$\bar{N u} = 0.021 R e^{0.8} P r_{f}^{0.43} {(\frac{P r_{f}}{P r_{w}})}^{0.25} ε_{L}$	10⁴ < Re < 5 × 10⁶ 0.6 < Pr < 2500	ε_L = f(L/D, Re)	Equation (4)
Petukhov [54]	$\bar{N u} = \frac{(f / 8) R e P r}{1.07 + 12.7 {(f / 8)}^{\frac{1}{2}} (P r^{\frac{2}{3}} - 1)}$	10⁴ < Re < 5 × 10⁶ 0.5 < Pr < 2000	$f = {(1.82 l n R e - 1.64)}^{- 2}$	Equation (5)
Notter and Sleicher [55]	$\bar{N u} = 4.8 + 0.0156 P e^{0.85} P r^{0.08}$ $\bar{N u} = 6.3 + 0.0167 P e^{0.85} P r^{0.08}$	10⁴ < Re < 10⁶ 0.004 < Pr < 0.1	T_w = const. q_w = const.	Equation (6) Equation (7)
Churchill and Ozoe [56]	$\bar{N u} = \frac{0.3387 P r^{1 / 3} R e^{1 / 2}}{{[1 + {(0.0468 / P r)}^{2 / 3}]}^{1 / 4}}$	Re > 100 10⁻⁴ < Pr → ∞	q_w = const.	Equation (8)
Hausen [57]	$N u = 0.0235 [1 + {(\frac{d}{L})}^{2 / 3}] [R e^{0.8} - 230] P r_{f}^{0.3} {(\frac{μ_{f}}{μ_{w}})}^{0.14}$	2300 < Re < 2 × 10⁶ 1.5 < Pr < 500 d/L < 1		Equation (9)
Gnieliński [58]	$\bar{N u} = \frac{(f / 8) (R e - 1000) P r}{1 + 12.7 {(f / 8)}^{0.5} (P r^{\frac{2}{3}} - 1)}$	3 × 10³ < Re < 5 × 10⁶ 0.5 < Pr < 2000	$f = {(0.79 l n R e - 1.64)}^{- 2}$	Equation (10)
Kutateladze [59]	$\bar{N u} = 1.61 {(P e \frac{D}{L})}^{1 / 3}$	Pe > 12 d/L < 12		Equation (11)

Table 3. Nu number correlation equations for water- Al₂O₃ nanofluids.

Authors	Equation	Remarks	Equation
Xuan and Li [60]	$\bar{N u} = 0.0059 (1 + 7.6286 φ_{v}^{0.6886} P e_{p}^{0.001}) R e_{}^{0.9238} P r_{}^{0.4}$	$P e_{p} = \frac{w d_{p}}{a_{n f}}$	Equation (12)
Vasu et al. [61]	$\bar{N u} = 0.0256 \cdot R e^{0.8} P r^{0.4}$	10⁴ < Re < 8 × 10⁴	Equation (13)
Hussein et al. [62]	$\bar{N u} = 0.02 \cdot R e^{0.788} P r^{0.45}$	5000 < Re < 5 × 10⁴ 6.8 < Pr < 11.97	Equation (14)
Sahin et al. [63]	$\bar{N u} = 0.106 \cdot R e^{0.588} \cdot (1 + φ_{v}^{- 0.1096}) \cdot P r^{0.258}$	4000 < Re < 20,000 5 < Pr < 7 0.5% < φ_v < 4%	Equation (15)
Chavan and Pise [64]	$\bar{N u} = 0.508358 \cdot R e^{0.7401} \cdot P r^{- 0.7026}$	6000 < Re < 14,000 0.3% < φ < 1%	Equation (16)
Durga and Gupta [65]	$\bar{N u} = 0.09589 \cdot R e^{0.8} \cdot P r^{0.4} \cdot {(1 + φ_{v})}^{2833}$	3000 < Re < 30,000 5.12 < Pr < 6.54 0% < φ_v < 0.03%	Equation (17)
Saha and Paul [66]	$\bar{N u} = 0.0126 R e_{}^{0.85589} P r_{}^{0.44709} {(\frac{d_{f}}{d_{p}})}^{- 0.00176}$	10⁴ < Re < 10⁵ 8.45 < Pr < 20.29 4% < φ_v < 6% 10 < d_p [nm] < 40	Equation (18)

Table 4. Correlations for viscosity of water- Al₂O₃ nanofluids.

Authors	Correlation								Remarks	Equation
Krieger and Dougherty [69]	$μ_{n f} = μ_{b f} (1 - {(\frac{φ_{a}}{φ_{v s}})}^{- 2.5 φ_{m}})$								$φ_{a} —$ volume fraction of aggregates $φ_{a} = φ_{v} {(d_{a} / d_{p})}^{3 - d_{f}}$ $φ_{v}$ —volume fraction of the well-dispersed individual particles, $d_{a}$ —diameter of aggregates, $d_{f}$ —fractal dimension of aggregates $φ_{v s}$ —volume fraction of densely packed spheres	Equation (19)
Palm et al. [70]	$μ_{b f} = 0.034 - 2 \cdot 10^{- 4} T + 2.9 \cdot 10^{- 7} T^{2}$ $μ_{b f} = 0.039 - 2.3 \cdot 10^{- 4} T + 3.4 \cdot 10^{- 7} T^{2}$								$φ_{v} = 1 %$ $φ_{v} = 4 %$	Equation (20) Equation (21)
Nguyen et al. [71]	$μ_{n f} = 0.904 e^{0.148 φ_{v}} μ_{b f}$ $μ_{b f} = (2.1275 - 0.0215 \cdot T + 0.0002 \cdot T^{2}) μ_{b f}$								d_p = 47 nm $φ_{v} = 4 %$	Equation (22) Equation (23)
Khanafer and Vafai [72]	$μ_{n f} = - 0.4491 + \frac{28.837}{t} + 0.574 φ_{v} - 0.1634 φ_{v}^{2} + 23.053 \frac{φ_{v}^{2}}{t^{2}} + 0.0132 φ_{v}^{3} - 2354.735 \frac{φ_{v}}{t^{3}} + 23.498 \frac{φ_{v}^{2}}{d_{p}^{2}} - 3.0185 \frac{φ_{v}^{3}}{d_{p}^{2}}$									Equation (24)
Pastoriza-Gallego et al. [73]	$μ_{n f} = e^{(A + \frac{B}{T - T_{o}})}$									Equation (25)
		ϕ_v
		0.000	0.005	0.010	0.015	0.021	0.031	0.048
	A	−3.694	−3.632	−2.381	−1.702	−3.450	−3.302	−1.379
	B [K]	999.0	999.0	689.3	534.7	999.0	999.0	518.4
	T_o [K]	145.7	145.5	169.8	185.5	146.2	145.3	189.9
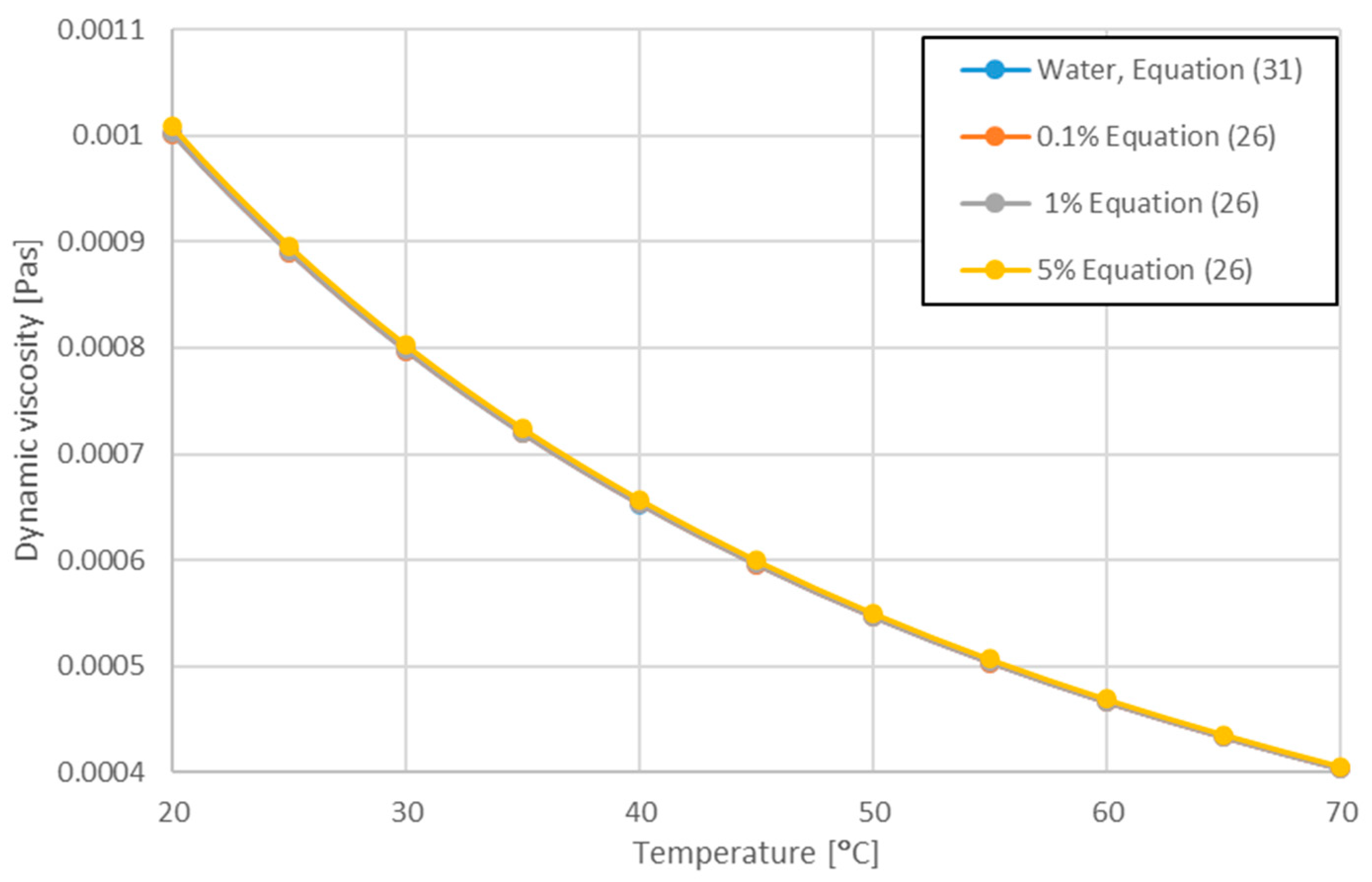
Corcione [74]	$μ_{n f} = μ_{b f} (\frac{1}{1 - 34.87 {(\frac{d_{p}}{d_{f}})}^{- 0.3} φ_{v}^{1.03}})$								d_f—equivalent diameter of liquid molecule $d_{f} = 0.1 {(\frac{6 M}{N π ρ_{f o}})}^{1 / 3}$ M—molecular weight of water N—Avogadro number $ρ_{f o}$ - density of water at T_o = 293 K	Equation (26)

Table 5. Correlations for viscosity of water.

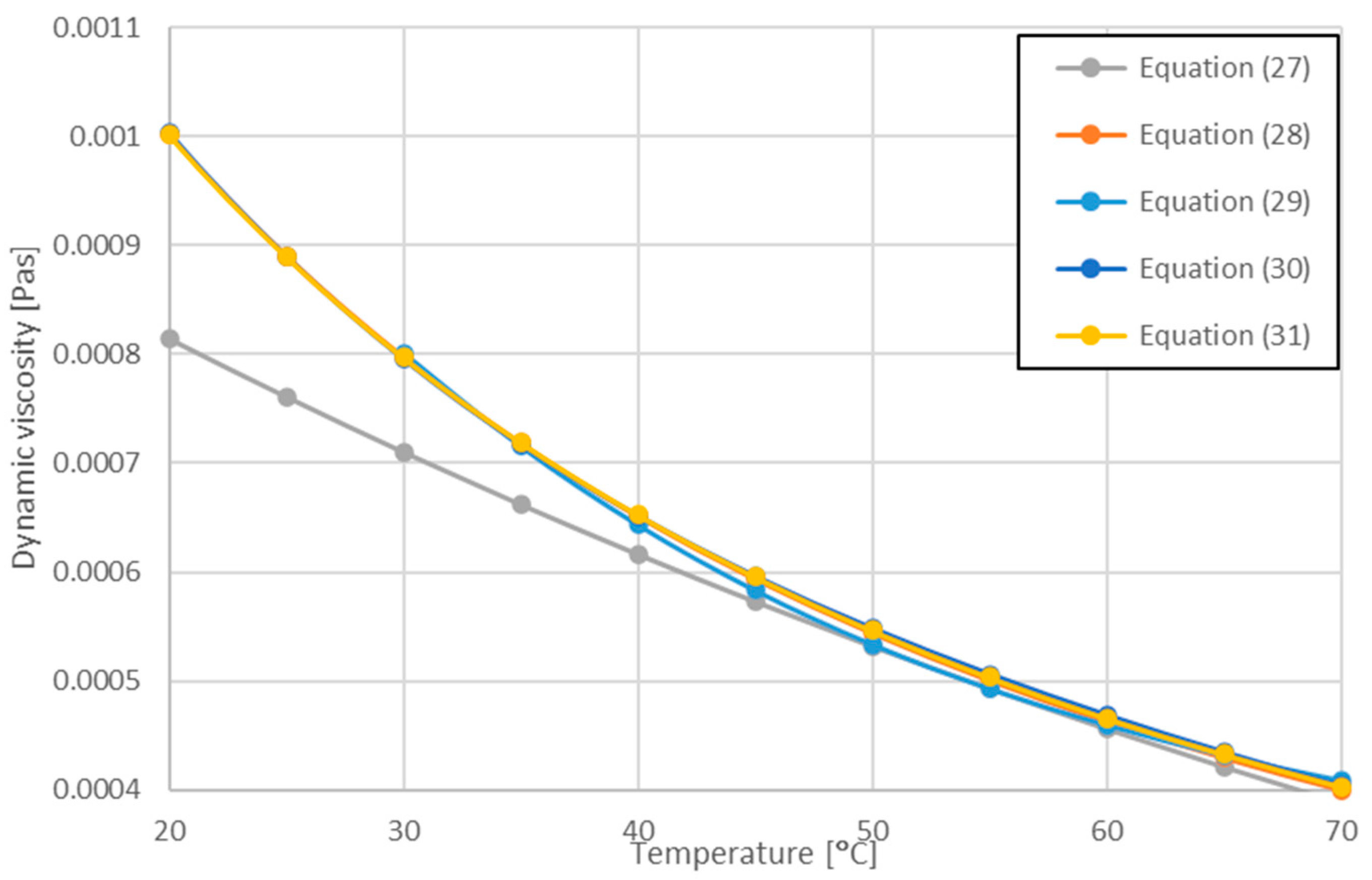
Authors	Correlation	Range	Equation
Minea et al. Equation (31) in [36]	$μ_{b f} = 1.055787 - 0.0132897 \cdot T + 0.00006309 \cdot T^{2} - 1.33730666 \cdot 10^{- 7} \cdot T^{3} - 1.0666666 \cdot 10^{- 10} \cdot T^{4}$	294 < T < 344	Equation (27)
Chon and Khim [75]	$μ_{b f} = 2.414 \cdot 10^{- 5} \cdot 10^{\frac{247.8}{T - 140}}$	294 < T < 344	Equation (28)
Purohit et al. [76]	$μ_{b f} = 999.79 + 0.068 \cdot t - 0.0107 \cdot t^{2} + 0.00082 \cdot t^{2.5} - 2.303 \cdot 10^{- 5} \cdot t^{3}$	300 < T < 350	Equation (29)
Saeed and Dulaimi [77]	$μ_{b f} = 0.414092804247831 - 4.792184560427 \cdot 10^{- 3} T + 2.0927097596 \cdot 10^{- 5} T^{2} - 4.0781184 \cdot 10^{- 8} T^{3} + 2.9885 \cdot 10^{- 11} \cdot T^{4}$		Equation (30)
Present work [78]	$μ_{b f} = 2.2551419 - 0.033948 \cdot T + 0.0002053 \cdot T^{2} - 6.229 \cdot 10^{- 7} \cdot T^{3} + 9.4741 \cdot 10^{- 10} \cdot T^{4} - 5.775 \cdot 10^{- 13} \cdot T^{5}$	283 < T < 343	Equation (31)

Table 6. Correlations for thermal conductivity of water- Al₂O₃ nanofluids.

Authors	Correlation	Remarks	Equation
Khanafer and Vafai [72]	$k_{n f} = k_{b f} (0.9843 + 0.398 φ_{v}^{0.7383} {(\frac{1}{d_{p}})}^{0.2246} {(\frac{μ_{n f}}{μ_{b f}})}^{0.0235} - 3.9517 \frac{φ_{v}}{t} + 34.034 \frac{φ_{v}^{2}}{t^{3}} + 32.509 \frac{φ_{v}}{t^{2}})$	water-Al₂O₃ $0.01 \leq φ_{v} \leq 0.09$ $20 \leq t [° C] \leq 70$ $13 nm \leq d_{p} \leq 131 nm$	Equation (32)
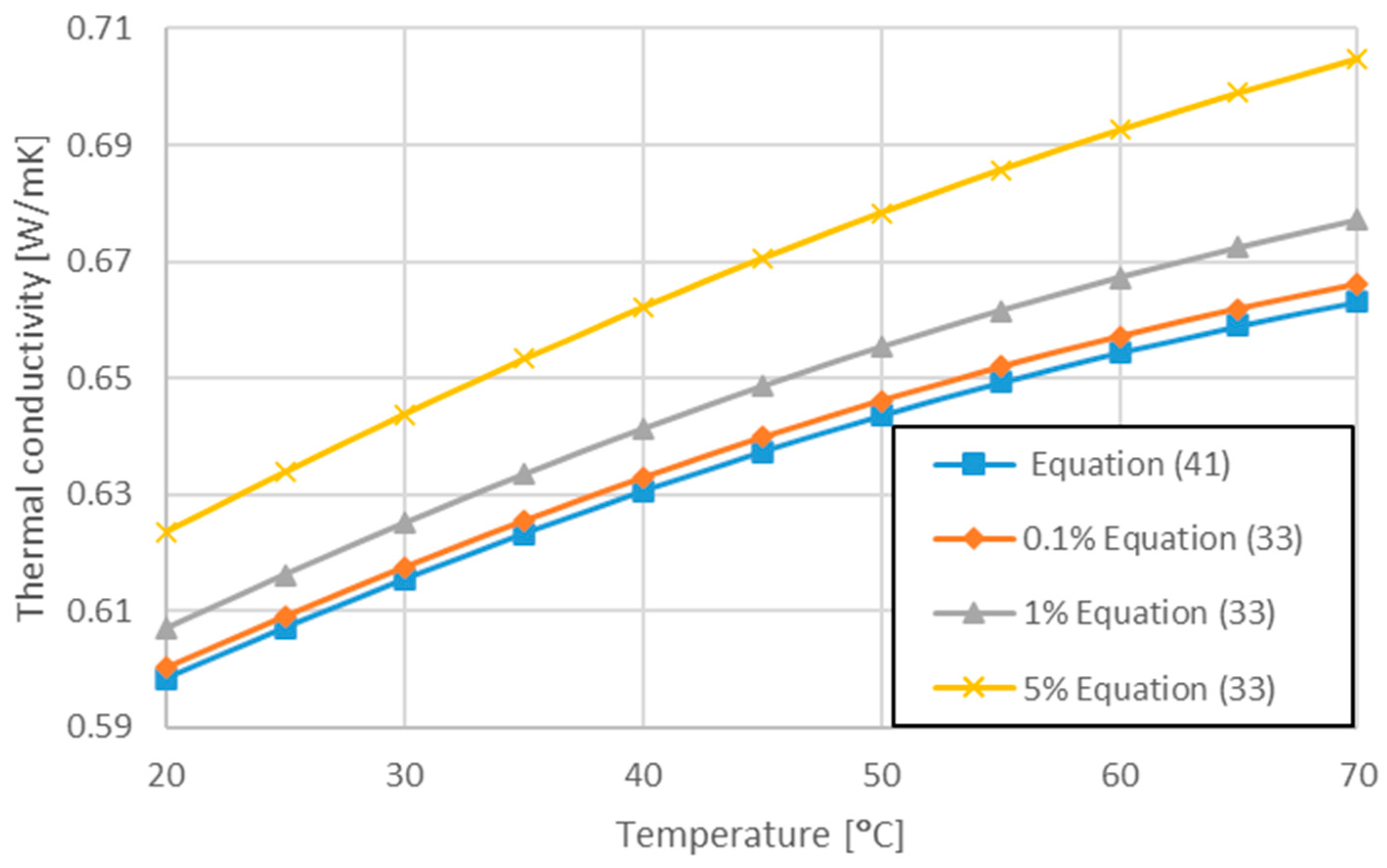
Corcione [74]	$k_{n f} = k_{b f} (1 + 4.4 R e_{p}^{0.4} P r^{0.66} {(\frac{T}{T_{f r}})}^{10} {(\frac{λ_{p}}{λ_{f}})}^{0.03} φ_{v}^{0.66}$	$R e_{p}$ —Re number based on nanoparticle diameter $R e_{p} = \frac{ρ_{b f} u_{B} d_{p}}{μ_{b f}}$ $u_{B}$ —Brownian velocity of the nanoparticle $u_{B} = \frac{2 k_{b} T}{π μ_{b f} d_{p}^{2}}$	Equation (33)
Chen [81]	$k_{p} = k_{n f} \frac{0.75 d_{p} / l_{p}}{0.75 d_{p} / l_{p} + 1}$	l_p—mean free path of nanoparticle	Equation (34)
Hassani et al. [82]	$k_{n f} = k_{b f} (1.04 + φ_{v}^{1.11} {(\frac{k_{p}}{k_{b f}})}^{0.33} P r^{- 1.7} [\frac{1}{P r^{- 1.7}} - \frac{262}{{(\frac{k_{p}}{k_{b f}})}^{0.33}} + (135 {(\frac{d_{r e f}}{d_{p}})}^{0.23} {(\frac{ν_{b f}}{d_{p} u_{B r}})}^{0.82}) {(\frac{c_{p}}{T^{- 1} u_{B r}^{2}})}^{- 0.1} {(\frac{T_{B}}{T})}^{- 7}])$	Various base fluids, metal and oxide nanoparticles	Equation (35)
Sawicka et al. [83]	$k_{n f} = k_{b f} (1 + 0.1046 φ_{m}^{0.2388} {(\frac{100}{d_{p}})}^{3.14 \cdot 10^{- 3}})$		Equation (36)

Table 7. Correlations for thermal conductivity of water.

Authors	Correlation	Range	Equation
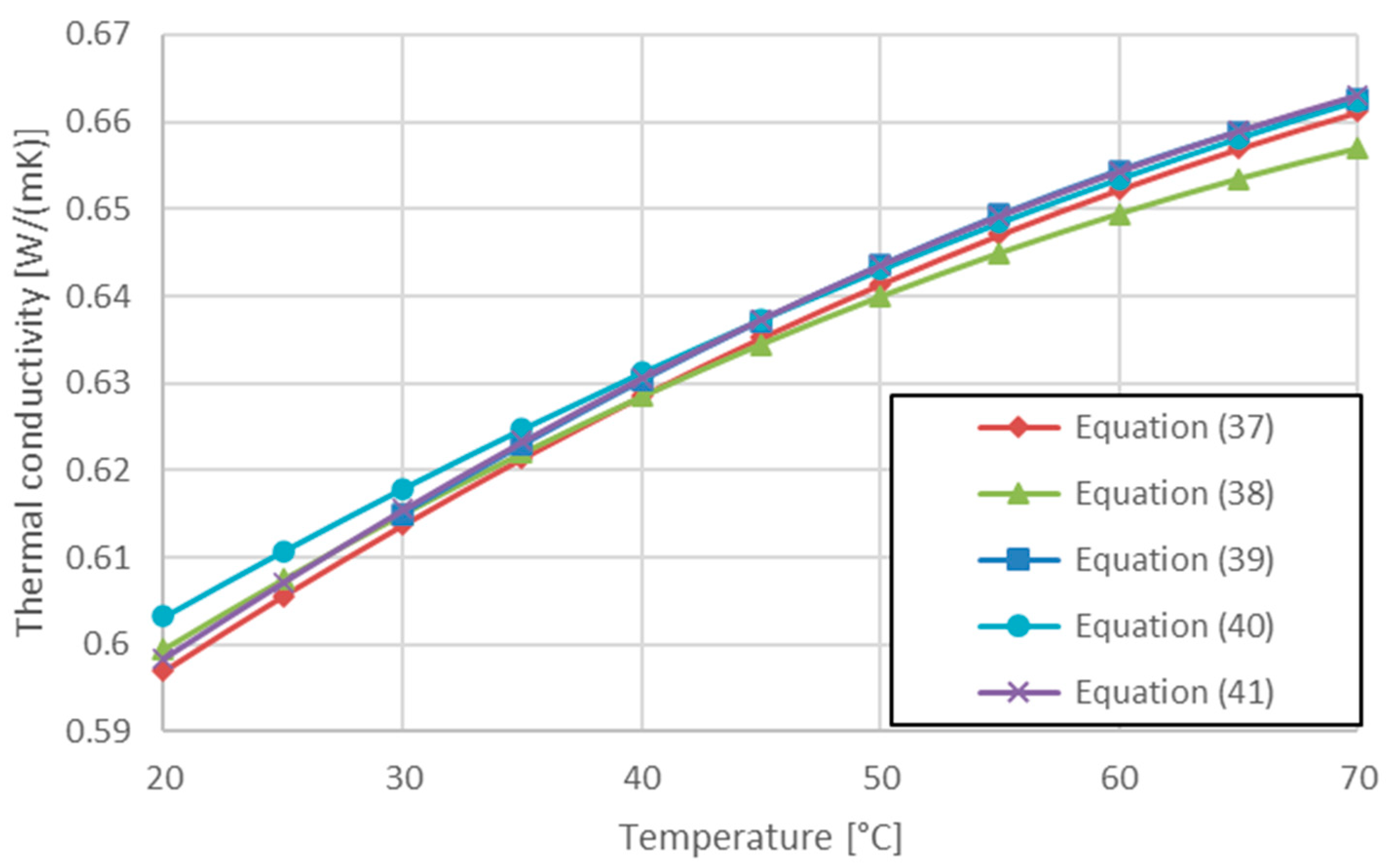
Minea et al. Equation (22) in [36]	$k_{b f} = - 0.98249 \cdot 10^{- 5} \cdot T^{2} + 7.535211 \cdot 10^{- 3} \cdot T - 0.76761$	294 < T < 344	Equation (37)
Minea et al. Equation (30) in [36]	$k_{b f} = - 0.743567 + 0.077513 \cdot T - 9.9999999 \cdot 10^{- 6} \cdot T^{2} - 8.63331959 \cdot 10^{- 18} \cdot T^{3} + 7.301424 \cdot 10^{- 21} \cdot T^{4}$	294 < T < 344	Equation (38)
Purohit [76]	$k_{b f} = 0.56112 + (0.00193 \cdot t) - (2.601 \cdot 10^{- 6} \cdot t^{2}) - (6.08 \cdot 10^{- 8} \cdot t^{3})$	300 < T < 350	Equation (39)
Saeed and Dulaimi [77]	$k_{b f} = - 0.46662403 + 0.00575419 \cdot T - 7.18 \cdot 10^{- 6} \cdot T^{2}$		Equation (40)
Present work [78]	$k_{b f} = 27.689 - 0.415 \cdot T + 0.000249 \cdot T^{2} - 7.389 \cdot 10^{- 6} \cdot T^{3} + 1.0839 \cdot 10^{- 8} - 6.3292 \cdot 10^{- 12}$	283 < T < 343	Equation (41)

Table 8. Correlations for density of nanofluids.

Authors	Correlation	Remarks	Equation
Khanafer and Vafai [72]	$ρ_{n f} = 1001.064 + 2738.6191 φ_{v} - 0.2095 \cdot t$	water-Al₂O₃ $0 \leq φ_{v} \leq 0.04$ $5 \leq t [° C] \leq 40$	Equation (42)
Pak and Cho [84]	$ρ_{n f} = φ_{v} ρ_{p} + (1 - φ_{v}) ρ_{b f}$	Mixture model	Equation (43)
Sharifpur et al. [85]	$ρ_{n f, n l} = \frac{ρ_{n f}}{(1 - φ_{v}) + φ_{v} {(r_{p} + t_{v})}^{3} / r_{p}^{3}}$	$r_{p}$ —radius of nanoparticle $t_{v}$ —nanolayer thickness $t_{v} = - 0002833 r_{p}^{3} + 0.0475 r_{p} - 0.1417$	Equation (44)

Table 9. Correlations for density of water.

Autors	Correlation	Range	Equation
Minea et al. Equation (20) in [36]	$ρ_{b f} = - 2.0546 \cdot 10^{- 10} \cdot T^{5} + 4.0505 \cdot 10^{- 7} \cdot T^{4} - 3.1285 \cdot 10^{- 4} \cdot T^{3} + 0.11576 \cdot T^{2} - 20.674 \cdot T + 2446$		Equation (45)
Minea et al. Equation (28) in [36]	$ρ_{b f} = - 413.15683 + 13.24245 \cdot T - 0.040578 \cdot T^{2} + 0.00004 \cdot T^{3} - 2.27018 \cdot 10^{- 17} \cdot T^{4}$		Equation (46)
Purohit et al. [76]	$ρ_{b f} = 999.79 + 0.068 \cdot t - 0.0107 \cdot t^{2} + 0.00082 \cdot t^{2.5} - 2.303 \cdot 10^{- 5} \cdot t^{3}$	300 < T < 350	Equation (47)
Saeed and Dulaimi [77]	$ρ_{b f} = 765.33 + 1.8142 \cdot T - 0.0035 \cdot 10^{- 2} \cdot T^{2}$		Equation (48)
Present work [78]	$ρ_{b f} = - 5859.3637 + 98.96855 \cdot T + 0.574747 \cdot T^{2} + 0.0016856 \cdot T^{3} - 2.4989 \cdot 10^{- 6} \cdot T^{4} - 1.4908 \cdot 10^{- 9} \cdot T^{5}$		Equation (49)
Saha and Paul [86]	$ρ_{b f} = 330.12 + 5.92 \cdot T - 1.63 \cdot 10^{- 2} \cdot T^{2} + 1.33 \cdot 10^{- 5} \cdot T^{3}$	278 < T < 363	Equation (50)

Table 10. Correlations for specific heat of nanofluids.

Authors	Correlation	Remarks	Equation
Pak and Cho [84]	$c_{p, n f} = φ_{v} c_{p, p} + (1 - φ_{v}) c_{p, b f}$	Mixture model	Equation (51)
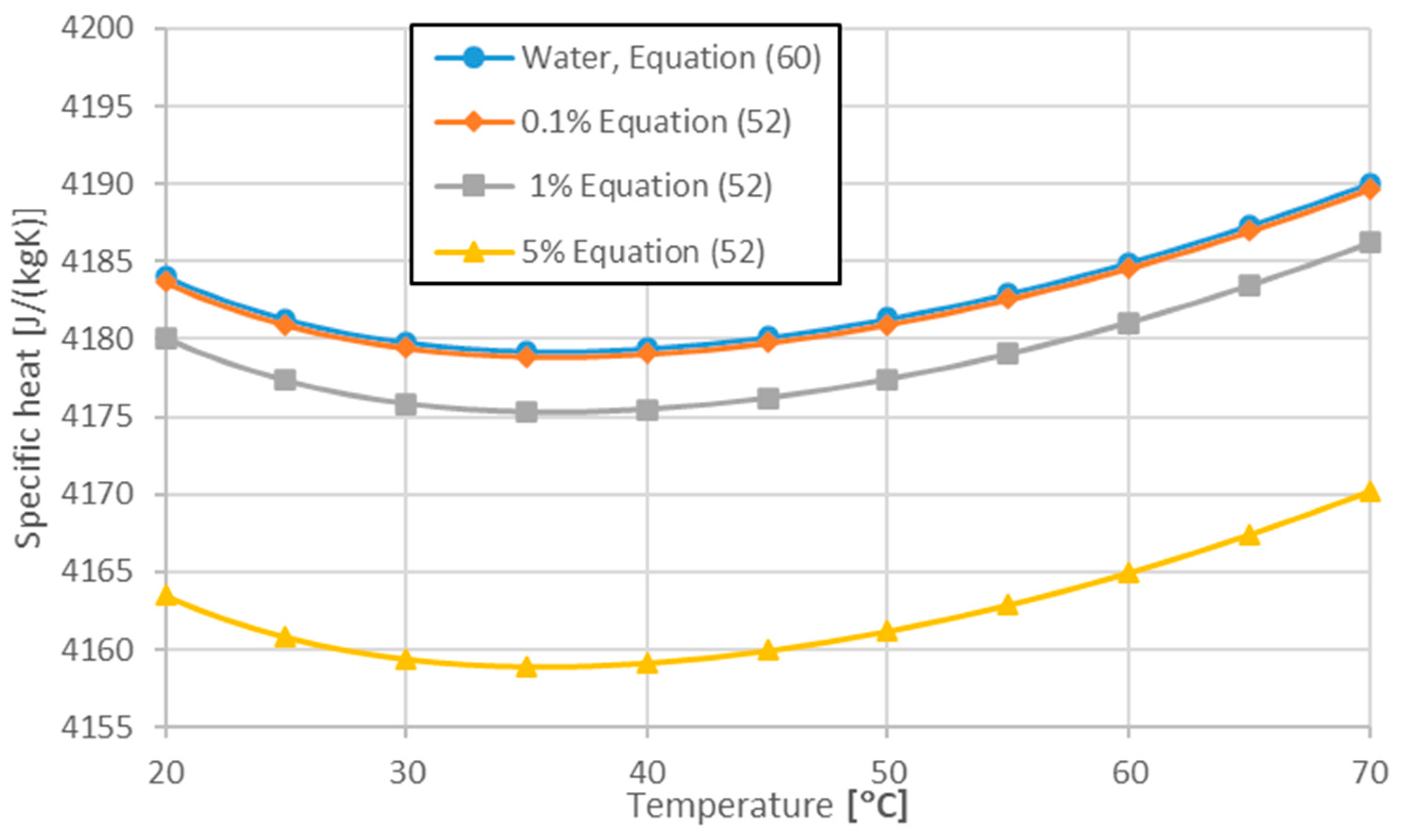
Williams et al. [90]	$c_{p, n f} = \frac{ρ_{b f} c_{p, b f} (1 - φ_{v}) + φ_{v} ρ_{p} c_{p, p}}{ρ_{b f}}$	water-Al₂O₃, water-ZrO₂	Equation (52)
Corcione et al. [91]	$c_{p, n f} = \frac{(1 - φ_{v}) {(ρ c_{p})}_{b f} + φ_{v} {(ρ c_{p})}_{p}}{(1 - φ_{v}) ρ_{b f} + φ_{v} ρ_{p}}$	water-Al₂O₃, water-CuO, water-TiO₂	Equation (53)
Sekhar and Sharma [92]	$c_{p, n f} = c_{p, H_{2} O} [0.8429 {(1 + \frac{t}{50})}^{- 0.3037} {(1 + \frac{d_{p}}{50})}^{0.4167} {(1 + \frac{φ_{v}}{100})}^{2.272}]$	water-Al₂O₃, water-CuO, water-TiO₂, water-SiO₂ $0.01 % \leq φ_{v} \leq 4 %$ , $20 \leq t [° C] \leq 50$ , $15 nm \leq d_{p} \leq 50 nm$	Equation (54)

Table 11. Correlations for specific heat of water.

Authors	Correlation	Range	Equation
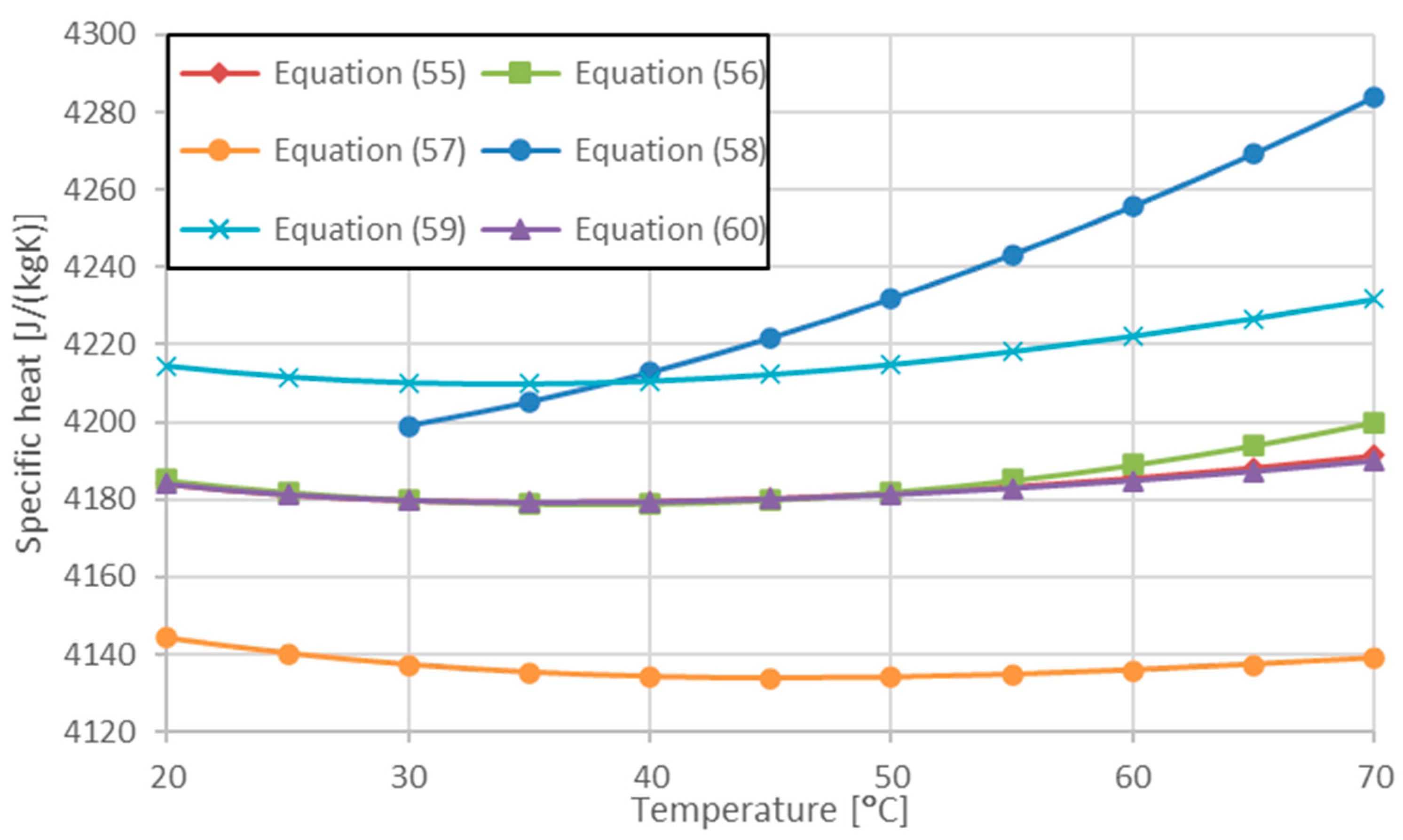
Minea et al. Equation (21) in [36]	$c_{p, b f} = - 2.0546 \cdot 10^{- 10} \cdot T^{5} + 4.0505 \cdot 10^{- 7} \cdot T^{4} - 3.1285 \cdot 10^{- 4} \cdot T^{3} + 0.11576 \cdot T^{2} - 20.674 \cdot T + 2446$	293 < T < 313	Equation (55)
Minea et al. Equation (25) in [36]	$c_{p, b f} = 6108.94345 - 12.426 \cdot T + 0.02 \cdot T^{2} - 5.540012 \cdot 10^{- 12} \cdot T^{3} + 6.25929269 \cdot 10^{- 21} \cdot T^{4}$	293 < T < 313	Equation (56)
Saha and Paul [66]	$c_{p, b f} = 10.01 - 5.14 \cdot 10^{- 2} \cdot T + 1.49 \cdot 10^{- 4} \cdot T^{2} - 2.62 \cdot 10^{- 12} \cdot T^{3}$	278 < T < 363	Equation (57)
Purohit et al. [76]	$c_{p, b f} = 4217.4 - 5.61 \cdot T + 1.299 \cdot T^{1.52} - 0.11 \cdot T^{2} + 4149.6 \cdot 10^{- 6} \cdot T^{2.5}$	300 < T < 350	Equation (58)
Saeed and Dulaimi [77]	$c_{p, b f} = 10444.58656104 - 54.08920728 \cdot T + 0.15359377 \cdot T^{2} - 0.00014301 \cdot T^{3}$		Equation (59)
Present work [78]	$c_{p, b f} = 185614 - 2737 \cdot T + 16.54446 \cdot T^{2} - 0.5006 \cdot T^{3} + 7.58 \cdot 10^{- 5} \cdot T^{4} - 4.5942 \cdot 10^{- 8} \cdot T^{5}$	283 < T < 343	Equation (60)

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Cieśliński, J.T.; Lubocki, D.; Smolen, S. Impact of Temperature and Nanoparticle Concentration on Turbulent Forced Convective Heat Transfer of Nanofluids. Energies 2022, 15, 7742. https://doi.org/10.3390/en15207742

AMA Style

Cieśliński JT, Lubocki D, Smolen S. Impact of Temperature and Nanoparticle Concentration on Turbulent Forced Convective Heat Transfer of Nanofluids. Energies. 2022; 15(20):7742. https://doi.org/10.3390/en15207742

Chicago/Turabian Style

Cieśliński, Janusz T., Dawid Lubocki, and Slawomir Smolen. 2022. "Impact of Temperature and Nanoparticle Concentration on Turbulent Forced Convective Heat Transfer of Nanofluids" Energies 15, no. 20: 7742. https://doi.org/10.3390/en15207742

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu

Impact of Temperature and Nanoparticle Concentration on Turbulent Forced Convective Heat Transfer of Nanofluids

Abstract

1. Introduction

2. Materials and Methods

2.1. Tested Nanofluids

2.2. Correlations for Forced Convection Heat Transfer inside Horizontal Tubes

2.3. Correlations for Thermophysical Properties of Nanofluids

3. Results and Discussion

3.1. Variation of Pr Number

3.2. Variation of Re Number

3.3. Variation of Nu Number

3.4. Variation of Heat Transfer Coefficient

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Nomenclature

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI