Abstract
The review presents the D2-law of droplet evaporation, which is used to describe the spraying process involving the evaporation of droplets. This law, the subject of numerous publications, can be successfully applied to describe the droplet evaporation process under various conditions, including the calculations of the process of feeding the boiler with a liquid that contains catalyst particles. To date, not a lot of work has been devoted to this issue. The paper is a continuation of previous research concerning the spraying of liquids with a catalyst, which improves the efficiency of the process. The conducted analysis showed that the experimental data from previously published work are very compatible with the data obtained from the D2-law of droplet evaporation. At the standard speed of about 20 m/s of an aerosol flowing through a dust duct, droplets in the stream should be observed up to a distance of 1 m from the outlet of the apparatus supplying the system. Under such flow conditions, a droplet’s lifetime must be above 0.05 s. The dependence between a droplet’s lifetime and its diameter and temperature was determined. The obtained results confirmed that the effective droplet diameter is above 30 µm. Such droplets must be generated and then fed to the boiler for the catalyst to work properly. This law is an engineering approach to the problem, which uses relatively simple model equations in order to determine the evaporation time of a droplet.
1. Introduction
In theory, mass transfer is at its maximum at the droplet surface that is subjected to the flow of gas around it, and at its minimum near the point of the detachment of its boundary layer. However, this exchange increases in the wake of the droplet. In order to determine the heat and mass transfer, a system of dimensionless differential equations of continuity, motion, and mass and heat balance can be written. However, the solution of such a coupled equations is of little practical importance, as it requires many simplifications. For this reason, experimental criterion formulas are used [1].
The mass transfer from an evaporating droplet of a liquid to the surrounding gas can take place due to molecular diffusion, diffusion caused by natural convection or forced convection, or a combination of these three phenomena simultaneously (with forced convection determining the mass transfer rate in most cases). Under free and forced convection conditions, the equation of the dimensionless mass transfer coefficient is described by the following general relationship:
In the case of systems with small droplet diameters and a small difference in fluid density in the immediate vicinity of the particle, and also at some distance from it (in the boundary layer and outside it), it is permissible to ignore the influence of natural convection on the intensity of the mass transfer. According to paper [2], in the case of flow around a droplet, the influence of free convection may be neglected when:
The fulfillment of this condition allows the equation of the dimensionless mass transfer coefficient to be written in a simplified form:
In engineering practice, the Sherwood number is calculated from empirical dependencies, and is a function of numbers that are easy to determine. The first classic study concerning forced evaporation of liquid droplets is the publication by Frossling [3]. By specifying the speed of the loss of substances from droplets of water, aniline, nitrobenzene and naphthalene, which were suspended in the air stream, the author gave the following equation:
The research was carried out for the Re numbers ranging from 2 to 800, and the Schmidt numbers from 0.6 to 2.56.
Ranz and Marshall [4], after carrying out an extensive program of research concerning the evaporation of water, benzene and aniline droplets (Sc values from 0.6 to 2.2) in the air at Re < 200, proposed the mass transfer equation in the following form:
The results of Frossling [3], Maisel and Sherwood [5], and also Ranz and Marshall [4], which referred to the analysis of the mass transfer from spherical surfaces conducted by Ranz [6], extended the scope of application of the Ranz–Marshall equation for dilute solutions and mixtures in which the concentration of liquid vapor is far from the saturated state. This equation is valid for the value of the Re number ranging from 1 to 70,000, and for the Sc number from 0.6 to 400. To date, this equation is considered as the reference and is used by many researchers to evaluate their results.
The research of Frossling [3] and Ranz–Marshall [4] regarding small Reynolds numbers Re < 6 is supplemented by the publication of Apashev and Malov [7]. Their research on the evaporation of small droplets of alcohol, ethyl ether, water, gasoline, kerosene, and diesel fuel in the air at a temperature of 20 to 370 °C led to the development of the Ranz–Marshall equation (Equation (5)).
In addition to the studies concerning the determination of the mass transfer coefficients of various substances from spherical surfaces, research was also carried out on the influence of stream turbulence, droplet vibrations, and liquid circulation inside the droplets on the rate of evaporation or sublimation. It is well known that an increase in the degree of stream turbulence results in the intensification of mass or heat transfer. However, it will have a different effect depending on the type of flow. Maisel and Sherwood [5] reported the first qualitative results of the influence of stream turbulence on the mass transfer rate during their evaporation studies conducted on spheres moistened with water and benzene (with a flow within the Re number ranging from 2000 to 50,000).
During the measurements, the degree of turbulence was increased from 3.5% to 24%, and the evaporation rate was increased by 18% at Re = 2.440, and by 25% at Re = 19.500. The measurement results showed that there is a clear reduction in the turbulence effect on the intensification of the mass transfer with decreasing Reynolds numbers. Moreover, it was found that the effect of stream turbulence can be completely neglected for droplets with a diameter smaller than 2 mm. The studies showed that the turbulence effect in the case of Re < 2000 is negligible [8,9,10]. They also proved that droplet vibrations do not have an influence on the increase of heat transfer coefficients if the linear vibration velocity is lower than the gas stream velocity [2]. The authors of paper [11] also indicated the lack of influence of liquid circulation inside a droplet on the speed of mass transfer by evaporation. Although this model is very successful in describing an evaporating droplet, the assumptions upon which the model was developed were subjected to criticism and several experimental and numerical analyses [12,13,14,15,16]. The model is also being improved for specific applications, e.g., for the systematic validation of computational solvers [17]. Paper [16] presents the analysis of the validity of the D2-law during n-decane droplet vaporization in a microgravity environment. The experimental results show that the D2-law is always valid in normal gravity within the range of the ambient temperatures explored in the study. The authors of article [18] proposed a revision of the D2-law that is capable of accurately determining the droplet evaporation rate in dilute conditions by properly estimating the asymptotic properties of a droplet. The authors of paper [18] tested the proposed model against data from direct numerical simulations, and found an excellent agreement for the predicted droplet evaporation time in dilute turbulent jet-sprays.
A simple model for heating and evaporation of non-isothermal droplets based on the parabolic approximation of the temperature profiles inside droplets was suggested by Dombrovsky and Sazhin [19]. The D2-law was modified to take into account droplet heating. Comparison with numerical solutions of the transient problem for moving droplets shows the applicability of this approximation to modelling the heating and evaporation processes of droplets. The simplicity of the model makes it particularly convenient for implementation into multidimensional CFD codes to replace the widely used model of isothermal droplets.
Droplet evaporation is a complicated process governed by the interplay of combined mass and heat transfer, surface tension and other thermal effects [20]. In the article [20], the time variation of the droplet temperature during evaporation was taken into account. For this purpose, the transient energy equation was solved numerically.
The literature concerning the evaporation of multicomponent droplets is relatively scarce. A modified model for both two- and three-component droplets is presented in paper [21]. The model has the following properties: the transport of one component can be augmented by the bulk (Stefan) flow of the other components, and a droplet can never exceed its boiling point. The ordinary differential equations that constitute the model were integrated numerically. Paper [22] shows the results of the detailed numerical modeling of the evaporation of an ethanol–water droplet. Analysis of the obtained data showed that the assumptions that liquid properties are constant, the liquid phase composition is homogeneous, and there is no differential volatility may not be valid—depending on the initial droplet temperature. The D2 model of the evaporation of droplets enables the diameter of the evaporating droplet to be calculated without the need to use complicated, cost-consuming and time-consuming numerical calculations. However, it does not give a broad picture of the process [23,24,25].
A model for the attenuation of fire radiation by water mist containing droplets of pure or sea water was developed by Dombrovsky et al. [26]. The new approach takes into account the kinetics of evaporation and also the effect of solidification of evaporated sea-salt droplets. The model was used to analyze the radiative heating and evaporation of droplets of pure water and more complex multi-phase processes in droplets of sea water. The proposed approach can be useful for engineering applications in fire protection.
Papers [24,25] describe fuel additives, which allow for the reduction of loading that is associated with coal combustion, and thus for the reduction of the amount of fuel that is required for the production of a unit amount of energy. Moreover, a method of feeding these additives into the boiler is also provided. These studies focused on the intensification of the combustion of solid fuels in a boiler with the use of alkyl alcohol and Al-Ni catalyst as combustion promoters. The most important aspect in this process is the selection and evaporation of the solvent, which in this case is alcohol, because the catalyst only works when it is in the droplets [24]. In the case of alcohol evaporating too early, the desired effect of intensifying the combustion of coal dust will not occur. Thanks to the application of this method, a greater degree of fuel burnout is obtained, which in turn results in a lower energy consumption for the production of the same power, and also an increased flame stability. The parameters of the emitted exhaust gases and ash are also improved. Despite numerous papers describing the D2-law of droplet evaporation, it is difficult to find any in which this law was used to describe the droplet evaporation process during the feeding of the boiler with a liquid containing catalyst particles. The main goal of this study was to present the literature data for the D2-law of droplet evaporation, and to attempt to perform calculations for the process of dosing the catalyst into a combustion chamber. The obtained results were analyzed, and confirmed its practical (i.e., engineering) approach to the problem, which uses relatively simple model equations that allow for the determination of the droplets’ evaporation time.
2. Analysis of the Evaporation Process
As a result of the temperature gradient, a heat flux with a density qt (W/m2) is generated, which in turn causes droplets to heat and evaporate:
where: qw—heat flux heating a droplet (W/m2), Lpar—latent heat of evaporation (J/kg), —mass flow rate (kg/(m2 × s)).
From the above equation, after many transformations, the D2-law of droplet evaporation is obtained:
where: D0, D—initial and final (current) diameter of a droplet, Kpar—evaporation constant, t—time.
The evaporation constant is described by the following relationship:
where: λp—thermal conductivity coefficient, B—exchange number, (Cp)p—isobaric specific heat of gas, ρc—liquid density.
The B is given by the following formula:
where: Lpar—latent heat of evaporation of the liquid (fuel) at temperature Ts, which is the surface temperature of the droplet. The calculation of Kpar requires knowledge of B, where B is a function of the generally unknown temperature Ts. It is possible to determine this temperature graphically or numerically, but it is very difficult. When simplifying this, however, it can be assumed that temperature Ts is equal to the boiling point of the liquid. It was also shown that the B value is close to zero at temperatures close to room temperature.
The combination of Equations (8) and (9) results in the formula for the evaporation time of a droplet in the form of:
In the paper by Lefebvre [25], the concept of the effective evaporation constant (Kpar)e was introduced as:
presented in papers [27,28], and also used in this paper.
It was assumed that the mass transfer coefficient on the air side can be determined from the previously quoted Frossling equation [3], which was modified by Ranz and Marshall [4] and has the following form:
in which the Reynolds number is:
and the Schmidt number is:
kp is the mass transfer coefficient in the gas phase (mol/N/s), βp is the mass transfer coefficient (kg/m2 × s), Dd is the dynamic diffusion coefficient (kg/m × s), and D is the dynamic molecular diffusion coefficient expressed in (m2/s). The gas constant in Equation (12) is equal to R = 8314 (J/mol/K). The speed of droplets was defined as the average velocity of the mixture in the outlet channel.
In the case of diffusion of water vapor in air, the kinematic diffusion coefficient can be described by relationship [29]:
in which temperature is expressed in Kelvin, and pressure is expressed in atm. The equation is correct for temperatures ranging from 280 to 450 K. The dependence between the kinematic diffusion coefficient for water and the temperature is shown graphically in Figure 1.
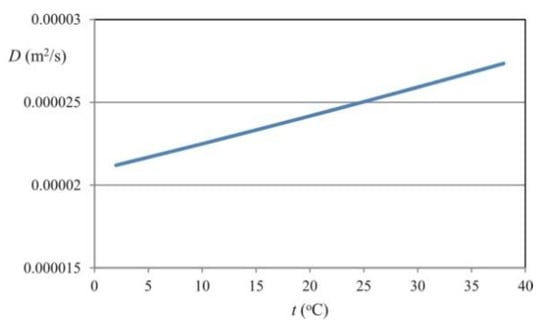
Figure 1.
Dependence between the kinematic diffusion coefficient and the temperature for the water-to-air vapor system.
Data regarding the dimensionless Colburn modulus jm of the mass transfer, defined as:
and obtained by various researchers, show relatively high convergence [30]. These data also perfectly match to the data obtained in this study, the graphical image of which is shown in Figure 2. The data were obtained for the aerosol temperature of 293 K, and for particles with diameters ranging from 0.1 to 100 µm. It was observed that an increase in temperature from 293 K to 308 K causes an increase in the Colburn modulus jm by about 3%. The process conditions were mapped on the basis of real data for a dust duct supplying coal dust to an existing coal dust boiler at a combined heat and power (CHP) plant in Poland [24].
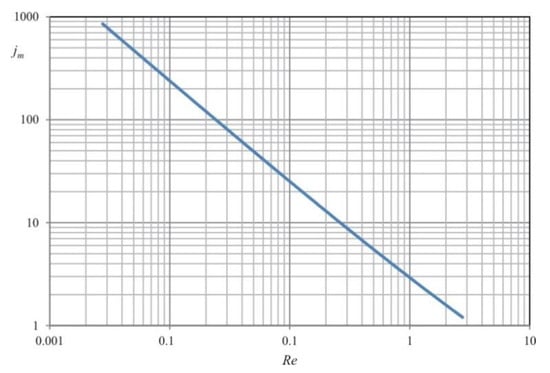
Figure 2.
Dependence between the dimensionless Colburn modulus jm of the mass exchange and the Reynolds number for the tested process.
The temperature in the dust duct was >100 °C, while the temperature of the fed liquid was around 20–35 °C. The catalyst feeding system was located 1 m from the burner. On an industrial scale, the gas flow rate through the dust duct is equal to 5000 m3n/h (at a speed of 26.8 m/s), the amount of supplied dust is 1.2 t/h, and its grain size ranges from 20 to 200 μm. The liquid with the catalyst is fed at a volumetric flow rate of 300 mL/h. Droplets of liquid containing the catalyst with diameters from 0.1 to 100 µm were analyzed. The diameter of the generated droplets should be >30 μm [24,25]. The analysis of the data presented in Figure 2 shows that the apparatus feeding a liquid containing the catalyst works in the laminar flow regime. It should be noted that the data presented in [30] show the values of the Colburn modulus for a Reynolds number from 1 to 1000, and the values of the Reynolds number 1–2 are consistent with the values shown in Figure 2.
Due to the fact that the diameter of a particle (droplet) is a characteristic dimension, it would be appropriate to present the dependence of jm with regard to the droplet’s diameter. An exemplary graph is shown in Figure 3. The analysis of the obtained dependence showed that the value of the Colburn modulus decreases with an increase in the droplet diameter.
Figure 3.
Dependence between the dimensionless Colburn modulus jm of the mass transfer and the droplet diameter at the temperature of aerosol of Ts = 308 K.
The analysis of the data presented in Figure 2 confirms that during the decomposition of the liquid stream into fine droplets, conditions arise in which the relative speed of the droplets and the Reynolds number are close to zero. It can even be simplified to (from the formula for the diffusion of a sphere with a radius reaching infinity):
where the Nusselt number is:
where: —average heat transfer coefficient, and —average thermal conductivity coefficient.
Ranz and Marshall [4] proposed an equation for heat transfer, which is analogous to the Frossling equation for mass transfer:
assuming that the Prandtl number is given by equation:
where a is the temperature uniformity coefficient (thermal diffusivity) (m2/s).
For relatively small droplet sizes, the evaporation time (lifetime) of the droplet is important. For example, in the case of heterogeneous combustion, it determines the time that is needed to complete the combustion, and in the case of homogeneous combustion, the time that is needed to prepare the combustible mixture. Time t of a droplet’s evaporation during its movement depends on various factors, including:
- -
- the physical properties of the surrounding gas, i.e., temperature, pressure, thermal conductivity, specific heat, and viscosity,
- -
- the droplet’s speed in relation to the environment,
- -
- the properties of the liquid and its vapor, i.e., density, vapor pressure, thermal conductivity, and specific heat,
- -
- the properties of the droplet in its initial state, especially its diameter and temperature.
The droplet’s evaporation time t results from Equation (7), i.e., from the D2-law of droplet evaporation. The concept of the effective evaporation constant, which is described by Equation (11), is very convenient from a practical point of view. The graph of the dependence between the effective evaporation constant and the temperature, which was obtained by extrapolating the data presented in the paper of Chin and Lefebvre [31], is shown in Figure 4.
Figure 4.
Diagram of the dependence between the effective evaporation constant and the temperature of the surrounding gas (the assumed boiling point of the liquid Twrz = 373 K).
The values of the droplet’s evaporation time at selected ambient temperatures and for droplets of different diameters calculated from Equation (11) are shown graphically in Figure 5. The obtained results confirm the observations conducted for the sprayed liquid stream [24,25]. In the case of the standard velocity of the aerosol flowing through the dust duct of even 120 m/s (usually from 20 to 25 m/s), the droplets in the stream should be observed at a distance of 1 m from the outlet of the apparatus supplying the system with the liquid containing the catalyst (e.g., nebulizer, reactor). Under such flow conditions, the droplet’s lifetime should be above 0.0084 s.
Figure 5.
Dependence between the evaporation time of a droplet and its diameter for selected temperatures.
At the actual flow velocity of 20 m/s, the minimum droplet lifetime is 0.05 s. Assuming that the droplets have a diameter of about 30 µm, the resulting droplet evaporation time is about 1.4 s for a temperature of 293 K, 0.1 s for a temperature of 308 K, 0.087 s for the temperature of 313 K, and 0.023 s for the temperature of 373 K. Therefore, such a droplet would be able to cover the required distance in the aerosol, taking into account the changes in temperature along the length of the dust duct leading to the boiler [24,25]. The obtained results are consistent with the simulation results presented in paper [24]. During the calculations, however, one should take into account the diversity of the composition of the liquid containing the catalyst, and also its rheological properties, which are described in detail in [25]. This is due to the fact that they may not only affect the diameters of the generated droplets, but also the droplet lifetime. During this time, smaller droplets evaporate and/or coalesce to form larger droplets and they also undergo other transformations.
3. Conclusions
The paper presents literature data that describe in detail the D2-law of droplet vaporization, which is used in the liquid spraying process. The aspect related to the evaporation of the liquid that carries catalyst particles is particularly interesting, because it is of a great practical importance—especially from the point of view of energy. As a result of the conducted analysis, earlier predictions regarding the size of a droplet, which were presented in articles [24,25], were confirmed. The obtained results confirmed that the effective diameter of a droplet is above 30 µm, which must be generated and then fed to the boiler for the catalyst to work properly. The use of the D2-law of droplet evaporation allows for a relatively simple calculation of a droplet’s diameter during the conducted process without the need for complicated, cost-intensive and time-consuming CFD calculations. It could be an alternative to process simulations. However, it should be borne in mind that this method does not give as broad a picture of the process as the one that can be obtained using CFD simulations.
Author Contributions
Conceptualization: M.O., Z.B., D.C. and R.L.; formal analysis: Z.B., M.O., M.B. and D.C.; writing: Z.B., M.O., M.M., A.K., S.W., M.B., D.C., R.L. and I.P. All authors have read and agreed to the published version of the manuscript.
Funding
The research was financed within the project “Development of an automatic system based on artificial intelligence in order to improve the economy of the boiler for variable loads” under the Sub-measure 1.1.1 of the Operational Program of Intelligent Development 2014-2020, co-financed by the European Regional Development Fund No. PO-IR contract. 01.01-00-2064/20-00. This research work was also supported by the Polish Ministry of Education and Science.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding authors (M.O.; Z.B.).
Acknowledgments
The authors would like to thank the Polish National Centre for Research and Development and the Polish Ministry of Education and Science for financial support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Orzechowski, Z.; Prywer, J. Preparation and Application of the Sprayed Liquid; Scientific and Technical Publishing House (WNT): Warsaw, Poland, 2008. [Google Scholar]
- Garner, F.H.; Keey, R.B. Mass transfer from single solid spheres—I. Transfer at low Reynolds numbers. Chem. Eng. Sci. 1958, 9, 119–129. [Google Scholar] [CrossRef]
- Frossling, N. Uber die verdunstung fallenden tropfen. Gerlands Beitr. Geophys. 1938, 52, 170–216. [Google Scholar]
- Hielscher, T. Ultrasonic Production of Nano-Size Dispersions and Emulsions; ENS’05: Paris, France, 2005; pp. 1–6. Available online: https://arxiv.org/ftp/arxiv/papers/0708/0708.1831.pdf (accessed on 18 October 2018).
- Maisel, D.S.; Sherwood, T.K. Evaporation of liquids into turbulent gas streams. Chem. Eng. Prog. 1950, 46, 131–138. [Google Scholar]
- Ranz, W.E. Friction and transfer coefficients for single panicles and packed beds. Chem. Eng. Prog. 1952, 48, 247–253. [Google Scholar]
- Apashev, M.D.; Malov, P.V. Evaporation of single free droplets of various liquids with small Reynolds number values for the stream flowing past the droplets. ARS J. 1962, 32, 467–471. [Google Scholar] [CrossRef]
- Brown, R.; Sato, K.; Sage, B. Material transfer in turbulent gas streams. Effect of turbulence on macroscopic transport from spheres. Ind. Eng. Chem. Data Ser. 1958, 3, 263–272. [Google Scholar] [CrossRef]
- Venezian, E.; Crespo, M.J.; Sage, B.H. Thermal and material transfer in turbulent gas stream: One inch spheres. AIChE J. 1962, 8, 383–388. [Google Scholar] [CrossRef]
- Van der Heoge Zijnen, B.G. Heat transfer from horizontal cylinders to a turbulent air flow. App. Sci. Res. 1958, A7, 205–223. [Google Scholar] [CrossRef]
- Constan, G.L.; Calvert, S. Mass transfer in drops under conditions that promote oscillation and internal circulation. AIChE J. 1963, 1, 109–115. [Google Scholar] [CrossRef]
- Faeth, G.M. Current status of droplet and liquid combustion. Prog. Energy Combust. Sci. 1977, 3, 191–224. [Google Scholar] [CrossRef]
- Faeth, G.M. Evaporation and combustion of sprays. Prog. Energy Combust. Sci. 1983, 9, 1–76. [Google Scholar] [CrossRef]
- Law, C.K. Recent advances in droplet vaporization and combustion. Prog. Energy Combust. Sci. 1982, 8, 171–201. [Google Scholar] [CrossRef]
- Sirignano, W.A. Fuel droplet vaporization and spray combustion theory. Prog. Energy Combust. Sci. 1983, 9, 291–322. [Google Scholar] [CrossRef]
- Chauveau, C.; Birouk, M.; Gökalp, I. An analysis of the d2-law departure during droplet evaporation in microgravity. Int. J. Multiphase Flow 2011, 37, 252–259. [Google Scholar] [CrossRef]
- Pathak, A.; Raessi, M. Steady-state and transient solutions to drop evaporation in a finite domain: Alternative benchmarks to the d2 law. Int. J. Heat Mass Trans. 2018, 127, 1147–1158. [Google Scholar] [CrossRef]
- Dalla, B.F.; Wang, J.; Picano, F. Revisiting d2-law for the evaporation of dilute droplets. Fluid Dyn. 2021, 33, 051701. [Google Scholar] [CrossRef]
- Dombrovsky, L.A.; Sazhin, S.S. A simplified non-isothermal model for droplet heating and evaporation. Int. Comm. Heat Mass Transfer 2003, 30, 5–787. [Google Scholar] [CrossRef]
- Dombrovsky, L.A.; Fedorets, A.A.; Levashov, V.Y.; Kryukov, A.P.; Bormashenko, E.; Nosonovsky, M. Modeling evaporation of water droplets as applied to survival of airborne viruses. Atmosphere 2020, 11, 965. [Google Scholar] [CrossRef]
- Newbold, F.R.; Amundson, N.R. A model for evaporation of a multicomponent droplet. AIChE J. 1973, 19, 22–30. [Google Scholar] [CrossRef]
- Lupo, G.; Duwig, C. A numerical study of ethanol–water droplet evaporation. J. Eng. Gas Turb. Power 2017, 140, 2. [Google Scholar]
- Lucci, F.; Frederix, E.; Kuczaj, A.K. AeroSolved: Computational fluid dynamics modeling of multispecies aerosol flows with sectional and moment methods. J. Aerosol. Sci. 2022, 159, 105854. [Google Scholar] [CrossRef]
- Bielecki, Z.; Ochowiak, M.; Włodarczak, S.; Krupińska, A.; Matuszak, M.; Lewtak, R.; Dziuba, J.; Szajna, E.; Choiński, D.; Odziomek, M. The Analysis of the Possibility of Feeding a Liquid Catalyst to a Coal Dust Channel. Energies 2021, 14, 8521. [Google Scholar] [CrossRef]
- Bielecki, Z.; Ochowiak, M.; Włodarczak, S.; Krupińska, A.; Matuszak, M.; Jagiełło, K.; Dziuba, J.; Szajna, E.; Choiński, D.; Odziomek, M. The Optimal Diameter of the Droplets of a High-Viscosity Liquid Containing Solid State Catalyst Particles. Energies 2022, 15, 3937. [Google Scholar] [CrossRef]
- Dombrovsky, L.A.; Levashov, V.Y.; Kryukov, A.P.; Dembele, S.; Wen, J.X. A comparative analysis of shielding of thermal radiation of fires using mist curtains containing droplets of pure water or sea water. Int. J. Thermal. Sci. 2020, 152, 106299. [Google Scholar] [CrossRef]
- Godsave, G.A.E. Studies of the combustion of drops in a fuel spray—the burning of single drops of fuel. Symp. Combust. 1953, 4, 818–830. [Google Scholar] [CrossRef]
- Lefebvre, A.H. Atomization and Spray; Hemisphere Publishing Corporation: New York, NY, USA, 1989. [Google Scholar]
- Marrero, T.R.; Mason, E.A. Gaseous diffusion coefficients. J. Phys. Chem. Ref. Data 1972, 1, 3–118. [Google Scholar] [CrossRef]
- Jasiewicz, J. Mass exchange from the surface of spheres and drops. Mech. Tech. Stos. 1957, 5, 45–56. (In Polish) [Google Scholar]
- Chin, J.S.; Lefebvre, A.H. Steady-state evaporation characteristics of hydrocarbon fuel drops. AIAA J. 1983, 21, 1437–1443. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).