Thermal Effect of Cylindrical Heat Sink on Heat Management in LED Applications
Abstract
1. Introduction
2. Materials and Methods
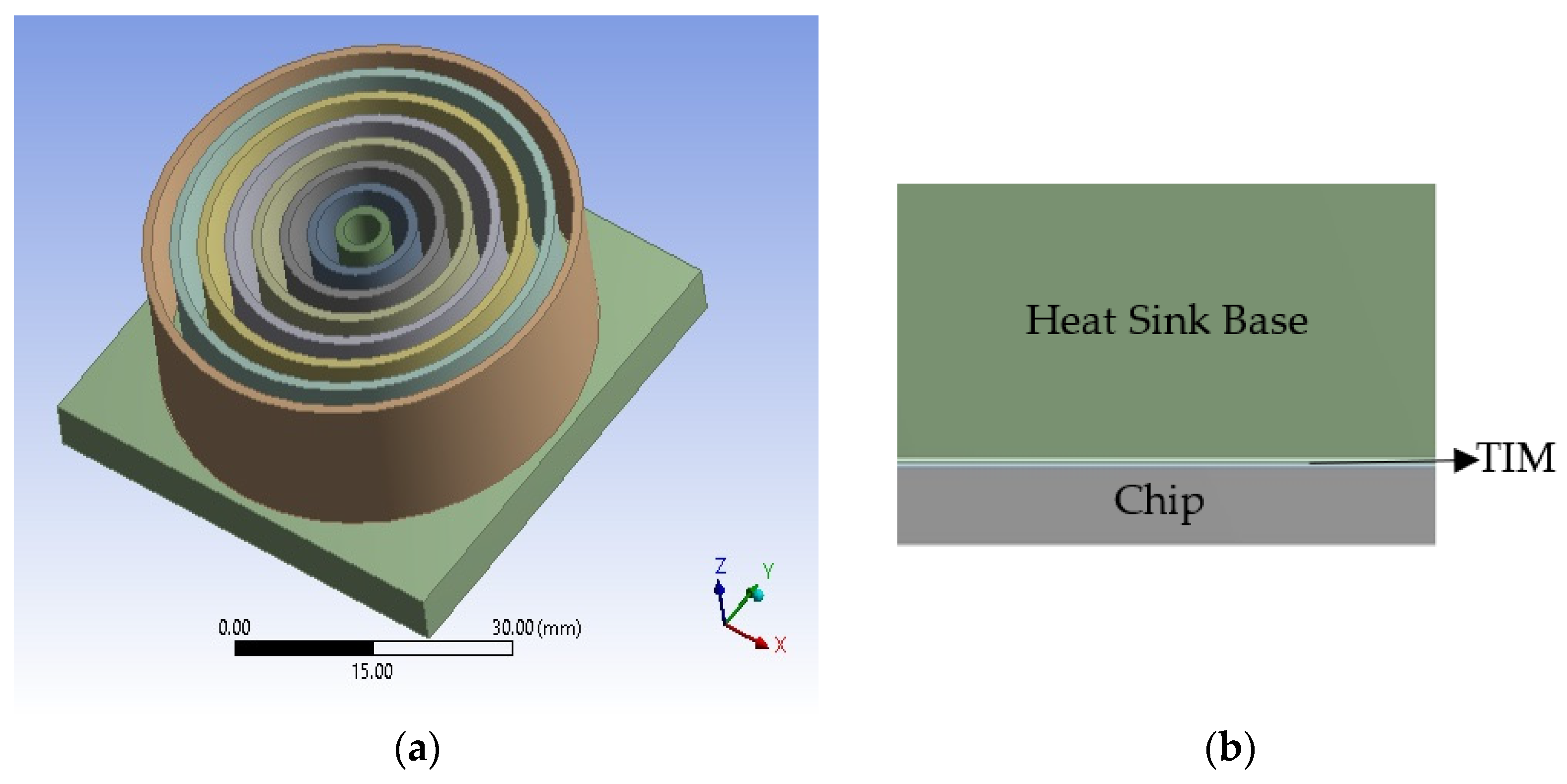
2.1. Description of Model
2.2. Materials
2.3. Load and Boundary Conditions
Governing Equation
3. Results and Discussion
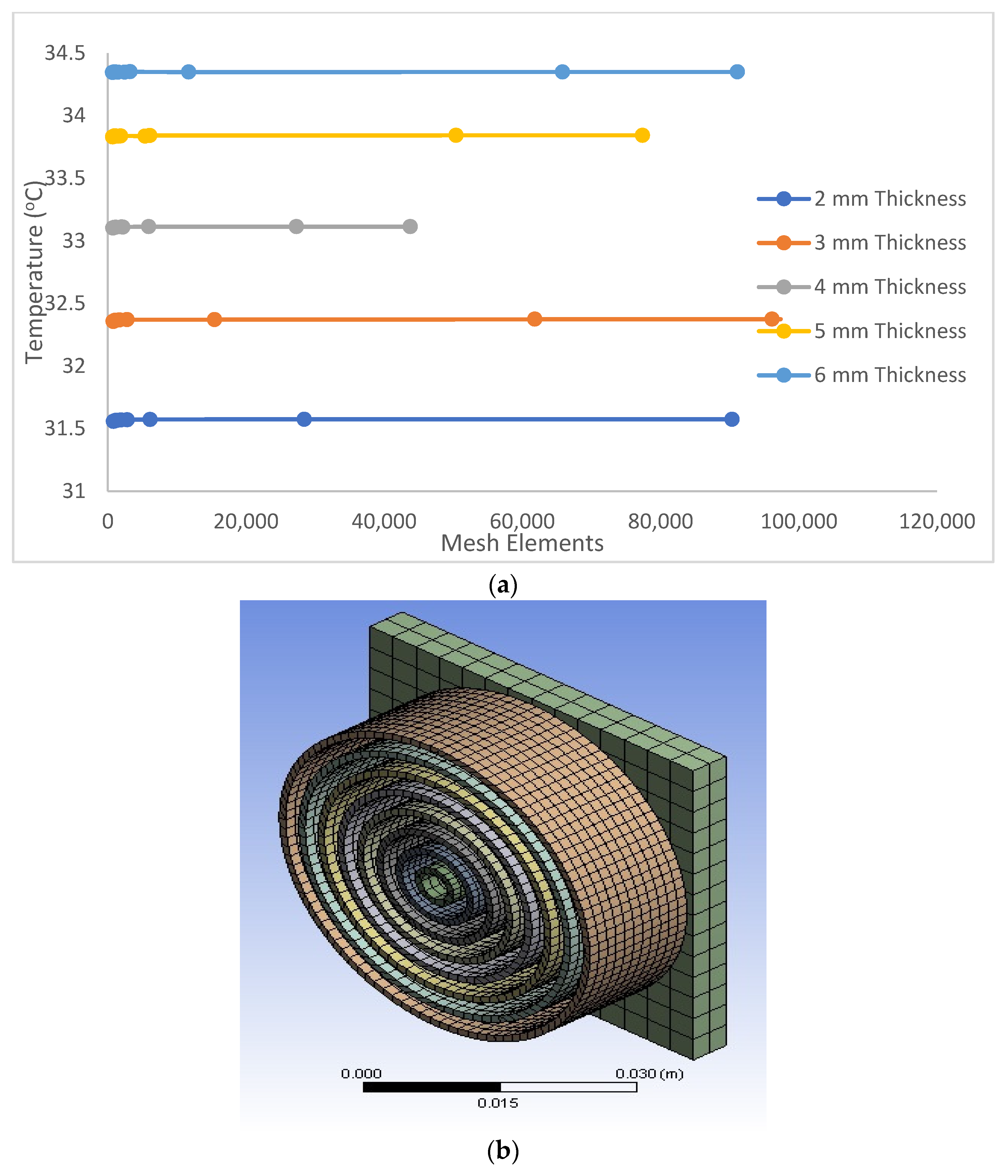
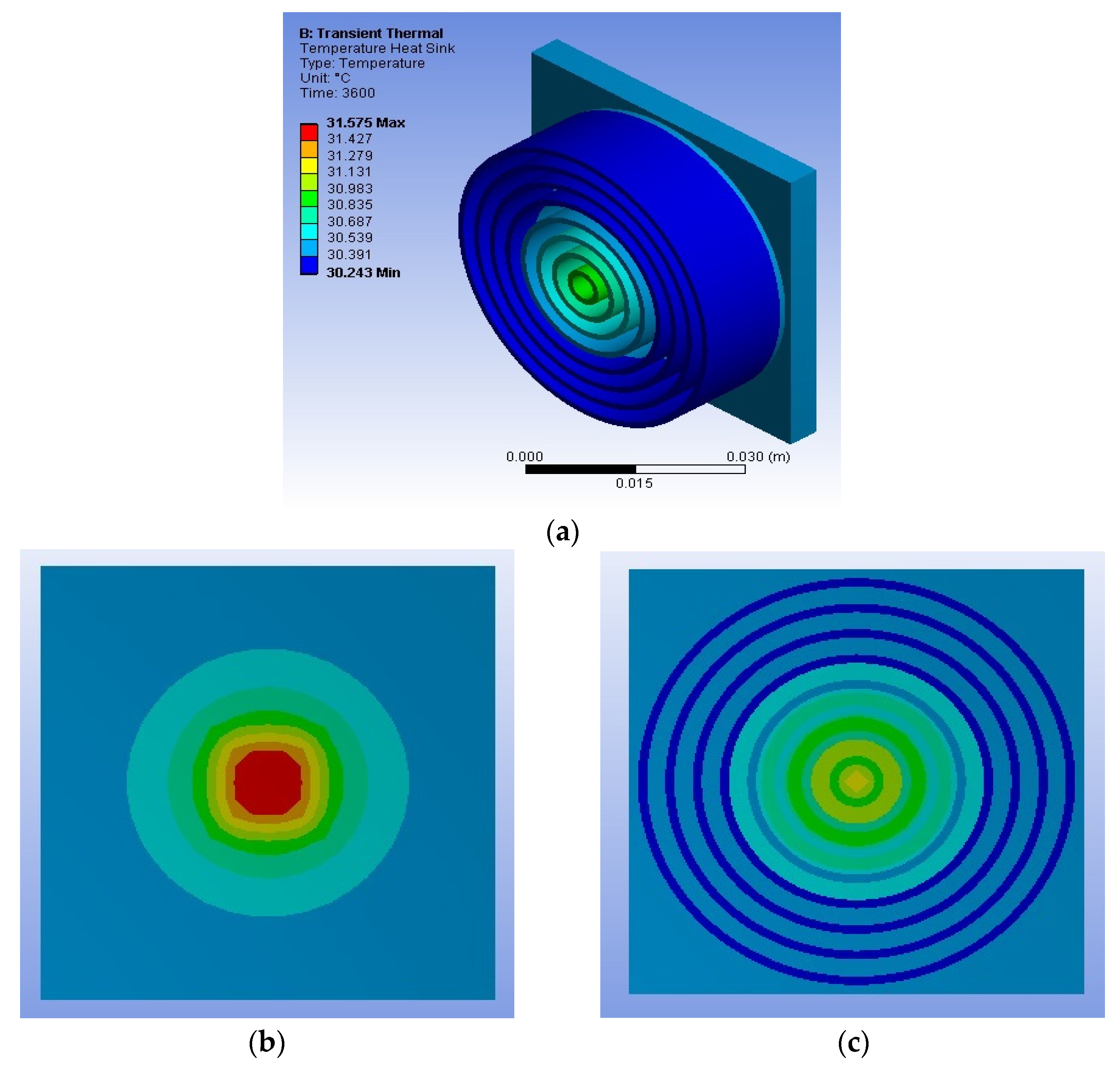
3.1. Mesh Dependency Study
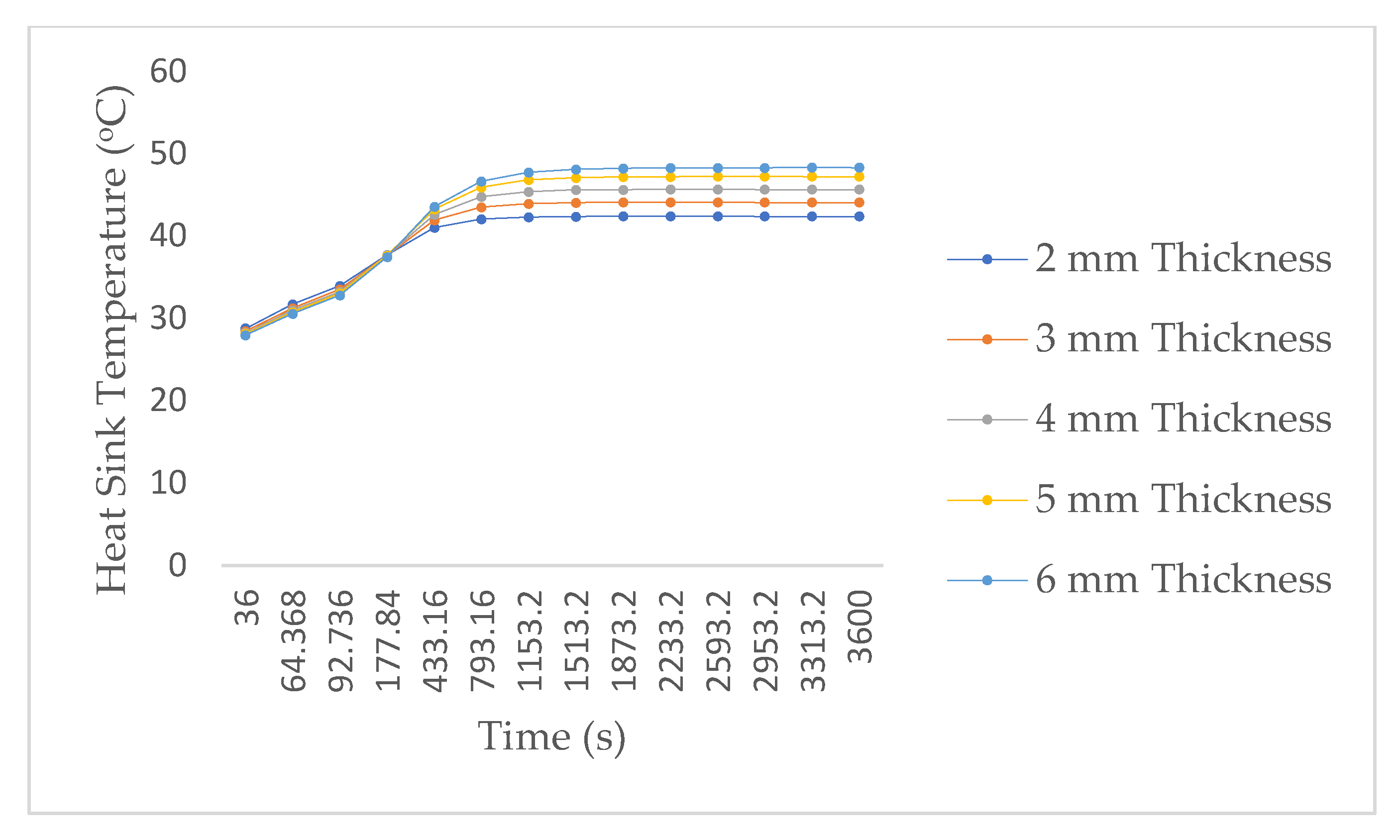
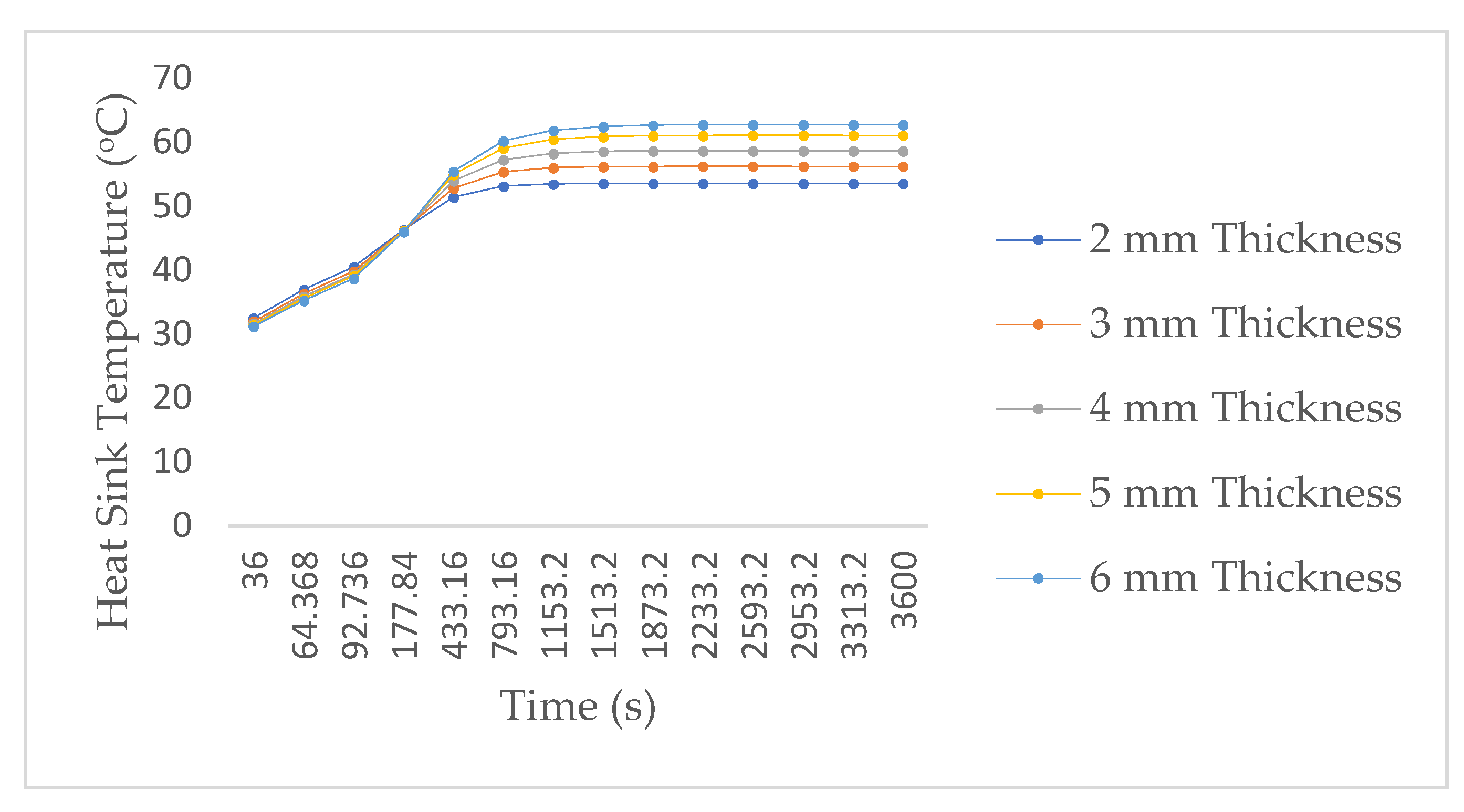
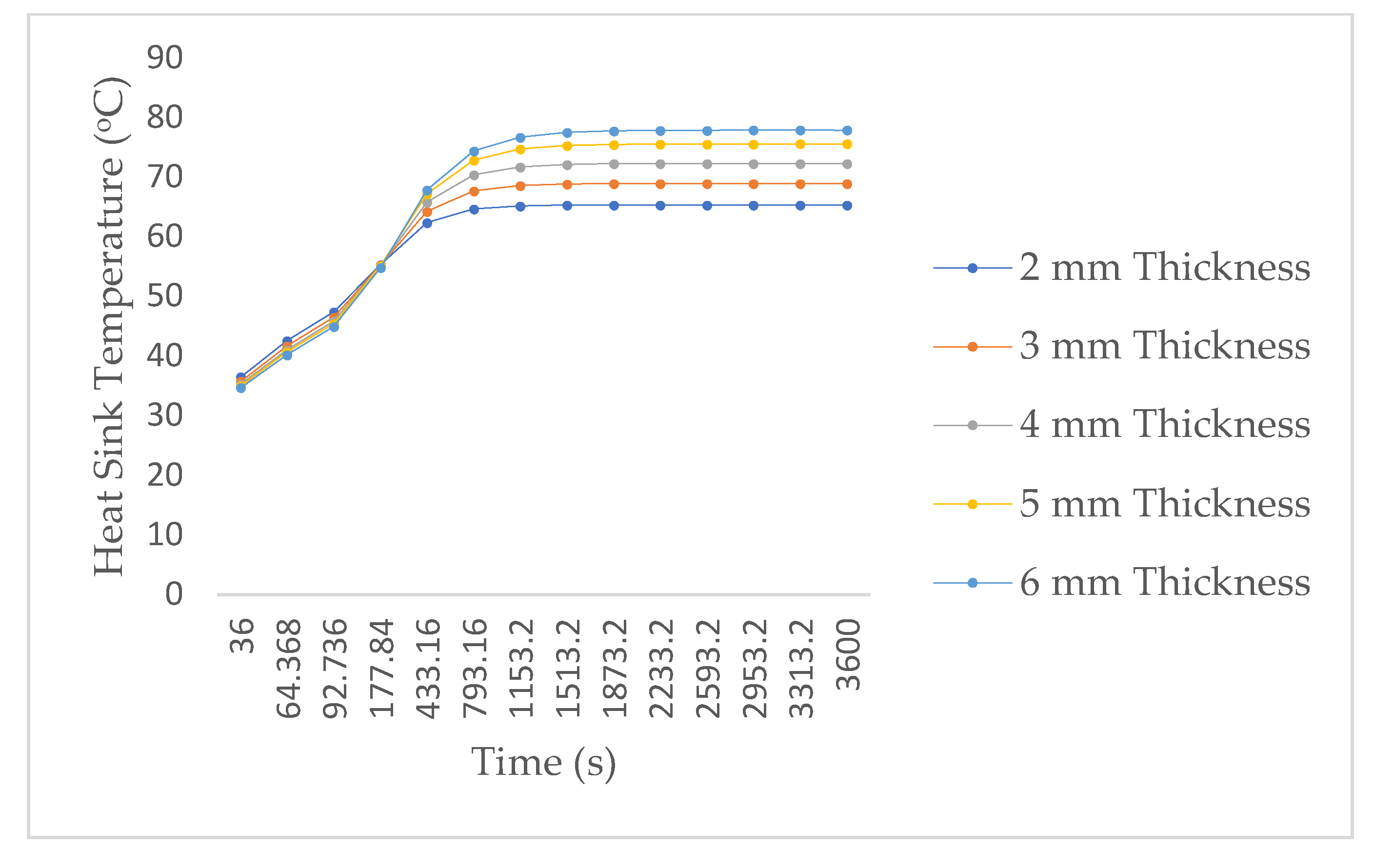
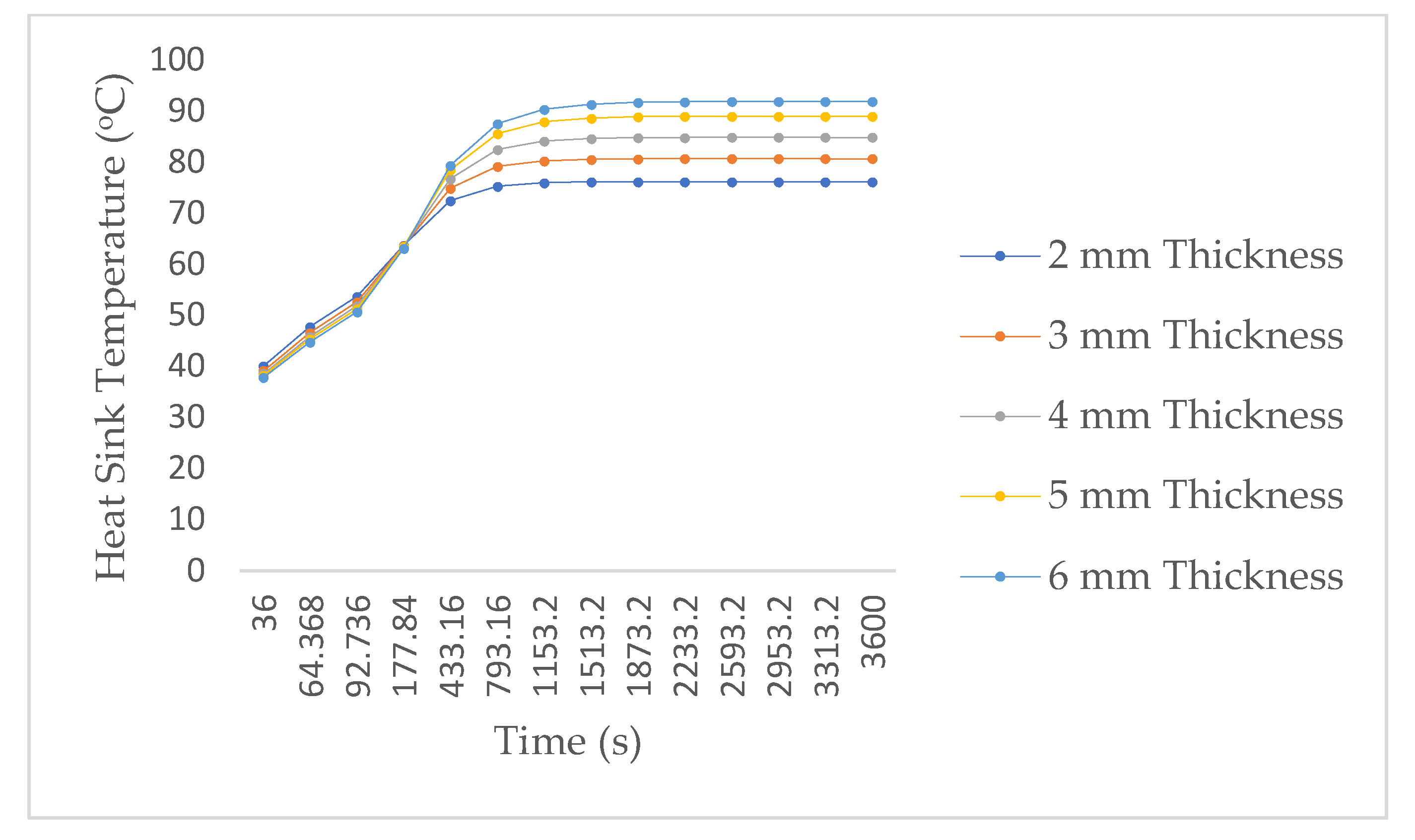
3.2. Effect of Power on Heat Sink Temperature
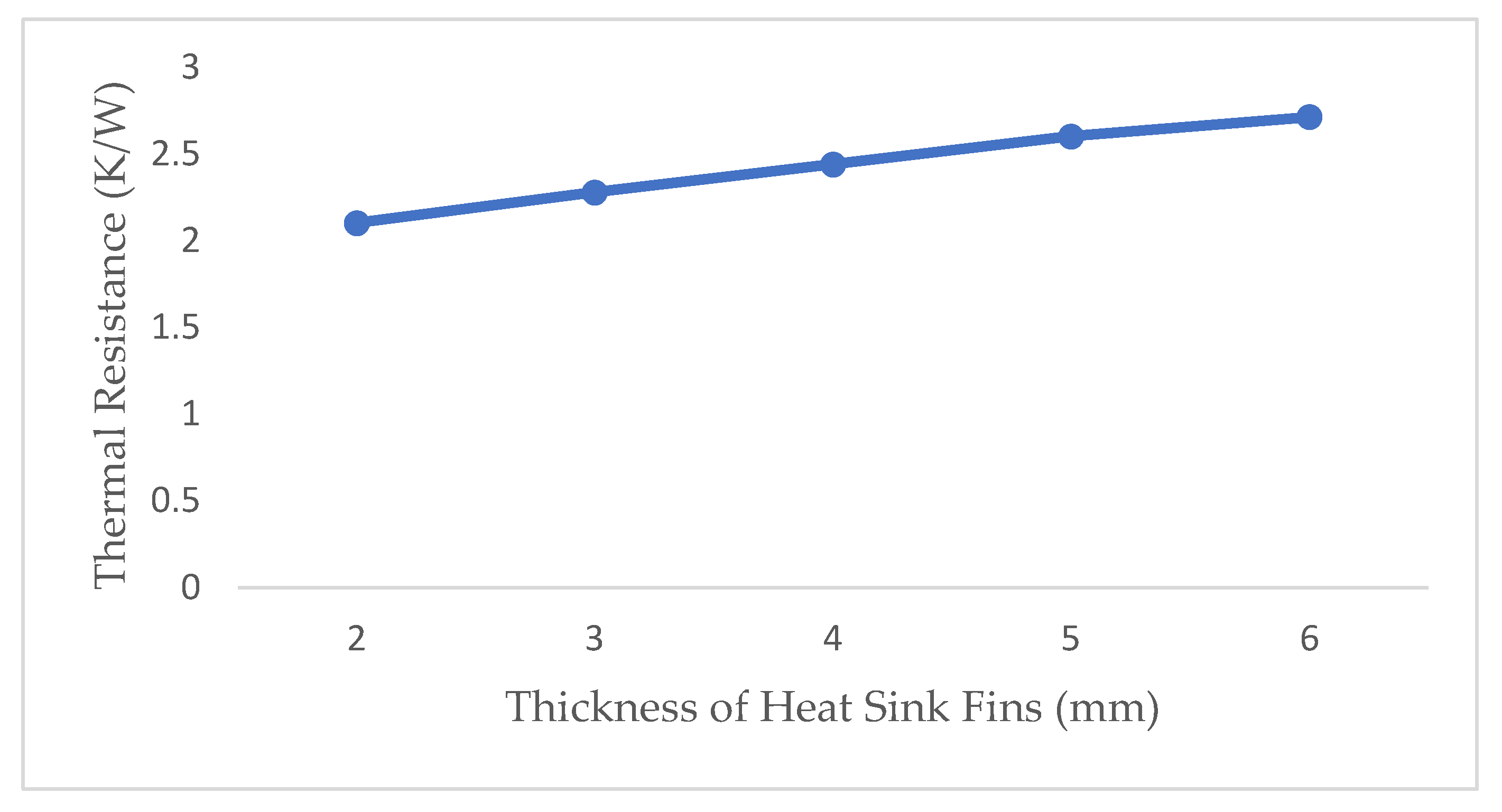
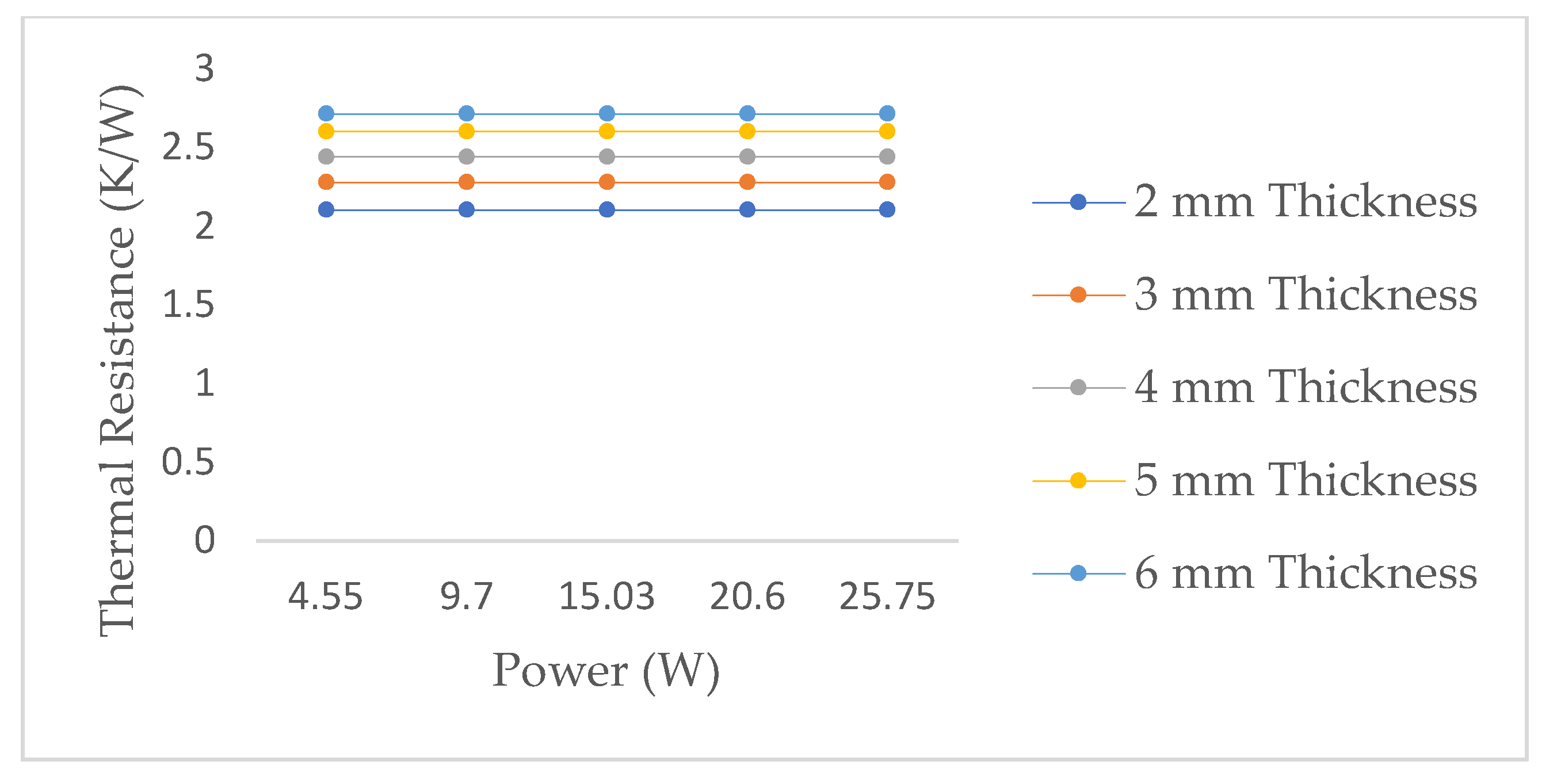
3.3. Effect of Thermal Resistance on the Cylindrical Heat Sink
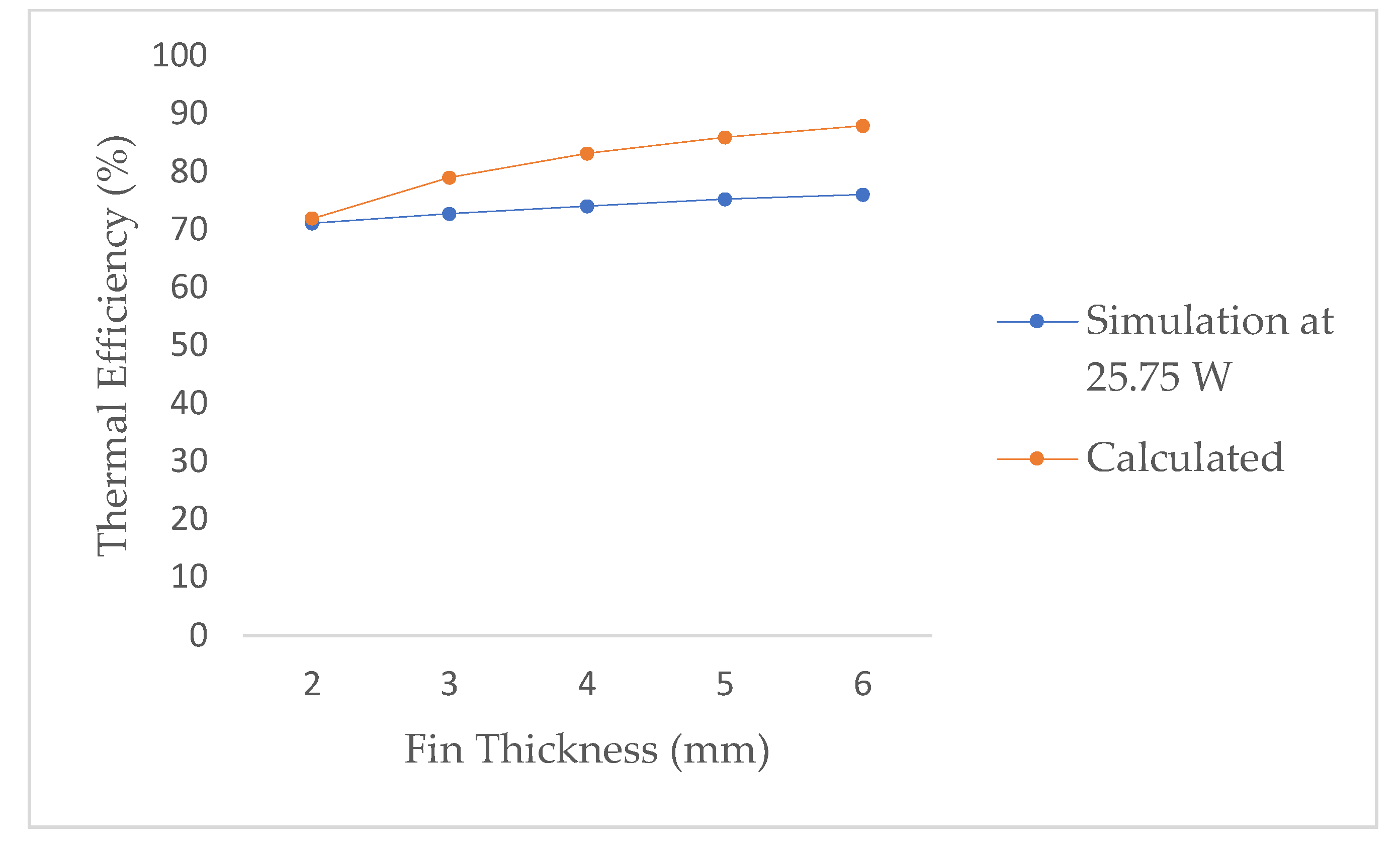
3.4. Thermal Efficiency Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Cp | constant pressure specific heat [J/(kg.°C)] |
| g | gravitational acceleration [m/s2] |
| hf | the convection coefficient |
| k | thermal conductivity [W/(m.°C)] |
| Lf | the height of fin [m] |
| M | mass [kg] |
| n | number of fins |
| p | pressure [Pa] |
| Q | heat flow/power [W] |
| R | thermal resistance [°C/W] |
| tf | the thickness of fin |
| T | temperature [°C] |
| T∞ | the ambient temperature |
| u, v, w | Cartesian velocity components [m/s] |
| x, y, z | Cartesian coordinates [m] |
| V | the volume [m3] |
| Greek symbols | |
| α | thermal diffusivity [m2/s] |
| β | coefficient of thermal expansion [1/K] |
| ρ | density [kg/m3] |
References
- Todorov, D.G.; Kapisazov, L.G. Led Thermal Management. Electronics 2008, 2008, 139–144. [Google Scholar]
- Buergel, E. Design of LEDS—Heat Management Challenge. Auto Tech. Rev. 2012, 1, 40–43. [Google Scholar] [CrossRef]
- Costa, V.A.F.; Lopes, A.M.G. Improved Radial Heat Sink for LED Lamp Cooling. Appl. Therm. Eng. 2014, 70, 131–138. [Google Scholar] [CrossRef]
- Ekpu, M.; Bhatti, R.; Okereke, M.I.; Mallik, S.; Otiaba, K.C. Prediction and Optimization of Design Parameters of Microelec- tronic Heat Sinks. J. Emerg. Trends Eng. Appl. Sci. 2013, 4, 493–500. [Google Scholar]
- Barbosa, J.; Simon, D.; Calixto, W. Design Optimization of a High Power LED Matrix Luminaire. Energies 2017, 10, 639. [Google Scholar] [CrossRef]
- Tang, Y.; Lin, L.; Zhang, S.; Zeng, J.; Tang, K.; Chen, G.; Yuan, W. Thermal Management of High-power LEDs based on Integrated Heat Sink with Vapor Chamber. Energy Convers. Manag. 2017, 151, 1–10. [Google Scholar] [CrossRef]
- Sobamowo, M.G.; Alaribe, K.C.; Adeleye, A.O. A Study on the Impact of Lorentz Force on the Thermal Behaviour of a Convective-Radiative Porous Fin using Differential Transformation Method. Int. J. Mech. Dyn. Anal. 2020, 6, 45–59. [Google Scholar]
- Ekpu, M. Effect of Fins Arrangement on Thermal Performance in Microelectronics Devices. J. Appl. Sci. Environ. Manag. 2018, 22, 1797–1800. [Google Scholar] [CrossRef]
- Staliulionis, Z.; Zhang, Z.; Pittini, R.; Andersen, M.A.E.; Tarvydas, P.; Noreika, A. Investigation of Heat Sink Efficiency for Electronic Component Cooling Applications. Elektron. IR Elektrotechnika 2014, 20, 49–54. [Google Scholar] [CrossRef]
- Ashad, M.; Karamti, H.; Awrejcewicz, J.; Grzelczyk, D.; Galal, A.M. Thermal Transmission Comparison of Nano-fluids over Stretching Surface under the Influence of Magnetic Field. Micromachines 2022, 13, 1296. [Google Scholar] [CrossRef]
- Ranjith, P.; Manimaran, A.; Praveen, A.S.; Ramesh, T. Experimental investigation of heat transfer characteristics of LED module using passive heat sinks. Int. J. Ambient. Energy 2018, 41, 1209–1213. [Google Scholar] [CrossRef]
- Mjallal, I.; Farhat, H.; Hammoud, M.; Ali, S.; Assi, I. Improving the Cooling Efficiency of Heat Sinks through the use of Different Types of Phase Change Materials. Technologies 2018, 6, 5. [Google Scholar] [CrossRef]
- Salah, S.B.; Hamida, M.B.B. Alternate PCM with air cavities in LED heat sink for transient thermal management. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4377–4393. [Google Scholar] [CrossRef]
- Chu, L.; Chang, W.; Huang, T.H. A Novel Heat Sink Design and Prototyping for LED Desk Lamps. Math. Probl. Eng. 2015, 1, 1–8. [Google Scholar] [CrossRef]
- Wengang, H.; Lulu, W.; Zongmin, Z.; Yanhua, L.; Mingxin, L. Research on simulation and experimental of thermal performance of LED array heat sink. Procedia Eng. 2017, 205, 2084–2091. [Google Scholar] [CrossRef]
- Jamil, M.A.; Goraya, T.S.; Rehman, A.U.; Yaqoob, H.; Ikhlaq, M.; Shahzad, M.W.; Zubair, S.M. A comprehensive design and optimization of an offset strip-fin compact heat exchanger for energy recovery systems. Energy Convers. Manag. X 2022, 14, 100191. [Google Scholar]
- Jamil, M.A.; Din, Z.U.; Goraya, T.S.; Yaqoob, H.; Zubair, S.M. Thermal-hydraulic characteristics of gasketed plate heat exchangers as a preheater for thermal desalination systems. Energy Convers. Manag. 2020, 205, 112425. [Google Scholar] [CrossRef]
- Ekpu, M.; Bhatti, R.; Okereke, M.I.; Mallik, S.; Otiaba, K. Fatigue life of lead-free solder thermal interface materials at varying bond line thickness in microelectronics. Microelectron. Reliab. 2014, 54, 239–244. [Google Scholar] [CrossRef]
- Ekpu, M.; Bhatti, R.; Okereke, M.I.; Mallik, S.; Otiaba, K. The effect of thermal constriction on heat management in a microelectronic application. Microelectron. J. 2014, 45, 159–166. [Google Scholar] [CrossRef]
- Ekpu, M. Finite Element Analysis of the Effect of Fin Geometry on Thermal Performance of Heat Sinks in Microelectronics. J. Appl. Sci. Environ. Manag. 2019, 23, 2059–2063. [Google Scholar] [CrossRef]
- Okereke, M.I.; Ling, Y. A computational investigation of the effect of three-dimensional void morphology on the thermal resistance of solder thermal interface materials. Appl. Therm. Eng. 2018, 142, 346–360. [Google Scholar] [CrossRef]
- Jeong, J.; Hah, S.; Kim, D.; Lee, J.H.; Kim, S. Thermal analysis of cylindrical heat sinks filled with phase change material for high-power transient cooling. Int. J. Heat Mass Transf. 2020, 154, 119725. [Google Scholar] [CrossRef]
- Incropera, F.P.; Dewitt, D.P. Introduction to Heat Transfer, 3rd ed.; John Wiley and Sons: New York, NY, USA, 1996; pp. 1–801. [Google Scholar]
- Wakefield-Vette. Heat Sink Design Facts and Guidelines for Thermal Analysis. Available online: https://www.digikey.com/en/pdf/w/wakefield-thermal-solutions/heat-sink-design-for-thermal-analysis (accessed on 15 February 2022).


| Material | Density (kg/m3) | Thermal Conductivity (W/mK) | Specific Heat (J/kgK) |
|---|---|---|---|
| Aluminium | 2689 | 237.5 | 951 |
| Silicon | 2330 | 148 | 712 |
| SAC 405 | 7440 | 62 | 236 |
| Heat Sink Fin Thickness (mm) | Number of Fins | Density (kg/m3) | Volume of Heat Sink (mm3) | Mass of Heat Sink (g) |
|---|---|---|---|---|
| 2 | 8 | 2689 | 22,301.69 | 59.97 |
| 3 | 7 | 2689 | 25,117.48 | 67.54 |
| 4 | 6 | 2689 | 27,202.69 | 73.15 |
| 5 | 5 | 2689 | 28,698.9 | 77.17 |
| 6 | 5 | 2689 | 30,171.46 | 81.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ekpu, M.; Ogbodo, E.A.; Ngobigha, F.; Njoku, J.E. Thermal Effect of Cylindrical Heat Sink on Heat Management in LED Applications. Energies 2022, 15, 7583. https://doi.org/10.3390/en15207583
Ekpu M, Ogbodo EA, Ngobigha F, Njoku JE. Thermal Effect of Cylindrical Heat Sink on Heat Management in LED Applications. Energies. 2022; 15(20):7583. https://doi.org/10.3390/en15207583
Chicago/Turabian StyleEkpu, Mathias, Eugene A. Ogbodo, Felix Ngobigha, and Jude E. Njoku. 2022. "Thermal Effect of Cylindrical Heat Sink on Heat Management in LED Applications" Energies 15, no. 20: 7583. https://doi.org/10.3390/en15207583
APA StyleEkpu, M., Ogbodo, E. A., Ngobigha, F., & Njoku, J. E. (2022). Thermal Effect of Cylindrical Heat Sink on Heat Management in LED Applications. Energies, 15(20), 7583. https://doi.org/10.3390/en15207583







