Analysis of Surface Texturing of Silicon with Surface Regular Microstructure Using C Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Method C
2.2. MATLAB Programming
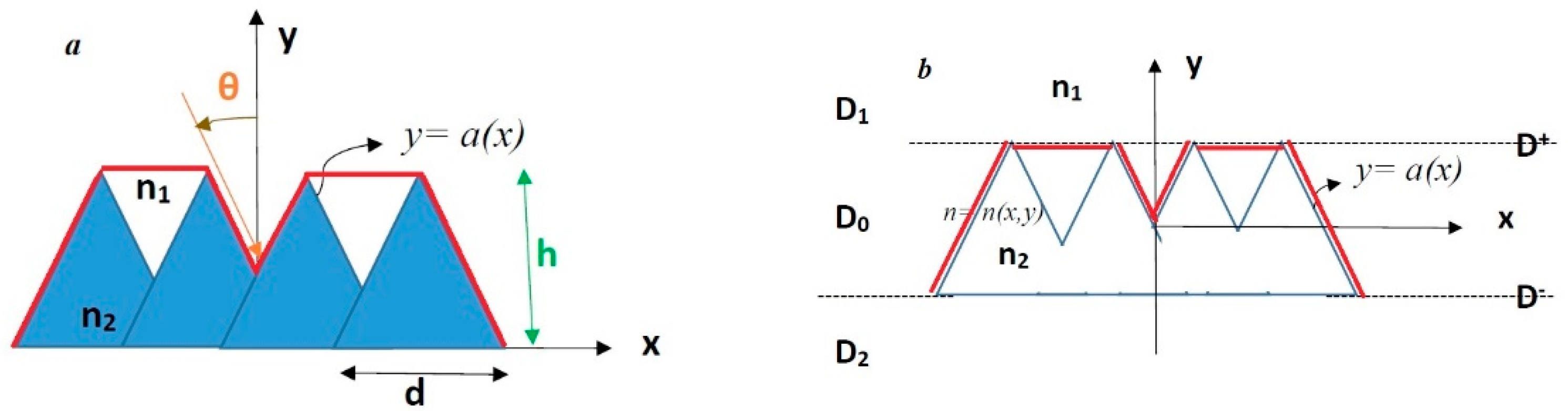
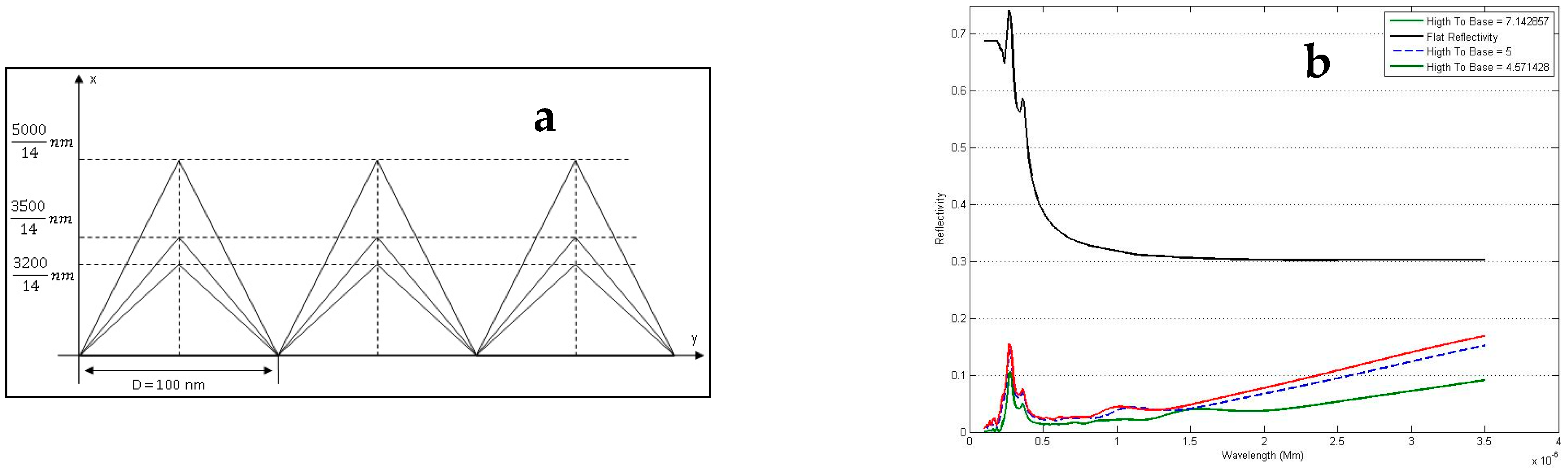
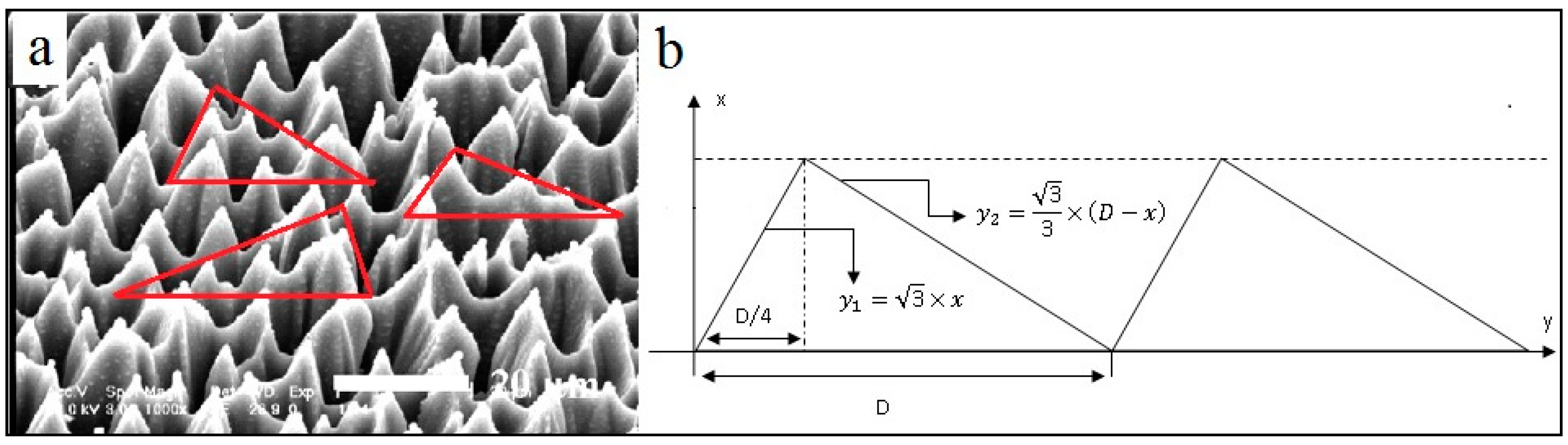
2.3. Simulation of Periodic Microstructures
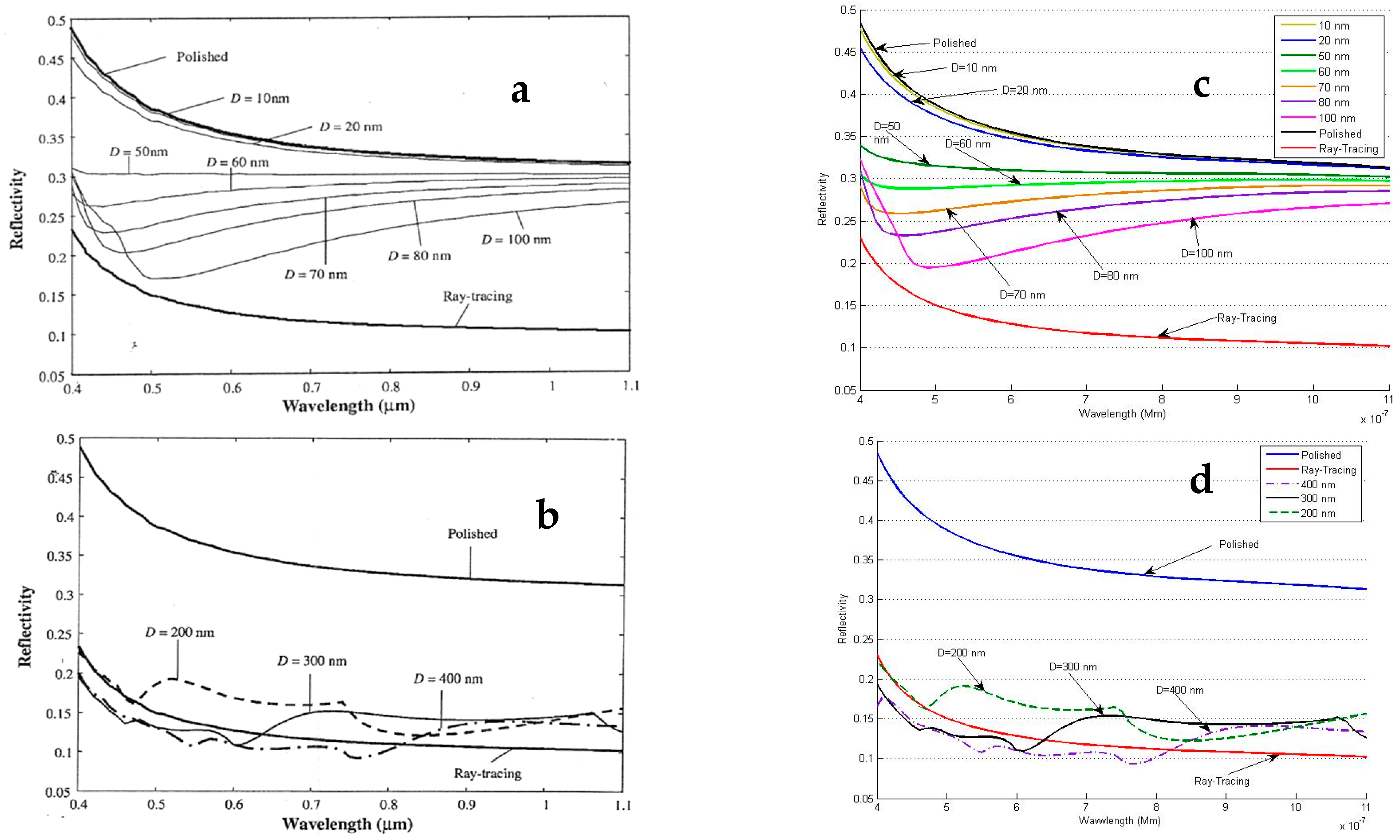
3. Results and Discussion
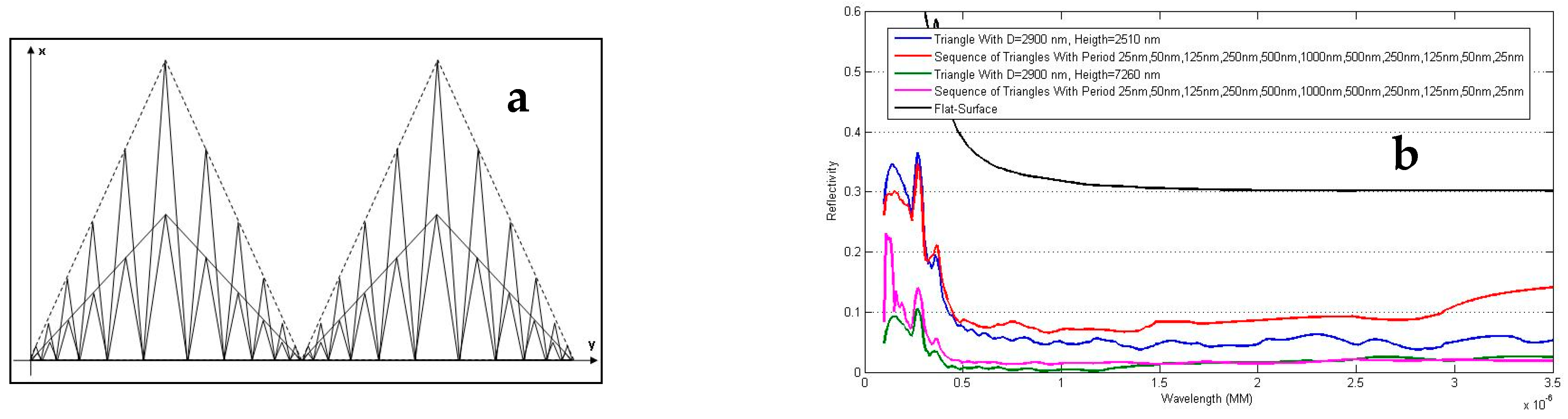
3.1. Triangular Model
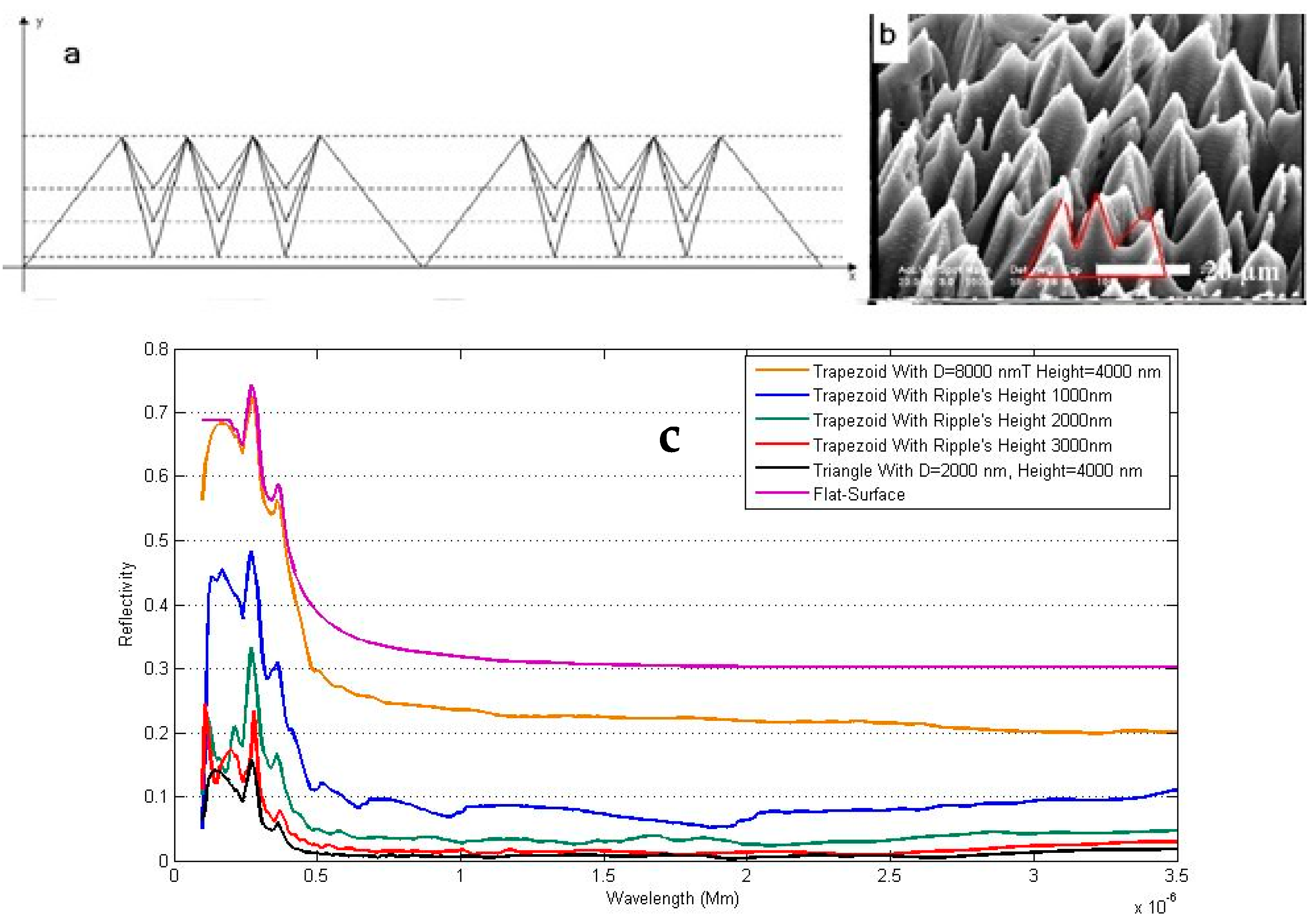
3.2. Trapezoid Model
3.3. Hybrid Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, V.; Verma, R.; Kango, S.; Sharma, V. Recent progresses and applications in Laser-based surface texturing. Systems. Mater. Today Commun. 2021, 26, 101736. [Google Scholar] [CrossRef]
- Wang, Z.; Song, J.; Wang, T.; Wang, H.; Wang, Q. Laser Texturing for Superwetting Titanium Alloy and Investigation of Its Erosion Resistance. Coatings 2021, 11, 1547. [Google Scholar] [CrossRef]
- Mao, B.; Siddaiah, A.; Liao, Y.; Menezes, P.L. Laser surface texturing and related techniques for enhancing tribological performance of engineering materials: A review. J. Manuf. Process. 2020, 53, 153–173. [Google Scholar] [CrossRef]
- Yaddadenea, C.; Djemaaa, A.; Belaroussib, Y.; Kerdjab, T.; Gabouzea, N.; Keffousa, A.; Guerbousc, L. Optical properties of silicon microcolumn grown by nanosecond pulsed laser irradiation. Opt. Commun. 2011, 284, 3308–3310. [Google Scholar] [CrossRef]
- Wu, C.; Crouch, C.H.; Zhao, L.; Carey, J.; Younkin, E.R.; Levinson, J.A.; Mazur, E.; Farrell, R.M.; Gothoskar, P.; Karger, A. Near-unity below-band-gap absorption by microstructured silicon. Appl. Phys. Lett. 2001, 78, 1850. [Google Scholar] [CrossRef]
- Lowndes, D.H.; Fowlkes, J.D.; Pedraza, A.J. Early stages of pulsed-laser growth of silicon microcolumns and microcones in air and SF6. Appl. Surf. Sci. 2000, 154–155, 647–658. [Google Scholar] [CrossRef][Green Version]
- Available online: http://www.mazur.harvard.edu/ (accessed on 2 September 2004).
- Her, T.H.; Finlay, R.J.; Wu, C.; Mazur, E. Femtosecond laser-induced formation of spikes on silicon. Appl. Phys. A 2000, 70, 383. [Google Scholar] [CrossRef]
- Bassam, M.A.; Parvin, P.; Sajad, B.; Moghimi, A.; Coster, H. Measurement of optical and electrical properties of silicon microstructuring induced by ArF excimer laser at SF6 atmosphere. Appl. Surf. Sci. 2008, 254, 2621–2628. [Google Scholar] [CrossRef]
- Dehghanpour, H.R.; Parvin, P.; Sajad, B.; Nour-Azar, S.S. Dose and pressure dependence of silicon microstructure in SF6 gas due to excimer laser irradiation. Appl. Surf. Sci. 2009, 255, 4664–4669. [Google Scholar] [CrossRef]
- Dehghanpour, H.R.; Parvin, P. Fluorine penetration into amorphous SiO2 glass at SF6 atmosphere using Q-switched Nd: YAG and excimer laser irradiations. Jpn. J. Appl. Phys. 2010, 49, 075803. [Google Scholar] [CrossRef]
- Dehghanpour, H.R.; Parvin, P. Glass surface modification using Nd: YAG laser in SF6 atmospheres. J. Theor. Appl. Phys. 2015, 9, 135–140. [Google Scholar] [CrossRef]
- Dehghanpour, H.R.; Parvin, P.; Abdolahi, S. Performance enhancement of solar panel by surface texturing using ArF excimer laser. Optik 2015, 126, 5496–5498. [Google Scholar] [CrossRef]
- Llopis, F.; Tobías, I. Influence of texture feature size on the optical performance of silicon solar cells. Prog. Photovol. 2005, 15, 27–36. [Google Scholar] [CrossRef]
- Refahizadeh, M.; Parvin, P.; Silakhori, K.; Mortazavi, S.Z.; Reyhani, A.; Abolhosseini, S.; Hojati Rad, H.; Majdabadi, A. Formation of ArF laser-induced self-assembled macrostructures on poly methyl methacrylate and CR-39 polymers. J. Laser Appl. 2017, 29, 022008. [Google Scholar] [CrossRef]
- Refahizadeh, M.; Parvin, P.; Silakhori, K.; Mortazavi, S.Z.; Mehdilo, A. Fabrication of self-ruled micro grating on CR-39 using ArF laser-induced rippling. Laser Phys. 2017, 27, 066101. [Google Scholar] [CrossRef]
- Refahizadeh, M.; Majdabadi, A.; Parvin, P.; Silakhori, K.; Mortazavi, S.Z.; Mehdilo, A.; Aghaii, P. Angular dependence of ArF laser induced self-aligning microstructures on CR39. Opt. Mater. Exp. 2015, 5, 1543–1549. [Google Scholar] [CrossRef]
- Parvin, P.; Refahizadeh, M.; Mortazavi, S.Z.; Silakhori, K.; Mahdiloo, A.; Aghaii, P. Regular self-microstructuring on CR39 using high UV laser dose. Appl. Surf. Sci. 2014, 292, 247–255. [Google Scholar] [CrossRef]
- Parvin, P.; Reyhani, A.; Mehrabi, M.; Refahizadeh, M.; Mortazavi, S.Z.; Ranjbar, A. Efficiency enhancement using ArF laser induced micro/nanostructures on the polymeric layer of solar cell. Opt. Laser Tech. 2017, 88, 242–249. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Reyhani, A.; Parvin, P.; Mortazavi, S.Z.; Mehrabi, M. Enhancement of Si solar cell efficiency using ZnO nanowires with various diameters. Mater. Res. Exp. 2018, 5, 015040. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Reyhani, A.; Parvin, P.; Mortazavi, S.Z. Efficiency enhancement of ZnO nanostructure assisted Si solar cell based on fill factor enlargement and UV-blue spectral down-shifting. J. Phys. D Appl. Phys. 2017, 50, 185501. [Google Scholar] [CrossRef]
- Smith, M.S.D. Application of the Differential Method to Diffraction Gratings That Utilize Total Internal Reflection Facets. Ph.D. Thesis, University of Manitoba, Winnipeg, MB, Canada, 1998. [Google Scholar]
- Bai, B.; Li, L. Improving the Fourier modal method for crossed gratings with C3 symmetry by using a group-theoretic approach. Proc. SPIE 2005, 5636, 1–11. [Google Scholar]
- Vincent, P. A finite-difference method for dielectric and conducting crossed gratings. Opt. Commun. 1978, 26, 293–296. [Google Scholar] [CrossRef]
- Maystre, D.; Nevière, M. Electromagnetic theory of crossed gratings. J. Opt. 1978, 9, 301–306. [Google Scholar] [CrossRef]
- Han, S.T.; Tsao, Y.L.; Walser, R.M.; Becker, M.F. Electromagnetic scattering of two-dimensional surfacerelief dielectric gratings. Appl. Opt. 1992, 31, 2343–2352. [Google Scholar] [CrossRef]
- Dobson, D.C.; Cox, J.A. An integral equation method for biperiodic diffraction structures. In International Conference on the Application and Theory of Periodic Structures; Lerner, J.M., McKinney, M.R., Eds.; 1991; Volume 1545, pp. 106–113. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-SPIE/1545.toc (accessed on 10 September 2022).
- Derrick, G.H.; McPhedran, R.C.; Maystre, D.; Nevière, M. Crossed gratings: A theory and its applications. Appl. Phys. 1979, 18, 39–52. [Google Scholar] [CrossRef]
- McPhedran, R.C.; Derrick, G.H.; Nevière, M.; Maystre, D. Metallic crossed gratings. J. Opt. 1982, 13, 209–218. [Google Scholar] [CrossRef]
- Harris, J.B.; Preist, T.W.; Sambles, J.R.; Thorpe, R.N.; Watts, R.A. Optical response of bigratings. J. Opt. Soc. Am. A 1996, 13, 2041–2049. [Google Scholar] [CrossRef]
- Granet, G. Analysis of diffraction by surface-relief crossed gratings with use of the Chandezon method: Application to multilayer crossed gratings. J. Opt. Soc. Am. A 1998, 15, 1121–1131. [Google Scholar]
- Bräuer, R.; Bryngdahl, O. Electromagnetic diffraction analysis of two-dimensional gratings. Opt. Commun. 1993, 100, 1–5. [Google Scholar] [CrossRef]
- Noponen, E.; Turunen, J. Eigenmode method for electromagnetic synthesis of diffractive elements with threedimensional profiles. J. Opt. Soc. Am. A 1994, 11, 2494–2502. [Google Scholar]
- Li, L. New formulation of the Fourier modal method for crossed surface-relief gratings. J. Opt. Soc. Am. A 1997, 14, 2758–2767. [Google Scholar] [CrossRef]
- Greffet, J.J.; Baylard, C.; Versaevel, P. Diffraction of electromagnetic waves by crossed gratings: A series solution. Opt. Lett. 1992, 17, 1740–1742. [Google Scholar] [CrossRef] [PubMed]
- Bagnoud, V.; Mainguy, S. Diffraction of electromagnetic waves by dielectric crossed gratings: A three-dimensional Rayleigh-Fourier solution. J. Opt. Soc. Am. A 1999, 16, 1277–1285. [Google Scholar] [CrossRef]
- Bruno, O.P.; Reitich, F. Numerical solution of diffraction problems: A method of variation of boundaries. III. Doubly periodic gratings. J. Opt. Soc. Am. A 1993, 10, 2551–2562. [Google Scholar] [CrossRef]
- Bruno, O.P.; Reitich, F. Calculation of electromagnetic scattering via boundary variations and analytic continuation. Appl. Computat. Electromagn. Soc. J. 1996, 11, 17–31. [Google Scholar]
- Li, L.; Chandezon, J.; Granet, G.; Plumey, J.P. Rigorous and efficient grating-analysis method made easy for optical engineers. Appl. Opt. 1999, 38, 304–313. [Google Scholar] [CrossRef]
- Chandezon, J.; Maystre, D.; Raoult, G. A new theoretical method for diffraction gratings and its numerical application. J. Opt. 1980, 11, 235–241. [Google Scholar] [CrossRef]
- Chandezon, J.; Dupuis, M.T.; Cornet, G.; Maystre, D. Multicoated gratings: A differential formalism applicable in the entire optical region. J. Opt. Soc. Am. 1982, 72, 839–846. [Google Scholar] [CrossRef]
- Liu, H. Coordinate transformation method for modeling three-dimensional photonic structures with curved boundaries. Opt. Exp. 2021, 29, 1516–1531. [Google Scholar] [CrossRef]
- Ming, X.; Sun, L. Simple reformulation of the coordinate transformation method for gratings with a vertical facet or overhanging profile. Appl. Opt. 2021, 60, 4305–4314. [Google Scholar] [CrossRef]
- Yue, L.; Cheng, D.; Qiao, Y.; Zhao, J. Error Calibration for Full Tensor Magnetic Gradiometer Probe Based on Coordinate Transformation Method. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar] [CrossRef]
- Petit, R. (Ed.) Electromagnetic Theory of Gratings; Springer-Verlag: Berlin-Heidelberg, Germany; New York, NY, USA, 1980. [Google Scholar]
- Popov, E. Gratings: Theory and Numeric Application; Institut Fresnel: Marseille, France, 2014. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dehghanpour, H.R.; Parvin, P.; Mortazavi, S.Z.; Reyhani, A.; Chegenizadeh, A.; Aghaei, M. Analysis of Surface Texturing of Silicon with Surface Regular Microstructure Using C Method. Energies 2022, 15, 7540. https://doi.org/10.3390/en15207540
Dehghanpour HR, Parvin P, Mortazavi SZ, Reyhani A, Chegenizadeh A, Aghaei M. Analysis of Surface Texturing of Silicon with Surface Regular Microstructure Using C Method. Energies. 2022; 15(20):7540. https://doi.org/10.3390/en15207540
Chicago/Turabian StyleDehghanpour, Hamid Reza, Parviz Parvin, Seyedeh Zahra Mortazavi, Ali Reyhani, Amin Chegenizadeh, and Mohammadreza Aghaei. 2022. "Analysis of Surface Texturing of Silicon with Surface Regular Microstructure Using C Method" Energies 15, no. 20: 7540. https://doi.org/10.3390/en15207540
APA StyleDehghanpour, H. R., Parvin, P., Mortazavi, S. Z., Reyhani, A., Chegenizadeh, A., & Aghaei, M. (2022). Analysis of Surface Texturing of Silicon with Surface Regular Microstructure Using C Method. Energies, 15(20), 7540. https://doi.org/10.3390/en15207540









