Tensor-Based Harmonic Analysis of Distribution Systems
Abstract
1. Introduction
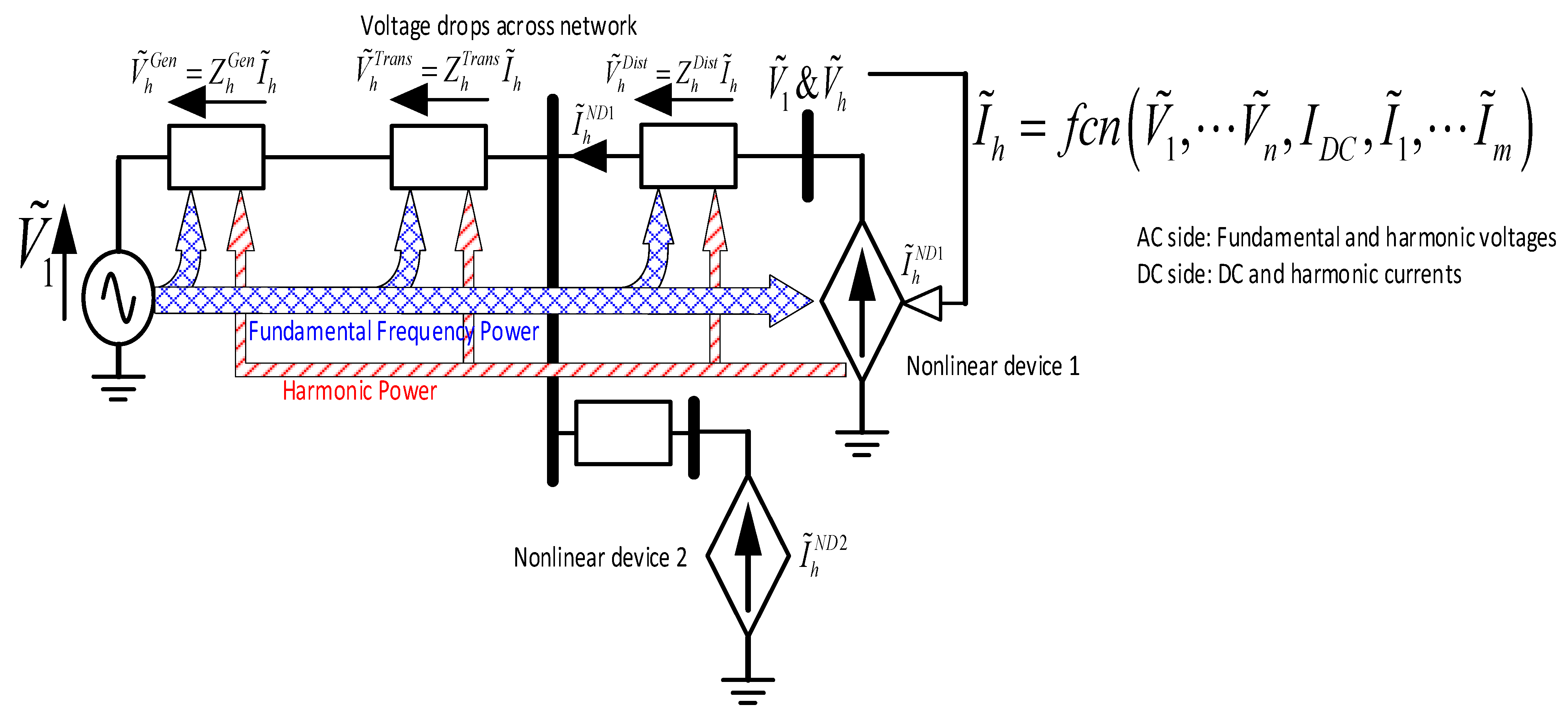
2. Phase Dependency and Harmonic Interaction
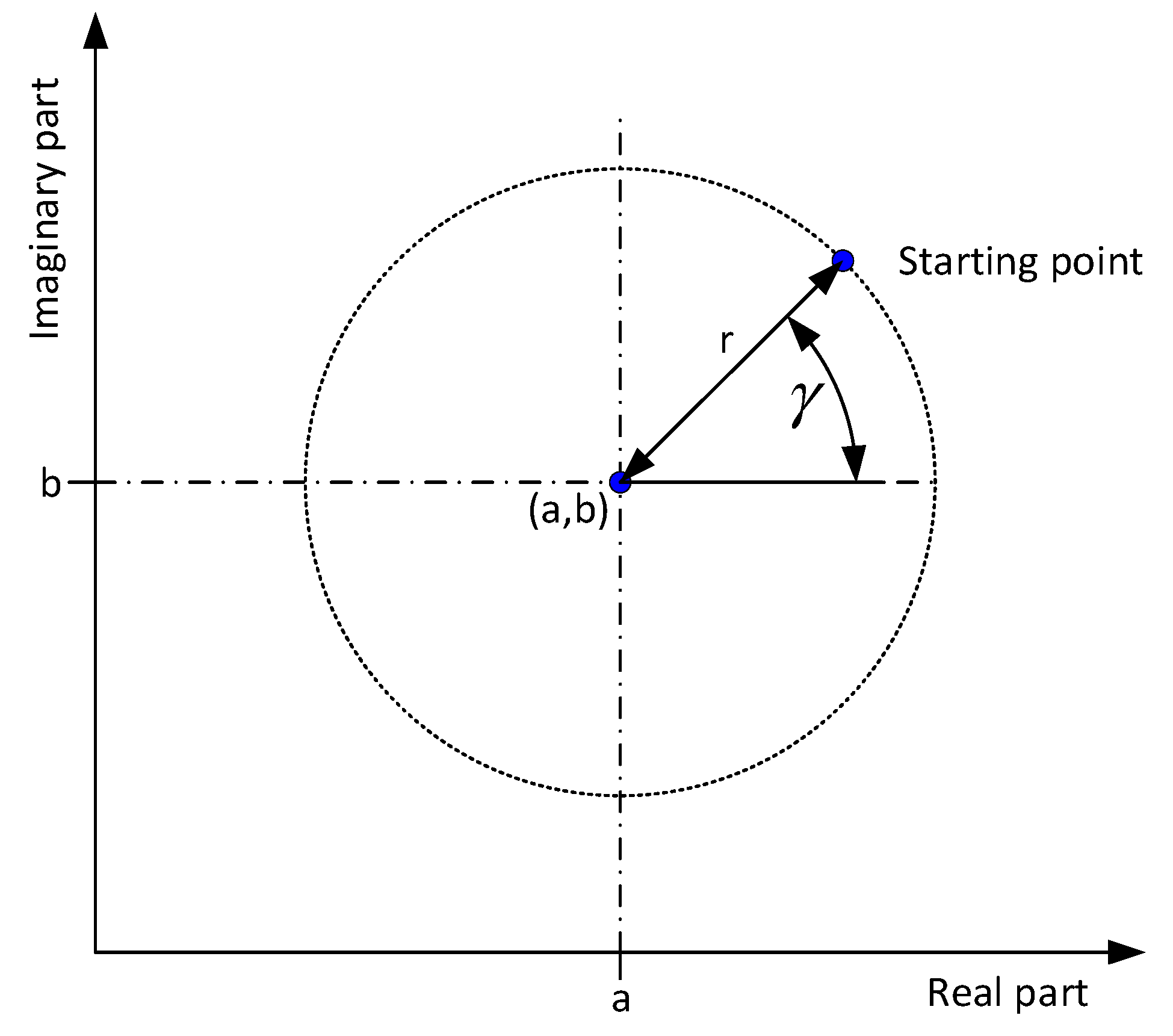
3. Tensor-based Harmonic Analysis Formulation
4. Numerical Experiment
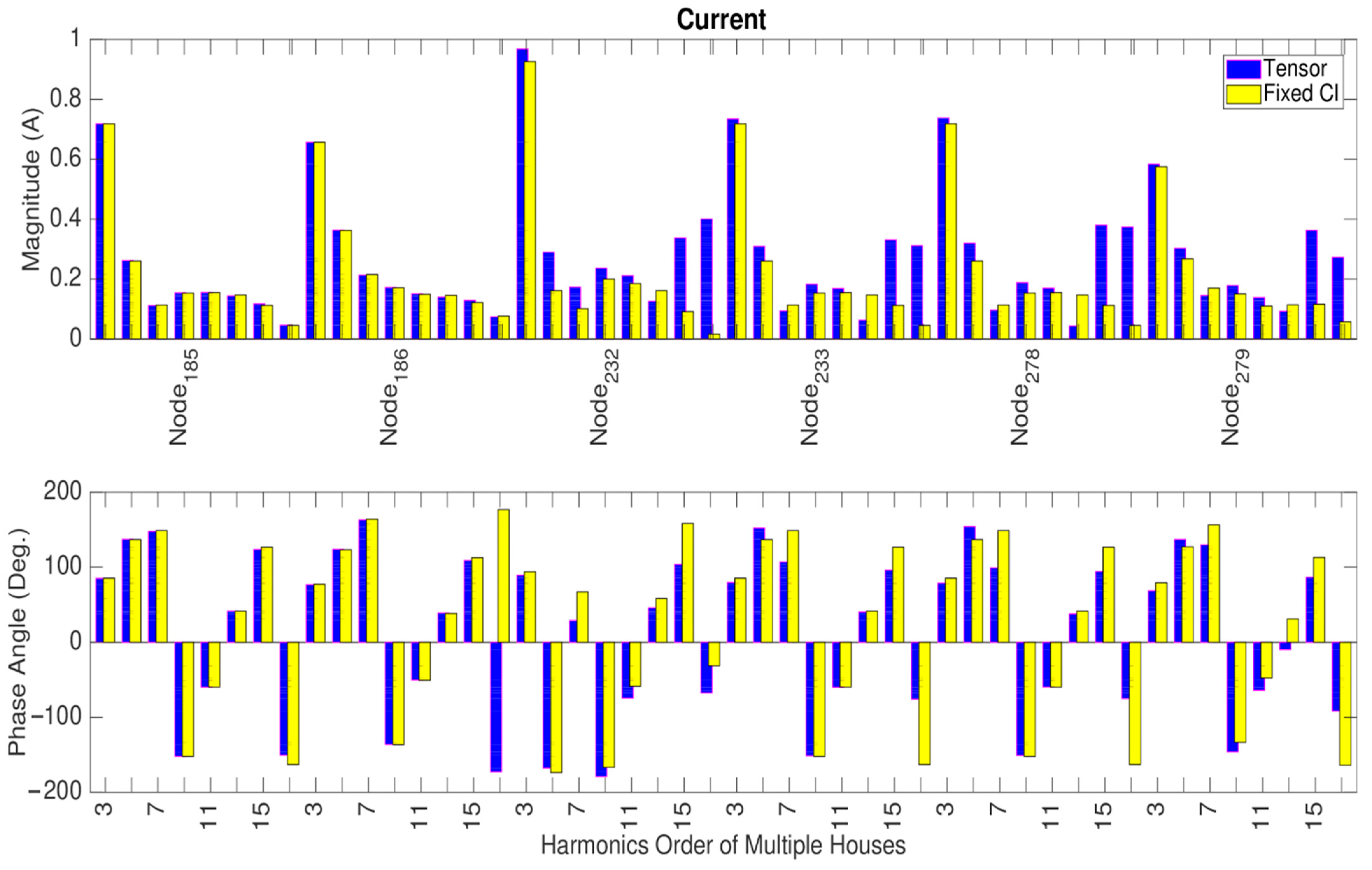
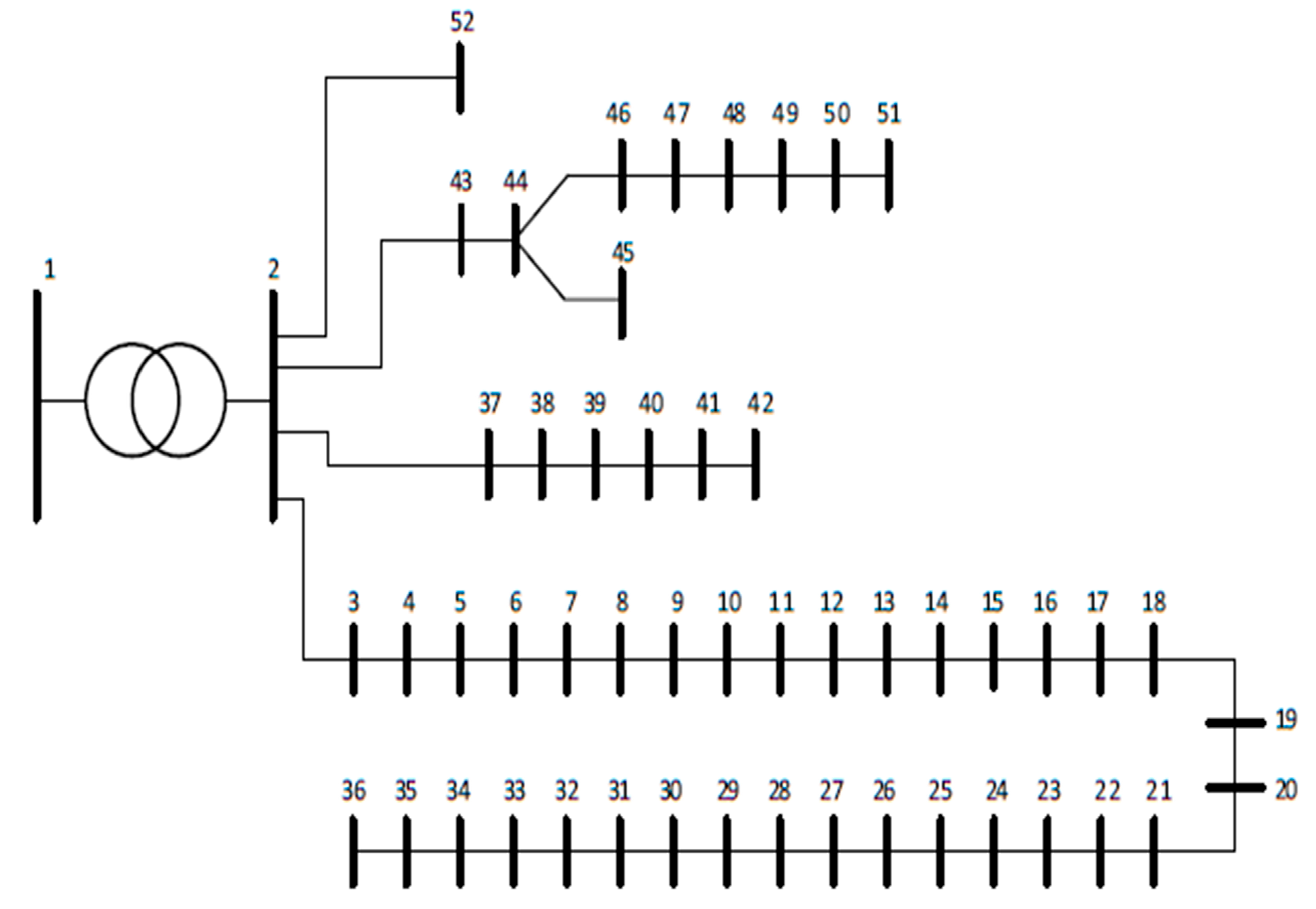
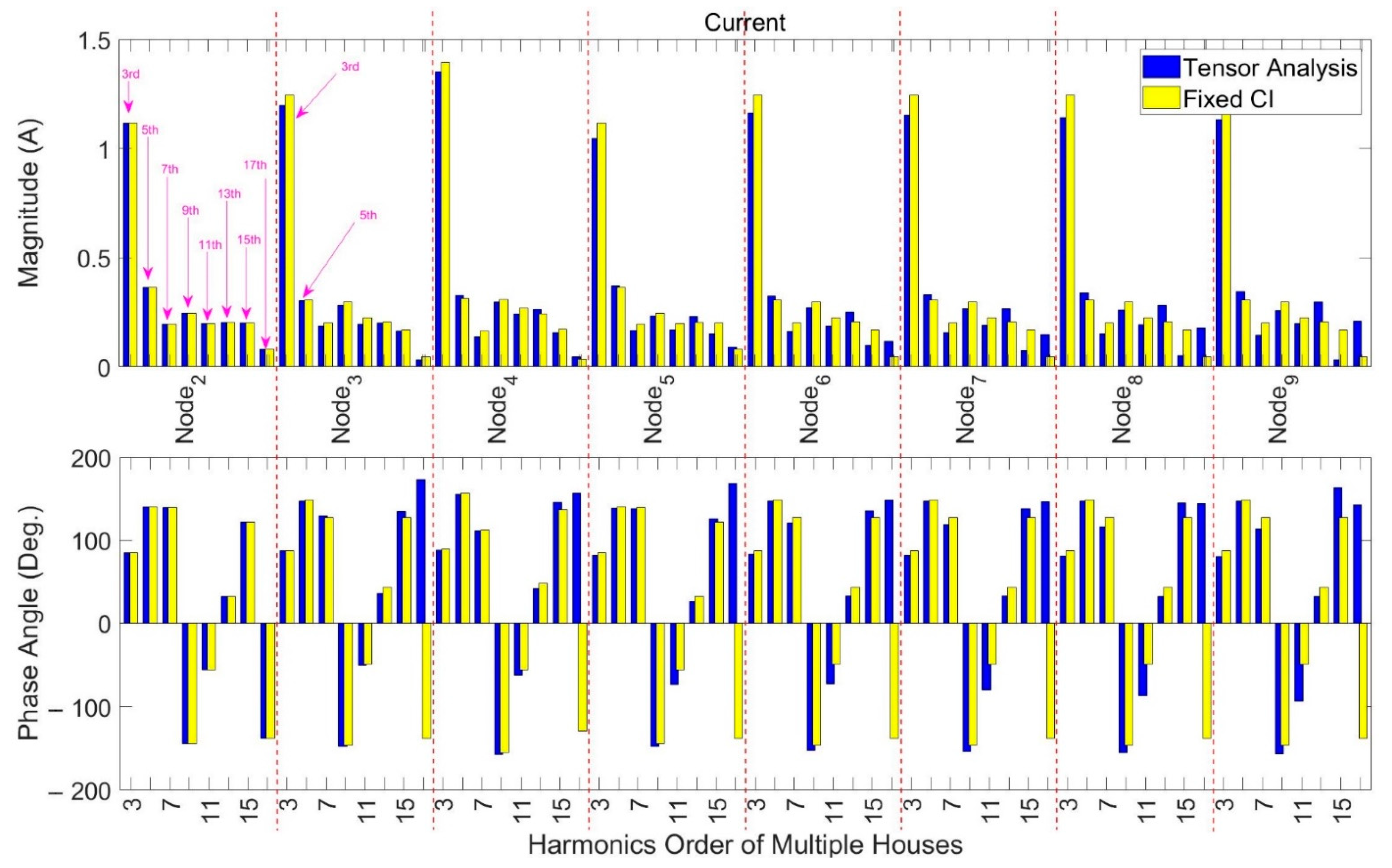
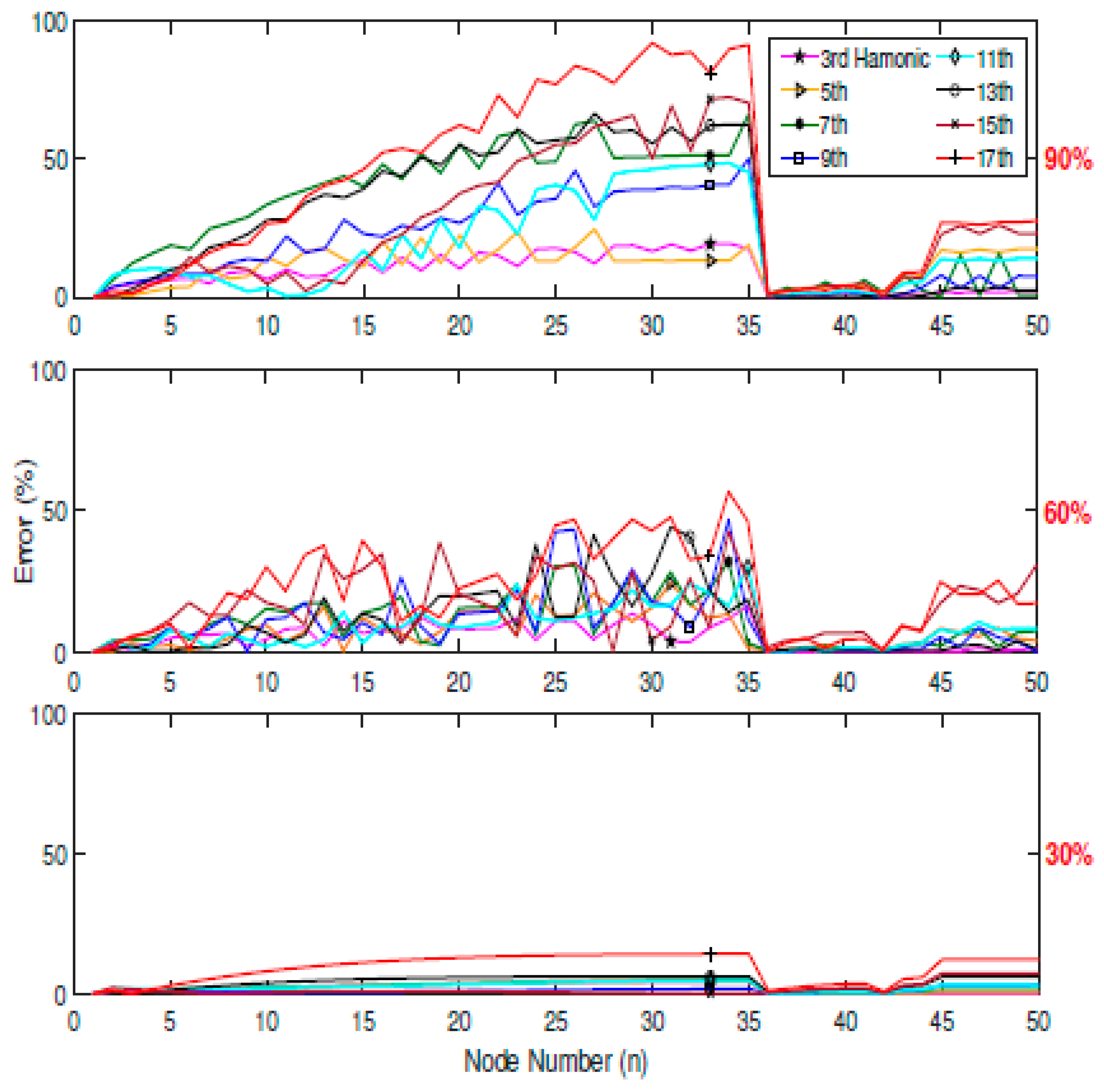
4.1. Urban LV Network
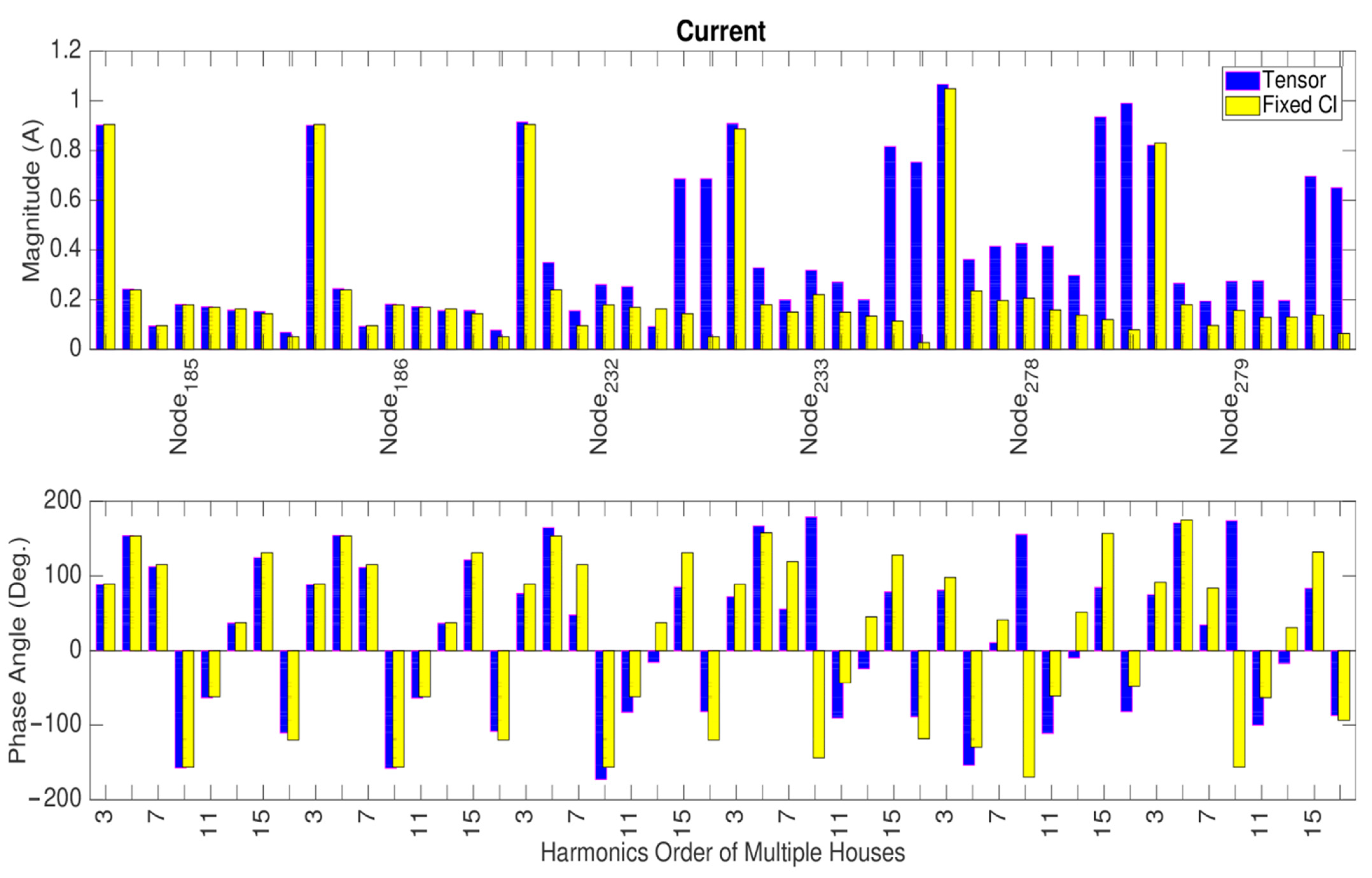
4.2. City Centre LV Network
5. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Strezoski, L.V.; Vojnovic, N.R.; Strezoski, V.C.; Vidovic, P.M.; Prica, M.D.; Loparo, K.A. Modeling challenges and potential solutions for integration of emerging DERs in DMS applications: Power flow and short-circuit analysis. J. Mod. Power Syst. Clean Energy 2019, 7, 1365–1384. [Google Scholar] [CrossRef]
- Watson, N.R.; Scott, T.L.; Hirsch, S.J.J. Implications for distribution networks of high penetration of compact fluorescent lamps. IEEE Trans. Power Deliv. 2009, 24, 1521–1528. [Google Scholar] [CrossRef]
- Carbone, R.; Menniti, D.; Testa, N.S.A. Iterative harmonic and interharmonic analysis in multiconverter industrial systems. In Proceedings of the 8th International Conference on Harmonics and Quality of Power. Proceedings (Cat. No.98EX227), Athens, Greece, 14–16 October 1998; Volume 1, pp. 432–438. [Google Scholar] [CrossRef]
- Carbone, R.; Fantauzzi, M.; Gagliardi, F.; Testa, A. Some considerations on the iterative harmonic analysis convergence. IEEE Trans. Power Deliv. 1993, 8, 487–493. [Google Scholar] [CrossRef]
- Collin, A.J.; Djokic, S.Z.; Drapela, J.; Guo, Z.; Langella, R.; Testa, A.; Watson, N.R. Analysis of Approaches for Modeling the Low Frequency Emission of LED Lamps. Energies 2020, 13, 1571. [Google Scholar] [CrossRef]
- Gallo, D.; Landi, C.; Langella, R.; Luiso, M.; Testa, A.; Watson, N.R. On the measurement of power electronic devices’ frequency coupling admittance. In Proceedings of the 2017 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Liverpool, UK, 20–22 September 2017; pp. 1–6. [Google Scholar]
- Gallo, D.; Langella, R.; Luiso, M.; Testa, A.; Watson, N.R. A new test procedure to measure power electronic devices frequency coupling admittance. IEEE Trans. Instrum. 2018, 67, 2401–2409. [Google Scholar] [CrossRef]
- Langella, R.; Testa, A.; Caicedo, J.E.; Romero, A.A.; Zini, H.C.; Meyer, J.; Watson, N.R. On the use of Fourier descriptors for the assessment of frequency coupling matrices of power electronic devices. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–6. [Google Scholar]
- Caicedo, J.E.; Romero, A.A.; Zini, H.C.; Langella, R.; Meyer, J.; Watson, N.R. Impact of reference conditions on the frequency coupling matrix of a plug-in electric vehicle charger. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Arrillaga, J.; Smith, B.C.; Watson, N.R.; Wood, A.R. Power System Harmonic Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Arrillaga, J.; Watson, N.R. Power System Harmonics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Smith, B.C.; Arrillaga, J.; Wood, A.R.; Watson, N.R. A review of iterative harmonic analysis for ac-dc power systems. IEEE Trans. Power Deliv. 1998, 13, 180–185. [Google Scholar] [CrossRef]
- Smith, B.C.; Watson, N.R.; Wood, A.R.; Arrillaga, J. Harmonic tensor linearisation of hvdc converters. IEEE Trans. Power Deliv. 1998, 13, 1244–1250. [Google Scholar] [CrossRef]
- Love, G.N.; Wood, A.R. Harmonic State Space model of power electronics. In Proceedings of the 2008 13th International Conference on Harmonics and Quality of Power, Wollongong, NSW, Australia, 28 September–1 October 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Malagon-Carvajal, G.; Duarte, C.; Ordoñez-Plata, G.; Almeida, C.F.M.; Kagan, N. A Harmonic Frequency Domain Modeling Method for Single-Phase Full Bridge Rectifiers. J. Control. Autom. Electr. Syst. 2020, 31, 1322–1333. [Google Scholar] [CrossRef]
- Ramzan, M. Modelling Distribution Network through Tensor Representation in the Presence of Power Electronic Devices. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2021. [Google Scholar]
- Ramzan, M.; Othman, A.; Watson, N.R. Comparison of Assessment Methods for Tensors of Nonlinear Devices. Electr. Power Syst. Res. 2022, submitted.
- Arrillaga, J.; Watson, N.R. Computer Modelling of Electrical Power Systems, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Watson, J.D.; Watson, N.R. Impact of Electric Vehicle Chargers on Harmonic Levels in New Zealand. In Proceedings of the 7th Innovative Smart Grid Technologies (ISGT Asia 2017), Auckland, New Zealand, 4–7 December 2017. [Google Scholar]
- Watson, J.D.; Watson, N.R. Impact of Residential PV on Harmonic Levels in New Zealand. In Proceedings of the 7th IEEE International Conference on Innovative Smart Grid Technologies (ISGT Europe 2017), Torino, Italy, 26–29 September 2017. [Google Scholar]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramzan, M.; Othman, A.; Watson, N.R. Tensor-Based Harmonic Analysis of Distribution Systems. Energies 2022, 15, 7521. https://doi.org/10.3390/en15207521
Ramzan M, Othman A, Watson NR. Tensor-Based Harmonic Analysis of Distribution Systems. Energies. 2022; 15(20):7521. https://doi.org/10.3390/en15207521
Chicago/Turabian StyleRamzan, Muhammad, Ali Othman, and Neville R. Watson. 2022. "Tensor-Based Harmonic Analysis of Distribution Systems" Energies 15, no. 20: 7521. https://doi.org/10.3390/en15207521
APA StyleRamzan, M., Othman, A., & Watson, N. R. (2022). Tensor-Based Harmonic Analysis of Distribution Systems. Energies, 15(20), 7521. https://doi.org/10.3390/en15207521








