Abstract
With respect to decision making by companies, normative approaches such as the net present value (NPV) method are widely applied, even though it is known that investors may make non-normative decisions. This study aimed to obtain new information on the decision-making behavior of renewable energy (RE) companies under uncertainty in the energy market, which is not provided by the conventional normative approach. In this study, we designed a novel framework that expressed both normative and non-normative perspectives of decision making, and developed a behavioral decision-making model of a power generation company investing in large-scale RE (RE company). We also examined the decisions of the RE company under uncertainty in the energy market using the developed model, considering the Kansai region in Japan as an example study area. As a result, compared to the conventional NPV method, we obtained the following information: (i) heavy investments in either photovoltaics (PV) or wind resulted in decreased variable renewable energy (VRE) capacity, even though financial support was sufficient; (ii) balanced investments in both PV and wind yielded a larger VRE capacity in cases where financial support was sufficient; and (iii) co-worker’s suggestions that lowered the decision-makers’ reference point (RFP) encouraged VRE investments despite insufficient financial support.
1. Introduction
1.1. Background
The transition from fossil fuels as the dominant source of energy to an era of clean and renewable energy (RE) is anticipated around the world. Although the endpoint of a renewable energy system with the elimination of fossil fuels is theoretically clear, during the transition period, power generation companies need to make the decision to invest (or not) in large-scale RE considering various uncertainties such as the level and duration of financial support for RE, fuel price trends, electricity demand, and the strategies of competitors. Given such uncertainties, power generation companies will follow different strategies based on their management culture, history, and interpretation of the information at hand. The elucidation of how uncertainties affect the investment decisions of power generation companies with regards to RE under different government energy and economic policies to encourage the introduction of large-scale RE is important for the continuous improvement of policy measures.
1.2. Literature Review
In the field of decision making, especially under uncertainty, approaches are typically categorized as either normative, prescriptive, or descriptive [1,2], as summarized in Table 1. The normative approach focuses on rational decision making and deductive discussions based on mathematical models. The net present value (NPV) method is widely applied in decision making in the case of company investments [3,4]. Though the NPV method is regarded as an effective measure for the evaluation of the advantages and disadvantages of investments under defined financial conditions [5], companies often do not make investment decisions even if the expected NPV of the investments is positive [6], especially in cases of capital investments under uncertainty, as these decisions are irreversible. The practical investment behavior of companies may therefore differ from their investment criterion under the conventional NPV approach. To explain this variation, the “value of the option of waiting to invest” has been introduced [7]; if the value of an option to wait is greater than that of the expected NPV of the investment at the current time, then the investment will be postponed. The application of such “real options” approaches became one of the major discussions in decision making regarding investments under uncertainty, including in power generation investment studies [8]. In the real options approach, decision makers have flexible investment options, and the value of options is evaluated via methods developed for finance such as the binominal model and the Black–Scholes model, in addition to traditional NPV approaches [7,9]. As shown by Kaslow and Pindyck, some electric utility companies are known to have applied real options when they made investment decisions under uncertainty [10]. Several studies have since used real options to evaluate investment in RE [11,12,13,14,15], nuclear [16], and thermal power plants [17]. These studies showed the effectiveness of flexibility for decision makers during decision making on investments under uncertainty. However, as real options still rely on traditional NPV approaches, the problem of previous studies is retained, in the assumption that the decision makers are supposed to make rational investment decisions. Thus, the question of whether power generation companies actually always make rational decisions persists.

Table 1.
Summary of approaches to decision-making in the field of energy investment.
The prescriptive approach supports decision makers to make rational decisions on a particular issue, and is sometimes regarded as a sub-category of the normative approach [1]. Multi-criteria Decision Making (MCDM) is representative of this approach, and some methods of MCDM have been applied to studies of decision making for RE investment. For example, several studies proposed supporting methods to select options for RE investment with the analytic hierarchy process (AHP) [18,19,20,21]. The AHP is one of the well-known MCDM methods to support organizing and analyzing complex decisions by quantifying the weights of decision criteria based on a structured technique [22]. Similarly, Hahn [23] demonstrated guidance of decision-making priorities for private entities in energy sustainability planning based on multi-attribute utility theory (MAUT), in which the total scores for alternatives were determined by the weighted utility scores for individual attributes. Although the prescriptive approach has prompted much research interest [1], this approach has the same issue as the normative approach, i.e., it does not sufficiently describe people’s or companies’ decisions in reality.
Here, it is important to discuss people’s and companies’ real decisions in society considering the non-normative perspective. As Hodgkinson et al. [24] found from experiments, positively framed decision scenarios for business investment led to different decisions when compared with negatively framed decision scenarios, even though the same value of income was expected from the business. Such framing bias is likely to be an important factor in decision making under uncertainty [24]. In addition, rational analysis was found to be insufficient, while behavioral aspects were necessary to explain RE diffusion. Masini and Menichetti, through a questionnaire survey, found that decisions of RE investors were sensitive to personal beliefs regarding technical adequacy and institutional pressures from peers [25,26]. Salm et al. showed that investors occasionally relied on their “gut feeling” in RE investments [27]. West et al. analyzed the influence of cultural and ideological identities in RE investments using a focus group approach with cultural theory, taking an example of the South West UK, developing deeper understandings of how individuals’ worldviews can inform opinions and behavior in relation to RE [28]. These studies indicate that the decisions made by RE investors, in reality, are not always normative, but are sometimes subjective, especially under uncertainty. As stated above, the conventional NPV approach is one useful method of evaluating the investments by a company, and the real options and prescriptive approach may compensate for the demerits of the NPV approach for decision making under uncertainty. However, these normative approaches do not express the non-normative perspectives of the decision makers, such as influences from personal beliefs, co-workers, and competitors, even though their importance has been recognized [25,26].
As contrasted with the normative and prescriptive approaches, the descriptive approach focuses on clarifying or modeling how people make decisions in reality, including the non-normative perspective of decision makers [1]. Prospect theory, which was developed by Kahneman and Tversky based on behavioral economics, is representative of the descriptive approach. The theory claims that preferences of decision makers in reality are reference dependent and exhibit loss aversion, and probabilities are subjectively weighted from the non-normative decision making point of view [29,30]. Some studies have applied prospect theory to the field of energy investment. Klein et al. analyzed household investment in solar photovoltaics in Germany based on prospect theory [31]. Heutel examined individuals’ behavior and its impacts on investments in energy saving in the US and suggested that the impact of prospect theory on a policy may be substantial [32]. Although these studies considered non-normative decisions, they did not focus on the company’s decision making for RE investments. Other studies have focused on behavioral decisions for RE investments, including non-normative aspects of people’s and company’s decisions. However, these studies are mostly based on the analysis of questionnaire surveys or qualitative analysis [25,26,27,28]. As stated above, previous studies have not attempted to quantify the values of RE investments from both normative and non-normative perspectives, particularly regarding the decision-making process of power generation companies to invest in large-scale RE (“RE companies” hereafter). Therefore, we infer that conventional normative and prescriptive approaches will be insufficient when governments formulate future policies and design mechanisms for the large-scale introduction of RE under uncertainty, and that a new approach that quantifies the non-normative decisions of RE companies is therefore necessary. In this study, focusing on the fact that non-normative perspectives influence decisions of RE investment in addition to normative perspectives, we designed a novel framework that incorporates both the normative and non-normative decision-making perspectives of RE companies to describe the investment behavior observed in reality, which the conventional normative approach overlooks. Based on this framework, we developed a quantitative decision-making model for an RE company. In addition, we defined various uncertainties that the RE company faces, including the power variation of variable renewable energy (VRE) and strategies of competitors and future policies. This study aimed to obtain novel information on the decision-making behavior of RE companies under uncertainty in the energy market, which is not yielded by the conventional normative approach. The Kansai region in Japan was used as the case study area, which is one of the most populous regions in Japan and is expected to install large-scale VRE in the next 30 years, for which there is sufficient and reliable data for the current study [33].
It should be noted that this field is not settled with regards to the extent and causal strengths of different parameters and influences. There are therefore a number of challenges to undertaking a quantitative evaluation of this sort, and in obtaining meaningful and useful outputs. Primarily, there is a high level of uncertainty when considering the reaction of specific individuals within a company, given a theoretical decision to be made under uncertainty. It could be argued that, in order to accurately model the decisions of a single individual, they would need to be monitored over a period of years, making a variety of decisions, within a relatively consistent company context. This is not possible here. The model described below integrates a number of approaches, each of which bring some uncertainty to the results. In addition, the inputs themselves are representative values or representative decision-making patterns, about which there is uncertainty. Although we do not claim to produce an absolute model that can definitively define this field, we have utilized sensitivity analysis with regards to the main parameters and inputs, in order to evaluate the model behavior and the changes of results in response to alternative inputs. We argue that these results can provide further information to support quantitative decision-making modeling for companies under uncertainty.
2. Materials and Methods
2.1. Design of the Framework
When decision making of a company is discussed, the company’s management functions can be summarized into three levels [34,35]—the top management (in charge of strategic decisions), the middle management (the operational decisions), and the first-line management (the administrative decisions)—although the company is normally composed of multi-level departments and sections. Because this study considers high-level decisions for RE investment, we focus on the top management and middle management as representing the decision-making processes of the RE company. Companies with bottom-up decision-making management, where the top management makes decisions based on reports and/or proposals from the sections in charge, are representative of the traditional infrastructure companies in Japan [36,37,38]. Figure 1 shows the designed framework of the decision of RE companies in this study. The middle management, in charge of investment planning, prepares possible investment options, analyzes outcomes and probabilities, and provides the analysis results such as the expected NPV of each option to the top management. The top management is the decision maker, who determines options to be invested in based on the analysis results. The novelty of the framework applied here is characterized by the non-normative perspectives of the decision maker being incorporated, in addition to the normative approach, assuming two layers of the RE company’s organization.
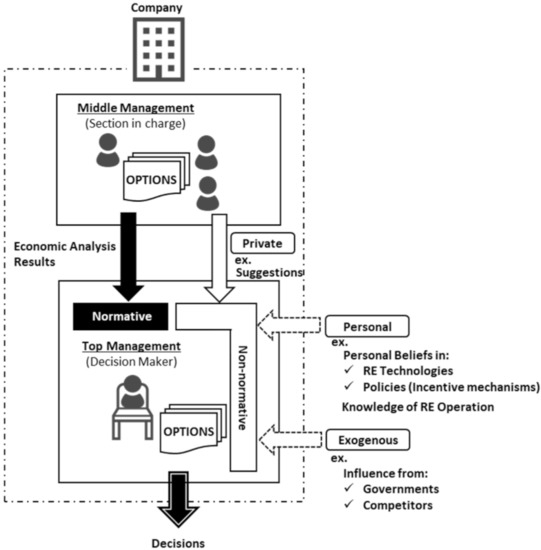
Figure 1.
Framework of decisions of RE companies based on normative and non-normative perspectives.
Non-normative perspectives were categorized into private, personal, and exogenous influences, considering the decision-making process of companies and a literature survey [25,26,27,28]. Private influence stems from within the company and includes suggestions from the middle management to the top management, which are usually given in addition to the economic analysis results. The decision of the top management may be influenced by the suggestions from the middle management. Personal influence expresses the personal beliefs and knowledge of the decision maker, such as beliefs regarding RE technologies. For instance, the decision maker should have objective information on the applied RE technologies; however, the adequacy for investments could depend on personal beliefs regarding the technologies [39]. Exogenous influence comes from outside the company. For example, RE investors usually take into account the investment decisions of their competitors [25,26]. Based on this framework, we developed the following behavioral decision model of the RE company in the energy market.
2.2. Development of the Behavioral Decision Model in the Energy Market
In this study, two power generation companies were assumed to compete in the energy market. One was a traditional power company that owns large-capacity conventional power generation plants (Company 1), and the other was a renewable power generation company that invests in VRE plants (Company 2), as shown in Figure 2a.
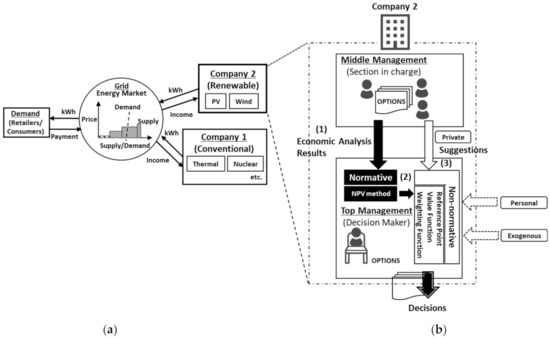
Figure 2.
Overview of the developed model based on the designed framework: (a) companies in the energy market and (b) application of the framework to the decision-making process Company 2.
Focusing on the investment behavior of Company 2, we developed a decision-making model based on the proposed framework. Figure 2b shows the concept of the developed model that applies concrete methods to quantitatively integrate normative and non-normative perspectives in the framework of Figure 1. First, the conventional NPV method was applied to the normative perspective of the decisions of the top management because the NPV method is widely used for companies’ decisions, as introduced in Section 1; that is, the middle management provided the expected NPV and the probabilities of each option to the top management (indicated by (1) in Figure 2b).
Second, to express the non-normative perspectives of the decision making by the top management in the framework, we referred to the approaches of behavioral economics, which were introduced by Kahneman and Tversky [29,30]. They classified an individual’s decision-making process into two phases: the editing phase and evaluation phase. In the editing phase, outcomes and stated probabilities of the decision maker’s options are analyzed and reformulated. They claimed that a decision maker converted the outcomes (NPV in this study) of each option into gains and losses relative to a “reference point” (RFP), which can be affected and shifted by the expectations of the decision maker [29,30]. The idea of an RFP makes their approach unique in that the basis of decisions changes depending on how people feel (the RFP applied to this study is defined in Section 2.4); in contrast, because conventional economics, including expected utility theory, assumes that people make decisions rationally, the basis for decisions does not change. In the evaluation phase, the converted gains/losses and probabilities of each option are evaluated with a “Value Function” and “Weighting Function”, and the value of each option is determined in the decision maker’s mind (indicated by (2) in Figure 2b). The value function expresses the decision maker’s tendency to be risk-averse in the case of a risky option leading to gains, and risk-seeking in the case of a risky option leading to losses. They also observed a trend that individuals tended to overestimate small probabilities and underestimate large probabilities, and a weighting function was introduced to express this trend [29,30].
The RFP of the decision maker can be expected to be affected by private, personal, and exogenous influences, which are incorporated in the designed framework in this study (indicated by (3) in Figure 2b). The decision given by the value and weighting functions may vary if the RFP is shifted despite the similarity of the incomes and probabilities of each option. We expected these ideas to fit well into the non-normative perspectives in the designed framework (see Appendix A for further details on reference point and value and weighting functions).
Considering the conventional NPV method for the normative perspective and the behavioral approach for the non-normative perspective as stated above, a decision-making model was developed to examine the decisions of Company 2 regarding preferred investments under various uncertainties. The model is summarized in Figure 3, which further elaborates on the details of Figure 2 and consists of the following five steps:
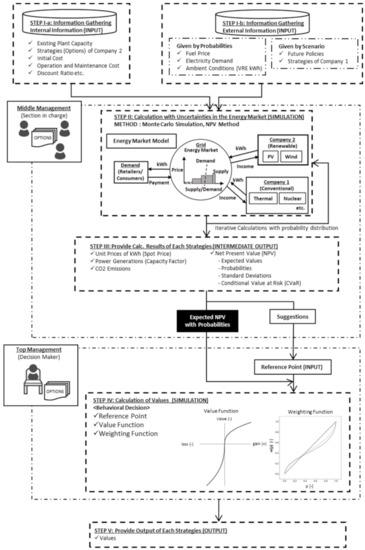
Figure 3.
Calculation steps of the developed behavioral decision model of Company 2.
STEP I: Information Gathering
Necessary information is defined as simulation input in this step. Private information (STEP 1-a) is the known data determined by Company 2: existing VRE capacity owned by Company 2, strategies for newly invested VRE capacity, the initial cost of VRE, operation and maintenance cost, and discount ratio. Exogenous information (STEP 1-b) is uncertain for Company 2 and some information is obtained from a probability distribution such as fuel price for fossil fuel-fired power plants owned by Company 1, electricity demand in the energy market, and VRE outputs affected by ambient conditions. The remaining factors are obtained by scenarios such as future policies and strategies of Company 1. The Kansai region in Japan was considered as the study area; details of input data are described in Section 2.3.
STEP II: Calculation with Uncertainties in the Energy Market
The middle management of Company 2 incorporates the gathered information into the energy market model to calculate NPV and other parameters for the evaluation of investment with respect to each strategy. Although there have been several previous studies of the energy market of RE [40,41], this study assumes that the energy market is competitive and not dominated by Company 1. The hourly spot price of electricity (Yen per kWh) is decided based on the supply curve generated by the energy supply capability of both companies and the demand obtained from the input of STEP I. Furthermore, the spot price is applied to all supply capacities of technology that are below the demand. Both companies simultaneously provide power generation cost (yen/kWh) and energy supply capacity (kW) of each technology to the market model hourly, and the merit order of power generation creates the supply curve. As the energy market is competitive, the marginal cost of power generation, which consists of fuel cost for power generation (only for thermal power) and O&M cost, is expected to encompass the cost of generating power. Both companies attempt to recover the initial investment using the income obtained from the energy market. However, if the cost of generating power of all technologies is the marginal cost, it is known that the capital investment of power generating facilities may never be recovered by the income obtained from the energy market, which the so-called “missing money problem” [42]. Therefore, the power generation cost of the replaced thermal power plants is assumed to include the initial investment only when Company 1 invests in the replacement of retiring thermal power plants to avoid the “missing money problem” in the market.
As some of the inputs are obtained through probability distributions, iterative calculations using the Monte Carlo method were adopted. The number of trials for each calculation case was set as 1000 considering calculation accuracy and time; each calculation case provided 1000 sets of the output of each company including NPV and CO2 emissions. The given probability distribution, expected value, standard deviation, and conditional value at risk (CVaR) of each output set were then obtained from the model (refer to Appendix B for the definition of NPV and other outputs in this study).
STEP III: Provision of Calculation Results of Each Strategy
Calculation results in STEP II, such as the expected value of NPV, are provided to the top management. As mentioned in Section 2.1, when the middle management reports to the top management, in reality, the middle management is supposed to provide suggestions on strategies, and these suggestions can affect the decisions made by the top management. As mentioned earlier, the influence of suggestions is considered as the reference point in this study, and the RFP of this study is obtained based on the calculation results in STEP II and the use of one of the inputs in STEP IV in the model. The RFPs in this study are defined in Section 2.4. As we defined the private, personal, and exogenous factors as influencers of the non-normative perspectives in the framework in Section 2.1, the belief in RE investments of the top management, the government’s announcement of new RE policies, or other factors may influence the top management’s decision. However, we only consider private suggestions as influences in the model for simplicity.
STEP IV and V: Calculation of Values and Provision of Output for Each Strategy
If the top management is ideally rational, they should select a strategy with the highest expected NPV. However, in reality, when the top management makes decisions, these decisions ordinarily include their objective and subjective perspectives. To reflect aspects in the decision-making process, the value function relative to the RFP and the weighting function of the top management are incorporated in the model. Figure 4 shows the calculation process of the RE investment value. (1) The NPV calculation and corresponding probability are provided from STEP III. (2) The gain/loss, which the top management “feels”, is given by subtracting RFP from NPV (the definition of RFP in this study is provided in Section 2.4.) (3) The gain/loss is converted to a value by the value function. (4) The given probability is then transformed to a subjective probability by the weighting function. (5) The value is multiplied by the subjective probability and the “Value” which the top management determine is obtained. “Value” with a capital V means the outcome calculated by the Value and weighting functions unless otherwise noted. (6) Summation of the Value of each calculation yields the expected Value for the decision. (See Appendix A for further details of the value and weighting function).
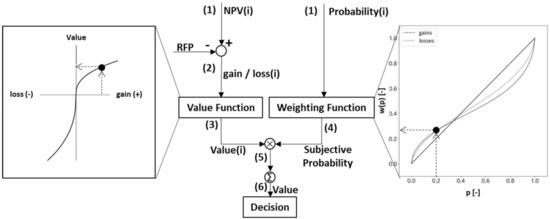
Figure 4.
Calculation process of the VRE investment value in STEP IV: (1)–(6) correspond to the numbers in the description of STEP VI. The black dots in the graphs are examples.
2.3. Application to Kansai Region, Japan
2.3.1. Overview of Electric Utility System in Japan
The power grid in Japan is characterized by a longitudinal transmission system (Figure 5), without international connections, and split into ten regions. Each region has one large conventional electric company, and the transmission system of each area is largely independent because power interconnection is limited to the neighboring area. Although any of these regions could be chosen as the case study, here, the Kansai region is selected, and the developed model is applied to the region in this study. The Kansai region is characterized by a large capacity of natural gas-fired and nuclear power plants, which is highly representative of the energy mix in Japan. Therefore, the Kansai region is considered to be a good example to discuss the energy transition in Japan. KEPCO is a large conventional electric company in the Kansai region, and is regarded as Company 1 in the model. Although there are several independent power producers (IPPs) other than KEPCO in the area, these IPPs are considered to be a single company, that is, Company 2, for simplicity in the model.
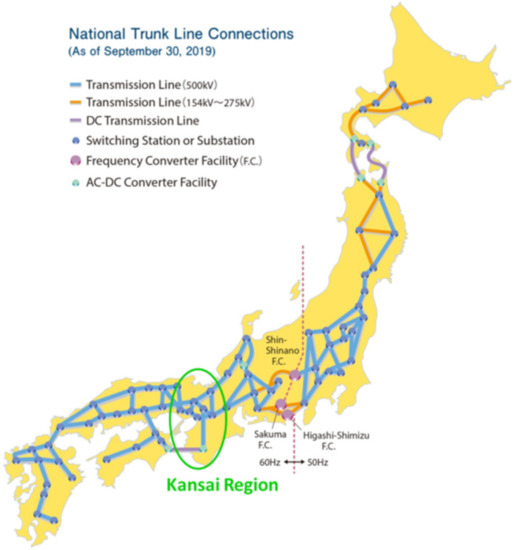
Figure 5.
National power grid in Japan and the Kansai region (Based on [43]).
An overview of the current and expected future electricity supply/demand system is shown in Table 2. The deregulation of the electrical utility system in Japan is still underway; most electricity trade is bilaterally conducted over the counter between electric companies and consumers; power generation companies supply electricity; a feed-in tariff is given to newly installed RE; and changes in fuel price can be passed on through the retail electricity price as of 2020. However, considering the timeframe of the energy transition discussed in this study, we incorporated the future expectation into the spot price market model; electricity is mainly traded in the spot price market, transmission operators are responsible for the supply of electricity, a feed-in-premium is applied as financial support for RE, and fuel price uncertainty risk is covered by the income of the spot price market.

Table 2.
Current and future electric utility system in Japan.
With regards to the timeframe of this study, Company 2 is expected to decide on investment in VRE in 2025, considering income from the spot price market for the coming 20 years in various scenarios because the lifetime of VRE is set at 20 years (Appendix C). Other properties of applied technologies are also listed in Appendix C.
2.3.2. Private Information of Company 2 (STEP I-a)
- (i.)
- Existing VRE Capacity
Existing VRE capacities owned by Company 2 were set, as shown in Table 3, considering installed capacity in the Kansai region as of 2019 [44]. The capacities decrease during 2035–2044 compared to the period ranging from 2025–2034 because the VRE lifetime ends; that is, since the lifetime of VRE was expected to be 20 years in this study (Appendix C), half the existing VRE were assumed to be retired in 10 years, whereas the remainder retire linearly thereafter. The initial cost of this existing VRE was considered to have been recovered, and the feed-in-premium (FIP) was not given to the power generation of the equipment.

Table 3.
Existing VRE capacity of Company 2.
- (ii.)
- Strategies of Company 2
Company 2 makes decisions to invest in PV and/or wind (onshore). Although there are several types of RE other than PV and wind (onshore), such as biomass, geothermal, and wind (off-shore), we focused on PV and/or wind (onshore) in this study. The strategies of Company 2 are summarized in Table 4. Each strategy has five different options (0 MW—7000 MW) of capacity to be invested, and 0 MW means that Company 2 keeps its existing capacity and does not make any investments in new VRE equipment. Because the target of RE introduction in the 2030s in Kansai is 6000 MW [45], we defined these capacity options to cover this target. Although a continuum of capacities, including 0, 1000, 3000, 5000, and 7000 MW may be selectable, it is difficult to calculate all continuous possible capacities in reality considering the calculation load, especially from a company’s decision-making point of view. Therefore, 1000, 3000, 5000, and 7000 MW were selected as the capacity options for calculation and evaluation of each strategy. As a result of the simulation, the top management was expected to select an option that earns the highest Value. MIX2 and MIX3 show “PV:Wind = 7:3” and “PV:Wind = 3:7” respectively in the strategy names for ease of understanding in the later sections; however the ratios do not exactly match some of the capacity investments in the table. In addition, because it is known that the “option to expand” may provide more value to the decision maker under uncertainties [8], we examine the “option to expand” in the developed model. Strategy names with “OE” mean that Company 2 has the option to expand the capacity of VRE; Company 2 decides to invest in half the capacity of each option in 2025 and decides to develop the remaining half in 2030 only if one-third of the first half capacity’s initial cost was expected to be recovered within five years (2025–2029) as a result of the simulation. Other than these cases, Company 2 decides to invest in VRE in 2025.

Table 4.
Strategies of Company 2 for investment in VRE.
2.3.3. Exogenous Information: Scenario Development (STEP I-b)
Uncertainties in Company 1’s strategy (Section 2.3.3 (i)) and FIP price (Section 2.3.3 (ii)) are considered by a variety of scenarios. The middle management of Company 2 calculates the NPV of RE investments for each scenario and option, and the top management evaluates each scenario and option from the investment Value point of view.
- (i.)
- Strategies of Company 1 Regarding Existing Power Plant Replacement
Company 1 owns a large capacity of thermal power and nuclear power plants, and some of these are expected to be retired chronologically, which is consistent with the lifetime of the existing facilities in the Kansai region. Therefore, Company 1 needs to make decisions on the retiring power plants, i.e., replace, scrap, or prolong them. The following strategies are given in this study.
Strategy T-1: Replacement of Retiring Thermal Power Plants with Gas Turbine Combined Cycle (GTCC)
Company 1 replaces retiring thermal power plants with the latest GTCC plants in each period if they have passed 40 years since the start of commercial operation.
Strategy T-2: Scrapping of Retiring Thermal Power Plant
Company 1 scraps retiring thermal power plants in each period if they have passed 40 years since the start of commercial operation.
Strategy N-1: Life Extension of Retiring Nuclear Power Plants
Company 1 gets the approval for extending the lifetime of retiring nuclear power plants from 40 to 60 years by the Japanese Government.
Strategy N-2: Scrapping of Retiring Nuclear Power Plants
Company 1 scraps retiring nuclear power plants in each period if they have passed 40 years since the start of commercial operation.
Three scenarios are developed from combinations of the strategies above, as shown in Table 5. However, a scenario composed of Strategy T-2 and N-2 (NO replacement of thermal power nor NO lifetime extension of nuclear power) is excluded because the power supply capacity of this scenario is very small compared to the expected maximum demand in the Kansai region [46,47]. Corresponding equipment capacities of each scenario are shown in Figure 6, and are estimated based on KEPCO’s existing power plants [48,49,50]. “wRP_NC60” is used as the base scenario.

Table 5.
Strategies of Company 1.
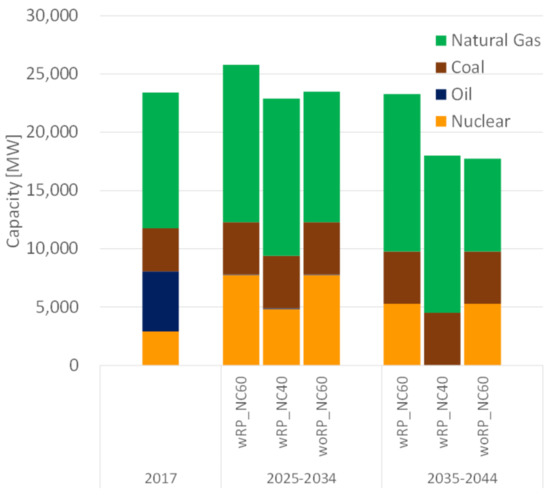
Figure 6.
National power grid in the Kansai region of Japan.
- (ii.)
- Future Policies
Feed-in Premium (FIP)
There are several types of financial support for RE examined by governments around the world, and “Fixed Feed-in Premium,” where a fixed premium is given on top of the spot price of the energy market, was selected as the financial support in this study. Because the FIP follows the spot price, it is expected to be suitable for the investigation of the impact of VRE introduction to the spot price market. In this study, different prices of FIP for PV and wind were set as scenarios as shown in Table 6. Because the future FIP price has not yet been decided in Japan, and is one of the key revenue uncertainties, we set the FIP price so that the difference in investment decision making due to the different FIP price becomes clear.

Table 6.
Scenarios of FIP.
2.3.4. Exogenous Information: Probability Distribution (STEP I-b)
Uncertainties of fuel price (Section 2.3.4 (i)), electricity demand (Section 2.3.4 (ii)) and ambient conditions (Section 2.3.4 (iii)) are given by probability distributions. The middle management of Company 2 executes iterative calculations based on the probability distributions in the spot market price for each strategy and option. The middle management then provides the calculation results with the probability to the top management.
- (i.)
- Fuel Price
Fuel prices of natural gas, coal, and oil in each year were assumed to stem from the triangular distribution in Table 7, and were used in the model to express the future uncertainty of the fuel price. Data from the World Energy Outlook of IEA were referenced [47].

Table 7.
Fuel price.
- (ii.)
- Electricity Demand
The recorded data of electricity demand of the Kansai region in 2017 were used as an input into the spot price market model as a basis. We also estimated the uncertainty of change in demand from 2025 to 2044 (20 years) to be ±10% in this model [46,47]. The probability distribution of the demand was given by a uniform distribution (rectangular distribution).
- (iii.)
- Ambient Conditions
Trends of unit output (kWh/unit) of PV and wind (onshore) were estimated using PV and wind output (kWh) recorded data of the Kansai region in 2017 [46]. The trends of unit output were implemented into the spot price market model as a basis. As changes in PV and wind output due to ambient conditions were highly uncertain for the investment of Company 2, the uniform distribution of ±15% was considered for changing output according to ambient conditions, based on historical data in the Kansai region.
2.4. Study Cases
Study cases are summarized in Table 8 and comprise the strategy of Company 2 and scenarios for the strategy of Company 1, FIP price, and CO2 restrictions. Company 2 has seven strategies defined in Table 4, and Company 1 has three strategies described in Table 5, respectively. Because there are numerous possible combinations of strategies and scenarios, we selected 10 representative cases to examine the boundary cases. Cases 1 and 2 examine the decisions of RE investment considering different FIP prices. The scenario “wRP_NC60” is used as Company 1’ s strategy, because the scenario is preferable in the Kansai region from a macroeconomic point of view, as per a previous study [50]. Cases 3 and 4 attempt to clarify the effect of Company 1’ s strategies. FIP-Low is applied because it is expected that the influence of Company 1 will be relatively less if the financial support is sufficient. Cases 5 and 6 compare differences in the mixture of PV and Wind. Cases 7, 8, 9, and 10 are for examining the option to expand. For Cases 5–10, the scenario of “wRP_NC60” is applied as in Cases 1 and 2.

Table 8.
Summary of study cases.
As mentioned in Section 2.2 (STEP III), the creation of RFPs in each case was necessary. Figure 7 shows the concept of RFP selection for the decision making of the top management in this study. The middle management provides the NPVs and probabilities of each investment option to the top management, which correspond to the histogram in Figure 7. We expect that the top management will decide the capacity of the VRE investment based on the anticipated income of each option compared to that of the option OP-0MW (defined in Table 4), where the existing facility owned by Company 2 earns income and there is no investment in new VRE. Although there are multiple possible RFPs in reality, as shown in Figure 7, two types of RFPs were adopted in this study for simplicity of the model: the expected value of NPV (Ref_EXP) and CVaR of NPV (Ref_CVaR) in the case of OP-0MW. We assume that the top management will evaluate the VRE investment based on the expected value of NPV of OP-0MW when the middle management emphasizes the “profit” of VRE investments (i.e., positively framed) in their suggestion to the top management. By comparison, the top management will evaluate the VRE investment based on the CVaR of NPV of OP-0MW when the middle management emphasizes the “risk” of the VRE investments (i.e., negatively framed). According to the definition of the reference point described in Appendix A, the different reference points result in different gains or losses even if the outcomes (NPV in this study) are the same; gains are smaller, and losses are bigger in the case of ReF_EXP compared to ReF_CVaR, which the decision maker “feels.” For example, in the case in which the expected value of NPV in OP-0MW (Ref_EXP) is 300 billion yen, the CVaR of NPV in OP-0MW is −100 Billion yen, and a 1000 MW PV investment yields 400 billion yen of NPV, the gain that the top management feels at Ref_EXP will be +100 billion yen (=400 billion yen − 300 billion yen), and +500 billion yen (=400 billion yen − (−100 billion yen)) at Ref_CVaR (these values are just examples.) Preparing for the two cases of RFP as shown in Table 8, the influence of suggestion (RFP) provided by the middle management was observed. Scenarios indicated by yellow highlighted areas with underscores in Table 8 are items for comparison in each case.
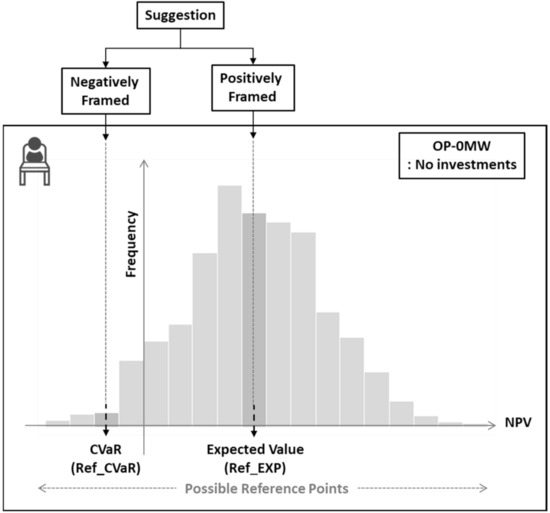
Figure 7.
Concept of selected reference points for the decision making of the top management.
3. Results and Discussion
Simulation results of each case are shown in the following subsections to examine the decision making by Company 2. If the top management is ideally rational, they should select a RE capacity with the highest expected NPV. However, the top management would invest in the RE capacity with the highest value from a behavioral decision perspective. Therefore, we evaluated the results by focusing on differences in the trend of expected NPV and the value in each strategy. Although graphs are shown to illuminate the trend, the data associated with the calculation results in each case corresponding to the figures are available in Appendix D. The cases of each subsection correspond to the case number in Table 8, and legends of the figures are in line with the scenario names in Table 4, Table 5, Table 6 and Table 7.
3.1. Effect of FIP Price (Cases 1 and 2)
Figure 8 shows the expected NPV reported to the top management by the middle management, the Value given by the NPV in the top management’s mind, and the average spot price in the spot price market. There are two alternative Values: Ref_EXP (high RFP) and Ref_CVaR (low RFP) cases, as defined in Table 9. The horizontal axis of each graph is the total VRE capacity in which Company 2 decides to invest. The error bars in the NPV graphs represent the standard deviation of the NPV. The left side of the figure represents the evaluation of the investment in PV, and the right side represents that of wind.
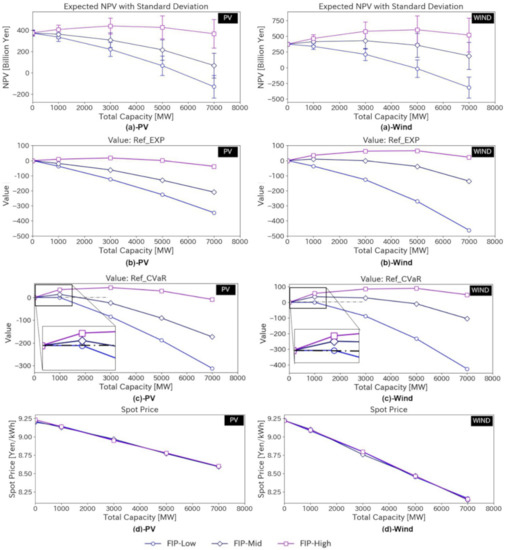
Figure 8.
Results of different FIP prices (Low, Middle, and High FIP): (a) Expected NPV with standard deviation, (b) Value in the case of high RFP, (c) Value in case of low RFP and (d) Spot price. The horizontal dashed lines show the zero axis in the Value graphs.

Table 9.
Types of reference point.
In the scenario with high FIP, investment in 5000 MW capacity earned the largest expected NPV (PV: 441.7 billion yen, Wind: 604. billion yen), and the 7000 MW investment yielded a relatively lower NPV (PV: 440.9 billion yen, Wind: 580.2 billion yen) due to a spot price decrease for both PV and wind cases (Figure 8a (a)-PV, (a)-Wind); Company 2 should decide to invest in 5000 MW of PV or wind, from the standpoint of economic rationality. By comparison, when the top management interpreted the expected NPV with probabilities through the Value and weighting functions, 3000 MW for PV and 5000 MW for wind yielded the highest Value for both Ref_EXP (high RFP) and Ref_CVaR (low RFP). The selected capacity shifted from 5000 to 3000 MW for PV (5000MW: Value 0.7 for high RFP, 29.1 for low RFP, 3000 MW: Value 17.5 for high RFP, 43.7 for low RFP) (Figure 8b (b)-PV, Figure 8c (c)-PV), and Company 2 decided to invest in a capacity that was lower than the economic optimum.
In the scenario with low FIP, additional investment in VRE yielded lower expected NPV because the initial cost of VRE could not be recovered by income from the spot price market (Figure 8a (a)-PV, (a)-Wind), and the same trend was given in the Value with Ref_EXP. However, observation of the Value with Ref_CVaR showed that the Value of 1000 MW remained slightly positive (1000 MW: Value 0.3 for PV, 0.6 for Wind) (Figure 8c (c)-PV, (c)-Wind). These results imply that the top management may decide to invest in a small capacity of VRE despite low financial support when the middle management made a suggestion that shifted the RFP of the top management downwards, as represented by Ref_CVaR in this study.
3.2. Effect of the Strategy of Company 1 (Cases 3 and 4)
Figure 9 shows the results of different strategies of Company 1 with low FIP. Company 2 achieved the largest expected NPV and Value in the case of wRP_NC40, which was the scenario in which Company 1 replaced retiring existing thermal power plants and scrapped retiring existing nuclear power plants. This is because Company 2 could expect higher spot prices because of the reduced capacity of nuclear power plants, allowing for a larger capacity factor of thermal power plants in this scenario. However, it should be noted that the CO2 emissions in this scenario were approximately 0.1 kg-CO2/kWh higher than those in the other two scenarios (Figure 9e (e)-PV FIP Low, (e)-Wind FIP Low).
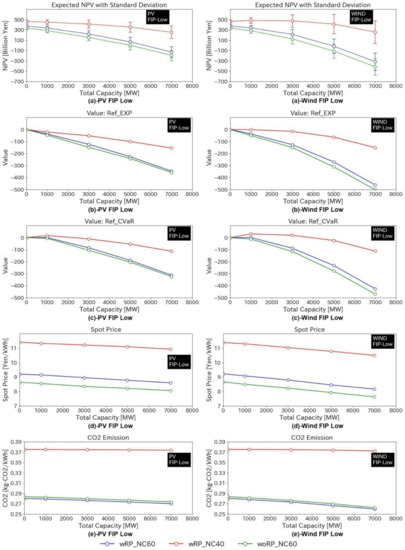
Figure 9.
Results of different strategies of Company 1 with low FIP: (a) Expected NPV with standard deviation, (b) Value in case of high RFP, (c) Value in case of low RFP, (d) Spot price, and (e) CO2 emissions.
Comparison of wRP_NC60 and woRP_NC60 showed that both NPV and Value of wRP_NC60 were higher than those of woRP_NC60. As retiring existing thermal power plants were replaced by the latest GTCC in wRP_NC60, the spot price was higher than that of woRP_NC60 due to the initial cost of GTCC replacement (Figure 9d (d)-PV, (d)-Wind FIP Low). Although the greater VRE introduction resulted in lower CO2 emissions, the new GTCC contributed to CO2 emissions, thus lowering the possible benefit.
As the financial support was insufficient in these cases, Company 2 was not encouraged to invest in VRE, even though the expected NPV was positive (Figure 9a (a)-PV FIP Low, (a)-Wind FIP Low). However, Company 2 may invest in VRE of 1000 MW, regardless of the strategies of Company 1 in case the top management has a lower RFP (Ref_CVaR) (Figure 9c (c)-PV FIP Low, (c)-Wind FIP Low).
3.3. Effect of VRE Mixture (Cases 5 and 6)
Figure 10 shows the results when Company 2 mixed the capacity of PV and wind for investment. The left side of the figure represents an evaluation with low FIP, and the right side represents one with high FIP. In the case of low FIP, even though Company 2 mixed the capacity of PV and wind, few differences were observed in the expected NPV and value yielded by the mixture of PV and wind, and the effect of the mixture on the decision made by Company 2 was limited (Figure 10a (a)-Mix FIP Low, Figure 10b (b)-Mix FIP Low). However, Company 2 invested in 1000 MW VRE, regardless of the ratio of PV to wind in case the top management had a lower RFP (Ref_CVaR) (Figure 10c (c)-Mix FIP Low), a trend that is similar to that of the results in Section 3.1 and Section 3.2.
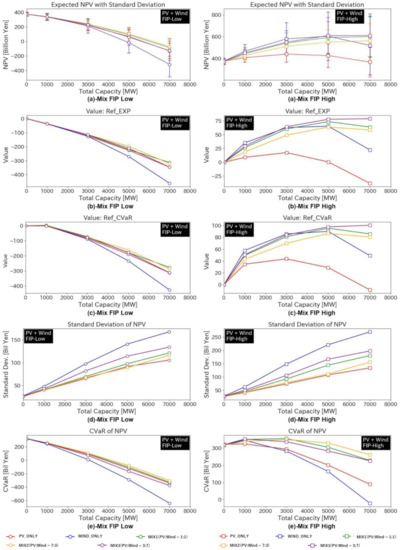
Figure 10.
Results of the mixture of VRE: (a) Expected NPV with standard deviation, (b) Value in case of high RFP, (c) Value in case of low RFP, (d) Standard deviation of NPV, and (e) CVaR of NPV.
By comparison, in the case of high FIP, when Company 2 adopted strategies to make a balanced investment in PV and wind, investment in VRE could be expedited compared to the strategies of PV or wind only (Figure 10a (a)-Mix FIP High, Figure 10b (b)-Mix FIP High, Figure 10c (c)-Mix FIP High). The expected NPV and Value of MIX1 (PV:Wind = 1:1), MIX2 (PV:Wind = 7:3), and MIX3 (PV:Wind = 3:7) were higher than those of PV_ONLY and WIND_ONLY; MIX3 (PV:Wind = 3:7) was optimal. Comparison of MIX3 (PV:Wind = 3:7) and WIND_ONLY showed that expected NPV and Value of the 7000 MW investment were the highest for MIX3 (PV:Wind = 3:7) and those of 5000 MW for WIND_ONLY. We found the standard deviation of MIX3 (PV:Wind = 3:7) was lower, and that of CVaR of MIX3 (PV:Wind = 3:7) was higher, than that of WIND_ONLY. As the standard deviation represents the uncertainty of the investment and CVaR expresses risk, VRE with a well-balanced mixture reduced the uncertainty and risk in investment. This can result in the increased capacity of VRE introduction (Figure 10d (d)-Mix FIP High, Figure 10e (e)-Mix FIP High). In the case of MIX3 (PV:Wind = 3:7), upon comparing 5000 MW to 7000 MW investments, the expected NPV was observed to increase from 610.7 billion yen at 5000 MW to 611.0 billion yen at 7000 MW (+0.05%; almost the same) (Figure 10a (a)-Mix FIP High), the Value with Ref_EXP from 78.0 to 79.1 (+1.4%) (Figure 10b (b)-Mix FIP High), and the Value with Ref_CVaR from 97.1 to 100.4 (+3.4%) (Figure 10c (c)-Mix FIP High). This implies that Company 2 may select a greater capacity of VRE than the NPV optimum capacity when it tries to invest in both PV and wind in a balanced manner and the middle management gives a negative framing to the top management.
3.4. Effect of Option to Expand in Cases 7, 8, 9, and 10
Figure 11 shows the results of the case “without” the option to expand (PV_ONLY, WIND_ONLY) and that “with” the option (PV_OE, WIND_OE) to expand in the case of low FIP. Company 2 was expected to simultaneously decide on investment in the entire capacity of VRE in 2025 and the case of PV_ONLY/WIND_ONLY. By comparison, Company 2 decided to invest in the first half of VRE in 2025 and had the option of expanding the second half in 2030 in the case of PV_OE/WIND_OE.
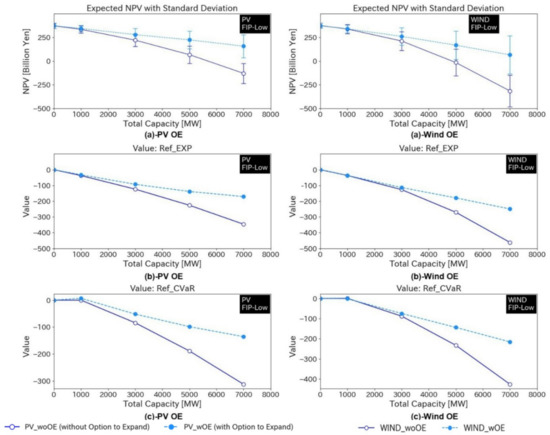
Figure 11.
Results of option to expand in case of low FIP: (a) Expected NPV with standard deviation, (b) Value in case of high RFP and (c) Value in case of low RFP.
In the scenario with Low FIP, the option to expand was found to result in a larger expected NPV and Value compared to the case without an option to expand because Company 2 could put the decision on hold until they reduced the risk of investment. However, as the Value for all cases with Ref_EXP (high RFP) was negative, Company 2 would not invest in additional VRE. Nevertheless, if the middle management could shift the RFP of the top management to Ref_CVaR (low RFP), the option to expand would possibly encourage the top management to invest in a small amount of VRE because the Value of 1000 MW with Ref_CVaR was slightly positive (Figure 11c (c)-PV).
By comparison, the scenario with high FIP provided the opposite trend, as shown in Figure 12; the option to expand reduced both expected VRE and Value, and did not promote investment in VRE. This is simply because a relatively earlier investment yields considerably more income if enough financial support for VRE is expected.
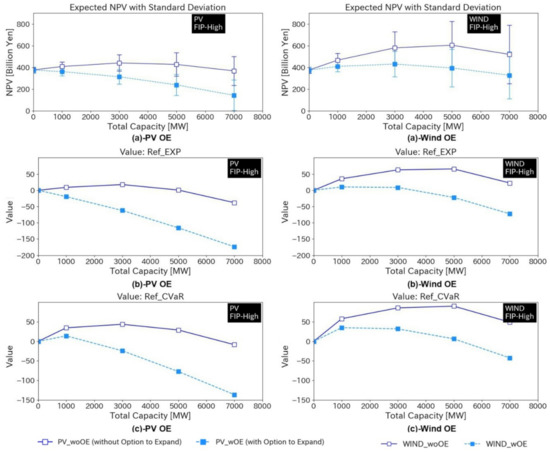
Figure 12.
Results of option to expand in case of high FIP: (a) Expected NPV with standard deviation, (b) Value in case of high RFP and (c) Value in case of low RFP.
4. Conclusions
In this study, it was highlighted that there have not yet been sufficient discussions on non-normative decisions of companies in the field of power generation, even though the decisions of these companies may not always be rational under uncertainty. Therefore, we designed a novel framework to model the decision-making process by RE companies, as shown in Figure 1, because the conventional NPV approaches do not reflect the non-normative perspectives of decision makers. A behavioral decision-making model was also developed based on the framework design to examine the decisions of the RE companies under uncertainty, as described in Figure 2 and Figure 3. From the analysis of the simulation results based on the developed model, we obtained the following important information on RE company decisions with respect to future investment compared to the conventional NPV approach.
First, in the case where high financial support is expected, and the RE company (Company 2) plans to invest in either PV or wind, the company may decide to make an investment decision that is below the economically optimum capacity gained by the highest expected NPV due to income uncertainties of large-scale VRE introduction (graphs with FIP-High in Figure 8, Section 3.1). This result is consistent with the fact that companies may be more conservative in capital investments under uncertainty in reality [6]. Heavy investments in either PV or wind may become a damper of large-scale VRE introduction, even though the high financial support attempts to expedite investments from a behavioral decision point of view.
Second, in contrast with the above point, in the case where high financial support is predicted and Company 2 attempts to make a balanced investment in both PV and wind, they possibly decide to invest in VRE that exceeds the capacity of the highest expected NPV (graphs with FIP-High in Figure 10, Section 3.3). This is because the balanced mixture of VRE maintains the increment in income uncertainties, and the risk is relatively smaller when the total VRE capacity increases. Some analyses in previous studies suggest that investments in both PV and wind reduce uncertainty and risk [51], and are economically preferable as renewable build-up pathways [52]. Modern portfolio theory also supports this result that an appropriate mixture ratio of PV to wind reduces the risk in VRE investment [53]. In addition, it was observed that the balanced mixture of PV and wind encourages RE investors, and the preferable capacity can be greater than the result obtained by the conventional NPV method, although the capacity to identify this investor behavior needs further verification from real-world case studies. Considering the results of the first and second points above, we suggest that governments implement policies to expedite investments in both PV and wind, in addition to offering adequate financial support. In addition, the influence of the RFP difference is relatively small in the case of high financial support.
Third, in the case where low financial support is anticipated and the middle management emphasizes the “risk” in their suggestions, the top management may decide to invest in a small amount of VRE even though no investment (0 MW) earns the highest expected NPV (FIP-low cases in Figure 8, Section 3.1). That is, the top management may progress in VRE investment if they have a relatively lower RFP due to the influence of the middle management. We observe a similar trend in different scenarios, regardless of the strategies of the competitor (Company 1; FIP-Low cases in Figure 9, Section 3.2), the mixture ratio of PV to wind (FIP-Low cases in Figure 10, Section 3.3), or the option to expand (in Figure 11, Section 3.4). As shown by a previous questionnaire survey, RE investors were sensitive to the influence of peers [26], and the RE investor’s behavior in the survey supports the simulation results of the model developed here; that is, our study shows that the top management can be more aggressive in RE investments if surrounding peers emphasize the risk of investment when financial support is lower. In this study, we should mention that decision makers are sensitive to the difference in RFP in the case of low financial support, in contrast with the first and second points discussed above.
In summary, we examined the behavior of RE companies regarding VRE investment decisions using the developed model based on the designed framework and concluded that, compared to the optimal results yielded by the conventional NPV approach: (1) heavy investments in either PV or wind lead to reduced VRE capacity in the case of sufficient financial support; (2) balanced investment in both PV and wind results in increased VRE capacity in the case of sufficient financial support; and (3) suggestions that reduce the RFP of the decision makers expedite a small amount of VRE investments, despite the insufficient financial support.
Despite the significant valuable results obtained from this study, and the contribution that will be made by emphasizing the proposed novel framework in future analysis of the decision making of VRE investment in the spot price market, certain conditions that may affect the results of this study are worth mentioning for the sake of future studies.
- This study assumed that the energy market was competitive, even though there were only two players (Company 1 and 2) in the market, in order to examine the novel decision-making model. Although renewable power generation companies were consolidated into Company 2 for simplicity, each renewable power generation company in the region may interact in reality. Moreover, although the strategies of Company 1 were provided by some scenarios in this study, the interactions between the decisions of Company 1 and the RE companies need to be considered in future work.
- In this study, only two types of RFPs were defined as the influence of the suggestions of the middle management for simplicity: Ref_EXP (higher RFP) and Ref_CVaR (lower RFP) for simplicity. However, as mentioned in the framework of Section 2.1, several factors will influence the RFP of the top management other than suggestions from the middle management, such as personal and exogenous influences. We should examine how the other non-normative perspectives affect the decisions made by the RE company.
- Although the NPV method was applied to the normative perspective of RE companies in the decision-making model, other methods such as IRR or Real Options approaches may be applicable. The Kahneman and Tversky approach [29,30] was used here to quantitatively express the non-normative perspective of RE companies; however, other approaches, such as the Regret theory, could be used for the non-normative perspective. Alternative methods should be further investigated in future studies.
- Energy storage was not applied as an option for technology. As the timeframe of decision making in this study was 2020–2030, we expected the effect of energy storage to be limited. However, energy storage should be considered in further studies of VRE introduction, such as the energy transition in the 2050s, on a larger scale.
- The electricity trade spot price and feed-in premium were the only financial supports considered for VRE to simplify the spot price market model. As emerging electricity markets and financial supports, such as the capacity market, are still being discussed in Japan, the effects of such new systems need to be examined.
Author Contributions
Conceptualization, R.G. and T.T.; methodology, R.G.; software, R.G.; validation, R.G. and T.T.; formal analysis, R.G.; investigation, R.G.; data curation, R.G.; writing—original draft preparation, R.G.; writing—review and editing, R.G., B.C.M. and T.T.; visualization, R.G.; supervision, T.T. and B.C.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Application of Reference Point, Value Function, and the Weighting Function
Essential characteristics of the reference point, value function, and weighting function [29,30] focused on in this study are as follows:
- Reference Point (RFP)
Values are evaluated by gains and losses relative to an RFP, and the RFP can be influenced and shifted by the expectation of the decision maker. This indicates that a change in RFP yields a different value for the decision makers, even though they acquire the same outcome from their decision.
where x is the gain/loss relative to the RFP, xoc is the outcome of the option, and xrp is the RFP.
- 2.
- The Value Function
The value function is defined as Equation (A2), and the expected shape is shown in Figure A1. This function shows that the decision maker tends to be risk-averse in the positive domain (x ≥ 0) and be risk-seeking in the negative domain (x < 0).
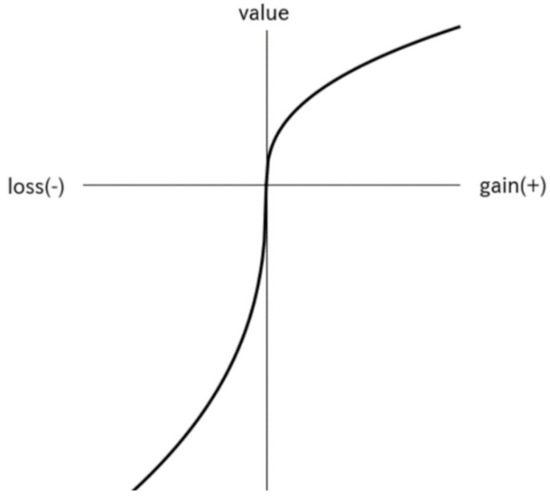
Figure A1.
The Value Function (based on [30]).
The median exponent α for gains of 0.88, β for losses of 0.88, and the median λ of 2.25 were used in this paper, which was shown by Tversky and Kahneman [29,30].
- 3.
- The Weighting Function
Although there are several studies on definitions of the Weighting Function [54,55,56], we applied the Weighting Function that was given by Tversky and Kahneman [30] because their definition is the most commonly used. The Value of each outcome is given by multiplying the Value Function by the Weighting Function (A3), which expresses the subjective probability of each outcome, as shown in (A4) and Figure A2. The median values γ of 0.61 for positive xi (gains) and 0.69 for negative xi (losses) are used in this study, which were shown by Tversky and Kahneman [30].
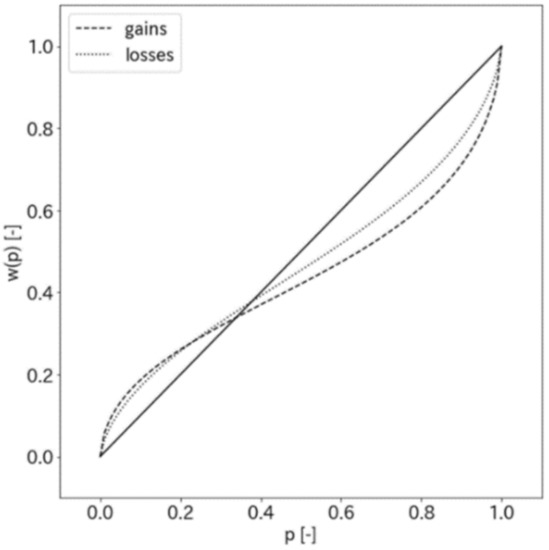
Figure A2.
The Weighting Function (based on [30]).
Appendix B. Definition of NPV and the Other Outputs
- 1.
- Net Present Value (NPV)
NPV in this study is defined as follows:
where parameters of capital letters mean exogenous variables or fixed values, and parameters of lower cases are endogenous variables. The indexes of i, j, t, and y express the number of trials in iterative calculations of the model, technologies (1: PV, 2: Wind), time, and year, respectively. The npvi is total NPV [yen], cfiy is cash flow earned in the spot price market, DR is the discount rate (set as 5% considering the Weighted Average Cost of Capital (WACC) of the electric utility companies in Japan [57]), CAPEXj is the initial cost of each technology, spity is the spot price in the spot price market, FIPj is the price of FIP, mcijy is the marginal cost of power generation [yen/kWh], and opijty is the power output of each technology [kWh].
The following equations give the expected value and standard deviation of NPV.
where N is the total number of trials in iterative calculations (=1000 times in this study). expNPV and sdNPV represent the expected value and standard deviation of NPV.
- 2.
- Value at Risk (VaR) and Conditional Value at Risk (CVaR)
VaR is one type of expected shortfall, and the “VaR at q%” is defined as the expected income in the worst q% of cases. CVaR is the average of values below VaR cases. In this study, 1000 cases of NPV are given for each calculation by the simulation in line with probability distributions, and CVaR calculated based on “VaR at 5%” is used; CVaR of NPV is the average of the 5% lowest cases of NPVi. CVaR is interpreted as the expected NPV, which Company 2 earns in the worst-case scenario for each calculation in this study.
Appendix C. Properties of Technology

Table A1.
Properties of each type of technology are shown in the following table.
Table A1.
Properties of each type of technology are shown in the following table.
| Item | Unit | Technology | Value | Remarks |
|---|---|---|---|---|
| Construction Cost | [yen/kW] | GTCC (Natural Gas) | 120,000 | [58] |
| PV | 273,500 | |||
| Wind (On-shore) | 287,000 | |||
| Operation & Maintenance | [%/Year] | GTCC (Natural Gas) | 3.0 | [58] |
| Steam Power (Oil) | 3.2 | |||
| Steam Power (Coal) | 4.0 | |||
| Nuclear | 5.2 | |||
| PV | 1.2 | |||
| Wind (On-shore) | 2.1 | |||
| Gross Plant Efficiency (LHV) | [%-LHV] | GTCC (Natural Gas, Existing) | 51.5 | Based on [58] |
| GTCC (Natural Gas, Replaced) | 58.6 | |||
| Steam Power (Oil) | 37.5 | |||
| Steam Power (Coal) | 40.8 | |||
| Payback Period | [Year] | GTCC | 15 | [58] |
| PV | 10 | |||
| Wind (On-shore) | 10 | |||
| Lifetime | [Year] | GTCC | 40 | [58] |
| PV | 20 | |||
| Wind (On-shore) | 20 | |||
| CO2 Emission Coefficient | [t-CO2/t] | GTCC (Natural Gas) | 2.7 | [59] |
| Steam Power (Oil) | 3.4 | |||
| Steam Power (Coal) | 2.3 |
Appendix D. Calculation Results of Each Case
Data of calculation results in each case are shown in Table A2, Table A3, Table A4, Table A5 and Table A6, which correspond to Figure 8, Figure 9, Figure 10 and Figure 11, respectively.
(“Exp.” means “Expected”, “SD” means “Standard Deviation” in the tables).

Table A2.
Calculation results of Cases 1 and 2 (corresponding to Figure 8).
Table A2.
Calculation results of Cases 1 and 2 (corresponding to Figure 8).
| Scenario | Case | 1 (Investments in PV) | 2 (Investments in Wind) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total Capacity | Unit | 0 | 1000 | 3000 | 5000 | 7000 | 0 | 1000 | 3000 | 5000 | 7000 | |
| FIP- Low | Exp. NPV | Billion yen | 372.9 | 335.8 | 221.1 | 67.7 | −129.6 | 372.9 | 339.2 | 212.3 | −15.5 | −316.1 |
| Exp.Value (Ref_EXP) | - | 0.0 | −37.7 | −123.6 | −225.9 | −346.1 | 0.0 | −37.0 | −126.7 | −270.2 | −461.6 | |
| Exp.Value (Ref_CVa) | - | 0.0 | 0.3 | −84.1 | −188.6 | −312.2 | 0.0 | 0.6 | −87.9 | −232.5 | −426.0 | |
| SD of NPV | Billion yen | 26.0 | 40.0 | 65.7 | 91.7 | 105.8 | 26.0 | 48.1 | 97.7 | 141.0 | 167.7 | |
| CVaR of NPV | Billion yen | 319.0 | 253.7 | 88.6 | −123.1 | −342.8 | 319.0 | 243.0 | 9.7 | −290.1 | −642.1 | |
| FIP- Mid | Exp.NPV | Billion yen | 372.9 | 363.3 | 308.4 | 217.0 | 69.2 | 372.9 | 415.0 | 428.9 | 357.3 | 188.9 |
| Exp.Value (Ref_EXP) | - | 0.0 | −19.2 | −61.7 | −129.9 | −209.2 | 0.0 | 9.9 | −0.4 | −38.4 | −135.9 | |
| Exp.Value (Ref_CVa) | - | 0.0 | 14.2 | −24.1 | −90.5 | −173.4 | 0.0 | 36.7 | 29.0 | −8.6 | −104.0 | |
| SD of NPV | Billion yen | 26.0 | 41.3 | 69.1 | 95.8 | 117.6 | 26.0 | 53.3 | 128.7 | 189.6 | 217.7 | |
| CVaR of NPV | Billion yen | 319.0 | 277.2 | 172 | 18.7 | −174.9 | 319.0 | 305.4 | 163.3 | −3.6 | −230.5 | |
| FIP- High | Exp.NPV | Billion yen | 372.9 | 407.8 | 440.9 | 441.7 | 367.8 | 372.9 | 466.2 | 580.2 | 604.4 | 520.4 |
| Exp.Value (Ref_EXP) | - | 0.0 | 9.0 | 17.5 | 0.7 | −38.1 | 0.0 | 35.4 | 62.8 | 65.6 | 22.4 | |
| Exp.Value (Ref_CVa) | - | 0.0 | 34.7 | 43.7 | 29.1 | −8.6 | 0.0 | 57.9 | 85.7 | 90.2 | 49.1 | |
| SD of NPV | Billion yen | 26.0 | 41.8 | 74.4 | 107.9 | 134.3 | 26.0 | 62.8 | 148.7 | 221.3 | 269.9 | |
| CVaR of NPV | Billion yen | 319.0 | 324.7 | 294.4 | 201.4 | 89.5 | 319.0 | 346.0 | 282.6 | 164.6 | −21.0 | |

Table A3.
Calculation results of Cases 3 and 4 (corresponding to Figure 9).
Table A3.
Calculation results of Cases 3 and 4 (corresponding to Figure 9).
| Scenario | Case | 3 (Investments in PV with FIP-Low) | 4 (Investments in Wind with FIP-Low) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total Capacity | Unit | 0 | 1000 | 3000 | 5000 | 7000 | 0 | 1000 | 3000 | 5000 | 7000 | |
| wRP _NC60 | Exp. NPV | Billion yen | 372.9 | 335.8 | 221.1 | 67.7 | −129.6 | 372.9 | 339.2 | 212.3 | −15.5 | −316.1 |
| Exp. Value (Ref_EXP) | - | 0.0 | −37.7 | −123.6 | −225.9 | −346.1 | 0.0 | −37.0 | −126.7 | −270.2 | −461.6 | |
| Exp. Value (Ref_CVa) | - | 0.0 | 0.3 | −84.1 | −188.6 | −312.2 | 0.0 | 0.6 | −87.9 | −232.5 | −426.0 | |
| SD of NPV | Billion yen | 26.0 | 40.0 | 65.7 | 91.7 | 105.8 | 26.0 | 48.1 | 97.7 | 141.0 | 167.7 | |
| CVaR of NPV | Billion yen | 319.0 | 253.7 | 88.6 | −123.1 | −342.8 | 319.0 | 243.0 | 9.7 | −290.1 | −642.1 | |
| wRP _NC40 | Exp. NPV | Billion yen | 464.6 | 451.3 | 413.2 | 354.3 | 255.5 | 464.6 | 483.3 | 475.5 | 413.6 | 258.7 |
| Exp. Value (Ref_EXP) | - | 0.0 | −21.6 | −52.2 | −100.6 | −154.2 | 0.0 | −1.9 | −15.9 | −63.5 | −151.0 | |
| Exp. Value (Ref_CVa) | - | 0.0 | 16.9 | −10.6 | −53.7 | −112.7 | 0.0 | 30.7 | 19.7 | −23.6 | −112.0 | |
| SD of NPV | Billion yen | 32.1 | 45.6 | 78.8 | 96.7 | 122.5 | 32.1 | 56.1 | 119.1 | 186.9 | 219.9 | |
| CVaR of NPV | Billion yen | 400 | 360 | 255 | 159 | 17 | 400 | 377 | 254 | 54 | −174 | |
| woRP _NC60 | Exp. NPV | Billion yen | 335.1 | 285.8 | 154.1 | 1.3 | −193.1 | 335.1 | 284.3 | 124.1 | −111.3 | −415.4 |
| Exp. Value (Ref_EXP) | - | 0.0 | −47.1 | −148.3 | −241.6 | −358.6 | 0.0 | −50.6 | −150.1 | −310.9 | −501.0 | |
| Exp. Value (Ref_CVa) | - | 0.0 | −5.8 | −105.4 | −204.1 | −323.9 | 0.0 | −12.2 | −115.8 | −277.0 | −469.8 | |
| SD of NPV | Billion yen | 27.9 | 37.3 | 59.9 | 82.7 | 101.3 | 27.9 | 45.0 | 96.4 | 135.9 | 160.6 | |
| CVaR of NPV | Billion yen | 278.7 | 211.4 | 31.7 | −163.0 | −402.4 | 278.7 | 196.6 | −64.5 | −372.5 | −730.2 | |

Table A4.
Calculation results of Cases 5 and 6 (corresponding to Figure 10).
Table A4.
Calculation results of Cases 5 and 6 (corresponding to Figure 10).
| Scenario | Case | 5 (with FIP-Low) | 6 (with FIP-High) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total Capacity | Unit | 0 | 1000 | 3000 | 5000 | 7000 | 0 | 1000 | 3000 | 5000 | 7000 | |
| PV _ONLY | Exp. NPV | Billion yen | 372.9 | 335.8 | 221.1 | 67.7 | −129.6 | 372.9 | 407.8 | 440.9 | 441.7 | 367.8 |
| Exp. Value (Ref_EXP) | - | 0.0 | −37.7 | −123.6 | −225.9 | −346.1 | 0.0 | 9.0 | 17.5 | 0.7 | −38.1 | |
| Exp. Value (Ref_CVaR) | - | 0.0 | 0.3 | −84.1 | −188.6 | −312.2 | 0.0 | 34.7 | 43.7 | 29.1 | −8.6 | |
| SD of NPV | Billion yen | 26.0 | 40.0 | 65.7 | 91.7 | 105.8 | 26.0 | 41.8 | 74.4 | 107.9 | 134.3 | |
| CVaR of NPV | Billion yen | 319.0 | 253.7 | 88.6 | −123.1 | −342.8 | 319.0 | 324.7 | 294.4 | 201.4 | 89.5 | |
| WIND _ONLY | Exp. NPV | Billion yen | 372.9 | 339.2 | 212.3 | −15.5 | −316.1 | 372.9 | 466.2 | 580.2 | 604.4 | 520.4 |
| Exp. Value (Ref_EXP) | - | 0.0 | −37.0 | −126.7 | −270.2 | −461.6 | 0.0 | 35.4 | 62.8 | 65.6 | 22.4 | |
| Exp. Value (Ref_CVaR) | - | 0.0 | 0.6 | −87.9 | −232.5 | −426.0 | 0.0 | 57.9 | 85.7 | 90.2 | 49.1 | |
| SD of NPV | Billion yen | 26.0 | 48.1 | 97.7 | 141.0 | 167.7 | 26.0 | 62.8 | 148.7 | 221.3 | 269.9 | |
| CVaR of NPV | Billion yen | 319.0 | 243.0 | 9.7 | −290.1 | −642.1 | 319.0 | 346.0 | 282.6 | 164.6 | −21.0 | |
| MIX1 (PV:Wind =1:1) | Exp. NPV | Billion yen | 372.9 | 340.4 | 240.3 | 93.0 | −84.7 | 372.9 | 443.3 | 542.0 | 593.5 | 601.0 |
| Exp. Value (Ref_EXP) | - | 0.0 | −35.3 | −116.8 | −221.1 | −312.7 | 0.0 | 26.6 | 60.5 | 73.7 | 63.9 | |
| Exp. Value (Ref_CVaR) | - | 0.0 | 3.6 | −72.1 | −178.6 | −276.2 | 0.0 | 49.4 | 81.1 | 95.5 | 85.9 | |
| SD of NPV | Billion yen | 26.0 | 40.7 | 69.9 | 97.9 | 121.4 | 26.0 | 46.0 | 92.9 | 144.5 | 180.7 | |
| CVaR of NPV | Billion yen | 319.0 | 257.5 | 99.8 | −106.1 | −330.0 | 319.0 | 350.6 | 356.0 | 305.5 | 228.7 | |
| MIX2 (PV:Wind =7:3) | Exp. NPV | Billion yen | 372.9 | 339.1 | 237.0 | 106.4 | −70.5 | 372.9 | 426.6 | 512.1 | 550.3 | 563.6 |
| Exp. Value (Ref_EXP) | - | 0.0 | −36.5 | −114.6 | −197.0 | −320.3 | 0.0 | 18.9 | 49.1 | 63.9 | 58.6 | |
| Exp. Value (Ref_CVaR) | - | 0.0 | 1.1 | −75.0 | −160.9 | −285.3 | 0.0 | 43.1 | 70.0 | 86.5 | 80.7 | |
| SD of NPV | Billion yen | 26.0 | 40.1 | 67.5 | 89.2 | 116.5 | 26.0 | 43.0 | 78.6 | 111.7 | 155.9 | |
| CVaR of NPV | Billion yen | 319.0 | 258.8 | 102.5 | −79.5 | −305.3 | 319.0 | 339.4 | 350.4 | 330.3 | 262.1 | |
| MIX3 (PV:Wind =3:7) | Exp. NPV | Billion yen | 372.9 | 338.0 | 231.6 | 60.2 | −126.4 | 372.9 | 451.4 | 550.3 | 610.7 | 611.0 |
| Exp. Value (Ref_EXP) | - | 0.0 | −37.8 | −115.0 | −211.3 | −345.6 | 0.0 | 29.3 | 64.5 | 78.0 | 79.1 | |
| Exp. Value (Ref_CVaR) | - | 0.0 | −1.2 | −77.3 | −177.2 | −311.3 | 0.0 | 50.6 | 84.0 | 97.1 | 100.4 | |
| SD of NPV | Billion yen | 26.0 | 42.8 | 82.2 | 114.4 | 134.2 | 26.0 | 50.4 | 106.1 | 166.8 | 198.0 | |
| CVaR of NPV | Billion yen | 319.0 | 251 | 69 | −167 | −379 | 319.0 | 353 | 338 | 283 | 227 | |

Table A5.
Calculation results of Cases 7 and 8 (corresponding to Figure 11).
Table A5.
Calculation results of Cases 7 and 8 (corresponding to Figure 11).
| Scenario | Case | 7 (Investments in PV with FIP-Low) | 8 (Investments in Wind with FIP-Low) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total Capacity | Unit | 0 | 1000 | 3000 | 5000 | 7000 | 0 | 1000 | 3000 | 5000 | 7000 | |
| PV (Case 7) WIND _OE (Case 8) | Exp NPV | Billion yen | 372.9 | 335.8 | 221.1 | 67.7 | −129.6 | 372.9 | 339.2 | 212.3 | −15.5 | −316.1 |
| Exp Value (Ref_EXP | - | 0.0 | −37.7 | −123.6 | −225.9 | −346.1 | 0.0 | −37.0 | −126.7 | −270.2 | −461.6 | |
| Exp Value (Ref_CVaR) | - | 0.0 | 0.3 | −84.1 | −188.6 | −312.2 | 0.0 | 0.6 | −87.9 | −232.5 | −426.0 | |
| SD of NPV | Billion yen | 26.0 | 40.0 | 65.7 | 91.7 | 105.8 | 26.0 | 48.1 | 97.7 | 141.0 | 167.7 | |
| CVaR of NPV | Billion yen | 319.0 | 253.7 | 88.6 | −123.1 | −342.8 | 319.0 | 243.0 | 9.7 | −290.1 | −642.1 | |
| PV (Case 7) WIND _OE (Case 8) | Exp NPV | Billion yen | 372.9 | 345.0 | 279.7 | 224.6 | 157.8 | 372.9 | 341.2 | 261.2 | 168.0 | 65.7 |
| Exp Value (Ref_EX) | - | 0.0 | −32.5 | −92.9 | −138.4 | −170.8 | 0.0 | −36.5 | −113.5 | −179.0 | −249.4 | |
| Exp. Value (Ref_CVaR) | - | 0.0 | 6.8 | −51.8 | −98.4 | −135.5 | 0.0 | −1.5 | −74.6 | −143.8 | −215.5 | |
| SD of NPV | Billion yen | 26.0 | 32.8 | 65.9 | 92.9 | 122.7 | 26.0 | 40.0 | 93.2 | 150.3 | 201.0 | |
| CVaR of NPV | Billion yen | 319.0 | 276.1 | 106.5 | −70.7 | −259.5 | 319.0 | 250.8 | 35.9 | −227.1 | −493.7 | |

Table A6.
Calculation results of Cases 9 and 10 (corresponding to Figure 11).
Table A6.
Calculation results of Cases 9 and 10 (corresponding to Figure 11).
| Scenario | Case | 9 (Investments in PV with FIP-Low) | 10 (Investments in PV with FIP-High) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total Capacity | Unit | 0 | 1000 | 3000 | 5000 | 7000 | 0 | 1000 | 3000 | 5000 | 7000 | |
| PV (Case 9) WIND _OE (Case 10) | Exp. NPV | Billion yen | 372.9 | 407.8 | 440.9 | 441.7 | 367.8 | 372.9 | 466.2 | 580.2 | 604.4 | 520.4 |
| Exp. Value (Ref_EXP) | - | 0.0 | 9.0 | 17.5 | 0.7 | −38.1 | 0.0 | 35.4 | 62.8 | 65.6 | 22.4 | |
| Exp. Value (Ref_CVaR) | - | 0.0 | 34.7 | 43.7 | 29.1 | −8.6 | 0.0 | 57.9 | 85.7 | 90.2 | 49.1 | |
| SD of NPV | Billion yen | 26.0 | 41.8 | 74.4 | 107.9 | 134.3 | 26.0 | 62.8 | 148.7 | 221.3 | 269.9 | |
| CVaR of NPV | Billion yen | 319.0 | 324.7 | 294.4 | 201.4 | 89.5 | 319.0 | 346.0 | 282.6 | 164.6 | −21.0 | |
| PV (Case 9) WIND _OE (Case 10) | Exp. NPV | Billion yen | 372.9 | 360.9 | 313.3 | 238.4 | 142.3 | 372.9 | 409.0 | 430.6 | 394.4 | 327.7 |
| Exp. Value (Ref_EXP) | - | 0.0 | −19.7 | −62.1 | −115.5 | −173.7 | 0.0 | 10.2 | 8.7 | −22.1 | −72.5 | |
| Exp. Value (Ref_CVaR) | - | 0.0 | 14.0 | −24.1 | −77.4 | −136.6 | 0.0 | 35.1 | 31.9 | 6.4 | −42.4 | |
| SD of NPV | Billion yen | 26.0 | 37.9 | 67.8 | 96.2 | 141.4 | 26.0 | 49.3 | 116.7 | 174.5 | 216.9 | |
| CVaR of NPV | Billion yen | 319.0 | 285.7 | 178.0 | 41.9 | −105.4 | 319.0 | 315.1 | 204.8 | 43.8 | −126.6 | |
References
- Raiffa, H.; Tversky, A. Decision Making: Descriptive, Normative, and Prescriptive Interactions; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Lepenioti, K.; Bousdekis, A.; Apostolou, D.; Mentzas, G. Prescriptive analytics: Literature review and research challenges. Int. J. Inf. Manag. 2020, 50, 57–70. [Google Scholar] [CrossRef]
- Block, S. Are real options actually used in the real world? Eng. Econ. 2007, 52, 255–267. [Google Scholar] [CrossRef]
- Baker, H.K.; Dutta, S.; Saadi, S. Management Views on Real Options in Capital Budgeting. J. Appl. Financ. 2011, 21, 18–29. [Google Scholar] [CrossRef]
- Luenberger, D. Investment Science; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Summers, L.H. Investment Incentives and The Discounting Of Depreciation Allowances. In The Effects of Taxation on Capital Accumulation; Martin, F., Ed.; University of Chicago Press: Chicago, IL, USA, 1987. [Google Scholar]
- McDonald, R.; Siegel, D. The Value of Waiting to Invest. Q. J. Econ. 1986, 101, 707–728. [Google Scholar] [CrossRef]
- Fernandes, B.; Cunha, J.; Ferreira, P. The use of real options approach in energy sector investments. Renew. Sustain. Energy Rev. 2011, 15, 4491–4497. [Google Scholar] [CrossRef]
- McDonald, R.; Siegel, D. Investment and the Valuation of Firms When There is an Option to Shut Down. Int. Econ. Rev. 1985, 26, 331–349. [Google Scholar] [CrossRef]
- Kaslow, T.; Pindyck, R. Valuing Flexibility in Utility Planning. Electr. J. 1994, 7, 60–65. [Google Scholar] [CrossRef]
- Hörnlein, L. The value of gas-fired power plants in markets with high shares of renewable energy: A real options application. Energy Econ. 2019, 81, 1078–1098. [Google Scholar] [CrossRef]
- Santos, L.; Soares, I.; Mendes, C.; Ferreira, P. Real Options versus Traditional Methods to assess Renewable Energy Projects. Renew. Energy 2014, 68, 588–594. [Google Scholar] [CrossRef]
- Zhang, M.M.; Wang, Q.; Zhou, D.; Ding, H. Evaluating uncertain investment decisions in low-carbon transition toward renewable energy. Appl. Energy 2019, 240, 1049–1060. [Google Scholar] [CrossRef]
- Li, Y.; Wu, M.; Li, Z. A real options analysis for renewable energy investment decisions under China carbon trading market. Energies 2018, 11, 1817. [Google Scholar] [CrossRef]
- Bigerna, S.; Wen, X.; Hagspiel, V.; Kort, P.M. Green electricity investments: Environmental target and the optimal subsidy. Eur. J. Oper. Res. 2019, 279, 635–644. [Google Scholar] [CrossRef]
- Naito, Y.; Takashima, R.; Kimura, H.; Madarame, H. Evaluating replacement project of nuclear power plants under uncertainty. Energy Policy 2010, 38, 1321–1329. [Google Scholar] [CrossRef]
- Glensk, B.; Madlener, R. The value of enhanced flexibility of gas-fired power plants: A real options analysis. Appl. Energy 2019, 251, 113125. [Google Scholar] [CrossRef]
- Ahmad, S.; Tahar, R.M. Selection of renewable energy sources for sustainable development of electricity generation system using analytic hierarchy process: A case of Malaysia. Renew. Energy 2014, 63, 458–466. [Google Scholar] [CrossRef]
- Amer, M.; Daim, T.U. Selection of renewable energy technologies for a developing county: A case of Pakistan. Energy Sustain. Dev. 2011, 15, 420–435. [Google Scholar] [CrossRef]
- Karger, C.R.; Hennings, W. Sustainability evaluation of decentralized electricity generation. Renew. Sustain. Energy Rev. 2009, 13, 583–593. [Google Scholar] [CrossRef]
- Theodorou, S.; Florides, G.; Tassou, S. The use of multiple criteria decision making methodologies for the promotion of RES through funding schemes in Cyprus, A review. Energy Policy 2010, 38, 7783–7792. [Google Scholar] [CrossRef]
- Saaty, T.L. Relative measurement and its generalization in decision making why pairwise comparisons are central in mathematics for the measurement of intangible factors the analytic hierarchy/network process. Rev. R. Spanish Acad. Sci. 2008, 102, 251–318. [Google Scholar] [CrossRef]
- Hahn, W.J. Making decisions with multiple criteria: A case in energy sustainability planning. EURO J. Decis. Process. 2015, 3, 161–185. [Google Scholar] [CrossRef]
- Hodgkingson, G.; Bown, N.; Manule, J.; Glaister, K.; Pearman, A. Research notes and communications breaking the frame: An analysis of strategic cognition and decision making under uncertainty. Strateg. Manag. J. 1999, 985, 977–985. [Google Scholar] [CrossRef]
- Masini, A.; Menichetti, E. The impact of behavioural factors in the renewable energy investment decision making process: Conceptual framework and empirical findings. Energy Policy 2012, 40, 28–38. [Google Scholar] [CrossRef]
- Masini, A.; Menichetti, E. Investment decisions in the renewable energy sector: An analysis of non-financial drivers. Technol. Forecast. Soc. Chan. 2013, 80, 510–524. [Google Scholar] [CrossRef]
- Salm, S.; Hille, S.L.; Wüstenhagen, R. What are retail investors ’ risk-return preferences towards renewable energy projects ? A choice experiment in Germany. Energy Policy 2016, 97, 310–320. [Google Scholar] [CrossRef]
- West, J.; Bailey, I.; Winter, M. Renewable energy policy and public perceptions of renewable energy: A cultural theory approach. Energy Policy 2010, 38, 5739–5748. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometlica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in Prospect Theory: Cumulative Representation of Uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Klein, M.; Deissenroth, M. When do households invest in solar photovoltaics? An application of prospect theory. Energy Policy 2017, 109, 270–278. [Google Scholar] [CrossRef]
- Heutel, G. Prospect theory and energy efficiency. J. Environ. Econ. Manag. 2019, 96, 236–254. [Google Scholar] [CrossRef]
- KEPCO Zero Carbon Vision 2050. Available online: https://www.kepco.co.jp/corporate/pr/2021/pdf/0226_3j_01.pdf (accessed on 15 July 2021).
- Ansoff, H.I. Corporate Strategy; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Janczak, S. The strategic decision-making process in organizations. Probl. Perspect. Manag. 2005, 3, 58–70. [Google Scholar]
- Ochi, W. Theory Z: How American Business Can Meet the Japanese Challenge; Avon Books: New York, NY, USA, 1981. [Google Scholar]
- Nonaka, I. Toward Middle-Up-Down Management: Accelerating Information Creation. Sloan Manage. Rev. 1988, 29, 9–18. [Google Scholar]
- Mom, T.J.M.; Van Den Bosch, F.A.J.; Volberda, H.W. Investigating managers’ exploration and exploitation activities: The influence of top-down, bottom-up, and horizontal knowledge inflows. J. Manag. Stud. 2007, 44, 910–931. [Google Scholar] [CrossRef]
- Loock, M. Going beyond best technology and lowest price: On renewable energy investors’ preference for service-driven business models. Energy Policy 2012, 40, 21–27. [Google Scholar] [CrossRef]
- Li, P.; Sekar, S.; Zhang, B. A capacity-price game for uncertain renewables resources. In Proceedings of the e-Energy ’18: Proceedings of the Ninth International Conference on Future Energy Systems, Karlsruhe, Germany, 12–15 June 2018; pp. 119–133. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, H.; Huang, J.; Lin, X. Storage or no storage: Duopoly competition between renewable energy suppliers in a local energy market. IEEE J. Sel. AREAS Commun. 2019, 38, 31–47. [Google Scholar] [CrossRef]
- Joskow, P.L. Capacity payments in imperfect electricity markets: Need and design. Util. Policy 2008, 16, 159–170. [Google Scholar] [CrossRef]
- The Federation of Electric Power Companies of Japan Electricity Review Japan. Available online: https://www.fepc.or.jp/english/library/electricity_eview_japan/__icsFiles/afieldfile/2020/03/11/2019ERJ_full.pdf (accessed on 10 May 2020).
- Kansai Electric Power Company Connected Capacity of Renewable Energy in Kansai Region. Available online: https://www.kansai-td.co.jp/denkiyoho/area-performance.html (accessed on 4 March 2020).
- Kansai Electric Power Company Renewable Energy of the Kansai Region. Available online: https://www.kepco.co.jp/energy_supply/energy/newenergy/index.html (accessed on 28 August 2021).
- Kansai Electric Power Company Electricity Supply and Demand Records in Kansai Region. Available online: https://www.kansai-td.co.jp/english/home/denkiyoho/area-performance.html (accessed on 4 March 2020).
- International Energy Agency. World Energy Outlook 2019; International Energy Agency: Paris, France, 2019. [Google Scholar]
- Kansai Electric Power Company Thermal Power Plants of KEPCO. Available online: https://www.kepco.co.jp/energy_supply/energy/thermal_power/plant/index.html (accessed on 4 March 2020).
- Kansai Electric Power Company Update of Nuclear Power Plants of KEPCO:2018. Available online: https://www.kepco.co.jp/ir/brief/earnings/2019/pdf/pdf2019_1029_02.pdf (accessed on 4 March 2020).
- Gotoh, R.; Tezuka, T. Study on power supply system for large scale renewable energy introduction under different strategies of existing power plant replacement. Jap. Soc. Energy Resour. 2020, 41, 38–50. [Google Scholar] [CrossRef]
- Schmidt, J.; Cancella, R.; Pereira, A.O. The role of wind power and solar PV in reducing risks in the Brazilian hydro-thermal power system. Energy 2016, 115, 1748–1757. [Google Scholar] [CrossRef]
- Becker, S.; Frew, B.A.; Andresen, G.B.; Jacobson, M.Z.; Schramm, S.; Greiner, M. Renewable build-up pathways for the US: Generation costs are not system costs. Energy 2015, 81, 437–445. [Google Scholar] [CrossRef]
- deLlano-Paz, F.; Calvo-Silvosa, A.; Antelo, S.I.; Soares, I. Energy planning and modern portfolio theory: A review. Renew. Sustain. Energy Rev. 2017, 77, 636–651. [Google Scholar] [CrossRef]
- Prelec, D. The Probability Weighting Function. Econometrica 1998, 66, 497. [Google Scholar] [CrossRef]
- Gonzalez, R.; Wu, G. On the Shape of the Probability Weighting Function. Cogn. Psychol. 1999, 166, 129–166. [Google Scholar] [CrossRef] [PubMed]
- Rieger, M.O.; Wang, M. Cumulative prospect theory and the St. Petersburg paradox. Econ. Theory 2006, 28, 665–679. [Google Scholar] [CrossRef][Green Version]
- Agency for Natural Resources and Energy; Organization for Cross-regional Coordination of Transmission Operators Setting of Demand Curves. Available online: https://www.occto.or.jp/iinkai/youryou/kentoukai/2018/files/youryou_kentoukai_16_04.pdf (accessed on 4 March 2020).
- Ministry of Economy Trade and Industry. Properties of Power Plants; Ministry of Economy Trade and Industry: Tokyo, Japan, 2015. [Google Scholar]
- Ministry of Environment of Japan List of Calculation Methods and Emission Factors. Available online: https://ghg-santeikohyo.env.go.jp/files/calc/itiran2019.pdf (accessed on 22 February 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).