Abstract
By conserving natural resources and reducing the consumption of fossil fuels, sustainable energy development plays a crucial role in energy planning. Specifically, demand-side planning must be researched and anticipated based on electricity consumption at the grounded level. Due to the global warming crisis, atmospheric conditions are among the most influential components that have altered electricity consumption patterns. In this study, 66 climate variables from the ERA5 reanalysis and the observed power demand at four grid substations (GSs) in Cambodia were examined using recurrent neural networks (RNNs). Using the cross-correlation function between power demand and each climate variable, statistically significant climate variables were sorted out. In addition, a wide range of feedback delays (FDs) was generated from the data on power demand and defined using 95% confidence intervals. The combination of the improved complete ensemble empirical mode decomposition with adaptive noise (ICEEMDAN) technique with a nonlinear autoregressive neural network with exogenous inputs (NARX) and a nonlinear autoregressive neural network (NAR) produced a hybrid electricity forecasting model. The data were decomposed into the intrinsic mode functions (IMFs) and were then used as inputs in optimized NARX and NAR models. The performance of the various benchmarked models was analyzed and compared using mainly statistical indicators such as the normalized root mean square error (NMSE) and the coefficient of determination (R2). The hybrid models perform exceptionally well in predicting electricity demand, and the ICEEMDAN-NARX hybrid model with correlated climate variables performs the best among the tested experiments as a useful prediction tool.
1. Introduction
Demand-side energy management is significant for tackling resilient sustainability under global warming. Decision-makers can use the future perspectives provided by electricity demand management to better coordinate renewable and clean energy in the power system. For emergency conditions, producing electricity from fossil fuels may be favored even though doing so may result in costly and environmentally damaging CO2 emissions for the global power market as a whole. While many meteorological and socioeconomic aspects (demographic, GDP, economic activity, habitation, family composition, average earnings, etc.) could influence electricity usage, well-prepared electrical demand planning is vital for ensuring the reliability and sustainability of the energy supply [1,2].
Many studies on power demand prediction have been conducted with different methods. Among them, machine learning (ML) algorithms are popularly used to predict future value in diverse fields, such as load forecasting [3,4,5]. groundwater level forecasting [6], flood forecasting [7], wind speed forecasting [8,9,10], and solar radiation prediction [11,12]. A large variety of prediction techniques have been introduced to improve the precision of calculations. Kazemzadeh et al. [13] stated that demand prediction techniques can be classified into univariate and multivariate methods. In multivariate methods, external variables such as socioeconomic parameters (population growth, prices, gross domestic product (GDP), and schedule holidays) and atmospheric parameters (temperature, humidity, and rainfall) are used to improve the predictions of electricity and energy demand. Univariate methods are commonly used in time series procedures in which a historical dataset is utilized to predict load demand [13].
In developed counties, economic growth potential could push energy demand to receive more attention since the reliability and sustainability of energy development have become crucial for all sectors. Some case studies presented various techniques to forecast electricity or energy demand, demonstrating promising outcomes.
For example, in Australia, Ahmed et al. [14] developed a multiple linear regression (MLR) model using climatic and socioeconomic variables as functions of the power demand for predicting long-term future electricity demand. In addition, a sensitivity analysis of the temperature rises in different seasons was conducted to demonstrate the cooling and heating needs for electricity consumption up to 2100 s. As a result, it was determined that a temperature rise alone could increase per capita electricity usage during the summer and spring seasons. For a microgrid power management, Tayab et al. [15] presented a feed-forward neural network (FFNN) featuring Harris hawk optimization (HHO) with three-level best-basis stationary wavelet packet transform decomposition (SWPT) as a combined short-term demand prediction models. To confirm the effectiveness and improvement of the suggested model, it was compared to a particle swarm optimization-based artificial neural network (PSO-ANN), a backpropagation-based neural network (BPNN), and a PSO-based least-squares support vector machine (PSO-LSSVM). As a result, the proposed SWPT-HHO-FNN was more effective than the other models tested in the study. Similarly, for short-term electricity demand predication, AL-Musaylh et al. [16] compared the performance of an artificial neural network (ANN) model to autoregressive integrated moving average (ARIMA), multivariate adaptive regression spline (MARS), and MLR models for short-term electricity demand forecasting. Moreover, input variables, such as historical demand, ground-based climate, and satellite variables via ERA-interim in the European Centre for Medium-Range Weather Forecasts (ECMWF), were simulated in each model with 6-h and daily forecast horizons. According to the study’s findings, the ANN fared the best among the compared ML methods.
In Canada, Runge et al. [17] developed a nonlinear autoregressive (NAR) neural network to forecast future values using the historical fan airflow supply rate with a 15-min interval dataset as input. Then, the airflow rate output (6 h ahead) of the NAR was used to calculate electricity consumption based on a physical model. Moreover, the comparisons were made between support vector regression (SVR) and ensemble approaches and the improved NAR architecture. The results of the study showed that automating the hyperparameter search process for an outstanding NAR model was advantageous for mitigating difficulty and achieving an optimized NAR model. Additionally, in terms of evaluation indices, the NAR model could provide slightly better performance than the SVR model.
On the other hand, in the last decade, studies on future energy predictions with various algorithms have been reported in Southeast Asian countries. Sulandari et al. [18] proposed a hybrid approach consisting of a linear recurrent formula (LRF), singular spectrum analysis (SSA), and an FFNN for hourly and half-hour electricity load forecasting in Indonesia. Concurrently, H.-Y. Lee et al. [19] used an ANN-based urban growth factor model for energy consumption forecasting in Vietnam.
In China, Shen et al. [20] proposed the combination of the variational mode decomposition (VMD) algorithm with a convolutional neural network (CNN) and a temporal convolutional network (TCN). The original input time series signal was decomposed using the VMD method to verify the impact of seasonal power load variation trends on the forecasting precision. Then, each decomposed feature was injected into the CNN, and a TCN was used to reshape the convolutional layer to improve forecasting accuracy. Similarly, R. Li et al. [21] proposed an original hybrid forecasting mechanism that coupled the adaptive Fourier decomposition (AFD) technique and an SVM for power demand time series.
In India, Bedi and Toshniwal [22] developed long–short-term memory (LSTM) network-based multi-input multioutput models that were built upon deep learning framework models to predict long-term future electricity demand. Moving window-based active learning was examined to increase forecasting accuracy.
Similarly, Kandananond [23] compared the ANN, ARIMA, and MLR methods based on yearly historical data (socioeconomic and electricity consumption data) in Thailand. Furthermore, Jaisumroum and Teeravaraprug [24] compared the performance of ANN and MLR methods to predict yearly electricity consumption in Thailand. In a study in the Philippines, Bantugon and Gallano [25] used a classical method (the Holt–Winters approach) and neural networks for short-term (hourly) and long-term (annual) load prediction.
Cambodia is one of the developing countries located in Southeast Asia. Cambodia’s economic growth of approximately 7% from 2010 to 2018 [26] has caused the country to require massive electricity consumption to supply industrial and commercial activities. The power development plan (PDP) of Cambodia was updated and studied mainly for electricity forecasting and future plant generation up to 2030 [27]. Based on regression techniques called the simple econometric simulation system (Simple E), it was discovered that GDP is one of the primary elements influencing the future trend of electricity. After the PDP was formed in 2015, the forecasted power lagged behind the actual power, which led to an imbalance between the demand and supply of the energy sector in Cambodia. Another challenge was determined regarding the dependence on large hydropower and coal plants in the previous PDP [28]. According to the EAC [29], the highest proportion of the energy mix was hydropower (46%), followed by coal (43%), diesel/heavy fuel oil (HFO) (9%), biomass (1%), and solar energy (1%). These two primary power resources caused some issues: (i) The vulnerability of the power system relied on the uncertainty of various seasons. Moreover, surplus energy was produced during the rainy season, while a lack of energy supply was encountered during the dry season. (ii) The inflexibility of the coal plants induced excess generation during off-peak times (low-demand times). Additionally, these problems could affect the electricity tariff faced by the country while the coal price fluctuates due to the global market [28].
Studies on the electricity and energy fields in Cambodia are limited. Among them, Lyheang and Limmeechokchai [30] used the long-range alternative energy planning (LEAP) model based on regression analysis using a linear equation with GDP to investigate the energy mix and CO2 mitigation from 2015 to 2050. Moreover, various scenarios were developed for the future injection of renewable energy and emission savings for future generation planning. San et al. [31] used a quantitative model to examine the impacts of rural household energy consumption on the economy and environment. The authors showed that economic and environmental costs for residents would be lower when biogas was introduced to replace nonconventional energy sources (fuelwood, plant waste, kerosene, and liquefied petroleum gas (LPG)). Hak et al. [32] designed qualitative and quantitative models using the Extended Snapshot (ExSS) tool for sustainable energy policy development in Cambodia and proposed five strategies for producing environmentally friendly plans for development towards 2050 that could reduce CO2 emissions by approximately 55% and 57% by 2030 and 2050, respectively. Promsen et al. [33] studied wind energy potential using Wind Atlas Analysis and Application Program (WAsP) software to estimate the installed capacity of wind energy potential in southern Cambodia. All energy-related reviews in Cambodia focused on energy policy, emission mitigation, renewable energy, and economic and environmental impact assessments for household energy consumption.
The literature review reveals that ML techniques have received increasing attention among the forecasting approaches utilized for both developing and developed countries. Among the ML techniques, ANNs can perform better than the support vector classification (SVC), MARS, MLR, and ARIMA models [16,17]. In addition, Altan et al. [9] presented that ML techniques combined with decomposition methods have achieved outstanding performance on wind speed forecasting compared with other techniques.
Therefore, based on the literature review and the energy plan in Cambodia, this study aims (1) to develop and design a new optimized recurrent neural network (RNN) and decomposition method hybrid model for future electricity demand prediction by using prediction algorithms for comparison, namely (i) a stand-alone NAR model using data in the past, (ii) a stand-alone NARX model with power demand and climate variables in the past, and (iii) hybrid models with the combination of decomposition techniques with NARX and NAR models; and (2) to identify the correlated climate variables with electricity demand and consider them in the prediction to improve the outcomes.
The goal of this study is to investigate medium- and long-term electricity forecasting models over a daily horizon dataset. Most previous studies have not concentrated on FDs, which could be defined by an autocorrelation function. Given a significant number of FDs for various datasets, as described in Section 3, this technique could replace the trial-and-error method. In addition, Section 3 presents the optimization of the NAR and NARX models, decomposition method, and hybrid models. Section 4 presents the compared results of the testing models. Finally, the discussion and conclusion are demonstrated in Section 5 and Section 6, respectively.
2. Materials
2.1. Study Area
The electricity supply covered fifteen provinces, such as Phnom Penh, Siem Reap, Preah Sihanouk, Kampong Cham, Battambang, Banteay Meanchey, Stung Treng, Rattanakkiry, Takeo, Kampot, Svay Rieng, Prey Veng, Mondulkiri, Kratie, and Kampong Speu, in 2013; however, only eight provinces had grid substations (GSs) for hourly power demand recording [34]. The power utility company in Cambodia, known as Electricité du Cambodia (EDC), is a state-owned company that has been authorized to generate, distribute, and transmit electricity throughout the country [35]. All GSs receive power from the national grid (NG) and supply energy to approximately 2,950,000 end users in each province throughout the country [36]. The GSs for which power demand records were available from 2013 to 2018 in four areas in Phnom Penh were selected, as shown in Table 1. The GS1, GS2, GS3, and west Phnom Penh (WPP) sites are located in Phnom Penh, the capital city, covering at least 60% of the total power load demand; this location is known as a load center in Cambodia, as shown in Figure 1.

Table 1.
Power demand information of the substations considered in this study and the nearest grid point information of ECMWF-ERA5 reanalysis with spatial and temporal resolutions.
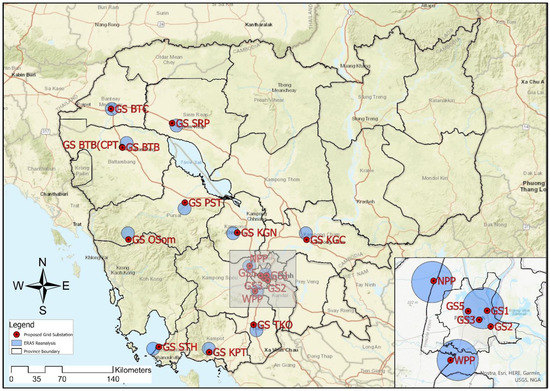
Figure 1.
Map of the study areas in Cambodia with the locations of grid substations (GSs) and the nearest grid points of the ECMWF-ERA5 reanalysis to the GSs in blue-shaded circles.
2.2. Data
2.2.1. Electricity Demand
A total of 52,584 datasets representing five years of electricity demand were collected, beginning on 1 January 2013 and ending on 31 December 2018. At each substation, the electricity data were tracked accurately by the supervisory control and data acquisition (SCADA) system. Hourly demand data (in MW) were recorded at each substation in the targeted provinces. The time series data required for the model were daily demand data; therefore, 1-h interval data were converted to a 24-h interval using the electricity consumption number at 10:00 a.m. (the highest demand of a day in the country) for a total of 2191 data points, as shown in Figure 2.
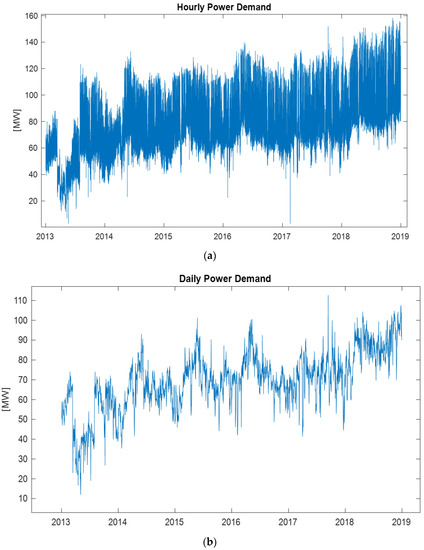
Figure 2.
(a) The original hourly power demand dataset at the GS1 site and (b) the converted daily power demand dataset from the hourly demand.
2.2.2. ERA5 Climate Reanalysis
The ERA5 climate reanalysis dataset from ECMWF was utilized for historical hourly climate data in Cambodia. ERA5 provides hourly climate variables such as atmospheric, land, and oceanic variables. The horizontal resolution of ERA5 is 0.1° × 0.1° with a 9 km spatial resolution. In this study, the latitudes and longitudes of the downloaded locations were derived from the coordinates of the selected GSs (Figure 1). The 66 climate variables presented in Table A1 were retrieved for five years from 1 January 2013 to 31 December 2018 for a total of 52,584 data points from ERA5 at each location. The time series data required for the model were daily demand data; therefore, 1-h interval data were also converted to 24-h intervals by taking the climate values at 10:00 a.m. for a total of 2191 data points.
3. Methodology
Empirical mode decomposition and its variations are used to decompose the input daily power demand into IMFs, and then, each IMF is predicted by RNN models. By combining all predicted IMFs in the end, the power demand is predicted. This is the data decomposition-RNN hybrid model of this study. The data preprocessing and decomposition techniques and RNN models are presented in the following.
3.1. Data Preprocessing
3.1.1. Imputation of Missing Values
The target data (electricity demand data) were checked, and the missing values in the power demand were imputed by a one-dimensional linear interpolation method since the missing data consisted of short intervals before they were input into decomposition and the neural network models.
is the time series electricity demand dataset and periodic variable having missing values at any time. It was assumed that in the periodic variable , there were missing data at on the interval [37]. The missing data are described in Equation (1).
where presents an application of trend interpolation to a single dimension, and presents the system disturbance caused by various variables on the periodic variable . The estimated calculation of was performed using the linear interpolation between data at and , respectively, as expressed in Equation (2).
3.1.2. Normalization of the Input Data
Normalization for the input (ERA5 climate variables) and target dataset (the power demand) before feeding them into the simulation model could improve the overall error of the neural network training process [38]. All input and target values were normalized to the range of −1 and 1 as described in Equation (3) [39].
where is the normalized value of , is , is is the actual parameter value (independent variable) of interest, is the minimum parameter value of interest, and is the maximum parameter value of interest.
3.2. Decomposition Techniques
The treated power demand is decomposed by empirical mode decomposition (EMD) and features after the missing data are imputed, as shown in the following [40].
3.2.1. Empirical Mode Decomposition (EMD)
EMD is an adaptive approach that breaks down a signal x(t) into a series of IMFs that serve as the foundation for the signal’s representation. This is how the algorithm can be explained [41]:
Step 1. Set the IMF index k = 0 and find all extrema of the 0th residue r0 = x.
Step 2. Interpolate between the minima (maxima) of rk to obtain the lower (upper) envelope emin (emax).
Step 3. Compute the mean envelope m = (emin + emax)/2.
Step 4. Compute the IMF candidate dk+1 = rk − m.
Step 5. Is dk+1 an IMF?
Yes. Save dk+1, compute the residue , iterate k = k + 1, and treat rk as input data in step 2.
No. Treat dk+1 as input data in step 2.
Step 6. Continue until the final residue rk satisfies some predefined stopping criterion.
The refinement process (steps 2 to 5) is needed to extract every mode with a certain number of iterations and is named the sifting process. EMD is adaptive and suitable for nonstationary and nonlinear data analysis. However, in the most complex case, where the processes are nonlinear, and the noises share the same time scale as the signal, EMD still fails to separate them (mode mixing).
3.2.2. Ensemble Empirical Mode Decomposition (EEMD)
By averaging the respective IMFs generated from an ensemble of the original signal x plus several realizations of finite-variance white noise, EEMD characterizes the “true” modes (denoted as in what follows). The approach of EEMD could be highlight as follows [42]:
Step 1. Generate x(i) = x + w(i), where w(i) (i = 1,…,I) presents various realizations of white noise with zero mean and unit variance, and I is the value of realizations in the ensemble and the magnitude of added noise > 0.
Step 2. Decompose each x(i) (i = 1,…,I) entirely by EMD, acquiring the modes , where k = 1, …, K presents the mode index.
Step 3. Define as the kth mode of x, acquired by averaging the corresponding modes .
The extraction of every needs a various value of sifting iterations. In EEMD, every x(i) can be decomposed independently of other realizations, and for every realization, a residue is acquired at each stage, without any connections between the various realizations. Due to this situation, some EEMD downsides may occur, including (i) an incomplete decomposition and (ii) the possibility that different realizations of signals plus noise may produce varying amounts of modes, especially at low frequencies.
3.2.3. Complete EEMD with Adaptive Noise (CEEMDAN)
To address these limitations, a new ensemble approach known as CEEMDAN was developed [43,44]. The overall concept includes the following: x(i) is produced from x, and the initial mode is calculated precisely as in EEMD. Then, a unique first residue is acquired independent of the noise realization:
After that, the first EMD mode is calculated from an ensemble of r1 values plus various realizations of a particular noise. The second mode is defined as the average of these modes. The next residue is . This technique is repeated until a termination requirement is met.
The following algorithm describes the CEEMDAN technique. Let Ek(·) be the operator that generates the kth mode obtained by EMD, and let w(i) be a realization of white noise with zero average and unit variance. Then, the following method is employed:
Step 1. For every i = 1, …, I, decompose each by EMD until receiving its initial mode and calculate
Step 2. In the initial phase (k = 1), calculate the initial residue as in Equation (4): .
Step 3. Acquire the first mode of , i = 1, …, I by EMD and determine the second CEEMDAN mode as:
Step 4. For k = 2, …, K, compute the kth residue:
Step 5. Acquire the first mode of , i = 1, …, I by EMD until the (k + 1)th CEEMDAN mode is defined as:
Step 6. Proceed to step 4 for the following k.
Iterating through steps 4 to 6 is done until the obtained residue can no longer be decomposed by EMD due to meeting the IMF criteria or having fewer than three local extrema.
Notice that by building the CEEMDAN mode, the final residue meets the following conditions:
where K presents the total number of modes. Therefore, the signal of interest x could be written as
providing a precise reconstruction of the original data by guaranteeing the completeness property of the suggested decomposition. The ultimate number of modes is determined only by the data and the stopping conditions. The coefficient allows for the selection of the signal-to-noise ratio (SNR) at each stage, where is the noise standard deviation.
There are, however, CEEMDAN features that need additional development: (i) there is some residual noise in its modes; and (ii) the signal attaches “later” than in EEMD due to the presence of “spurious” modes in the initial stages of decomposition.
Let us recall the operator Ek(·), and let M(·) be the operator that produces the local mean of the signal to which it is applied. It can be noticed that E1(x) = x − M(x). Let w(i) be a realization of white Gaussian noise, x(i) = x + w(i), and ⟨·⟩ be the action of mean throughout the realizations. For the first EEMD and original CEEMDAN modes, we have:
By anticipating only the local mean and subtracting it from the raw signal, we have:
In this manner, the quantity of noise present in the modes is minimized.
3.2.4. Improved CEEMDAN
To address these two issues, a new method for CEEMDAN is presented (hence referred to as ICEEMDAN) [45]:
Step 1. Compute the local means of I realizations by EMD to acquire the initial residue:
Step 2. In the initial phase (k = 1), compute the initial mode: .
Step 3. Determine the second residue as the average of the local means of the realizations and define the second mode:
Step 4. For k = 3, …, K, compute the kth residue:
Step 5. Calculate the kth mode:
Step 6. Go to step 4 for the next k.
The constants are chosen to achieve a desired SNR between the added noise and the residue to which the noise is added. We employ the noise produced by EMD preprocessing to obtain noise realizations with lower amplitudes for the next stages of the process of decomposition in the remaining modes, i.e., without normalizing them by their standard deviation . In this study, , , a few hundred realizations, and the same SNR were used for all the stages in all analyses.
3.3. RNN
The ANN model is comprised of numerous sub-models of neural networks. The NAR and NARX models are included in the classification of recurrent neural networks (RNNs). In addition, nonlinear dynamical models, such as NARX and NAR, are used to solve time series prediction problems [46].
3.3.1. NAR Architecture
To make projections for the future, the NAR neural network model requires as its sole input the provided historical dataset [47]. Mathematical equations for the NAR model’s output function are described in Equation (17):
where represents the historical electricity usage dataset through (t) time, presents the activation function of neural network model, and presents the FD or lagged feedback output. The FD influences both the simulated closed-loop output and the multistep predictive outcome. Additionally, it was defined by using the autocorrelation function of the input dataset (electricity demand). As a result, a sufficient FD is essential, as it allows the training process to see the peculiarities of prior data. The critical settings of the NAR model used in this investigation are as follows:
- (1)
- Feedback delay (FD): The autocorrelation of the training dataset was utilized to identify the FDs, and all significant values were employed as FDs in the model. (Figure 3).
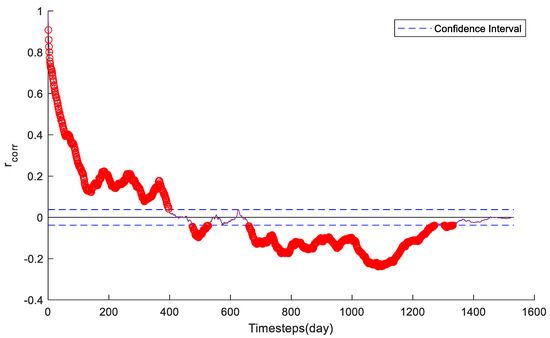 Figure 3. Autocorrelation function result for the power demand. These significant points (red circles) were used as the FDs in the model development process.
Figure 3. Autocorrelation function result for the power demand. These significant points (red circles) were used as the FDs in the model development process. - (2)
- Hidden layers: The number of hidden layer neurons was defined individually each time, for example, 10 neurons [48] and 15 neurons [12], ranging between 3 and 10 [49] and between 1 and 20 [50]. Therefore, the trial-and-error procedure was applied to investigate the number of hidden layer neurons by ranging it from 1 to 20.
- (3)
- Transfer function: Since FDs were utilized in a variety of values, the training time performance is technically the model’s constraint. Therefore, to lessen the need for both memory and time during training, Kumar and Murugan [51] proposed using scaled conjugate gradient-based back-propagation (trainscg) for this model.
- (4)
- Activation function: Sarkar et al. [52] and Vogl et al. [53] stated that the hyperbolic tangent-sigmoidal (tansig) transfer function Equation (18) could provide better results based on an error evaluation during the training process, and this function was accordingly considered as the activation function for the hidden layer and linear function (purelin) (Equation (19)) in the output layer in this study.
- (5)
- Weights and bias: The trial-and-error method employed a double loop for each number of hidden layer neurons, leading to 200 tests with randomly determined beginning weights and biases ranging from 1 to 10.
3.3.2. NARX Architecture
The NARX model is similar to the NAR model in terms of its framework; however, NARX has external inputs. The NARX model’s equation can be expressed as Equation (20).
where the exogenous input dataset is denoted by and the input delay (ID) is denoted by . While the NAR configuration served as the basis for the NARX configurations, further investigation into the ID and connected input factors was necessary. Since 66 ERA5 climate variables were used as inputs to the NARX model (Table A1), the statistically relevant variables were identified from the entire ERA5 climate variables using the cross-correlation function between the power demand and ERA5 climate variables (Figure A1). The six most associated climate variables at site GS1 were used as the exogenous inputs of the NARX model, with input delays selected as vector values between 0 and 2. . The NARX algorithm is described below as follows.
- Step 1.
- Examine the input (climate variables) and target (power demand) from the extracted files, normalize or preprocess these raw data, and convert the data file from an hourly to daily dataset by extracting data at 10:00 a.m. (the peak hour) to represent the daily data.
- Step 2.
- Define the correlated climate variables using a cross-correlation function between the input (each climate variable) and the target (power demand). Set the bounds for eliminating the variables with low correlations and set the correlation coefficient of lag from 0 to 2 as the ID.
- Step 3.
- For random weight generation, use MAX_TRIAL and MAX_HIDDEN_NEURON to set the maximum number of trials and the maximum number of neurons, respectively, in the hidden layer.
- Step 4.
- Calculate the significant lags using the autocorrelation function and define the number of significant lags as the FD for the network.
- Step 5.
- For the first loop, starting from HIDDEN_NEURON = 1 to MAX_HIDDEN_NEURON = 20.
- Step 6.
- For the second loop, starting from TRIAL = 1 to MAX_TRIAL = 10.
- Step 7.
- Construct an NARX neural network algorithms; specify the input and target vectors, setting up number of hidden layers, training function (trainscg), and the transfer function used in the hidden (tansig) and output (purelin) layers.
- Step 8.
- Divide the dataset in half. First, there is a section for TRAINING, and then, there is a section for MULTISTEP TESTING. In the Section 1, the dataset is divided into training (75 percent), validation (15 percent), and testing (15 percent) datasets using the divideint function. The multistep testing period is utilized to validate the derived prediction in the Section 2.
- Step 9.
- Prepare the data using the preparet function with the input and target of the training period.
- Step 10.
- Train the open-loop neural network using the training function.
- Step 11.
- Simulate the closed-loop neural network using the closeloop function, then use the preparets function to prepare the closed-loop system with closed-loop parameters and execute it with the train function. By using the trained closed-loop network, multistep prediction is simulated with the second part of the dataset.
- Step 12.
- Denormalize or postprocess the simulated output data of the open-loop and closed-loop neural networks. Then, calculate the performance indices of the open-loop (normalized root mean square error (NMSE), , mean absolute error (MAEo), mean absolute percentage error (MAPEo), and root mean square error (RMSEo)), closed-loop (NMSEc, , MAEc, MAPEc, and RMSEc), and multistep prediction networks (NMSEp, , MAEp, MAPEp, and RMSEp).
- Step 13.
- Record the results of the open-loop, closed-loop, and multistep prediction neural networks (the neuron size, number of trials, and performance indices in step 12) if the calculated performance indices are lower than those in the previous iteration. Skip this step otherwise.
- Step 14.
- END\\TRIAL
- Step 15.
- END\\HIDDEN_NEURON
- Step 16.
- From step 13, select the optimum NARX model.
- Step 17.
- Use the optimized NARX model for prediction.
3.4. Hybrid Model
The hybrid computational structure was proposed by combining the ICEEMDAN and RNN (NAR and NARX) models. The original dataset was decomposed into IMFs, and the NAR and NARX models were then fed the information from each IMF. The composition procedure was used to establish the initial amplitude of the dataset after the forecast results of each IMF were received. In the last phase, the optimal hybrid model between the ICEEMDAN-NAR and ICEEMDAN-NARX techniques was sought. Figure 4 illustrates the detailed structure of the hybrid model.
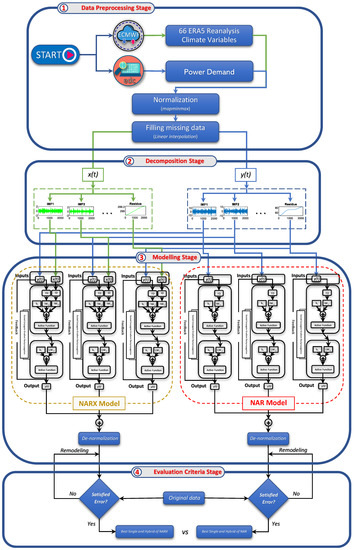
Figure 4.
Structures of the NARX and NAR models. The NAR and NARX models have basically the same structure, but the NAR model has no exogenous inputs.
3.4.1. Data Decomposition
In this stage of the study, the ICEEMDAN decomposition method generated IMFs from the power demand and climate variables. Each IMF was used as the input of an NAR (only power demand) and NARX model for the forecasting model at the next stage.
3.4.2. Experiments
Each dataset was separated into three major sections. The Section 1 was used as training (70% of data), validation (15%), and testing (15%) data from 1 January 2013 to 30 November 2018 for the open-loop and closed-loop learning models at site GS1. The Section 2 was for multistep and targetless predictions from 30 November 2018 to 20 December 2018. The last section was used for prediction beyond the known data from 20 December 2018 to 31 December 2018 (Figure 5). The open-loop system was used for training, validation, and testing the model in one particular period; however, the output of the open-loop (series-parallel) system was deducted by FDs, making it difficult to utilize that period to understand the model. This could benefit the closed-loop (parallel) system. After the closed-loop system was determined, its architecture was employed to predict the next period (multistep prediction). By using the same period and closed-loop architecture for multistep prediction, x inputs were still used, but the target was no longer used in this model for predicting the next period; this is called targetless prediction. This procedure was used to test the fitness of the model, while the target was not available in the model for future prediction. The last ten days of the known data were used to test the predicted future values by using the closed-loop architecture; this is called prediction beyond the known data. This procedure was used to test the prediction outcomes, while future x inputs were available for injection into the model. The main models for the simulations were constructed on the Intel CPU i7 processor at 2.60 GHz platform using MATLAB® 2020a with Neural Network Toolbox™.
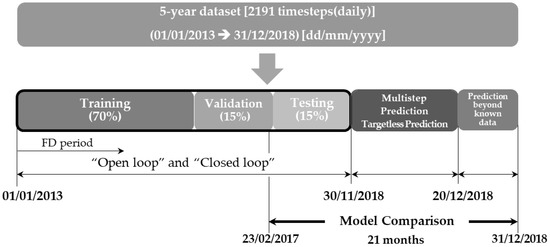
Figure 5.
Experimental design of neural network modelling for power demand prediction.
After applying decomposition for the power demand in the above stage, all IMF and residue pairs were simulated in the NAR and NARX models, respectively. The prediction results were subsequently merged into a single dataset. For the NARX model, the ICEEMDAN model was used to decompose the power demand and the statistically significant climate variables chosen by cross-correlation.
Each decomposed output (IMF and residue) of the power demand (henceforth called the target) and selected climate variables (henceforth called the x inputs) were simulated in the NARX model, and the predicted values of each IMF were merged into a single dataset. Finally, the ICEEMDAN-NAR and ICEEMDAN-NARX hybrid models were evaluated.
3.5. Performance Evaluation
Error indices were applied to assess the performance of the models: the NMSE [54], coefficient of determination , , , and , as given in Equation (21) to Equation (25).
where presents the actual value, the average of the actual values in period N , the forecasted value, and the average of the predicted values in period N for the electricity demand, respectively, and presents the overall value for the duration of the testing period. The value close to 1 indicates a perfect linear relationship between the actual and forecasted values [55,56]. The MAPE value is near to zero, and it depicts the behavior of the optimal model. Differences between actual and forecasted MW values are measured using the MAE and RMSE [57]. According to Guiamel and Lee [58], the value, as explained in Table 2, can be used to determine the goodness of fit.

Table 2.
The statistical performance evaluation for determining goodness of fit.
4. Results
4.1. Climate Variables
Among the 66 extracted climate variables from ERA5, there were several variables that were relevant to the electricity demand characteristics. Moreover, irrelevant climate variables could lead the models to follow erroneous directions in terms of future aspects. Furthermore, the elimination of irrelevant variables could prevent the heavy training process since many variables would consume the simulation memory. By calculating the cross-correlation coefficient at the k (0, 1, 2)-lag between the electricity demand and each variable dataset, six climate variables were selected, as shown in Figure 6.
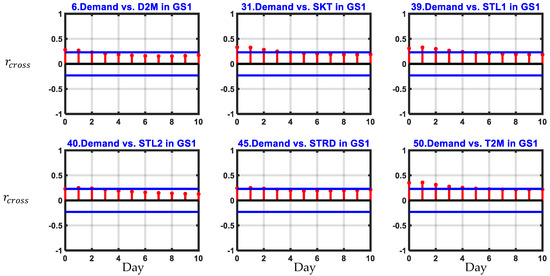
Figure 6.
Six climate variables from ERA5 reanalysis were selected by using the cross-correlation function. The upper and lower bounds (blue lines) of the confidence interval were set between −0.23 and 0.23. The chosen variables needed to have 3 (0:2) cross-correlation coefficients that were higher or lower than the bounds.
Figure 6 presents the cross-correlation coefficients for 0 to 10 lags between the electricity demand and climate variables. The confidence intervals (blue lines) were set with a minimum bound of −0.23 and a maximum bound of 0.23. These assumptions were used to increase the correlation capability and eliminate the weak relationships in the variable selection stage. Finally, the six climate variables with cross-correlation coefficients at 0 to 2 lags (daily) greater than the positive bound or smaller than the negative bound were chosen and used in the training of neural network models. The 2-meter dewpoint temperature (D2M), skin temperature (SKT), soil temperature level 1 (STL1), soil temperature level 2 (STL2), surface thermal radiation downwards (STRD), and 2-meter temperature are the six climate variables for the GS1 site (T2 M).
4.2. Decomposition Result
The power demand and six correlated climate variables were subjected to decomposition using ICEEMDAN. Figure 7 depicts the decomposition results of the power demand with nine IMFs and the residue. IMF1 is the highest frequency mode, while IMF9 represents the lowest frequency mode. IMFs 1 to 9 are statistically significant at the 5% and 95% confidence intervals. The residue indicates the nonlinear trend of the power demand over the data period.
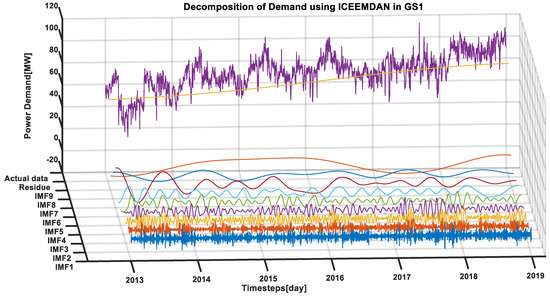
Figure 7.
Decomposition results of the daily power demand using the ICEEMDAN method at the GS1 site with nine IMFs and the residue. The dark blue color, brown color, dark yellow color, dull violet color, green color, deep blue color, red color, navy color, tawny brown color, gold color, and purple color represent the characteristic of IMF1, IMF2, IMF3, IMF4, IMF5, IMF6, IMF7, IMF8, IMF9, residue, and actual data (daily power demand), respectively.
4.3. Stand-Alone Models
A stand-alone model refers to the NAR or NARX model without the combination with the decomposition technique. The typical workflow of the NAR model is to train the open-loop network (including validation and testing stages), and then, the open-loop network is transferred to a closed-loop system for multistep-ahead forecasting.
Figure 8 demonstrates the iterative prediction process by applying the NAR model. The blue line is the original electricity demand dataset, and the red line is the predicted values yielded by the NAR neural network. The output response of the NAR model performed poorly compared to the original time series dataset even though the optimization of the model was completed during the training process. Figure 8 also illustrates the iterative prediction results in the yellow line obtained by using the NARX model. The model configurations had the same structure as that of the NAR model; however, the correlated variables (D2 M, SKT, STL1, STL2, STRD, and T2 M) became the improvement factors for NARX’s outcome. It is clearly seen that values predicted by the NARX model achieved higher accuracy than values predicted by the NAR model. Moreover, the statistical indices of both models, presenting improvements in terms of the NMSE = 14.65, MAE = 5.192 MW, RMSE = 6.745 MW, and MAPE = 0.435 (for NAR) were compared with NMSE = 1.343, MAE = 2.288 MW, RMSE = 3.713 MW, and MAPE = 0.432 (for NARX), as shown in Table 3.
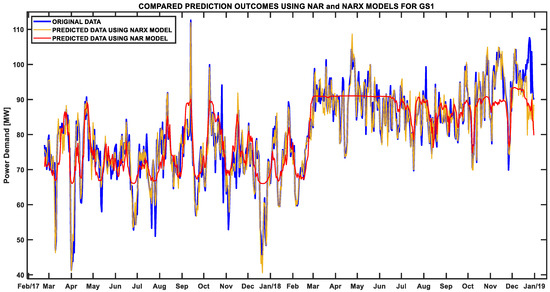
Figure 8.
Prediction results over the model comparison period obtained using the stand-alone NAR and stand-alone NARX models for the GS1 site.

Table 3.
Statistical comparisons between the stand-alone NAR and NARX models for the GS1 site.
4.4. Hybrid Models
The hybrid ICEEMDAN-NAR and ICEEMDAN-NARX models were applied to predict future daily electricity demand values. In the analysis and prediction of the power demand with the hybrid models, the IMFs generated by the ICEEMDAN were injected into the NAR and NARX models as input. Figure 9 shows and compares the prediction results of the ICEEMDAN-NAR model (Figure 9a) and the ICEEMDAN-NARX model (Figure 9b) with those of the stand-alone NAR and NARX results. The prediction results of each IMF are also illustrated in Figure 9.
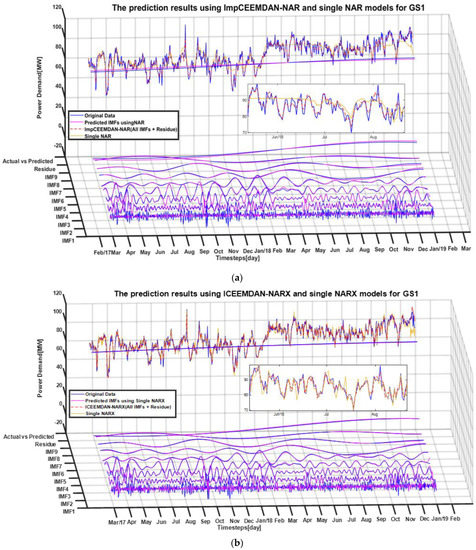
Figure 9.
Prediction results of the power demand at GS1 using (a) the hybrid ICEEMDAN−NAR and (b) the hybrid ICEEMDAN−NARX models. The prediction results of each IMF are also presented, and the prediction results of the stand-alone models are shown for comparison.
Figure 10 illustrates the anticipated outcomes from the stand-alone and hybrid models, while Table 4 provides error statistics for model performances. For site GS1, the suggested ICEEMDAN-NARX hybrid model produced excellent NMSE, , MAE, RMSE, and MAPE values of 0.048, 0.952, 1.923, 2.605, and 0.032%, respectively. Among the various models, the ICEEMDAN-NAR hybrid model could also provide good performance in terms of the NMSE, MAE, RMSE, and MAPE, with values of 0.074, 0.926, 2.519, 3.240, and 0.214%, respectively. While the stand-alone NAR and NARX models yielded relatively poor performance, the stand-alone NARX model is still capable of outperforming the stand-alone NAR model in terms of the NMSE; their values were 1.343 and 14.654, respectively. Clearly, the ICEEMDAN-NARX hybrid model attained the highest performance.
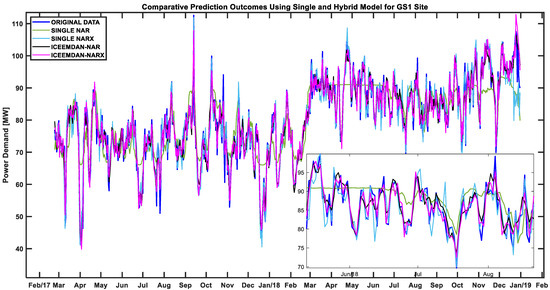
Figure 10.
Comparison of the predicted power demands among the stand−alone and hybrid models over the model comparison period with the power demand record at the GS1 site.

Table 4.
Statistical comparisons among various predictive models for the GS1 site.
5. Discussion
5.1. Sensitivity to the Number of Climate Variables
The climate variables are the motivational factors for improving the model outputs since exogenous inputs highly impact electricity demand behavior. The temperature was found to be closely related to electricity consumption since the temperature rose parallel to the demand. However, the other variables could also be affected by the geographical terrain and atmosphere; for instance, the electricity demand curve in coastal areas was influenced by the total cloud cover and total precipitation. These necessities require serious attention when deciding which variables are useful for raising the performance of the utilized forecasting model.
Experiments investigated the climate variables to understand the impacts of climate variables with low and high correlations. The thirty-four (34) climate variables, including low- and high-correlation climate variables, were simulated in the NARX models; however, the statistics of this experiment provided poor performance in terms of evaluation indices (NMSE = 3.814, R2 = 0.830, MAE = 3.814 MW, RMSE = 4.897 MW, and MAPE = 0.354) compared with the stand-alone NARX model with six high-correlation climate variables at the GS1 site (NMSE = 1.343, = 0.902, MAE = 2.228 MW, RMSE = 3.713 MW, and MAPE = 0.432), and the evaluation indices of thirty four climate variables of hybrid ICEEMDAN-NARX (NMSE = 0.062, = 0.937, MAE = 2.225 MW, RMSE = 2.967 MW, and MAPE = 0.302) underperformed compared to the six climate variables of hybrid ICEEMDAN-NARX (NMSE = 0.048, = 0.952, MAE = 1.923 MW, RMSE = 2.605 MW, and MAPE = 0.302), as shown in Table 5. Due to this experiment, the combination of low- and high-correlation climate variables probably prevented the improvement of the prediction models. Therefore, defining the bounds for highly correlated variable selection is the ideal solution that leads to outstanding prediction performance.

Table 5.
Statistical comparisons among highly correlated (HC) and all correlated (AC) variables using NARX for the GS1 site.
5.2. Sensitivity to the Key Parameters in RNNs
Among the key parameters of RNNs, the identification of FDs is extremely crucial and mainly determines the overall model performance. The calculation of the FDs is based on the target (electricity demand) time series dataset and performed by using the autocorrelation function. The different electricity demand curves at the various stations cause the number of FDs to vary in diverse ranges. The second key parameter is the optimization of the weight and bias. The trial-and-error approach was utilized to determine the optimal weight and bias for the model to reduce error propagation. Moreover, the double loop of the trial-and-error algorithm was also used to find the numbers of hidden neurons for the optimized model. The third key parameter is the transfer function of the neural network. Since a wide range of FDs was used in the model, the transfer function needs to be defined as a transfer function that consumes less memory, exhibits less calculation variation, and possesses sufficient efficiency. The fourth key parameter is the activation function of the hidden and output layers. The activation function of both layers also plays a crucial part in each layer after being exported to another layer using mathematical properties. The detailed configuration of the neural networks is described in Section 3.
6. Conclusions
The understanding of the future demand for power systems could enable policy makers to visualize a clear path for managing the operation system environmentally, efficiently, securely, and economically for the country. A ground-based investigation of electricity demand forecasting is an ideal analysis method for system operations.
Medium-term electricity demand prediction could affect system planning within several weeks or months, making it more realistic for energy experts to balance demand and supply. There are many types of factors that influence the shape of the electricity demand curve; however, weather or climate factors can provide insight into customer behaviors during different seasons. The available climate variables obtained from reliable sources can address the uncertainty of the local climate variables since data management is a major challenge for developing countries.
In this study, an RNN was introduced to estimate future electricity demand. By using a historical electricity demand dataset, RNNs allowed the developed model to learn the sharpness of the electricity demand during the training period. After treating the missing values and converting the hourly dataset into a daily demand dataset, decomposition techniques were applied to decompose the nonlinear and nonstationary power demand data into IMFs from the high-frequency to the low-frequency bands and the residue. In general, IMF1 and IMF2 gained the high-frequency nature of the original dataset, while IMF3 and onward depicted the relatively low-frequency oscillatory behavior of the data. The residue represents the nonlinear trend of the power demand. Then, each IMF is input and predicted with trained NAR and NRAX models. The predicted results of each mode showed very good performance, particularly for the low-frequency modes from IMF3 and onward. Relatively low performance and large RMSE were obtained for the high-frequency mode predictions (IMF1 and IMF2). The hybrid models of this study illustrate very good performance for power demand forecasting. If the low-frequency modes are utilized for prediction depending on a specific need, then mid-term and long-term power demand forecasts would be possible with significant information on sustainable power development and management.
This study was focused on and limited to the normal condition of electricity usage from 2013 to 2018. The effects on power generation or energy consumption were not considered in the analysis. The electricity trend was based on consumers’ behaviors, economic activities, and development activities during the study period.
In regard to the error propagation section of the study, numerous aspects could be improved, and the first improvement would be the climate variables. Various climate resources could be measured in terms of the reliability of the input data, which would benefit future research. The second improvement would be to randomly initialize the weight and bias. Optimizers for weights and biases were introduced, such as the grey wolf optimizer, PSO, the genetic algorithm, the harmony search algorithm, simulated annealing, tabu search, and ant colony optimization. These optimizations could be compared to improve the learning process of the network. The major improvement would be the real-time measurement of climate variables (maximum temperature, minimum temperature, sunshine, humidity, etc.) at a local station, which is essentially necessary for consideration in the model’s prediction process. Moreover, socioeconomic variables (such as the electricity consumption levels of different consumers, energy policies, energy consumption levels on weekdays and holidays, electricity usage behaviors, etc.) could also be used as improvement factors for the ANN model.
Author Contributions
Method, program, visualization, validation, critical evaluation, research, data curation, and writing—first draft preparation, K.C., H.S.L. and S.T.; writing—review and editing and supervision, H.S.L. All authors have read and agreed to the published version of the manuscript.
Funding
The first and third authors are supported by The Project for Human Resource Development Scholarship (JDS), Japan, at Hiroshima University. Additionally, we highly appreciate the ECMWF and EDC for providing the used dataset for this study.
Data Availability Statement
Electricity demand data at grid substations are available from the authors upon request.
Conflicts of Interest
The authors state that they have no conflict of interest.
Abbreviations
| AC | All correlated |
| ADB | Asian Development Bank |
| AFD | Adaptive Fourier decomposition |
| ANN | Artificial neural network |
| ARIMA | Autoregressive integrated moving average |
| BPNN | Back-propagation-based neural network |
| CEEMDAN | Complete ensemble empirical mode decomposition with adaptive noise |
| CNN | Convolution neural network |
| CO2 | Carbon dioxide |
| EAC | Electricity Authority of Cambodia |
| ECMWF | European Center for Medium-Range Weather Forecast |
| EDC | Electricité du Cambodge |
| EEMD | Ensemble empirical mode decomposition |
| EMD | Empirical mode decomposition |
| ExSS | Extended snapshot |
| FFNN | Feed-forward neural network |
| GDP | Gross domestic production |
| GS | Grid substation |
| HC | Highly correlated |
| HFO | Heavy fuel oil |
| HFT | Hidden transfer function |
| HHO | Harris hawks optimization |
| ICEEMDAN | Improved complete ensemble empirical mode decomposition with adaptive noise |
| IMF | Intrinsic mode function |
| LEAP | Long-range alternatives energy planning |
| LPG | Liquefied petroleum gas |
| LRF | Linear recurrent formula |
| LSSVM | Least-square-support vector machine |
| LSTM | Long–short-term memory network |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| MARS | Multivariate adaptive regression spline |
| ML | Machine learning |
| MLR | Multiple linear regression |
| NAR | Nonlinear autoregressive neural network |
| NARX | Nonlinear autoregressive neural network with exogenous inputs |
| NMSE | Normalized mean square error |
| OFT | Output transfer function |
| PDP | Power development plan |
| PSO | Particle swarm optimization |
| RMSE | Root-mean square error |
| RNN | Recurrent neural network |
| SCADA | Supervisory control and data acquisition |
| SDGs | Sustainable development goals |
| SSA | Singular spectrum analysis |
| SVR | Support vector regression |
| SWPT | Stationary wavelet packet transform decomposition |
| TCN | Temporal convolutional network |
| VMD | Variational mode decomposition |
| WAsP | Wind Atlas Analysis and Application Program |
| WPP | West Phnom Penh grid substation |
Appendix A. ERA5 Climate Variables

Figure A1.
For the GS1 site, the outcomes of cross-correlation coefficient (daily) between electricity demand and climate variables from the ECMWF-ERA5 reanalysis dataset. The climate variables were selected based on their 95% confidence intervals and are demonstrated by the blue lines. The six chosen blue variables were based on the number of significant daily lags (from 0 to 2) and the number of decomposed power demand outputs. The details are described in Table A1.

Table A1.
Input climate variables from the ECMWF-ERA5 climate reanalysis.
Table A1.
Input climate variables from the ECMWF-ERA5 climate reanalysis.
| Data Description | No. | Main Climate Variables | Acronym | Daily Dataset |
|---|---|---|---|---|
| Mean (1 January 2013) | ||||
| ERA5 climate reanalysis | 1 | Boundary layer dissipation | BLD | 4303.75 |
| 2 | Boundary layer height | BLH | 563.93 | |
| 3 | Convective available potential energy | CAPE | 0.04 | |
| 4 | CHNK | 0.02 | ||
| 5 | Convective precipitation | CP | 0.00 | |
| 6 | 2-metre dewpoint temperature | D | 292.15 | |
| 7 | Evaporation | E | 0.00 | |
| 8 | Eastward turbulent surface stress | EWSS | −109.38 | |
| 9 | Forecast albedo | FAL | 0.16 | |
| 10 | 10-metre wind gusts since previous postprocessing | FG10 | 6.12 | |
| 11 | Forecast logarithm of surface roughness for heat | FLSR | −3.84 | |
| 12 | Forecast surface roughness | FSR | 0.47 | |
| 13 | High cloud cover | HCC | 0.87 | |
| 14 | Instantaneous moisture flux | IE | 0.00 | |
| 15 | Instantaneous eastward turbulent surface stress | IEWS | −0.04 | |
| 16 | Instantaneous northward turbulent surface stress | INSS | −0.15 | |
| 17 | Instantaneous surface sensible heat flux | ISHF | −52.10 | |
| 18 | Low cloud cover | LCC | 0.17 | |
| 19 | Large-scale precipitation fraction | LSPF | 0.00 | |
| 20 | MCC | 0.06 | ||
| 21 | Mean sea level pressure | MSL | 101,139.75 | |
| 22 | Northward turbulent surface stress | NSSS | −528.31 | |
| 23 | Vertical integral of potential, internal, and latent energy | P62.162 | 2,780,152,438.89 | |
| 24 | Vertical integral of total energy | P63.162 | 2,780,456,503.09 | |
| 25 | Vertical integral of eastward kinetic energy flux | P67.162 | −1,832,177.66 | |
| 26 | Vertical integral of eastward geopotential flux | P73.162 | −2,982,667,364.29 | |
| 27 | Vertical integral of northward geopotential flux | P74.162 | 2,069,308,190.16 | |
| 28 | Vertical integral of eastward total energy flux | P75.162 | −14,986,239,992.45 | |
| 29 | Vertical integral of eastward ozone flux | P77.162 | 0.02 | |
| 30 | RO | 0.00 | ||
| 31 | Skin temperature | SKT | 300.50 | |
| 32 | Surface latent heat flux | SLHF | −286,915.24 | |
| 33 | SP | 100,833.20 | ||
| 34 | Skin reservoir content (m of water equivalent) | SRC | 0.00 | |
| 35 | Surface sensible heat flux | SSHF | −186,000.54 | |
| 36 | Surface net solar radiation | SSR | 692,607.54 | |
| 37 | Surface net solar radiation, clear sky | SSRC | 721,085.09 | |
| 38 | Surface net solar radiation, downwards | SSRD | 818,633.89 | |
| 39 | Soil temperature level 1 | STL1 | 301.93 | |
| 40 | Soil temperature level 2 | STL2 | 301.76 | |
| 41 | Soil temperature level 3 | STL3 | 302.18 | |
| 42 | Soil temperature level 4 | STL4 | 301.95 | |
| 43 | Surface net thermal radiation | STR | −222,398.82 | |
| 44 | Surface net thermal radiation, clear sky | STRC | −254,379.87 | |
| 45 | Surface thermal radiation, downwards | STRD | 1,435,890.80 | |
| 46 | Volumetric soil water layer 1 | SWVL1 | 0.21 | |
| 47 | Volumetric soil water layer 2 | SWVL2 | 0.22 | |
| 48 | Volumetric soil water layer 3 | SWVL3 | 0.29 | |
| 49 | Volumetric soil water layer 4 | SWVL4 | 0.29 | |
| 50 | T2 M | 300.33 | ||
| 51 | Total cloud cover | TCC | 0.88 | |
| 52 | Total column cloud liquid water | TCLW | 0.02 | |
| 53 | TCO3 | 0.00 | ||
| 54 | Total column cloud ice water | TCIW | 0.00 | |
| 55 | Total column water | TCW | 37.75 | |
| 56 | TCWV | 37.71 | ||
| 57 | TOA incident solar radiation | TISR | 1,260,279.10 | |
| 58 | Total precipitation | TP | 0.00 | |
| 59 | Temperature of snow layer | TSN | 273.05 | |
| 60 | Top net solar radiation | TSR | 1,009,476.83 | |
| 61 | Top net solar radiation, clear sky | TSRC | 1,043,013.34 | |
| 62 | Top net thermal radiation | TTR | −863,546.10 | |
| 63 | Top net thermal radiation, clear sky | TTRC | −1,037,561.45 | |
| 64 | 10-metre U wind component | U10 | −0.48 | |
| 65 | Downward U.V. radiation at the surface | UVB | 95,201.23 | |
| 66 | 10-metre V wind component | V10 | −2.65 |
References
- Thatcher, M.J. Modelling Changes to Electricity Demand Load Duration Curves as a Consequence of Predicted Climate Change for Australia. Energy 2007, 32, 1647–1659. [Google Scholar] [CrossRef]
- Wang, C.; Grozev, G.; Seo, S. Decomposition and Statistical Analysis for Regional Electricity Demand Forecasting. Energy 2012, 41, 313–325. [Google Scholar] [CrossRef]
- Abbas, F.; Feng, D.; Habib, S.; Rahman, U.; Rasool, A.; Yan, Z. Short Term Residential Load Forecasting: An Improved Optimal Nonlinear Auto Regressive (NARX) Method with Exponential Weight Decay Function. Electronics 2018, 7, 432. [Google Scholar] [CrossRef]
- Buitrago, J.; Asfour, S. Short-Term Forecasting of Electric Loads Using Nonlinear Autoregressive Artificial Neural Networks with Exogenous Vector Inputs. Energies 2017, 10, 40. [Google Scholar] [CrossRef]
- Netsanet, S.; Zhang, J.; Zheng, D. Short Term Load Forecasting Using Wavelet Augmented Non-Linear Autoregressive Neural Networks: A Single Customer Level Perspective. In Proceedings of the IEEE 3rd International Conference on Big Data Analysis (ICBDA), Shanghai, China, 9–12 March 2018; pp. 407–411. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Forecasting Groundwater Levels Using Nonlinear Autoregressive Networks with Exogenous Input (NARX). J. Hydrol. 2018, 567, 743–758. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Xu, C.-Y.; Chang, F.-J.; Yin, J. Improving the Reliability of Probabilistic Multi-Step-Ahead Flood Forecasting by Fusing Unscented Kalman Filter with Recurrent Neural Network. Water 2020, 12, 578. [Google Scholar] [CrossRef]
- Cadenas, E.; Rivera, W.; Campos-Amezcua, R.; Cadenas, R. Wind Speed Forecasting Using the NARX Model, Case: La Mata, Oaxaca, México. Neural Comput. Applic. 2016, 27, 2417–2428. [Google Scholar] [CrossRef]
- Altan, A.; Karasu, S.; Zio, E. A New Hybrid Model for Wind Speed Forecasting Combining Long Short-Term Memory Neural Network, Decomposition Methods and Grey Wolf Optimizer. Appl. Soft Comput. 2021, 100, 106996. [Google Scholar] [CrossRef]
- Blanchard, T.; Samanta, B. Wind Speed Forecasting Using Neural Networks. Wind Eng. 2020, 44, 33–48. [Google Scholar] [CrossRef]
- Alzahrani, A.; Kimball, J.W.; Dagli, C. Predicting Solar Irradiance Using Time Series Neural Networks. Procedia Comput. Sci. 2014, 36, 623–628. [Google Scholar] [CrossRef]
- Boussaada, Z.; Curea, O.; Remaci, A.; Camblong, H.; Mrabet Bellaaj, N. A Nonlinear Autoregressive Exogenous (NARX) Neural Network Model for the Prediction of the Daily Direct Solar Radiation. Energies 2018, 11, 620. [Google Scholar] [CrossRef]
- Kazemzadeh, M.-R.; Amjadian, A.; Amraee, T. A Hybrid Data Mining Driven Algorithm for Long Term Electric Peak Load and Energy Demand Forecasting. Energy 2020, 204, 117948. [Google Scholar] [CrossRef]
- Ahmed, T.; Muttaqi, K.M.; Agalgaonkar, A.P. Climate Change Impacts on Electricity Demand in the State of New South Wales, Australia. Appl. Energy 2012, 98, 376–383. [Google Scholar] [CrossRef]
- Tayab, U.B.; Zia, A.; Yang, F.; Lu, J.; Kashif, M. Short-Term Load Forecasting for Microgrid Energy Management System Using Hybrid HHO-FNN Model with Best-Basis Stationary Wavelet Packet Transform. Energy 2020, 203, 117857. [Google Scholar] [CrossRef]
- AL-Musaylh, M.S.; Deo, R.C.; Adamowski, J.F.; Li, Y. Short-Term Electricity Demand Forecasting Using Machine Learning Methods Enriched with Ground-Based Climate and ECMWF Reanalysis Atmospheric Predictors in Southeast Queensland, Australia. Renew. Sustain. Energy Rev. 2019, 113, 109293. [Google Scholar] [CrossRef]
- Runge, J.; Zmeureanu, R.; Le Cam, M. Hybrid Short-Term Forecasting of the Electric Demand of Supply Fans Using Machine Learning. J. Build. Eng. 2020, 29, 101144. [Google Scholar] [CrossRef]
- Sulandari, W.; Subanar, S.S.; Lee, M.H.; Rodrigues, P.C. Indonesian Electricity Load Forecasting Using Singular Spectrum Analysis, Fuzzy Systems and Neural Networks. Energy 2020, 190, 116408. [Google Scholar] [CrossRef]
- Lee, H.-Y.; Jang, K.M.; Kim, Y. Energy Consumption Prediction in Vietnam with an Artificial Neural Network-Based Urban Growth Model. Energies 2020, 13, 4282. [Google Scholar] [CrossRef]
- Shen, Y.; Ma, Y.; Deng, S.; Huang, C.-J.; Kuo, P.-H. An Ensemble Model Based on Deep Learning and Data Preprocessing for Short-Term Electrical Load Forecasting. Sustainability 2021, 13, 1694. [Google Scholar] [CrossRef]
- Li, R.; Jiang, P.; Yang, H.; Li, C. A Novel Hybrid Forecasting Scheme for Electricity Demand Time Series. Sustain. Cities Soc. 2020, 55, 102036. [Google Scholar] [CrossRef]
- Bedi, J.; Toshniwal, D. Deep Learning Framework to Forecast Electricity Demand. Appl. Energy 2019, 238, 1312–1326. [Google Scholar] [CrossRef]
- Kandananond, K. Forecasting Electricity Demand in Thailand with an Artificial Neural Network Approach. Energies 2011, 4, 1246–1257. [Google Scholar] [CrossRef]
- Jaisumroum, N.; Teeravaraprug, J. Forecasting Uncertainty of Thailand’s Electricity Consumption Compare with Using Artificial Neural Network and Multiple Linear Regression Methods. In Proceedings of the 12th IEEE Conference on Industrial Electronics and Applications (ICIEA), Siem Reap, Cambodia, 18–20 June 2017; pp. 308–313. [Google Scholar] [CrossRef]
- Bantugon, M.J.T.; Gallano, R.J.C. Short- and Long-Term Electricity Load Forecasting Using Classical and Neural Network Based Approach: A Case Study for the Philippines. In Proceedings of the IEEE Region 10 Conference (TENCON), Singapore, 22–26 November 2016; pp. 3822–3825. [Google Scholar] [CrossRef]
- World Bank Group. Cambodia Economic Update. 2019. Available online: https://documents1.worldbank.org/curated/en/707971575947227090/pdf/Cambodia-Economic-Update-Upgrading-Cambodia-in-Global-Value-Chains.pdf (accessed on 23 May 2021).
- MME. Power Development Master Plan (PDP) (Power Development Master Plan in Kingdom of Cambodia); MME: Phnom Penh, Cambodia, 2015. [Google Scholar]
- ADB. Cambodia: Energy Sector Assessment, Strategy, and Road Map. 2018. Available online: http://search.ebscohost.com/login.aspx?direct=true&scope=site&db=nlebk&db=nlabk&AN=2029528 (accessed on 23 April 2021).
- EAC. Salient Feature of Power Development in the Kindom of Cambodia Until December 2019; EAC: Phnom Penh, Cambodia, 2019. [Google Scholar]
- Lyheang, C.; Limmeechokchai, B. The Role of Renewable Energy in CO2 Mitigation from Power Sector in Cambodia. Int. Energy J. 2018, 18. Available online: http://www.rericjournal.ait.ac.th/index.php/reric/article/view/1970 (accessed on 11 June 2021).
- San, V.; Sriv, T.; Spoann, V.; Var, S.; Seak, S. Economic and Environmental Costs of Rural Household Energy Consumption Structures in Sameakki Meanchey District, Kampong Chhnang Province, Cambodia. Energy 2012, 48, 484–491. [Google Scholar] [CrossRef]
- Hak, M.; Matsuoka, Y.; Gomi, K. A Qualitative and Quantitative Design of Low-Carbon Development in Cambodia: Energy Policy. Energy Policy 2017, 100, 237–251. [Google Scholar] [CrossRef]
- Promsen, W.; Janjai, S.; Tantalechon, T. An Analysis of Wind Energy Potential of Kampot Province, Southern Cambodia. Energy Procedia 2014, 52, 633–641. [Google Scholar] [CrossRef][Green Version]
- EDC. Annual Report 2013; EDC: Phnom Penh, Cambodia, 2013; Available online: http://edc.com.kh/images/Annual%20Report%202013%20Publish.pdf (accessed on 23 February 2021).
- EDC. Annual Report 2017; EDC: Phnom Penh, Cambodia, 2017; Available online: http://edc.com.kh/images/Annual%20Report%202017%20(English)__pdf (accessed on 4 February 2021).
- EAC. Annual Report on Power Sector for Year 2019; EAC: Phnom Penh, Cambodia, 2019. Available online: https://eac.gov.kh/uploads/annual_report/english/Annual-Report-2019-en.pdf (accessed on 31 July 2020).
- Su, T.; Shi, Y.; Yu, J.; Yue, C.; Zhou, F. Nonlinear Compensation Algorithm for Multidimensional Temporal Data: A Missing Value Imputation for the Power Grid Applications. Knowl. -Based Syst. 2021, 215, 106743. [Google Scholar] [CrossRef]
- Li, M.; Yang, B.; Zhai, W.; Ma, X.; Xia, Y.; Lin, Y. Non-Mechanism Model for Superheater Pollution Diagnosis of Waste Incinerator Based on BP Neural Network. IOP Conf. Ser. Mater. Sci. Eng. 2019, 612, 052015. [Google Scholar] [CrossRef]
- Abidoye, L.K.; Mahdi, F.M.; Idris, M.O.; Alabi, O.O.; Wahab, A.A. ANN-Derived Equation and ITS Application in the Prediction of Dielectric Properties of Pure and Impure CO2. J. Clean. Prod. 2018, 175, 123–132. [Google Scholar] [CrossRef]
- Lee, H.S. Improvement of Decomposing Results of Empirical Mode Decomposition and Its Variations for Sea-Level Records Analysis. J. Coast. Res. 2018, 85, 526–530. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E.; Flandrin, P. NOISE-ASSISTED EMD METHODS IN ACTION. Adv. Adapt. Data Anal. 2012, 4, 1250025. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; IEEE: Prague, Czech Republic, 2011; pp. 4144–4147. [Google Scholar] [CrossRef]
- Colominas, M.A. Improved Complete Ensemble EMD: A Suitable Tool for Biomedical Signal Processing. Biomed. Signal Process. Control 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Yang, S.; Yang, D.; Chen, J.; Zhao, B. Real-Time Reservoir Operation Using Recurrent Neural Networks and Inflow Forecast from a Distributed Hydrological Model. J. Hydrol. 2019, 579, 124229. [Google Scholar] [CrossRef]
- Zhang, G.; Zhou, H.; Wang, C.; Xue, H.; Wang, J.; Wan, H. Forecasting Time Series Albedo Using NARnet Based on EEMD Decomposition. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3544–3557. [Google Scholar] [CrossRef]
- Khalid, A.; Sundararajan, A.; Sarwat, A.I. A Multi-Step Predictive Model to Estimate Li-Ion State of Charge for Higher C-Rates. In Proceedings of the IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Di Piazza, A.; Di Piazza, M.C.; La Tona, G.; Luna, M. An artificial neural network-based forecasting model of energy-related time series for electrical grid management. Math. Comput. Simul. 2021, 184, 294–305. [Google Scholar] [CrossRef]
- Ryu, J.-A.; Chang, S. Data Driven Heating Energy Load Forecast Modeling Enhanced by Nonlinear Autoregressive Exogenous Neural Networks. IJSCER 2019, 8, 246–252. [Google Scholar] [CrossRef]
- Kumar, D.A.; Murugan, S. Performance Analysis of NARX Neural Network Backpropagation Algorithm by Various Training Functions for Time Series Data. IJDS 2018, 3, 308. [Google Scholar] [CrossRef]
- Sarkar, R.; Julai, S.; Hossain, S.; Chong, W.T.; Rahman, M. A Comparative Study of Activation Functions of NAR and NARX Neural Network for Long-Term Wind Speed Forecasting in Malaysia. Math. Probl. Eng. 2019, 2019, 1–14. [Google Scholar] [CrossRef]
- Vogl, T.P.; Mangis, J.K.; Rigler, A.K.; Zink, W.T.; Alkon, D.L. Accelerating the Convergence of the Back-Propagation Method. Biol. Cybern. 1988, 59, 257–263. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.; Yang, J.; Li, B. Long Range Dependence Prognostics for Bearing Vibration Intensity Chaotic Time Series. Entropy 2016, 18, 23. [Google Scholar] [CrossRef]
- Hussainzada, W.; Lee, H.S.; Vinayak, B.; Khpalwak, G.F. Sensitivity of Snowmelt Runoff Modelling to the Level of Cloud Coverage for Snow Cover Extent from Daily MODIS Product Collection 6. J. Hydrol. Reg. Stud. 2021, 36, 100835. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Tong, C.W.; Arif, M.; Petković, D.; Ch, S. A New Hybrid Support Vector Machine–Wavelet Transform Approach for Estimation of Horizontal Global Solar Radiation. Energy Convers. Manag. 2015, 92, 162–171. [Google Scholar] [CrossRef]
- Prasad, R.; Deo, R.C.; Li, Y.; Maraseni, T. Input Selection and Performance Optimization of ANN-Based Streamflow Forecasts in the Drought-Prone Murray Darling Basin Region Using IIS and MODWT Algorithm. Atmos. Res. 2017, 197, 42–63. [Google Scholar] [CrossRef]
- Guiamel, I.A.; Lee, H.S. Watershed Modelling of the Mindanao River Basin in the Philippines Using the SWAT for Water Resource Management. Civ. Eng. J. 2020, 6, 626–648. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).