Heat Transfer Characteristics of Cold Water Phase-Change Heat Exchangers under Active Icing Conditions
Abstract
1. Introduction
2. Physical Model
3. Mathematical Model
3.1. Energy Equation
3.2. Momentum Equation
3.3. Mass Equation
4. Computational Analysis
4.1. Geometric Models and Computational Grids
4.2. Simulation Scheme and Boundary Conditions
5. Model Error Analysis
6. Results and Analysis
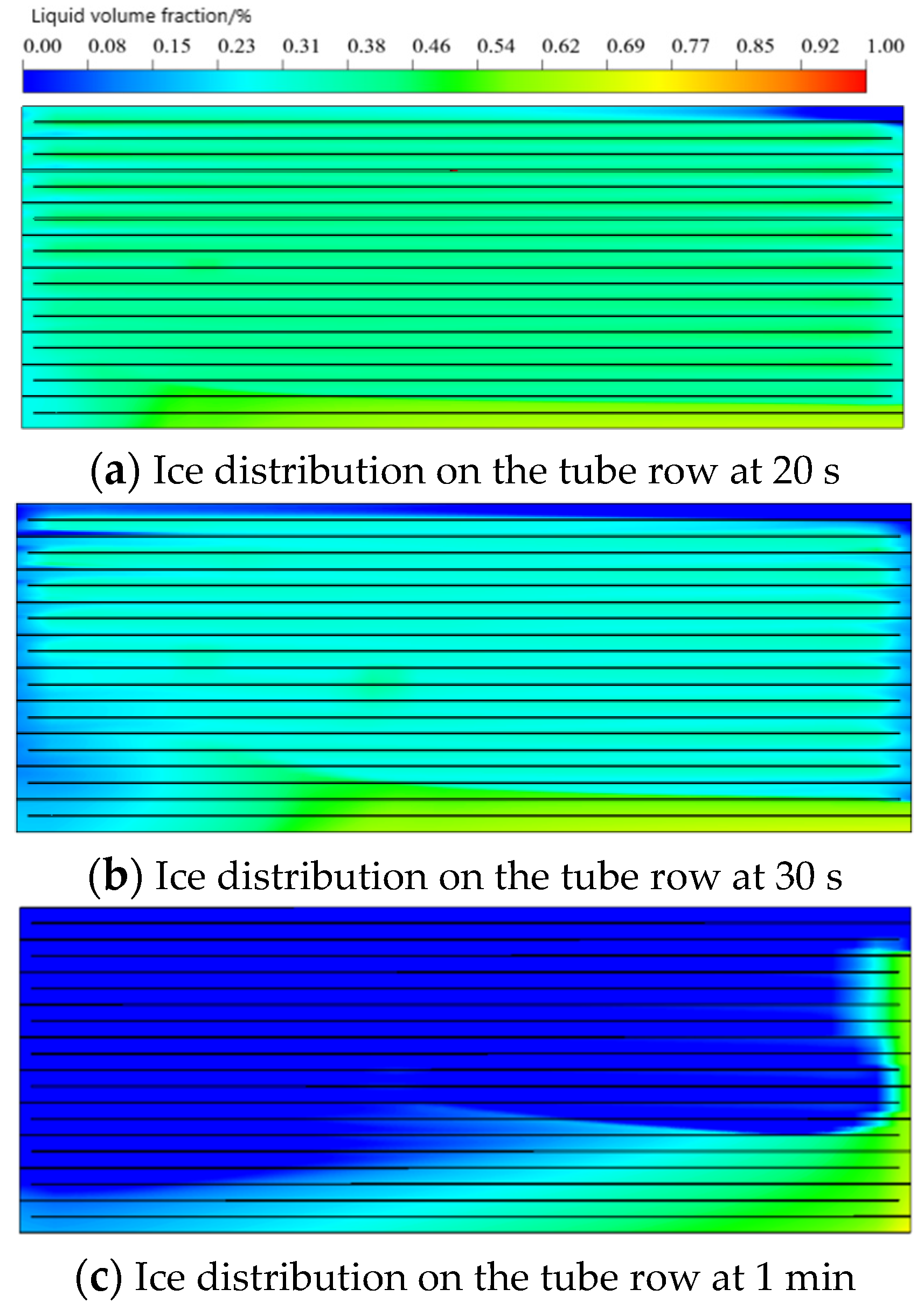
6.1. Ice Layer Growth Law under Active Icing Condition
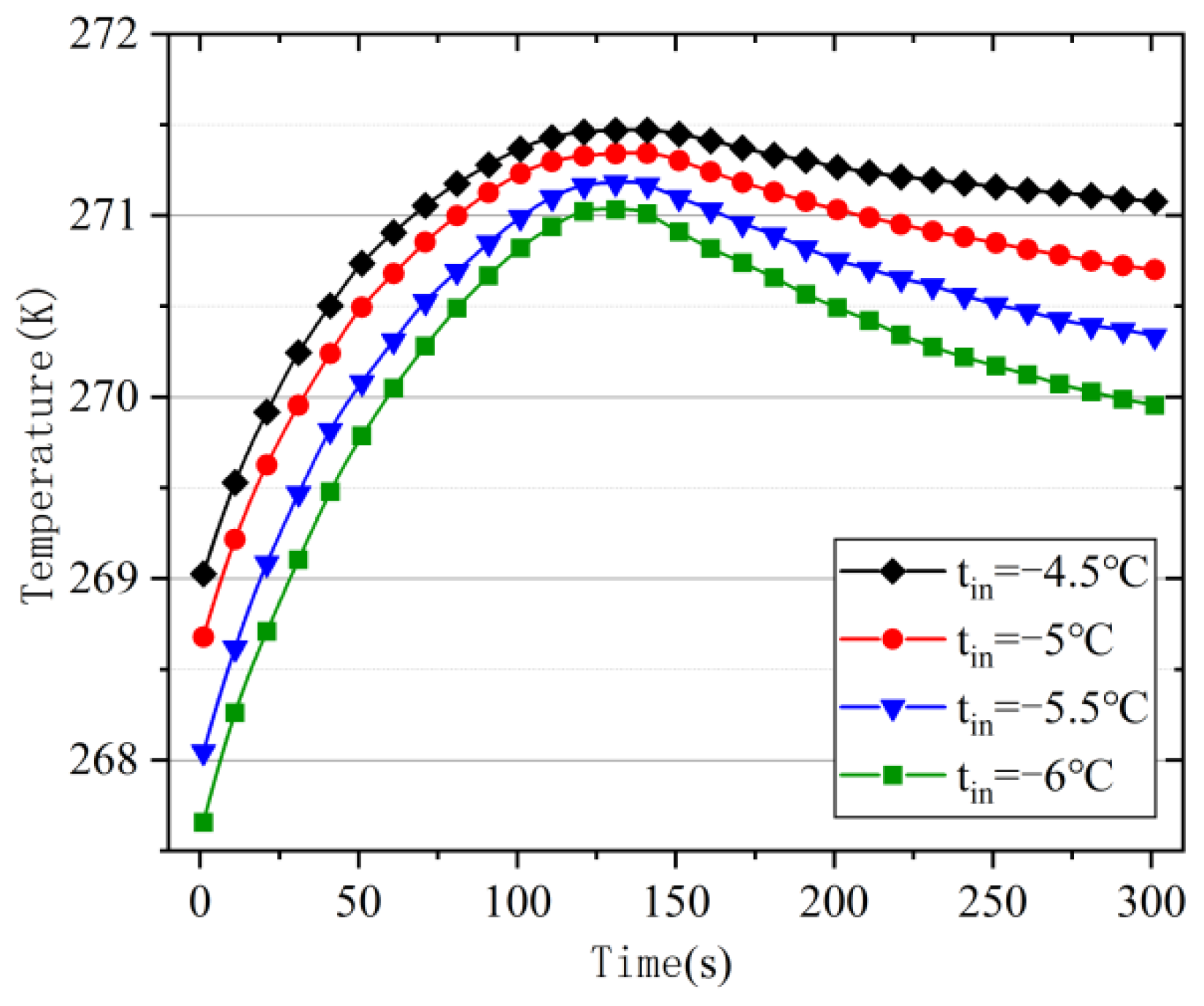
6.2. Heat Transfer Characteristics under Variable Intermediate Water Temperature Conditions
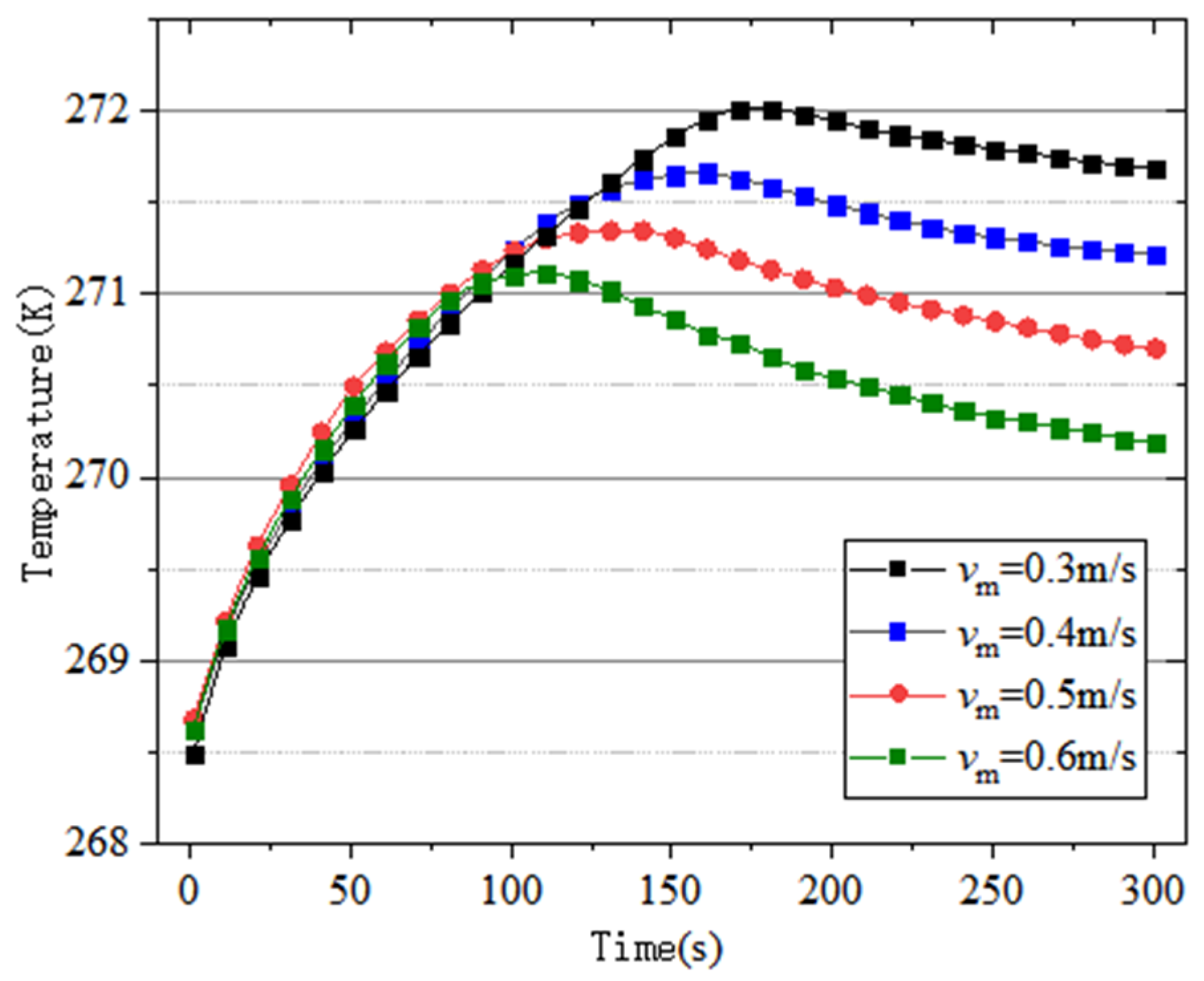
6.3. Heat Transfer Characteristics under Variable Intermediate Water Velocity Conditions
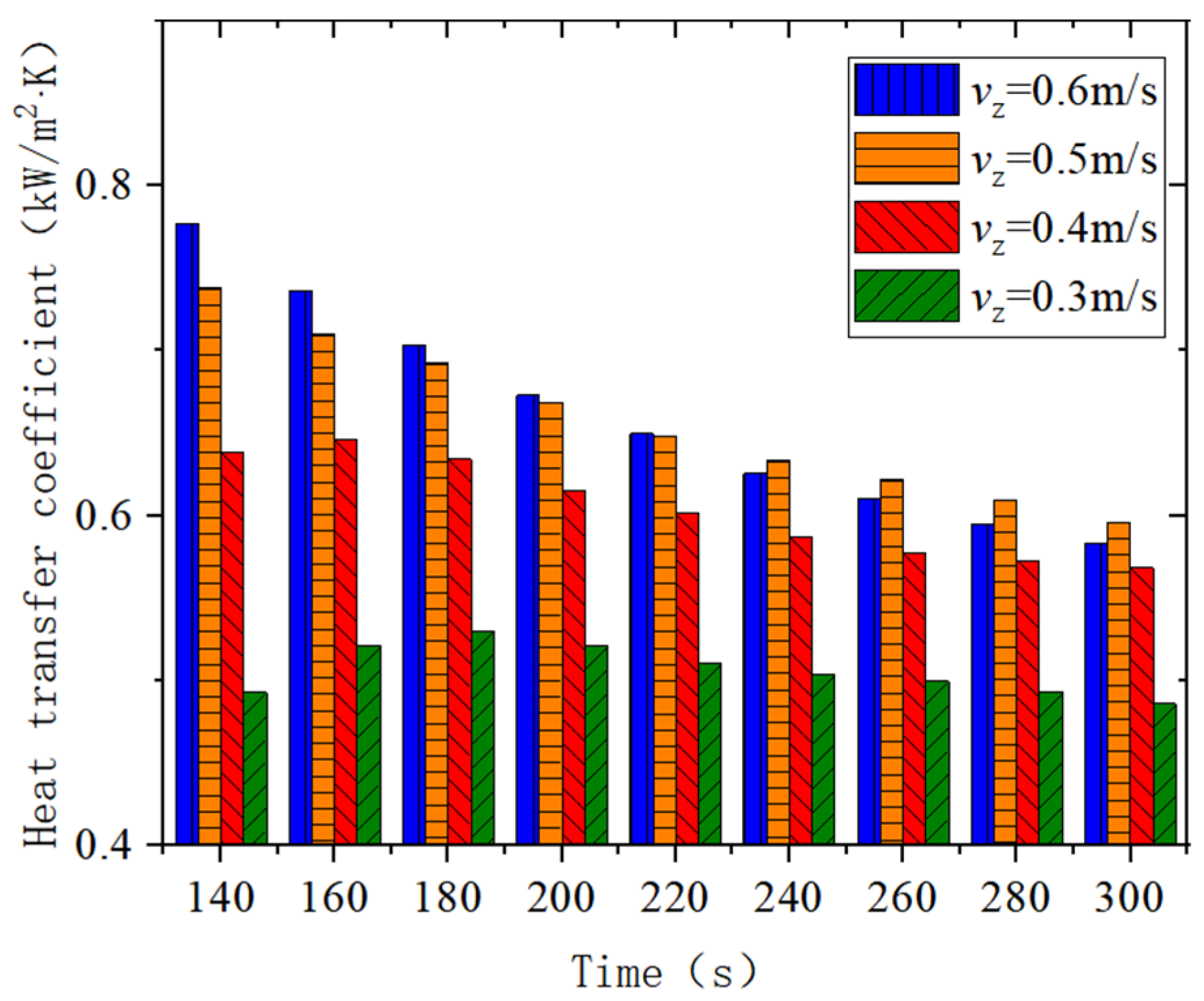
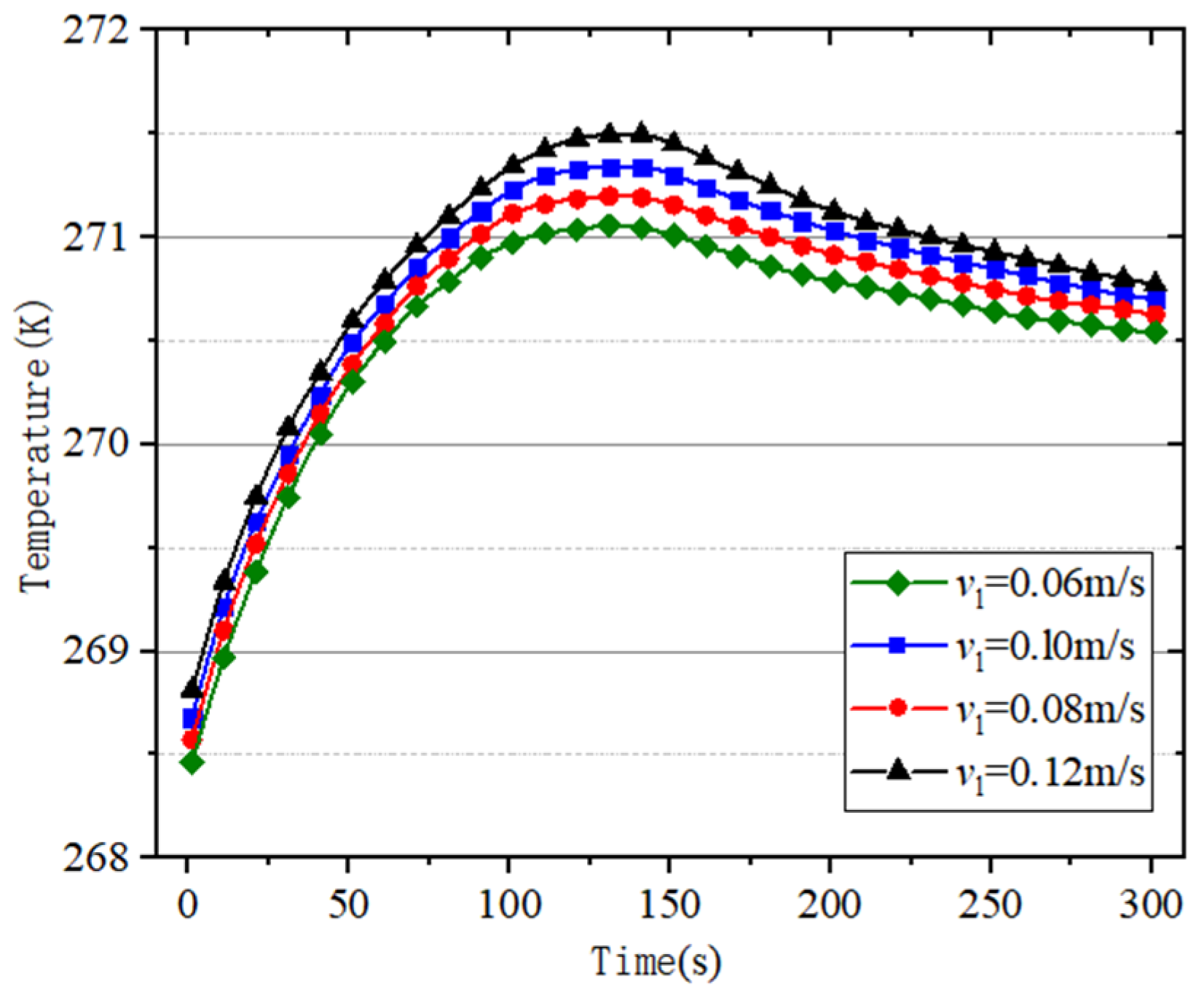
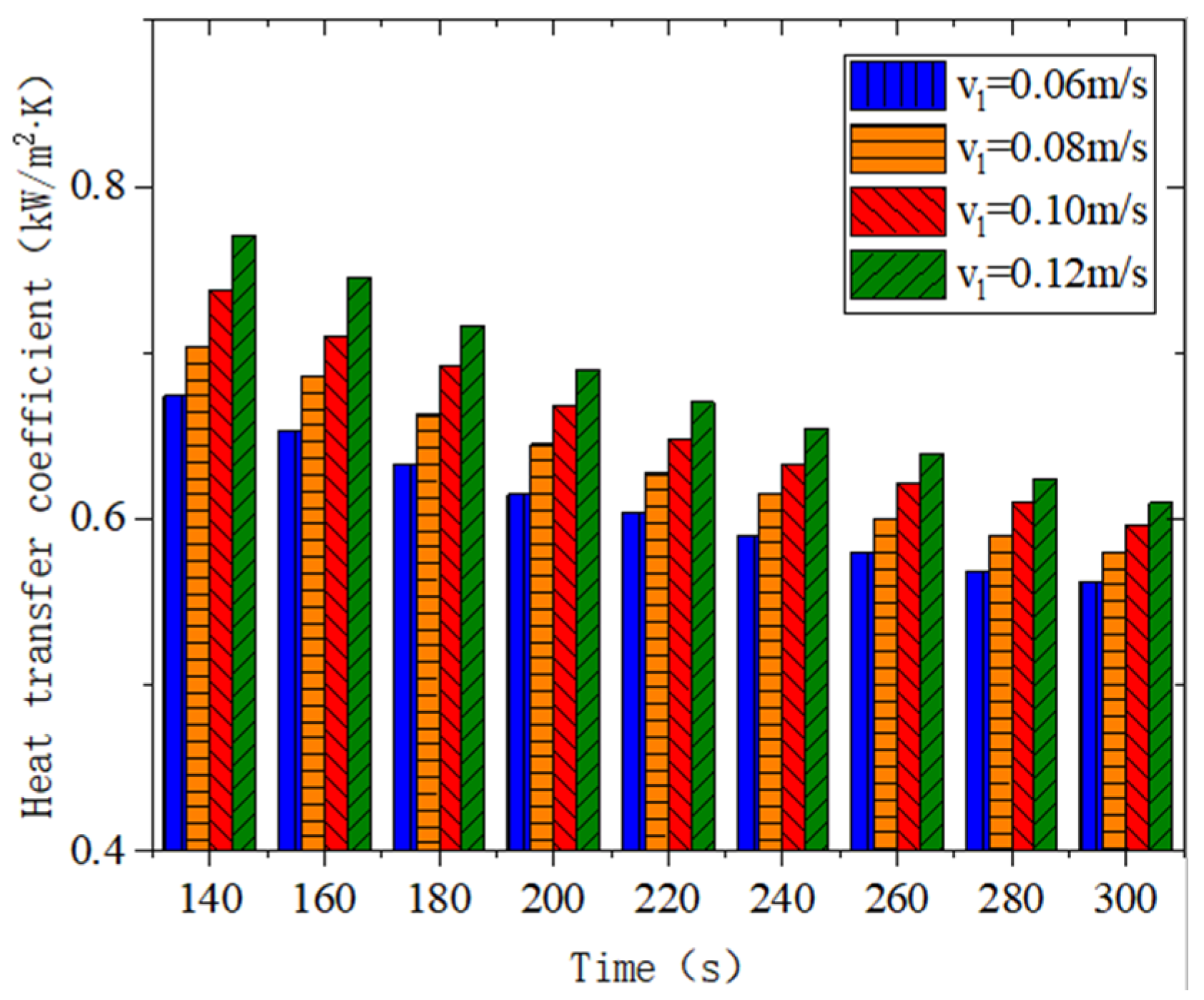
6.4. Heat Transfer Characteristics under Variable Cold Water Flow Rate Conditions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nomenclature | Nomenclature | ||
| time (s) | gravitational acceleration (m·s−2) | ||
| total heat release (kJ/kg) | decayed momentum (N/m3) | ||
| velocity vector (m/s) | very small value to prevent divergence, Equal to 0.001 | ||
| thermal conductivity (W/m·K) | solidification zone constant | ||
| Temperature (K) | mass added to the continuous phase (kg/m2·s) | ||
| other source items | rate of ice formation on pipe rows (m2/s) | ||
| apparent heat (kJ/kg) | area of ice on the pipe row at time t (m2) | ||
| latent heat (kJ/kg) | area of ice on the pipe row at time t-30 (m2) | ||
| the corresponding enthalpy at the reference temperature (kJ/kg) | specific heat capacity of intermediate water (J/kg·K) | ||
| enthalpy variable (kJ/kg) | mass flow rate of intermediate water (kg/s) | ||
| reference temperature (K) | import and export temperature difference of the intermediate water (K) | ||
| specific heat capacity at constant pressure (kJ/kg·K) | heat transfer coefficient of the CPHE (W/m2·K) | ||
| volume fraction of liquid phase | iheat transfer area of single-row tube (m2) | ||
| latent heat of phase change for complete solidification (kJ/kg) | logarithmic mean temperature difference of CPHE (K) | ||
| pressure (Pa) | sectional area of single heat exchange tube (m2) | ||
| dynamic viscosity (Pa·s) | intermediate water velocity (m/s) | ||
| momentum source term | intermediate water outlet temperature (K) | ||
| Greek symbols | intermediate water inlet temperature (K) | ||
| density (kg/m3) | cold water temperature (K) | ||
| Acronym | |||
| CPHE | cold water phase change heat exchanger | ||
| p | phase-change energy heat pump | ||
| EVAP | evaporator | ||
| COND | condenser |
References
- Gaur, A.S.; Fitiwi, D.Z.; Curtis, J. Heat pumps and our low-carbon future: A comprehensive review. Energy Res. Soc. Sci. 2021, 71, 101764. [Google Scholar] [CrossRef]
- Chen, Q.; Wei, W.; Li, N. Techno-economic control strategy optimization for water source heat pump coupled with ice storage district cooling system. Int. J. Refrig. 2022, 138, 148–158. [Google Scholar] [CrossRef]
- Xu, X.; Xu, Z.; Li, G. Research and development of photovoltaic air source heat p-ump. J. Sol. Energy 2022, 43, 356–361. (In Chinese) [Google Scholar]
- Ma, G.; Sun, Y.; Cong, D.; Wu, Z.; Yang, W. Simulation study on sand erosion and wear of air source heat pump heat exchange. Fluid Mach. 2021, 49, 62–69. (In Chinese) [Google Scholar]
- Li, H.; Cai, Y. Experimental study on closed cooling tower ground source heat pump system in summer. Fluid Mach. 2019, 47, 81–88. (In Chinese) [Google Scholar]
- Liu, J.; Wan, P.; Guo, J.; Zhou, E.; Guo, W. Optimization of solar ground source heat pump combined heating system. Therm. Sci. Technol. 2019, 18, 155–162. (In Chinese) [Google Scholar]
- Yan, B.; Sun, J.; Wang, X.; Li, X.; Sun, F.; Fu, D. Suitability zoning of groundwater source heat pump in Shijiazhuang based on gis-fahp. J. Jilin Univ. (Earth Sci.) 2021, 51, 1172–1181. [Google Scholar]
- Yuanyuan, S. Research and Application of Lake Water Source Heat Pump System in Cold Area. Master’s Thesis, Qingdao University, Qingdao, China, 2016. [Google Scholar]
- Fu, Y.; Pan, L.; Liu, Y.; Liang, Y. Research on energy saving control method of sewage source heat pump system. Therm. Power Engi-Neering 2020, 35, 80–88. (In Chinese) [Google Scholar]
- Xinrui, Z. Research on a New Absorption Refrigeration and Heat Pump System for Efficient Recovery of Industrial Waste Heat. Master’s Thesis, Shanghai Jiaotong University, Shanghai, China, 2019. [Google Scholar]
- An, M.; Zhao, X.; Xu, Z.; Wang, R. Coupled compression absorption high temperature heat pump cycle for industrial waste heat recovery. J. Shanghai Jiaotong Univ. 2021, 55, 434–443. [Google Scholar]
- Wu, S.; Yunzhun, F.; Lijie, C. Experimental study on refrigeration performance of closed river water source heat pump system. Fluid Mach. 2018, 46, 63–67 + 28. (In Chinese) [Google Scholar]
- Zhang, Y.; Jiaqi, Y.; Gang, W. Influence of multi-source uncertainty on the performance of surface water source heat pump system. HVAC 2022, 52, 138–143. (In Chinese) [Google Scholar]
- Yidong, Q. Performance Analysis and Operation Strategy Optimization of Energy Storage Surface Water Source Heat Pump System. Master’s Thesis, Zhejiang University, Hangzhou, China, 2020. [Google Scholar]
- Wang, W.; Lianghong, W.; Zhenzu, L.; Li, J.; Jia, R.; Hongqiang, Z. Optimal scheduling of surface water source heat pump units based on neighborhood adaptive particle swarm optimization algorithm. Syst. Sci. Math. 2021, 41, 1520–1532. (In Chinese) [Google Scholar]
- Chengliang, X.; Yanjie, L.; Zhang, J.; Sun, C.; Huanxin, C.; Jiangyu, W.; Huang, Y. Study on operation strategy optimization of a groundwater source heat pump system. J. Refrig. 2018, 39, 72–76. (In Chinese) [Google Scholar]
- Ronghua, W.; Zonghui, Z.; Xu, L.; Li, K.; Yuanyuan, S.; Yu, H.; Shirui, T.; Yinghui, Z.; Dexing, S.; Yusheng, X.; et al. A Cold Water Phase Change Energy Heat Extraction Device and Its System. C.N. Patent 108036549a, 15 May 2018. [Google Scholar]
- Wenfang, C. Study on the Characteristics of Water Source Heat Pump Air Conditioning at Low Temperature. Master’s Thesis, Tianjin University of Science and Technology, Tianjin, China, 2013. [Google Scholar]
- Vakiloroaya, V.; Samali, B.; Fakhar, A.; Pishghadam, K. A review of different strategies for HVAC energy saving. Energy Convers. Manag. 2014, 77, 738–754. [Google Scholar] [CrossRef]
- Vasiliev, A.N.; Ershova, I.G.; Belov, A.A.; Timofeev, V.N.; Uhanova, V.Y.; Sokolov, A.V.; Smirnov, A.A. Energy-saving system development based on heat pump. Amazon. Investig. 2018, 7, 219–227. [Google Scholar]
- Chua, K.J.; Chou, S.K.; Yang, W.M. Advances in heat pump systems: A review. Appl. Energy 2010, 87, 3611–3624. [Google Scholar] [CrossRef]
- Niezgoda-Żelasko, B. The enthalpy-porosity method applied to the modelling of the ice slurry melting process during tube flow. Procedia Eng. 2016, 157, 114–121. [Google Scholar] [CrossRef]
- Sánta, R.; Garbai, L.; Fürstner, I. Optimization of heat pump system. Energy 2015, 89, 45–54. [Google Scholar] [CrossRef]
- Nenkaew, P.; Tangthien, C. A study of Transient Performance of a Cascade Heat Pump System. Energy Procedia 2015, 79, 131–136. [Google Scholar] [CrossRef][Green Version]








| Parameters | a | b | c | d | H |
|---|---|---|---|---|---|
| Value/(mm) | 20.5 | 56 | 16.5 | 52 | 3000 |
| Parameters | Value |
|---|---|
| Sizing | |
| Transition | Slow |
| Span angle center | Fine |
| Curvature normal angle | 90° |
| Min cell size [m3] | 2.1 × 10−9 |
| Max face size [m2] | 1.6 × 10−4 |
| Growth rate | 1.2 |
| Quality | |
| Smoothing | Medium |
| Statistics | |
| Elements | 3,200,000 |
| Under-Relaxation Factors | Numerical Value |
|---|---|
| Pressure | 0.3 |
| Density | 1 |
| Body Forces | 1 |
| Momentum | 0.5 |
| Turbulent Kinetic Energy | 0.8 |
| Specific Dissipation Rate | 0.8 |
| Turbulent Viscosity | 1 |
| Liquid Fraction Update | 0.5 |
| Energy | 1 |
| Materials | Density [kg/m3] | Specific Heat Capacity [J/kg·K] | Thermal Conductivity [W/m·K] | Latent Heat [J/kg] | Solidification Temperature [K] |
|---|---|---|---|---|---|
| Solid | |||||
| Steel | 8030 | 460 | 48 | / | / |
| Fluid | |||||
| Intermediate water | 1079 | 3678 | 0.48 | 315,325 | 256 |
| Cold water | 998 | 4182 | User-Defined Function (UDF) | 333,193 | 273 |
| Equipment Name | Related Parameters |
|---|---|
| Water source heat pump unit | Rated heating capacity: 326 kW Rated heating power: 87 kW Source side rated flow: 68 m3/h End side rated flow: 83 m3/h Source side rated inlet and outlet water temperature: −1 °C/−4 °C End side rated inlet and outlet water temperature: 45 °C/50 °C |
| Cold water phase change machine | Heat transfer rate: 300 kW Rated inlet and outlet water temperature of primary side: 2 °C/0 °C Secondary side rated inlet and outlet water temperature: −5 °C/−1 °C |
| Intermediate circulation pump | Rated power: 7.5 kW Flow rate: 107 m3/h Head: 12 m |
| Cold water circulation pump | Rated power: 4 kW Flow rate: 96 m3/h Head: 10 m |
| Parameters | Value/Unit |
|---|---|
| Intermediate water inlet temperature | −5 °C |
| Intermediate water flow rate | 0.5 m/s |
| Cold water inlet temperature | 2 °C |
| Cold water flow rate | 0.1 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Wu, R.; Yu, H.; Zhan, H.; Xu, L. Heat Transfer Characteristics of Cold Water Phase-Change Heat Exchangers under Active Icing Conditions. Energies 2022, 15, 7392. https://doi.org/10.3390/en15197392
Liu C, Wu R, Yu H, Zhan H, Xu L. Heat Transfer Characteristics of Cold Water Phase-Change Heat Exchangers under Active Icing Conditions. Energies. 2022; 15(19):7392. https://doi.org/10.3390/en15197392
Chicago/Turabian StyleLiu, Changqing, Ronghua Wu, Hao Yu, Hao Zhan, and Long Xu. 2022. "Heat Transfer Characteristics of Cold Water Phase-Change Heat Exchangers under Active Icing Conditions" Energies 15, no. 19: 7392. https://doi.org/10.3390/en15197392
APA StyleLiu, C., Wu, R., Yu, H., Zhan, H., & Xu, L. (2022). Heat Transfer Characteristics of Cold Water Phase-Change Heat Exchangers under Active Icing Conditions. Energies, 15(19), 7392. https://doi.org/10.3390/en15197392






