A Novel Classification of the 330 kV Nigerian Power Network Using a New Voltage Stability Pointer

Abstract

The incessant power outages that characterize the Nigerian power network (NGP), as in all developing countries, are not limited to the shortage of fuel for power generation. However, differential power shortages between the generated power and the load demand are alarming. In this study, we propose a new voltage stability pointer (NVSP) based on a reduced one-line power network to act as a classifier. The NVSP was trained with a support vector machine (SVM) using a medium Gaussian kernel classification toolbox (mGkCT) in the MATLAB environment. This classification is based on the power network susceptibility to voltage instability. NGP 28-bus 330 kV data were extracted and modeled in the MATLAB environment and tested with the NVSP-mGkCT classifier. The NVSP-mGkCT was able to classify the lines viz. stable and unstable lines for the base and contingency cases. Similarly, the linear load dynamics and non-linear load dynamics were evaluated on the basis of critical buses using the NVSP. The aim of this work was to help the Transmission Company of Nigeria (TCN) and the National Control Centre (NCC) to be pre-emptive with respect to possible voltage collapse due to voltage instability. The simulation results show that NVSP was able to flag vulnerable lines in the NGP.

1. Introduction

Power system planning in most developing countries is associated with several challenges due to the non-linear relationship between the increasing population and power generation, low reliability on capital investment, dispersed utilities, etc. [1]. Gross deficiency in power generation has driven many developing countries to forced load shedding to ensure that the meager generated power reaches the considerable population. In such a context, power system operators are concerned about active power control, which is invariably associated with the frequency stability [2], and rarely consider reactive power control, which is associated with voltage stability [3]. Furthermore, the rotor, frequency and voltage stability control are essential components of a reliable power system [4].

The Nigerian power network (NGP) comprised approximately twenty-six power plants with a combined optimal power generation of slightly more than seven thousand megawatts (7000 MW) [5], which are provided hydro and thermal power plants [6]. This generated power serves a population of more than two hundred million (200,000,000) people [7]. The NGP is faced several crises, including insufficient generation of electric power to match the demand [8,9], overstretched transmission lines and support, [10] and the inability to withstand transient conditions [11]. The average number of the recorded power outages, both partial and total, in the NGP every year is alarming [12], and there seems to be no end in sight with respect to addressing this increasing figure. The high rate of blackouts in Nigeria has driven many small-scale businesses out of operation [13], and the few remaining companies operate at a high cost of production due to the increase in prices of alternative sources of fuel, for example, diesel, gas, etc. Hence, there is a need to develop a tool to identify the weak buses and lines that are vulnerable to voltage collapse, which could lead to a national blackout.

The framework of this research is to (1) develop a new voltage stability pointer (NVSP) for evaluation of voltage stability, (2) train the NVSP with the support vector machine using a medium Gaussian kernel classification toolbox in a MATLAB environment and (3) adapt it to the Nigerian power network to classify it into two classes, i.e., stable and unstable. The lines and buses under the unstable classification will be flagged as vulnerable.

2. Related Work

The effort of the Nigerian government to increase the power generation capacity of the country has not yielded satisfactory results despite the considerable capital investment in the power sector over the years. According to the World Bank Energy Progress Report, only 55.4 percent of the Nigerian population had access to electricity in the year 2020 [7]. The geographical structure of the transmission lines in Nigeria is shown in Figure 1.

Figure 1. Geographical structure of the NGP transmission lines [6].

The load demand is predicted to reach 50,000 MW by the year 2035 [6]. However, there little effort has been made to date to scale up the generation capacity to meet this future demand. The recorded cases of power outages in the NGP between January and June 2022 are estimated to be five [14]. This number is high compared to other developed nations [7]. The variation in load demand is among the factors that affect the power network stability [15]. Ramirez-Gonzalez M. et al. [16] studied contingencies in a power network and their effects on security. A convolutional neural network was used to allocate power injection stations in the power network, with the result proving the effectiveness of the proposed method.

Similarly, Abdulkareem A. et al. [10] suggested that the NGP topology be changed from a radial to ring structure to minimize losses and voltage instability. The TCN annual technical report also set a goal to achieve this transition before the year 2030 [6]. However, such a transition will be time-consuming and cost-intensive, and a solution is urgently required before it can be implemented. In addition, Obi P. I. et al. [17] presented a technique to improve the NGP with static Var compensators to fulfill the voltage quality requirements. However, this technique is regarded as a short-term solution to the lingering problem faced by the Nigerian power grid. Moreover, Adebayo et al. [18] proposed two methods to identify vulnerable buses in a power network. The first method was achieved through the maximum loading limit technique, and the other was based on the configuration of the power network. The NGP 24-bus and IEEE 30-bus systems were used to evaluate the proposed method. The critical buses were strengthened with FACTS components. Simulation results showed that optimal placement of a compensating device could improve the voltage profile. In [19], a stability concept for power systems based on the frequency control of synchronous machines was presented. The system was tested with various loading patterns, and the results were compared with conventional synchro-converter models.

In a research paper presented by Kasis A. et al. [20], a technique was evaluated to solve the problem associated with fluctuations of renewable energy sources and the effects on power stability. Multiple possibilities for frequency dynamics were modeled, considering the variability of the inherent power supply. The results showed the immunity of the power stability to a high-frequency cycle. A surge in renewable power penetration in power distribution networks might result in overvoltage at network buses in the absence of an effective control mechanism. Heidari Yazdi et al. [21] proposed a method to regulate voltage magnitude based on the load demand. Power demand usually varies; therefore, means to compensate for the peak consumption period is necessary. An overvoltage resulting from excessive reactive power injection was considered and addressed for a stable power system.

In an effort to solve problems associated with power network configuration, Narimani et al. [22] proposed a novel method of analyzing several contingency problems associated with the architecture of the network. This was achieved through a graph theory approach that identifies different power components responsible for contingency, especially between two successive contingencies. The results showed that the proposed method could rapidly identify multiple contingencies. In the same vein, Randey A et al. [23] proposed a network reconfiguration technique for NGP to secure the network from a possible grid collapse and thereby improve the voltage profile. Contingency analysis resulted suggested that the redistribution of notable generators to defined voltage set-points would reduce power outages.

In a paper presented by Nkan et al. [24], several compensative devices were investigated with the aim of combining two similar controllers. The method was tested on NGP in the power system analysis toolbox (PSAT) in MATLAB. Analysis results showed that the combination of similar compensating devices could reduce power losses to a considerable extent. Some NGP buses are currently operating below their standard rated voltage [25] as a result of overload and congestion, with no adequate plan for contingency. Moreover, Liu S. et al. [26] presented a study on the dynamism of a stability point in a power network through the injection of noise and time delay. The aim of this method is to improve the integrity of the power network in a smart grid. The authors assessed the effect of noise on power system stability.

The power stability problem has recently received attention from many researchers, and efforts are being made to address the problems associated with power stability. Alnasseir et al. [27] addressed the power stability problem by introducing a static synchronous compensator (STATCOM) and a thyristor-controlled series capacitor (TCSC). The two compensators were assessed independently, and their results were compared. The results showed that the TCSC is relatively effective in securing power stability. Similarly, Calma E. and Pacis M. [28] studied voltage stability indices for different states of operation in a power system. The proposed approach involved an artificial neural network, and the Newton–Raphson power flow was employed in the MATLAB environment. The results demonstrated the feasibility of the proposed approach, especially compared with other machine learning techniques in terms of assessing the voltage stability of a power network. In addition, Collados-Rodriguez et al. [29] analyzed the effect of power electronics components on power system stability. Several cases of stability were evaluated to assess the minimum power generation expected to ensure power network security with the installation of compensative components. The stability indices considered for the evaluation were frequency and voltage, which were sufficient to identify the vulnerable lines in the network [2,3].

The effect of harmonics on power stability cannot be overemphasized [30]. Abirami and Ravi [31] recommended a technique to reduce harmonic distortion, especially with the advent of electric car charging stations in the distribution network. They suggested that a shunt capacitive filter be connected in parallel with dynamic loads in a radial distribution network. Simulation results revealed that adequate control of harmonic could enhance the power quality delivery to end consumers. Similarly, Zaheb H. et al. [32] investigated the effect of inductive load dynamics on various voltage stability indices. The researchers emphasized the suitability of these indices for online application. The obtained results were used to classify the indices in terms of their ability to assess, formulate and analyze the voltage stability.

The NVSP proposed in this study was developed to (a) verify the voltage stability status of the Nigerian power network, (b) assess the vulnerability of each transmission line to voltage instability, (c) flag unstable lines and buses and (d) suggest a reactive power injection station. With this approach, it is expected that the outcome of this research will help to tame the frequent power outages in the NGP, and thus, improves the economic viability of the country.

3. Proposed Methodology

The proposed method is based on successive dependence of three approaches viz. power flow solution, development of a new voltage stability pointer for voltage stability evaluation from the power flow data and training of the NVSP through a support vector machine.

3.1. Power Flow Solution

In this research, the Newton–Raphson method was adopted, owing to its fast convergence time. Saadat [33] considered an n-bus network (Figure 2) for as a power flow solution.

$$I_i={\displaystyle \sum }_{j=1}^n{Y}_{ij}{V}_j$$

(1)

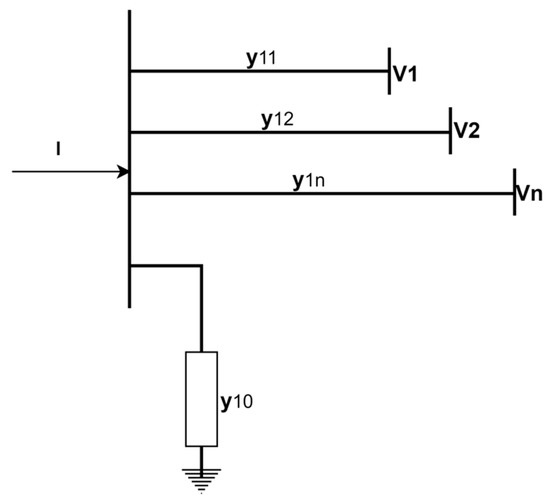
Figure 2. n-bus power network [33].

The polar-form representation of the equation is:

$$I_i={\displaystyle \sum }_{j=1}^n\begin{array}{c}\left|Y_{ij}\left|V_j\right|\right|\angle {\theta }_{ij}+{\delta }_{j }\end{array}$$

(2)

The power at bus 1 is expressed as:

$$P_i-j{Q}_i=V_i^{*}{I}_{i }$$

(3)

Substituting Equation (2) into Equation (3) yields:

$$P_i-j{Q}_i=\left|V_i\right|\angle -{\delta }_i{\displaystyle \sum }_{j=1}^n\left|Y_{ij}\right|\left|V_j\right|\angle {\theta }_{ij}+{\delta }_j$$

(4)

Separating the real from the imaginary part yields:

$$P_i={{\displaystyle \sum }}_{j=1}^n\left|V_i\right|\left|V_j\right|\left|Y_{ij}\right|\cos \left({\theta }_{ij}-{\delta }_j+{\delta }_j\right)$$

(5)

$$Q_i=-{{\displaystyle \sum }}_{j=1}^n\left|V_i\right|\left|V_j\right|\left|Y_{ij}\right|\sin \left({\theta }_{ij}-{\delta }_j+{\delta }_j\right)$$

(6)

Expanding Equations (5) and (6) using Taylor’s series yields:

$$\left[\begin{array}{c}\Delta P_2^{\left(k\right)}\\ ⋮\\ \Delta P_n^{\left(k\right)}\\ -\\ \Delta Q_2^{\left(k\right)}\\ ⋮\\ \Delta Q_n^{\left(k\right)}\end{array}\right]=\left[\frac{\begin{array}{cccccc}\frac{\partial P_2^{\left(k\right)}}{\partial {\delta }_2}& \dots & \frac{\partial P_2^{\left(k\right)}}{\partial {\delta }_n}& \frac{\partial P_2^{\left(k\right)}}{\partial {\delta }_2}& \dots & \frac{\partial P_2^{\left(k\right)}}{\partial {\delta }_n}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ \frac{\partial P_n^{\left(k\right)}}{\partial {\delta }_2}& \dots & \frac{\partial P_n^{\left(k\right)}}{\partial {\delta }_n}& \frac{\partial P_n^{\left(k\right)}}{\partial {\delta }_2}& \dots & \frac{\partial P_n^{\left(k\right)}}{\partial {\delta }_n}\end{array}}{\begin{array}{cccccc}\frac{\partial P_2^{\left(k\right)}}{\partial {\delta }_2}& \dots & \frac{\partial P_2^{\left(k\right)}}{\partial {\delta }_n}& \frac{\partial P_2^{\left(k\right)}}{\partial {\delta }_2}& \dots & \frac{\partial P_2^{\left(k\right)}}{\partial {\delta }_n}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ \frac{\partial P_n^{\left(k\right)}}{\partial {\delta }_2}& \dots & \frac{\partial P_n^{\left(k\right)}}{\partial {\delta }_n}& \frac{\partial P_n^{\left(k\right)}}{\partial {\delta }_2}& \dots & \frac{\partial P_{n_k}^{\left(k\right)}}{\partial {\delta }_n}\end{array}}\right]\left[\begin{array}{c}\Delta {\delta }_2^{\left(k\right)}\\ ⋮\\ \Delta {\delta }_n^{\left(k\right)}\\ -\\ \Delta \left|V_2^{\left(k\right)}\right|\\ ⋮\\ \Delta \left|V_n^{\left(k\right)}\right|\end{array}\right]$$

(7)

Equation (7) can be expressed in short form as:

$$\left[\begin{array}{c}\Delta P\\ \Delta \mathrm{Q}\end{array}\right]=\left[\begin{array}{cc}{J}_1& J_2\\ J_3& J_4\end{array}\right]\left[\begin{array}{c}\Delta \delta \\ \Delta \left|V\right|\end{array}\right]$$

(8)

The diagonal and off-diagonal components of J₁, J₂, J₃ and J₄ are estimated to obtain the differential residual power and bus voltages:

$$\Delta P_i^{\left(k\right)}=P_i^{sch}-P_i^{\left(k\right)}$$

(9)

$$\Delta Q_i^{\left(k\right)}=Q_i^{sch}-Q_i^{\left(k\right)}$$

(10)

$${\delta }_i^{\left(k+1\right)}={\delta }_2^{\left(k\right)}+\Delta {\delta }_i^{\left(k\right)}$$

(11)

$$\left|V_n^{\left(k+1\right)}\right|=\left|V_i^{\left(k\right)}\right|+\Delta \left|V_i^{\left(k\right)}\right|$$

(12)

3.2. Derivation of the Proposed New Voltage Stability Pointer

The proposed NVSP is derived from a reduced one-line diagram as shown in Figure 3.

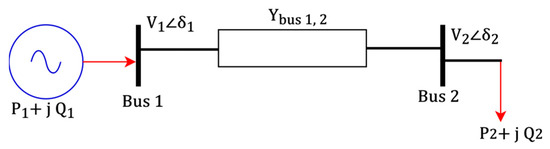
Figure 3. A reduced one-line diagram.

The line current (I) from the generator bus is expressed as:

$$I=\left(V_1-V_2\right).Y_{bus}$$

(13)

The current at the load bus can also be calculated as:

$$I=\left(\frac{S_2}{V_2}\right)=\frac{P_2-j{Q}_2}{V_2\angle -{\delta }_2}$$

(14)

Assuming the line loss due to the load current is neglected, then Equation (13) will equate to Equation (14):

$$P_2-j{Q}_2=\left(V_1-V_2\right).Y_{bus} . V_2\angle -{\delta }_2$$

(15)

$$P_2-j{Q}_2=\left|V_1{V}_2{Y}_{bus}\right|\angle (\theta -{\delta }_2)-{\left|V_2\right|}^2.\left|Y_{bus}\right|\angle \theta$$

(16)

Dividing Equation (16) by $\left|Y_{bus}\right|\angle \theta$ yields:

$$\frac{P_2-j{Q}_2}{\left|Y_{bus}\right|\angle \theta }=\left|V_1{V}_2\right|\angle -{\delta }_2-{\left|V_2\right|}^2$$

(17)

Equation (17) can be rewritten as:

$${\left|V_2\right|}^2-\left|V_1{V}_2\right|\angle -{\delta }_2+\frac{P_2-j{Q}_2}{\left|Y_{bus}\right|\angle \theta }=0$$

(18)

From Equation (18):

$$a=1;b=\left|V_1\right|\angle -{\delta }_{2 } and c=\frac{P_2-j{Q}_2}{\left|Y_{bus}\right|\angle \theta }$$

$$V_2=\left|V_1\right|\angle -{\delta }_{2 }\pm \frac{\sqrt{\left|V_1\right|\angle -{\delta }_2{|}^2-4\frac{P_2-j{Q}_2}{\left|Y_{bus}\right|\angle \theta } }}{2}$$

(19)

If $\left(\left|V_1\right|\angle -{\delta }_2{|}^2-4\frac{P_{2-}j{Q}_2}{\left|Y_{bus}\right|\angle \theta }\right)$ is discriminated to zero, the real roots of $V_2$ can be expressed as $\left|V_1\right|\angle -{\delta }_2{|}^2-4\frac{P_{2-}j{Q}_2}{\left|Y_{bus}\right|\angle \theta }\le 0$; then:

$$\frac{4\left(P_2-j{Q}_2\right)}{\left|G-jB\right|\angle \theta \left|V_1\right|\angle -{\delta }_{2 }{|}^2} \le 1$$

(20)

If Equation (20) is rearranged into real and imaginary parts, then the real part is $\frac{4P_2}{G cos\theta . {\left|V_1\right|}^2 co{s}^2 \left(-{\delta }_{2 }\right)}\le 1$, and if the voltage angle (${\delta }_{2 }$) is very small, then it is reduced to$\approx \frac{4P_2\left|Z\right|}{{\left|V_1\right|}^2}$ $\le 1$.

Likewise, the imaginary part is $\frac{4Q_2}{B sin \theta . {\left|V_1\right|}^2 si{n}^2 \left(-{\delta }_{2 }\right)}$ $\le 1$; if the voltage angle (${\delta }_{2 }$) is assumed to be negligible, then it is reduced to$\approx \frac{4Q_2\left|Z\right|}{{\left|V_1\right|}^2} \le 1$.

Therefore, the new voltage stability pointer (NVSP) is:

$$\mathrm{N}\mathrm{V}\mathrm{S}\mathrm{P}=\frac{4Q_2\left|Z\right|}{{\left|V_1\right|}^2}\le 1$$

(21)

where V₁ is the voltage at the sending end bus, Q₂ is the reactive power at the load bus and Z is the line impedance. The index Equation (21) depends on the extracted data from the power flow solution of Equations (8), (10) and (12). The NGP 28-bus line diagram is shown in Figure 4.

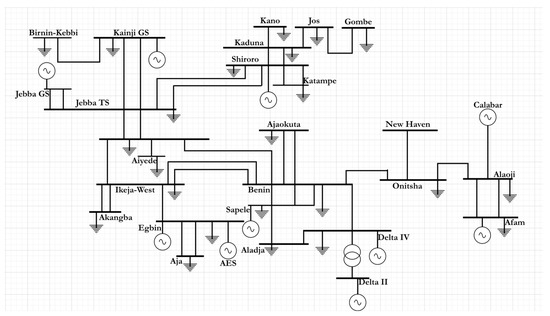
Figure 4. Single-line diagram of the 28-bus, 330 kV NGP.

3.3. Classification through Support Vector Machine Algorithm

The support vector machine (SVM) algorithm has been widely used to classify data of different sets that are separable into classes [34]. Squires [35] defined the Gaussian elimination with a function $f\left(x\right)=\exp \left(-x\right)$ with parametric extension:

$$f\left(x\right)=a\exp \left(-\frac{{\left(x-b\right)}^2}{2c^2}\right)$$

(22)

where a and b are real constants, and c is a non-zero variable. However, the Gaussian function is usually expressed as:

$$g\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{1}{2} \frac{{\left(x-\mu \right)}^2}{{\sigma }^2}\right)$$

(23)

where $\sigma \mathrm{is}\mathrm{the}\mathrm{expected}\mathrm{value}$ $\mathrm{and}\mu \mathrm{is}\mathrm{the}\mathrm{variance}$.

Assuming [36] that the training data $\left(x_i,y_i\right)$ for $i=1\dots \dots N with X_i\in {ℝ}^d and y_i\in \left\{-1,1\right\}$, the classifier $f\left(x\right)$ is:

$$f(x_i)=\left\{\begin{array}{c}\ge 0 y_i=+1 \\ <0 y_i=-1\end{array}\right.$$

(24)

and

$$f\left(x\right)=W^{T}X+b$$

(25)

where $X$ is the input vector, $W$ is the vector weight and $b$ is the bias. The NVSP was trained by the support vector machine algorithm in MATLAB using the medium Gaussian kernel classification tool according to the function $k(x_{ij})$ in Equation (26):

$$k_{ij}=\left\{\begin{array}{c}+1 if 0.00<\mathrm{N}\mathrm{V}\mathrm{S}\mathrm{P}<0.80 \left(Stable\right)\\ -1 if 0.80<\mathrm{N}\mathrm{V}\mathrm{S}\mathrm{P}<1.00 \left(Unstable\right)\end{array}\right.$$

(26)

where $k_{ij }$ is the NVSP-mGkCT trained index value between the two buses.

4. Results and Discussion

4.1. Assessment of the NGP 28-Bus, 330 kV Base Case

The simulation results obtained from the voltage stability assessment of the NGP using the NVSP are presented in Table 1, and the training results from the support vector machine in the MATLAB environment are shown in Figure 5. The NGP 28-bus voltage magnitude in the base case is depicted in Figure 6.

Table 1. Voltage stability assessment of 28-bus 330 kV NGP transmission line using NVSP in the base case.

From	Bus Name	To	Bus Name	NVSP
3	Aja	1	Egbin	0.0087
4	Akangba	5	Ikeja-west	0.1033
1	Egbin	5	Ikeja-west	0.0777
5	Ikeja-west	8	Benin	0.9673
5	Ikeja-west	9	Ayede	0.3404
5	Ikeja-west	10	Osogbo	0.4711
6	Ajaokuta	8	Benin	0.5410
2	Delta	8	Benin	0.3432
2	Delta	7	Aladja	0.0242
7	Aladja	24	Sapele	0.0109
8	Benin	14	Onitsha	0.2159
8	Benin	10	Osogbo	0.4213
8	Benin	24	Sapele	0.0080
9	Aiyede	10	Osogbo	0.2290
15	Birnin	21	Kanji	0.0171
10	Osogbo	14	Jebba TS	0.0153
11	AFAM	12	Alaoji	0.0818
12	Alaoji	14	Onitsha	0.2210
13	New Haven	14	Onitsha	0.1656
16	Gombe	19	Jos	0.1335
17	Jebba TS	18	Jebba GS	0.0000
17	Jebba TS	23	Shiroro	0.0986
17	Jebba TS	21	Kanji	0.0041
19	Jos	20	Kaduna	0.0275
20	Kaduna	22	Kano	0.3689
20	Kaduna	23	Shiroro	0.0389
23	Shiroro	26	Katempe	0.2223
12	Alaoji	25	Calabar	0.1797
14	Onitsha	27	Okpai	0.0000
25	Calabar	27	Okpai	0.0000
5	Ikeja-west	28	AES GS	0.0000

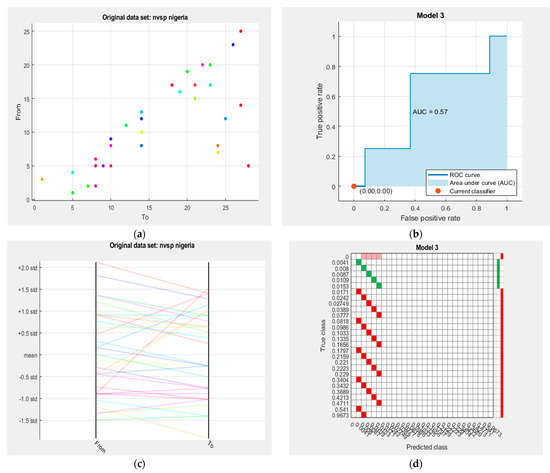
Figure 5. Training results of NVSP using support vector machine in the MATLAB environment. (a) Scatter plot of the NGP. (b) Receiver operating characteristic (ROC) curve. (c) Parallel coordinate plot. (d) Confusion matrix.

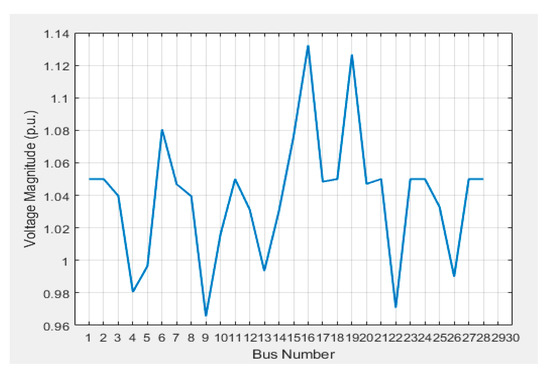
Figure 6. The NGP 28-bus voltage per unit in the base case.

4.2. Analysis of the 28-Bus, NGP 330 kV Base Case

The overall percentage accuracy of the predicted class of NVSP, 28-bus NGP 330 kV line to the true class is 72.48, with a training time of about 2.02 s. The area under the curve from the receiver operating characteristic (ROC) is 0.57. All lines and buses are stable in the base case, except the Ikeja-west bus and the Ikeja-west–Benin line. The NVSP index value is 0.9673, and the voltage magnitude is 0.997 (p.u), indicating the vulnerability of the line to voltage instability. In the base case, the Ikeja-west load bus has 474. 5 MVar, as shown in Table A1, as a result of heavy industrial presence in the region. The NVSP index values for all other lines are far less than unity, indicating their immunity to voltage instability in the base case, as shown in Figure 7.

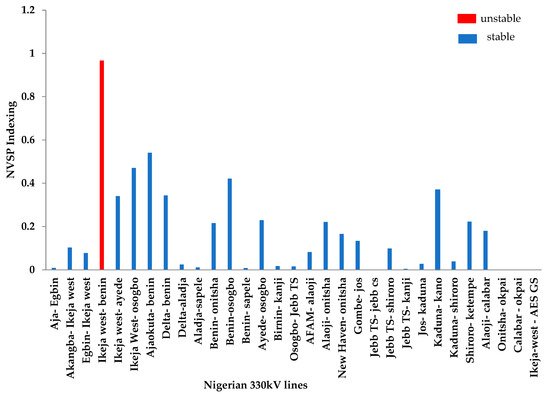
Figure 7. Classification of the NGP transmission lines using NVSP in the base case.

The placement of the static synchronous compensator (STATCOM) at the Ikeja-west bus provides stability at the bus, as the NVSP index value from the Ikeja-west–Benin line changes from 0.9673 to 0.7621. The voltage magnitude of the Ikeja-west bus also changes from 0.997 (p.u) to 1.023 (p.u). This effect yielded a positive result with respect to the overall performance of the NGP, as none of the lines are near the unity NVSP index value, and the voltage profile is also improved, as shown in Figure 8.

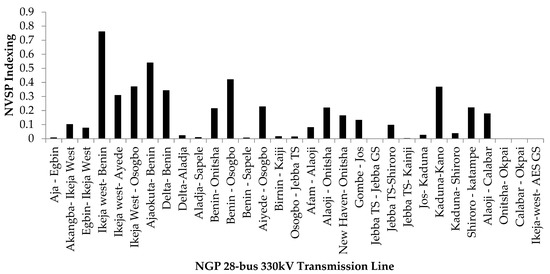
Figure 8. The NGP 28-bus 330 kV transmission lines after STATCOM compensation in the base case.

4.3. Contingency Assessment of the NGP 28-Bus Using NVSP

The contingency analysis is among the performance indices used to evaluate the power network stability, especially with respect to its loading capacity limit [15]. Contingency analysis can assist the system operator in identifying the most critical and vulnerable lines and buses to voltage instability. The contingency analysis of the NGP, 28-bus using NVSP is presented in Table 2. The NVSP index and the power flow convergence methods were used to evaluate the loadability of all the NGP P-Q buses. The power flow solution is programmed to return non-convergence after 100 iterations without convergence.

Table 2. Realization of the NGP critical lines and the maximum reactive power loading points.

P-Q Bus	From	To	NVSP	Voltage Mag. (p.u)	Qmax (MVar)	Remark
Aja	Aja	Egbin	0.0260	0.600	6005.58	Non-convergence
Akangba	Akangba	Ikeja-west	0.2527	0.6270	2050.8	Non-convergence
Ikeja-west	Ikeja-west	AES-GS	0.0000	0.9760	774.9	NVSP indexing
	Egbin	Ikeja-west	0.1268
	Ikeja-west	Benin	1.0077
	Ikeja-west	Osogbo	0.4908
	Akangba	Ikeja-west	0.1758
	Ikeja-west	Ayede	0.3546
Ajaokuta	Ajaokuta	Benin	0.9980	0.7960	355.3	NVSP-indexing
Aladja	Aladja	Sapele	0.0174	0.8280	2972.4	NVSP-indexing
	Delta	Alajda	0.9946
Benin	Benin	Sapele	0.0080	1.0390	295.5	NVSP-indexing
	Delta	Benin	0.3528
	Benin	Osogbo	0.4318
	Ikeja-west	Benin	0.9944
	Benin	Onitsha	0.2161
	Akaokuta	Benin	0.5566
Aiyede	Aiyede	Osogbo	0.6678	0.5650	906.8	NVSP-indexing
Osogbo	Osogbo	Jebba TS	0.0171	0.9840	300.9	NVSP indexing
	Benin	Osogbo	0.8660
	Ikeja-west	Osogbo	0.9501
	Ayede	Osogbo	0.4776
Alaoji	Afam	Alaoji	0.9763	0.7450	3820.2	NVSP-indexing
	Alaoji	Onitsha	0.4231
	Alaoji	Calabar	0.3440
New Haven	New Haven	Onitsha	0.3602	0.6740	633.4	NVSP-indexing
Onitsha	Benin	Onitsha	0.9591	0.9840	605.4	NVSP-indexing
	Alaoji	Onitsha	0.9787
	New Haven	Onitsha	0.8013
Birni-Kebbi	Birni-Kebbi	Kainji	0.3560	0.7470	285.9	NVSP-indexing
Gombe	Gombe	Jos	0.1358	1.1230	100.9	Non-convergence
Jebba TS	Jebba Ts	Shiroro	0.1004	1.0390	500.2	NVSP-indexing
	Jebba TS	Kainji	0.0048
	Jebba TS	Jebba GS	0.0000
	Osogbo	Jebba TS	0.9436
Jos	Gombe	Jos	0.6662	0.8860	142.7	Non-convergence
	Jos	Kaduna	0.4442
Kaduna	Kaduna	Shiroro	0.0512	0.9120	332.7	NVSP indexing
	Kaduna	Kano	0.4858
	Jos	Kaduna	0.9508
Calabar	Alaoji	Calabar	0.9517	0.9050	459	NVSP indexing
	Calabar	Okapi	0.0000
Katampe	Shiroro	Katampe	0.7128	0.7980	465	Non-convergence
Kano	Kaduna	Kano	0.6185	0.8080	210.9	Non-convergence

The maximum reactive power at all the P-Q buses of the NGP 28-bus is presented in Table 3. The results show the peak loading limit of all the load buses, and a step above this threshold results in voltage instability. The contingency ranking was obtained based on the increment of reactive power at the load buses. The maximum reactive power that drives the NVSP index value to unity or the power flow solution to non-convergence is regarded as maximum loadability. In other words, the safe operating limit of reactive power at the load buses was attained by considering the power flow convergence and the NVSP indexing value. The NVSP of every line should be maintained well below unity in order to ensure voltage stability.

Table 3. Contingency analysis of the NGP buses and lines.

Ranking	Bus Name	From	To	NVSP	Voltage Mag. (p.u)	Qmax (MVar)
1	Gombe	Gombe	Jos	0.1358	1.1230	100.9
2	Jos	Gombe	Jos	0.6662	0.8860	142.7
3	Kano	Kaduna	Kano	0.6185	0.8080	210.9
4	Birni-Kebbi	Birni-Kebbi	Kainji	0.3560	0.7470	285.9
5	Benin	Ikeja-west	Benin	0.9944	1.0390	295.5
6	Osogbo	Ikeja-west	Osogbo	0.9501	0.9840	300.9
7	Kaduna	Jos	Kaduna	0.9508	0.9120	332.7
8	Ajaokuta	Ajaokuta	Benin	0.9980	0.7960	355.3
9	Calabar	Alaoji	Calabar	0.9517	0.9050	459
10	Katampe	Shiroro	Katampe	0.7128	0.7980	465
11	Jebba TS	Osogbo	Jebba TS	0.9436	1.0390	500.2
12	Onitsha	Alaoji	Onitsha	0.9787	0.9840	605.4
13	New Haven	New Haven	Onitsha	0.3602	0.6740	633.4
14	Ikeja-west	Ikeja-west	Benin	1.0077	0.9760	774.9
15	Ayede	Ayede	Osogbo	0.6678	0.5650	906.8
16	Akangba	Akangba	Ikeja-west	0.2527	0.6270	2050.8
17	Aladja	Delta	Alajda	0.9946	0.8280	2972.4
18	Alaoji	Afam	Alaoji	0.9763	0.7450	3820.2
19	Aja	Aja	Egbin	0.0260	0.6000	6005.58

The results presented in Table 3 show that the most critical bus and line under contingency rankings are Gombe and Gombe-Jos, with a maximum operating limit of 100.9 MVar and an NVSP index value of 0.1358, respectively. The Jos, Kano, Birni-Kebbi and Benin buses, which are ranked second, third, fourth and fifth, with maximum reactive power limits of 142.7 MVar, 210.9 MVar, 285.9 MVar and 295.5 MVar, respectively, are also vulnerable to perturbation or transient conditions. The voltage magnitude and maximum reactive power limit of the NGP P-Q bus are presented in Figure 9 and Figure 10, respectively.

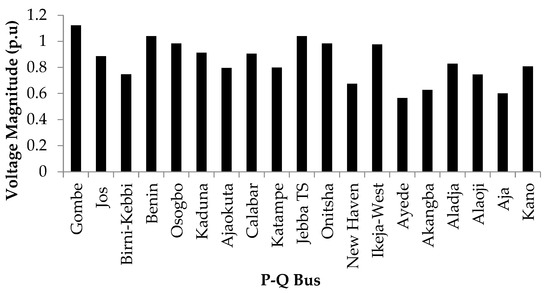
Figure 9. Voltage magnitude of the NGP P-Q bus under contingency conditions.

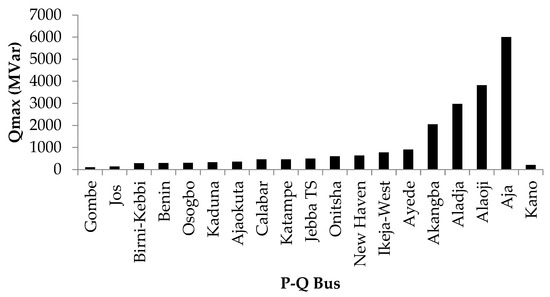
Figure 10. Maximum loading limit of the NGP P-Q bus.

The results presented in Table 3 show that the order of stable buses of the NGP under contingency conditions is: Aja, Alaoji, Aladja, Akangba, Ayede, Ikeja-west and New Haven. Conversely, the order of unstable P-Q buses under contingency conditions is: Gombe, Jos, Kano, Birni-Kebbi, Osogbo, Kaduna, Calabar, Katampe, Jebba TS and Onitsha. Based on the results presented in Figure 9 and Figure 10 and a stamp to ensure a safe margin of operation at the vulnerable buses in the NGP, we recommended that the loads at the critical P-Q buses be optimally shed, especially during peak load hours. However, this approach is regarded as a short-term solution to power system stability [37].

4.4. Assessment of Dynamic Load on 28-Bus NGP Critical Lines and Vulnerable Buses

The effect of the dynamic load on the vulnerable P-Q buses in the NGP 28-bus system were considered for this analysis, including the first, second and third rankings in Table 3, i.e., Gombe, Jos and Kano, respectively. In addition, we evaluated both linear load dynamics and non-linear load dynamics to assess the power stability of the NGP.

4.4.1. Linear Load Dynamics

The linear increment in both P and Q at Gombe, Jos and Kano buses of the 28-bus NGP are presented in Table 4, Table 5 and Table 6, respectively. The results presented in Table 4 show that the lowest power consumption at Gombe bus is 60.0 MW and 70.0 MVar. The power flow solution using the Newton–Raphson method did not converge at this loading point after 100 iterations, implying that any further drop in the load-active power and reactive power would lead to voltage instability. However, maximum dynamic loads of 145.0 MW and 150.0 MVar were recorded at Gombe bus, as shown in Table 4.

Table 4. Linear load dynamics at Gombe bus in the 28-bus NGP.

Bus Name	Critical Line		Load Dynamics		NVSP	Voltage Mag. (p.u)
	From	To	Active Power, P, (MW)	Reactive Power, Q, (MVar)
Gombe	Gombe	Jos	60.0	70.0	Non-convergence	-
			90.6	50.9	0.1242	1.174
			95.0	105.0	0.1284	1.155
			100.0	110.0	0.1331	1.134
			105.0	115.0	0.1385	1.112
			125.0	135.0	0.1711	1.000
			145.0	150.0	Non-convergence	-

Table 5. Linear load dynamics at Jos bus in the 28-bus NGP.

Bus Name	Critical line		Load Dynamics		NVSP	Voltage Mag. (p.u)
	From	To	Active Power, P, (MW)	Reactive Power, Q, (MVar)
Jos	Gombe	Jos	40.3	55.7	0.1372	1.140
			30.3	45.7	0.1079	1.161
			20.0	25.7	0.0567	1.195
			10.0	10.0	0.0210	1.221
			100.0	85.0	0.2604	1.042
			120.0	105.0	0.3936	0.962
			140.0	125.0	Non-convergence	-

Table 6. Linear load dynamics at Kano bus in the 28-bus NGP.

Bus Name	Critical Line		Load Dynamics		NVSP	Voltage Mag. (p.u)
	From	To	Active Power, P, (MW)	Reactive Power, Q, (MVar)
Kano	Kaduna	Kano	50.6	40.0	Non-convergence	-
			80.6	90.9	0.2091	1.112
			100.0	120.0	0.2848	1.068
			150.0	120.0	0.3206	1.033
			250.0	150.0	0.4006	0.933
			350.0	250.0	Non-convergence	-

According to the results presented in Table 5, the Jos bus is relatively stable, even at the lowest load consumption. However, a shunt reactor should be installed at the Jos bus to prevent cases of overvoltage, especially during the lowest power consumption period. In the same vein, the maximum active power and reactive power at the Jos bus are 140 MW and 125 MVar, respectively.

As shown in Table 6, the lowest stable power consumptions at Kano bus are 50.6 MW and 40.9 MVar for active power and reactive power, respectively. The maximum linear load dynamics before instability are 350 MW and 250 MVar for active and reactive power, respectively.

4.4.2. Non-Linear Dynamic Load

An evident load disagreement pattern often occurs when a surge in reactive power load occurs as a result of a massive drop in active power load and vice-versa. The results obtained from the non-linear load dynamic on the critical P-Q buses of the 28-bus NGP are presented in Table 7, Table 8 and Table 9. The Gombe bus was subjected to various incoherent loading patterns of active and reactive power, and the stability of the NGP was evaluated accordingly. The results presented in Table 7 depict voltage instability at Gombe bus during an uneven loading pattern of 40.0 MW and 200 MVar.

Table 7. Non-linear load dynamics at Gombe bus in the 28-bus NGP.

Bus Name	Critical Line		Load Dynamics		NVSP	Voltage Mag. (p.u)
	From	To	Active Power, P, (MW)	Reactive Power, Q, (MVar)
Gombe	Gombe	Jos	50.6	120.9	0.1291	1.152
			170.6	40.9	0.1119	1.237
			250.6	20.9	0.1278	1.157
			40.0	200.0	Non-convergence	-

Table 8. Non-linear load dynamics at Jos bus in the 28-bus NGP.

Bus Name	Critical Line		Load Dynamics		NVSP	Voltage Mag. (p.u)
	From	To	Active Power, P, (MW)	Reactive Power, Q, (MVar)
Jos	Gombe	Jos	30.0	90.7	0.2511	1.086
			20.0	100.7	0.2868	1.073
			10.0	250.7	Non-convergence	-
			150.0	30.7	0.0815	1.050
			350.0	20.0	Non-convergence	-

Table 9. The non-linear load dynamics at Kano bus in the 28-bus NGP.

Bus Name	Critical Line		Load Dynamics		NVSP	Voltage Mag. (p.u)
	From	To	Active Power, P, (MW)	Reactive Power, Q, (MVar)
Kano	Kaduna	Kano	90.6	182.9	0.4664	0.977
			70.6	200.0	0.5124	0.955
			50.6	220.0	0.5752	0.925
			30.0	280.0	0.8250	0.768
			10.0	300.0	Non-convergence	-
			350.0	50.0	0.1272	1.019
			450	30.0	0.0865	0.914
			650	20.0	Non-convergence	-

After several load permutations at the Jos bus, it was deduced that the nonlinear load pattern combinations that may lead to voltage instability at the Jos bus are 10.0 MW-250.7 MVar and 350.0 MW-20 MVar for the P-Q, as presented in Table 8.

Similarly, Kano bus appeared to be stable under a nonlinear load combination of 450 MW and 30.0 MVar. However, as voltage instability set in, a step in an almost inverse progression of P and Q occurred. As shown in Table 9, load combinations of 650 MW-20.0 MVar and 10.0 MW-300.0 MVar for the P-Q are the unstable load set points for the Kano bus.

4.5. Comparison of Past Research Work

Many researchers have assessed the NGP in the last couple of years and suggested ways to improve the stability of the network. However, there is a need to improve on this existing knowledge, which was the motivation for the present study. Oluseyi et al. [11] suggested that Ikeja-west be supported by increasing the injection capacity of the Egbin power plant. However, the issue was addressed through the NVSP by placing the STATCOM device close to the Ikeja-west bus, as shown in Figure 8; this approach was also corroborated by Obi et al. [17]. The NGP contingency ranking results obtained in [18] for the first to fourth rankings were consistent with the NVSP analysis; however, the contingency ranking by the NVSP were more accurate, with a relatively faster computing time. In addition, this research assessed the load dynamics of the NGP. The authors of [10,23,38] recommended that the Gombe bus and Kano bus be changed from radial to ring structures. However, such a transition would be cost-intensive and time-consuming. Similarly, renewable energy incorporation at the weak buses was suggested to improve the stability of power network [39,40,41]. However, there are some notable problems associated with the injection of renewable energy sources into a power network, such as intermittency, fluctuations, etc. [20].

5. Conclusions

In this paper, we presented a novel voltage stability index, the NVSP, for the classification of the 28-bus NGP, 330 kV transmission lines and buses. The classification was based on the vulnerability of each line to voltage collapse for the base and contingency cases. The results presented in Table 1 show that the Ikeja-west–Benin line was the only unstable line in the base case, with an NVSP index value of 0.9672 and a voltage magnitude of 0.997 (p.u). However, the problem was remedied by the installation of a STATCOM at the Ikeja-west bus, which improved the voltage stability of the line to an NVSP index value of 0.7621, as presented in Figure 8, with the voltage magnitude enhanced to 1.023 (p.u). A contingency analysis was carried out to evaluate the loadability of the P-Q buses of the 28-bus, 330 kV NGP. The Gombe, Jos and Kano P-Q buses were ranked as the most critical buses, with a maximum reactive power limit of 100.9 MVar, 142.9 MVar and 210.9 MVar, respectively. The most stable P-Q buses are Aja, Alaoji, Aladja and Akangba, with a maximum reactive power limit of 6005.58 MVar, 3820.2 MVar, 2972.4 MVar and 2,0508 MVar, respectively. Furthermore, the results obtained in this research show that (1) the installation of injection substations close to the flagged points will reduce the number possible blackouts, especially at Gombe, Jos and Kano buses; (2) increasing the power generation capacity from the Shiroro plant will also help to prevent the P-Q buses at these critical buses from operating close to their maximum capacity limit; and (3) the load at the P-Q buses for the critical buses—Gombe, Jos and Kano—could be optimally shed, especially during peak load hours, to maintain the stability of the NGP.