Effects of Composite Electrode Structure on Performance of Intermediate-Temperature Solid Oxide Electrolysis Cell

Abstract

The composite electrode structure plays an important role in the optimization of performance of the intermediate-temperature solid oxide electrolysis cell (IT-SOEC). However, the structural influence of the composite electrode on the performance of IT-SOEC is not clear. In this study, we developed a three-dimensional macroscale model coupled with the mesoscale model based on percolation theory. We describe the electrode structure on a mesoscopic scale, looking at the electrochemical reactions, flow, and mass transport inside an IT-SOEC unit with a composite electrode. The accuracy of this multi-scale model was verified by two groups of experimental data. We investigated the effects of operating pressure, volume fraction of the electrode phase, and particle diameter in the composite electrode on electrolysis reaction rate, overpotential, convection/diffusion flux, and hydrogen mole fraction. The results showed that the variation in the volume fraction of the electrode phase had opposite effects on the electrochemical reaction rate and multi-component diffusion inside the composite electrode. Meanwhile, an optimal range of 0.8–1 for the particle diameter ratio was favorable for hydrogen production. The analysis of IT-SOEC with composite electrodes using this multi-scale model enables the subsequent optimization of cell performance and composite electrode structure.

1. Introduction

In the current context of vigorously developing green and sustainable energy, hydrogen energy is considered a key energy carrier due to its unique and excellent performance characteristics. In general, electrolytic hydrogen production has advantages of cleanliness and high purity compared with other current industrial hydrogen production methods. It is the most promising technology to achieve large-scale hydrogen production [1,2]. The technology of hydrogen production through electrolysis using a solid oxide electrolysis cell (SOEC) under high temperature conditions was first proposed by Doenitz in 1980 [3], which differed from other conventional electrolysis cells in their working mechanisms and material characteristics. Compared with the low-temperature proton exchange membrane (PEM) electrolysis cell and alkaline electrolysis cell, SOEC has higher electrolytic efficiency [4,5].

In response to limitations of the SOEC under high temperature operating conditions, such as material fabrication processes and performance degradation of the electrolysis cell [6], an increasing number of scholars have started to investigate intermediate-temperature SOECs (IT-SOECs) and fuel cells (IT-SOFCs) with operating temperatures between 723 and 1073 K [7,8,9]. However, from a thermodynamic viewpoint, the decrease in the operating temperature also inevitably has a negative impact on the cell performance [10]. In the technological development of IT-SOECs or IT-SOFCs, many scholars have focused on developing new electrode materials or improving the electrode structure to expand the triple phase boundary (TPB) area while obtaining more stable electrochemical reactions and multi-component diffusion processes inside the SOEC [6,11]. Thus, many studies have been carried out on the composite electrode.

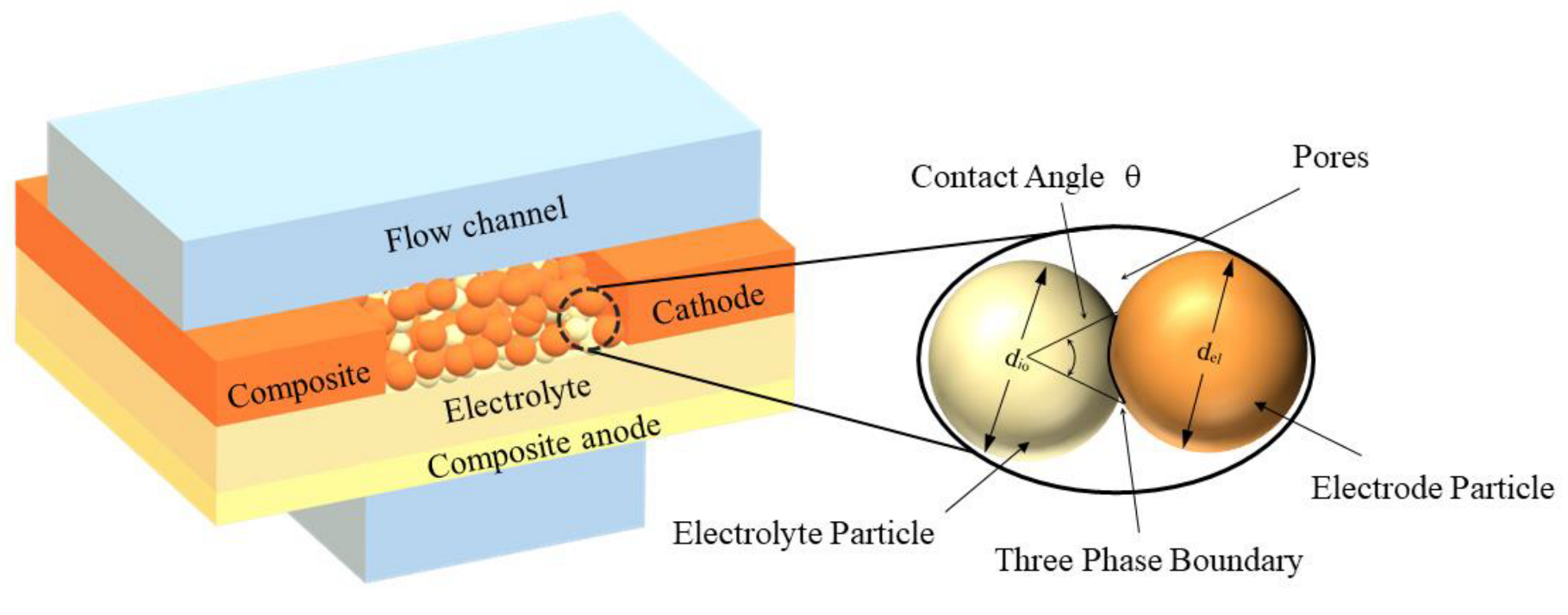
The composite electrode is a multi-phase material made by mixing electrode materials with electrolyte materials. Due to the structural features of the composite material, the TPB area is effectively enlarged [12,13]. The yttria-stabilized zirconia (YSZ), gadolinium-doped ceria (GDC), scandium-ceria-stabilized-zirconia (ScSZ), cobalt-samarium-doped ceria (Co-SDC), and other electrolyte materials that are combined with nickel (Ni) to form the composite electrode have received extensive attention [1,14].

For understanding and analyzing the complex coupling process of electrochemical reactions, flow, and multi-component diffusion in composite electrodes, numerical research has more advantages compared with experimental research [15,16,17]. Grondin et al. [16] developed a one-dimensional (1D) model to simulate the cathodic kinetic behavior of a composite cathode (Ni-ceramic) in SOEC and discussed the effects of chemical and electrochemical kinetic steps on the polarization curves. It is worth noting that the composite electrode is the main place where the above complex coupling process occurs. The composite electrode structure on the mesoscopic scale, including particle diameter, the volume fraction of electrode or electrolyte phase, and so on, will also affect the electrochemical reactions, flow, and multi-component diffusion process inside the electrode [18].

Therefore, many scholars have adopted different mesoscale mathematical models to study the species transport phenomena and reactions in the microporous structure of composite electrodes. Moussaoui et al. [19] adopted a so-called 3D Gaussian ‘random field model’ to carry out a mechanistic study about the relationship between the structural properties and performance of the electrode. Laurencin et al. [13] similarly reconstructed single-phase La_1−xSr_xCo_yFe_1−yO_3−δ (LSCF) electrodes as well as composite electrodes LSCF-CGO. It was found that the LSCF and ceria-doped gadolinium oxide (CGO) composites exhibited higher performance than the LSCF single-phase electrodes. Ren et al. [20] developed a microkinetic model to investigate the reduction mechanism of CO₂ at the TPB surface based on Ni-SDC. Density functional theory (DFT) was also used to analyze the rate-controlling step in different surface models. Schneider et al. [21] used a discrete element method (DEM) to study the influence of parameters, including electrode composition, thickness, and density, on the resistance and effective conductivity of the electrode. Gaiselmann et al. [22] quantitatively analyzed the effects of different sinter temperatures and different pore former contents in production processes on microstructures, using stochastic microstructural models. Deseure et al. [23] also used a one-dimensional flooded homogeneous model and microscopic approach to conclude that the grain size determined the rate-controlling step of the reaction and that optimum porosity was close to 0.3.

Therefore, when using the model to analyze the influence of the macro process on a SOEC unit performance, the corresponding internal structure of the composite electrode cannot be ignored. However, considering the fundamental differences in the scale of the SOEC unit and the internal structure of the composite electrode on the mesoscopic scale, it is difficult for the analysis of the unit performance to describe the composite electrode by mesoscale method [24,25,26,27,28,29,30]. In some studies, when analyzing the unit performance using macroscale models in different dimensions, some scholars have directly ignored [15] or adopted constants to reflect the internal structured features of composite electrodes [31,32,33,34], which certainly affect the accuracy and reliability of the model. Demin et al. [15] used the 0D equivalent circuit model to simulate and analyze the SOEC of ionic and proton conductive electrolytes in different feeding modes (downstream and countercurrent) while considering the influence of mass transport, but only external structural parameters, such as thickness, were considered. Grondin et al. [31] built a 2D macroscopic continuity model to describe the electrochemical reactions, mass transport, and temperature distribution inside a SOEC unit. However, this model assumed the internal TPB area to be 1 m² m⁻³.

Earlier, in fields related to SOFC, some scholars [35,36] established a more accurate and easier mathematical model by coupling the percolation theory with the continuity model to solve the above problem. This method can preserve the relationship between the structural features of the composite electrode on the mesoscopic scale and the macroscopic physical processes involved inside the electrode by calculating the interparticle coordination number and percolation threshold in a binary particle random stacking system. Chen et al. [37] analyzed the effect of various parameters on the performance of the composite cathode inter-layer of the SOFC by combining the equivalent circuit model and percolation theory. Although the electrochemical reactions and multi-component diffusion processes involved in SOEC and SOFC are quite different, they have similar structural parameter or electrode characteristics. Therefore, some scholars [38,39] have applied this method to the field of SOEC for hydrogen production. Ni et al. [38] established a mathematical model of SOEC coupled with percolation theory. In this study, the authors point out that the particle diameter affects the activation overpotential and concentration overpotential and that the volume fraction of the electrode phase affects the overall overpotential. Li et al. [39] similarly proposed a 1D solid oxide cell (SOC) model, incorporating percolation theory. They investigated the effects of structured features on the mesoscopic scale, including particle diameter and porosity, on the overpotential, ion current density, oxygen partial pressure, and polarization characteristics in both SOEC and SOFC models.

The above studies on the structural influences of the composite electrode mainly focused on comparisons of overall electrochemical performance. However, the corresponding composite electrode structure evidently also has an effect on the process of flow and multi-component diffusion in the IT-SOEC unit. Taking only the electrochemical behavior into account cannot ensure that the influence of the composite electrode structure will be fully reflected. Meanwhile, the processes of flow and mass transport inside the composite electrode are also important factors to optimize the performance of IT-SOEC. However, there are few systematical studies on the analysis of variation in the flow and mass transfer process with composite electrode structure. Therefore, the effect of composite electrode structure on IT-SOEC performance from a perspective of flow and multi-component diffusion processes needs to be further explored. In this study, we developed a 3D multi-scale model. The effects of the composite electrode structure on the mesoscopic scale and external operating pressures on electrochemical performance were investigated. Furthermore, we studied the influence of the composite electrode structure on the multi-component diffusion process in the different positions of composite electrodes.

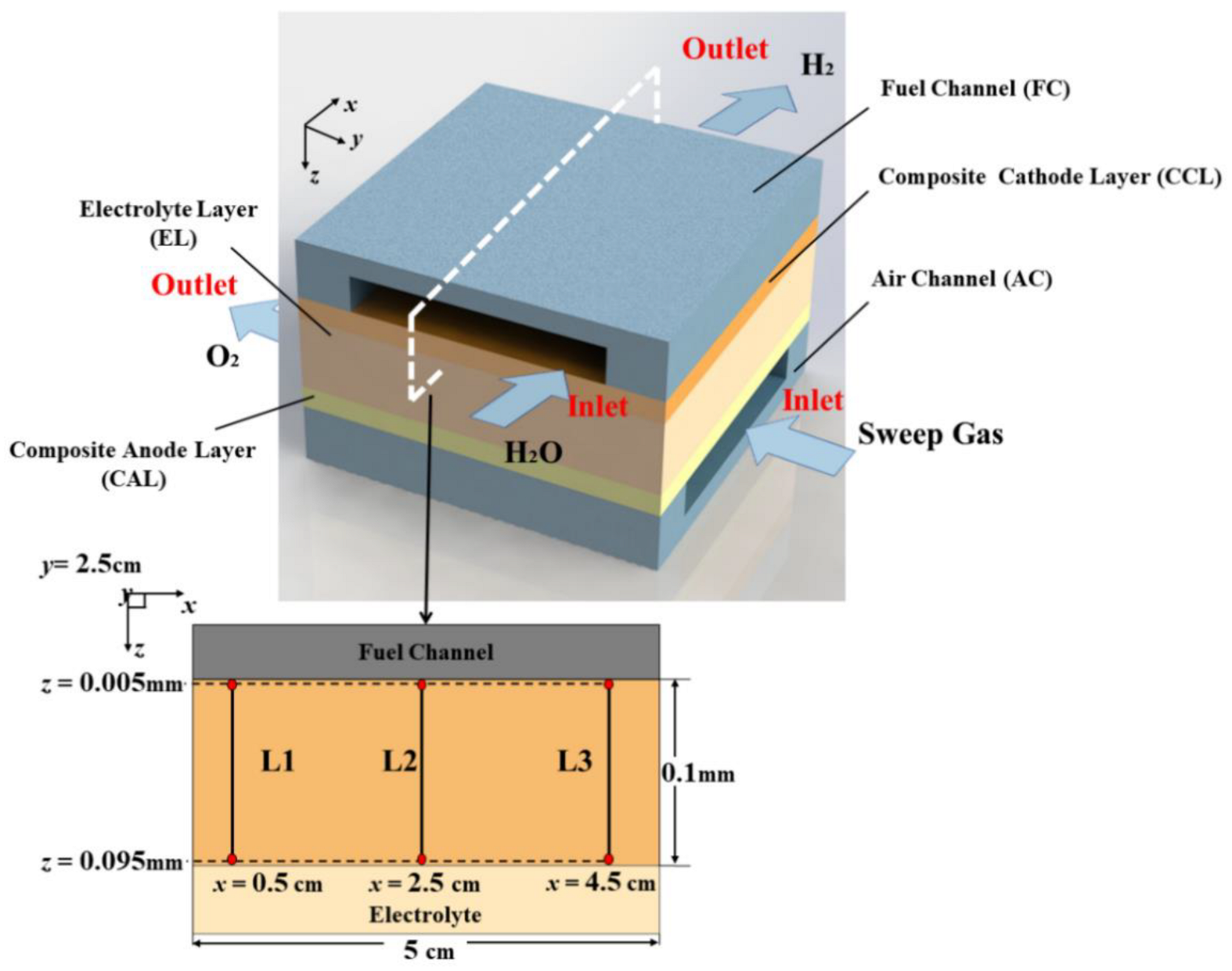
In this paper, the adopted method and 3D multi-scale mathematical model of IT-SOEC unit are introduced in Section 2. In Section 3, we validate our mathematical model using experimental data. Finally, in Section 4, we study the influence of operating pressure, volume fraction of the electrode phase, and particle diameter on the electrochemical reaction rate, overpotential, hydrogen molecular diffusion flux, hydrogen concentration gradient, hydrogen convection diffusion flux, and hydrogen mole fraction.

This aim of this study is not only to propose a 3D multi-scale model to describe the IT-SOEC with a composite electrode, but to also provide guidance for performance optimization, design, and manufacturing of the IT-SOEC unit through a comprehensive performance-based parameter analysis.

2. Method and Models

In this study, we adopted a numerical simulation method based on a multi-scale model. The geometric unit of IT-SOEC was separated into several sub-regions. The physical processes in a sub-region were described by the corresponding continuity model. These continuity models in different sub-regions were coupled and solved by a damped Newton method. Considering the scale difference between composite electrode structure on the mesoscopic scale and the IT-SOEC unit, the mesoscale model based on percolation theory was used to describe the composite electrode structure on the mesoscopic scale. By coupling the mesoscale model with continuity models, we considered the composite electrode structure on the mesoscopic scale, electrochemical reactions, flow, and multi-component diffusion inside an IT-SOEC unit. This multi-scale model evaluates of electrode performance by considering the morphology and composition of the electrode and the effective conductivity of the solid phase in the electrode. However, the mesoscopic model is only valid within the percolation threshold of the corresponding particles. It is suitable for cases where the electrode is regarded as a binary mixture [25,37]. The 3D multi-scale model is presented in the following section.

2.1. Assumptions and Geometric Model

In the modeling process, the following assumptions are considered [34]:

• Steady state.
• All the gas species are ideal gases.
• IT-SOEC operates at an adiabatic state.
• The gas flow in the channel has laminar flow and is a fully developed flow.
• The effect of gravity is ignored.

The computational domain consisted of a composite cathode consisting of nickel and SCSZ (Ni–SCSZ), a composite anode consisting of La_1−xSr_xMnO_3−δ and SCSZ (LSM–SCSZ), and an electrolyte (SCSZ). It also consisted of the fuel/air flow channel, which was arranged in a convective manner. To quantitatively analyze the results at different positions of the composite electrode, three characteristic lines, L1, L2, and L3, were set in the cross-section at y = 2.5 cm, in the entrance, middle, and exit sections with distances of 0.05, 2.5, and 4.5 cm from the entrance boundary, respectively. The geometric model is shown in Figure 1, and the corresponding geometric and basic operating parameters are listed in

Table 1. Geometric and basic operating parameters [34,38].

Parameters	Unit	Value
Channel width	cm	2.5
Channel height	mm	0.5
Channel length	cm	5
Composite cathode width	cm	5
Thickness of composite cathode	mm	0.1
Composite cathode length	cm	5
Electrolyte width	cm	5
Thickness of electrolyte	mm	1
Electrolyte length	cm	5
Composite anode width	cm	5
Thickness of composite anode	mm	0.1
Composite anode length	cm	5
Operating pressure	atm	1–5, 10
Operating temperature	K	973.15

. The sub-models and sub-regions of the IT-SOEC unit are shown in

Table 2. Sub-models and regions.

Sub-Model	Physical Problems	Sub-Region
Mathematical model for flow channel	Gas flow and mass transfer	Fuel/air channel
Mathematical model for composite electrode	Gas flow in porous media, mass transfer in porous media, and electrochemical reaction	Composite cathode/anode
Mathematical model for electrolyte	Ion transfer	Electrolyte

. The electrode material characteristic parameters, reaction kinetic parameters, and other relevant parameters are listed in

Table 3. Modeling parameters [39,40].

Parameters	Unit	Value
Electronic conductivity of Ni	S m−1	3.27 × 106 (−1065.3T)
Electronic conductivity of LSM	S m−1	4.2 × 107/T exp(−1150/T)
Ionic conductivity of ScSZ	S m−1	6.92 × 104 exp(−9681/T)
Ionic conductivity of YSZ	S m−1	3.34 × 104 exp(−10,300/T)
Pre-exponential factor for anode γa	A m−2	2.051 × 109
Pre-exponential factor for cathode γc	A m−2	1.344 × 1010
Activation energy for anode, Eact,a	J mol−1	1.2 × 105
Activation energy for cathode, Eact,c	J mol−1	1.0 × 105
Anode transfer coefficient, αa		0.35
Cathode transfer coefficient, αc		0.3
Gas diffusion volume of H2O	m3	13.1
Gas diffusion volume of H2	m3	6.12
Gas diffusion volume of N2	m3	18.5
Gas diffusion volume of O2	m3	16.3

. The parameters of the mesostructure model used to characterize the internal structure of the composite electrode are listed in

Table 4. Modeling parameters in the mesostructure model [39,41].

Parameters	Unit	Value
Electrode porosity, ψp		0.335
Contact angle between the electronic and ionic particles, θ	deg	15
Average pore diameter of cathode, ravre,c	μm	0.258
Average pore diameter of anode, raver,a	μm	0.322

. The boundary conditions for each domain are described later in the paper.

2.2. Mathematical Model

2.2.1. Mathematical Model for Composite Electrode

The Brinkman equation was used to describe the flow and permeation process of each component inside the composite electrode [42,43]; the equations are as follows:

$$\frac{1}{{\psi }_{\mathrm{p}}}\rho (\overrightarrow{u}\cdot \nabla )\overrightarrow{u}\frac{1}{{\psi }_{\mathrm{p}}}=\nabla \cdot \left(-p+\frac{\mu }{{\psi }_{\mathrm{p}}}(\nabla \overrightarrow{u}+{(\nabla \overrightarrow{u})}^T)-\frac{2}{3}\frac{\mu }{{\psi }_{\mathrm{p}}}(\nabla \cdot \overrightarrow{u})\right)-(\mu {\kappa }^{-1}+\beta \rho \left|\overrightarrow{u}\right|+\frac{Q_{\mathrm{i}}}{{\psi }_{\mathrm{p}}{}^2})\overrightarrow{u}$$

(1)

$$\kappa =\frac{{\psi }_{\mathrm{p}}{}^3\cdot r_{\mathrm{avre}}{}^2}{150\cdot {(1-{\psi }_{\mathrm{p}})}^2}$$

(2)

$$\nabla \cdot (\rho \overrightarrow{u})=Q_{\mathrm{i}}$$

(3)

where ρ is the density of the working medium, u is the velocity, μ is the dynamic viscosity, T is the temperature, and p represents the operating pressure. ψ_p indicates the porosity of the composite electrode and r_avre denotes the average pore size of the composite electrode. The isothermal compressibility coefficient β is also considered. κ denotes the permeability magnitude, which can be calculated by Equation (2). Q_i denotes the mass source term of component i.

The mass transfer process within a composite electrode remains a complex problem involving porous media. The description of the multi-component diffusion process is achieved by the Dusty-Gas Model (DGM), considering the effect of Knudsen diffusion [38]. The equations are as follows:

$$\nabla \cdot j_{\mathrm{i}}+\rho (\overrightarrow{u}\cdot \nabla ){\omega }_{\mathrm{i}}=Q_{\mathrm{i}}$$

(4)

$$j_{\mathrm{i}}=-\left(\rho D_{\mathrm{i}}{}^{\mathrm{m}}\nabla {\omega }_{\mathrm{i}}+\rho {\omega }_{\mathrm{i}}{D}_{\mathrm{i}}{}^{\mathrm{m}}\frac{\nabla M_{\mathrm{n}}}{M_{\mathrm{n}}}-j_{\mathrm{c},\mathrm{i}}\right)$$

(5)

$$j_{\mathrm{c},\mathrm{i}}=\rho {\omega }_{\mathrm{i}}{\displaystyle \sum _{\mathrm{j}}\frac{M_{\mathrm{i}}}{M_{\mathrm{n}}}{D}_{\mathrm{j}}{}^{\mathrm{m}}\nabla x_{\mathrm{j}}}$$

(6)

$$D_{\mathrm{i}}{}^{\mathrm{m}}={\left(\frac{1}{D_{\mathrm{i}}{}^{\mathrm{eff}}}+\frac{1}{D_{\mathrm{i}}{}^{\mathrm{K}}}\right)}^{-1}$$

(7)

$$D_{\mathrm{i}}{}^{\mathrm{eff}}=\frac{1-{\omega }_{\mathrm{i}}}{{\displaystyle \sum _{\mathrm{j}\ne \mathrm{i}}\frac{c_{\mathrm{j}}}{D^{\mathrm{Q}}{}_{\mathrm{i},\mathrm{j}}}}}$$

(8)

$$D^{\mathrm{Q}}{}_{\mathrm{i},\mathrm{j}}=\frac{{\psi }_{\mathrm{p}}}{\tau }{D}_{\mathrm{i},\mathrm{j}}$$

(9)

$$D_{\mathrm{i}}{}^{\mathrm{K}}=\frac{4{\psi }_{\mathrm{p}}{r}_{\mathrm{avre}}}{3\tau }\sqrt{\frac{8RT}{\pi M_{\mathrm{i}}}}$$

(10)

The heat diffusion flux caused by temperature variation is neglected here. So, the total flux is mainly composed of the molecular diffusion flux and convective flux. j_c,i is the correction term for the mixture diffusion flux [44]. j_i is the molecular diffusion flux of species i, ω_i denotes the mass fraction of species i, and c_j denotes the mole fraction of species j. M_n, M_i, and M_j denote the average mole mass and the mole mass of each species, respectively. D_i^m is the effective mixing diffusion coefficient and D^Q_i,j denotes the effective binary diffusion coefficient, after corrections using the Millington–Quirk model. D_i^K is the Knudsen diffusion coefficient. τ is the fluid tortuosity factor. D_i^eff denotes the effective binary diffusion coefficient in the composite electrode.

There are also complex electrochemical reactions within the composite electrode; thus, a reasonable description of the internal electrode kinetic processes is equally important.

When calculating the applied voltage of the IT-SOEC unit, it is necessary to consider the effects of the concentration overpotential η_conc, activation overpotential η_act, and ohmic overpotential η_ohimc [40]. The applied voltage can be expressed as:

$$V=E_{\mathrm{a}}-E_{\mathrm{c}}=\underset{E_{\mathrm{eq}}}{\underbrace{E_{\mathrm{eq},\mathrm{a}}-E_{\mathrm{eq},\mathrm{c}}}}+{\eta }_{\mathrm{act},\mathrm{a}}+{\eta }_{\mathrm{act},\mathrm{c}}+{\eta }_{\mathrm{conc},\mathrm{a}}+{\eta }_{\mathrm{conc},\mathrm{c}}+{\eta }_{\mathrm{ohmic}}$$

(11)

where E_eq,c and E_eq,a represent the equilibrium potential of each electrode, respectively. E_eq is the equilibrium voltage, which is expressed by the Nernst equation:

$$E_{\mathrm{eq}}=E_0+\frac{RT}{2F}\ln \left(\frac{c^{\mathrm{TPB}}{}_{{\mathrm{H}}_2}{c}^{\mathrm{TPB}}{{}_{{\mathrm{O}}_2}}^{\frac{1}{2}}}{c^{\mathrm{TPB}}{}_{{\mathrm{H}}_2\mathrm{O}}}\right)$$

(12)

where F is the Faraday constant and R is the mole gas constant. c^bulk_H2, c^bulk_H2O, and c^bulk_O2 are the mole fractions of hydrogen, vapor, and oxygen at the electrode/gas interface, respectively; E₀ is the standard potential. The value of E₀ in this model can be calculated by the empirical equation [40]:

$$E_0=1.253-2.4516\times {10}^{-4}T$$

(13)

When describing the kinetics of the electrode process inside the composite electrode, the exchange current density I₀ is an important performance index. It can be calculated by the following equations [40]:

$$I_{0,\mathrm{c}}={\gamma }_{\mathrm{c}}\exp \left(-\frac{E_{\mathrm{act},\mathrm{c}}}{RT}\right)$$

(14)

$$I_{0,\mathrm{a}}={\gamma }_{\mathrm{a}}\exp \left(-\frac{E_{\mathrm{act},\mathrm{a}}}{RT}\right)$$

(15)

where E_act represents the reaction activation energy of the corresponding electrode and γ is the corresponding pre-exponential coefficient.

Due to the presence of a significant change in the concentrations of reactants and products, the net reaction rate of the kinetics of the electrode process within the composite electrode is described using the generalized B–V equation [42].

$$I_{\mathrm{c}}=I_{0,\mathrm{c}}\left(\left(\frac{c^{\mathrm{TPB}}{}_{{\mathrm{H}}_2\mathrm{O}}}{c^{\mathrm{bulk}}{}_{{\mathrm{H}}_2\mathrm{O}}}\right)\exp \left(\frac{\alpha nF{\eta }_{\mathrm{act},\mathrm{c}}}{RT}\right)-\left(\frac{c^{\mathrm{TPB}}{}_{{\mathrm{H}}_2}}{c^{\mathrm{bulk}}{}_{{\mathrm{H}}_2}}\right)\exp \left(-\frac{\left(1-\alpha \right)nF{\eta }_{\mathrm{act},\mathrm{c}}}{RT}\right)\right)$$

(16)

$$I_{\mathrm{a}}=I_{0,\mathrm{a}}\left(\exp \left(\frac{\alpha nF{\eta }_{\mathrm{act},\mathrm{a}}}{RT}\right)-\left(\frac{c^{\mathrm{TPB}}{}_{{\mathrm{O}}_2}}{c^{\mathrm{bulk}}{}_{{\mathrm{O}}_2}}\right)\exp \left(-\frac{\left(1-\alpha \right)nF{\eta }_{\mathrm{act},\mathrm{a}}}{RT}\right)\right)$$

(17)

where I_c and I_a represent the net reaction ion current density on the unit’s percolated TPB area in the cathode and anode, respectively. c^TPB_H2 and c^TPB_H2O are the mole fractions of hydrogen and vapor at the reactive interface, respectively. α is the transfer coefficient.

The charge/ion transfer process is described by using Ohm’s law and the conservation of charge/ion. The net reaction rate expressed in the B–V equation is coupled with the ion or charge transfer process in the form of an electrode reaction source term; the expressions can be written as [11]:

$$\nabla \cdot i_{\mathrm{c},\mathrm{el}}=\nabla \cdot \left(-{\delta }_{\mathrm{eff},\mathrm{el}}\nabla {\varphi }_{\mathrm{io}}\right)=\{\begin{array}{l}-I_{\mathrm{c}}\left(\mathrm{in} \mathrm{cathode}\right)\\ -I_{\mathrm{a}}\left(\mathrm{in} \mathrm{anode}\right)\end{array}$$

(18)

$$\nabla \cdot i_{\mathrm{c},\mathrm{io}}=\nabla \cdot \left(-{\delta }_{\mathrm{eff},\mathrm{io}}\nabla {\varphi }_{\mathrm{el}}\right)=\{\begin{array}{l}{I}_{\mathrm{c}}\left(\mathrm{in} \mathrm{cathode}\right)\\ I_{\mathrm{a}}\left(\mathrm{in} \mathrm{anode}\right)\end{array}$$

(19)

where i_c,io and i_c,el denote the electrolyte and electrode current densities, respectively. ϕ_el and ϕ_io is the electrode and electrolyte potential, respectively.

The Bruggeman model [45,46] was used to describe the effect of the intermixing of electrode and electrolyte particles inside the composite electrode on the structured features of the composite electrode. So, the corresponding effective conductivity δ_eff is obtained by correcting the electrode conductivity δ_el and the electrolyte conductivity δ_io, with the following equations:

$${\delta }_{\mathrm{eff},\mathrm{el}}=k_{\mathrm{el}}{}^{1.5}{\delta }_{\mathrm{el}}$$

(20)

$${\delta }_{\mathrm{eff},\mathrm{io}}=k_{\mathrm{io}}{}^{1.5}{\delta }_{\mathrm{io}}$$

(21)

The k_el and k_io are set as (1 − ψ_io − ψ_p) and (1 − ψ_el − ψ_p), respectively.

The relationship between the mass source term Q_i of each component and the net electrochemical reaction rate is reflected by Faraday’s law, as described in Equation (22).

$$Q_{\mathrm{i}}=\frac{A_{\mathrm{TPB}}{I}_{\mathrm{el}}{v}_{\mathrm{i}}}{nF}$$

(22)

where v_i is the stoichiometric number of oxidized/reduced species, and A_TPB denotes the volumetric percolation TPB area, as expanded on in Section 2.2.4.

2.2.2. Mathematical Model for Flow Channel

The N–S equation in compressible form and continuity equation were used to describe the flow process in the gas channel.

The mass diffusion process of each component in the gas flow channel was described by the Stefan–Maxwell model (SMM), which ignores the influence of Knudsen diffusion. The diffusion coefficients can be expressed as [39,42]:

$$D_{\mathrm{i}}{}^{\mathrm{eff}}=\frac{1-{\omega }_{\mathrm{i}}}{{\displaystyle \sum _{\mathrm{j}\ne \mathrm{i}}\frac{c_{\mathrm{j}}}{D_{\mathrm{ij}}}}}$$

(23)

$$D_{\mathrm{i},\mathrm{j}}=\frac{0.00101T^{1.75}{\left(\frac{1}{M_{\mathrm{i}}}+\frac{1}{M_{\mathrm{j}}}\right)}^{\frac{1}{2}}}{P{\left(V_{\mathrm{d},\mathrm{i}}{}^{\frac{1}{3}}+V_{\mathrm{d},\mathrm{j}}{}^{\frac{1}{3}}\right)}^2}$$

(24)

D_i^eff in Equation (23) is the effective binary diffusion coefficient in the flow channel. D_i,j denotes the binary diffusion coefficients of species i and j. V_i and V_j are the respective diffusion volumes of each species.

2.2.3. Mathematical Model for Electrolyte

In the electrolyte layer, only oxygen ion transport processes occur. The effect of ohmic polarization is obvious in this region and no electrode reaction occurs. By using the ion conservation equation and combining it with Ohm’s law to describe the oxygen ion transport process. The expression can be written in the following form [11]:

$$\nabla \cdot i_{\mathrm{c},\mathrm{io}}=\nabla \cdot \left(-{\delta }_{\mathrm{eff},\mathrm{io}}\nabla {\varphi }_{\mathrm{io}}\right)=0$$

(25)

It is worth noting that the effective conductivity is the actual conductivity of the electrolyte material YSZ, as the electrolyte layer is not doped with electrode particles.

2.2.4. The Mesostructure Model of the Composite Electrode

Percolation theory was used to preserve the connection between the effective characteristics and structured features of the composite electrode on the mesoscopic scale. For a given porosity, the composite electrode structure can be considered as a binary system consisting of a random accumulation of spheres corresponding to electrode particles (denoted as el) and electrolyte particles (denoted as io). The contact angle, particle diameter, and volumetric percolation TPB area were used to characterize the structure inside the composite electrode on the mesoscopic scale [44,47], which is shown schematically in Figure 2.

Considering the existence of a multi-component gas transport process and permeation process within the pores of the composite electrode, ψ_io and ψ_el denote the corresponding volume fractions of the electrolyte phase and electrode phase inside the electrode, respectively, satisfying the following equations [14,47]:

$$1-{\psi }_{\mathrm{p}}={\psi }_{\mathrm{io}}+{\psi }_{\mathrm{el}}$$

(26)

The volumetric percolation TPB area can be expressed as [38]:

$$A_{\mathrm{TPB}}=\pi {\sin }^2\theta {\min }^2\left(d_{e\mathrm{l}},d_{io}\right)n_{\mathrm{t}}{n}_{\mathrm{el}}{n}_{\mathrm{io}}\frac{Z_{\mathrm{el}}{Z}_{\mathrm{io}}}{6}{P}_{\mathrm{el}}{P}_{\mathrm{io}}$$

(27)

where θ is the contact angle between the ion and electron conductors. d_el is the electrode particle diameter. d_io is the electrolyte particle diameter. n_t is the total number of particles in each cell volume. n_e is the number fraction of the electron conductor and n_i is the number fraction of the ion conductor:

$$n_{\mathrm{t}}=\frac{1-{\psi }_{\mathrm{p}}}{\frac{4}{3}\pi d_{\mathrm{el}}{}^3\left[n_{\mathrm{el}}+(1-n_{\mathrm{el}})d^3\right]}$$

(28)

$$n_{\mathrm{el}}=\frac{{\psi }_{\mathrm{el}}}{{\psi }_{\mathrm{el}}+\frac{(1-{\psi }_{\mathrm{el}})}{d^3}}$$

(29)

$$n_{\mathrm{el}}+n_{\mathrm{io}}=1$$

(30)

where d is the ratio of electrolyte particle diameter to electrode particle diameter, $d=\raisebox{1ex}{$d_{\mathrm{io}}$}\!\left/ \!\raisebox{-1ex}{$d_{\mathrm{el}}$}\right.$.

Z_el and Z_io represent the average coordination number of the electronic and ionic conductors, respectively:

$$Z_{\mathrm{el}}=3+\frac{3}{n_{\mathrm{el}}+\left(1-n_{\mathrm{el}}\right)d^2}$$

(31)

$$Z_{\mathrm{io}}=3+\frac{3d^2}{n_{\mathrm{io}}+\left(1-n_{\mathrm{io}}\right)d^2}$$

(32)

P_el and P_io denote the probability of formation of percolation clusters by electrode and electrolyte particles, respectively [38,40]:

$$P_{\mathrm{el}}={\left[1-{\left(\frac{4.236-Z_{\mathrm{el}-\mathrm{el}}}{2.472}\right)}^{2.5}\right]}^{0.4}$$

(33)

$$P_{\mathrm{io}}={\left[1-{\left(\frac{4.236-Z_{\mathrm{io}-\mathrm{io}}}{2.472}\right)}^{2.5}\right]}^{0.4}$$

(34)

Z_el-el and Z_io-io represent the average coordination number between the same particle [38], which can be expressed in the following equations:

$$Z_{\mathrm{el}-\mathrm{el}}=\frac{6n_{\mathrm{el}}}{n_{\mathrm{el}}+\left(1-n_{\mathrm{el}}\right)d^2}$$

(35)

$$Z_{\mathrm{io}-\mathrm{io}}=\frac{6n_{\mathrm{io}}}{n_{\mathrm{io}}+\left(1-n_{\mathrm{io}}\right)d^{-2}}$$

(36)

2.3. Boundary Conditions

To apply the above 3D multi-scale model describing electrode mesostructure, electrochemical reactions, flow, and mass transfer within the IT-SOEC,

Table 5. Boundary conditions.

Boundary	Ionic Charge	Electronic Charge	Flow	Mass Transport
FC inlet	Insulation	Insulation	Inlet velocity	cbulkH2, cbulkH2O
FC outlet	Insulation	Insulation	Pressure	Outflow
AC inlet	Insulation	Insulation	Inlet velocity	cbulkO2, cbulkN2
AC outlet	Insulation	Insulation	Pressure	Outflow
CCL/FC interface	Grounding	Grounding	Continuity	Continuity
CCL/EL interface	Continuity	Insulation	Wall	Wall
CAL/EL interface	Continuity	Insulation	Wall	Wall
CAL/AC interface	Insulation	Current density	Continuity	Continuity
Others	Insulation	Insulation	Wall	Wall

lists the boundary conditions.

The inlet flow velocity of both cathode and anode channels were 1 mm s⁻¹. The inlet component of the cathode channel was 60 mol% H₂O and 40 mol% H₂. The inlet component of the anode channel was 21 mol% O₂ and 79 mol% N₂. The external current density at the anode boundary was 4000 A m⁻².

3. Numerical Simulation and Model Validation

The 3D macroscopic model describing the multi-physics processes in the IT-SOEC with the composite electrode described in Section 2.2.1, Section 2.2.2 and Section 2.2.3 was calculated using the finite element method using the commercial software COMSOL Multiphysics. The mesostructure model of the composite electrode shown in the Section 2.2.4 was coupled with a macroscopic model by directly writing a custom function. The detailed parameters used to analyze the effect of the variation of operating pressure and structured parameters on the comprehensive performance of the IT-SOEC are listed in

Table 6. Parameter analysis.

Parameters	Pressure Analysis	Electrode Phase Volume Fraction Analysis	Particle Diameter Analysis
P (atm)	1–5, 10	1	1
ψel	0.35	0.2–0.4	0.35
del (μm)	0.5	0.5	0.2–0.5
d	1	1	0.5–1.5

.

To verify the reliability of the multi-scale model, the experimental I–V curves obtained by electrolyzing different inlet H₂O concentrations with tubular SOC (LSCF-LSM-YSZ|YSZ|Ni-YSZ) at 1023.15 K were cited. Figure 3 shows the comparison between simulation results and experimental data [48]. The detailed structure parameters and operating conditions of the electrolysis unit are listed in

Table 7. Basic operating parameters for model validation by different inlet H₂O mole fractions [48].

Parameters	Unite	Value
Thickness of electrolyte layer	μm	8.53
Thickness of composite anode layer	μm	25
Thickness of cathode functional layer	μm	11.7
Operating temperature, T	K	1023.15
Operating temperature, P	atm	1
Anode flowrate	cc min−1	100
Cathode flowrate	cc min−1	100

. According to the Figure 3, the modeling results were consistent with the experimental results. The maximum deviation obtained by our calculations were 0.0135 and 0.0571 V, respectively.

Although the heat transfer process was neglected in this multi-scale model, the above relationships verify the reliability and accuracy of the model.

4. Results and Discussion

The effect of macro-operating pressures on the performance of IT-SOEC was analyzed by performance indices of the hydrogen mole fraction distribution, overpotential, and electrochemical reaction rate using the multi-scale model. The corresponding results were then compared with those of other scholars to further verify the effectiveness of the multi-scale model. Finally, from mesoscopic perspective, the effect of the mesostructural parameters on the performance of IT-SOEC was studied. The parametric analysis of performance indices, such as hydrogen molecular diffusion/convective flux, overpotential, and electrochemical reaction rate, was carried out under different electrode phase volume fractions and particle diameters in the composite electrode.

4.1. Effects of the Operating Pressure on IT-SOEC Electrolysis Performance

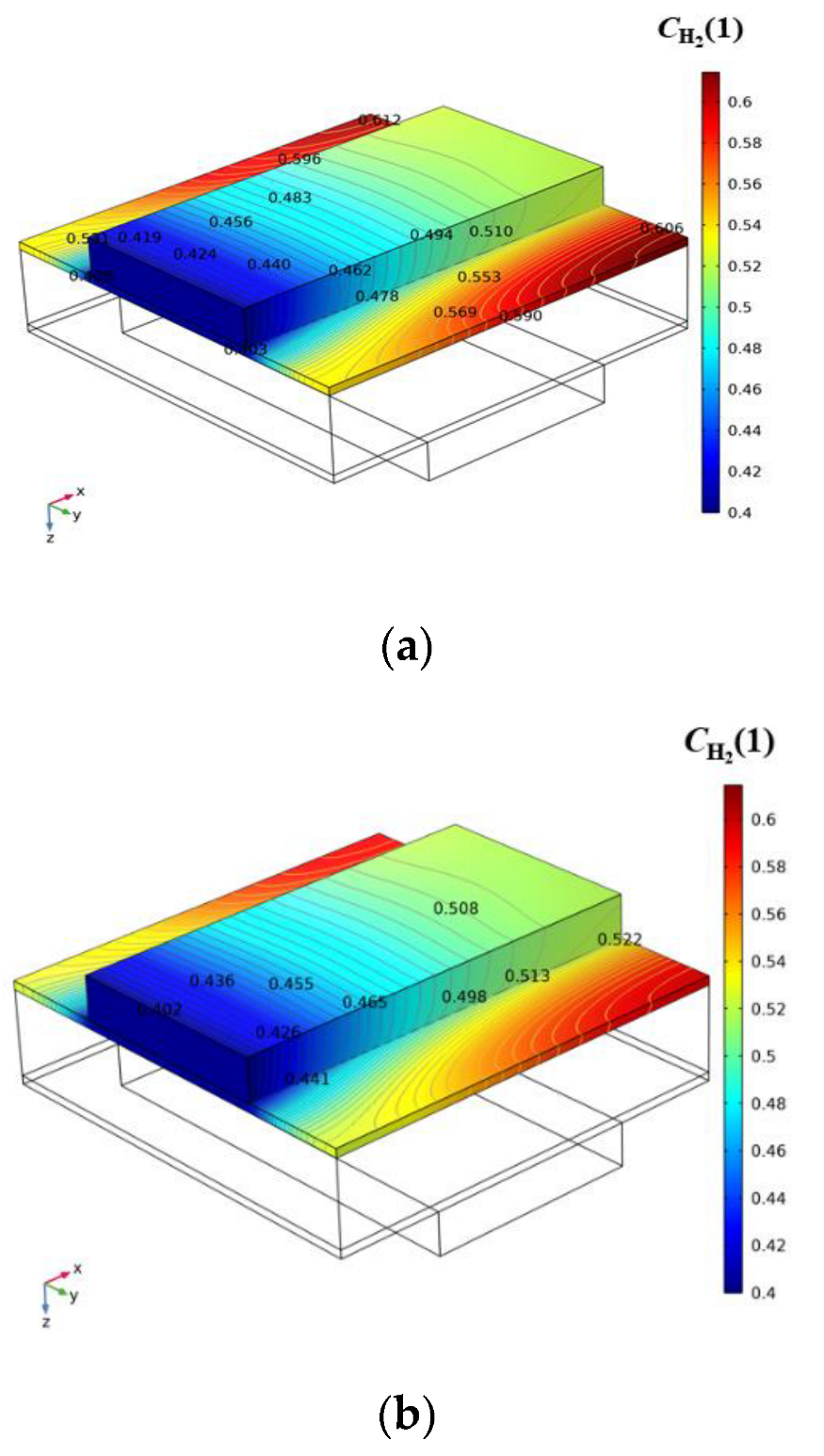
Figure 4a,b shows the distribution of the hydrogen mole fraction in the fuel channel and inside the composite cathode under the operating pressure of 1 and 10 atm, respectively. It can be seen from the figures that under any operating pressure, along the direction of the flow channel, the hydrogen mole fraction is gradually increasing. However, there is a large accumulation of hydrogen inside the composite electrode and the value of the hydrogen mole fraction reaches a maximum at the edges. This suggests that the mass transport process of hydrogen inside the composite electrode cannot be neglected.

Comparing the distribution of the hydrogen mole fraction under the conditions of 1 and 10 atm, we found that with an increase in operating pressure, the local accumulation of hydrogen inside the electrode edge was reduced to a certain extent. The appearance of this phenomenon exerts a certain impact on the kinetic characteristics of the electrode and electrochemical reactions. Interestingly, when the operating pressure increased from 1 to 10 atm, the hydrogen accumulated in the cathode edge decreased by 3.63%. The increase in pressure only reduced the hydrogen mole fraction at the outlet of the flow channel by 0.522%, under these external conditions. Therefore, the increase in operating pressure had no significant effect on the hydrogen output, but greatly improved the hydrogen accumulation phenomenon inside the cathode.

Figure 5a shows the relationship between the overpotential and operating pressure along the characteristic line L2. We found that the overpotential reached a maximum near the electrolyte boundary, regardless of the operating pressure. This may have been because the component mass transfer process became a rate-determining step. The concentration overpotential increased as the diffusion of the vapor into the electrode and diffusion of the generated hydrogen out of the electrode became more difficult to carry out.

Further analysis illustrated that, as the pressure increased, the overpotential inside the composite electrode adjacent to the electrolyte boundary as well as the overall electrode showed a tendency to decrease. These results corroborate the findings of Bernadet et al. [43], who found that an increase in pressure improved the mass transport of vapor and hydrogen in the porous medium to some extent, and improved diffusion conditions may inhibit the increase in overpotential. Du et al. [34] also reported that an increase in pressure weakens electrochemical polarization, and thus, reduces the activation overpotential. In summary, these results show that an increase in pressure leads to a decrease in overpotential in the composite cathode.

To further investigate the effect of operating pressure on the electrochemical performance of the electrolysis cell, the electrolysis reaction rate in the volumetric percolation TPB unit area, R_H2, was introduced as an indicator of the electrolysis reaction rate inside the composite cathode, which can be calculated from the following equation:

$$R_{{\mathrm{H}}_2}=\frac{{\nu }_{{\mathrm{H}}_2}{I}_{\mathrm{c}}}{nF}$$

(37)

Figure 5b shows the effect of operating pressure on R_H2 in the composite electrode along the characteristic line L2. Evidently, the maximum value of R_H2 under each operating pressure is obtained near the electrolyte boundary. This suggests that the electrolysis reaction is the most intense in the electrode region near the electrolyte boundary. Chen et al. [37] pointed out that in the case of equivalent electric particle loading, the region near the electrolyte boundary is identified as the electrochemically active zone (EAZ). Interestingly, from Figure 5b, the effect of pressure on the electrolysis reaction rate was observed to be different in the regions near and away from the electrolyte. This indicates that the operating pressure affects the positioning of the region covered by the reaction. In the region close to the electrolyte, the pressure has a facilitating effect on the electrolysis reaction. However, in the region far away from the electrolyte, the electrolysis reaction is inhibited. When the operating pressure was increased from 1 to 10 atm, the electrolysis reaction rate in the near region, with a higher ionic current density inside the composite electrode, increased by 47.13% and, in the region away from the electrolyte, was reduced by 66.15%. Generally, the region near the electrolyte has a higher ionic current density and electrolytic reaction rate [38]. It was also observed that when the position of electrode was greater than 0.07 mm, the electrolysis reaction rate increased.

Therefore, to increase the electrolysis reaction rate in the composite electrode by increasing the operating pressure of the IT-SOEC, it is necessary to control the area near the electrolyte region, i.e., the thickness of the composite electrode, within an appropriate range. In other words, the smaller the thickness of the composite electrode, the more obvious the gain effect of operating pressure on electrode performance. However, it has also been pointed out in the literature [37] that when the thickness of the composite electrode is less than the corresponding thickness of the EAZ, the activation overpotential will inevitably increase, which affects the economy of SOEC.

According to the above results, the effectiveness of the multi-scale model was validated by predicting performance changes of IT-SOEC with composite electrodes at the macroscale. Meanwhile, it should be noted that almost no electrolysis reaction occurred in the composite electrode near the flow channel, regardless of the operating pressure value. Therefore, when the ability to change the external conditions is limited, it is necessary to optimize the internal structure of the composite electrode to improve the overall performance of the SOEC. This will be discussed in detail in the following section.

4.2. Effect of Composite Electrode Structure on the Comprehensive Performance of IT-SOEC

In this section, through the structural parametric analysis of the volume fraction of the electrode phase and the particle diameter within the composite electrode, the effects of different structural features on the electrochemical reaction rate, applied voltage, and diffusion/convection flux of the IT-SOEC unit are discussed.

4.2.1. Effect of Volume Fraction of Electrode Phase

When investigating the effect of different electrode phase volume fractions within the composite electrode, the gas phase volume fraction ψ_p was taken as 0.335. According to Equations (26), (33) and (34), when d = 1 within the composite cathode, the electrode and electrolyte particle percolation thresholds are ψ_el = 0.47 and 1 − ψ_p − ψ_io = 0.195, respectively.

Therefore, ψ_el < 0.195 is the case of low electrode particle loading and ψ_el > 0.47 is the case of high electrode particle loading. Chen et al. [12] discussed in their study that either case is detrimental to electrode performance and has strict requirements on the percolation TPB area. Therefore, we discuss the cases when 0.195 < ψ_el < 0.47 for 0.2, 0.25, 0.3, 0.35, and 0.4, respectively. When the volume fraction of the electrode phase is 0.665, the composite electrode is a pure electron conductor porous electrode.

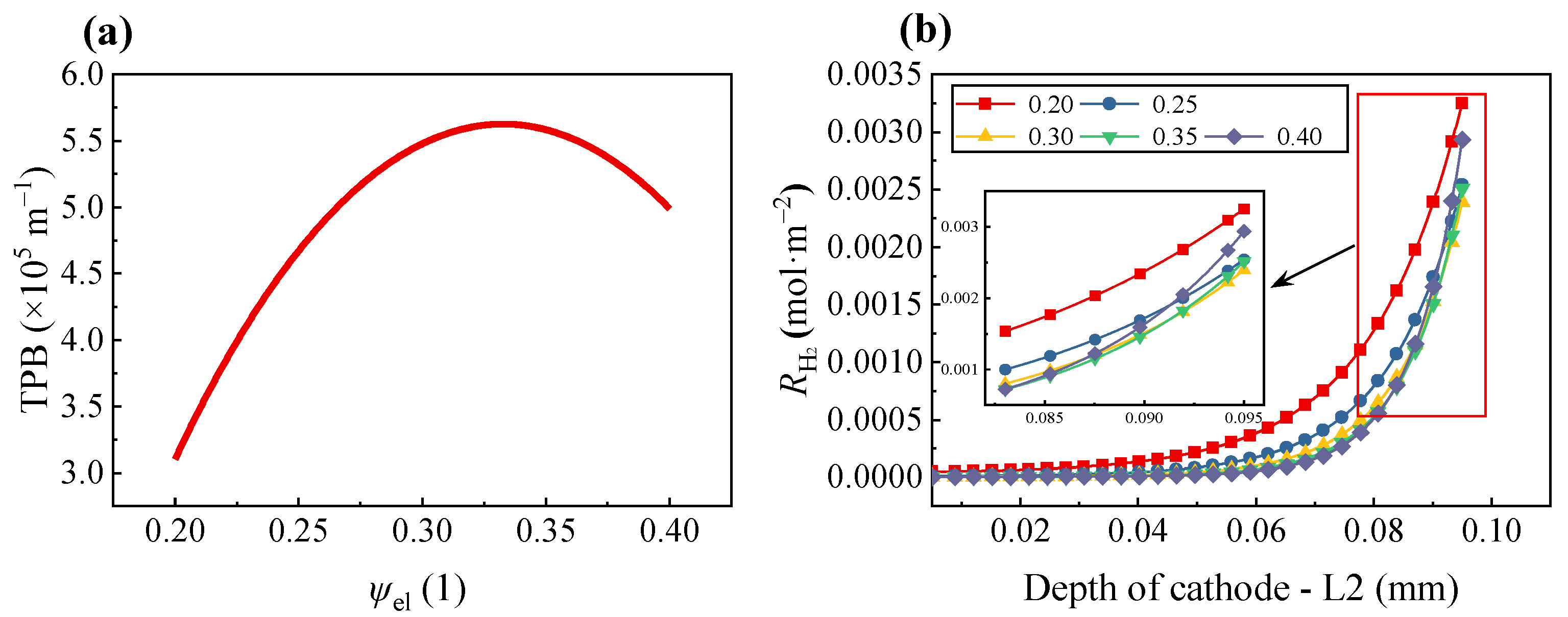
As shown in Figure 6a, as ψ_el gradually increases, the volumetric percolation TPB area also increases, reaching a maximum at ψ_el = 0.348. However, when ψ_el > 0.348, the composite electrode gradually transits to a high electrode particle loading structure and the volumetric percolation TPB area gradually decreases with the increase in ψ_el. This phenomenon can be attributed to the increase in electrode particles at a certain electrode volume; most of the electrode particles form corresponding percolation clusters, but the electrolyte particles only appear in some short connection networks near the electrolyte. This results in the TPB belonging to percolation clusters that are too small and percolated only near the electrolyte, similar with the results obtained by Chen et al. [37]. According to Equations (26), (20), and (21), the increases in ψ_io will lead to an increase in the effective electrolyte conductivity δ_eff,s within the composite electrode.

Figure 6b shows the relationship between the value of ψ_el and R_H2 in the composite electrode along the characteristic line L2. Overall, it was found that, regardless of the value of ψ_el, the most intense electrolysis reaction occurred in the region near the electrolyte and the electrolysis reaction rate was decreased in the region away from the electrolyte. When the electrode position was greater than 0.07 mm, the electrolysis reaction rate was significantly increased.

Figure 6b also indicates that when ψ_el decreases, the region where the electrolysis reaction occurs is closer to the flow channel and the electrolysis reaction rate also becomes more intense. Therefore, in the range of the percolation threshold, an increase in ψ_io improved the electrolytic performance of the composite electrode. For example, at 0.06 mm inside the electrode, when ψ_el was 0.25 and 0.4, the R_H2 was 1.747 × 10⁻⁴ and 5.53 × 10⁻⁵ mol m⁻², respectively. The relative difference between them was 68.34%. Meanwhile, the growth rate of R_H2 corresponding to ψ_el = 0.4 was larger in the region near the electrolyte and R_H2 was only smaller than that corresponding to the ψ_el = 0.2. So, by comparing Figure 6a,b, we can observe that the effective electrolyte conductivity of composite electrode plays a more important role in the reaction rate than the value of volumetric percolation TPB area.

The composite electrode structure on the mesoscopic scale also had a significant influence on the flow and mass transport processes inside the IT-SOEC unit. Figure 7a–c shows the relationship between the hydrogen molecular diffusion flux j_H2 and the electrode volume fraction ψ_el at different positions inside the composite cathode along the characteristic lines L1, L2, and L3. As shown in the figures, regardless of the value of ψ_el in the front (L1), middle (L2), and end (L3) of the composite cathode, being situated closer to the electrolyte (when the position of the electrode is greater than 0.04 mm) is the main determining factor of j_H2. Our results indicated that being positioned closer to the electrolyte or having a thicker electrode increased the resistance to the diffusion of hydrogen, making it more difficult to carry out the diffusion process. Therefore, a proper reduction in the electrode thickness is also beneficial for the mass transport process.

From these findings shown in Figure 6b, we can conclude that a small ψ_el increases the electrolysis reaction rate and the area of the EAZ region to a certain extent. However, Figure 7a–c shows that a decrease in ψ_el is unfavorable to the effective diffusion of the mass inside the electrode and the location of the reduced diffusion flux also occurs earlier. When the position is greater than 0.04 mm, the difference in j_H2 is significant. Along the characteristic line L3, at 0.06 mm inside the electrode, when ψ_el = 0.2 and ψ_el = 0.25, the j_H2 in the composite electrode was 0.072 and 0.076 mg m⁻², respectively. When ψ_el = 0.4, the j_H2 had the maximum value of 0.078 mg m⁻². j_H2 decreased by 8.3% for ψ_el = 0.2, compared with ψ_el = 0.4. However, j_H2 increased by 5.6% when ψ_el = 0.25, compared with ψ_el = 0.2.

As shown in Equation (5), in addition to the density of the working medium and the effective diffusion coefficient, the driving force of the diffusion process mainly depended on the concentration gradient of each mass at the corresponding position. Figure 7d–f shows the relationship between the concentration gradient of hydrogen and ψ_el at different positions inside the composite cathode. Similarly, regardless of the value of ψ_el, the hydrogen concentration gradient showed a decreasing trend near the electrolyte. As ψ_el increased, the concentration gradient at the same position inside the composite electrode also increased to a certain extent. This phenomenon mainly occurred in the electrode region far from the flow channel.

The comparison between the molecular diffusion flux and concentration gradient corresponding to characteristic lines L1, L2, and L3 in Figure 7a–f reveals a decreasing trend. Thus, as the electrolysis process proceeds, the molecular diffusion process inside the electrode gradually weakens from the inlet to the outlet side; however, there is also a trend toward a more uniform distribution of hydrogen.

When considering the effect of ψ_el on the mass transport inside the electrode, we need to consider not only the molecular diffusion flux driven by the concentration gradient, but also the convective flux. Figure 7g–i shows the relationship between the convective flux of hydrogen at different positions inside the composite cathode and different values of ψ_el. Similar to the relationships of j_H2 shown in Figure 7a–c, in regions closer to the electrolyte, it is more difficult for the mass transport process driven by convection in the electrode to occur, especially when the position is greater than 0.04 mm. However, in the region away from the flow channel, it is conducive to the development of the convection, as ψ_el increases. As this study was carried out at a given initial velocity and could be considered as forced convection, there was not much difference between the convective flux at the different locations in L1, L2, and L3.

4.2.2. Effect of the Particle Diameter

To investigate the effect of the particle diameter on IT-SOEC performance, we used percolated TPB size, applied voltage, and maximum value of the hydrogen mole fraction inside the composite electrode as indicators. The corresponding parameters are presented in Table 6. The value of the ratio d indirectly reflects the uniformity of the particle diameter distribution within the composite electrode. The overall particle diameter level within the composite electrode is also reflected by the combination of d and particle diameter d_el.

According to the mesostructure model described in Section 2.2.4, the description of the volumetric percolation TPB area was nonlinear. Figure 8a reflects the effect of different d_el and d on the volumetric percolation TPB area. We found that, for the same value of d, there was a monotonically decreasing relationship between d_el and the TPB area. However, regardless of the value of d_el, the TPB area did not vary monotonically with d. A larger value was achieved at d = 0.75. When d = 1.5 and d_el = 0.5 μm, the TPB area was minimal; thus, we can infer that a larger particle diameter will limit the TPB area. So, to increase the TPB area, it is necessary to reduce the particle diameter and keep the size difference between the electrode and electrolyte particles at an optimal range.

Figure 8b depicts the relationship between the applied voltage of the IT-SOEC unit, d_el and d. The variation in the applied voltage also reflects the economics of the electrolysis process. As shown in Figure 8b, the applied voltage decreases as d_el decreases. When d is closer to 1, the particle diameter is more homogeneous, and the applied voltage is closer to the minimum value. For example, when d_el = 0.5 μm and the electrolyte particle diameter was 1.5 times the electrode particle diameter, the applied voltage reached a maximum value and was at its worst, economically. For the appearance of such a phenomenon, it can be seen from Figure 8a that the smaller the particle diameter of the electrode and electrolyte and the more uniform the size of both particles, the greater the percentage of TPB belonging to the percolation clusters. This allows for effective electrolysis reactions. Ni et al. [38] also pointed out in their research that when the particle diameter is less than a certain value, the concentration overpotential becomes the main constraint for the performance enhancement of the SOEC. This also indicates that the diffusion process of the reactants becomes the rate-determining step of the electrolysis reaction.

Figure 8c also demonstrates the effects of d_el and d on the hydrogen production rate per unit electrode volume. The results showed that properly reducing the particle diameter (0.2–0.3 μm) was more conducive to hydrogen production inside the electrode. Meanwhile, there was also an optimal range of 0.8–1 for d to obtain the maximum hydrogen production rate.

5. Conclusions

In this paper, we presented a 3D multi-scale model that describes the electrolysis of vapor to hydrogen in an IT-SOEC unit with a composite electrode (fuel flow channel|Ni-SCSZ|SCSZ|LSM-SCSZ|air flow channel). After comparing our model with other experimental results, we validated the accuracy of this novel model. In addition, by analyzing the effect of operating pressure on performance and comparing it with the results of other scholars, we found that the multi-scale model could be used to predict performance changes on a macroscale level. This model was used to predict the effects of the composite electrode structure, on a mesoscopic scale, on the comprehensive performance of IT-SOEC. Meanwhile, the effects of the composite electrode structure on the flow and multi-component diffusion processes at different positions in the electrode were also studied. We obtained the following conclusions:

• Under certain external conditions, when the pressure was increased from 1 to 10 atm, the hydrogen accumulated in the cathode edge was reduced by 3.63%, even though it reduced the hydrogen mole fraction at the outlet of the flow channel by 0.522%.
• To improve the electrolysis reaction rate by increasing operating pressure, it is necessary to control the thickness of the composite electrode within an appropriate range. When the pressure was increased from 1 to 10 atm, the electrolysis reaction rate increased by 47.13% in the region near the electrolyte, but decreased by 66.15% in the region away from electrolyte.
• The volume fraction of the electrode phase, ψ_el, has a very important effect on the comprehensive performance of the IT-SOEC. A decrease in ψ_el improved the electrochemical reaction rate, but it also had an adverse impact on the multi-component gas transport process inside the composite electrode.
• Properly reducing the particle diameter (0.2–0.3 μm) and avoiding particle size differences are favorable in improving the volumetric percolation TPB area. It is also beneficial to reduce the applied voltage to improve hydrogen production rate. There is an optimal range of d (0.8–1) that is conducive to more hydrogen production inside the composite electrode.

Based on the above conclusions, we can use the 3D multi-scale model proposed in this study to complete a comprehensive performance analysis of IT-SOEC from the perspective of electrolytic reaction and multi-component diffusion. At the same time, this model also provides guidance for the numerical analysis of the SOEC with composite electrodes. This could be helpful in optimizing the design of SOEC cells and related composite electrode structures on a mesoscopic scale. In future work, this multi-scale model should be improved to achieve a more comprehensive description of electrolysis performance. Further investigations on the impact of various internal structures from multi-layer SOEC with composite electrodes on electrolysis performance are needed.