On the Existence and Applicability of Extremal Principles in the Theory of Irreversible Processes: A Critical Review
Abstract
1. Introduction
2. Equilibrium Thermodynamics
3. Thermodynamics of Irreversible Processes
4. Extremal Principles for Dissipative Systems Not Directly Related to Thermodynamic Quantities
5. Optimality and Illusion of Optimality
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
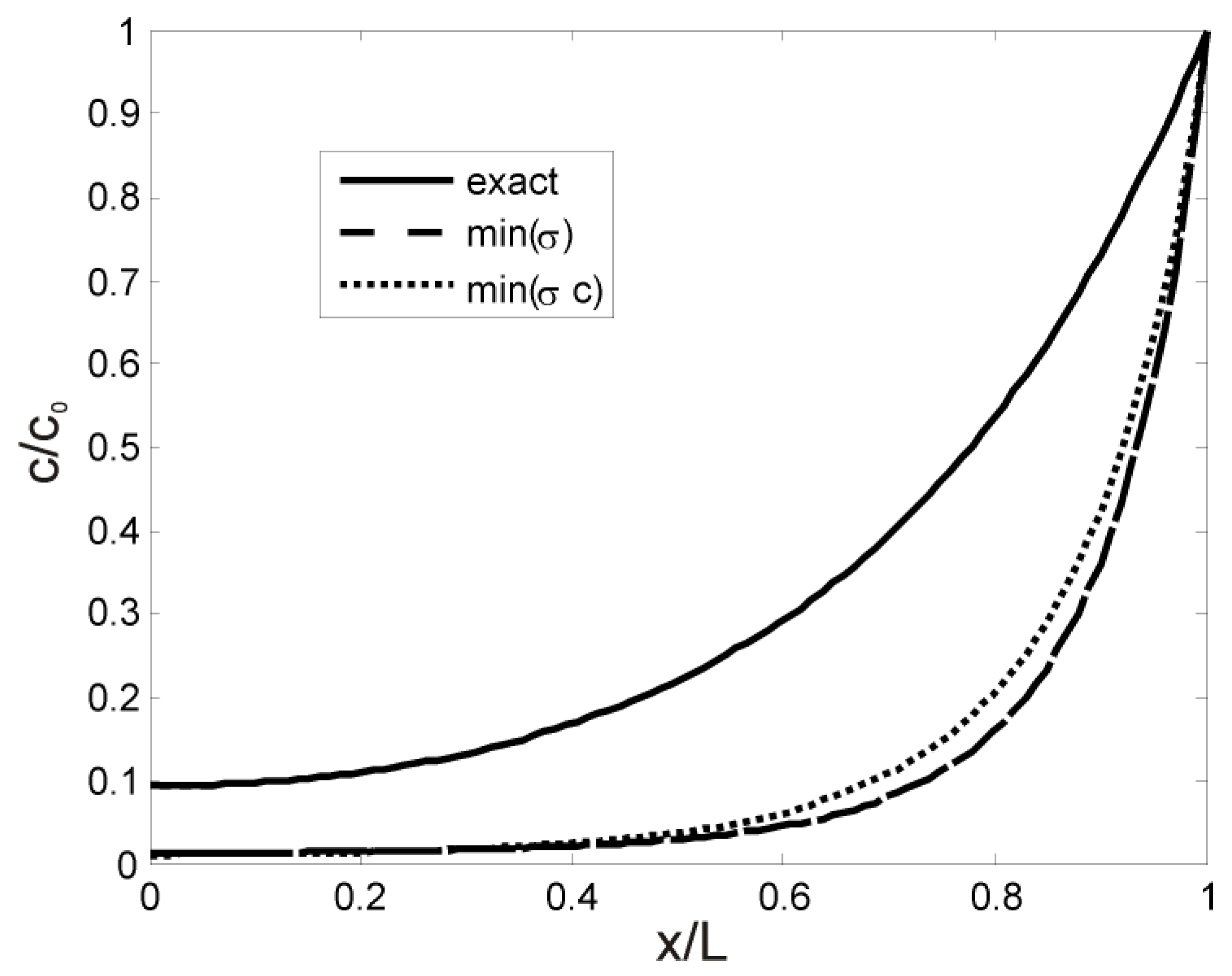
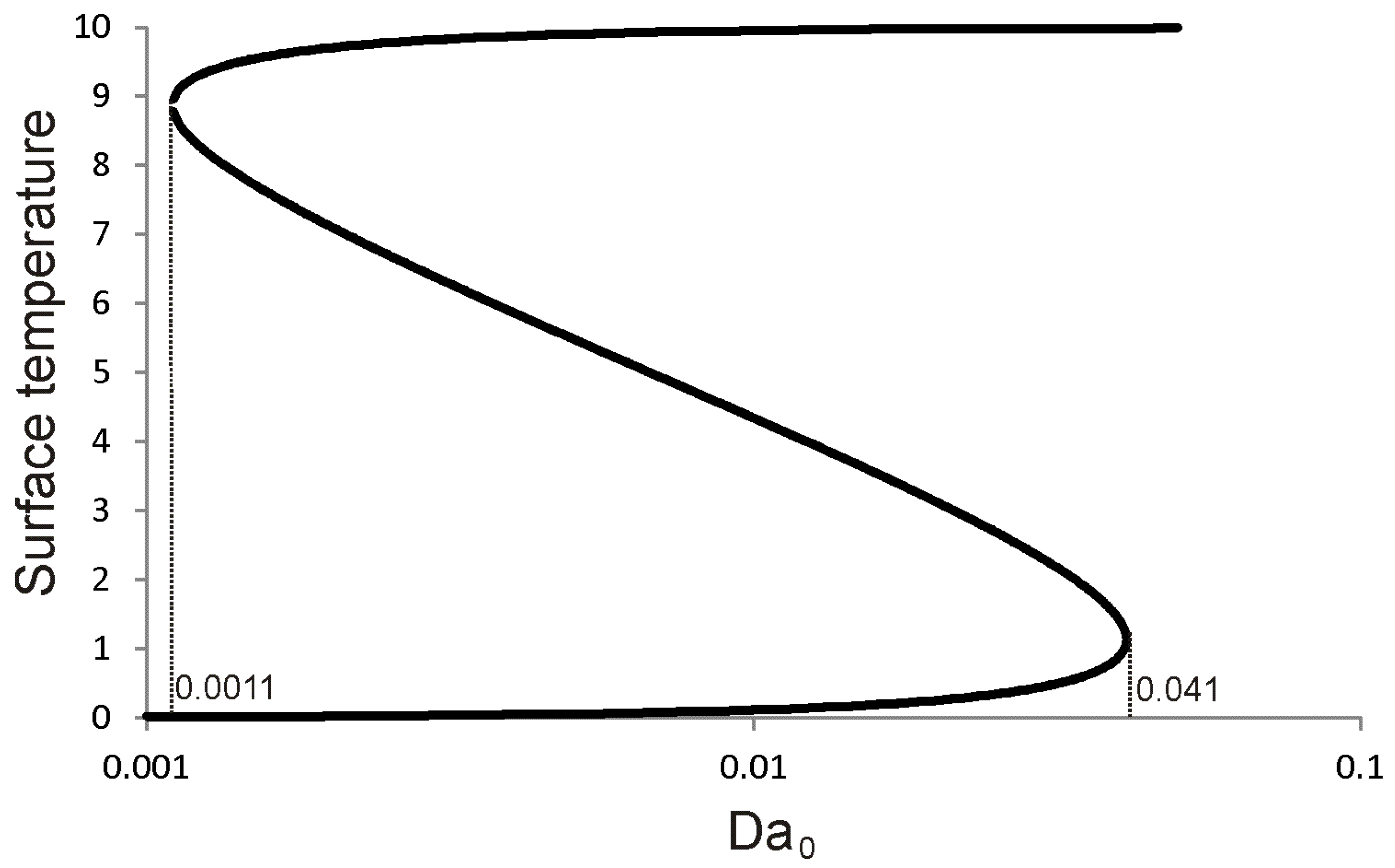

References
- Tikhonov, A.N. On solution of ill-posed problems and regularization method. Dokl. Akad. Nauk USSR 1963, 151, 501–504. [Google Scholar]
- Jaynes, E.T. The minimum entropy production principle. Ann. Rev. Phys. Chem. 1980, 31, 579–601. [Google Scholar] [CrossRef]
- Gorban, A.N.; Karlin, I.V. Method of invariant manifolds for chemical kinetics. Chem. Eng. Sci. 2003, 58, 4751–4768. [Google Scholar] [CrossRef]
- Kaganovich, B.M.; Keiko, A.V.; Shamansky, V.A. Equilibrium thermodynamic modeling of dissipative macroscopic systems. In Advances in Chemical Engineering. 39; West, D.H., Yablonsky, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 1–74. [Google Scholar] [CrossRef]
- Leontovich, M.A. On the free energy of the nonequilibrium state. JETP 1938, 8, 844–854. [Google Scholar]
- Sobczyk, K.; Trebicki, J. Maximum entropy principle in stochastic dynamics. Probab. Eng. Mech. 1990, 5, 102–110. [Google Scholar] [CrossRef]
- Gorban, A.N.; Mirkes, E.M.; Bocharov, A.N.; Bykov, V.I. Thermodynamic consistency of kinetic data. Combust. Explos. Shock Waves 1989, 25, 593–600. [Google Scholar] [CrossRef]
- Vom Lehn, F.; Cai, L.; Pitsch, H. Sensitivity analysis, uncertainty quantification, and optimization for thermochemical properties in chemical kinetic combustion models. Proc. Combust. Inst. 2019, 37, 771–779. [Google Scholar] [CrossRef]
- Kojima, S. Low-Dimensional Manifolds Based on Entropy Production Rate of Reaction Kinetics. In Proceedings of the 24th ICDERS, Taipei, Taiwan, 28 July–2 August 2013; Available online: http://www.icders.org/ICDERS2013/abstracts/ICDERS2013-0019.pdf (accessed on 26 September 2022).
- Kooshkbaghi, M.; Frouzakis, C.E.; Boulouchos, K.; Karlin, I.V. Entropy production analysis for mechanism reduction. Combust. Flame 2014, 161, 1507–1515. [Google Scholar] [CrossRef]
- Valorani, M.; Paolucci, S.; Ciottoli, P.P.; Galassi, R.M. Enthropy production and timescales. Combust. Theory Model. 2017, 21, 137–157. [Google Scholar] [CrossRef]
- Porras, S.; Bykov, V.; Gol’dshtein, V.; Maas, U. Joint Characteristic Timescales and Entropy Production Analyses for Model Reduction of Combustion Systems. Entropy 2017, 19, 264. [Google Scholar] [CrossRef]
- Keck, J.C. Rate-controlled constrained-equilibrium theory of chemical reactions in complex systems. Progr. Energy Combust. Sci. 1990, 16, 125–154. [Google Scholar] [CrossRef]
- Hiremath, V.; Pope, S.B. A study of the rate-controlled constrained equilibrium dimension reduction method and its different implementations. Combust. Theory Model. 2013, 17, 260–293. [Google Scholar] [CrossRef]
- Popkov, Y.S. Dynamical systems with entropy operator. Comput. Math. Model. 2000, 11, 181–186. [Google Scholar] [CrossRef]
- Popkov, Y.S. Equilibria and Stability of One Class of Positive Dynamic Systems with Entropy Operator: Application to Investment Dynamics Modeling. Mathematics 2020, 8, 859. [Google Scholar] [CrossRef]
- Rigopoulos, S.; Lovas, T. A LOI-RCCE methodology for reducing chemical kinetics, with application to laminar premixed flames. Proc. Combust. Inst. 2009, 32, 569–576. [Google Scholar] [CrossRef]
- Koniavitis, P.; Rigopoulos, S.; Jones, W. A methodology for derivation of RCCE-reduced mechanisms via CS. Combust. Flame 2017, 183, 126–143. [Google Scholar] [CrossRef]
- Gallavotti, G. Entropy production and thermodynamics of nonequilibrium stationary states: A point of view. Chaos 2004, 14, 680. [Google Scholar] [CrossRef]
- Peters, M.H. Nonequilibrium Entropy Conservation and the Transport Equations of Mass, Momentum, and Energy. Energies 2021, 14, 2196. [Google Scholar] [CrossRef]
- Arnol’d, V.I. What Is Mathematics? MCNMO: Moscow, Russia, 2002; p. 104. [Google Scholar]
- Rubi, J.M.; Perez-Madrid, A. Coarse-graining and thermodynamics in far-from-equilibrium systems. Acta Phys. Pol. B 2013, 44, 913. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. II. Phys. Rev. 1931, 38, 2265. [Google Scholar] [CrossRef]
- Loytsyanskii, L.G. Mechanics of Liquids and Gases; Nauka: Moscow, Russia, 1950. [Google Scholar]
- Mamedov, M.M. On the incorrectness of the traditional proof of the Prigogine principle of minimum entropy production. Tech. Phys. Lett. 2003, 29, 340–341. [Google Scholar] [CrossRef]
- Ross, J.; Vlad, M.O. Exact Solutions for the Entropy Production Rate of Several Irreversible Processes. J. Phys. Chem. A 2005, 109, 10607–10612. [Google Scholar] [CrossRef] [PubMed]
- Barbera, E. On the principle of minimal entropy production for Navier-Stokes-Fourier fluids. Contin. Mech. Thermodyn. 1999, 11, 327–330. [Google Scholar] [CrossRef]
- Bertola, V.; Cafaro, E. A critical analysis of the minimum entropy production theorem and its application to heat and fluid flow. Int. J. Heat Mass Transf. 2008, 51, 1907–1912. [Google Scholar] [CrossRef]
- Kolenda, Z.; Donizak, J.; Hubert, J. On the minimum entropy production in steady state heat conduction processes. Energy 2004, 29, 2441–2460. [Google Scholar] [CrossRef]
- Lampinen, M.J. A problem of the principle of minimum entropy production. J. Non-Equilib. Thermodyn. 1990, 15, 397–402. [Google Scholar] [CrossRef]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability and Fluctuations; Wiley-Interscience: Hoboken, NJ, USA, 1971; p. 305. [Google Scholar]
- Glansdorff, P.; Nicolis, G.; Prigogine, I. The Thermodynamic Stability Theory of Non-Equilibrium States. PNAS 1974, 71, 197–199. [Google Scholar] [CrossRef]
- Biot, M.A. Variational-lagrangian thermodynamics of evolution of collective chemical systems. Chem. Phys. 1978, 29, 97–115. [Google Scholar] [CrossRef]
- Dyarmati, I. Irreversible Thermodynamics. The Field Theory and Variation Principles; Mir: Moscow, Russia, 1974; p. 304. [Google Scholar]
- Verhas, J. Gyarmati’s Variational Principle of Dissipative Processes. Entropy 2014, 16, 2362–2383. [Google Scholar] [CrossRef]
- Sieniutycz, S. From a least action principle to mass action law and extended affinity. Chem. Eng. Sci. 1987, 42, 2697–2711. [Google Scholar] [CrossRef]
- Reina, C.; Zimmer, J. Entropy production and the geometry of dissipative evolution equations. Phys. Rev. E 2015, 92, 052117. [Google Scholar] [CrossRef] [PubMed]
- Salamon, P.; Nitzan, A.; Andresen, B.; Berry, R.S. Minimum entropy production and the optimization of heat engines. Phys. Rev. A 1980, 21, 2115. [Google Scholar] [CrossRef]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191. [Google Scholar] [CrossRef]
- Tsirlin, A.; Sukin, I. Averaged Optimization and Finite-Time Thermodynamics. Entropy 2020, 22, 912. [Google Scholar] [CrossRef]
- Ziegler, H.; Wehrill, C. On a Principle of Maximal Rate of Entropy Production. J. Non-Equilib. Thermodyn. 1987, 12, 229–243. [Google Scholar] [CrossRef]
- Lucia, U. Irreversibility, entropy and incomplete information. Phys. A 2009, 388, 4025–4033. [Google Scholar] [CrossRef]
- Presse, S.; Ghosh, K.; Lee, J.; Dill, K.A. Principles of maximum entropy and maximum caliber in statistical physics. Rev. Mod. Phys. 2013, 85, 1115. [Google Scholar] [CrossRef]
- Kohler, M. Behandlung von Nichtgleichgewichtsvorgangen mit Hilfe eines Extremalprinzips. Z Phys. 1948, 124, 772–789. [Google Scholar] [CrossRef]
- Ziman, J.M. The general variational principles of transport theory. Can. J. Phys. 1956, 34, 1256–1273. [Google Scholar] [CrossRef]
- Ross, J.; Corlan, A.D.; Muller, S.C. Proposed Principles of Maximum Local Entropy Production. J. Phys. Chem. B 2012, 116, 7858–7865. [Google Scholar] [CrossRef]
- Beretta, G. The fourth law of thermodynamics: Steepest entropy ascent. Phil. Trans. R Soc. A 2020, 378, 20190168. [Google Scholar] [CrossRef] [PubMed]
- Sonnino, G.; Evslin, J. The minimum rate of dissipation principle. Phys. Lett. A 2007, 365, 364–369. [Google Scholar] [CrossRef]
- Bruers, S. A discussion on maximum entropy production and information theory. J. Phys. A Math. Theor. 2007, 40, 7441. [Google Scholar] [CrossRef]
- Dewar, R.C. Maximum Entropy Production as an Inference Algorithm that Translates Physical Assumptions into Macroscopic Predictions: Don’t Shoot the Messenger. Entropy 2009, 11, 931–944. [Google Scholar] [CrossRef]
- Dyke, J.; Kleidon, A. The Maximum Entropy Production Principle: Its Theoretical Foundations and Applications to the Earth System. Entropy 2010, 12, 613–630. [Google Scholar] [CrossRef]
- Martyushev, L.M. The maximum entropy production principle: Two basic questions. Phil. Trans. R Soc. B 2010, 365, 1333–1334. [Google Scholar] [CrossRef]
- Martyushev, L.M. Entropy and Entropy Production: Old Misconceptions and New Breakthroughs. Entropy 2013, 15, 1152–1170. [Google Scholar] [CrossRef]
- Kleidon, A. Nonequilibrium thermodynamics and maximum entropy production in the Earth system. Naturwissenschaften 2009, 96, 1–25. [Google Scholar] [CrossRef]
- Paltridge, G.W. Climate and thermodynamic systems of maximum dissipation. Nature 1979, 279, 630–631. [Google Scholar] [CrossRef]
- Ozawa, H.; Ohmura, A.; Lorenz, R.D.; Pujol, T. The second law of thermodynamics and the global climate system: A review of the maximum entropy production principle. Rev. Geophys. 2003, 41, 4. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. The restrictions of the maximum entropy production principle. Phys. A 2014, 410, 17–21. [Google Scholar] [CrossRef]
- Ross, J. Thermodynamics and Fluctuations Far from Equilibrium; Springer: Berlin, Germany, 2008. [Google Scholar] [CrossRef]
- Endres, R.G. Entropy production selects nonequilibrium states in multistable systems. Sci. Rep. 2017, 7, 14437. [Google Scholar] [CrossRef] [PubMed]
- Dobovisek, A.; Zupanovic, P.; Brumen, M.; Bonacic-Losic, Z.; Luic, D.; Juretic, D. Enzyme kinetics and the maximum entropy production principle. Biophys. Chem. 2011, 154, 49–55. [Google Scholar] [CrossRef] [PubMed]
- Mahulikar, S.; Sengupta, T.; Sharma, N.; Rastogi, P. Thermodynamic Merger of Fluctuation Theorem and Principle of Least Action: Case of Rayleigh–Taylor Instability. J. Non-Equilib. Thermodyn. 2019, 44, 363–371. [Google Scholar] [CrossRef]
- Chavanis, P.H.; Sommeria, J.; Robert, R. Statistical Mechanics of Two-Dimensional Vortices and Collisionless Stellar Systems. Astrophys. J. 1996, 471, 385. [Google Scholar] [CrossRef]
- Keizer, J.; Fox, R.F. Qualms Regarding the Range of Validity of the Glansdorff-Prigogine Criterion for Stability of Non-Equilibrium States. PNAS 1974, 71, 192–196. [Google Scholar] [CrossRef]
- Bradford, R.A.W. An investigation into the maximum entropy production principle in chaotic Rayleigh–Benard convection. Phys. A 2013, 392, 6273–6283. [Google Scholar] [CrossRef]
- Bartlett, S.; Bullock, S. Natural convection of a two-dimensional Boussinesq fluid does not maximize entropy production. Phys. Rev. E 2014, 90, 023014. [Google Scholar] [CrossRef]
- Paltridge, G.W. A Story and a Recommendation about the Principle of Maximum Entropy Production. Entropy 2009, 11, 945–948. [Google Scholar] [CrossRef]
- Attard, P. The Second Entropy: A Variational Principle for Time-dependent Systems. Entropy 2008, 10, 380–390. [Google Scholar] [CrossRef]
- Wei, J. Irreversible thermodynamics in engineering. Ind. Eng. Chem. 1966, 50, 55–60. [Google Scholar] [CrossRef]
- Truesdell, C. The Tragicomedy of Classical Thermodynamic; Springer: Udine, Italy, 1971; p. 41. [Google Scholar]
- Bejan, A.; Lorente, S. The constructal law of design and evolution in nature. Phil. Trans. R Soc. B 2010, 365, 1335–1347. [Google Scholar] [CrossRef] [PubMed]
- Reis, A.H. Use and validity of principles of extremum of entropy production in the study of complex systems. Ann. Phys. 2014, 346, 22–27. [Google Scholar] [CrossRef]
- Lucia, U. Entropy generation: Minimum inside and maximum outside. Phys. A 2014, 396, 61–65. [Google Scholar] [CrossRef]
- Yourgrau, W.; Raw, C.J.G. Variational principles and chemical reactions. Il Nuovo Cim. 1957, 5, 472–478. [Google Scholar] [CrossRef]
- Reti, P.; Ropolyi, L. On the geometrical structure of equilibrium chemical systems. Utilization of analogies between point mechanics and reaction kinetics. Il Nuevo Cim. B 1986, 94, 16–28. [Google Scholar] [CrossRef]
- Moroz, A. On a variational formulation of the maximum energy dissipation principle for non-equilibrium chemical thermodynamics. Chem. Phys. Lett. 2008, 457, 448–452. [Google Scholar] [CrossRef]
- Trusov, B.G.; Malanichev, A.G. Application of variational principle for solving chemical kinetic problem. Dokl. Akad. Nauk 1994, 339, 771–775. (In Russian) [Google Scholar]
- Trusov, B.G. Simulation of Kinetics of Chemical Conversions: Thermodynamic Approach. Her. Baumann MSTU 2005, 18, 26–38. Available online: http://vestniken.ru/articles/385/385.pdf (accessed on 26 September 2022).
- Reinhardt, V.; Winckler, M.; Lebiedz, D. Approximation of Slow Attracting Manifolds in Chemical Kinetics by Trajectory-Based Optimization Approaches. J. Phys. Chem. A 2008, 112, 1712–1718. [Google Scholar] [CrossRef]
- Lebiedz, D.; Reinhardt, V.; Siehr, J. Minimal curvature trajectories: Riemann geometry concepts for slow manifold computation in chemical kinetics. J. Comp. Phys. 2010, 229, 6512–6533. [Google Scholar] [CrossRef]
- Lebiedz, D.; Unger, J. On unifying concepts for trajectory-based slow invariant attracting manifold computation in kinetic multiscale models. Math. Comp. Model. Dyn. Syst. 2016, 22, 87–112. [Google Scholar] [CrossRef]
- Adrover, A.; Creta, F.; Giona, M.; Valorani, M. Stretching-based diagnostics and reduction of chemical kinetic models with diffusion. J. Comput. Phys. 2007, 225, 1442–1471. [Google Scholar] [CrossRef]
- Adrover, A.; Creta, F.; Giona, M.; Valorani, M. Explosion limits and runaway criteria: A stretching-based approach. Chem. Eng. Sci. 2007, 62, 1171–1183. [Google Scholar] [CrossRef]
- Orlov, V.N.; Rozonoer, L.I. The variational principle for the equations of macroscopic dynamics and its applications to chemical kinetics. USSR Comput. Math. Math. Phys. 1981, 21, 120–133. [Google Scholar] [CrossRef]
- Okunev, A.G.; Parmon, V.N. Application of the thermodynamic form of kinetic equations to analysis of reversible chemical processes. Functional of a stationary state. Kinet. Catal. 1997, 38, 498–506. [Google Scholar]
- Parmon, V.N. Catalysis and non-equilibrium thermodynamics: Modern in situ studies and new theoretical approaches. Catal. Today 1999, 51, 435–456. [Google Scholar] [CrossRef]
- Pagonabarraga, I.; Perez-Madrid, A.; Rubi, J.M. Fluctuating hydrodynamics approach to chemical reactions. Phys. A 1997, 237, 205–219. [Google Scholar] [CrossRef]
- Rubi, J.M.; Perez-Madrid, A. Far-from-equilibrium kinetic processes. J. Non-Equilib. Thermodyn. 2015, 40, 275–281. [Google Scholar] [CrossRef]
- Keizer, J. Nonequilibrium thermodynamics and the stability of states far from equilibrium. Acc Chem. Res. 1979, 12, 243–249. [Google Scholar] [CrossRef]
- Ross, J.; Vlad, M.O. Nonlinear Kinetics and New Approaches to Complex Reaction Mechanisms. Ann. Rev. Phys. Chem. 1999, 50, 51–78. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Berdichevsky, V. Variational Principles of Continuum Mechanics. V. 1. Fundamentals; Springer: Berlin, Germany, 2009. [Google Scholar] [CrossRef]
- Horne, W.; Karamcheti, K. Extrema principles of entropy production and energy dissipation in fluid mechanics. In Proceedings of the 1st National Fluid Dynamics Conference, Cincinnati, OH, USA, 25–28 July 1988. No. 88-3830-C2159-2165. [Google Scholar]
- Douglas, J. Solution of the inverse problem of the calculus of variations. Trans. Amer Math. Soc. 1941, 50, 71–128. [Google Scholar] [CrossRef]
- Vujanovic, B. A Variational Principle for Non-Conservative Dynamical Systems. J. Appl. Math. Mech. 1975, 55, 321–331. [Google Scholar] [CrossRef]
- Gafiichuk, V.V.; Lubashevskii, I.A. Variational principles of dissipative systems. J. Sov. Math. 1993, 67, 2943–2949. [Google Scholar] [CrossRef]
- Filippov, V.M.; Savchin, V.M.; Shorokhov, S.G. Variational principles for nonpotential operators. J. Math. Sci. 1994, 68, 275–398. [Google Scholar] [CrossRef]
- Musielak, Z.E. Standard and non-standard Lagrangians for dissipative dynamical systems with variable coefficients. J. Phys. A Math. Theor. 2008, 41, 055205. [Google Scholar] [CrossRef]
- Finlayson, B.A.; Scriven, L.E. On the search for variational principles. Int. J. Heat Mass Transf. 1967, 10, 799–821. [Google Scholar] [CrossRef]
- Van, P.; Muschik, W. Structure of variational principles in nonequilibrium thermodynamics. Phys. Rev. E 1995, 52, 3584. [Google Scholar] [CrossRef]
- Van, P.; Kovacz, R. Variational principles and nonequilibrium thermodynamics. Phil. Trans. R Soc. A 2020, 378, 20190178. [Google Scholar] [CrossRef]
- Denman, H.H. Approximate invariants and Lagrangians for autonomous, weakly non-linear systems—II. Linear friction. Int. J. Non-Linear Mech. 1998, 33, 301–314. [Google Scholar] [CrossRef]
- He, J.-H. Variational principles for some nonlinear partial differential equations with variable coefficients. Chaos Solitons Fractals 2004, 19, 847–851. [Google Scholar] [CrossRef]
- Gitman, D.M.; Kupriyanov, V.G. The action principle for a system of differential equations. J. Phys. A Math. Theor. 2007, 40, 40. [Google Scholar] [CrossRef][Green Version]
- Kong, X.; Wang, Z.; Wu, H. Variational integrators for forced Lagrangian systems based on the local path fitting technique. Appl. Math. Comput. 2022, 416, 126739. [Google Scholar] [CrossRef]
- Mobbs, S.D. Variational principles for perfect and dissipative fluid flows. Proc. R Soc. A 1982, 381, 457–468. [Google Scholar] [CrossRef]
- Ecer, A.; Rout, R.K.; Ward, P. Investigation of solution of Navier-Stokes equations using a variational formulation. Int. J. Numer. Methods Fluids 1983, 3, 23–31. [Google Scholar] [CrossRef]
- Marra, R. Variational principles for conservative and dissipative diffusions. Phys. Rev. D 1987, 36, 1724. [Google Scholar] [CrossRef]
- Kerswell, R.R. Variational principle for the Navier-Stokes equations. Phys. Rev. E 1999, 59, 5482. [Google Scholar] [CrossRef]
- Fukugawa, H.; Fujitani, Y. A Variational Principle for Dissipative Fluid Dynamics. Prog. Theor. Phys. 2012, 127, 921–935. [Google Scholar] [CrossRef]
- Maximov, G.A. Generalized variational principle in dissipative hydrodynamics and continuum mechanics. Comput. Contin. Mech. 2009, 2, 92–104. [Google Scholar] [CrossRef][Green Version]
- Gol’dshtik, M.A.; Stern, V.N. Hydrodynamic Stability and Turbulence; Nauka: Novosibirsk, Russia, 1977; p. 368. (In Russian) [Google Scholar]
- Benzi, R.; Vitaletti, M.; Vulpiani, A. A variational principle for the statistical mechanics of fully developed turbulence. J. Phys. A 1982, 15, 883. [Google Scholar] [CrossRef]
- Qian, J. Variational approach to the closure problem of turbulence theory. Phys. Fluids 1983, 26, 2098. [Google Scholar] [CrossRef]
- Eyink, G.L. Turbulence noise. J. Stat. Phys. 1996, 83, 955–1019. [Google Scholar] [CrossRef]
- Finlayson, B.A.; Scriven, L.E. The method of weighted residuals and its relation to certain variational principles for the analysis of transport processes. Chem. Eng. Sci. 1965, 20, 395–404. [Google Scholar] [CrossRef]
- Sieniutycz, S. The variational principles of classical type for non-coupled non-stationary irreversible transport processes with convective motion and relaxation. Int. J. Heat Mass Transf. 1977, 20, 1221–1231. [Google Scholar] [CrossRef]
- Glazunov, Y.T. The variational method for the solution of the combined heat and mass transfer problems. Int. J. Heat Mass Transf. 1983, 26, 1815–1822. [Google Scholar] [CrossRef]
- Lorenzini, E. A variational formulation applied to heat conduction equation. Bull. Acad. Roy. Belg. 1970, 56, 367–379. [Google Scholar] [CrossRef]
- Busse, F.H. Bounds for turbulent shear flow. J. Fluid Mech. 1970, 41, 219–240. [Google Scholar] [CrossRef]
- Stern, M.E. Inequalities and variational principles for turbulent transport. J. Fluid Mech. 1979, 91, 513–540. [Google Scholar] [CrossRef]
- Lazareva, T.Y.; Tsirlin, A.M. Variational approach in assessment of quasi stationary approximation method applicability. J. Appl. Chem. 1981, 54, 2225–2230. (In Russian) [Google Scholar]
- Amat, S.; Lopez, D.J.; Pedregal, P. Numerical approximation to ODEs using a variational approach. I: The basic framework. Optimization 2014, 63, 337–358. [Google Scholar] [CrossRef]
- Amat, S.; Legaz, M.J.; Ruiz-Alvarez, J. On a Variational Method for Stiff Differential Equations Arising from Chemistry Kinetics. Mathematics 2019, 7, 459. [Google Scholar] [CrossRef]
- Phythian, R. Some variational methods in the theory of turbulent diffusion. J. Fluid Mech. 1972, 53, 469–480. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Variational Method in Turbulence Theory. Phys. Rev. Lett. 1979, 42, 1263. [Google Scholar] [CrossRef]
- Gorla, R.; Canter, M.; Pallone, P.J. Variational approach to unsteady flow and heat transfer in a channel. Heat Mass Transf. 1998, 33, 439–442. [Google Scholar] [CrossRef]
- Chavanis, P.-H.; Sommeria, J. Thermodynamical Approach for Small-Scale Parametrization in 2D Turbulence. Phys. Rev. Lett. 1997, 78, 3302. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Calo, V.M.; Cottrell, J.A.; Hughes, T.J.R.; Reali, A.; Scovazzi, G. Variational multiscale residual-based turbulence modeling for large eddy simulation of incompressible flows. Comp. Methods Appl. Mech. Eng. 2007, 197, 173–201. [Google Scholar] [CrossRef]
- Eyink, G.L.; Alexander, F.J. Predictive Turbulence Modeling by Variational Closure. J. Stat. Phys. 1998, 91, 221–283. [Google Scholar] [CrossRef]
- Gravemeier, V. The variational multiscale method for laminar and turbulent flow. Arch. Comput. Methods Eng. 2006, 13, 249. [Google Scholar] [CrossRef]
- Doi, M. A New Variational Approach to the Diffusion and the Flow Problem in Porous Media. J. Phys. Soc. Jpn. 1976, 40, 567–572. [Google Scholar] [CrossRef]
- Rubinstein, J.; Torquato, S. Flow in random porous media: Mathematical formulation, variational principles, and rigorous bounds. J. Fluid Mech. 1989, 206, 25–46. [Google Scholar] [CrossRef]
- Korshiya, T.K.; Tishkin, V.F.; Favorskii, A.N.; Shashkov, M.Y. A variational approach to the construction of difference schemes on curvilinear meshes for the heat-conduction equation. USSR Comput. Math. Math. Phys. 1980, 20, 135–155. [Google Scholar] [CrossRef]
- Ramos, J.I. Finite element methods for one-dimensional combustion problems. Int. J. Numer. Methods Fluids 1990, 11, 893–906. [Google Scholar] [CrossRef]
- Liseikin, V.D. The construction of structured adaptive grids: A review. Comput. Math. Math. Phys. 1996, 36, 1–32. [Google Scholar]
- Moon, K.-S.; Szepessy, A.; Tempone, R.; Zouraris, G.E. A variational principle for adaptive approximation of ordinary differential equations. Numer. Math. 2003, 93, 131–152. [Google Scholar] [CrossRef]
- Liu, C.; Wang, C.; Wang, Y. A structure-preserving, operator splitting scheme for reaction-diffusion equations with detailed balance. J. Comput. Phys. 2021, 436, 110253. [Google Scholar] [CrossRef]
- Gostintsev, Y.A. Method of reduction to ordinary differential equations in problems of the nonstationary burning of solid propellants. Combust. Explos. Shock Waves 1967, 3, 218–220. [Google Scholar] [CrossRef]
- Tsirelman, N.M. Variational Solutions of Complex Heat and Mass Transfer Problems. Adv. Heat Transf. 1989, 19, 191–245. [Google Scholar] [CrossRef]
- Kuzin, I.; Pohozaev, S. Entire Solutions of Semilinear Elliptic Equations; Birkhauser: Basel, Switzerland, 1997; p. 254. [Google Scholar]
- Anisimov, S.I.; Vitkin, E.I. Some variational problems in thermal explosion theory. J. Appl. Mech. Tech. Phys. 1966, 7, 109–110. [Google Scholar] [CrossRef]
- Grishin, A.M. Some problems of ignition theory. J. Appl. Mech. Tech. Phys. 1962, 3, 75–79. (In Russian) [Google Scholar]
- Wake, G.C.; Rayner, M.E. Variational methods for nonlinear eigenvalue problems associated with thermal ignition. J. Differ. Equ. 1973, 13, 247–256. [Google Scholar] [CrossRef]
- Graham-Eagle, J.G.; Wake, G.C. Theory of thermal explosions with simultaneous parallel reactions. II. The two- and three-dimensional cases and the variational method. Proc. R Soc. A 1985, 401, 195–202. [Google Scholar] [CrossRef]
- Ajadi, S.O. The influence of viscous heating and wall thermal conditions on the thermal ignition of a poiseuille/couette reactive flow. Russ. J. Phys. Chem. B 2010, 4, 652–659. [Google Scholar] [CrossRef]
- Blouquin, R.; Joulin, G. On a Variational Principle for Reaction/Radiation/Conduction Equilibria. Combust. Sci. Tech. 1996, 112, 375–385. [Google Scholar] [CrossRef]
- Kuvyrkin, G.N.; Savelyeva, I.Y.; Zarubin, V.S. Estimations of the parameters of a thermal explosion in a triaxial ellipsoid. Z Angew. Math. Phys. 2020, 71, 113. [Google Scholar] [CrossRef]
- Volpert, V.A.; Volpert, V.A. Propagation Velocity Estimation for Condensed Phase Combustion. SIAM J. Appl. Math. 1991, 51, 1074–1089. [Google Scholar] [CrossRef]
- Benguria, R.D.; Depassier, M.C. Variational Principles for the Speed of Traveling Fronts of Reaction-Diffusion Equations. In Variational and Extremum Principles in Macroscopic Systems; Elsevier: Amsterdam, The Netherlands, 2005; pp. 339–354. [Google Scholar] [CrossRef]
- Stevens, A.; Papanicolaou, G.; Heinze, S. Variational Principles for Propagation Speeds in Inhomogeneous Media. SIAM J. Appl. Math. 2001, 62, 129–148. [Google Scholar] [CrossRef]
- Lucia, M.; Muratov, C.B.; Novaga, M. Linear vs. nonlinear selection for the propagation speed of the solutions of scalar reaction-diffusion equations invading an unstable equilibrium. Comm. Pure Appl. Math. 2004, 57, 616–636. [Google Scholar] [CrossRef]
- Rodrigo, M.R.; Miura, R.M. Exact and approximate travelling waves of reaction-diffusion systems via a variational approach. Anal. Appl. 2011, 9, 187–199. [Google Scholar] [CrossRef]
- Gerasev, A. Variational principles in irreversible thermodynamics with application to combustion waves. J. Non-Equilib. Thermodyn. 2011, 36, 55–73. [Google Scholar] [CrossRef]
- Karpov, A.I.; Kudrin, A.V.; Alies, M.Y. Calculation of the stationary flame propagation velocity by the variational principle of irreversible thermodynamics. Case Stud. Therm. Eng. 2022, 30, 101767. [Google Scholar] [CrossRef]
- Tavadyan, L.A.; Martoyan, G.A. Value-Based Numerical Identification and Analysis of Critical States of Chemical Reaction Systems. Russ. J. Phys. Chem. B 2021, 15, 447–456. [Google Scholar] [CrossRef]
- Vellela, M.; Qian, H. Stochastic dynamics and non-equilibrium thermodynamics of a bistable chemical system: The Schlogl model revisited. J. R Soc. Interface 2009, 6, 925–940. [Google Scholar] [CrossRef] [PubMed]
- Bochkov, G.N.; Kuzovlev, Y.E. Nonlinear fluctuation-dissipation relations and stochastic models in nonequilibrium thermodynamics: II. Kinetic potential and variational principles for nonlinear irreversible processes. Phys. A 1981, 106, 480–520. [Google Scholar] [CrossRef]
- Bertini, L.; De Sole, A.; Gabrielli, D.; Jona-Lasinio, G.; Landim, C. Minimum Dissipation Principle in Stationary Non-Equilibrium States. J. Stat. Phys. 2004, 116, 831–841. [Google Scholar] [CrossRef]
- Van, P. Nonequilibrium thermodynamics: Emergent and fundamental. Phil. Trans. R Soc. A 2020, 378, 20200066. [Google Scholar] [CrossRef]
- Jaynes, E.T. Gibbs vs Boltzmann Entropies. Am. J. Phys. 1965, 33, 391. [Google Scholar] [CrossRef]
- Lloyd, S. Use of mutual information to decrease entropy: Implications for the second law of thermodynamics. Phys. Rev. A 1989, 39, 5378. [Google Scholar] [CrossRef]
- Koukkari, P.; Pajarre, R. A Gibbs energy minimization method for constrained and partial Equilibria. Pure Appl. Chem. 2011, 83, 1243–1254. [Google Scholar] [CrossRef]
- Donskoy, I.G.; Shamansky, V.A.; Kozlov, A.N.; Svishchev, D.A. Coal gasification process simulations using combined kinetic-thermodynamic models in one-dimensional approximation. Combust. Theory Model. 2017, 21, 529–559. [Google Scholar] [CrossRef]
- Strieder, W.; Aris, R. Variational Methods Applied to Problems of Diffusion and Reaction; Springer: Berlin/Heidelberg, Germany, 1973. [Google Scholar] [CrossRef]
- Kiss, E. In the validity of the principle of minimum entropy production. Period. Polytech. Chem. Eng. 1994, 38, 183–197. [Google Scholar]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; Interscience: New York, NY, USA, 1967. [Google Scholar]
- Frank-Kamenetskii, D.A. Diffusion and Heat Exchange in Chemical Kinetics; Princeton Univ. Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Zarubin, V.S.; Kuvyrkin, G.N.; Savelyeva, I.Y. Variational estimates of the parameters of a thermal explosion of a stationary medium in an arbitrary domain. Int. J. Heat Mass Transf. 2019, 135, 614–619. [Google Scholar] [CrossRef]
- Donskoy, I.G. Determining critical conditions in the thermal explosion problem using approximate variational formulations. Inf. Math. Technol. Sci. Manag. 2022, 1, 7–20. [Google Scholar] [CrossRef]
- Kapila, A.K.; Matkowski, B.J.; Vega, J. Reactive-Diffusive System with Arrhenius Kinetics: Peculiarities of the Spherical Geometry. SIAM J. Appl. Math. 1980, 38, 382–401. [Google Scholar] [CrossRef]
- Balakotaiah, V.; Luss, D. Multiplicity features of reacting systems: Dependence of the steady-states of a CSTR on the residence time. Chem. Eng. Sci. 1983, 38, 1709–1721. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Donskoy, I. On the Existence and Applicability of Extremal Principles in the Theory of Irreversible Processes: A Critical Review. Energies 2022, 15, 7152. https://doi.org/10.3390/en15197152
Donskoy I. On the Existence and Applicability of Extremal Principles in the Theory of Irreversible Processes: A Critical Review. Energies. 2022; 15(19):7152. https://doi.org/10.3390/en15197152
Chicago/Turabian StyleDonskoy, Igor. 2022. "On the Existence and Applicability of Extremal Principles in the Theory of Irreversible Processes: A Critical Review" Energies 15, no. 19: 7152. https://doi.org/10.3390/en15197152
APA StyleDonskoy, I. (2022). On the Existence and Applicability of Extremal Principles in the Theory of Irreversible Processes: A Critical Review. Energies, 15(19), 7152. https://doi.org/10.3390/en15197152







