Parameter Matching, Optimization, and Classification of Hybrid Electric Emergency Rescue Vehicles Based on Support Vector Machines

Abstract

Based on the requisition for an ideal precise power source for a hybrid electric emergency rescue vehicle (HE-ERV), we present an optimistic parameter matching and optimization schemes for the selection of a HE-ERV. Then, given a set of optimized power source components, they are classified into different types of HE-ERV. In this study, due to the different design objectives of different types of emergency rescue vehicles and the problems of hybrid electric vehicle parameter matching, a multi-island genetic algorithm (MIGA) and non-linear programming quadratic Lagrangian (NLPQL) is proposed for the matched parameters. The vehicle dynamic model is established based on the AVL Cruise simulation platform. The power source performance parameters are matched by theoretical analysis and coupled to the simulation platform. Finally, the optimized matched parameters are classified based on the support vector machines classification model to determine the category of the HE-ERV. The classification results showed that there is an unprecedented level for categorizing several factors of the power source parameters. This research showed that its more logical and reasonable to match HE-ERVs with medium motor/engine power output and battery capacity, as these can attain dynamic performance, extended driving range, and reduced energy consumption.

1. Introduction

When faced with increasingly severe environmental pollution, urban traffic congestion, and energy shortages, priority development of hybrid electric vehicles (HEVs) can effectively alleviate the current environmental pollution and energy crisis and, as such, is the main development trend of the automobile industry [1,2]. The key powertrain parameters and energy management strategies of hybrid electric vehicles determine the energy consumption and power performance. It is imperative that a particular set of layouts be taken into consideration when designing and matching the parameters of a hybrid electric vehicle powertrain system, since each of these layouts directly impacts the vehicle performance or design objectives, including fuel consumption and emissions [3,4]. For a given set of design layouts, identifying the appropriate design parameters that maximize the design objectives of a hybrid electric vehicle is necessary to solve the hybrid electric vehicle design problem [5,6]. The study of matching and optimizing the key powertrain parameters can effectively reduce the emissions and energy consumption of the vehicle, hence, in the face of the requirements of energy conservation and environmental protection, hybrid electric vehicles have gradually become a research focus [7,8]. Zhao et al. studied the parameter matching and configuration analysis of a fuel cell electric vehicle (EV) driving system. In their study, the hybrid, compensation, and full power type of the fuel EV powertrain were analyzed. Their results showed that the cost, performance, and portability were improved in the full-power type powertrain [9].

Tran et al. designed a HEV powertrain configuration and components that can satisfy the performance criteria of acceleration, braking, driving range, fuel economy, and emissions given at the EcoCAR Mobility Challenge competition. Their design deduced a P4 powertrain system with a 2.5 L engine, a 150 kW electric motor, and a 133 kW battery pack [10]. Multi-objective optimization of the HEV transmission system based on an immune genetic algorithm is proposed by Wang, Z. et al. The authors considered the powertrain components and the control strategy as the design variables, the fuel consumption and emissions as the design objectives, and the vehicle’s dynamic performance as the primary constraint condition [11]. Verbruggen, F.J.R. et al. developed a nested optimization routine which is used to optimize the battery, electric machine size, and the gear ratio values in an outer loop with the particle swarm optimization algorithm and, in the inner loop, the gear shifting is optimized as a local minimization problem. The simulation results showed that electric machine size can be reduced −16% without compromising the vehicle’s top speed and acceleration performance, and with a moderate reduction in energy usage of 1.4% [12]. Pengxiang et al. proposed a genetic algorithm based on a multi-objective optimization method for matching power sources for PHEV.

Fuel economy and a lightweight quality were considered as the objectives under the performance constraints. In their results, the fuel economy and lightweight quality were increased by 2.26 and 8.26%, respectively [13]. Xu adopted a hybrid Toyota PRIUS for the optimization and performance analysis of the power system. The author built and optimized the hybrid power system with AVL Cruise, resulting in an optimized system with better performance [14]. In order to solve the problems of the cumbersome calibration process and the inability of calibration parameters to meet the requirements of different driving cycles, Li et al. proposed an optimization method for calibration parameters for HEV [15]. Hong et al. designed a parameter tuning-based co-optimization for the HEV powertrain system by leveraging V2V/V2I information to maximize fuel efficiency. The authors achieved an average of 9.22% fuel savings for a random driving cycle on a Toyota Prius test model [16]. With the aim of guaranteeing the vehicle’s comprehensive performance, a parameter matching and optimization for the power system of range-extended EV based on PSO and sensitivity analysis was proposed by Liu et al. Their results showed a significant influence on the characteristic parameters and the coupling effect in the vehicle performance indicators [17]. He et al. put forward the parameter matching and simulation analysis of electromechanical coupling devices with the engine, motor, and generator as the characteristic parameters. They recorded fuel consumption of 4.6 L/100 km in NEDC, and the SOC battery was in line with the requirements of the control strategy [18].

Aiming at problems of large computational complexity and poor reliability, Fu et al. proposed a multi-objective optimization (MOO) scheme for solving the parameter matching optimization of the HEV powertrain system. The authors streamlined the MOO problem for fuel consumption and emission with the weight coefficient method to analyze the parameter ranges of different components. Their results showed a significant reduction in fuel consumption and emissions of the vehicle [19]. Cao et al. used the hybrid PSO method to solve the parameter matching of dual-clutch transmission for axle-split HEV [20]. In order to improve the overall performance of EV, Wang and Sun used the quantum genetic intelligent algorithm to determine the parameter optimization of a dual-motor hybrid driving system for EV. According to their results, the quantum GA exhibited good global optimization capabilities, satisfying the design’s dynamic performance and economic requirements. A reduced energy consumption of 15.6% compared with conventional EV was reported in their study [21]. Due to the fact that less attention is given to electric agricultural machinery, Chen et al. proposed a powertrain parameter matching and optimal design of a dual-motor electric tractor. A PSO algorithm based on a mixed penalty function was used for parameter optimization and designed in MATLAB [22]. Zhang, Z., et al. proposed a master–slave hybrid electric vehicle (MSHEV) with multiple energy sources, selected the battery SOC of MSHEV as the optimization objective and optimized applicable parameters further. An approximate model was constructed based on the response surface model (RSM), and an optimization model was built based on the multi-island genetic algorithm (MIGA). Their results showed an enhanced SOC and a reasonably optimized MSHEV [23]. Zhao, Z. et al. introduced a new method for optimizing the energy management strategy (EMS) for a fuel cell vehicle (FCV) to reduce fuel consumption.

A multi-island genetic algorithm was used to optimize the MFs and demonstrated optimized fuzzy control EMS in simulations of two EMSs under four driving cycles. The simulation results confirmed that the optimized fuzzy control EMS provided smoother and more stable output power from FCS, reducing hydrogen consumption by 8.4%, 1.1%, 5.1%, and 7.6%, respectively, compared to the original fuzzy control EMS [24]. Jibin et al. proposed a parameter matching approach for a hybrid energy storage system based on a multi-objective optimization algorithm with a system simulation model in the loop designed by using an NSGA-II-type genetic algorithm. Considering the important indicator of capacity decay of hybrid energy storage systems in service life, a cumulative penalty factor was added. However, the adopted method did not consider the type of battery and supercapacitor monomer, meaning that the combined consideration of lifetime, price, and cost was highly constrained. Their results indicated a reduction in the performance degradation rate of battery by at least 31.1% when compared with the parameter matching result of the hybrid energy storage system based on the equivalent calculation approach [25]. Zhang et al. proposed an improved genetic algorithm based on adaptive crossover probability and mutation probability; the algorithm solves the accuracy problem effectively, but the optimization process is complicated [26].

In the field of classification and prediction, the support vector machine (SVM) based on the kernel method has been used as a powerful tool for solving practical binary classification problems [27,28,29]; it is superior to other supervised learning methods, and the training time is short. Due to their good theoretical foundations and good generalization capacity, SVMs have become one of the most used classification methods. Decision functions are determined directly from the training data by using SVM in such a way that the existing separation (margin) between the decision borders is maximized in a highly dimensional space called the feature space [30,31]. This classification strategy minimizes the classification errors of the training data and obtains a better generalization ability, i.e., classification skills of SVMs and other techniques differ significantly, especially when the number of input data is small. Furthermore, SVMs are a powerful technique used in data classification and regression analysis [32,33]. Alimi, O.A. et al. presented a hybrid classification technique using support vector machine (SVM) with the evolutionary genetic algorithm (GA) model to detect and classify power system unwanted events in an accurate yet straightforward manner. The performance of the proposed GA-SVM model was evaluated and compared with other models using key classification metrics. In their experimental results, the proposed model improved the classification rate of unwanted events in power systems [34].

As a popular machine learning algorithm, Jayadeva and Chandra designed two proximal class hyperplanes that theoretically reduce SVM’s training cost by one-fourth [35]. The twin support vector machines (TSVM) have been developed as successful variants of support vector machines (SVM). They consist of nonparallel hyperplanes, where each hyperplane is either at least one distance from the other class or closer to one of the two classes. Compared to classical classifiers, non-parallel SVMs consider intra-class information and possess vital advantages. As a method of improving the generalization performance of twin-bounded support vector machines, Borah and Gupta proposed a truncated loss function-based algorithm with reduced sensitivity to noise and outliers and for handling class imbalance learning [36]. The twin bounded support vector machine (TBSVM) was improved by Wang et al. by adding regularization terms to the objective functions [37]. Using two non-parallel hyperplanes, Zhao adopted two methods to classify the diversity between classes, thereby boosting the performance of non-parallel support vector machine active learning [38]. In a paper by Chen et al., they developed structural non-parallel support vector machines by using prior knowledge of data to improve generalization performance [39]. According to Tian et al., non-parallel support vector machines were extended to large data learning by ν-nonparallel support vector machines and a divide-and-conquer method [40,41]. Additionally, Ju et al. [42] proposed a divide-and-conquer method for large scale ν-non-parallel SVMs, similar to [40].

In this study, a foam fire truck hybrid electric emergency rescue vehicle is used as the research object. In summary, the contributions of this study are as follows: (1) Classifying and determining the particular type of emergency rescue vehicle from sets of optimized matched power source parameters of the hybrid electric emergency rescue vehicle using non-parallel SVM classification (NPSVM); (2) combinatorial optimization of theoretical analysis of matching parameters of hybrid electric emergency rescue vehicle using MIGA and NLPQL.

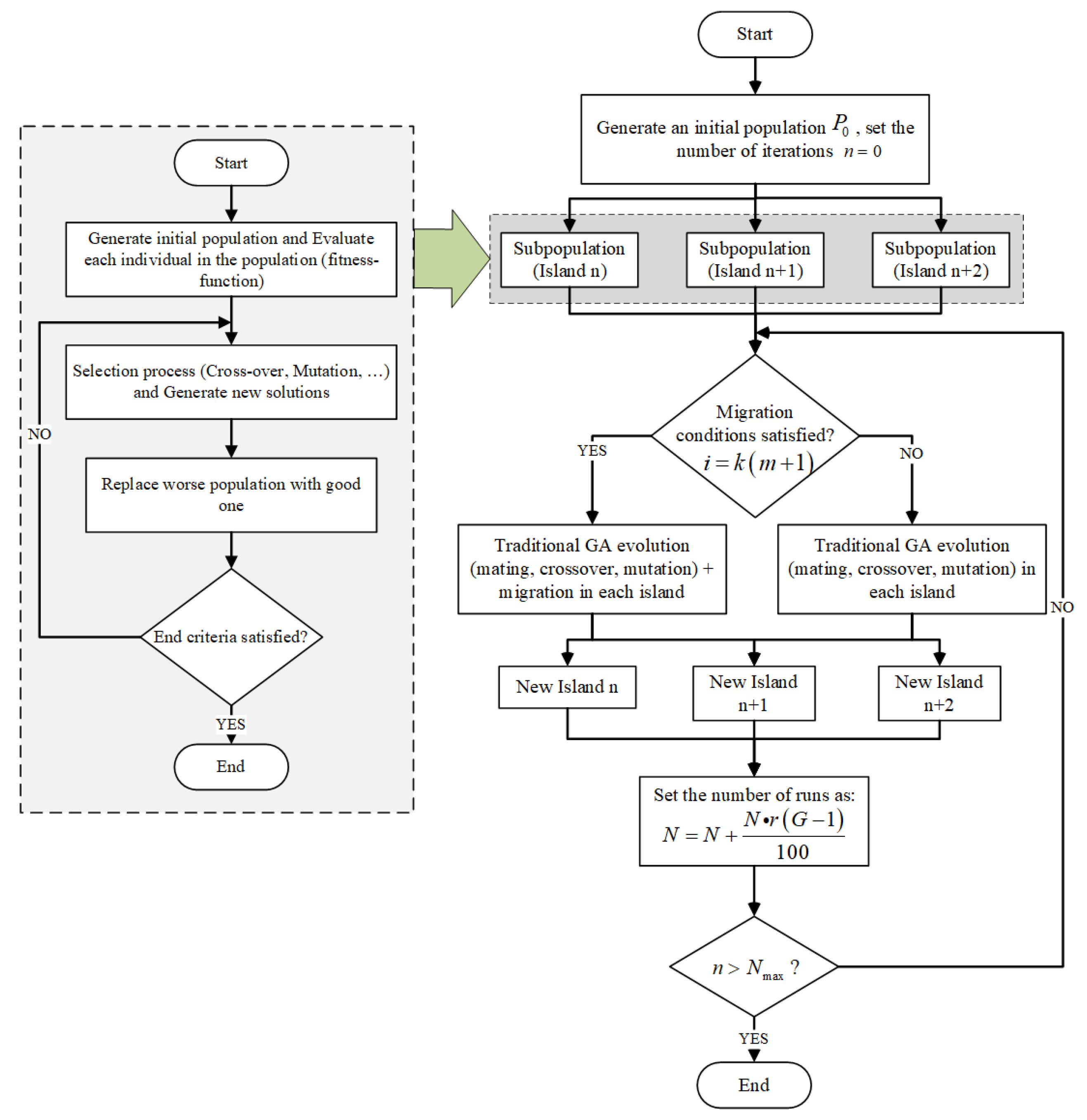
The following methodology was used in the study. Firstly, the matching parameters of the emergency rescue vehicle is achieved by theoretical analysis. Secondly, the matched parameters are optimized using a combined optimization methods of multi-island genetic algorithm (MIGA) and non-linear programming quadratic Lagrangian (NLPQL) methods to determine the dynamic performance of the energy source power output and the battery SOC according to the power request from the driver input. Finally, the optimized matched parameters are classified into different types of emergency rescue vehicles. The proposed method adopted in this study is comprised of the discriminant and Gaussian mixture methods to distinctly classify the optimized matched parameters with a linear kernel function in SVM classification.

The research organization is summarized as follows. Section 2 presents the parameter matching theoretical analysis of the HE-ERV powertrain system. In Section 3, MIGA and NLPQL optimization methods are applied to the power source matched parameters. In Section 4, the support vector machines classification is presented and discussed for the optimized matched parameters. The optimization and classification results are presented and analyzed in Section 5. Finally, in Section 6, the conclusion is presented.

2. Parameter Matching of HE-ERV Powertrain System

2.1. Powertrain Modeling of HE-ERV

In this study, a power-split parallel hybrid electric emergency rescue vehicle is selected as the research object to study the parameter matching and optimization of the hybrid powertrain system. The powertrain system consists of the engine, electric motor, generator, DC–DC converter, battery pack, planetary gear, transmission, and control units. The powertrain configuration is shown in Figure 1. The vehicle basic parameters used in this study are shown in

Table 1. Basic parameters of the HE-ERV.

Parameter Properties	Parameter Value	Parameter Unit
Vehicle parameters
Mass of vehicle $\left(m\right)$	9750	kg
Full mass of vehicle $\left(m_f\right)$	12,495	kg
Wheelbase $\left(L\right)$	2700	mm
Wheel radius $\left(r\right)$	465	mm
Frontal area $\left(A\right)$	6.8	m2
Drag coefficient $\left(C_D\right)$	0.64
Rolling resistance coefficient $\left(f\right)$	0.01
Driveline efficiency $\left({\eta }_t\right)$	0.9
Engine parameters
Peak power	150	kW
Peak torque	200	Nm
Maximum power speed	2350	RPM
Maximum torque speed	1400–1600	RPM
Electric motor parameters
Rated/Peak power	70/150	kW
Rated/Peak torque	210/1090	Nm
Generator parameters
Rated/Peak power	25/35	kW
Rated/Peak torque	80/150	Nm
Battery parameters
Capacity	48	Ah
Voltage	400	V

.

2.2. Parameter Matching of HEV Key Components

2.2.1. Vehicle Performance Indicators

In this study, the vehicle dynamic standard is the most important performance indicator. Under extensive pondering of the scope of performance, the vehicle performance indicators designed are shown in

Table 2. Vehicle performance indicators.

Description	Target Value	Unit
Maximum speed	90	km/h
Maximum gradeability	15	%
0–50 km/h	20	s
Maximum climbing slope	20	%
100 km fuel consumption	32	L/100 km
Driving range	100	km

.

2.2.2. Parameter Matching of Power Sources

In a typical hybrid electric vehicle and depending on the powertrain configuration, the electric motor is required to provide the peak power to the driveline system. In a hybrid mode, the power demand of the engine, which is determined according to the acceleration performance and the peak power of the electric motor, is the focal point to be considered. To ensure that the engine has the ability to guarantee the balance of battery power under the whole working condition, the power output of the engine needs to be greater than the average power under the working condition. In contrast to the hybrid mode is the purely electric mode of HEV, when the electric motor is the sole provider of energy sources [43,44]. Hence, in determining the maximum speed and acceleration, the demanded power of the drive cycle should meet the power demand of the electric motor.

Engine Parameter Matching

The engine power demand at maximum speed should meet the power requirements of the vehicle driving at the maximum speed, as follows:

$$P_{eng\_dem1}=\frac{v_m}{3600{\eta }_t}\left(mgf+\frac{C_{D}A{v}_{max}^2}{21.15}\right)$$

(1)

The engine power demand corresponds to the acceleration performance, as follows:

$$\begin{gathered} P_{eng\_dem2}=\frac{1}{3600{\eta }_t{t}_m}{{\displaystyle \int }}_0^{t_m}\left(mgf+\frac{C_{D}Av{t}^2}{21.15}+\delta m\frac{dv\left(t\right)}{dt}\right) \\ v\left(t\right)=v_m{\left(\frac{t}{t_m}\right)}^{0.5} \end{gathered}$$

(2)

where $\delta$ is the conversion coefficient of vehicle rotating mass, $t_m$ is the acceleration time, and $v_{max}$ is the maximum vehicle speed.

Electric Motor Parameter Matching

In electric motor peak power matching analysis, according to the requirements of the target design as shown in Table 2, the peak power demand is expressed as follows:

$$P_{em\_dem}=\frac{\frac{\delta m}{2t_b}\left(v_n^2+v_f^2\right)+\frac{2}{3}mgf{v}_f+\frac{1}{5}{\rho }_a{C}_{D}A{V}_f^3}{1000\eta }$$

(3)

where $v_n$ is the base speed of the electric motor, and $v_f$ is the final speed of acceleration.

Battery Parameter Matching

The battery pack is the energy storage unit of the HEV; hence, the peak discharge power has to meet the requirements of the motor, and the battery capacity has to meet the requirements of the driving range of the vehicle. In order to determine the maximum power and number of battery groups during the operation of the vehicle, the power provided by the battery must meet the requirements of the peak power of the electric motor. The maximum power of a single battery is expressed as follows:

$$P_{b\_max}=\frac{2E^2}{9R_{int}}$$

(4)

where $E$ is the electromagnetic force of the cell, and $R_{int}$ is the internal resistance of the cell. The number of batteries is, thus, calculated as follows:

$$n_p=\frac{P_{em\_max}}{P_{b\_max}{\eta }_{em}{\eta }_{em,c}}$$

(5)

where $P_{em\_max}$ is the peak power of the electric motor, $P_{b\_max}$ is the maximum power achieved by a single battery, ${\eta }_{em,c}$ is the efficiency of the electric motor controller, and ${\eta }_{em}$ is the efficiency of the electric motor.

According to the targeted driving range of the vehicle, the total energy required is expressed as follows:

$$W_{ess}=\frac{U_{ess}C}{1000}$$

(6)

where $W_{ess}$ is the total energy required, $U_{ess}$ is the voltage of the battery park, and $C$ is the battery capacity.

The energy consumed by the vehicle at a constant speed $u_a$ is given as follows:

$$\begin{array}{c}W=\frac{P}{u_a}\\ P=\frac{1}{3600{\eta }_t}\left(mgf{u}_a+\frac{C_{D}A{u}_a^3}{21.15}\right)\end{array}$$

(7)

The battery capacity can, thus, be expressed as follows:

$$C=\frac{1000S}{3600{\eta }_t{\xi }_{SOC}{U}_{ess}}\left(mgf+\frac{C_{D}A{u}_a^2}{21.15}\right)$$

(8)

where ${\xi }_{SOC}$ is the discharge depth of the battery during discharge, which can also represent the performance of the battery in different stages of its life cycle.

2.3. Selection of HEV Key Components

According to the parameter matching equations for the energy sources of the HEV powertrain to meet the vehicle speed of 90 km/h,

Table 3. Matched parameters of HEV key powertrain components.

Powertrain Components	Characteristic’s Evaluation	Value	Units
Engine	Power demand for maximum speed	≥50.62	kW
	Power demand for climbing power	≥142.06	kW
	Power demand for acceleration performance	≥71.55	kW
Electric motor	Peak power	≥138.72	kW
	Rated power	≥52.14	kW
Battery	Maximum output power of a single battery	2.832	kW
	Number of battery sets	24

shows the selected parameter values according to the characteristic’s evaluation. Considering the power losses of each component and the demand of other components, 10–20 kW is added to the selection to create a margin to ensure a more accurate performance.

3. Optimization of Power-Split PHEV (PS-PHEV) Parameters

The parameter matching of power-split parallel hybrid electric vehicles affects the vehicle’s performance, fuel economy, and emissions, so it is very important to consider during the initial stages of HEV design. In modern times, parameter matching of a HEV is primarily a non-linear optimization problem involving multi-parameter and multi-object optimization under certain simulation environments. This study describes the parameter optimization of the power-split PHEV system from the following three perspectives: a mathematical model, simulation environment, and optimization algorithm.

3.1. Mathematical Modeling of PS-PHEV

With reference to Figure 1, a quasi-static modeling approach is adopted for the energy analysis of the powertrain system. The inertia and dynamics of the engine, electric machines, gears, and shaft are ignored [45].

3.1.1. Engine Model

The torque at the wheels is expressed as follows:

$$T_{p\_w}=g_{fd}·\left(T_r+T_{em}\right)$$

(9)

where $T_{em}$ is the electric motor torque, $T_r$ is the planetary ring torque, and $g_{fd}$ is the final drive ratio.

The torque at the engine and generator are given as follows:

$$\begin{array}{c}{T}_{eng}=\left(1+\rho \right)T_r\\ T_{gen}=\rho ·T_r\end{array}$$

(10)

where $\rho =N_s/N_r$.

In this instance, the kinematics constraint is expressed as follows:

$$\left(1+\rho \right){\omega }_{eng}=\rho {\omega }_{gen}+{\omega }_{em}$$

(11)

Furthermore, since there is a fixed gear between the ring/EM shaft and the wheels, the EM is directly proportional to the wheel speed, which is also proportional to the vehicle’s longitudinal speed. This can be seen as follows:

$${\omega }_{em}=g_{fd}\frac{v_{veh}}{r}$$

(12)

The engine speed is, thus, related to the generator and vehicle speed, as in the following:

$${\omega }_{eng}=\frac{\rho {\omega }_{gen}}{1+\rho }+\frac{g_{fd}{v}_{veh}}{\left(1+\rho \right)r}$$

(13)

where $v_{veh}$ is the vehicle speed, and $r$ is the wheel radius.

3.1.2. Electric Motor Model

In this study, the optimization scheme is set along two degrees of freedom, namely the engine torque and generator speed. In relation to the engine torque and speed, the generator and electric motor power is given as follows:

$$\begin{array}{c}{P}_{gen}=\frac{{\omega }_{gen}·\rho ·T_{eng}}{1+\rho }\\ P_{em}={\omega }_{em}{T}_{em}\end{array}$$

(14)

The total electric power at the battery is as follows:

$$P_{batt}=P_{em}+P_{gen}$$

(15)

$$P_{gen}=\left\{\begin{array}{cc}{\eta }_{gen}{P}_{gen}& if P_{gen}<0\\ \frac{P_{gen}}{{\eta }_{gen}}& if P_{gen}\ge 0\end{array}\right.$$

(16)

$$P_{em}=\left\{\begin{array}{cc}{\eta }_{em}{P}_{em}& if P_{em}<0\\ \frac{P_{em}}{{\eta }_{em}}& if P_{em}\ge 0\end{array}\right.$$

(17)

3.1.3. Battery Model

The evolution of the battery state of charge in a system dynamic equation is a representation of the state itself and the control input $T_{em}$ and $T_{gen}$. The battery model is as follows:

$$\dot{SOC}=-\frac{1}{{\eta }_{coul}^{sign\left(I\left(t\right)\right)}{Q}_{nom}}\left[\frac{V_{oc}\left(SOC\right)}{2R_o\left(SOC\right)}-\sqrt{\frac{V_{oc}\left(SOC\right)}{2R_o\left(SOC\right)}-\frac{P_{batt}}{R_o\left(SOC\right)}}\right]$$

(18)

where $Q_{nom}$ is the nominal charge capacity, and ${\eta }_{coul}$ is the coulombic efficiency.

Introducing the electrochemical energy variation in place of the state of charge gives the following:

$$E_{ech}=E_{batt}·\left(SOC\left(t_0\right)-SOC\left(t\right)\right)$$

(19)

where ${\mathit{E}}_{\mathit{batt}}={\mathit{V}}_{\mathit{oc},\mathit{nom}}{\mathit{Q}}_{\mathit{nom}}{\mathit{\eta }}_{\mathit{coul}}$. The system dynamic is, therefore, expressed as follows:

$${\dot{E}}_{ech}=P_{batt}=-E_{batt}\dot{SOC}$$

(20)

The total electric power at the battery is as follows:

$$P_{batt}=P_{em}\left(T_{em},{\omega }_{em}\right)+P_{gen}$$

(21)

where $P_{em}\left(T_{em},{\omega }_{em}\right)$ is the electrical power required by the electric motor to produce the torque $T_{em}$ at speed ${\omega }_{em}$.

3.2. Simulation Environment

The system optimization problem of HEV is generally based on the optimization of the simulation environment. The objective function and constraint functions of the optimization model are not the explicit expression of design variables. In this case, the objective function, constraint function, and design variables are implicit relationships determined by the simulation system. This implicit mathematical relationship depends on the vehicle simulation system used, the dynamic multi-modal and nonlinear response of the vehicle system. In this study, MATLAB programming and AVL Cruise is used to call out the vehicle Simulink model to obtain the energy control variables from the matched parameters. Figure 2 shows the extracted vehicle model used in the simulation.

3.3. Optimization Algorithm

Genetic algorithms (GAs) have been widely used in the optimization of HEVs as a global optimum algorithm solution. However genetic algorithms achieve local optimization quickly and converge slowly. For parameter matching optimization in this study, qulti-island GA (MIGA) and non-linear programming using a quadratic Lagrangian (NLPQL) method are proposed to overcome the disadvantages of slow convergence speeds and stagnation behavior. The multi-island genetic algorithm is an improvement of the parallel distributed genetic algorithm; it is suitable for global optimization design of univariate function and has a better global solving ability and computational efficiency than a traditional genetic algorithm [46]. Its calculation process is shown in Figure 3. Firstly, an initial population P_0 is randomly generated and divided into several sub-populations, which are called “islands”. Secondly, the selection, crossover, and mutation operations of the traditional genetic algorithm are carried out on each island. If the migration conditions are met, the genetic algorithm can be migrated from one subpopulation to another subpopulation to continue the evolution of the genetic algorithm. The periodic migration operation of the multi-island genetic algorithm keeps the diversity of optimization solutions and improves the optimization speed, which can solve the problem of premature convergence of traditional genetic algorithm, making it easy to fall into the local optimum to a certain extent [47]. Finally, it converges to the optimal parameters through continuous generation selection, and the optimization process ends when the number of genetic generations n reaches the maximum $N_{max}$. In essence, the multi-island genetic algorithm (MIGA) divides an island into sub-islands that compute in the form of a traditional genetic algorithm. Each sub-island population executes the process of selection, cross-over, and mutation, and periodically migrates to different sub-islands. With the continuous migration from different sub-islands, MIGA becomes efficient in limiting ill-timed convergence, and makes it possible to merge with other algorithms.

In addition to its ability to solve local numerical optimum problems, NLPQL can also be used to solve a problem that has nonlinear constrained optimization constraints. With NLPQL and the genetic algorithm together, during the early phase, the genetic algorithm can be used as a powerful global search technique. In the later stage, NLPQL is used to deal with the overall pre-optimal solution. In order to converge to the local solution, the latter part of the NLPQL capability of local search is fully utilized. Finally, the multi-island genetic algorithm is used to optimize the matched parameters, taking into consideration the battery, engine, and electric motor. In this instance, the fuel economy, emissions, and battery SOC are taken as the design objectives. The MIGA optimization process is shown in Figure 3, and the total population size of the multi-island genetic algorithm is 300, the number of islands is 30, the total evolutionary algebra is 150, the inter-island mobility is 0.4, the migration interval algebra is 5, the crossover rate is 0.95, and the mutation rate is 0.05.

3.4. Determination of Objective Function

The objective of parameter optimization of a power-split parallel hybrid system is to improve the fuel economy of the whole vehicle as far as possible under the premise of satisfying the design indexes of dynamic performance and the performance constraints of each component. Hence, the objective function $f\left(x\right)$ of parameter optimization is as follows:

$$\left\{\begin{array}{cc}f\left(x\right)=\min \left(fuel\left(x\right)+\alpha \ast ecom\left(x\right)\right)& x\in \mathsf{\Omega }\\ h_i\left(x\right)\le 0& i=1,2,\cdots ,N\end{array}\right.$$

(22)

where $fuel\left(x\right)$ is fuel consumption, $ecom\left(x\right)$ is electrical energy consumption, $\alpha$ is the conversion coefficient of oil to electricity, $x$ is the vector of planetary unit design parameters and control strategy parameters to be optimized, $\mathsf{\Omega }$ is the space of possible solutions, $h_i\left(x\right)\le 0$ is the dynamic constraint condition, and $N$ is the number of constraints. To ensure the balance of battery power in the optimization process of the system, the limiting conditions shown in Equation (25) are set, that is, the optimization parameters should ensure that the system’s electric power changes less, and $\epsilon$ is the upper limit of electric power changes.

$$\left|Ele\left(x\right)\right|<\epsilon$$

(23)

4. Support Vector Machine Classification (SVM)

The support vector machine (SVM) offers a combination of parametric and non-parametric characteristics. In addition to being resistant to dimensionality, they can approximate complex functions and are more prone to overfitting. Support vector classification is a preferential method based on the given constraints. Thus, SVMs are used in machine learning to separate data into categories. The technique aims to divide data into two or more categories by using a hyperplane [48,49]. The SVM classifier is represented based on the following mathematical programming model:

$$T=\left\{\left(x_1,y_1\right),\cdots ,\left(x_l,y_l\right)\right\}\in {\left({\Re }^n\ast \mathcal{Y}\right)}^l$$

(24)

where $x_i\in {\Re }^n,y_i\in \mathcal{Y}=\left\{1,-1\right\},i=1,2,\cdots ,l$, and $x_i$ is the eigenvector.

The SVM’s linear soft margin algorithm is used to solve the following primal quadratic programming problem:

$$\begin{gathered} \underset{w,b,\xi }{\min }\frac{1}{2}{||w||}_2^2+C{\displaystyle \sum }_{i=1}^m{\xi }_i \\ s.t. y_i\left(w^T{x}_i+b\right)\ge 1-{\xi }_i and {\xi }_i\ge 0 for all i=1,2,\cdots ,l \end{gathered}$$

(25)

where $C$ is a penalty parameter added to maximize the margin and minimize the classification error, and ${\xi }_i$ are the slack variables. The goal is to find an optimal separating hyperplane.

$$w^{T}x+b=0$$

(26)

where $x\in {\Re }^n$. The Wolfe dual of (27) can be expressed as follows:

$$\begin{gathered} \underset{\alpha }{\min }\frac{1}{2}{\displaystyle \sum }_{i=1}^j{\displaystyle \sum }_{j=1}^l{\alpha }_i{\alpha }_j{y}_i{y}_{j}K\left(x_i,x_j\right)-{\displaystyle \sum }_{j=1}^l{\alpha }_j \\ s.t. {\displaystyle \sum }_{i=1}^l{\alpha }_i{y}_i=0, and 0\le {\alpha }_i\le C for all i=1,\cdots ,l. \end{gathered}$$

(27)

Taking ${\alpha }^{\ast }$ as the positive component of $0<{\alpha }_j^{\ast }<C$, and calculate the threshold as follows:

$$\begin{gathered} w={\displaystyle \sum }_{i=i}^l{\alpha }_i^{\ast }{y}_i{x}_i, \\ b=\frac{1}{N_{sv}}\left(y_j-{\displaystyle \sum }_{i=1}^{N_{sv}}{\alpha }_i^{\ast }{y}_{i}K\left(x_i-x_j\right)\right) \end{gathered}$$

(28)

where ${\alpha }^{\ast }={\left({\alpha }_1^{\ast },\cdots ,{\alpha }_l^{\ast }\right)}^T$ is the optimal solution, $N_{sv}$ represents the number of support vectors such that $0<\alpha <C$, and $K$ is the linear kernel, and it is expressed as $K\left(x_i,x_j\right)=x_i^T x_j$. A new sample is classified as $+1$ or $-1$ according to the final decision function.

$$f\left(x\right)=sgn\left(\left(w·x\right)+b\right)$$

(29)

4.1. Nonparallel Support Vector Machine

A linear nonparallel SVM [50,51] consists of two hyper-planes which can be solved by the following:

$$\begin{array}{c}\underset{w_{+}}{\min }\frac{1}{2}||w_{+}||{}^2+C_1{e}_{+}^T\left({\eta }_{+}+{\eta }_{+}^{\ast }\right)+C_2{e}_{-}^T{\xi }_{-}\\ s.t. \left\{\begin{array}{c}A{w}_{+}+b_{+}{e}_{+}\le \epsilon e_{+}+{\eta }_{+},\\ -A{w}_{+}-b_{+}{e}_{+}\le \epsilon e_{+}+{\eta }_{+}^{\ast },\\ \begin{array}{c}B{w}_{+}+b_{+}{e}_{-}\le e_{-}+{\xi }_{-},\\ {\eta }_{+}\ge 0,{\eta }_{+}^{\ast }\ge 0,{\xi }_{-}\ge 0\end{array}\end{array}\right.\end{array}$$

(30)

and:

$$\begin{array}{c}\underset{w_{-}}{\min }\frac{1}{2}||w_{-}||{}^2+C_3{e}_{-}^T\left({\eta }_{-}+{\eta }_{-}^{\ast }\right)+C_4{e}_{+}^T{\xi }_{+}\\ s.t. \left\{\begin{array}{c}B{w}_{-}+b_{-}{e}_{-}\le \epsilon e_{-}+{\eta }_{-},\\ -B{w}_{-}-b_{-}{e}_{-}\le \epsilon e_{-}+{\eta }_{-}^{\ast },\\ \begin{array}{c}A{w}_{-}+b_{-}{e}_{+}\ge e_{+}+{\xi }_{+},\\ {\eta }_{-}\ge 0,{\eta }_{-}^{\ast }\ge 0,{\xi }_{+}\ge 0\end{array}\end{array}\right.\end{array}$$

(31)

where $c_1, c_2, c_3, c_4, \epsilon$ are non-negative parameters and ${\eta }_{+},{\eta }_{+}^{\ast },{\xi }_{+}$ and ${\eta }_{-},{\eta }_{-}^{\ast },{\xi }_{-}$ are slack variables of appropriate dimensions, and $e_{+}$ and $e_{-}$ stand for an all-one vector of appropriate dimensions. Applying a sequential minimization optimization, the corresponding dual formulations can be solved, as follows:

$$\begin{array}{c}\min \frac{1}{2}{\left(\alpha -{\alpha }^{\ast }\right)}^{T}A{A}^T\left(\alpha -{\alpha }^{\ast }\right)+{\left(\alpha -{\alpha }^{\ast }\right)}^{T}A{B}^T\beta +\frac{1}{2}{\beta }^{T}B{B}^T\beta +\epsilon e_1^T\left(\alpha +{\alpha }^{\ast }\right)-e_2^T\beta \\ s.t. \left\{\begin{array}{c}{e}_1^T\left(\alpha -{\alpha }^{\ast }\right)+e_2^T\beta =0,\\ 0\le \le c_1{e}_1, 0\le \stackrel{\ast }{i}\le c_1{e}_1\\ 0\le \mathrm{fi}\le c_2{e}_2\end{array}\right.\end{array}$$

(32)

Additionally, Equation (33) is as follows:

$$\begin{array}{c}\min \frac{1}{2}{\left(\alpha -{\alpha }^{\ast }\right)}^{T}B{B}^T\left(\alpha -{\alpha }^{\ast }\right)-{\left(\alpha -{\alpha }^{\ast }\right)}^{T}B{A}^T\beta +\frac{1}{2}{\beta }^{T}B{B}^T\beta +\epsilon e_1^T\left(\alpha +{\alpha }^{\ast }\right)-e_2^T\beta \\ s.t. \left\{\begin{array}{c}{e}_1^T\left(\alpha -{\alpha }^{\ast }\right)+e_2^T\beta =0,\\ 0\le \le c_3{e}_1, 0\le \stackrel{\ast }{i}\le c_3{e}_1\\ 0\le \mathrm{fi}\le c_4{e}_2\end{array}\right.\end{array}$$

(33)

where $\alpha , {\alpha }^{\ast }, \mathrm{and} \beta$ are defined as non-negative Lagrange multipliers, one for each classification constraints.

The framework for the SVM classification for the matched parameters of emergency rescue vehicles is shown in Figure 4. This method consists of three steps, namely test and support vectors, mapped and dot product, and finally the evaluation of classification outputs.

4.2. Performance Evaluation and Dataset

Fifty datapoints were retrieved from each of the optimized matched parameters of the energy source component from ten emergency rescue vehicles and summed up to one hundred datapoints. Due to different design objectives and targets, the research can choose the energy source components that fits the purpose. In order to validate the datapoints from the optimized matched parameters, a reference dataset, namely the ‘Car Evaluation dataset’, is used to verify the classification pattern of the optimized matched parameters for the ERVs, which can be retrieved from https://archive.ics.uci.edu/ml/datasets.php (accessed on 15 June 2022). Further validation and a comparison study with previous research was conducted. The SVM classification model was developed in MATLAB software.

4.3. Gaussian Mixture Model (GMM)

The Gaussian mixture model (GMM) provides a good approximation of the originally observed feature probability density functions by a mixture of weighted Gaussians. This considers a set of feature vectors $X=\left\{x_1,x_2,\cdots ,x_T\right\}$, where $x_T$ is a feature vector of discrete time $t\in \left[1,2,\cdots ,T\right]$. The mixture coefficients were computed using an expectation maximization (EM) algorithm. Each density is modeled in a separate GMM, and the decision is made on the basis of the maximum likelihood model. In this study, diagonal covariance GMM is used as a baseline classifier. For a D-dimensional feature vector, $x$, the mixture density used for the likelihood function can be written as follows:

$$p_{GMM}\left(\left.X\right|w,\mu ,\mathsf{\Sigma }\right)={\displaystyle \sum }_{k=1}^K{w}_{k}N\left(x^{\left(n\right)}\left|{\mu }_k,{\mathsf{\Sigma }}_k\right.\right)$$

(34)

$$N\left(x,{\mu }_k,{\mathsf{\Sigma }}_k\right)=\frac{1}{{\left(2\pi \right)}^{\raisebox{1ex}{$d$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\left|\mathsf{\Sigma }\right|}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\ast exp\left[-\frac{1}{2}{\left(x-\mu \right)}^T{\mathsf{\Sigma }}^{-1}\left(x-\mu \right)\right]$$

(35)

where $w_k$, ${\mu }_k$, and ${\mathsf{\Sigma }}_k$ are the mixture weights, mean vector, and covariance matrix, respectively. The mixture weights should satisfy the condition that ${{\displaystyle \sum }}_{i=1}^M{w}_i=1$. The maximum likelihood function for maximizing the mixture density is, thus, expressed as follows:

$$\ln p\left(\left.X\right|w,\mu ,\mathsf{\Sigma }\right)={\displaystyle \sum }_{n=1}^M\ln \left({\displaystyle \sum }_{k=1}^K{w}_k\mathcal{N}\left(x^{\left(n\right)}\left|{\mu }_k,{\mathsf{\Sigma }}_k\right.\right)\right)$$

(36)

5. Optimization Results and Analysis

5.1. Optimization Results

With the purpose of enhancing the robustness of the parameter matching technique, the NEDC driving cycle is selected for the vehicle model. The characteristic parameters of the drive cycle, namely mileage, average speed, driving time, maximum speed, and acceleration (10.93 km, 32.21 km/h, 1184 s, 120 km/h, and 1.06 m/s²) are extracted to compute the energy maximum power demand. As shown in Figure 5, the positive and negative peak powers are recorded as 27.18 and −15 kW, respectively.

In this study, the power request responsible for starting the vehicle is used to simulate the optimization of the parameter matching of the PS-PHEV energy source components. In order to obtain the optimal solution, the objective function corresponding to the weights and power request are analyzed. Considering the fuel consumption and after effect of the power output from the engine and motor, the following algorithm is used to find the optimal solution:

$$F_{fuel}=\min \left(f_{eng}·w_1+f_{mot}·w_2+f_{req}·w_3\right)$$

(37)

where $w_1, w_2, w_3$ are the allocated weights of 0.9, 0.9, and 1, respectively. The iteration process for the power request in relation to the fuel consumption is shown in Figure 6.

It can be seen that the fitness function converges after the 280th iteration. The parameters of the energy source components are optimized simultaneously in the optimization algorithm. The individual output of the first layer is known as the population, and it generates its own population in the second layer. This process re-calibrates until it reaches the objective function and converges. Although the fuel consumption gradually converged with minimal fluctuations, MIGA showed a stronger global search capability, and the local search capability of NLPQL can be demonstrated by the number of generated iterations.

The logic of parameter matching should be checked by comparing the simulation results of dynamic vehicle performance and economy with the design objectives of the vehicle model in AVL Cruise. Based on the dynamic and economic evaluation indexes of the vehicle, the performance of acceleration, climbing, and energy consumption during the cycle from 0 to 50 km/h is simulated. In order to evaluate vehicle dynamic performance, acceleration time, climbing grade, and maximum speed were used. To optimize the energy strategy for the matched parameters at the requested power at the wheels, the battery SOC, fuel consumption, and emissions are evaluated. In this instance, the initial SOC is modified in order to obtain the same value at the end of the drive cycle as at the beginning.

Figure 7 shows the evolution of the battery SOC in each case. The simulation results indicate that the optimized results fluctuate according to the requested power at the wheel, showing performance degradation of the battery SOC by 13.83%, 28.25%, and 52.6%, respectively. From the figure, it can be seen that, the higher the power request, the greater the battery usage, which will affect the battery’s state of health. Figure 8 shows the impact of the power request value on fuel consumption. It can be seen that the fuel consumption is a little lower when we increase the use of the purely electric mode i.e., when using a higher power request value. This can be explained by the fact that the less we use the engine, the more we increase its power when we use it. Finally, the engine is used at operating points where the engine has better efficiency. The impact on fuel consumption reaches 2% on the NEDC drive cycle with the extreme values of the power request.

Across the total fuel consumption of the different power requests with the NEDC drive cycle, the optimized value was reduced by 8.75% after optimization.

The fuel consumption after optimization decreased by 3.68%, CO emissions decreased by 17.56%, HC decreased by 7.89%, and NOx decreased by 6.56% as shown in Figure 9. In line with the optimization of the matched parameters, the comparison of the matching parameters and the optimized parameters is shown in

Table 4. Comparison of parameter matching optimization results.

Optimization Parameters	Before Optimization	After Optimization
Engine power (kW)	142.06	131.64
Electric motor rated power (kW)	52.14	57.26
Battery capacity (%)	48	52
Fuel consumption (L/100 km)	30.27	27.62

. It can be seen that though the engine power is reduced, there is a slight increment in the rated power of the electric motor and an increased battery capacity.

The characteristic performance of the PS-PHEV of the matched parameters after optimization is shown in

Table 5. Characteristic performance of single-axis power-split PHEV after optimization.

Description		Value
Characteristic conditions	Maximum velocity (km/h)	93.85
	Maximum gradeability (%)	18.48
	Acceleration time 0–50 km/h	17.56
Driving cycle	Path tracking absolute error (km/h)	2.05
Fuel consumption	Fuel consumption of driving cycle (L/100 km)	26.25
	Total fuel consumption of driving cycle (L/100 km)	27.63
Rate of fuel saving	Rate of fuel saving of driving cycle (%)	35.82

. It can be seen that the dynamic performance of the vehicle performance indexes has been improved, the acceleration time between 0–50 km/h is reduced to 17.56 s, and the maximum gradeability increased to 18.48%. Concerning the total fuel consumption, a 3.58% reduction was recorded against the theoretical value after optimization, and the fuel saving for the NEDC drive cycle is 35.82%.

5.2. SVM Classification Results and Discussion

For the Gaussian mixture model (GMM) classifier, the “gmdistribution” function was used to train the model by maximum likelihood, using the Expectation-Maximization algorithm. The testing method was based on minimum distance classification, and 100 Gaussian Mixtures were used for the simulation.

On average, 500 feature vectors for each matched parameter were obtained. The system was trained in two steps: in the first step, 250 feature vectors for computing the target GMM for computing the background model. In the second step of training, using these models we computed the 100 scores for 100 segments of parameter data in which 50 were from the matched electric motor parameters and 50 were from matched engine parameters. Based on these 100 scores, a single threshold for individual matched parameters that provided the minimum equal error rate was selected. Figure 10 shows the GMM classifier output for the electric motor and engine power of the matched parameters. It can be seen that motor and engine power are segregated and fairly distributed according to the allocated mixture weights.

Using the combination of the weights and matched parameters (motor and engine power output) of the emergency rescue vehicle as the test vectors, the discriminant method of SVM classification is used to classify the motor and engine power output according to three categories of a foam fire truck emergency rescue vehicle (FFT-ERV).

Figure 11 shows that the classification of the average motor/engine power output in small, medium, and heavy FFT-ERV were recorded as 60/52 kW, 145/134 kW, and 142/145 kW, respectively, whilst Figure 12 shows the classification of both weight and quantity of small, medium, and heavy FFT-ERV. The output distribution between the vehicles was 19, 32, and 46. In comparison to [50,52], an improved accuracy of 97% was achieved when two non-parallel hyperplanes were used to distinguish between categories.

Furthermore, a SVM classification was carried out on the matched power output required for the onboard system of an emergency rescue vehicle. The objectives indexes used were the range of power output from the vehicle energy source components and the total input power required by the onboard system. Figure 13 shows the power input from the ERV for communication and fire truck emergency rescue vehicles. The classification indexes are shown in

Table 6. SVM classification of emergency rescue vehicle.

Name	Number of Vehicles	Onboard System Devices	Total Power Input (kW)
Communication ERVs	13	Transmitters, Digital communication systems, Electric motor	20–30
Fire truck ERVs	13	Electric pumps and motors	35–45

. It can be seen from the figure that the onboard system’s power input of the communication ERVs requires a lesser amount of power when compared to the onboard system of the fire truck ERVs.

6. Conclusions

According to the structural characteristics, design, and classification of HEV to meet the performance requirements, it is necessary to match and optimize the energy source parameters to obtain better vehicle performance. This study is summarized as follows:

• A simulation model of PS-HEV is built in the AVL Cruise platform, which is used to establish the corresponding HEV power system, vehicle maximum speed, acceleration, and climbing performances. The matching results were simulated under NEDC driving conditions, and the rationality of the vehicle structure and parameter matching were proved from the perspective of power performance and fuel economy.
• Using this model, an optimization problem was formulated to minimize fuel consumption and emissions. Multi-island GA and NLPQL are used to optimize the matched parameters, which included the dynamic and economic performances. In the process of simulation, the optimal range for the requested power varied between 2.17 and 3.85% for 10, 12.5, and 15 kW, while other parameters are improved to varying degrees.
• Finally, SVM classification and a Gaussian mixture model is employed for classifying the optimized match parameters, and the results are presented. The classifications are carried out according to the optimized matched parameters and classified to the different types of a particular emergency rescue vehicle. Additionally, the power required for the onboard system of an emergency rescue vehicle is used to classify the peculiar type of emergency rescue vehicle.

The SVM classification discriminant method allowed for the detection and categorization of optimized matched parameters in specifying the emergency rescue vehicle from the performance indicators of a vehicle.