Abstract
The regenerator plays an extremely important role in the Stirling circulation. A grid regenerator can be used for inverse Stirling machines at room temperature due to its low flow resistance. This paper proposes a hexagonal grid regenerator to theoretically explore heat transfer properties in the inverse Stirling cycle and establishes an approximate analytical model to analyze the effect mechanism of working frequency, thermal diffusivity and wall thickness on the oscillation flow. The results show that the wall thickness is one of the key factors affecting the equivalent heat transfer coefficient. Specifically, too small or too large wall thickness increases the instability of the heat transfer process. The ultimate wall thickness is determined by the equivalent heat transfer coefficient and thermal penetration depth, whose optimal value ensures not only sufficient heat exchange but also the full utilization of materials. With the increase in frequency, heat exchange performance is improved monotonously. Therefore, high–frequency operation can improve the heat exchange performance of the regenerator. In addition, an optimization criterion for the size of regenerator with the specific capacity of heat transfer as the objective parameter is proposed based on the equivalent heat transfer coefficient. The optimal parameters were obtained when relative thickness was set as 0.8 mm and the equivalent heat transfer coefficient was up to 104–105 W/m2·K indicating that the grid regenerator has broad application prospects in the inverse Stirling cycle.
1. Introduction
The refrigeration and heating of the inverse Stirling cycle at room temperature has been proved to have the advantages of energy saving, environmental protection and high efficiency and has always been one of the focuses of research. Compared with steam compression cycle technology, inverse Stirling cycle technology does not use a refrigerant and does not emit carbon dioxide. It is a perfect alternative to sustainable technologies in the future. At the same time, the theoretical efficiency of the inverse Stirling cycle is equivalent to the efficiency of the Carnot cycle, which is the maximum possible efficiency of any engine cycle technology under the specific temperature limit operation, which is unmatched by other technologies. For instance, the use of inverse Stirling cycle technology to develop air–conditioning compressors for pure electric vehicles has outstanding technical advantages; efficient and environmentally friendly inverse Stirling air conditioning technology is an important issue to overcome the short battery range of pure electric vehicles [1,2,3]. Hachem et al. studied a Stirling machine at room temperature and under normal pressure with air as the working medium. Their results show that the machine achieved the bi–directional function of cooling/heating by driving a crank slider mechanism and rotating counterclockwise/clockwise with the help of a motor [4,5]. Haywood studied the inverse Stirling cycle technology at ambient temperature (−233–313 K) and modified the Stirling engine with a 4α double–acting structure to provide the bi–directional function of heating and cooling. The COP value of the Stirling machine was up to 4.5 when the temperature at hot and cold ends was 293 K and 278 K, respectively [6].
The heat exchange performance of the regenerator, a key unit of energy conversion in Stirling cycle, has the most significant impact on the Stirling engine efficiency [7]. The temperature difference between hot and cold chambers of the Stirling engine is mostly more than 500 K. For instance, the temperature ratio of the two chambers of 40 HP and 4–235 engines is 691 K/71 K and 683 K/43 K, respectively. The temperature of the hot chamber at the Stirling heat pump at room temperature ranges from 290 K to 350 K, while that of the cold chamber from −250 K to 280 K, with a difference between the two of less than 100 K [8]. Compared with incomplete heat loss and axial thermal conductivity loss, the loss of flow resistance pressure drop can be ignored, while that of loss cannot [9].
The regenerator can be in the form of screen type [10], packing type [11], porous medium [12], parallel plate [13], pin–array stack [14,15], etc. Some new types of regenerators are also being developed, such as a novel freeze–cast regenerators [16].
At present, research mostly focuses on screen or packing regenerators, which have strong heat storage capacity but high flow resistance [17]. York found that no matter what stacking method was adopted, the average misalignment rate was 44–49%, and that flow resistance was mainly caused by such misalignment [18]. Dellali et al. experimentally studied the pressure, pressure drop, speed and friction coefficient of the pin–array stack regenerator under the condition of reciprocating flow, and found that pressure drop was related to frequency and might be mainly caused by the viscous effect arising from the increased speed with the increase in frequency [19]. Yuan et al. investigated the frequency–dependent heat transfer characteristics of the magnetothermal regenerator of the parallel plate and found that, different from steady–state flow, the convective heat transfer coefficient in the matrix of the parallel plate depended not only on the fluid velocity but also the operating frequency due to the oscillating flow in the regenerator. Compared with steady–state flow, the heat transfer coefficient varies from −17% to 68% [20]. Pan proposed a novel method to calculate the pressure drop loss in the regenerator of a VM refrigerator, and pointed out that the pressure drop loss in the regenerator would reduce refrigeration capacity in two ways: one was friction, that is, the pressure drop in the regenerator would be converted into heat, directly reducing refrigeration capacity, and the other was pressure drop in the regenerator that would reduce the pressure ratio at the cold end [21]. The advantage of pin–array stack regenerators can be more available for high frequencies, but in thermoacoustic engines and pulse tube refrigerators only [22].
Existing regenerators cannot meet the requirements of small temperature difference and low flow resistance, so it is necessary to design and develop a new type of regenerator to make the pressure drop small when the gas passes by while possessing excellent heat exchange performance [23]. Wang et al. developed a hexagonal tube grid regenerator based on additive manufacturing technology to reduce the flow resistance by 96.2% compared with screen regenerators under the same condition. Meanwhile, the accuracy of the theoretical analysis method under the condition of single blowing was verified by combining simulation and experimental methods [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Many studies focus on the optimization of wire diameter size of a wire mesh regenerator. For example, Boroujerdi et al. proposed a new relationship between heat transfer and pressure drop characteristics of a wire mesh regenerator to calculate the oscillating flow. According to the deduced relation, the thinner the wire, the greater the pressure drop and the higher the heat transfer rate [25]. At the same time, there are also some questionable suggestions on the selection of regenerative material. Compared with traditional metal materials, a rotary regenerator made of polymer is light in weight and has strong corrosion resistance, which can reduce the operating cost and maintenance time of the thermal system [26].
To sum up, there is little research on regenerators with small temperature difference and low flow resistance. The hexagonal tube grid regenerator (HTGR) proposed in this paper is a novel regenerator with small temperature difference and low flow resistance, which has been granted an invention patent (authorization number ZL202110300042.7). Its structural characteristics are similar to those of the circular tube bundle and the pin–array structure, but the geometric structure has better uniformity, which can reduce the flow resistance and make full use of the heat storage capacity of solid materials. The existing research gap is that the influence law of oscillatory flow frequency, solid material, structure size and wall thickness on the heat transfer performance of the HTGR is not clear at present. The idea for addressing these research gaps is: according to the structural characteristics of the HTGR, an approximate geometric model is established according to the theory of heat conduction, the analytical solution is further derived, and the numerical verification is carried out based on the N–S equation. The objective of this study is to reveal the temperature distribution and heat transfer performance of the HTGR under oscillating flow. According to the parameters of oscillating flow frequency, solid material, structure size and wall thickness, the optimal design procedure of the HTGR is then established.
Aiming at the above problems, this paper focuses on the heat conduction law, such as the equivalent heat transfer coefficient (EHTC) of temperature distribution, by taking oscillation frequency, grid geometry, and material thermal diffusivity as the variable, and finally determines the optimal design mainly from the following perspectives:
- According to the heat conduction theory under periodic boundary conditions, an analytical expression of temperature distribution in a single grid is established.
- The influence of oscillation frequency, grid geometry, material thermal diffusivity and other parameters on temperature distribution and EHTC is discussed to further demonstrate the superiority of the HTGR in the inverse Stirling cycle at room temperature.
- Taking the maximum specific volume heat transfer capacity (SVHTC) as the objective function and the oscillation frequency, grid geometry and material thermal diffusivity as variables, the methods for identifying the optimal solution are explored.
This work provides theoretical guidance and reference for the design and operation of an HTGR. This paper is structured as follows: Section 1 describes the current situation and main problems of regenerators used at room temperature at home and abroad; Section 2 simplifies the physical model of the HTGR; in Section 3, the one–dimensional quasi–steady temperature field of a single circular tube in cylindrical coordinates is solved and its analytical expression is obtained; and Section 4 studies the temperature distribution and its influencing factors, analyzes the heat transfer coefficient under oscillation [27], discusses the optimization of circular tube thickness under specific surface area, and finally gives the conclusion of this paper.
2. Physical Model of HTGR
An HTGR that met the requirements in small temperature difference and low flow resistance is designed based on additive manufacturing technology [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24], whose geometric model is shown in Figure 1.

Figure 1.
Physical model of HTGR (a) model (b) 3D–printed regenerator.
The grid is shaped like a hexagonal straight tube, which is a complex structure. In order to build an analytical model, the physical model of the grid was simplified. One of the grids was selected for research, and the regular hexagonal tube was equivalently converted into a circular tube, as shown in Figure 2. Figure 2a is the local section shape of the HTGR and Figure 2b is the physical model of a single grid. The heat exchange boundary of the inner tube wall is indicated by a solid line and the adiabatic boundary by the symmetric center line, or dotted line.
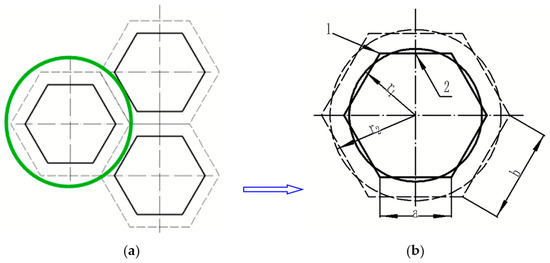
Figure 2.
Simplified diagram of single–grid physical model (a) HTGR section (b) single–grid physical model.
Assuming that the inner side length of the regular hexagonal tube is a, the outer length is b, the inner diameter of the circular tube is r1, and the outer diameter is r2, then the geometry of the equivalent transformation between the regular hexagonal tube and the circular tube is essentially the geometric space transformation between the inner and outer lengths of the hexagonal tube (a, b) and the inner and outer radius of the circular tube (r1, r2). Since the main function of a regenerator is to store and release heat by means of frequent heat transfer between the wall surface and thickness, the equivalent conditions should be: (1) heat transfer areas are equal to ensure the same heat transfer; (2) the volume–specific surface areas are equal to ensure the same heat storage.
The heat exchange area per unit tube length is equal:
The wall thickness of the unit tube length is equal to the volume:
Thus, the thermal conductivity of the HTGR can be studied by replacing the hexagonal tube with a circular tube (as shown in Appendix A).
A simplified model of a single circular tube is shown in Figure 3. Assumptions are made as follows:
- (1)
- The temperature field is distributed in the circumferential direction of the tube, so the problem is simplified to a two–dimensional problem in the axial and radial directions, and the model is symmetrical in the axial direction. The temperature distribution is expressed as T(r,z,t), where r is the radius and r1 ≤ r ≤ r2, t is the time and t ≥ 0.
- (2)
- To explore the mechanism of radial heat transfer, it is assumed that the length of circular tube Z is far greater than r2, and that the influence of axial Z heat conduction is negligible; then, the temperature distribution could be simplified as T(r,t).
- (3)
- At each axial position Z, the temperature of the fluid changes periodically with respect to a certain equilibrium temperature, which constitutes the boundary condition of heat transfer in a circular tube.

Figure 3.
Simplified model of a single circular tube.
Since a Stirling machine regenerator works by continuously exchanging compression and expansion, assuming that the temperature distribution observed the law of cosine periodic change, then the boundary conditions of the inner wall r = r1 at each position Z can be written as:
where T0,z is the average temperature fluctuation at each axial position Z of the regenerator, and ω is the circular frequency of temperature fluctuation, whose relationship with the working frequency f can be expressed as:
3. Mathematical Model and Its Solution
Based on hypothesis (1), the governing equation of the above physical model is the unsteady heat conduction equation in a cylinder, which can be expressed as Equation (5) in a cylindrical coordinate system [28]:
Based on hypothesis (2), and given that the influence of axial heat conduction is ignored, the equation can be simplified into:
The problem is further simplified as one–dimensional unsteady heat conduction along radial r, and the boundary conditions satisfy Equations (7) and (8):
The boundary conditions of the inner circle are of the first type, which is non–homogeneous:
The boundary condition of the outer circle is of the second type, which is homogeneous:
where r1 and r2 are the inner and outer diameters of the circular tube. When the Stirling machine is working stably, the temperature at each position in the tube would change periodically with the same frequency as the boundary condition, and the average temperature would be the same as the boundary condition.
The difference between the temperature at each location and its mean is defined as θ; then, . Hence, the original problem is transformed into:
The corresponding boundary conditions become:
To solve the problem constituted by Equation (9) and its boundary conditions (10) and (11), it can be assumed that:
In order to separate the time and space variables of the governing equation, the solution in the form of a complex function is:
Substituted into the governing Equation (9), we can obtain R© from:
The corresponding boundary conditions of Equation (14) are:
Equation (14) is a typical zero–order Bessel equation. Let ; the general solution is [29]:
where is a zero–order Bessel function of the first kind, is a zero–order Bessel function of the second kind, and B and C are undetermined constants determined by boundary conditions.
B and C are solved by:
Substituting B and C into Equation (17), we obtain ©(r) as:
Substituting Equation (20) into Equation (13), we can obtain θ(r,t) as:
where is the amplitude, noted ©©(r), and ϕ(r) is the phase angle. They are, respectively, expressed as:
4. Discussion on Analytical Solutions
The logical flow chart discussed in this paper based on theoretical analysis is shown in Figure 4. Based on the simplified model of a single–grid regenerator under the condition of unsteady heat conduction, the equivalent transformation condition of the hexagonal tube and the circular tube is obtained. The distribution of the temperature field in the tube is obtained through theoretical derivation, which laid a foundation for the research of this paper. According to the temperature distribution, the heat storage within a period is obtained, and the EHTC K is determined. The relative thickness w is calculated by the dimensionless analysis. The EHTC K is transformed, and SVHTC Kv is obtained. Taking the maximum SVHTC as the objective function and the oscillation frequency f, the grid geometry (r1, r2) and the material thermal diffusivity α as variables, how to obtain the optimal working and structural parameters of the grid HTGR is analyzed. Finally, the general law in the heat transfer performance of HTGR is summarized on the basis of the above discussion.
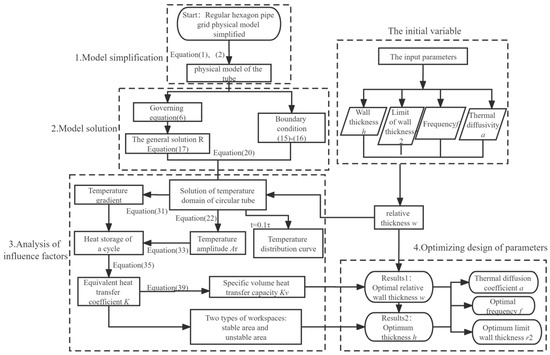
Figure 4.
Logical flow chart.
4.1. Factors Influencing Temperature Distribution
4.1.1. Influence of Thermal Diffusivity α on Temperature Distribution
The thermal diffusivity of a material a is the ratio of the thermal conductivity λ multiplied by the specific heat capacity cp and the density ρ [30].
Taking 1060 aluminum alloy (AA) and carbon fiber (CF) for 3D printing as examples, the temperature distribution in a grid regenerator unit is studied. The thermophysical properties of these two materials are shown in Table 1.

Table 1.
Thermophysical properties of aluminum alloy and carbon fiber.
The temperature distribution at different moments calculated by Equation (21) is shown in Figure 5. Initially, the inner diameter r1 is 3 mm, the outer diameter r2 is 5 mm, the frequency f is 30 Hz, and the temperature fluctuation amplitude A is 20 K. The results indicate that the temperature distribution in the circular tube changes periodically under the boundary conditions, accompanied by a phase lag, as shown in Figure 5.
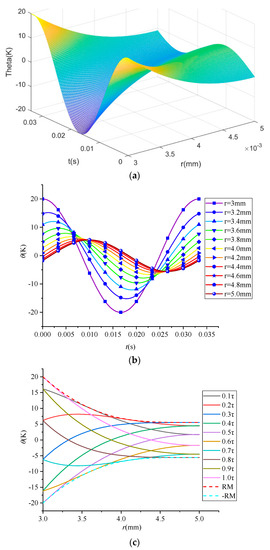
Figure 5.
Amplitude curve with time and radius (a) three–dimensional amplitude–time–radius (θ–t–r) panorama of a period (b) θ–r diagram (c) θ–t diagram.
Figure 5 shows the amplitude variation curve with time and radius. Figure 5a is a three–dimensional amplitude–time–radius (θ–t–r) panorama of a period. As can be seen from the figure, the curve varies with time and radius in periodic cosine. The amplitude–radius (θ–r) curve and amplitude–time (θ–t) curve are plotted, as shown in Figure 5b and Figure 5c, respectively. Figure 5b shows the amplitude variation with time at different tube thicknesses. It can be seen from the figure that with the increase in the thickness, the amplitude gradually decreases and the phase angle gradually shifts backward. Figure 5c shows the temperature distribution curve within a period τ at different moments. The dotted lines are the envelope line. The figure indicates that the amplitude decreased with the increase in wall thickness.
The temperature distribution curves for aluminum alloy and carbon fiber are shown in Figure 6a,b, respectively. The temperature distribution curves within a period τ at different moments are plotted on the horizontal axis of r1 ≤ r ≤ r2.

Figure 6.
The distribution of θ–r temperature in wall thickness (a) tube made from aluminum alloy, r1 = 3 mm, r2 = 5 mm, f = 30 Hz (b) tube made from carbon fiber, r1 = 3 mm, r2 = 5 mm, f = 30 Hz.
By comparing the two figures, we can see that the influence of physical property difference on the temperature distribution of the tube made from aluminum alloy is that the temperature distribution in the tube wall thickness is relatively uniform due to the large thermal diffusivity and small change rate of the temperature distribution curve. However, the heat diffusion coefficient of the carbon fiber circular tube is small, the temperature distribution curve change rate is large, the temperature distribution in the tube wall thickness is not uniform, and the temperature of the near–adiabatic part of the outer diameter of the circular tube (4.25 mm–5 mm) basically remains unchanged, and no more heat exchange occurs.
4.1.2. The Influence of Frequency f on Temperature Distribution
The expression of Ar, the temperature distribution amplitude of the regenerator, was obtained according to Equation (22). The change in the temperature distribution amplitude was affected by frequency, as shown in Figure 7. The amplitude distribution curve reflects the heat storage capacity of the regenerator at different frequencies. The smaller the frequency, the stronger the heat storage capacity of the regenerator, and the larger the heat exchange capacity of each cycle, which is also proved by the subsequent calculation of the periodic heat transfer Qen (Equation (34)). The results also indicate that the temperature distribution became increasingly less uniform with the increase in frequency under the condition of the same tube wall thickness. In terms of circular tubes made from carbon fiber, the temperature at the near–adiabatic part tended to be constant at a frequency of more than 50 Hz, suggesting that no heat exchange occurred at the near–adiabatic part and that such part no longer contributed to heat transfer.
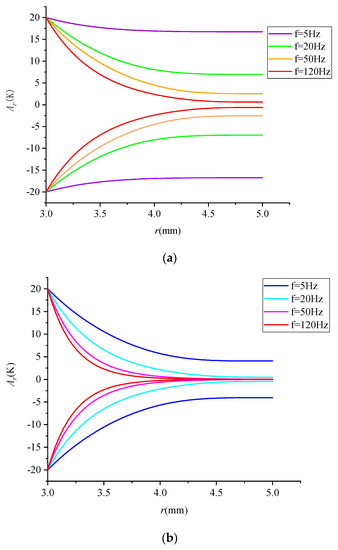
Figure 7.
Distribution curve of Ar–r temperature amplitude in wall thickness (a) aluminum alloy tube, r1 = 3 mm, r2 = 5 mm (b) carbon fiber tube, r1 = 3 mm, r2 = 5 mm.
4.1.3. The Influence of Relative Wall Thickness w on Temperature Distribution
h is defined as the tube wall thickness; then:
The attenuation of amplitude has a significant influence on the performance of the regenerator, which is affected by material thermal diffusivity α, working frequency f, and internal and external radius r1 and r2, which can be expressed as:
Therefore, the dimensionless parameter w is the ratio of the tube wall thickness h to the thermal penetration depth δk, which is also known as “relative wall thickness”. It involves all the parameters affecting the change in amplitude and is an important parameter to be discussed later. δk is widely used in regenerators and is expressed as [32]:
If r2 is assumed to be a constant, then h can be changed by changing r1*, and the dimensionless h* is defined as:
where r1 < r1* < r2, the dimensionless amplitude corresponding to the dimensionless wall thickness h* is defined as:
When the relative wall thickness w is 0.4, 0.8, 1.0, 1.4, 2.0, 3.2, and 4.4, the variation rule of dimensionless temperature fluctuation amplitude distribution along the dimensionless wall thickness h* is shown in Figure 8a. As can be seen from the figure, with the increase in the relative wall thickness w, temperature distribution became less uniform and heat transfer capacity significantly decreased.
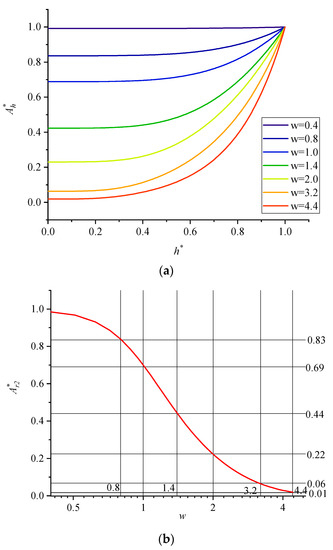
Figure 8.
Dimensionless temperature fluctuation amplitude distribution at different relative wall thickness w (a) distribution along the dimensionless wall thickness h* (b) temperature distribution along the adiabatic surface r = r2.
Figure 8b shows the variation in the dimensionless temperature fluctuation amplitude along the adiabatic boundary with w. It can be calculated by:
In Figure 8b, the horizontal axis is scaled in logarithmic coordinates. The figure shows the variation law of the dimensionless temperature fluctuation amplitude A0* of the adiabatic wall with the relative wall thickness w, which is analyzed from three perspectives:
First, when 0 < w < 1, decreases slowly with the increase in w. Second, when 1 < w < 2, decreases rapidly with the increase in w, especially when w = 1.4. Third, when 2 < w < 4.4, decreases rapidly with the increase in w, especially after w > 4.4, → 0. When the relative wall thickness w = 4.4, the fluctuation range at the center of the tube is close to 0, and the contour lines are, respectively, drawn when is equal to 0.83, 0.69, 0.44, 0.22, 0.06 and 0.01.
4.2. Heat Transfer Coefficient of Circular Tube Regenerator under Oscillation
The regenerator periodically stores and releases heat. The heat stored in a period could be calculated by integrating the temperature gradient of the wall surface. According to Equation (20), the temperature gradient equation can be derived as:
The temperature gradient curve at the inner–wall surface is shown in Figure 9.

Figure 9.
Temperature gradient curve.
In a cycle, the amount of heat absorbed through the inner wall of the tube Qen is equal to the amount of heat discharged Qex; thus, we have:
In Figure 9, t1 and t2 are the heat Qen releases within a cycle, which could be calculated by integrating the temperature gradient at time [t1, t2] and expressed as:
After solving:
where S is the heat transfer area of a single circular tube, which is directly related to the wall thickness h and length l. The total heat exchange time of the Qen is the period τ, and the temperature difference ∆T = 2A. Therefore, the EHTC K of the circular tube regenerator could be calculated by temperature gradient Equation (31) and heat Equation (34).
The change in the EHTC K with wall thickness h at different frequencies is shown in Figure 10. According to the structural characteristics of the hexagonal grid tube, the outer diameter r2 of the equivalent circular tube is assumed to be the ultimate wall thickness. In other words, the wall thickness h changes based on constant r2, and could be changed by changing r2.
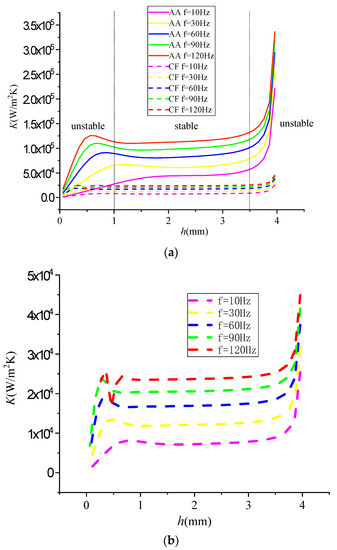
Figure 10.
Variation in heat transfer coefficient K with tube wall thickness h. (a) Aluminum alloy and carbon fiber (b) Enlarged view of carbon fiber.
Figure 10 shows the relationship between the heat transfer coefficient K and the tube wall thickness. It can be known from that h is a function of r2 and r1. When r2 remains unchanged (r2 = 4 mm for research), the larger r1 is, the smaller h is and the thinner the tube wall is. As can be seen from Figure 10, at a certain frequency, the heat transfer coefficient increases with the wall thickness when the wall thickness h of circular tube is small (0 < h < 1 mm). In the area where the tube wall is at medium thickness (1 < h < 3.5), the heat transfer coefficient increases slowly and then remains basically stable. When the tube wall thickness h is large (3.5 < h < 4 mm), the heat transfer coefficient approaches infinity. The heat transfer coefficient is unstable when the wall thickness is too large or too small. In addition, it also remains unstable with the change in heat transfer coefficient. The heat transfer coefficient is unstable when the tube wall thickness is larger or smaller, and the heat transfer coefficient is also unstable with the change in heat transfer coefficient. The variation trend of carbon fiber is the same as that of aluminum alloy, except that the heat transfer coefficient of carbon fiber is small, the variation amplitude of the heat transfer coefficient with frequency is relatively small, and the cut–off point of the stability zone is moved forward compared with aluminum alloy. Therefore, the selection of wall thickness is required, and the appropriate wall thickness should avoid the unstable zone at both ends. Due to the large range of the stability zone, taking aluminum alloy as an example, the wall thickness is between 1 < h and < 3.5 mm, so the concept of “limit wall thickness” is introduced to determine the optimal value of wall thickness.
The relationship between the inner–wall thickness and the outer diameter of the tube can be explained from three perspectives. The influence mechanism of the wall thickness of the tube on the heat transfer coefficient is explored in three cases: ultra–thin wall thickness, normal wall thickness, and ultra–thick wall thickness, as shown in Figure 11a–c.
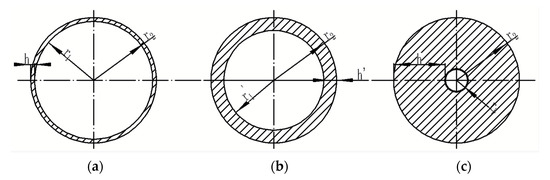
Figure 11.
Relationship between wall thickness and inner and outer diameters; (a) ultra–thin wall thickness (b) normal wall thickness (c) ultra–thick wall thickness.
The following conclusions can be drawn from the analysis and numerical verification of Equation (32). First, in the case of ultra–thin wall thickness, when r1 → r2, the wall thickness h → 0 and the heat storage volume is V → 0. In the case of ultra–thin wall thickness, the heat storage Qen → 0 in a cycle and the EHTC is sharply reduced, approaching 0, K → 0, which is an unstable condition of the failure of the heat storage capacity. Second, if the wall is ultra–thick when the inner diameter of the circular tube r1 → 0, the heat exchange area S → 0, resulting in the EHTC K → +∞, and the heat exchange capacity of the regenerator is reduced, an unstable working condition in which the EHTC could only meet the heat exchange requirements when it becomes infinite. Therefore, the practical conditions of ultra–thin wall thickness and ultra–thick wall thickness should be avoided. In the case of normal wall thickness (1 mm < r1 < 3.5 mm), the heat transfer coefficient remains basically unchanged with the change in wall thickness, but is positively correlated with the frequency, which conforms to the heat transfer theory. Therefore, it should be selected in practical applications, as shown in Figure 10.
The above analysis brings about an interesting and critical question, which is the choice of ultimate wall thickness r2. The heat transfer coefficients when the ultimate wall thickness r2 is 1, 2, 4, 6 and 8 mm are shown in Figure 12; the heat transfer coefficient increases with the increase in wall thickness h. When r2 = 1, in the “narrow” wall thickness, the heat transfer coefficient basically has no stable region, and its value varies from zero to infinity. However, when taking the other values of r2 > 1, the K value is stable in a certain area, and the sizes of the stable areas are basically the same; first it goes up, then it goes down, and then it goes to infinity. Therefore, the increase in wall thickness is not beneficial for the increase in K value. So, in the value of the limited wall thickness r2, we avoid the narrow area () and consider the full use of materials at the same time, so the limited wall thickness should not be large. This is the purpose of the concept of “ultimate wall thickness”. Combined with the requirements of the thermal penetration depth of the material, the ultimate wall thickness r2 is 2 mm in this case. According to Figure 10 and Figure 12, it can be determined that there is an optimal value of h and r2.
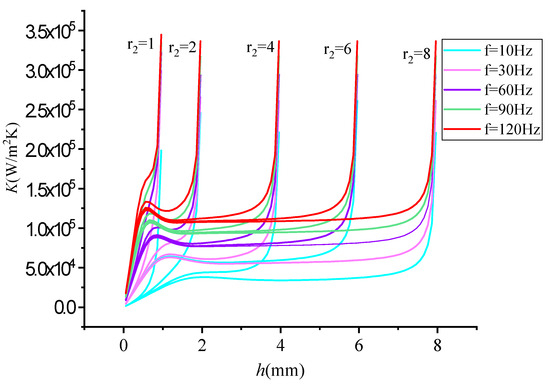
Figure 12.
Heat transfer coefficient K of different ultimate wall thickness r2.
4.3. Optimization of Tube Thickness Considering Specific Surface Area
It would be a key task to determine the wall thickness and inner diameter of a circular tube in the design process. Theoretically, heat transfer area is independent of heat transfer coefficient, but some constraints need to be considered in practical applications. The size of the regenerator cannot be arbitrarily large, so it is of practical significance to explore heat transfer process under the constraints of a given regenerator volume. The constraints can be described by specific surface area, the ratio of the surface area of the inner circle to the tube volume. The calculation results are:
Therefore, the product of heat transfer coefficient and specific surface area was selected as the target parameter to determine the optimal size of the circular tube in this paper. It is called specific volume heat transfer capacity, denoted as Kv, and can be calculated by:
This parameter actually reflects the relationship between the overall heat exchange performance of the regenerator and the wall thickness h and the frequency f, as shown in Figure 13.
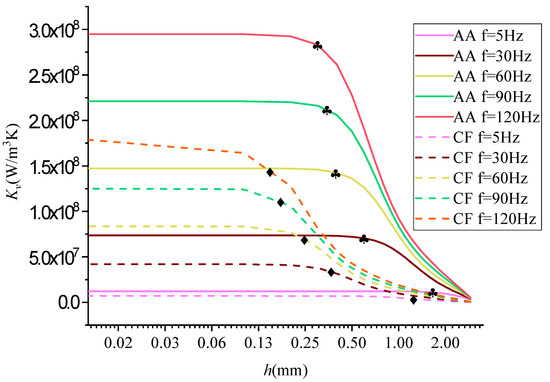
Figure 13.
Variation in Kv with wall thickness h.
It can be found that Kv decreased monotonically with the wall thickness h, indicating that the larger the specific surface area, the better the overall heat transfer performance. At the same time, when the wall thickness was small enough, the overall heat transfer performance was stable, reaching its optimum. Therefore, the heat exchange performance was not significantly changed by further increasing specific surface area, implying that there is an optimal wall thickness. If the wall thickness exceeded its optimal value, specific surface area would increase, and flow resistance would also rapidly increase, which could not improve the overall efficiency of the Stirling machine.
Take aluminum alloy as an example; when the frequency f = 30 Hz, the corresponding thickness h = 1 mm, and when f > 30 Hz, h was between 0.5 and 1 mm. This conclusion verifies the relationship between the heat transfer coefficient K and the wall thickness h in Figure 10. As can be seen from Figure 13, the SVHTC of the aluminum alloy was greater than that of carbon flux, and the difference between the two increased with frequency. The optimal wall thickness of tube made from aluminum alloy should not exceed the “♣” number marked in the figure. Before “♣” number, the SVHTC Kv was at a high level and then decreased slowly with the increase in the wall thickness h. After “♣” number, the SVHTC Kv decreased rapidly with the increase in the wall thickness h until it approached 0. The optimal wall thickness h of the tube made from carbon fiber should not exceed the mark “♦” in the figure, and its forward and backward variation trend was the same as that of the aluminum alloy. The SVHTC Kv of the same material increased with the increase in frequency f. Compared with the aluminum alloy, the SVTHC of carbon fiber decreased with the increase in frequency. Take aluminum alloy as an example; when the frequency f = 30 Hz, the corresponding thickness h = 1 mm, and when f > 30 Hz, h was between 0.5 and 1 mm. This conclusion verifies the relationship between the heat transfer coefficient K and the wall thickness h in Figure 10.
When the regenerator was made of aluminum alloy, the outer diameter r2 was 2.5 mm, the inner diameter r1 was 1.5 mm, the thickness h was 1 mm, the working frequency f was 20 Hz, the heat transfer capacity Kv was 2 × 107 W/m3K, the heat transfer difference ∆T was 1 K, the porosity of the regenerator was 0.46, and the total volume Vr was 65.2 cm3; then, the heat exchange of the regenerator was calculated by:
It reached the magnitude of kW, as Equation (38) shows; when and , the heat transfer was numerically equal to Kv. The higher the frequency, the greater the heat change. Under such working conditions, the heat exchange performance of the regenerator is undoubtedly satisfactory.
According to the research results of this paper, some suggestions are put forward for the design of a Stirling machine regenerator: Firstly, according to Figure 8b, the relative thickness w was set at about 0.8 and w < 1, making the heat storage material basically in the state of thermal permeability. Secondly, according to Equation (34) for heat exchange, thermal diffusivity α and working frequency f of several materials were comprehensively considered. Thirdly, the ultimate wall thickness r2 and h were selected according to the analysis results in Figure 12 to obtain the inner diameter r1 further. At this point, the parameters of HTGR were primarily determined. Then, the working point of h was verified, as displayed in Figure 13. If Kv is at a high level and locates in the slow decline area at the beginning stage, the optimization design is completed. If Kv does not meet the requirement, then one should return to the second step, which means continuing to search for the optimal design by jointly considering the thermal spreading coefficient of the material and working frequency.
4.4. Verifying the Analytical Solution
The circular tube model was established, and the outer diameter of the circular tube was r1 = 3 mm and r2 = 5 mm, respectively. The numerical simulation was carried out using Fluent software. The inner–wall temperature changed periodically: , the outer wall was an adiabatic boundary; a transient model, first–order upwind difference scheme and SIMPLE algorithm were adopted; the convergence condition of the energy equation was that the residual was less than ; so, the temperature cloud diagram of the circular tube at a time τ was obtained, as shown in Figure 14. Through the cloud image, the process of heat absorption and emission through the wall of the circular tube regenerator can be clearly seen.

Figure 14.
Temperature distribution cloud diagram of circular tube at different times.
The numerical solution was compared with the analytical solution, and the result is shown in Figure 15.

Figure 15.
Comparative analysis of numerical solution and analytical solution (a) temperature distribution (b) error analysis.
In Figure 15a, the solid line is the analytical solution and the dashed line is the numerical solution. The two curves are in good agreement, which directly verifies the correctness of the analytical method for the circular tube regenerator. Figure 15b shows the degree of difference between the two curves. The maximum mean square error is not more than 2.3%.
The model of a regular hexagonal tube was established in the same way, according to the equivalent relation with the circular tube; the regular hexagon tube edge a = 3.14 mm and b = 5.24 mm. The temperature cloud diagram of the regular hexagonal tube at a time τ was obtained, as shown in Figure 16. The process of heat absorption and emission through the regular hexagonal tube wall in a period τ can be clearly seen through the cloud image.
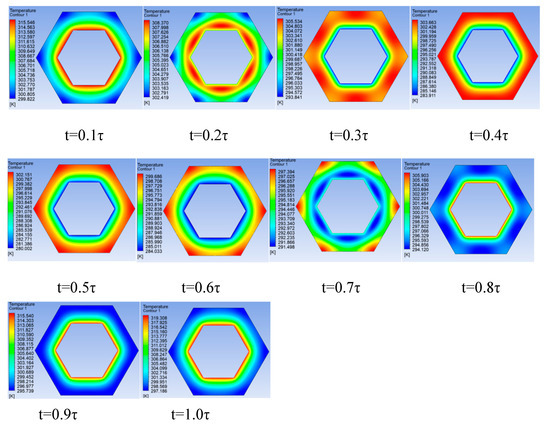
Figure 16.
Temperature distribution cloud diagram of regular hexagonal tube at different times.
The numerical solution of the regular hexagon tube was compared with that of the circular tube. The result is shown in Figure 17a, where 1 and 2 are the two endpoints of the regular hexagon (Figure 2b); the dashed line stands for the numerical solution of the circular tube. The error between the end points 1 and 2 of the regular hexagonal tube and the circular tube is shown in Figure 17b.

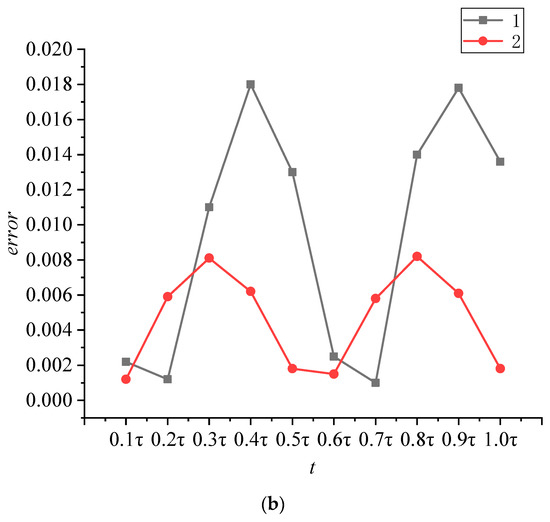
Figure 17.
Numerical solution of regular hexagon and circular tube (a) temperature distribution (b) error analysis.
5. Conclusions
In this paper, based on the two basic conditions of equal heat exchange area and equal heat storage, the geometric space of a regular hexagonal tube was equivalently transformed into a circular tube, and the HTGR was proved to be suitable for a inverse Stirling cycle at room temperature through theoretical analysis. Taking aluminum alloy and carbon fiber as examples, this paper provided a reference case for the design and operation of a regenerator at room temperature. The analytical expression of the Bessel function for temperature distribution was derived and the heat transfer coefficient of the HTGR was obtained. Two dimensionless parameters affecting the heat transfer mechanism of the HTGR were proposed: one is the relative thickness w, which is composed of four factors: operating frequency f, wall thickness h, ultimate wall thickness r2, and thermal diffusivity α; and the other is the SVHTC Kv of the specific surface area, which reflects the overall heat transfer performance of the regenerator. The conclusions of this paper are summarized as follows:
- Based on the influence of wall thickness on the heat transfer coefficient, the heat transfer mechanism of the HTGR was explored. When the heat transfer coefficient of the tube was ultra–thin or ultra–thick, the EHTC decreased sharply or increased infinitely, leading to the failure of the regenerator to store or exchange heat due to functional failure or a loss of heat transfer capacity. Therefore, it is necessary to avoid two unstable areas and select normal wall thickness in the selection of wall thickness. In the stable area, the EHTC could reach 104–105 W/m2·K, indicating that HTGR exhibits excellent heat transfer capacity.
- With the increase in specific surface area, the SVHTC increased, but there was a limit value. When the specific surface area was large enough, the SVHTC was in the high position, and the wall thickness of the grid was optimal at this moment. The relative thickness w was about 0.8, which is the appropriate boundary for heat penetration.
- The limited wall thickness was selected mainly to ensure that the regenerator had a stable heat exchange working area. In the stable working region, the heat transfer coefficient remained constant with the increase in the limited wall thickness, so the appropriate limited wall thickness is very important. When the limited wall thickness was too small, heat transferred quickly through, the heat transfer coefficient was unstable; with the increase in the limited wall thickness, the stable working area became longer and the heat transfer coefficient did not increase. So, an appropriate value can not only ensure sufficient heat exchange but also save materials.
- The frequency had a positive influence on heat transfer performance. With the increase in frequency, the heat exchange performance increased monotonically, so high–frequency operation is beneficial to improve the heat transfer performance of the regenerator.
- The numerical solution of the circular tube was in good agreement with the analytical solution, and the error was less than 2.3%, which indicates the correctness of solving the HTGR with the analytical model. The approximate numerical solution of the regular hexagon tube and the circular tube verifies that the regular hexagon can be transformed into a circle with an error less than 1.8%. In the next step, the heat exchange of a regular hexagonal pipe and circular pipe can be solved to further verify the equivalence of the two structures.
6. Patent
Chinese invention patent “Air Conditioning Temperature Zone Layered Honeycomb Structure with Variable Porosity Regenerator” was invented with the authorization number “ZL202110300042.7”.
Author Contributions
Y.W.: Investigation, data curation, visualization, software, writing—original draft, writing—original review and editing. J.Z.: Conceptualization, methodology, formal analysis, investigation, resources, supervision, funding acquisition, writing—review and editing. Z.L.: Formal analysis, data curation. J.L.: Validation, visualization. B.L.: Investigation, review and editing. H.D.: Resources, review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (No. 51705390), the Natural Science Basic Research Program of Shaanxi Province (General Program) (No. 2020JM–720), and Coal Mine Intelligent Machinery Equipment Research and Innovation Team (2021KYTD04) of Shaanxi Energy Institute.
Data Availability Statement
The data presented in this study are available from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a | hexagon pipe inner side length, mm |
| b | hexagonal pipe outside length, mm |
| r | diameter of the circular tube, mm |
| r1 | the inner diameter of the circular tube, mm |
| r2 | the outer diameter of the circular tube, mm |
| T | temperature, K |
| Z | axial position, mm |
| A | temperature amplitude, K |
| ω | frequency of temperature fluctuations |
| θ | the difference between the temperature of each place and the average, K |
| J0 | zero–order first–class Bessel functions |
| Y0 | zero–order Bessel functions of the second kind |
| Ar(r) | amplitude, K |
| h | circular tube wall thickness, mm |
| ϕ | phase angle |
| w | relative wall thickness |
| δk | depth of thermal penetration |
| h* | dimensionless wall thickness |
| dimensionless amplitude | |
| the dimensionless amplitude of temperature fluctuation on an adiabatic boundary | |
| Qen | heat absorbed through the inner wall of a tube during one cycle, W |
| Qex | heat released through the inner wall of a tube during one cycle, W |
| S | the heat transfer area of a single circular tube, mm2 |
| l | tube length, mm |
| τ | one cycle |
| V | storage volume, mm3 |
| K | equivalent heat transfer coefficient, W/m2K |
| Kv | specific volume heat transfer capacity, W/m3K |
Appendix A
The following can be obtained from Equation (A1):
Then, the minimum wall thickness h0 of the regular hexagonal pipe is:
The maximum wall thickness of the regular hexagonal pipe is:
Figure A1 is a schematic diagram of unilateral wall thickness. h is any wall thickness between the maximum and minimum wall thickness, and its value range is between ; the average value of any point can be obtained:
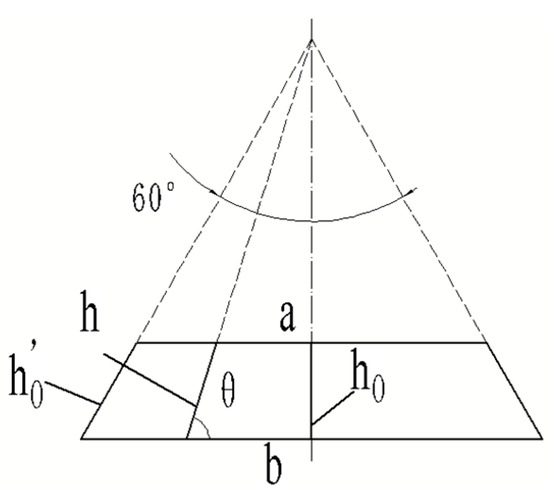
Figure A1.
Schematic diagram of wall thickness of a unilateral pipe.
The integral mean value theorem is used to obtain:
The equivalent thickness should meet the following requirements:
According to this, the volume–specific surface area equals:
By (A7):
Substitute (A7) into (A8) to obtain:
Substitute (A9) into (A6) to obtain the expression of . So, once a and b are evaluated, can be evaluated, and then can be evaluated.
References
- Wang, Y.J.; Zhang, J.A.; Liu, B.; Dong, H.; Liu, X.Y. Progress in Applications of Reverse Stirling Cycle Technology in Air Conditioning System of Pure Electric Vehicles. J. Xi’an Technol. Univ. 2021, 6, 609–620. [Google Scholar]
- Scheunert, M.; Masser, R.; Khodja, A.; Paul, R.; Schwalbe, K.; Fischer, A.; Hoffmann, K.H. Power-Optimized Sinusoidal Piston Motion and Its Performance Gain for an Alpha-Type Stirling Engine with Limited Regeneration. Energies 2020, 13, 4564. [Google Scholar] [CrossRef]
- Khan, U.; Zevenhoven, R.; Tveit, T.M. Evaluation of the Environmental Sustainability of a Stirling Cycle-Based Heat Pump Using LCA. Energies 2020, 13, 4469. [Google Scholar] [CrossRef]
- Hachem, H.; Gheith, R.; Aloui, F.; Naseallah, S.B.; Dincer, I. Exergy Assessment of Heat Transfer inside a Beta Type Stirling Engine. Int. J. Exergy 2016, 20, 186–202. [Google Scholar]
- Hachem, H.; Gheith, R.; Naseallah, S.B. Energetic and Exergetic Performance Evaluations of an Experimental Beta Type Stirling Machine; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Haywood, D. Investigation of Stirling-type Heat-pump and Refrigerator Systems Using Air as the Refrigerant. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2004. [Google Scholar]
- Bitsikas, P.; Rogdakis, E.; Dogkas, G. CFD study of heat transfer in Stirling engine regenerator. Therm. Sci. Eng. Prog. 2020, 17, 100492. [Google Scholar] [CrossRef]
- Chen, X.; Ling, F.; Liu, X.; Peng, W.T.; Huo, Q.Z.; Yang, W.L.; Yang, J.X. Optimization design of regenerator of free piston Stirling cryocooler in air-conditioning temperature zone. Vac. Cryog. 2019, 25, 231–236. [Google Scholar]
- Zhang, T.L.; Zhang, J.A.; Wang, Y.J.; Liu, B. Design and analysis of new type regenerator for Stirling engine. Cryogenics 2021, 2, 18–24. [Google Scholar]
- Cui, Y.; Qiao, J.; Song, B.; Wang, X.; Yang, Z.; Li, H.; Dai, W. Experimental study of a free piston Stirling cooler with wound wire mesh regenerator. Energy 2021, 234, 121287. [Google Scholar] [CrossRef]
- Park, P.M.; Cho, H.C.; Shin, H.D. Unsteady thermal flow analysis in a heat regenerator with spherical particles. Int. J. Energy Res. 2003, 27, 161–172. [Google Scholar] [CrossRef]
- Srinivasan, K.; Manimaran, A.; Arulprakasajothi, M.; Revanth, M.; Arolkar, V.A. Design and development of porous regenerator for Stirling cryocooler using additive manufacturing. Therm. Sci. Eng. Prog. 2019, 11, 195–203. [Google Scholar] [CrossRef]
- Ismail, A.; Perrin, M.; Giurgea, S.; Bailly, Y.; Roy, J.; Barriere, T. Multiphysical and multidimensional modelling of Parallel-Plate active magnetic regenerator. Appl. Energy 2022, 314, 118963. [Google Scholar] [CrossRef]
- Tu, Q.; Li, Q.; Liu, X.X.; Li, Z.Y. Optimization design of pin-array thermoacoustic stack. Int. J. Heat Exch. 2004, 5, 287–300. [Google Scholar]
- Tu, Q.; Zhang, X.Q.; Chen, Z.J.; Guo, F.Z. Design of miniature thermoacoustic refrigerator with pin-array stack. Acta Acust. United Acust. 2006, 92, 16–23. [Google Scholar]
- Liang, J.; Christiansen, C.D.; Engelbrecht, K.; Nielsen, K.K.; Bjørk, R.; Bahl, C.R. Heat transfer and flow resistance analysis of a novel freeze-cast regenerator. Int. J. Heat Mass Transf. 2020, 155, 119772. [Google Scholar] [CrossRef]
- Nielsen, A.S.; York, B.T.; MacDonald, B.D. Stirling engine regenerators: How to attain over 95% regenerator effectiveness with sub-regenerators and thermal mass ratios. Appl. Energy 2019, 253, 113557. [Google Scholar] [CrossRef]
- York, B.T.; MacDonald, B.D. Influence of misalignment and spacing on the pressure drop through wire mesh Stirling engine regenerators. Energy Convers. Manag. 2021, 245, 114588. [Google Scholar] [CrossRef]
- Dellali, E.; Bégot, S.; Lanzetta, F.; Gavignet, E.; Rauch, J. Pressure drop analysis of oscillating flows through a miniature porous regenerator under isothermal and nonisothermal conditions. Exp. Therm. Fluid Sci. 2019, 103, 394–405. [Google Scholar] [CrossRef]
- Yuan, L.; Yu, J.; Qian, S. Frequency correlated heat transfer characteristics of parallel plate active magnetocaloric regenerator. Int. J. Refrig. 2019, 108, 103–112. [Google Scholar] [CrossRef]
- Pan, C.; Zhou, Y.; Wang, J.; Chen, L. A new method to calculate the pressure drop loss of the regenerator in VM refrigerator. Cryogenics 2013, 61, 107–110. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, B.; Liu, M.; Rao, Z. Analytical solution of heat transfer performance of pin-array stack regenerator in stirling cycle. Int. J. Therm. Sci. 2021, 167, 107015. [Google Scholar] [CrossRef]
- Chen, L.-B.; Kong, C.-H.; Wu, X.-L.; Zhou, Y.; Wang, J.-J. Specific heat capacities and flow resistance of an activated carbon with adsorbed helium as a regenerator material in refrigerators. New Carbon Mater. 2018, 33, 47–52. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Zhang, T.; Lu, Z.; Dong, H. Analysis and Experiment of Heat Transfer Performance of Straight-Channel Grid Regenerator. Int. J. Heat Technol. 2022, 40, 781–791. [Google Scholar] [CrossRef]
- Boroujerdi, A.; Esmaeili, M. Characterization of the frictional losses and heat transfer of oscillatory viscous flow through wire-mesh regenerators. Alex. Eng. J. 2015, 54, 787–794. [Google Scholar] [CrossRef]
- Gupta, S.K.; Ghosh, P.; Nandi, T.K. Theoretical and CFD investigations on a 200 Hz thermoacoustic heat engine using pin array stack for operations in a pulse tube cryocooler. IOP Conf. Ser. Mater. Sci. Eng. 2019, 502, 012025. [Google Scholar] [CrossRef]
- Fan, H.T.; Xiao, G.; Lai, H.S.; Peng, H.; Ni, M.J. Numerical Study of the Heat Transfer Characteristics in Stirling Engine Regenerators Under Oscillating Flow. J. Eng. Thermophys. 2019, 40, 2595–2602. [Google Scholar]
- Ren, Y.H. Improved Numerical Solving Method of Unsteady Heat Conduction Problem Under Cylindrical Coordinate System. Contemp. Chem. Ind. 2015, 44, 1634–1637. [Google Scholar]
- Yan, Z.J. Mathematical Physical Equation, 2nd ed.; University of Science and Technology of China Press: Hefei, China, 2002; pp. 82–123. [Google Scholar]
- Luo, X.Q.; Yang, Z.P.; Chen, Z.D. Investigation on Transient Measurement of Thermal Conductivity and Thermal Diffusion by Thermal Line Method. J. Sichuan Norm. Univ. 2013, 36, 792–794. [Google Scholar]
- Wang, T.T.; Gu, Y.Z.; Wang, S.K.; Li, M.; Fang, Z.N.; Zhang, Z.G. Characterization on axial thermal conductivity of carbon fiber and its influence factors. J. Beijing Univ. Aeronaut. Astronaut. 2017, 43, 8. [Google Scholar]
- Wu, Z.; Chen, Y.; Dai, W.; Luo, E.; Li, D. Investigation on the thermoacoustic conversion characteristic of regenerator. Appl. Energy 2015, 152, 156–161. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).