Integrated Economic Optimization of Hybrid Thermosolar Concentrating System Based on Exact Mathematical Method
Abstract
1. Introduction
2. Literature for Hybrid Thermosolar Systems and EDC Optimization
3. Economic Dispatch and Commitment Optimization of Hybrid Thermosolar System
3.1. External Data
3.2. Generation Constraints
3.3. The Objective Function
3.4. Thermal Energy System
3.5. Solar Energy System
3.6. Solution
- Fixed data for generating units: characteristics of heat rates, number and rates of thermal units, prices of fuels, power bounds constraints, solar irradiation data, and load demand data.
- Parameter for accuracy of the results is the size of increment .
4. Study Case: Thermosolar System in North-West Greece
5. Results, Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Thermal Units | (MW) | (MW) | Heat Consumption Rates | Locations | ||
|---|---|---|---|---|---|---|
| Th1 | 28 | 70 | 0.005102 | 1.7286 | 12.80 | Ptolemaida I |
| Th2 | 120 | 300 | 0.000254 | 1.6410 | 44.19 | Ptolemaida IV |
| Th3 | 120 | 300 | 0.001217 | 1.3095 | 73.20 | Kardia III–IV |
| Th4 | 120 | 300 | 0.000254 | 1.6410 | 44.19 | Kardia I–II |
| Th5 | 170 | 300 | 0.000222 | 1.7318 | 30.99 | Agios Dimitrios I–II |
| Th6 | 170 | 310 | 0.000399 | 1.6253 | 42.47 | Agios Dimitrios III–IV |
| Th7 | 170 | 300 | 0.000622 | 1.5386 | 49.49 | Amidaio I–II |
| Totals | 898 | 1880 | ||||
| Technology | Hybrid, Parabolic Trough |
| Power Cycle | Steam Rankine |
| Nominal Capacity (MW) | 22.5 |
| Turbine efficiency % | 37 |
| Expected Generation (GWh/year) | 44.1 |
| Latitude/Longitude Location (o) | 41.529/0.8 |
| Solar Field Aperture Area (m2) | 183120 |
| Number of Solar Collector Assemblies (SCAs) | 336 |
| Number of Loops | 56 |
| Number of SCAs per Loop | 6 |
| Number of Modules per SCA | 8 |
| SCA Aperture Area (m2) | 545 |
| SCA Length (m) | 96 |
| Total Construction Cost (2012) M EUR | 149.94 |
| Total Cost (2020) M EUR | 211.67 |
| Specific Cost (2020) EUR/kW | 9407.41 |
| Remuneration EUR/kWh | 0.27 |
| Remuneration Start Year | 2012 |
| Remuneration Deflated (2020) EUR/kWh | 0.37 |
| PPA or Tariff Period (Years) | 25 |
| Operation and Maintenance O/M (%) (% of investment cost per year) | 1.5 |
| Levelized Cost of Electricity (2020) EUR/kWh (LCOE with 5% weighted average cost of capital and 25-year payback period) | 0.41 |
References
- Harsem, T.T.; Nourozi, B.; Behzadi, A.; Sadrizadeh, S. Design and Parametric Investigation of an Efficient Heating System, an Effort to Obtain a Higher Seasonal Performance Factor. Energies 2021, 14, 8475. [Google Scholar] [CrossRef]
- Stamatakis, M.E.; Ioannides, M.G. State Transitions Logical Design for Hybrid Energy Generation with Renewable Energy Sources in LNG Ship. Energies 2021, 14, 7803. [Google Scholar] [CrossRef]
- Ladakakos, P.D.; Ioannides, M.G.; Vionis, P.S.; Fragoulis, A.N. Development of a simulation model for investigating the dynamic operation of autonomous wind-diesel system. In Proceedings of the 7th European Wind Energy Conference EWEC-1997, Dublin, Ireland, 6–9 October 1997; European Wind Energy Association: Brussels, Belgium, 1997; pp. 833–836. [Google Scholar]
- Papazis, S.A.; Ioannides, M.G.; Fotilas, P.N. An Information System for Multiple Criteria Assessment of Renewable Energy Power Plants. Wind Eng. 2000, 24, 81–99. [Google Scholar] [CrossRef]
- Gayme, D.; Topcu, U. Optimal power flow with large-scale storage integration. IEEE Trans. Power Syst. 2012, 28, 709–717. [Google Scholar] [CrossRef]
- IRENA. Renewable Power Generation Costs in 2021; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2022; ISBN 978-92-9260-452-3. Available online: https://www.irena.org/publications/2022/Jul/Renewable-Power-Generation-Costs-in-2021 (accessed on 16 July 2022).
- CNN.gr. 2022. Available online: https://fox24.gr/2022/07/09/dimioyrgeitai-neo-ergostasio-lignit/ (accessed on 9 July 2022).
- Conejo, A.J.; Baringo, L. Power System Operations; Springer International Publishing AG: Cham, Switzerland, 2018; pp. 197–216. [Google Scholar] [CrossRef]
- Wood, A.J.; Wollenbeg, B.F.; Sheble, G.B. Power Generation, Operation and Control, 3rd ed.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Papazis, S.A.; Bakos, G.C. Generalized Model of Economic Dispatch Optimization as an Educational Tool for Management of Energy Systems. Adv. Electr. Comput. Eng. 2021, 21, 75–86. [Google Scholar] [CrossRef]
- García, J.M.G.-V.; García-Carmona, M.; Trujillo Torres, J.M.; Moya-Fernández, P. Teacher Training for Educational Change: The View of International Experts. Contemp. Educ. Technol. 2022, 14, ep330. [Google Scholar] [CrossRef]
- Klaassen, R.; de Vries, P.; Ioannides, M.G.; Papazis, S.A. Tipping your toe in the ‘Emerging Technologies’ pond from an educational point of view. In Proceedings of the 45th SEFI Annual Conference 2017—Education Excellence for Sustainability, SEFI 2017, Azores, Portugal, 18–21 September 2017; pp. 1190–1197. Available online: https://www.sefi.be/proceedings/?conference=2017-azores (accessed on 17 July 2022).
- Ioannides, M.G.; Papazis, S.A. Teaching and Research in Emerging Electrical Energy Engineering Education. In Proceedings of the 2021 International Conference on Applied and Theoretical Electricity (ICATE), Craiova, Romania, 27–29 May 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Papazis, S.A.; Ioannides, M.G. Emerging Energy Engineering Education on the Way to Employment. In Learning with Technologies and Technologies in Learning; Auer, M.E., Pester, A., May, D., Eds.; Lecture Notes in Networks and Systems, 456; Springer Nature: Cham, Switzerland, 2022; pp. 655–677. [Google Scholar] [CrossRef]
- Fotilas, P.N.; Papazis, S.A. A multiple criteria decision support system for the assessment of renewable energy power plants. In Proceedings of the 3rd International Symposium on Advanced Electromechanical Motion Systems, Electromotion, Patras, Greece, 8–9 July 1999; Volume 2, pp. 921–927. [Google Scholar]
- Ladakakos, P.D.; Ioannides, M.G. Estimation of wind parameter variation effect on the power quality of hybrid weak grids. Wind. Eng. 1999, 23, 353–364. Available online: https://www.jstor.org/stable/43749905 (accessed on 17 July 2022).
- Papazis, S.A.; Ioannides, M.G.; Fotilas, P.N. Development of an Information System for Wind Power Stations. In Enterprise Information Systems II; Sharp, B., Filipe, J., Cordeiro, J., Eds.; Springer: Dordrecht, The Netherlands, 2001; pp. 101–107. [Google Scholar] [CrossRef]
- Ioannides, M.G.; Tuduce, R.; Cristea, P.-D.; Papazis, S.A. Wind power generating systems based on double output induction machine: Considerations about control techniques. In Proceedings of the 20th International Conference on Systems, Signals and Image Processing (IWSSIP), Bucharest, Romania, 7–9 July 2013; pp. 103–107. [Google Scholar] [CrossRef]
- Ioanides, M.G.; Stamelos, A.; Papazis, S.A.; Papoutsidakis, A.; Vikentios, V.; Apostolakis, N. IoT Monitoring System for Applications with Renewable Energy Generation and Electric Drives. Renew. Energy Power Qual. J. 2021, 19, 565–570. [Google Scholar] [CrossRef]
- Østergaard, P.A.; Duic, N.; Noorollahi, Y.; Kalogirou, S.A. Latest progress in Sustainable Development using renewable energy technology. Renew. Energy 2020, 162, 1554–1562. [Google Scholar] [CrossRef]
- Østergaard, P.A.; Duic, N.; Noorollahi, Y.; Mikulcic, H.; Kalogirou, S. Sustainable development using renewable energy technology. Renew. Energy 2020, 146, 2430–2437. [Google Scholar] [CrossRef]
- Østergaard, P.A.; Duic, N.; Noorollahi, Y.; Kalogirou, S.A. Recent advances in renewable energy technology for the energy transition. Renew. Energy 2021, 179, 877–884. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, Y.; Zhang, J.; Wang, Z. The Knowledge Mapping of Concentrating Solar Power Development Based on Literature Analysis Technology. Energies 2020, 13, 1988. [Google Scholar] [CrossRef]
- Bakos, G.C.; Papazis, S.A. Solar Aided Power Generation (SAPG) System Using Parabolic Troughs: Techno-Economic Scenarios. In Proceedings of the 3rd International Conference on Advances in Energy Research and Applications (ICAERA’22), Seoul, Korea, 27–29 October 2022; Paper No. 102. pp. 1–5. [Google Scholar]
- Maffezzoni, P.; Codecasa, L.; D’Amore, D. Modeling and Simulation of a Hybrid Photovoltaic Module Equipped with a Heat-Recovery System. IEEE Trans. Ind. Electron. 2009, 56, 4311–4318. [Google Scholar] [CrossRef]
- Rehman, A.U.; Wadud, Z.; Elavarasan, R.M.; Hafeez, G.; Khan, I.; Shafiq, Z.; Alhelou, H.H. An Optimal Power Usage Scheduling in Smart Grid Integrated with Renewable Energy Sources for Energy Management. IEEE Access 2021, 9, 84619–84638. [Google Scholar] [CrossRef]
- Kalogirou, S.; Lloyd, S.; Ward, J.; Eleftheriou, P. Design and performance characteristics of a parabolic-trough solar-collector system. Appl. Energy 1994, 47, 341–354. [Google Scholar] [CrossRef]
- Montes, M.; Abánades, A.; Martínez-Val, J. Performance of a direct steam generation solar thermal power plant for electricity production as a function of the solar multiple. Sol. Energy 2009, 83, 679–689. [Google Scholar] [CrossRef]
- Ranjan, S.; Chandra Das, D.; Latif, A.; Sinha, N.; Suhail Hussain, S.M.; Selim Ustun, T. Maiden Voltage Control Analysis of Hybrid Power System with Dynamic Voltage Restorer. IEEE Access 2021, 9, 60531–60542. [Google Scholar] [CrossRef]
- Valenzuela, L.; Zarza, E.; Berenguel, M.; Camacho, E. Control scheme for direct steam generation in parabolic troughs under recirculation operation mode. Sol. Energy 2006, 80, 1–17. [Google Scholar] [CrossRef]
- López-Álvarez, J.A.; Larrañeta, M.; Pérez-Aparicio, E.; Silva-Pérez, M.A.; Lillo-Bravo, I. An Approach to the Operation Modes and Strategies for Integrated Hybrid Parabolic Trough and Photovoltaic Solar Systems. Sustainability 2021, 13, 4402. [Google Scholar] [CrossRef]
- Poullikkas, A. Economic analysis of power generation from parabolic trough solar thermal plants for the Mediterranean region—A case study for the island of Cyprus. Renew. Sustain. Energy Rev. 2009, 13, 2474–2484. [Google Scholar] [CrossRef]
- Riahi, A.; Haj Ali, A.B.; Guizani, A.; Balghouthi, M. Performance study of a concentrated photovoltaic thermal hybrid solar system. In Proceedings of the 2019 10th International Renewable Energy Congress (IREC), Sousse, Tunisia, 26–28 March 2019; pp. 1–5. [Google Scholar] [CrossRef]
- ASHRAE American Society of Heating, Refrigerating, and Air-Conditioning Engineers. Standard Method of Testing to Determine the Thermal Performance of Solar Collectors; U.S. Department of Energy, Office of Scientific Technical Information: Oak Ridge, TN, USA, 1991.
- Bouhal, T.; Agrouaz, Y.; Kousksou, T.; Jamil, A.; Zeraoulia, Y.; El-Rhafiki, T.; Bakkas, M. CSP plants optimization in Morocco: Best practices and real challenges. In Proceedings of the 2016 International Renewable and Sustainable Energy Conference (IRSEC), Marrakesh, Morocco, 17 November 2016; pp. 269–274. [Google Scholar] [CrossRef]
- Kannaiyan, S.; Bokde, N.D.; Geem, Z.W. Solar Collectors Modeling and Controller Design for Solar Thermal Power Plant. IEEE Access 2020, 8, 81425–81446. [Google Scholar] [CrossRef]
- Mufti, G.M.; Jamil, M.; Naeem, D.; Mukhtiar, M.U.; Al-Awami, A.T. Performance analysis of parabolic trough collectors for Pakistan using mathematical and computational models. In Proceedings of the 2016 Clemson University Power Systems Conference (PSC), Clemson, SC, USA, 8–11 March 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Shabbir, N.S.K.; Alam Chowdhury, M.S.; Liang, X. A Guideline of Feasibility Analysis and Design for Concentrated Solar Power Plants. Can. J. Electr. Comput. Eng. 2018, 41, 203–217. [Google Scholar] [CrossRef]
- Valan-Arasu, A.; Sornakumar, T. Theoretical analysis and experimental verification of parabolic trough solar collector with hot water generation system. Therm. Sci. 2007, 11, 119–126. [Google Scholar] [CrossRef]
- Zaaoumi, A.; Bouramdane, Z.; Bah, A.; Alaoui, M.; Mechaqrane, A. Energy production estimation of a parabolic trough solar power plant using artificial neural network. In Proceedings of the 2020 International Conference on Electrical and Information Technologies (ICEIT), Rabat-Salé, Morocco, 4–7 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Bentouba, S.; Bourouis, M. Feasibility study of a wind-photovoltaic hybrid power generation system for a remote area in the extreme south of Algeria. Appl. Therm. Eng. 2016, 99, 713–719. [Google Scholar] [CrossRef]
- Karnavas, Y.L. The Autonomous Electrical Power System of Crete Island-A Review. Int. Rev. Electr. Eng. Praise Ed. 2006, 1, 1–8. [Google Scholar]
- Bakos, G.; Tsechelidou, C. Solar aided power generation of a 300 MW lignite fired power plant combined with line-focus parabolic trough collectors’ field. Renew. Energy 2013, 60, 540–547. [Google Scholar] [CrossRef]
- Huang, C.; Madonski, R.; Zhang, Q.; Yan, Y.; Zhang, N.; Yang, Y. On the use of thermal energy storage in solar-aided power generation systems. Appl. Energy 2022, 310, 118532. [Google Scholar] [CrossRef]
- Huang, C.; Hou, H.; Hu, E.; Liang, M.; Yang, Y. Impact of power station capacities and sizes of solar field on the performance of solar aided power generation. Energy 2017, 139, 667–679. [Google Scholar] [CrossRef]
- Liu, H.; Zhai, R.; Patchigolla, K.; Turner, P.; Yang, Y. Model predictive control of a combined solar tower and parabolic trough aided coal-fired power plant. Appl. Therm. Eng. 2021, 193, 116998. [Google Scholar] [CrossRef]
- Petrovic, R. Economic dispatching in power systems using optimal control theory. In Optimization and Control of Dynamic Operational Research Models; Tzafestas, S.G., Ed.; North-Holland Publishing: Amsterdam, The Netherlands, 1982; Volume 4, pp. 217–250. [Google Scholar]
- Khare, V.; Nema, S.; Baredar, P. Solar wind hybrid renewable energy system: A review. Renew. Sustain. Energy Rev. 2016, 58, 23–33. [Google Scholar] [CrossRef]
- Chen, C.; Wang, F.; Zhou, B.; Chan, K.W.; Cao, Y.; Tan, Y. An interval optimization-based day-ahead scheduling scheme for renewable energy management in smart distribution systems. Energy Convers. Manag. 2015, 106, 584–596. [Google Scholar] [CrossRef]
- Reddy, S.S.; Momoh, J.A. Realistic and transparent optimum scheduling strategy for hybrid power system. IEEE Trans. Smart Grid 2015, 6, 3114–3125. [Google Scholar] [CrossRef]
- Dike, D.; Adinfono, M.I.; Ogu, G. Economic Dispatch of Generated Power Using Modified Lambda-Iteration Method. IOSR-JEEE J. Electr. Electron. Eng. 2013, 7, 49–54. [Google Scholar] [CrossRef]
- Han, X.; Gooi, H. Effective economic dispatch model and algorithm. Int. J. Electr. Power Energy Syst. 2007, 29, 113–120. [Google Scholar] [CrossRef]
- Zhan, J.P.; Wu, Q.H.; Guo, C.X.; Zhou, X.X. Fast λ-Iteration Method for Economic Dispatch with Prohibited Operating Zones. IEEE Trans. Power Syst. 2013, 29, 990–991. [Google Scholar] [CrossRef]
- Farag, A.; Al-Baiyat, S.; Cheng, T. Economic load dispatch multiobjective optimization procedures using linear programming techniques. IEEE Trans. Power Syst. 1995, 10, 731–738. [Google Scholar] [CrossRef]
- Sinha, N.; Chakrabarti, R.; Chattopadhyay, P. Evolutionary programming techniques for economic load dispatch. IEEE Trans. Evol. Comput. 2003, 7, 83–94. [Google Scholar] [CrossRef]
- Ding, T.; Bie, Z. Parallel augmented Lagrangian relaxation for dynamic economic dispatch using diagonal quadratic approximation method. IEEE Trans. Power Syst. 2017, 32, 1115–1126. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.; Zhang, B.; Sun, H.; Guo, Q. Dynamic economic dispatch using Lagrangian relaxation with multiplier updates based on a quasi-Newton method. IEEE Trans. Power Syst. 2013, 28, 4516–4527. [Google Scholar] [CrossRef]
- Solar Irradiance Calculations. 2022. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/tools.html (accessed on 30 June 2022).
- Reddy, S.S.; Bijwe, P.R.; Abhyankar, A.R. Real-Time Economic Dispatch Considering Renewable Power Generation Variability and Uncertainty Over Scheduling Period. IEEE Syst. J. 2014, 9, 1440–1451. [Google Scholar] [CrossRef]
- Chen, C.L.; Lee, T.Y.; Jan, R.M. Optimal wind-thermal coordination dispatch in isolated power systems with large integration of wind capacity. Energy Convers. Manag. 2006, 47, 3456–3472. [Google Scholar] [CrossRef]
- Reddy, S.S. Optimal scheduling of thermal-wind-solar power system with storage. Renew. Energy 2017, 101, 1357–1368. [Google Scholar] [CrossRef]
- Xie, L.; Chiang, H.D.; Li, S.H. Optimal power flow calculation of power system with wind farms. In Proceedings of the IEEE Power Energy Society General Meeting, Detroit, MI, USA, 24–29 July 2011; pp. 1–6. [Google Scholar]
- Hetzer, J.; Yu, D.C.; Bhattarai, K. An economic dispatch model incorporating wind power. IEEE Trans. Energy Convers. 2008, 23, 603–611. [Google Scholar] [CrossRef]
- Jabr, R.; Pal, B. Intermittent wind generation in optimal power flow dispatching. IET Gener. Transm. Distrib. 2009, 3, 66–74. [Google Scholar] [CrossRef]
- Hoffmann, L.D.; Bradley, G.L. Calculus for Business, Economics, and the Social and Life Sciences, 10th ed.; McGraw Hill: New York, NY, USA, 2010; pp. 613–647. ISBN 978-0-07-353231-8. [Google Scholar]
- Papanikolaou, D.N. Economic Operation of Power Systems. Master’s Thesis, University of Patras, Patras, Greece, 21 February 2008. Available online: http://nemertes.lis.upatras.gr/jspui/handle/10889/725 (accessed on 11 August 2022). (In Greek).
- Hybrid Parabolic Trough Projects. 2022. Available online: https://solarpaces.nrel.gov/by-technology/hybrid-parabolic-trough (accessed on 16 July 2022).

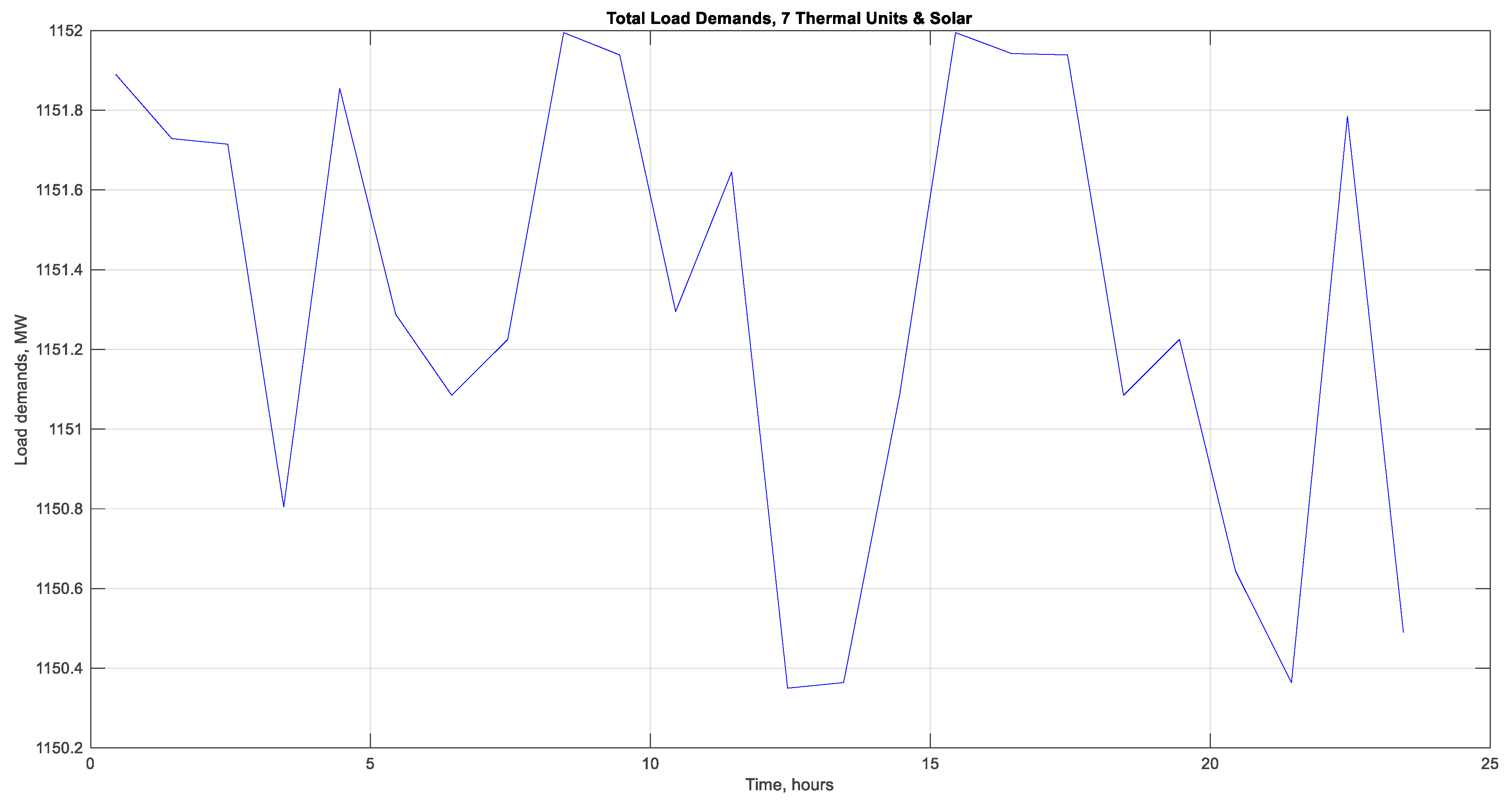
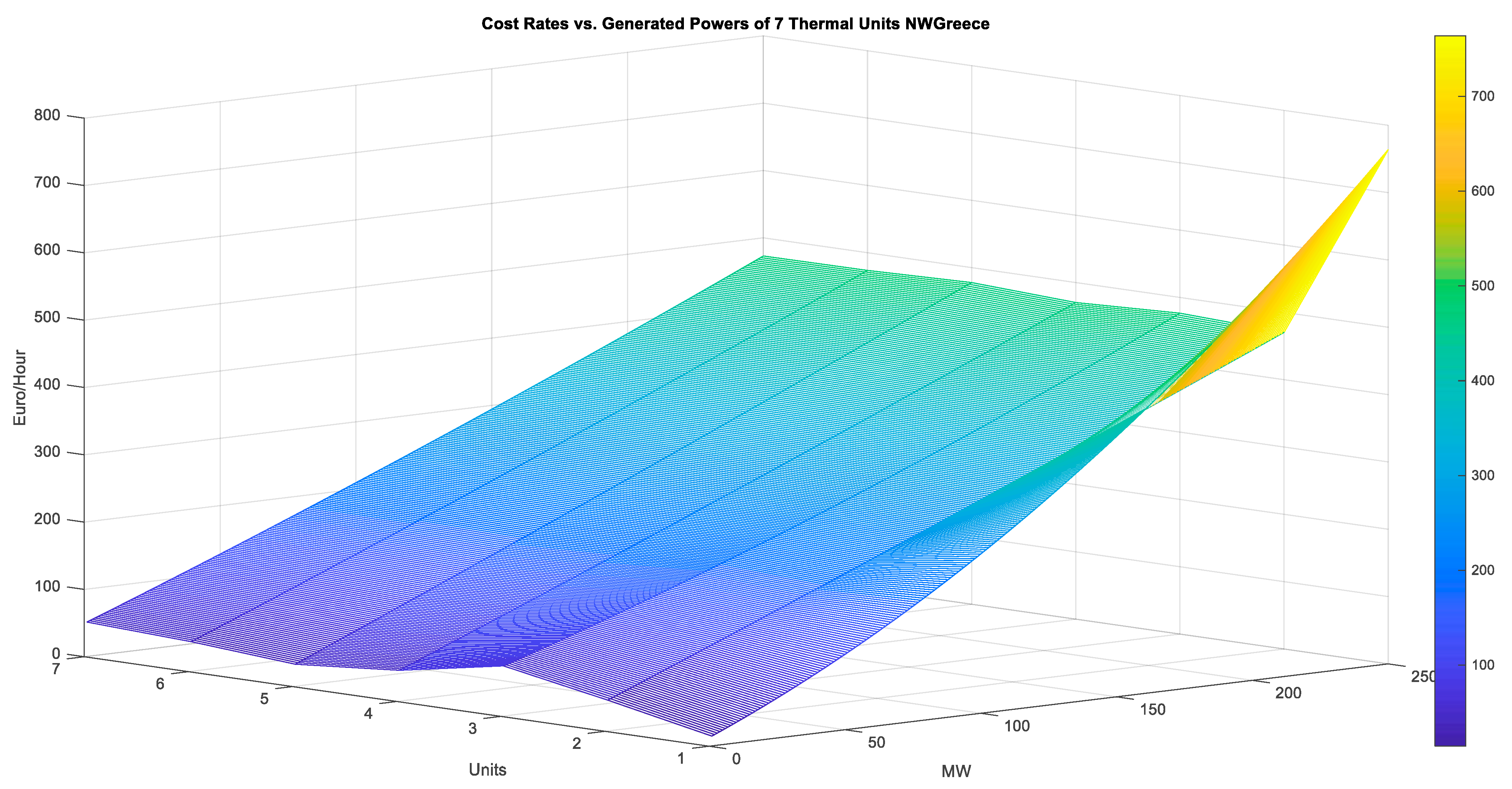

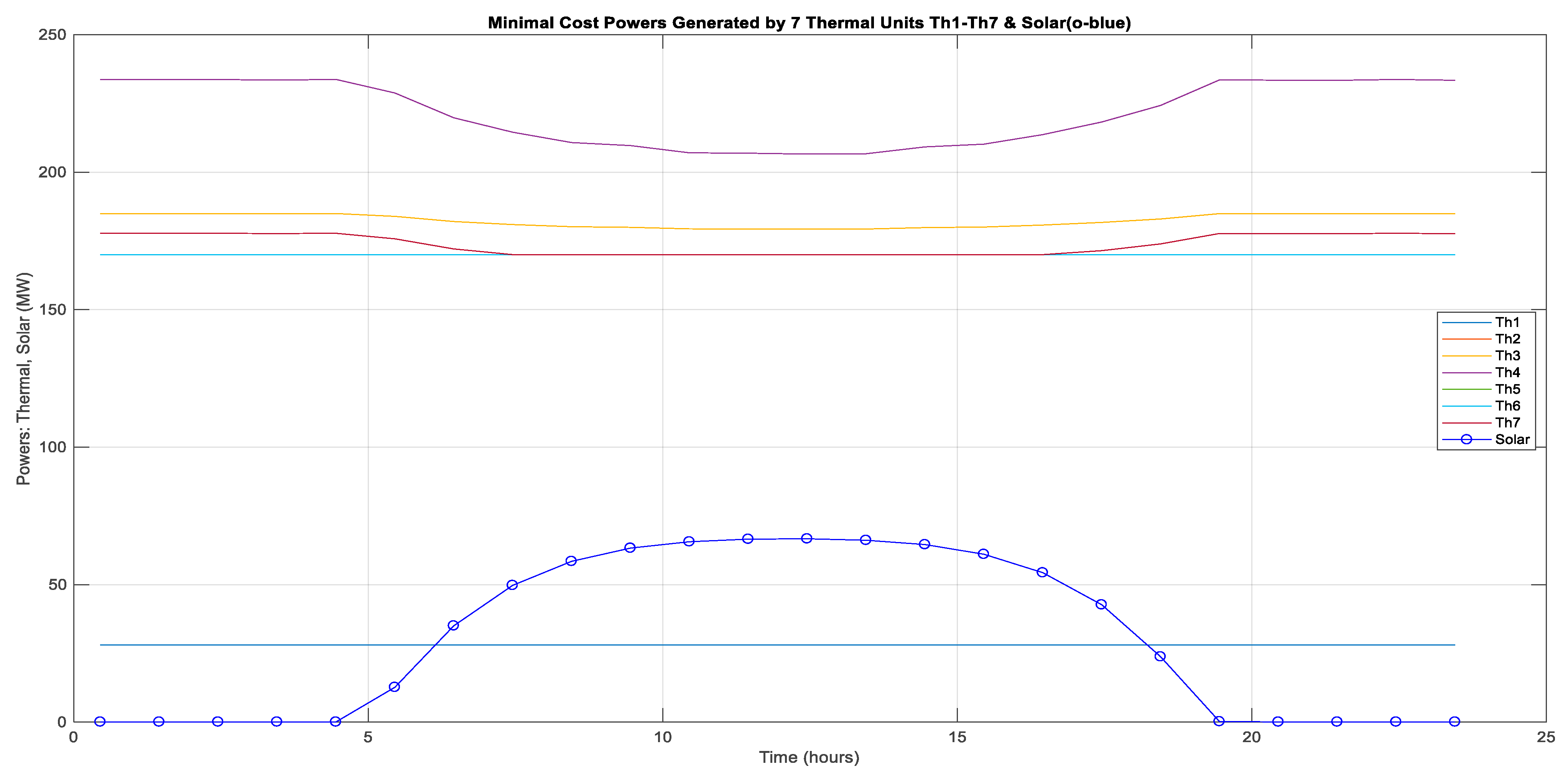
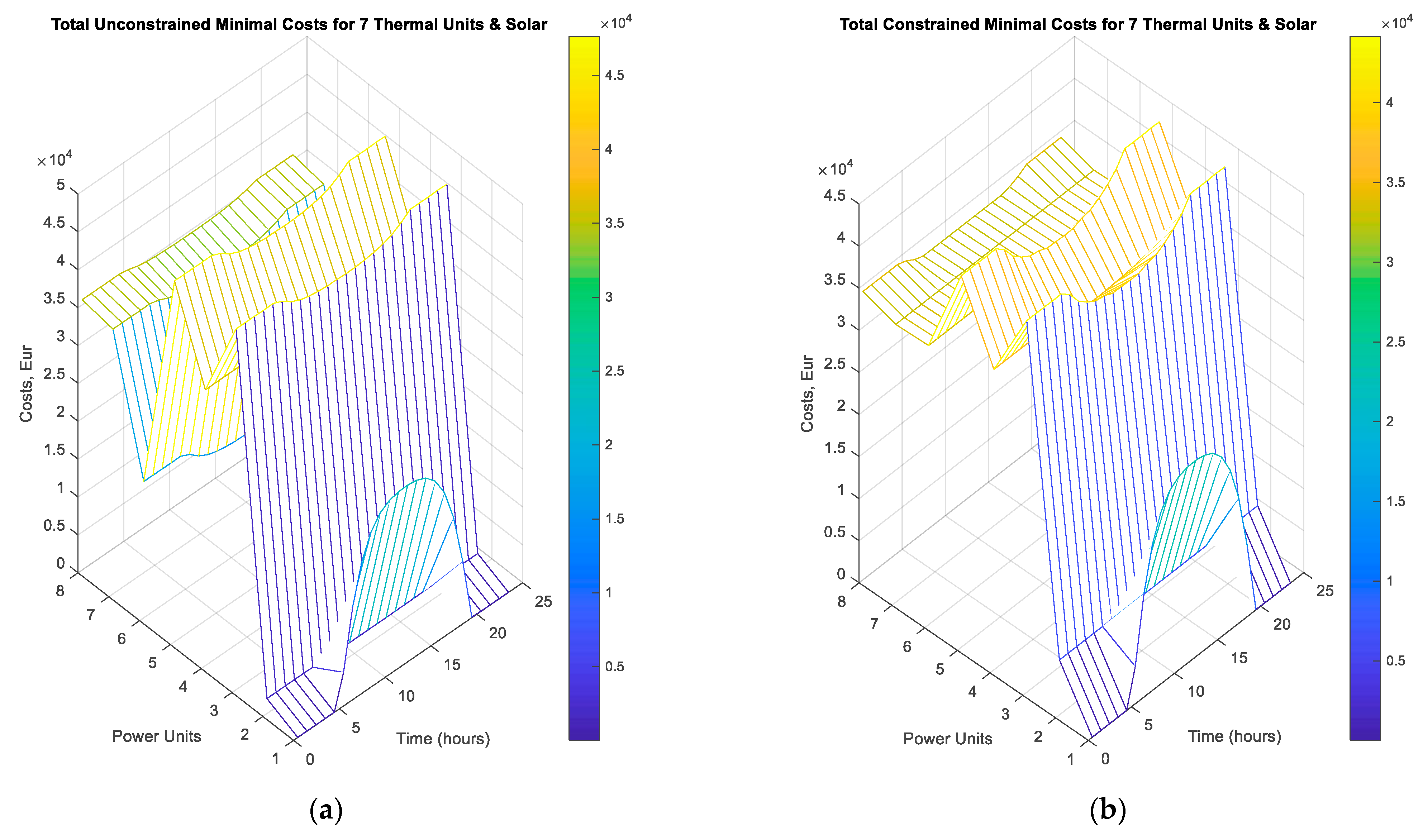
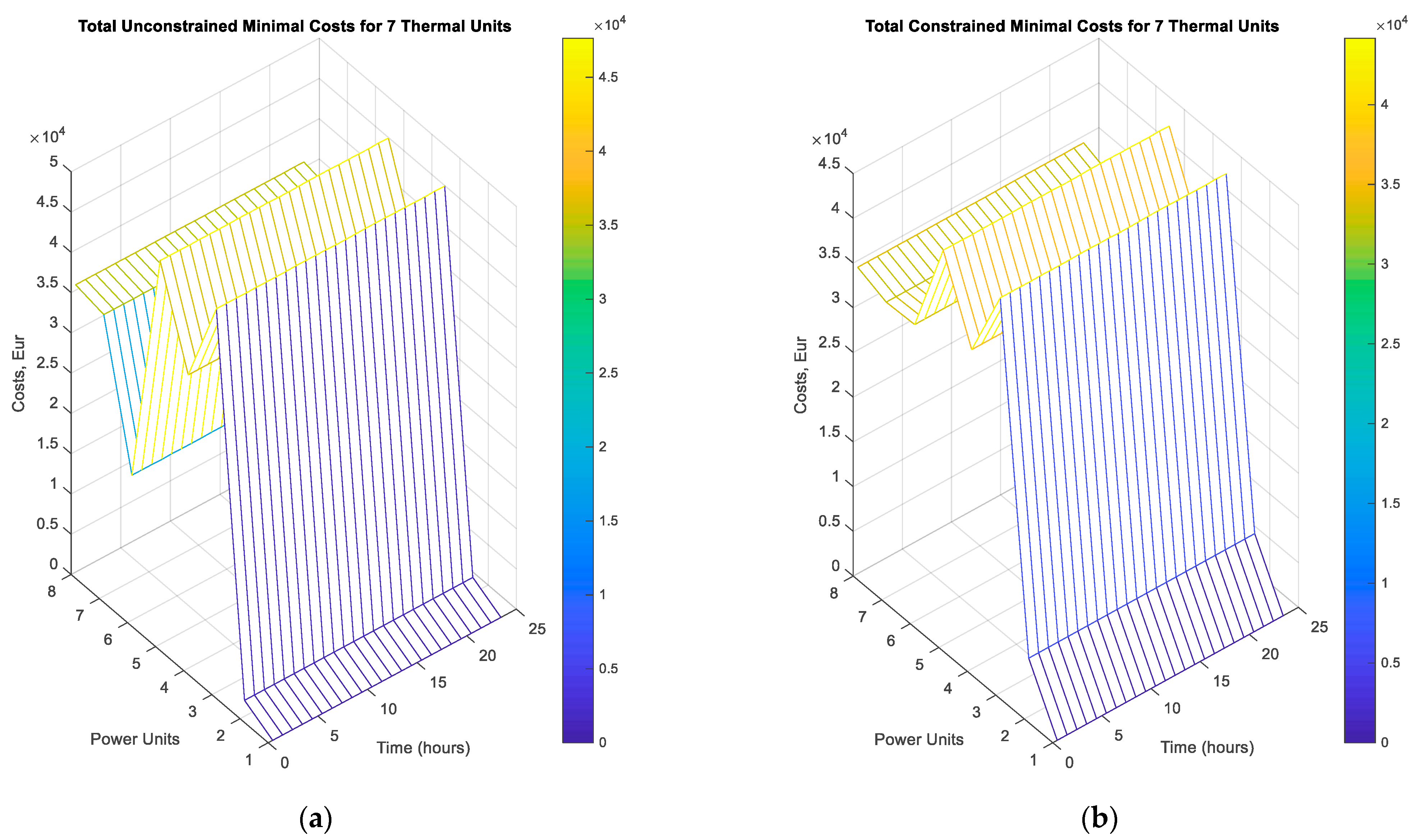
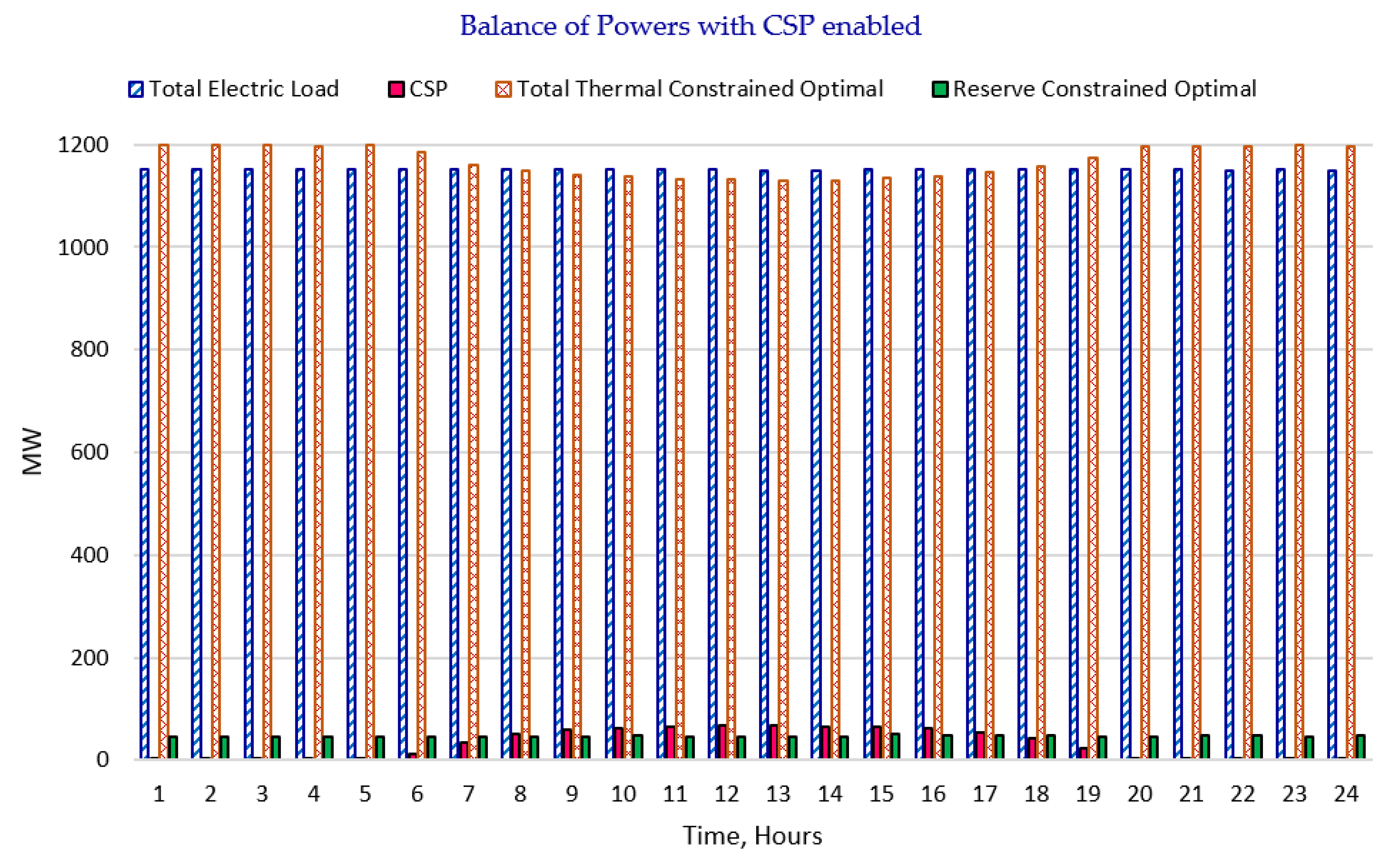

| Thermal Units | Scenario 1 CSP Enabled | Scenario 2 CSP Disabled | Differences: Scenario 1–Scenario 2 | |||||
|---|---|---|---|---|---|---|---|---|
| Constraints—Boundary Values | Total Generated Energy (MWh) | Total Operational Costs (EUR) | Constraints—Boundary Values | Total Generated Energy (MWh) | Total Operational Costs (EUR) | Total Generated Energy (MWh) | Total Operational Costs (EUR) | |
| Th1 | 672.00 | 156,480 | 672.00 | 156,480 | 0 | 0 | ||
| Th2 | 5321.77 | 1,009,361 | 5606.49 | 1,059,295 | −284.73 | −49,934 | ||
| Th3 | 4378.62 | 846,277 | 4437.97 | 856,686 | −59.35 | −10,409 | ||
| Th4 | 5321.77 | 1,009,361 | 5606.49 | 1,059,295 | −284.73 | −49,934 | ||
| Th5 | 4080.00 | 796,330 | 4080.00 | 796,330 | 0 | 0 | ||
| Th6 | 4080.00 | 792,694 | 4080.00 | 792,694 | 0 | 0 | ||
| Th7 | 0:45–6:45 and 17:45–23:45: 6:45–17:45: | 4170.17 | 805,430 | 4265.17 | 822,102 | −95.00 | −16,673 | |
| CSP | - | 731.34 | 255,969 | - | 0 | 0 | 731.34 | 255,969 |
| Totals | 28,755.67 | 5,671,901 | 28,748.13 | 5,542,882 | 7.54 | 129,019 | ||
| Thermal Units | Scenario 1 CSP Enabled | Scenario 2 CSP Disabled | Differences Scenario 1–Scenario 2 | |||
|---|---|---|---|---|---|---|
| Mean Operational Costs per 1 MWh (EUR/MWh) | Mean Operational Costs per 1 MW (EUR/MW) | Mean Operational Costs per MWh (EUR/MWh) | Mean Operational Costs per 1 MW (EUR/MW) | Mean Operational Costs per MWh (EUR/MWh) | Mean Operational Costs per 1 MW (EUR/MW) | |
| Th1 | 232.86 | 9.70 | 232.86 | 9.70 | 0 | 0 |
| Th2 | 189.67 | 7.90 | 188.94 | 7.87 | 0.73 | 0.03 |
| Th3 | 193.27 | 8.05 | 193.04 | 8.04 | 0.24 | 0.01 |
| Th4 | 189.67 | 7.90 | 188.94 | 7.87 | 0.73 | 0.03 |
| Th5 | 195.18 | 8.13 | 195.18 | 8.13 | 0 | 0 |
| Th6 | 194.29 | 8.10 | 194.29 | 8.10 | 0 | 0 |
| Th7 | 193.14 | 8.05 | 192.75 | 8.03 | 0.39 | 0.02 |
| CSP | 350.00 | 14.58 | 0 | 0 | 350.00 | 14.58 |
| Totals | 197.24 | 8.22 | 192.81 | 8.03 | 4.44 | 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papazis, S.A. Integrated Economic Optimization of Hybrid Thermosolar Concentrating System Based on Exact Mathematical Method. Energies 2022, 15, 7019. https://doi.org/10.3390/en15197019
Papazis SA. Integrated Economic Optimization of Hybrid Thermosolar Concentrating System Based on Exact Mathematical Method. Energies. 2022; 15(19):7019. https://doi.org/10.3390/en15197019
Chicago/Turabian StylePapazis, Stylianos A. 2022. "Integrated Economic Optimization of Hybrid Thermosolar Concentrating System Based on Exact Mathematical Method" Energies 15, no. 19: 7019. https://doi.org/10.3390/en15197019
APA StylePapazis, S. A. (2022). Integrated Economic Optimization of Hybrid Thermosolar Concentrating System Based on Exact Mathematical Method. Energies, 15(19), 7019. https://doi.org/10.3390/en15197019





