A Novel Hybrid Machine Learning Model for Wind Speed Probabilistic Forecasting
Abstract
1. Introduction
- (1)
- A new machine learning method named LGB is used to predict wind-speed sequences, which can provide accurate wind-speed prediction results.
- (2)
- A novel hybrid model combining LGB and GPR is proposed for wind-speed probability prediction.
- (3)
- The proposed hybrid model is applied to a real case in the United States and compared with eight contrasting models.
2. Methodology
2.1. Light Gradient Boosting Machine
2.1.1. Model Formulation
2.1.2. Model Optimization Mechanism
- (1)
- Gradient-based One-Side Sampling (GOSS): Without changing the distribution of sample data, some samples with small gradients can be eliminated, and only the remaining samples with larger gradients can be retained to estimate information gain, thereby reducing the number of training samples. Since samples with smaller gradients also contribute little to information gain, GOSS technology can make the LGB model faster while ensuring accuracy.
- (2)
- Exclusive Feature Bundling: In practical applications, high-dimensional data is often sparse. LGB model adopts the histogram (Histogram) algorithm to merge those mutually exclusive features after discretizing continuous features to form new features, reduce feature dimension, reduce memory usage, and speed up model training.
- (3)
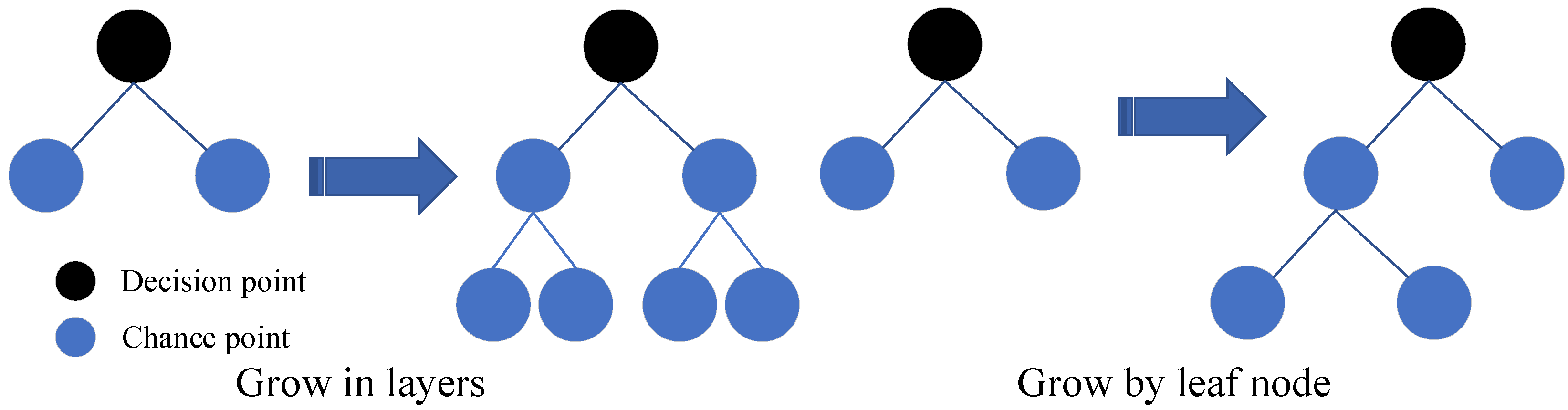
- Leaf-wise Tree Growth with Depth Limit: Change the level-wise tree growth adopted by most decision tree models to a leaf-wise growth strategy. Compared to the original, each leaf node was split, but now only the leaf node with the largest split gain is split, which reduces unnecessary overhead. In the case of the same number of classifications, the latter is more accurate than the former. LGB avoids model overfitting by setting the maximum tree depth parameter. The growth diagram of the decision tree is shown in Figure 1:
2.1.3. Model Implementation Process
- (1)
- Initialize, find the constant value that minimizes the overall loss function.where L(.) is the loss function. At this point, the model is a tree with only one root node.
- (2)
- For m = 1, 2, , M.
- (a)
- For i = 1, 2, , N, the residual is estimated by the negative gradient of the loss function.
- (b)
- Fit a regression tree to rm to obtain the leaf node area Rmj of the m-th tree, that is, j = 1, 2, , J.
- (c)
- For j = 1, 2, , J, estimate the value of the leaf node region using a linear search fit to minimize the loss function.
- (d)
- Iteratively update with the following formula.
- (3)
- Get the final model.
2.2. Gaussian Process Regression
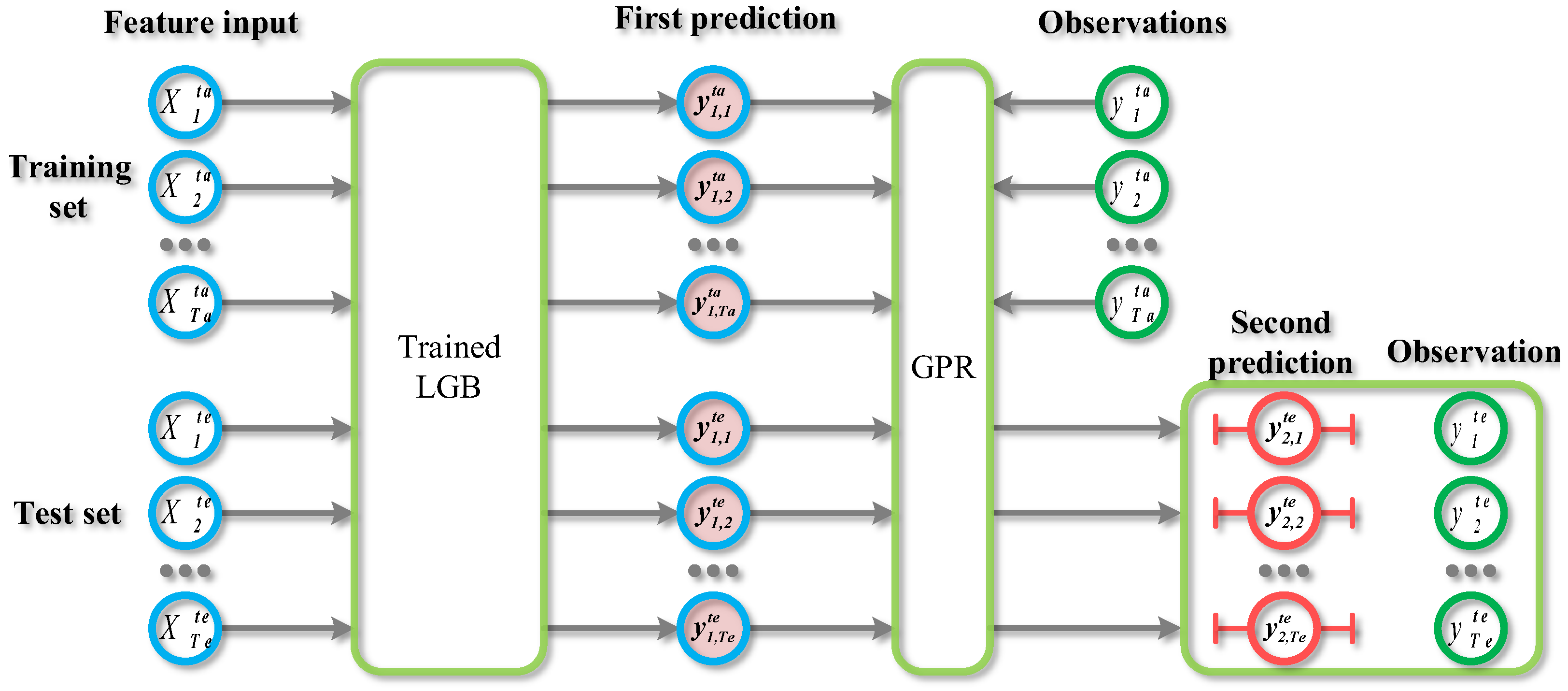
2.3. LGB-GPR
3. Scoring Metrics
3.1. Deterministic Forecasting Evaluation Metrics
3.2. Probabilistic Forecasting Evaluation Metric
4. Case Study
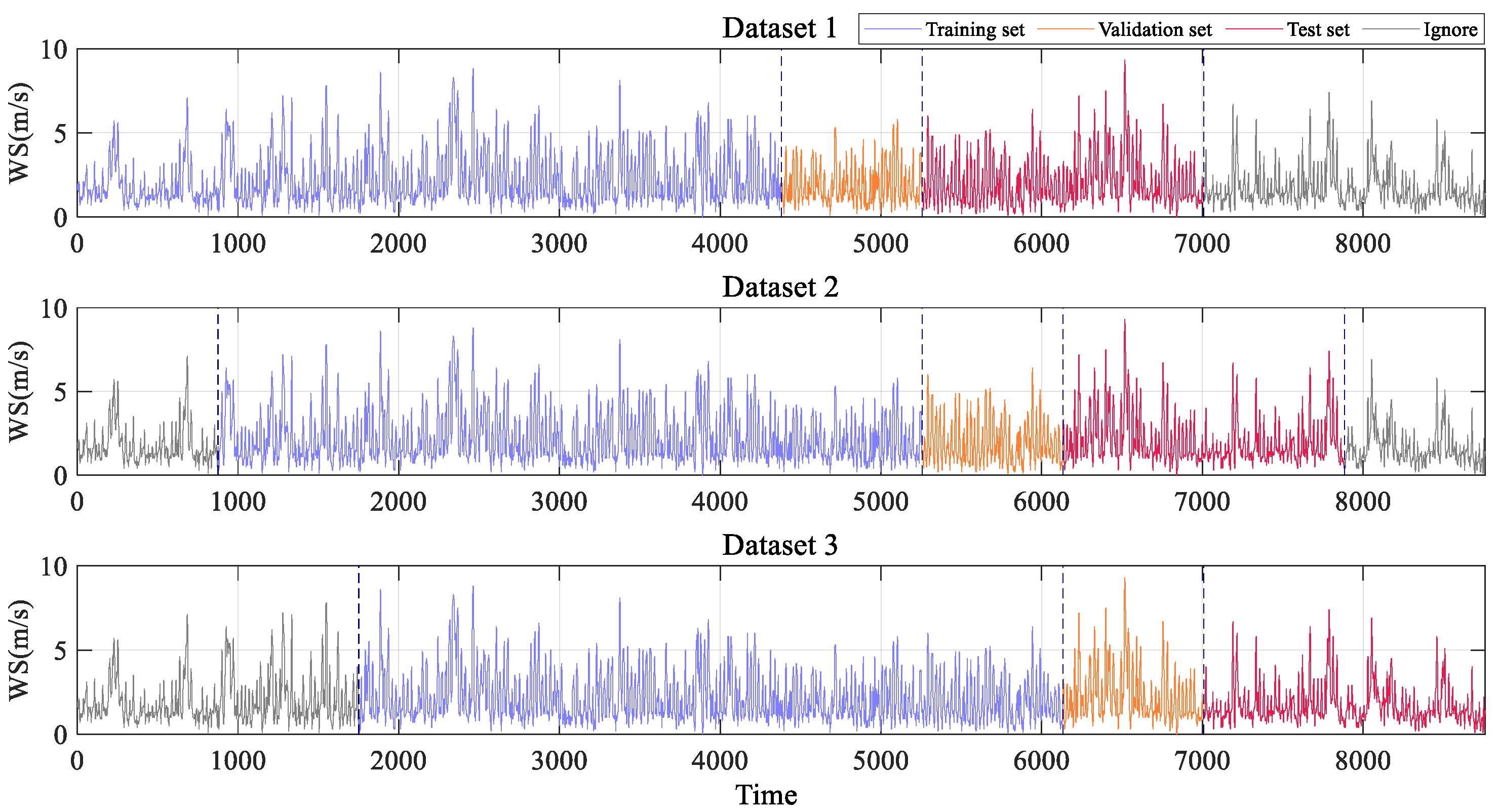
4.1. Case Introduction
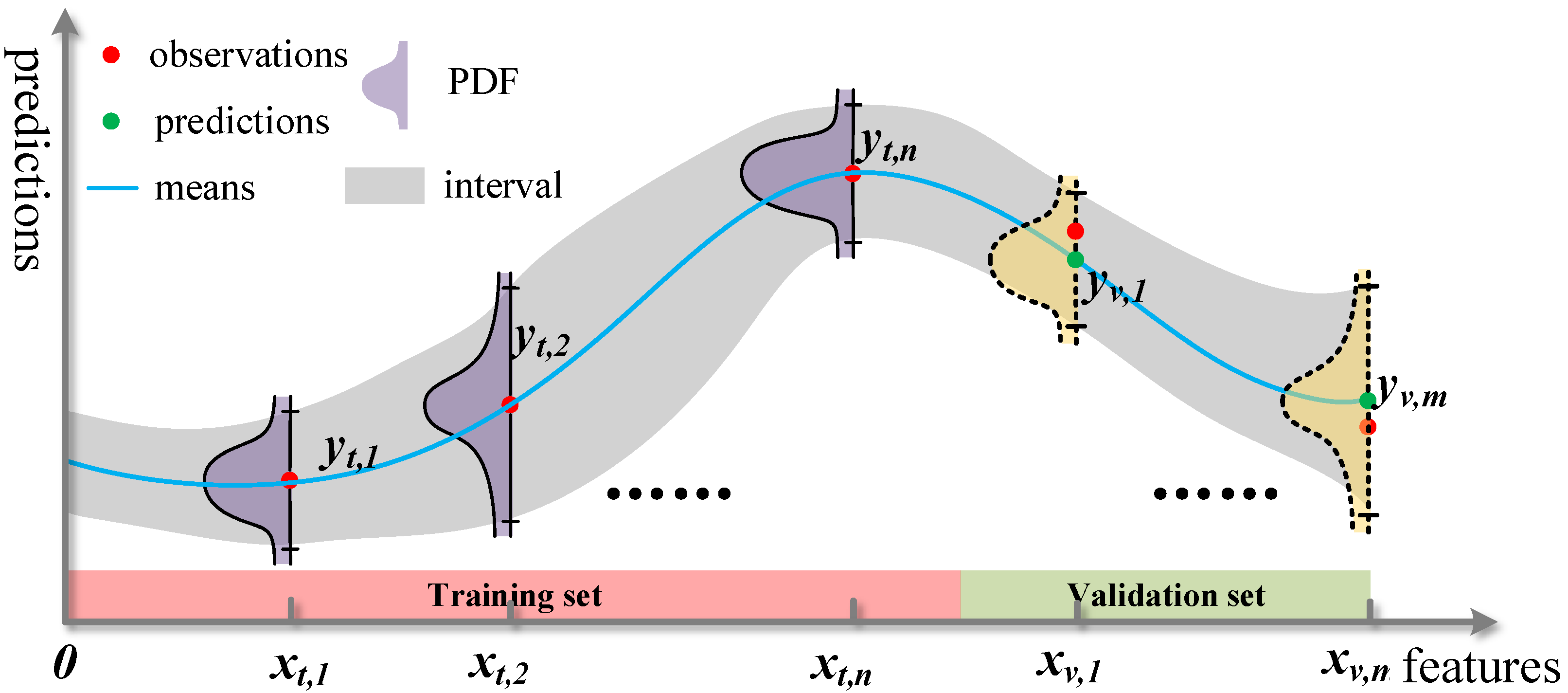
4.2. Data Processing
4.2.1. Data Normalized
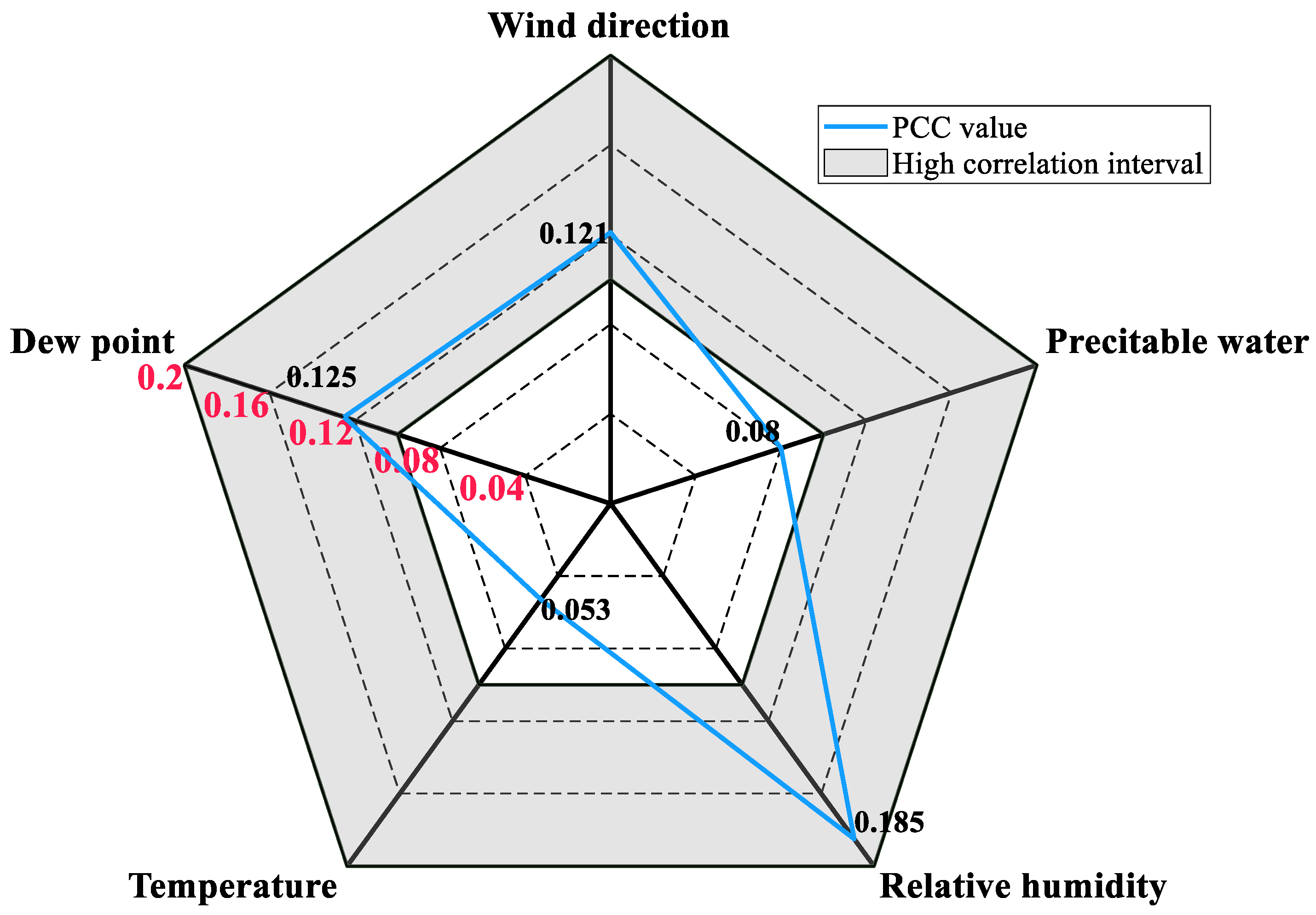
4.2.2. Feature Selection
4.3. Model Selection and Hyperparameter Optimization
5. Result and Discussion
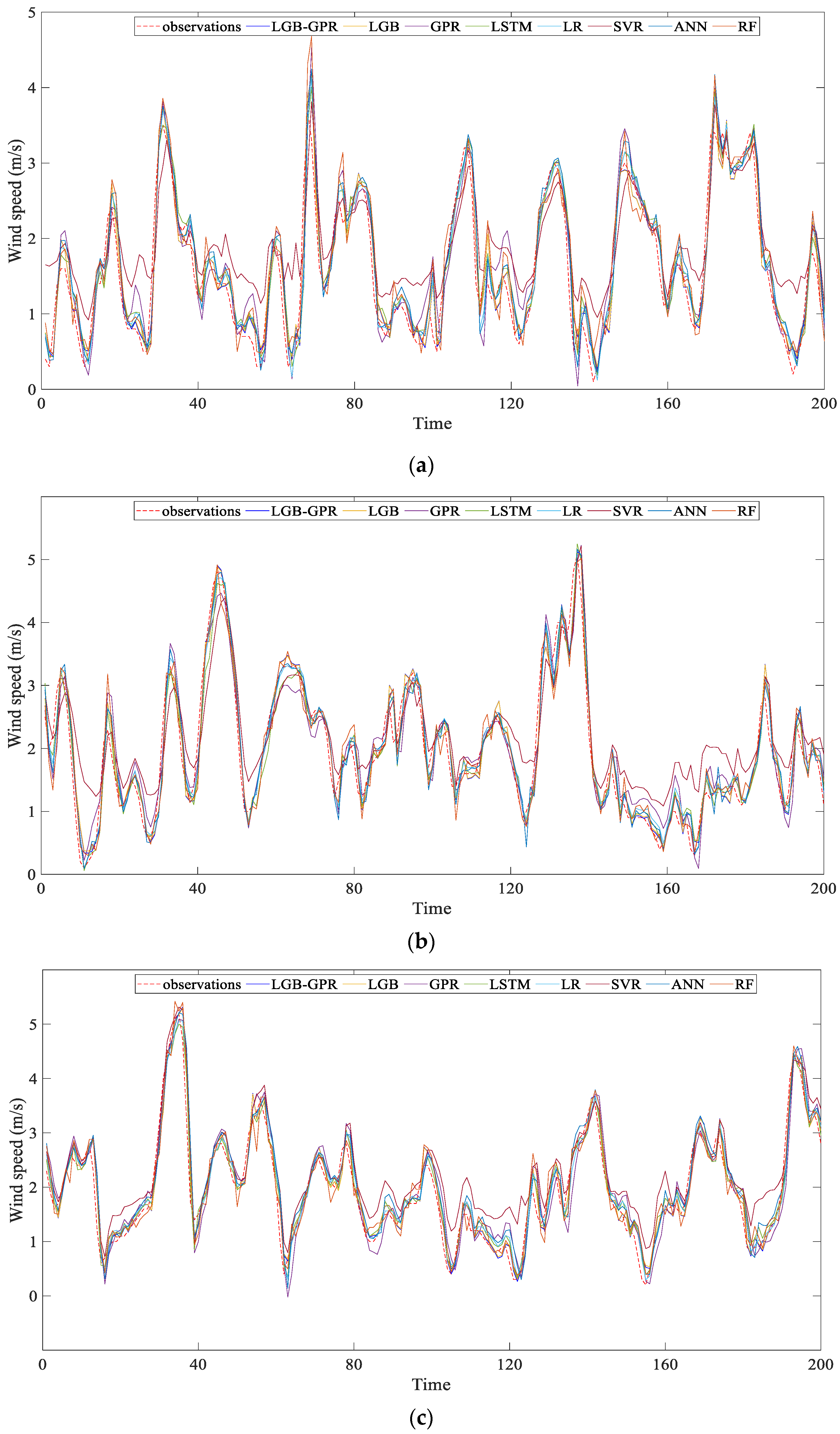
5.1. Deterministic Prediction Result Evaluation
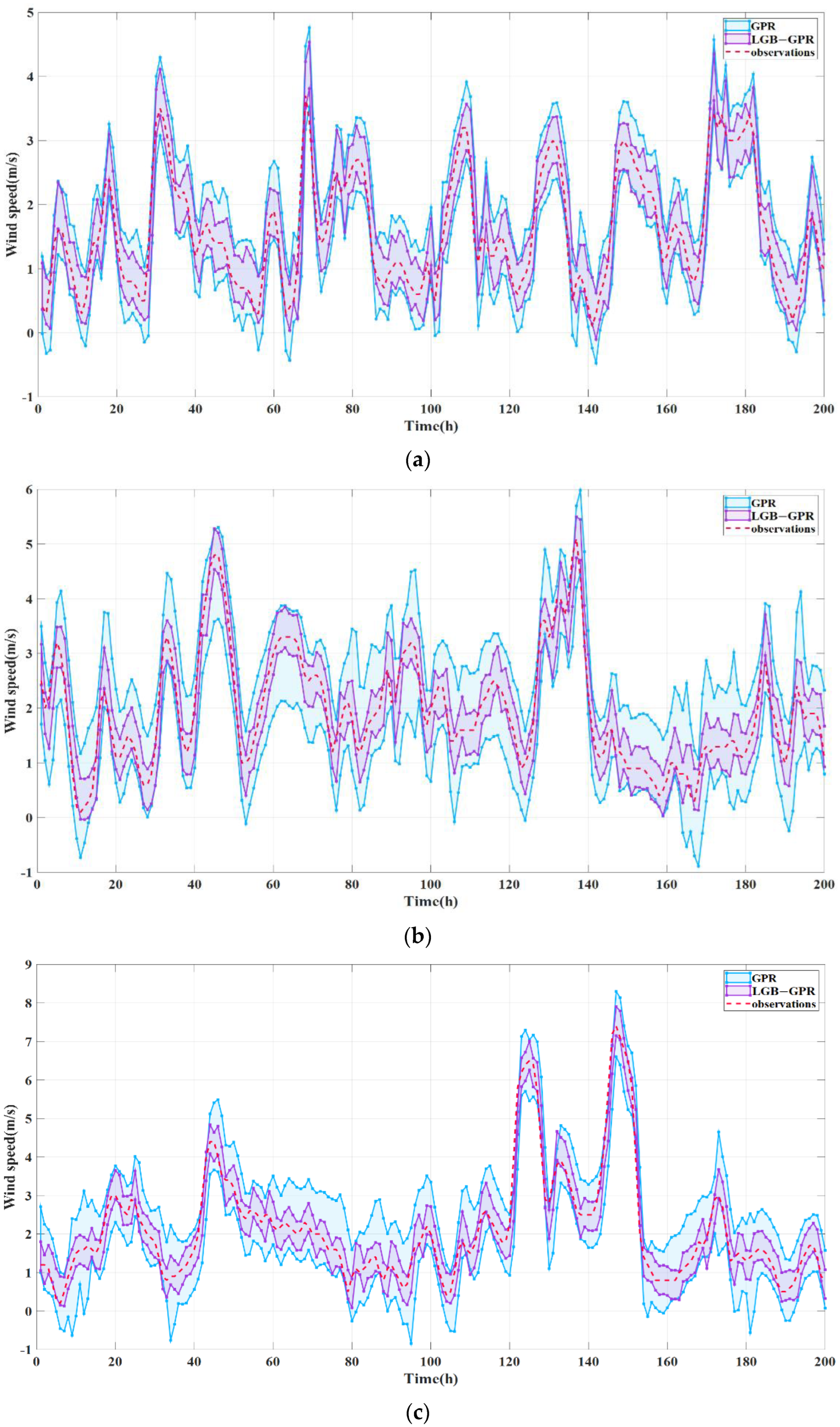
5.2. Probability Prediction Result Evaluation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, G.; Qin, H.; Shen, Q.; Lyv, H.; Qu, Y.; Fu, J.; Liu, Y.; Zhou, J. Probabilistic spatiotemporal solar irradiation forecasting using deep ensembles convolutional shared weight long short-term memory network. Appl. Energy 2021, 300, 117379. [Google Scholar] [CrossRef]
- Zhang, Z.; Ye, L.; Qin, H.; Liu, Y.; Wang, C.; Yu, X.; Yin, X.; Li, J. Wind speed prediction method using Shared Weight Long Short-Term Memory Network and Gaussian Process Regression. Appl. Energy 2019, 247, 270–284. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, G.; Zhou, W.; Du, W.; Lu, K. Wind speed forecasting using nonlinear-learning ensemble of deep learning time series prediction and extremal optimization. Energy Convers. Manag. 2018, 165, 681–695. [Google Scholar] [CrossRef]
- Hong, Y.; Rioflorido, C.L.P.P. A hybrid deep learning-based neural network for 24-h ahead wind power forecasting. Appl. Eneryg 2019, 250, 530–539. [Google Scholar] [CrossRef]
- Yang, Z.; Zhan, X.; Zhou, X.; Xiao, H.; Pei, Y. The Icing Distribution Characteristics Research of Tower Cross Beam of Long-Span Bridge by Numerical Simulation. Energies 2021, 14, 5584. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, M.; Øiseth, O.; Rønnquist, A. Wind deflection analysis of railway catenary under crosswind based on nonlinear finite element model and wind tunnel test. Mech. Mach. Theory 2022, 168, 104608. [Google Scholar] [CrossRef]
- Memarzadeh, G.; Keynia, F. A new short-term wind speed forecasting method based on fine-tuned LSTM neural network and optimal input sets. Energy Convers. Manag. 2020, 213, 112824. [Google Scholar] [CrossRef]
- Peng, Z.; Peng, S.; Fu, L.; Lu, B.; Tang, J.; Wang, K.; Li, W. A novel deep learning ensemble model with data denoising for short-term wind speed forecasting. Energy Convers. Manag. 2020, 207, 112524. [Google Scholar] [CrossRef]
- Shahid, F.; Zameer, A.; Mehmood, A.; Raja, M.A.Z. A novel wavenets long short term memory paradigm for wind power prediction. Appl. Energy 2020, 269, 115098. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Liu, Y.; Wang, Y.; Yao, L.; Li, Q.; Li, J.; Pei, S. Long Short-Term Memory Network based on Neighborhood Gates for processing complex causality in wind speed prediction. Energy Convers. Manag. 2019, 192, 37–51. [Google Scholar] [CrossRef]
- Liu, G.; Tang, Z.; Qin, H.; Liu, S.; Shen, Q.; Qu, Y.; Zhou, J. Short-term runoff prediction using deep learning multi-dimensional ensemble method. J. Hydrol. 2022, 609, 127762. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, G.; Huang, F.; Qin, H.; Wang, B.; Yi, L. Directed graph deep neural network for multi-step daily streamflow forecasting. J. Hydrol. 2022, 607, 127515. [Google Scholar] [CrossRef]
- Zhao, Y.; Ye, L.; Li, Z.; Song, X.; Lang, Y.; Su, J. A novel bidirectional mechanism based on time series model for wind power forecasting. Appl. Energy 2016, 177, 793–803. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H.; Song, J. Deep belief network based k-means cluster approach for short-term wind power forecasting. Energy 2018, 165, 840–852. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Liu, Y.; Yao, L.; Yu, X.; Lu, J.; Jiang, Z.; Feng, Z. Wind speed forecasting based on Quantile Regression Minimal Gated Memory Network and Kernel Density Estimation. Energy Convers. Manag. 2019, 196, 1395–1409. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, H.; Zhang, Z.; Pei, S.; Jiang, Z.; Feng, Z.; Zhou, J. Probabilistic spatiotemporal wind speed forecasting based on a variational Bayesian deep learning model. Appl. Energy 2020, 260, 114259. [Google Scholar] [CrossRef]
- Optis, M.; Kumler, A.; Brodie, J.; Miles, T. Quantifying sensitivity in numerical weather prediction-modeled offshore wind speeds through an ensemble modeling approach. Wind Energy 2021, 24, 957–973. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Ishihara, T. Maximum Instantaneous Wind Speed Forecasting and Performance Evaluation by Using Numerical Weather Prediction and On-Site Measurement. Atmosphere 2021, 12, 316. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, Z.; Guo, Y.; Lin, W.; Zhu, W. A self-organizing forecast of day-ahead wind speed: Selective ensemble strategy based on numerical weather predictions. Energy 2021, 218, 119509. [Google Scholar] [CrossRef]
- Chen, N.; Qian, Z.; Nabney, I.T.; Meng, X. Wind Power Forecasts Using Gaussian Processes and Numerical Weather Prediction. IEEE Trans. Power Syst. 2014, 29, 656–665. [Google Scholar] [CrossRef]
- Niu, Z.; Yu, Z.; Tang, W.; Wu, Q.; Reformat, M. Wind power forecasting using attention-based gated recurrent unit network. Energy 2020, 196, 117081. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Li, Y. A Novel Hybrid Strategy Using Three-Phase Feature Extraction and a Weighted Regularized Extreme Learning Machine for Multi-Step Ahead Wind Speed Prediction. Energies 2018, 11, 321. [Google Scholar] [CrossRef]
- Loukatou, A.; Howell, S.; Johnson, P.; Duck, P. Stochastic wind speed modelling for estimation of expected wind power output. Appl. Energy 2018, 228, 1328–1340. [Google Scholar] [CrossRef]
- Jiang, W.; Yan, Z.; Feng, D.; Hu, Z. Wind speed forecasting using autoregressive moving average/generalized autoregressive conditional heteroscedasticity model: Wind speed forecasting using arma-garch model. Eur. Trans. Electr. Power 2012, 22, 662–673. [Google Scholar] [CrossRef]
- Erdem, E.; Shi, J. ARMA based approaches for forecasting the tuple of wind speed and direction. Appl. Energy 2011, 88, 1405–1414. [Google Scholar] [CrossRef]
- Ailliot, P.; Monbet, V. Markov-switching autoregressive models for wind time series. Environ. Model. Softw. Environ. Data News 2012, 30, 92–101. [Google Scholar] [CrossRef]
- Arenas-López, J.P.; Badaoui, M. Stochastic modelling of wind speeds based on turbulence intensity. Renew. Energy 2020, 155, 10–22. [Google Scholar] [CrossRef]
- Karakuş, O.; Kuruoğlu, E.E.; Altınkaya, M.A. One-day ahead wind speed/power prediction based on polynomial autoregressive model. Iet Renew. Power Gen. 2017, 11, 1430–1439. [Google Scholar] [CrossRef]
- Tang, J.; Brouste, A.; Tsui, K.L. Some improvements of wind speed Markov chain modeling. Renew. Energy 2015, 81, 52–56. [Google Scholar] [CrossRef]
- Azeem, A.; Fatema, N.; Malik, H.; Srivastava, S.; Malik, H.; Sharma, R. k-NN and ANN based deterministic and probabilistic wind speed forecasting intelligent approach. J. Intell. Fuzzy Syst. 2018, 35, 5021–5031. [Google Scholar] [CrossRef]
- Vassallo, D.; Krishnamurthy, R.; Sherman, T.; Fernando, H.J.S. Analysis of Random Forest Modeling Strategies for Multi-Step Wind Speed Forecasting. Energies 2020, 13, 5488. [Google Scholar] [CrossRef]
- Jamil, M.; Zeeshan, M. A comparative analysis of ANN and chaotic approach-based wind speed prediction in India. Neural Comput. Appl. 2018, 31, 6807–6819. [Google Scholar] [CrossRef]
- Chen, K.; Yu, J. Short-term wind speed prediction using an unscented Kalman filter based state-space support vector regression approach. Appl. Energy 2014, 113, 690–705. [Google Scholar] [CrossRef]
- Santamaría-Bonfil, G.; Reyes-Ballesteros, A.; Gershenson, C. Wind speed forecasting for wind farms: A method based on support vector regression. Renew. Energy 2016, 85, 790–809. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, G.; Chen, B.; Han, J.; Zhao, Y.; Zhang, C. Short-term wind speed prediction model based on GA-ANN improved by VMD. Renew. Energy 2020, 156, 1373–1388. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.N.; Srikanth, N. A Novel Empirical Mode Decomposition With Support Vector Regression for Wind Speed Forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1793–1798. [Google Scholar] [CrossRef]
- Wang, H.; Sun, J.; Sun, J.; Wang, J. Using Random Forests to Select Optimal Input Variables for Short-Term Wind Speed Forecasting Models. Energies 2017, 10, 1522. [Google Scholar] [CrossRef]
- Shukur, O.B.; Lee, M.H. Daily wind speed forecasting through hybrid KF-ANN model based on ARIMA. Renew. Energy 2015, 76, 637–647. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.; Li, Y. Comparison of two new ARIMA-ANN and ARIMA-Kalman hybrid methods for wind speed prediction. Appl. Energy 2012, 98, 415–424. [Google Scholar] [CrossRef]
- Cadenas, E.; Rivera, W. Wind speed forecasting in three different regions of Mexico, using a hybrid ARIMA-ANN model. Renew. Energy 2010, 35, 2732–2738. [Google Scholar] [CrossRef]
- Zhang, D.; Peng, X.; Pan, K.; Liu, Y. A novel wind speed forecasting based on hybrid decomposition and online sequential outlier robust extreme learning machine. Energy Convers. Manag. 2019, 180, 338–357. [Google Scholar] [CrossRef]
- Wang, L.; Guo, Y.; Fan, M.; Li, X. Wind speed prediction using measurements from neighboring locations and combining the extreme learning machine and the AdaBoost algorithm. Energy Rep. 2022, 8, 1508–1518. [Google Scholar] [CrossRef]
| Model | Hyperparameter | Optimization Range |
|---|---|---|
| LGB-GPR | Tree Maximum depth | (3–15) |
| Max number of leaves | (10–150) | |
| Learning rate | (0.005–0.2) | |
| Minimal number of data | (20–300) | |
| Kernel | (‘RBF’, ‘W’, ‘RQ’) | |
| LGB | Tree Maximum depth | (3–15) |
| Max number of leaves | (10–150) | |
| Learning rate | (0.005–0.2) | |
| Minimal number of data | (20–300) | |
| RF | Tree Maximum depth | (3–15) |
| Learning rate | (0.005–0.2) | |
| LSTM | Hidden layer nodes | (8–32) |
| Dropout | (0.01–0.5) | |
| Batch-size | (8–32) | |
| Epochs | 100 | |
| Optimizer | Adam | |
| ANN | Hidden layer nodes | (8–32) |
| Dropout | (0.01–0.5) | |
| Batch-size | (8–32) | |
| Epochs | 100 | |
| Optimizer | Adam | |
| SVR | Kernel | (‘rbf’, ‘poly’, ‘sigmoid’) |
| GPR | Kernel | (‘C’, ‘RBF’, ‘RQ’) |
| Model (R2) | Dataset 1 | Dataset 2 | Dataset 3 | Average |
|---|---|---|---|---|
| SVR | 0.851 | 0.878 | 0.818 | 0.849 |
| LR | 0.947 | 0.956 | 0.949 | 0.951 |
| RF | 0.932 | 0.951 | 0.940 | 0.941 |
| ANN | 0.940 | 0.956 | 0.924 | 0.940 |
| LSTM | 0.946 | 0.960 | 0.953 | 0.953 |
| LGB | 0.950 | 0.961 | 0.952 | 0.954 |
| GPR | 0.917 | 0.936 | 0.949 | 0.934 |
| LGB-GPR | 0.954 | 0.963 | 0.956 | 0.958 |
| Model (RMSE) | Dataset 1 | Dataset 2 | Dataset 3 | Average |
|---|---|---|---|---|
| SVR | 0.539 | 0.521 | 0.569 | 0.543 |
| LR | 0.321 | 0.311 | 0.301 | 0.311 |
| RF | 0.364 | 0.331 | 0.328 | 0.341 |
| ANN | 0.342 | 0.311 | 0.368 | 0.340 |
| LSTM | 0.326 | 0.299 | 0.290 | 0.305 |
| LGB | 0.305 | 0.291 | 0.285 | 0.294 |
| GPR | 0.401 | 0.377 | 0.301 | 0.360 |
| LGB-GPR | 0.300 | 0.286 | 0.280 | 0.288 |
| Model (MAPE) | Dataset 1 | Dataset 2 | Dataset 3 | Average |
|---|---|---|---|---|
| SVR | 0.409 | 0.350 | 0.367 | 0.375 |
| LR | 0.156 | 0.138 | 0.136 | 0.143 |
| RF | 0.182 | 0.143 | 0.142 | 0.156 |
| ANN | 0.170 | 0.138 | 0.170 | 0.159 |
| LSTM | 0.167 | 0.133 | 0.141 | 0.147 |
| LGB | 0.156 | 0.130 | 0.119 | 0.135 |
| GPR | 0.209 | 0.170 | 0.130 | 0.170 |
| LGB-GPR | 0.152 | 0.128 | 0.118 | 0.133 |
| Model (ICPC) | Dataset 1 | Dataset 2 | Dataset 3 | Average |
|---|---|---|---|---|
| GPR | 0.868 | 0.961 | 0.798 | 0.876 |
| LGB-GPR | 0.945 | 0.980 | 0.989 | 0.971 |
| Model (CRPS) | Dataset 1 | Dataset 2 | Dataset 3 | Average |
|---|---|---|---|---|
| GPR | 0.225 | 0.209 | 0.165 | 0.200 |
| LGB-GPR | 0.165 | 0.157 | 0.148 | 0.157 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Wang, C.; Qin, H.; Fu, J.; Shen, Q. A Novel Hybrid Machine Learning Model for Wind Speed Probabilistic Forecasting. Energies 2022, 15, 6942. https://doi.org/10.3390/en15196942
Liu G, Wang C, Qin H, Fu J, Shen Q. A Novel Hybrid Machine Learning Model for Wind Speed Probabilistic Forecasting. Energies. 2022; 15(19):6942. https://doi.org/10.3390/en15196942
Chicago/Turabian StyleLiu, Guanjun, Chao Wang, Hui Qin, Jialong Fu, and Qin Shen. 2022. "A Novel Hybrid Machine Learning Model for Wind Speed Probabilistic Forecasting" Energies 15, no. 19: 6942. https://doi.org/10.3390/en15196942
APA StyleLiu, G., Wang, C., Qin, H., Fu, J., & Shen, Q. (2022). A Novel Hybrid Machine Learning Model for Wind Speed Probabilistic Forecasting. Energies, 15(19), 6942. https://doi.org/10.3390/en15196942






