Abstract
Many systems in use today require strong cryptographic primitives to ensure confidentiality and integrity of data. This is especially true for energy systems, such as smart grids, as their proper operation is crucial for the existence of a functioning society. Because of this, we observe new developments in the field of cryptography every year. Among the developed primitives, one of the most important and widely used are iterated block ciphers. From AES (Advanced Encryption Standard) to LEA (Lightweight Encryption Algorithm), these ciphers are omnipresent in our world. While security of the encryption process of these ciphers is often meticulously tested and verified, an important part of them is neglected—the key expansion. Many modern ciphers use key expansion algorithms which produce reversible sub-key sequences. This means that, if the attacker finds out a large-enough part of this sequence, he/she will be able to either calculate the rest of the sequence, or even the original key. This could completely compromise the cipher. This is especially concerning due to research done into side-channel attacks, which attempt to leak secret information from memory. In this paper, we propose a novel scheme which can be used to create key expansion algorithms for modern ciphers. We define two important properties that a sequence produced by such algorithm should have and ensure that our construction fulfills them, based on the research on hashing functions. In order to explain the scheme, we describe an example algorithm constructed this way, as well as a cipher called IJON which utilizes it. In addition to this, we provide results of statistical tests which show the unpredictability of the sub-key sequence produced this way. The tests were performed using a test suite standardized by NIST (National Institute for Standards and Technology). The methodology of our tests is also explained. Finally, the reference implementation of the IJON cipher is published, ready to be used in software. Based on the results of tests, we conclude that, while more research and more testing of the algorithm is advised, the proposed key expansion scheme provides a very good generation of unpredictable bits and could possibly be used in practice.
1. Introduction
Data integrity and confidentiality are the crucial security requirements of information systems and communication networks, including smart grids [1,2]. Deployment of protection methods allows for secure data transmission in cyberspace. However, the security services need efficient cryptography algorithms, such as symmetric block ciphers [3]. These kinds of algorithms are building blocks of modern security services—from privacy protection to authentication of smart meters [4].
Although nowadays most discussion on security focuses on modern algorithms and protocols, cryptography itself is a very old art. One of the oldest mentions of encryption is the Caesar’s cipher, allegedly used by the ruler of ancient Rome. It was a simple cipher operating on text written in Latin alphabet. As centuries passed, other ciphers have improved on its design, with a notable example being the Vigènere cipher. It was also based on Latin alphabet but used a secret key in a way similar to modern constructions. Much later, in the 20th century, the Enigma machine was used by German army during World War II to encrypt classified military information. The next step in evolution of cryptography came with the invention of a computer which surpassed humans’ computing ability. This made it necessary to create more complex encryption algorithms that would be able to withstand the newfound computing power without breaking. Works in the field of telecommunication and information theory, based on research of Claude Shannon (among others) served an important role in this development. This led to invention of Data Encryption Standard (DES). This could be considered the beginning of era of modern cryptography, based on ciphers designed for digital computers. Following into the 1990s and early 2000s, improvements made in the area of processing units and other integrated circuits caused DES to become obsolete. Its key sizes were deemed too small and attempts to improve its security through multiple iterations (Triple DES) were thwarted by new attacks. A new standard for cryptography became a necessity. Out of this necessity, Advanced Encryption Standard (AES) was introduced. Despite the time passed since its inception, AES remains in widespread use and is still considered a secure choice for data confidentiality. Nonetheless, new algorithms are still being created in order to improve—if not in terms of security then in terms of performance and ease of implementation [5,6]. Both DES and AES, as well as many modern ciphers, follow a structure called an iterated cipher in which the encryption process is split into a number of rounds. Every round requires a separate secret sub-key. To fulfill this requirement, each cipher of this type defines its own key expansion algorithm. The role of the algorithm is to derive a sequence of sub-keys from the main key.
1.1. Motivation
A lot of effort has been put over the years into making modern symmetric ciphers secure. A lot of this effort was focused on the encryption process itself, and less on the process of key expansion. This may be observed in the fact that many currently used and upcoming ciphers have fully reversible key expansion algorithms. This means that, given a long enough sequence of sub-keys, the attacker is able to decipher not only the rest of the sequence, but often the main key itself. Example ciphers which exhibit this behaviour include AES and LEA. AES has been the standard for symmetric encryption for around 20 years, and no practical attacks against it have been found. Specifically, no attacks were found that would target its key expansion. Despite this, we cannot be certain that a new attack is not developed in 1, 5 or perhaps 10 years. Modern constructions should not ignore this possibility. This is especially true when one takes into account the research into side-channel attacks, which do not attack the cipher directly. Instead, they attack the environment the algorithm is performed in. The goal of such attacks is to leak secret values from memory. If a sufficiently large part of the sub-key sequence was to be leaked this way, any cipher with reversible key expansion would be instantly compromised. To prevent this from happening, the sub-key sequence should have two important properties:
- The main key should not be directly used as part of the sub-key sequence;
- Every sub-key should be sufficiently difficult to derive from any other sub-key, including the one happening before and after it in the sequence.
The word “sufficiently” in this context means a varying degree of security, but, in general, it should be practically impossible to guess one sub-key based on the knowledge of another. This would mean that, in order to break the encryption, an attacker would have to leak every sub-key in the sequence. Given the cost, complexity and low reliability of side-channel attacks should render this attack vector impractical.
1.2. Contribution
The authors of this paper propose a key expansion scheme based on the sponge construction. This solution can be used to create key expansion algorithms for modern block ciphers. The scheme produces a sequence of sub-keys which is difficult to reverse thanks to the properties of the sponge construction. This makes it difficult to retrieve the original key or other sub-keys from part of the sequence. This is achieved by using the excess bits of the state of the sponge as a variable unknown to the attacker, as well as increasing the work performed between absorbing the input and squeezing the output. This is done to protect ciphers from attacks on block ciphers which aim to retrieve original key material from singular sub-keys, e.g., slide attacks or attacks based on side-channel data extraction.
In addition to the scheme itself, a cipher called IJON (pronounced “e-yon”) is proposed. It serves as an example application of the scheme. It is a block cipher with 128 bits of block and key size optimized for processing units capable of operating on 32-bit words. The sequence of sub-keys used in the cipher is generated using a key expansion algorithm based on the sponge construction with 96 bits of sponge state and 32 bitrate.
Finally, the test results are described. The sequence of sub-keys produced by the key expansion algorithm of IJON was tested using a suite of tests for cryptographically secure pseudo-random number generators (CSPRNGs) standardized by National Institute of Standards and Technology (NIST) [7]. The suite checks whether a sequence behaves like a truly random, unpredictable stream of bits. Specific methodology which was assumed during tests is described as well.
The remainder of the paper proceeds as follows: Section 2 provides an introduction to cryptography techniques applied in modern block ciphers. Sponge construction is explained in Section 3. In Section 4, a new sponge-based key expansion scheme is proposed. The IJON cipher is explained in Section 5 in detail, including both the key expansion as well as the encryption processes. Section 6 describes security considerations, testing methodology and results of statistical tests of the cipher. Finally, Section 7 concludes the paper.
The paper is intended for cryptographers working on new symmetric block ciphers. The authors hope it provides them with tools necessary to create secure key expansion algorithms for their constructions. Additionally, any readers interested in developments of cryptography should find the paper interesting.
1.3. Related Works
The problems arising from usage of reversible sub-key sequences have been noticed before. Latest developments meant to create a secure key expansion scheme have been mostly focused on advanced mathematics, specifically chaos maps [8,9,10]. While these approaches are most likely to result in a solution, they are also difficult to follow for readers unfamiliar with the topic. When new ciphers are created, it is not only important that they are safe, but also that it is relatively easy to prove that they are safe, or to approximate their level of security. That is why we propose a solution that is based on less complex concepts and constructions—specifically, the sponge construction. Instead of placing the trust in mathematics, we place it in the research previously performed in the field of hashing functions. This way, the resulting solution is much easier to understand for people not acquainted with advanced mathematics—for example software developers, project managers, and smart grid engineers. We believe that, since those are the people who will benefit from results of our work, it is important that they are able to comprehend it. At the same time, we strongly believe that the increase in simplicity will not negatively impact the practical application of our solution. In fact, we provide a reference implementation of the proposed cipher which is ready to be used in software which needs symmetric ciphers with strong key expansion algorithms.
1.4. Acronyms
The acronyms used in the paper are listed and expanded in Table 1 below. The name “IJON” is not an acronym.

Table 1.
Acronyms used in the paper.
2. Symmetric Block Ciphers
An algorithm is a set of instructions meant to be performed in specific order with a certain purpose behind it. Therefore, a cipher can be viewed as a set of algorithms. Every cipher defines at least two algorithms: encryption and decryption. Purpose of encryption is to transform secret data (called plaintext) in a way that prevents anyone without the knowledge of the special secret key from recovering it. At the same time, anyone who knows the key can easily recover plaintext from the encrypted data (called ciphertext) using the decryption algorithm. Additional algorithms may also be a part of the cipher if they are necessary.
Ciphers are divided into two categories as seen in Figure 1: symmetric ciphers and asymmetric ciphers. Symmetric ciphers use the same key during encryption and decryption, while asymmetric ciphers use two distinct, albeit related keys for each operation. The difference does not have any security implications—neither type of cipher is inherently “more secure”. Instead, it necessitates different assumptions about the privacy of the key. This in turn causes each type of ciphers to have different use cases. In practice, both types often are used together. This way they are able to complement each other. Symmetric ciphers can further be divided into stream and block ciphers. Stream ciphers encrypt and decrypt one bit at a time. Block ciphers operate on blocks of data, which have fixed length usually defined in bits or bytes. Encryption and decryption algorithms of such ciphers take a block of data of specified length as input and produce a different block of data of the same length.
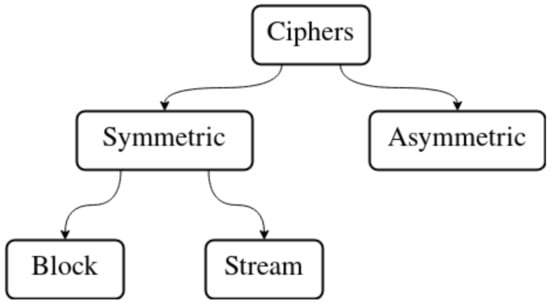
Figure 1.
Types of ciphers.
A popular design choice for block ciphers is a construction called an iterated cipher, shown in Figure 2. Instead of creating one large algorithm for encryption, a round function is defined. It modifies internal state of the cipher during execution. It is applied to the plaintext a certain number of times called number of rounds. Output of the last round is the ciphertext. Each iteration of the round function usually uses a sub-key. It is a smaller piece of data generated from the original key. An inverse round function must also be defined. It is used during decryption, to undo the work performed during encryption. Decryption usually applies sub-keys in reverse order. This approach not only makes creating a cipher simpler, but also minimizes code size. It makes it necessary to define additional algorithm within the cipher, called the key expansion algorithm. Its role is to generate a sequence of sub-keys from the main key.
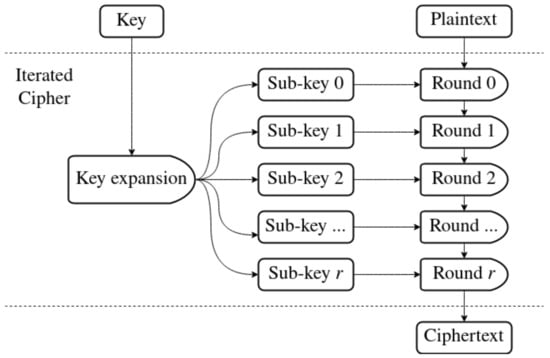
Figure 2.
Encryption in an iterated cipher with r number of rounds.
Iterated ciphers may be implemented in a multitude of ways. One of them is a substitution–permutation network (SPN), as seen in Figure 3. This type of construction is divided into two layers: the substitution layer and permutation layer. The role of the first one is to achieve nonlinearity. This means that the cipher is more difficult to approximate with linear functions. This mitigates attacks based on linear cryptanalysis [11]. Nonlinearity is achieved by using a function usually called an S-BOX. Substitution is the act of replacing one value with another. It is often implemented using a lookup-table (LUT) to allow any possible mapping from input to output. The other part of an SPN is a permutation layer. Its role is to mix the bits of the state together. This layer might only swap bits around, or also mix them using XOR, matrix multiplication or other operations. In the end, the purpose of the P-BOX is to increase diffusion. Making bits of state change positions with each round causes each bit of the output to depend on multiple input bits.
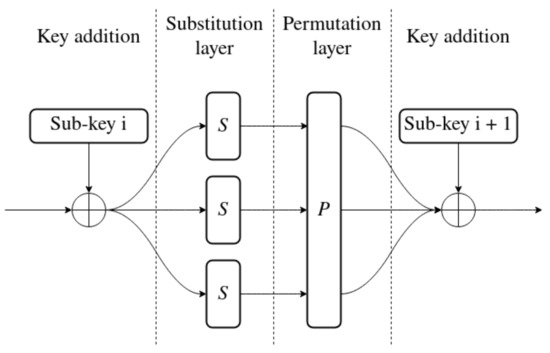
Figure 3.
Full round of SPN.
An alternative to SPN is a construction called Feistel network. Assume that desired block size of the cipher is N bits. To create a Feistel network, an F function needs to be defined. The function has to accept two inputs: half of the block ( bits long) and a sub-key. The Feistel network begins by splitting the input block into two halves. During each round, the left half is combined with a sub-key by the F function. The output of the function is then combined with the right half using the XOR operation. As the last step in a round, the halves are reordered. The left half becomes the right and vice versa. This may continue for any number of rounds. After the last round, the two halves are concatenated into an N bit block of ciphertext. Feistel network is a simple construction with great potential. It was proven to be secure even with a small number of rounds as long as the input of the F function is sufficiently hard to predict based on its output [12]. Additionally, the function F does not need to be reversible as the decryption algorithm uses the function itself rather than its inverse. The only requirement is that the sub-keys have to be supplied to the round function in reverse order during decryption.
In contrast to a Feistel network or an SPN, Add-Rotate-XOR (ARX) does not directly refer to the construction of a block cipher. Instead, ARX can be thought of as a special category of ciphers. Ciphers of this category are built entirely out of three operations: addition modulo , XOR of n-bit words and n-bit rotations by a constant amount. These operations are very simple and easy to approximate in various ways by potential attackers. Because of this, creation of a secure cipher based solely on them is not a trivial task. However, if used properly, the ARX operations provide the resulting cipher with important advantages, listed below.
- All three operations are very fast, usually taking small number of cycles on various CPU architectures. This causes software implementations of such ciphers to be very efficient.
- Not only is the time of their execution low but also constant. This means that ciphers built out of them are naturally immune to side-channel attacks based on the time of execution of certain parts of code [13].
- Since the ciphers use only basic operations, they are often very easy to implement and analyze.
3. Sponge Construction
Sponge construction [14] is a scheme most often considered as the core of hashing algorithms rather than block ciphers. It was introduced as a part of the Keccak hash algorithm, the winner of the SHA-3 (Secure Hashing Algorithm 3) competition [15]. Since it is intended to be used in hashing functions, a sequence of bits generated using a sponge construction is usually difficult to reverse. By “reversing” a sequence, we mean calculating one part of the sequence knowing another part of it, or finding the “seed” it was based on. This property also makes it useful for creation of key expansion algorithms.
Sponge construction requires three elements. The first is a function f which takes b-bit data block as input and outputs another b-bit data block (b is the size of the internal state of the sponge construction). The second is the bitrate r, which defines the size of chunks in which sponge consumes input and returns output (r should be always smaller than b). Finally, the third element is a pad function, which makes sure that input to the sponge is always a multiple of r. In this paper, we can ignore the pad function and assume that input always has correct length.
The sponge construction allows creation of a function which generates output of any size (limited to multiples of bitrate) from input of any size. Sponge functions work in the way visualized in Figure 4. In the figure, the vertical dashed line divides the absorbing and squeezing stages. The horizontal lines mark the part of the state directly modified by the input and directly copied to output. Other bits of the state have to be populated by the f function. The steps of the function are presented below.
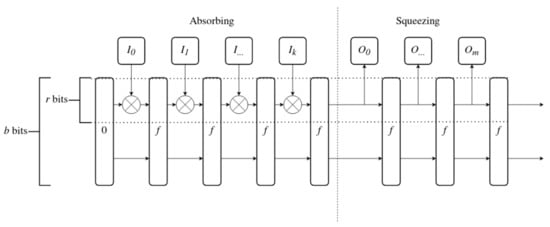
Figure 4.
Sponge function.
- 1.
- Set all b bits of internal state to 0.
- 2.
- Divide input data into chunks of r bits: , , up to for selected k.
- 3.
- For each chunk of input data perform the absorbing procedure:
- (a)
- Apply the input chunk to the first r bits of internal state through the XOR operation,
- (b)
- Apply the f function to the internal state.
- 4.
- After all input has been absorbed by the sponge, start squeezing out the output:
- (a)
- Append first r bits of the state to the output,
- (b)
- Apply the f function to the internal state.
- 5.
- Stop after all necessary output has been squeezed out.
4. Sponge-Based Key Expansion
The role of the key expansion algorithm in an iterated cipher is to generate sub-keys for all the rounds of encryption and decryption. The sub-keys have to depend on the value of the main key. The bits of the main key are also collectively known as key material. At the same time, we suggest that it should be difficult to guess one part of the sequence of sub-keys from another. It should also be difficult to guess the seed that the sequence was generated from. To make it possible, we propose usage of the sponge construction as the framework for key expansion algorithms. In order to explain how one would use the sponge this way, we propose a novel key expansion algorithm to serve as an example. Our key expansion algorithm is based entirely on 32-bit ARX operations. This way it should be easy to implement and be optimized for 32-bit processing units. The size of its internal state is 96 bits, which can be easily implemented as three 32-bit words. The input to the key expansion algorithm is 128 bits (16 bytes) of key material, divided into four input words. In terms of the sponge construction, the bitrate parameter is equal to 32 bits [14]. Output is also split into 32-bit words, and each output word is a single sub-key.
Key expansion is split into four stages, as seen in Figure 5. The stages, in order, are: initialization, absorbing, mixing and squeezing. Initialization, absorbing and squeezing are all standard phases of the sponge construction.The mixing stage might be thought of as part of the squeezing stage, with output discarded. It is added to increase the amount of work performed on the internal state before output words are collected. The function f is defined later in this section.
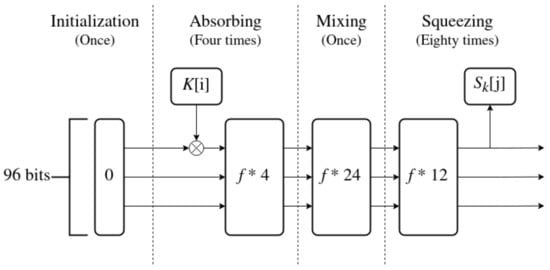
Figure 5.
Sponge-based key expansion algorithm.
The algorithm is described in steps below.
- 1.
- Initialization: Set 96 bits of internal state to 0.
- 2.
- Absorbing:
- (a)
- Absorb a word of input through a XOR operation with the first 32 bits of the state
- (b)
- Apply 4 iterations of the f function to the internal state;
Repeat until all of the key material has been absorbed (4 times). - 3.
- Mixing: Apply 24 iterations of the f function
- 4.
- Squeezing:
- (a)
- Apply 12 iterations of the f function to the internal state;
- (b)
- Squeeze an output word , by saving first 32 bits of the internal state.
Repeat until all of the sub-keys have been squeezed out.
The number of iterations of each stage of the algorithm as well as the number of applications of the f function is based on the length of the input and required length of the output. They also take into account the results of security analysis, to find a good trade-off between security and performance of the algorithm.
The f Function
The f function used in the key expansion algorithm transforms 96-bit input into 96-bit output. Its purpose is to fill the bits of state that are not modified by input data and to mix all the bits of the state. The security of the key expansion algorithm relies heavily on the excess bits of the state. Because of this, the design of the f function is very important.
The function is designed as three applications of a function (“f one-third”), which is presented in Figure 6. It splits input state into three 32-bit words a, b and c. Then, it applies constants , and to the state using XOR. This is followed by a series of ARX operations between the words. In the end, the state is rotated one position to the right to produce the output words, , and .
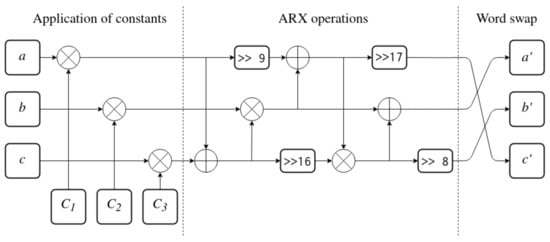
Figure 6.
The fot function (one third of the entire f function).
The application of constants as the first step of the function ensures that any bits are set to 1 prior to the additions, XORs and rotations being performed. This mitigates a fundamental weakness of ARX operations. Every ARX operation will produce an all-zero word as output if given an all-zero input. Thanks to the constants, if the initial state of a, b and c is set to 0, some of the bits will change value to 1 before any other operations take place. In case the input state happens to be equal to the constants, applying the constants will actually have the opposite effect and clear all bits. However, those will be again set back to 1 in the next iteration of the function. Usage of constants at the beginning removes an entire class of trivial weak keys with all bits set to 0 or with a very small number of bits set to 1.
The values of the constants proposed by the authors are given below:
These are so called nothing-up-my-sleeve numbers. A nothing-up-my-sleeve number is a type of a constant generated in a complicated manner, based on values which are hard to control. Oftentimes, fractional parts of mathematical constants are used or values derived from the name of the algorithm. This is done to eliminate any suspicion—a skilled cryptanalyst could theoretically develop a cipher with meticulously chosen constants that allow a backdoor into the algorithm. By using nothing-up-my-sleeve numbers, this is made significantly harder. This, in turn, makes the algorithm more trustworthy.
The function constants have been generated from the name “IJON” (The algorithm was developed in the year 2021, which also marked the hundredth anniversary of the birth of Stanisław Lem—a Polish writer of science fiction and futurologist. Ijon Tichy is the main character in many of his novels and the cipher was named after him.) in the way described in steps below:
- 1.
- Four bytes which form the string IJON (in ASCII encoding) were interpreted as a 32-bit floating point number. In addition to the number itself, its square root and second power were calculated. This resulted in a total of three floating point values.
- 2.
- All three values from previous step were reinterpreted as unsigned integers. The following procedure was performed on each of them;
- (a)
- The integer was multiplied by itself, generating a 64-bit value;
- (b)
- The upper and lower halves of the result from previous step were XORed together to make a 32-bit number;
- (c)
- This number then served as input to the next iteration of the procedure, for a total of 128 iterations;
- 3.
- The result of the last iteration of the procedure became the output of the entire algorithm. Since procedure was performed on three integers, it resulted in three constants: , and .
The ARX operations performed after the application of constants are the core of the function. The order of operations was decided by attempting to obtain the highest possible diffusion between all three words of the state to utilize the state to its full potential. Both order and rotation amounts were determined by trial and error, with resulting sub-key sequences rated by statistical tests which measure randomness [7]. Another consideration was performance on various CPUs—some architectures support shifts by any amount, but some 8-bit architectures might only support rotations through arithmetic shifts, which are limited to 8 bits at most. In those cases, amounts chosen are a multiple of 8, with a potential additional shift by 1 (for example 17 = 8 + 8 + 1, which results in only three rotations).
The last part of the function is 32-bit words swap. During each of three iterations, every word enters the function at a different position to perform different operations. This allows for chaining of three iterations into one full f iteration and results in a larger and more complex procedure being constructed out of smaller steps. The full f function is presented in Figure 7. The first word of the state and its path through the function are highlighted. This construction both increases the diffusion and allows for memory/time trade-off during implementation. If performance is more important than space, loop unrolling might be performed as is usually done. However, if the implementation targets the embedded environment, space might be more important than speed of execution. In such case, the key expansion algorithm may be implemented as a loop which repeatedly executes the function. Since is relatively small—consisting of only 5 XORs, 3 additions and 4 rotations—it would result in very small code size, at the expense of performance.
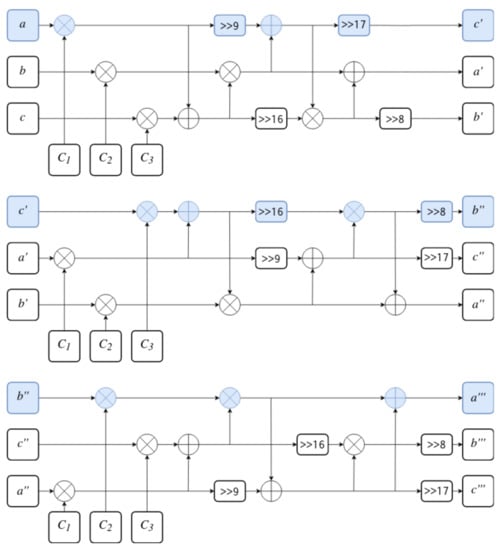
Figure 7.
The f function made of three iterations of .
5. IJON Cipher
The proposed sponge-based key expansion algorithm was used in a selected iterated cipher. The authors proposed such cipher and decided to call it IJON. The IJON cipher encrypts data over the span of 10 rounds. Each round consumes eight sub-keys. This results in a total of 80 sub-keys in a sequence generated by the key expansion algorithm.
The design of IJON was based on the research into the Long Trail Strategy (LTS) [16]. LTS is a cipher design strategy applicable to ARX ciphers. It was inspired by previous work on AES and the Wide Trail Strategy (WTS) [17]. Its aim is to allow bounding of the possible probabilities of differential trails within the ciphers. To achieve that, the ciphers are constructed in a way similar to traditional substitution–permutation networks, except with S-BOXes implemented as series of ARX operations (called ARX-BOX).
LTS focuses on the substitution layer, by introducing multiple applications of the S-BOX intertwined with sub-key applications before the permutation layer. This is done to place the primary burden of achieving diffusion on the substitution layer. This allows differential probabilities to be bounded, approximating complexity of an attack. All of this is reflected in the architecture of IJON encryption algorithm. To match the nomenclature of the LTS research, in this section, applications of the S-BOX will be referred to as rounds, while what is usually called a round in iterated ciphers will be referred to as a step.
5.1. Encryption Algorithm
The encryption algorithm is visualized in Figure 8 and described below.
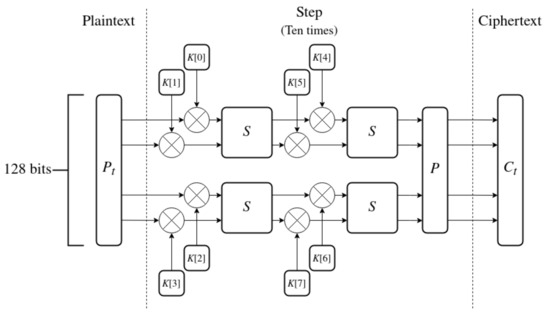
Figure 8.
The encryption algorithm of IJON.
- 1.
- Plaintext contains 128 bits of data and serves as an input to the algorithm.
- 2.
- Split into 4 words of 32 bits each.
- 3.
- Perform ten steps on the words of the state. Each step has 8 sub-keys K assigned from the sequence generated by the key expansion.
- (a)
- Combine four first sub-keys with the words of the state using XOR.
- (b)
- Apply the S-BOX S twice in parallel to the state.
- (c)
- Combine four last sub-keys.
- (d)
- Perform the second application of S-BOXes.
- (e)
- Apply the P-BOX P.
- 4.
- The output of the last step is the resulting ciphertext .
As the core of the substitution layer IJON can use a selected S-BOX. The authors decided to use a 64-bit ARX-BOX called Alzette [18]. It offers great statistical properties even at just two applications while being very efficient in both software and hardware. Due to the IJON block size being 128 bits long, two parallel applications of this S-BOX are performed on the input during each application.
The permutation layer, while deemphasized in the LTS, still remains a vital part of the SPN construction. It ensures mixing of all the bits of the input together. A construction similar to a Feistel network is used in IJON as the permutation layer. The F function is inspired by the one used in the SPARX family of ciphers, introduced as part of the LTS research [16]. The entire Feistel-like P-BOX is shown in Figure 9, while the F function itself is shown in Figure 10.
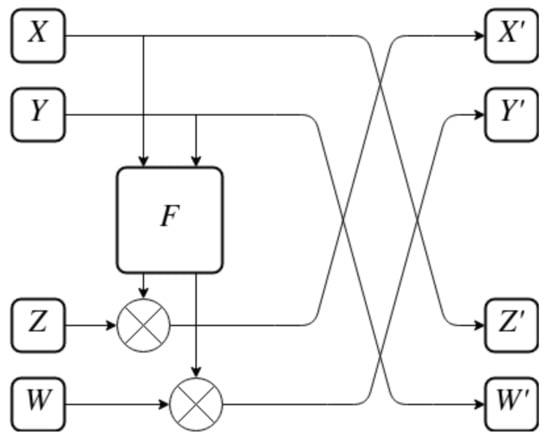
Figure 9.
Feistel-like P-BOX of IJON.
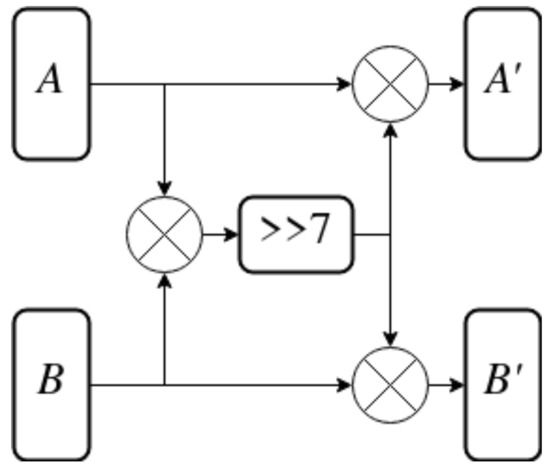
Figure 10.
F function used in P-BOX.
5.2. Decryption Algorithm
The role of the decryption algorithm is to reverse the work performed by encryption—a given ciphertext and sub-key sequence should return the original plaintext. Because of this, its design is closely related to the encryption function through inverse operations. Luckily, all ARX operations have trivial inverses: inverse of XOR is the XOR itself, inverse of rotation right by N bits is either rotation left by the same amount, or rotation right by bits (when working with 32-bit words) and inverse of addition modulo is subtraction. Thanks to this, many complex functions built out of those three operations are easily invertible. When defining the decryption algorithm, the goal is to find those inversions and perform them in reverse order.
The decryption algorithm is listed in steps below and is presented in Figure 11.
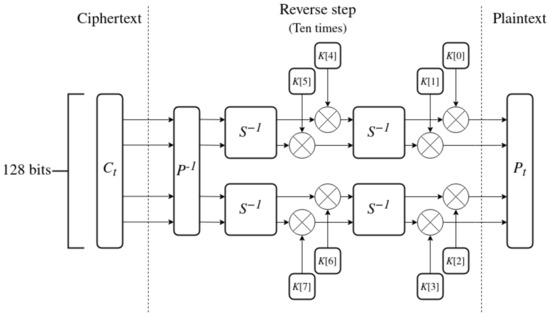
Figure 11.
Decryption algorithm.
- 1.
- Ciphertext contains 128 bits of encrypted data and serves as the input to the algorithm.
- 2.
- Split into 4 words of 32 bits each.
- 3.
- Perform ten reverse steps on the words of the state. Each step has 8 sub-keys K assigned from the sequence generated by the key expansion.
- (a)
- Apply the inverse P-BOX to reverse the mixing of bits.
- (b)
- Apply the inverse S-BOX twice in parallel to the state.
- (c)
- Combine four last sub-keys with the words of the state using XOR.
- (d)
- Apply the inverse S-BOX again.
- (e)
- Combine the four first sub-keys with the state.
- 4.
- The output of the last decryption step is the resulting plaintext .
It is worth mentioning that the inverse of the P-BOX must be found. This structure is presented in Figure 12. It is used to reverse the order of operations: the application of the F function and the reordering of halves. What is important is that the F function itself stays the same. It is one of the advantages of the Feistel-like structure on which the P-BOX is based.
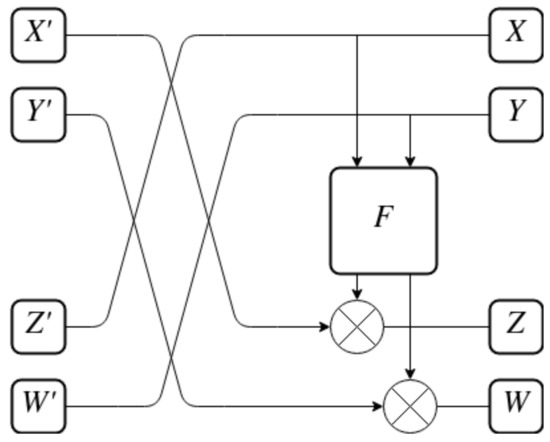
Figure 12.
Inverse P-BOX.
An inverse of the S-BOX is harder to find, although still trivial. This is due to the fact that ARX operations are easily invertible. In fact, most of the operations in the S-BOX do not even have to be replaced—they are their own inverse. The only operation that has to be replaced by its inverse is addition modulo which becomes subtraction.
6. Security Considerations
The functionality of the IJON cipher which contains a sponge-based key expansion algorithm was verified. Additionally, basic diffusion and confusion properties have been tested. This means that a single bit changed in key or plaintext results in massive changes in the ciphertext, with around 50% of bits changing value. This is important to verify, but it is not enough to fully evaluate the security of the cipher. IJON, like many iterated ciphers, has parameters—for example, the number of steps, the number of rounds within a step (S-BOX applications), block size, key size, etc. All of them should have values that are justified either by tests and experiments or by common practice and logic. This section contains security considerations and explains the choices made in design of the cipher.
6.1. Key Size and Block Size
Minimal values for these two parameters are slowly growing as hardware evolves. Ciphers with 64-bit block or key size, albeit sometimes still used in memory-constrained environments, are usually deemed not secure enough. This is mostly due to the key space being too small and prone to a brute force attack. The block size and shortest key of AES cipher is 128 bits, which still holds up very well today after more than 20 years in use. Therefore, 128 bits seems to be the perfect middle-ground between ’too small to be secure’ and ’too big to be practical’. Due to those reasons, this key size was chosen.
The introduced key expansion algorithm may theoretically use keys of any length, as long as the length is a multiple of 32 bits. This can be done by performing the absorbing stage of the algorithm different amount of times. In the future, if 128 bits of key material proves to be insufficient, the algorithm could easily be expanded for longer keys.
6.2. Side-Channel Attacks
The cipher was consciously designed with resistance against time-based side-channel attacks [13] in mind. Thanks to the exclusive usage of constant-time ARX operations, it is easier to implement the cipher in a way that is immune to this type of attack. This includes the reference implementation created to verify functionality of the proposed algorithm [19].
6.3. Slide Attack
Slide attack is a technique which targets iterated ciphers that base their security on a large number of rounds and re-use a single sub-key between multiple rounds [20]. Since IJON is an iterated cipher, it may be susceptible to a slide attack. To counter that, a lot of effort was directed into creating a strong, secure key expansion algorithm. Every sub-key is used only once, in order to make potential attack as complicated as possible. Additionally, even if an attacker comes in possession of a single sub-key, it should be difficult to retrieve the main key or other sub-keys from that information. This is due to the non-invertible sponge construction used as the framework for the key expansion algorithm.
6.4. Construction of Encryption
The important component of the encryption algorithm is the selected S-BOX (in IJON, the Alzette S-BOX was chosen) due to Long Trail Strategy [16] guiding the design of the cipher. Because of that, security approximation was based entirely on its properties. Authors of the Alzette S-BOX [18] claim that two iterations of the ARX-BOX have the Maximum Expected Differential Characteristic Probability (MEDCP) bounded at around . This was decided to be reasonably low for a single step of encryption, and so the number of rounds within a single step was set to 2. The number of steps was set to 10, which allows approximation of maximum differential trail probability at around under the assumption that no other characteristics arise from the repeated use of the S-BOX or from connection with P-BOX within the encryption algorithm. This probability is very small, which means that the number of steps could have been lowered to possibly 8 or 7. However, a security margin was assumed and number of steps during encryption was chosen to be 10.
6.5. Randomness of Key Expansion
Key expansion of IJON has been tested as a Cryptographically Secure Pseudo-Random Number Generator (CSPRNG). The tests were performed according to a specification published by the National Institute of Standards and Technology (NIST) [7].
6.5.1. Methodology
The suite defines a number of tests meant to measure the unpredictability of a random sequence of bits. Each test generates a p-value as an output which characterizes randomness in quantitative way. The sequence should result in a p-value bigger than to pass a test. The tests are listed below:
- 1.
- Frequency (monobit) test
- 2.
- Frequency test within a block
- 3.
- Runs test
- 4.
- Test for the longest run of ones in a block
- 5.
- Binary matrix rank test
- 6.
- Discrete Fourier transform (spectral) test
- 7.
- Non-overlapping template matching test
- 8.
- Overlapping template matching test
- 9.
- Maurer’s “Universal Statistical” test
- 10.
- Linear complexity test
- 11.
- Serial test
- 12.
- Approximate entropy test
- 13.
- Cumulative sums (cusum) test
- 14.
- Random excursions test
- 15.
- Random excursions variant test
All tests put constraints on the input given to them, with one of the constraints being the minimal length of the input sequence. When testing IJON, tests with numbers 5, 8, 9, 10, 14 and 15 have been omitted due to their requirements on length. Additionally, in tests where an arbitrary length of a block was to be chosen, a value of 256 bits was used—the total length of 8 sub-keys used during a single round of encryption.
Sequences generated from expansion of a set of keys have been tested using the test suite. Out of all the keys, most attention was given to the theoretical weak keys. This is a group of keys with only 0, 1 or 2 bits set to 1. Those keys could become trivial weak keys if the algorithm was not properly designed and tested due to the nature of ARX operations used. Additionally, two variants of pseudorandom keys have been tested. In the first variant, 128 bits of the main key were generated, and then expanded using the IJON key expansion algorithm. In the second variant, the entire sequence of 320 bytes was generated, and no expansion was used. All pseudorandom data in both cases have been generated using/dev/urandom—Pseudo-Random Number Generator (PRNG) present in Linux environment. The second variant has been performed to compare the results of IJON key expansion algorithm to a well-known PRNG.
6.5.2. Test Results
Test results for the three sets of keys are presented in Table 2, Table 3 and Table 4. Meaning behind values in columns is described below:

Table 2.
Test results for potential weak keys (8257 samples total).

Table 3.
Test results for the first variant random (10,000 samples total).

Table 4.
Test results for the second variant random (10,000 samples total).
- Max Diff—applicable only to the monobit test, it is the maximal absolute difference between expected and actual number of ones in the sequence. The percentage in the brackets is given in relation to the expected value (100% = 1280 bits).
- Success rate—number of samples from the given set that successfully passed a given test. Percentage in brackets is in relation to the number of samples in the set.
- Min/Max/Avg P—respectively minimal, maximal and average value of P among all samples, both successful and failing. The p-value has to be greater than to pass a test.
The results for the second pseudorandom variant should be treated as a benchmark. They were generated using an industry-standard PRNG and are independent from the IJON cipher structure. Overall, results for all three groups are very similar. Success rates in all cases are above , and average p-values are relatively high: and more. In some rare cases, the IJON-based sequences achieve better results than those generated through Linux PRNG (an example would be the Min P for the longest run of ones test). The differences are so small that they can be attributed to the randomness during bit generation. Therefore, IJON key expansion algorithm could be considered comparable to the Linux/dev/urandom PRNG in terms of generating an unpredictable sequence of bits. What is worth emphasizing is that the difference between results for potential weak keys and first variant random keys is also very small. This means that the potential weak keys are not weaker than random keys generated using a PRNG. In turn, they should not be considered weak at all.
7. Conclusions
Development of modern ciphers leads us towards higher security of smart grids. This paper describes a novel key expansion scheme based on the sponge construction. This construction is able to produce a sequence of subkeys which is difficult to reverse and can be used in iterated modern ciphers. The authors also introduced a new block cipher called IJON. The design of this solution was described in details and a reference implementation was developed. The cipher is able to encrypt and decrypt data as long as the same key is used in both operations, which is a standard way of operation of symmetric ciphers. The new construction is well suited to execute on 32-bit CPUs. The algorithm is based on fast operations on 32-bit words that perfectly fit into registers of such processing units. At the same time, it does not require hardware implementation to perform well, due to low clock cycles required for used operations.
Tests and approximations of security bounds were performed. The results indicate that the algorithm is safe to use. The sequence generated by the key expansion algorithm is very unpredictable and hard to reverse. It is worth mentioning that the security margin left by the number of rounds is very high. It was calculated based on differential probabilities of the used Alzette S-BOX. However, this does not give a guarantee about the cipher’s security. Further tests and analysis are still required in this area. On the other hand, research might also assess that the number of rounds is actually too big. In such case, it may be reduced in future versions of the algorithm to increase efficiency. This could help to increase performance and resolve potential memory requirement problem. However, results of security analysis indicate that the cipher seems to have great potential.
IJON with the sponge-based key expansion algorithm is a fully functional cipher; however, there are still a lot of possibilities for improvements. First of all, further tests are needed to fully evaluate the encryption process in terms of security. In addition, further performance tests and benchmarks are needed. Speed of execution should be tested and compared to other modern ciphers. In addition to that, further optimizations in assembly may be possible using vector processing instructions on various architectures—for instance, SIMD extensions to the x86 instruction set. Furthermore, while the cipher should execute very well on 32-bit microcontrollers, its memory requirements may be a problem in embedded environments. The length of the buffer necessary to hold all sub-keys after key expansion is equal to 320 bytes. This is by no means a small amount, even by today’s standards. This problem could be mitigated by generating sub-keys as needed during encryption, but it is a solution which wastes a lot of cycles by duplicating work. It also does not work with decryption, as sub-keys are used in reverse order. In summary, further research on cipher’s security as well as performance optimizations are required before the algorithm could be widely used. However, the cipher is pretty much ready to be incorporated into software thanks to the reference implementation.
Author Contributions
Conceptualization, M.S. and M.N.; methodology, M.S. and M.N.; software, M.S.; validation, M.S.; formal analysis, M.S. and M.N.; investigation, M.S. and M.N.; writing—original draft preparation, M.S. and M.N.; writing—review and editing, M.S. and M.N.; visualization, M.S.; supervision, M.N.; project administration, M.N.; funding acquisition, M.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been funded by the European Union’s Horizon 2020 Research and Innovation Programme, under Grant Agreement No. 830943, project ECHO (European network of Cybersecurity centres and competence Hub for innovation and Operations). The research was also partially supported by the National Centre for Research and Development, Grant No. CYBERSECIDENT/381319/II/NCBR/2018 on “The federal cyberspace threat detection and response system” (acronym DET-RES) as part of the second competition of the CyberSecIdent Research and Development Program–Cybersecurity and e-Identity.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study—reference implementation of the IJON block cipher—are available online in: https://github.com/msaw328/ijon (accessed on 8 September 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tufail, S.; Parvez, I.; Batool, S.; Sarwat, A. A Survey on Cybersecurity Challenges, Detection, and Mitigation Techniques for the Smart Grid. Energies 2021, 14, 5894. [Google Scholar] [CrossRef]
- Alghassab, M. Analyzing the Impact of Cybersecurity on Monitoring and Control Systems in the Energy Sector. Energies 2022, 15, 218. [Google Scholar] [CrossRef]
- Jain, N.; Chauhan, S.S. Novel Approach Transforming Stream Cipher to Block Cipher. In Proceedings of the 2021 International Conference on Technological Advancements and Innovations (ICTAI), Tashkent, Uzbekistan, 10–12 November 2021; pp. 182–187. [Google Scholar]
- Di Matteo, S.; Baldanzi, L.; Crocetti, L.; Nannipieri, P.; Fanucci, L.; Saponara, S. Secure Elliptic Curve Crypto-Processor for Real-Time IoT Applications. Energies 2021, 14, 4676. [Google Scholar] [CrossRef]
- Rodinko, M.; Oliynykov, R. Comparing Performances of Cypress Block Cipher and Modern Lighweight Block Ciphers on Different Platforms. In Proceedings of the 2019 IEEE International Scientific-Practical Conference Problems of Infocommunications, Science and Technology (PIC S&T), Kyiv, Ukraine, 8–11 October 2019; pp. 113–116. [Google Scholar]
- Alasaad, A.; Alghafis, A. Key-Dependent S-box Scheme for Enhancing the Security of Block Ciphers. In Proceedings of the 2019 2nd International Conference on Signal Processing and Information Security (ICSPIS), Dubai, United Arab Emirates, 30–31 October 2019; pp. 1–4. [Google Scholar]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; National Institute of Standards & Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Xu, Y.; Zhao, M.; Liu, H. Design an irreversible key expansion algorithm based on 4D memristor chaotic system. Eur. Phys. J. Spec. Top. 2022. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Li, Y. Cryptanalyze and design strong S-Box using 2D chaotic map and apply to irreversible key expansion. arXiv 2021, arXiv:2111.05015. [Google Scholar]
- Zhao, M.; Liu, H. Construction of a Nondegenerate 2D Chaotic Map with Application to Irreversible Parallel Key Expansion Algorithm. Int. J. Bifurc. Chaos 2022, 32, 2250081. [Google Scholar] [CrossRef]
- Matsui, M. Linear Cryptanalysis Method for DES Cipher. In Proceedings of the Advances in Cryptology— EUROCRYPT’93; Helleseth, T., Ed.; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Luby, M.; Rackoff, C. How to Construct Pseudorandom Permutations from Pseudorandom Functions. SIAM J. Comput. 1988, 17, 373–386. [Google Scholar] [CrossRef]
- Kocher, P.C. Timing Attacks on Implementations of Diffie-Hellman, RSA, DSS, and Other Systems. In Proceedings of the Advances in Cryptology—CRYPTO’96; Koblitz, N., Ed.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 104–113. [Google Scholar]
- Bertoni, G.; Daemen, J.; Peeters, M.; Van Assche, G. Cryptographic Sponge Functions. 2011. Available online: https://keccak.team/files/CSF-0.1.pdf (accessed on 8 September 2022).
- Dworkin, M. SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions; Federal Inf. Process. Stds. (NIST FIPS); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. [Google Scholar]
- Dinu, D.; Perrin, L.; Udovenko, A.; Velichkov, V.; Großschädl, J.; Biryukov, A. Design Strategies for ARX with Provable Bounds: Sparx and LAX. In Proceedings of the Advances in Cryptology—ASIACRYPT 2016; Cheon, J.H., Takagi, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 484–513. [Google Scholar]
- Daemen, J.; Rijmen, V. The Wide Trail Design Strategy. In Proceedings of the Cryptography and Coding; Honary, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 222–238. [Google Scholar]
- Beierle, C.; Biryukov, A.; Cardoso dos Santos, L.; Großschädl, J.; Perrin, L.; Udovenko, A.; Velichkov, V.; Wang, Q. Alzette: A 64-Bit ARX-box. In Proceedings of the Advances in Cryptology—CRYPTO 2020; Micciancio, D., Ristenpart, T., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 419–448. [Google Scholar]
- Sawka, M. Reference Implementation of the IJON Block Cipher. 2021. Available online: https://github.com/msaw328/ijon (accessed on 8 September 2022).
- Biryukov, A.; Wagner, D. Slide Attacks. In Proceedings of the Fast Software Encryption; Knudsen, L., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 245–259. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).