Study on Aerodynamic Characteristics of a Savonius Wind Turbine with a Modified Blade
Abstract
:1. Introduction
2. Wind Turbine Model
2.1. Performance Parameter
2.2. Numerical Simulation
2.2.1. Turbulence Model
2.2.2. Establishment of Computational Domain
2.2.3. Grid Division
2.2.4. Grid and Time Step Independence Verification
2.2.5. Comparison between Wind Tunnel Test and Numerical Simulation
2.3. Wind Tunnel Test
3. Results and Analysis
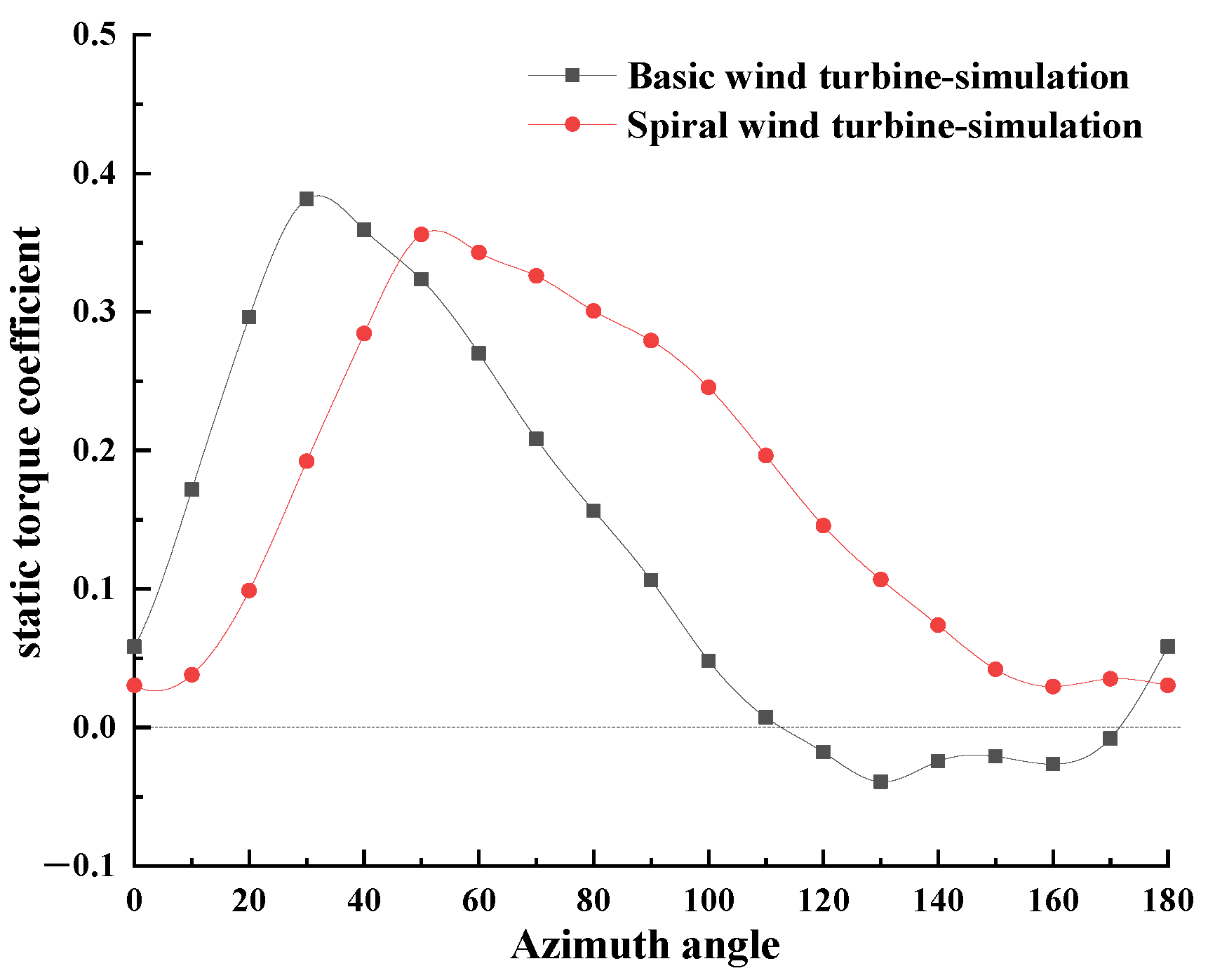
3.1. Static Starting Characteristic
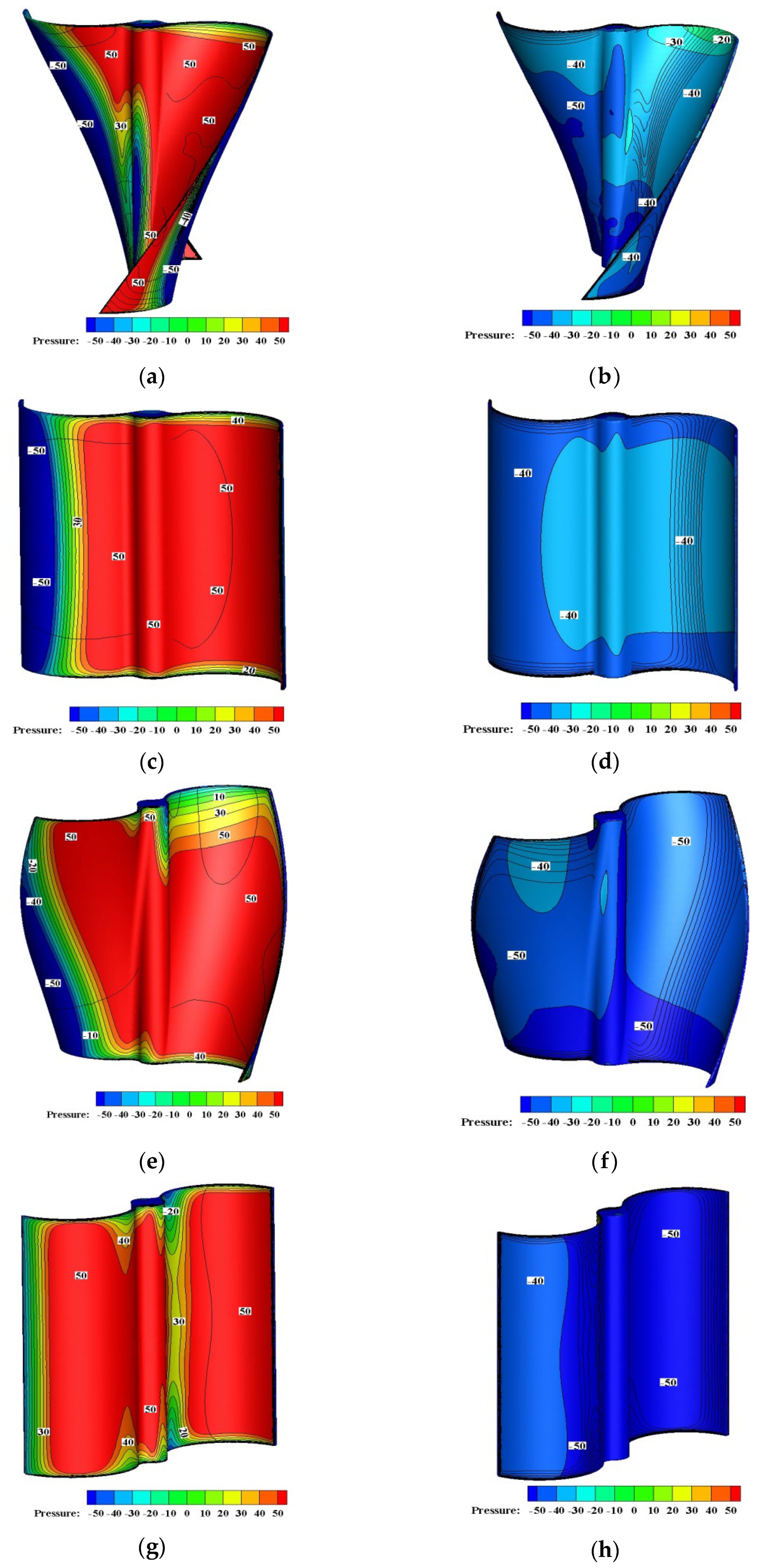
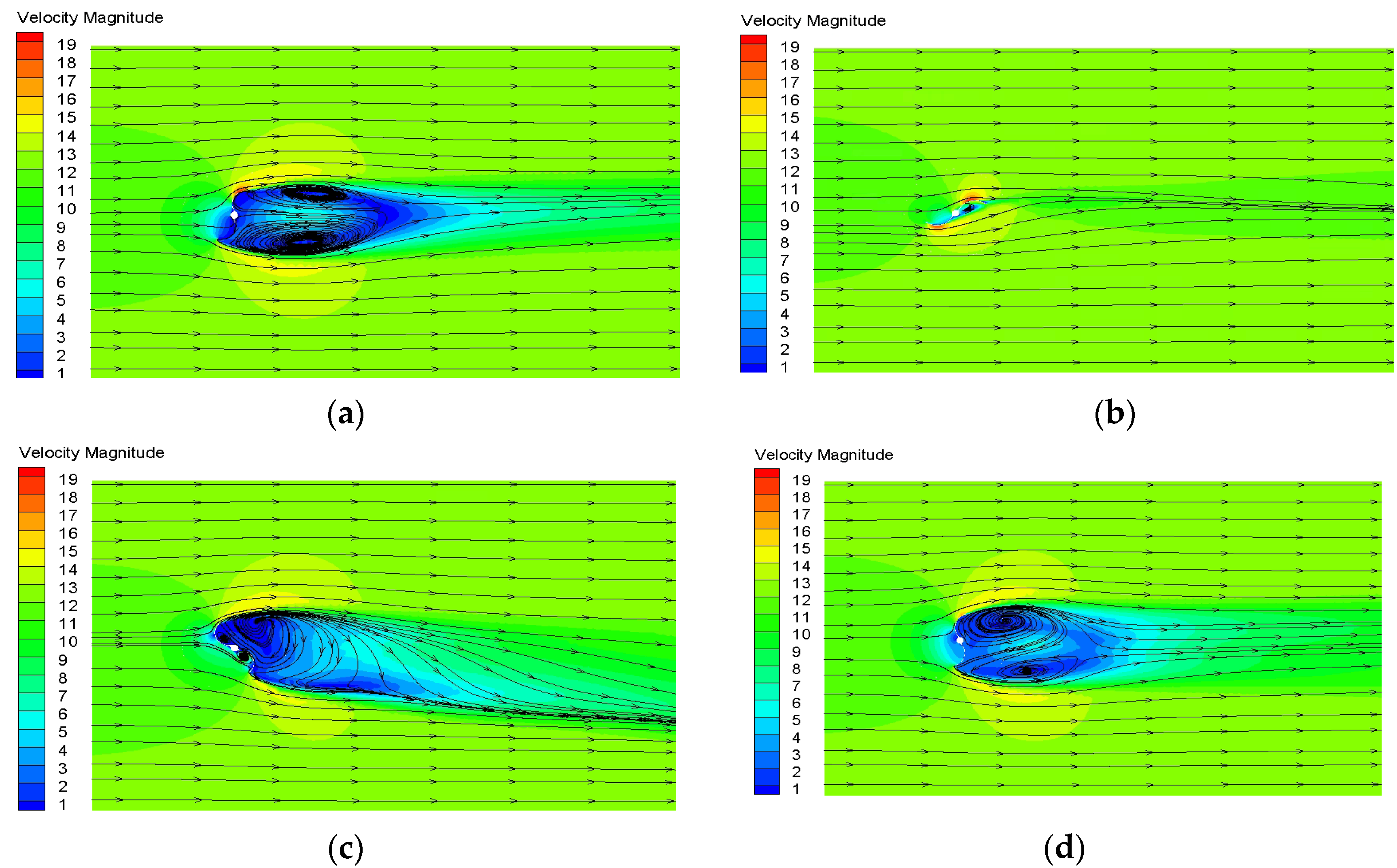
3.2. Static Flow Field
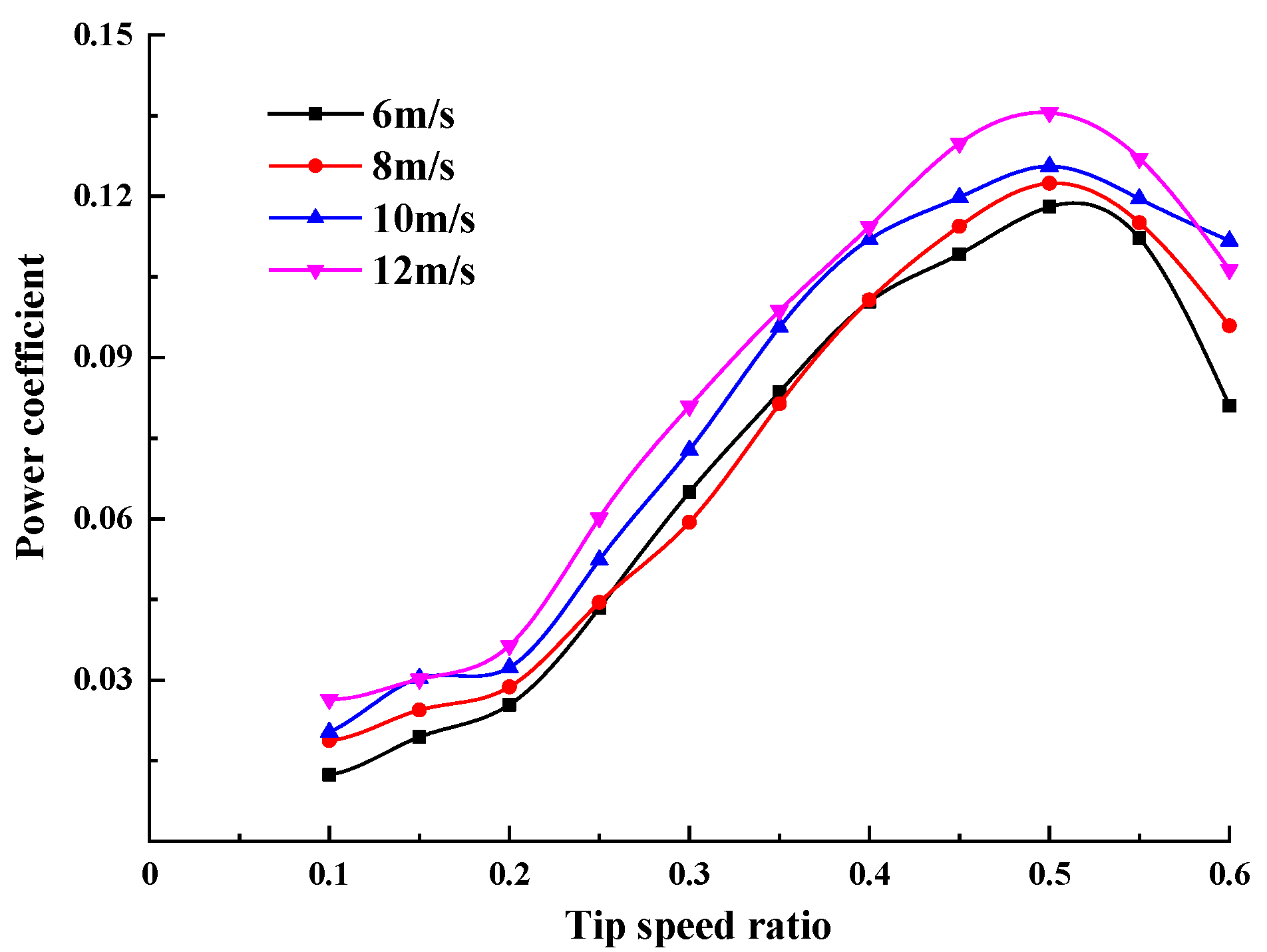
3.3. Power Characteristic
3.4. Rotational Speed Characteristic
4. Conclusions
- (1)
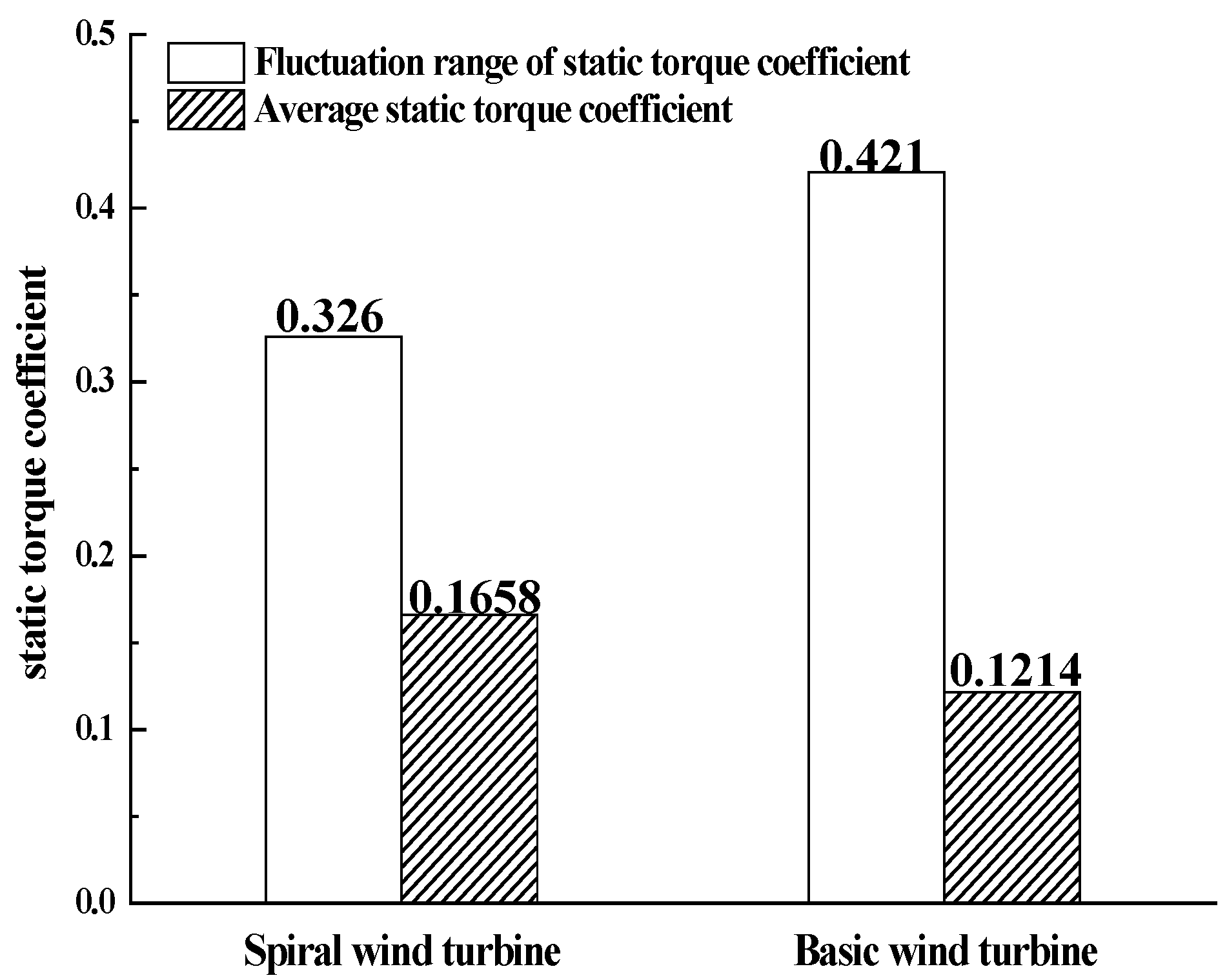
- The basic Savonius wind turbine could not start between an azimuth of 120° and 170°, while the spiral Savonius wind turbine could start between an azimuth of 0° and 180°. The static torque coefficient of the improved wind turbine was 72.2% higher.
- (2)
- Compared with the basic Savonius wind turbine, the stability and efficiency of the spiral Savonius wind turbine was improved. The average torque coefficient was increased by 36.6%.
- (3)
- Through the analysis of flow field characteristics, the velocity flow field and pressure of the spiral Savonius wind turbine were better than that of the basic Savonius wind turbine.
- (4)
- Through the wind tunnel test, the static torque coefficient of the spiral Savonius wind turbine under 12 m/s, the power coefficient and instantaneous rotational speed under different wind speeds were obtained. When the azimuth was 50°, the maximum static torque coefficient was 0.31. When the wind speed was 12 m/s and the tip speed ratio was 0.5, the maximum power coefficient was 0.136.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| CP | Output power coefficient, |
| CTs | Static torque coefficient, |
| λ | Tip speed ratio, |
| Ts | Torque acting on Savonius turbine, N·m |
| ρ | Air density, kg/m3 |
| A | Wind turbine swept area, m2 |
| U | Incoming wind speed, m/s |
| R | Wind turbine radius, m |
| V | Wind turbine outer diameter tangent speed, m/s |
| ω | Wind turbine rotation angular speed, rad/s |
| P | Wind turbine power, W |
| C | Chord length, m |
| D | Rotor diameter, m |
| R | Blade radius, m |
| T | Blade thickness, m |
| H | Blade height, m |
| d | Clearance between two blades, m |
| θ | Arc angle, ° |
| α | Azimuth angle of rotor against wind, ° |
References
- Amjith, L.; Bavanish, B. A review on biomass and wind as renewable energy for sustainable environment. Chemosphere 2022, 293, 133579. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y.; Zhang, H.; Xu, X.; Yang, Z.; Xu, W. A review of the potential of district heating system in Northern China. Appl. Therm. Eng. 2021, 188, 116605. [Google Scholar] [CrossRef]
- Tummala, A.; Velamati, R.K.; Sinha, D.K.; Indraja, V.; Krishna, V.H. A review on small scale wind turbines. Renew. Sustain. Energy Rev. 2016, 56, 1351–1371. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, S.; Tagawa, K.; Feng, F. Starting performance effect of a truncated-cone-shaped wind gathering device on small-scale straight-bladed vertical axis wind turbine. Energy Convers. Manag. 2018, 167, 70–80. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, X. Review on the application of variable-pitch to performance improvement of the lift-type vertical axis wind turbine. Renew. Resour. Res. 2020, 36, 194–200. [Google Scholar]
- Maalouly, M.; Souaiby, M.; ElCheikh, A.; Issa, J.; Elkhoury, M. Transient analysis of H-type Vertical Axis Wind Turbines using CFD. Energy Rep. 2022, 8, 4570–4588. [Google Scholar] [CrossRef]
- Celik, Y.; Ma, L.; Ingham, D.; Pourkashanian, M. Aerodynamic investigation of the start-up process of H-type vertical axis wind turbines using CFD. J. Wind Eng. Ind. Aerodyn. 2020, 204, 104252. [Google Scholar] [CrossRef]
- Gao, R.; Chen, K.; Li, Y.; Yao, W. Investigation on aerodynamic performance of wind turbine blades coupled with airfoil and herringbone groove structure. J. Renew. Sustain. Energy 2021, 13, 053301. [Google Scholar] [CrossRef]
- Khamlaj, T.A.; Rumpfkeil, M.P. Analysis and optimization of ducted wind turbines. Energy 2018, 162, 1234–1252. [Google Scholar] [CrossRef]
- Kang, C.; Liu, H.; Yang, X. Review of fluid dynamics aspects of Savonius-rotor-based vertical-axis wind rotors. Renew. Sustain. Energy Rev. 2014, 33, 499–508. [Google Scholar] [CrossRef]
- Jureczko, M.; Mrówka, M. Multiobjective Optimization of Composite Wind Turbine Blade. Materials 2022, 15, 4649. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Li, F.; Chen, J.; Su, Z.; Yu, J. Development status of vertical axis resistance Type Savonius turbine. J. Harbin Eng. Univ. 2020, 41, 298–308. [Google Scholar]
- Akwa, J.V.; Vielmo, H.A.; Petry, A.P. A review on the performance of Savonius wind turbines. Renew. Sustain. Energy Rev. 2012, 16, 3054–3064. [Google Scholar] [CrossRef]
- Kim, K.C.; Ji, H.S.; Kim, Y.K.; Lu, Q.; Baek, J.H.; Mieremet, R. Experimental and numerical study of the aerodynamic characteristics of an archimedes spiral wind turbine blade. Energies 2014, 7, 7893–7914. [Google Scholar] [CrossRef]
- Lee, J.-H.; Lee, Y.-T.; Lim, H.-C. Effect of twist angle on the performance of Savonius wind turbine. Renew. Energy 2016, 89, 231–244. [Google Scholar] [CrossRef]
- Cuevas-Carvajal, N.; Cortes-Ramirez, J.; Norato, J.A.; Hernandez, C.; Montoya-Vallejo, M. Effect of geometrical parameters on the performance of conventional Savonius VAWT: A review. Renew. Sustain. Energy Rev. 2022, 161, 112314. [Google Scholar] [CrossRef]
- Al Noman, A.; Tasneem, Z.; Sahed, M.F.; Muyeen, S.M.; Das, S.K.; Alam, F. Towards next generation Savonius wind turbine: Artificial intelligence in blade design trends and framework. Renew. Sustain. Energy Rev. 2022, 168, 112531. [Google Scholar] [CrossRef]
- Tian, W.; Mao, Z.; Zhang, B.; Li, Y. Shape optimization of a Savonius wind rotor with different convex and concave sides. Renew. Energy 2018, 117, 287–299. [Google Scholar] [CrossRef]
- Kerikous, E.; Thévenin, D. Optimal shape of thick blades for a hydraulic Savonius turbine. Renew. Energy 2018, 134, 629–638. [Google Scholar] [CrossRef]
- Alom, N. Influence of curtain plates on the aerodynamic performance of an elliptical bladed Savonius rotor (S-rotor). Energy Syst. 2021, 13, 265–280. [Google Scholar] [CrossRef]
- Wang, W.; Song, B.W.; Mao, Z.Y.; Tian, W. Optimization of Savonius wind turbine impeller with bilateral contour. J. Harbin Eng. Univ. 2019, 40, 254–259+272. [Google Scholar]
- Pan, C.; Kang, C.; Zhang, W. Numerical investigation of combination and interfence of vertical-axis spiral wind impeller. Acta Energ. Sol. Sin. 2018, 39, 2118–2124. [Google Scholar]
- Zhu, J.; Liu, P. Experimental study on aerodynamic characteristics of helical Savonius rotor with twist of 180°. J. Mech. Eng. 2020, 56, 155–161. [Google Scholar]
- Li, Y.; Zhao, S.; Qu, C.; Tong, G.; Feng, F.; Zhao, B.; Kotaro, T. Aerodynamic characteristics of Straight-bladed Vertical Axis Wind Turbine with a curved-outline wind gathering device. Energy Convers. Manag. 2019, 203, 112249. [Google Scholar] [CrossRef]
- Guo, W.; Shen, H.; Li, Y.; Feng, F.; Tagawa, K. Wind tunnel tests of the rime icing characteristics of a straight-bladed vertical axis wind turbine. Renew. Energy 2021, 179, 116–132. [Google Scholar] [CrossRef]
- Feng, F. Research on Aerodynamic Characteristics of Combined Vertical Axis Wind Turbine with Lift Drag Combined Starting Structure. Ph.D. Thesis, Northeast Agricultural University, Harbin, China, 2018. [Google Scholar]
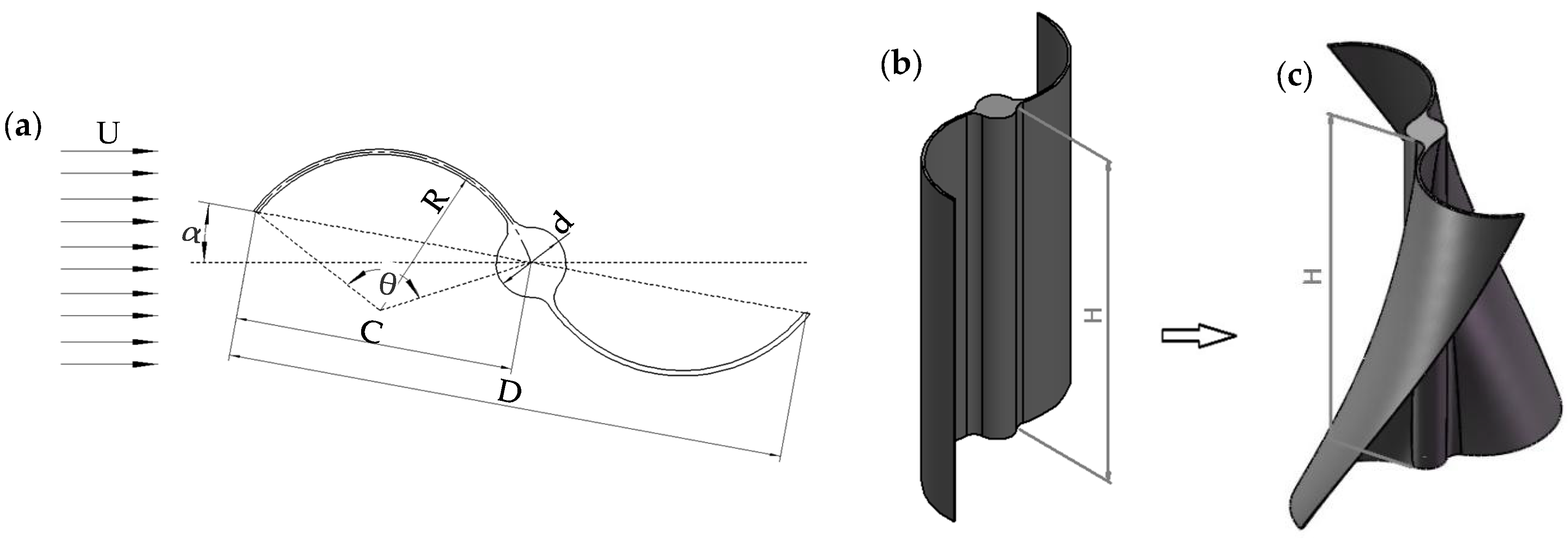
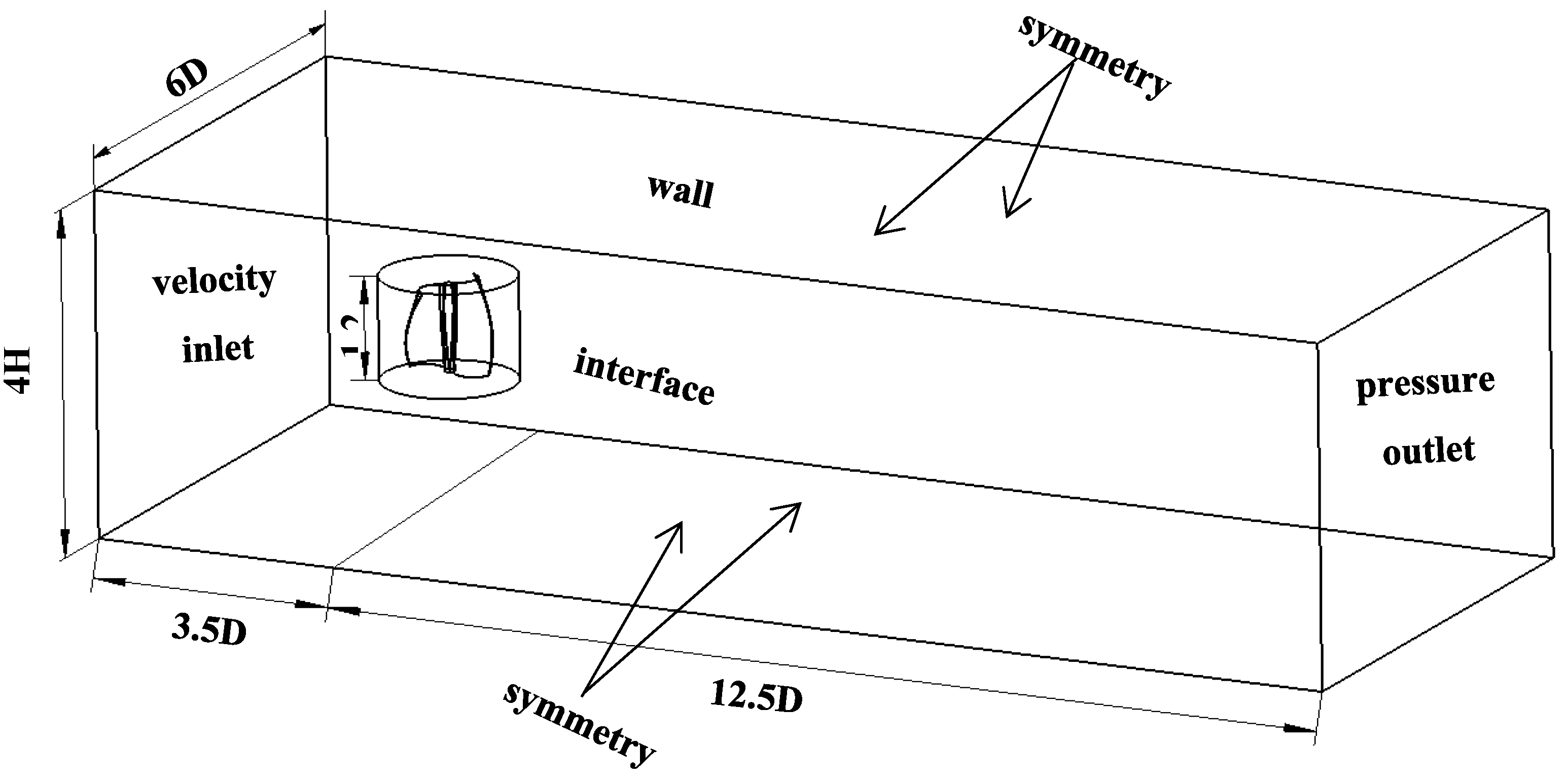
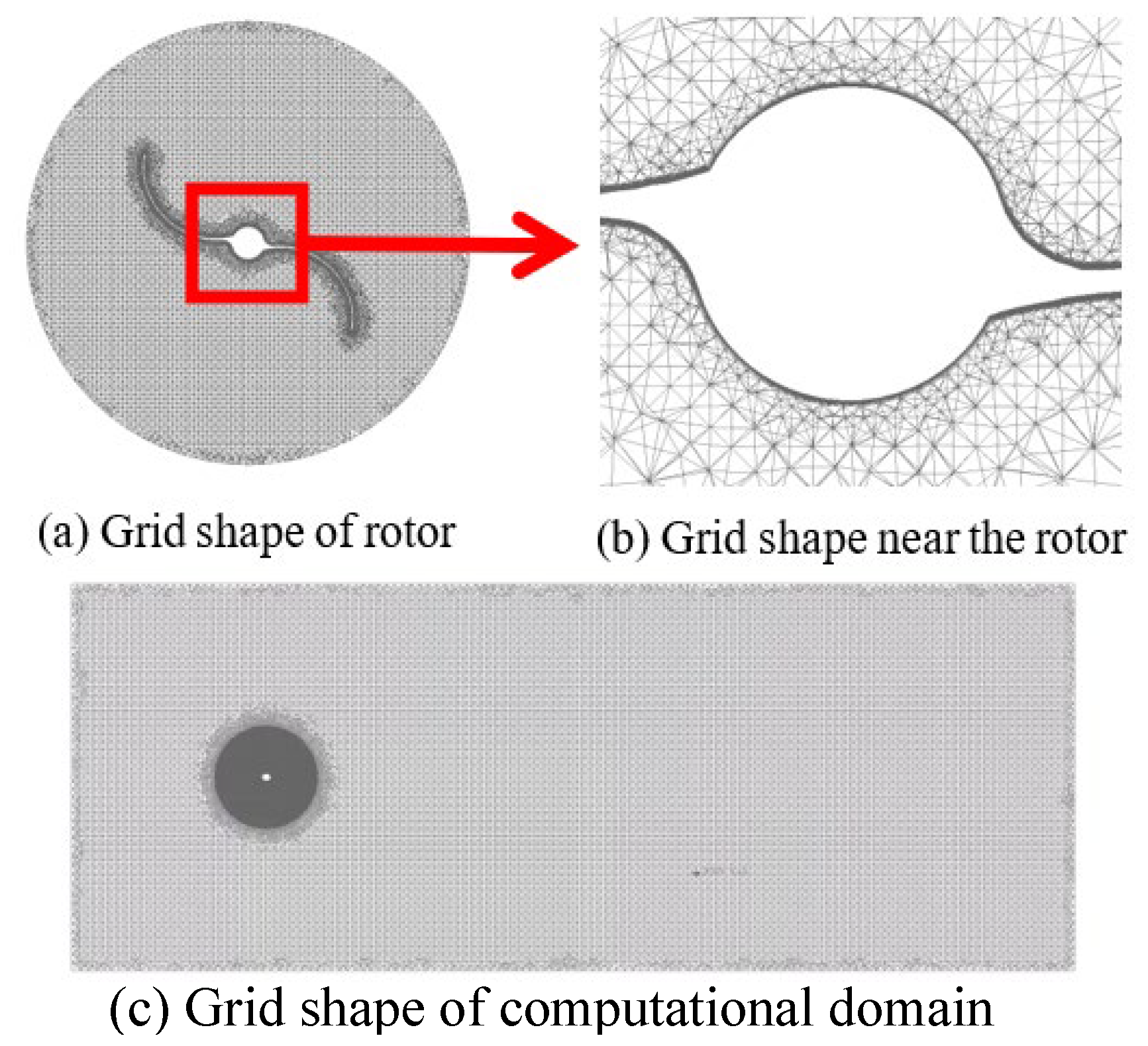
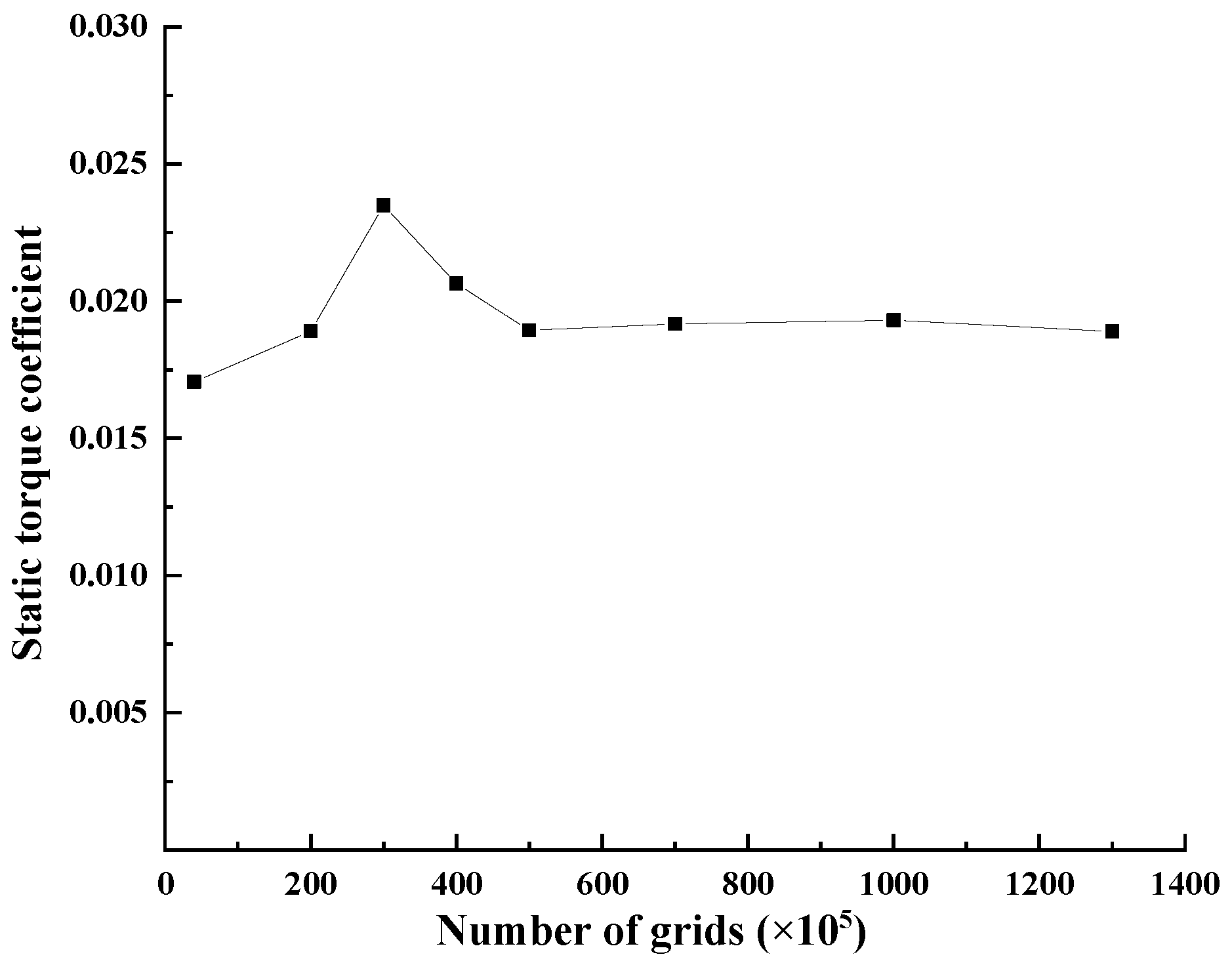




| Parameters | Value |
|---|---|
| Blade airfoil | Spiral blade |
| Blade number | 2 |
| Chord length (C) [m] | 0.112 |
| Rotational diameter (D) [m] | 0.224 |
| Blade height (H) [m] | 0.252 |
| Blade radius (R) [m] Blade thickness (T) [m] | 0.1 0.002 |
| Clearance between two blades (d) [m] | 0.024 |
| Arc angle (θ) [°] | 125 |
| Origin of Variance | Sum of Squares | df | Mean Squares | F Value | p Value |
|---|---|---|---|---|---|
| Different groups | 0.00381 | 1 | 0.00381 | 0.2788 | 0.60092 |
| Interior group | 0.46431 | 34 | 0.01366 | ||
| Total | 0.46812 | 35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, Z.; Tong, G.; Xiao, Z.; Deng, Q.; Feng, F.; Li, Y.; Arne, G.V. Study on Aerodynamic Characteristics of a Savonius Wind Turbine with a Modified Blade. Energies 2022, 15, 6661. https://doi.org/10.3390/en15186661
Mu Z, Tong G, Xiao Z, Deng Q, Feng F, Li Y, Arne GV. Study on Aerodynamic Characteristics of a Savonius Wind Turbine with a Modified Blade. Energies. 2022; 15(18):6661. https://doi.org/10.3390/en15186661
Chicago/Turabian StyleMu, Zhongqiu, Guoqiang Tong, Zhenjun Xiao, Qingyue Deng, Fang Feng, Yan Li, and Garrel Van Arne. 2022. "Study on Aerodynamic Characteristics of a Savonius Wind Turbine with a Modified Blade" Energies 15, no. 18: 6661. https://doi.org/10.3390/en15186661
APA StyleMu, Z., Tong, G., Xiao, Z., Deng, Q., Feng, F., Li, Y., & Arne, G. V. (2022). Study on Aerodynamic Characteristics of a Savonius Wind Turbine with a Modified Blade. Energies, 15(18), 6661. https://doi.org/10.3390/en15186661








