Abstract
Due to its significance in the operation of power systems, the optimal power flow (OPF) problem has attracted increasing interest with the introduction of smart grids. Optimal power flow developed as a crucial instrument for resource planning effectiveness as well as for enhancing the performance of electrical power networks. Transmission line losses, total generation costs, FACTS (flexible alternating current transmission system) costs, voltage deviations, total power transfer capability, voltage stability, emission of generation units, system security, etc., are just a few examples of objective functions related to the electric power system that can be optimized. Due to the nonlinear nature of optimal power flow problems, the classical approaches may become locked in local optimums, hence, metaheuristic optimization techniques are frequently used to solve these issues. The most recent optimization strategies used to solve optimal power flow problems are discussed in this paper as the state of the art (according to the authors, the most pertinent studies). The presented optimization techniques are grouped according to their sources of inspiration, including human-inspired algorithms (harmony search, teaching learning-based optimization, tabu search, etc.), evolutionary-inspired algorithms (differential evolution, genetic algorithms, etc.), and physics-inspired methods (particle swarm optimization, cuckoo search algorithm, firefly algorithm, ant colony optimization algorithm, etc.).
1. Introduction
With the advent of smart grids, the optimal power flow (OPF) problem has gained more and more attention due to its importance in power system operation. Optimal power flow developed as a crucial instrument for resource planning effectiveness as well as for enhancing the performance of electrical power networks. Through the use of control variables, starting from predetermined objective functions, and adhering to predetermined limitations, optimum power flow seeks to find the best or the most secure operating point. Transmission line losses, total generating costs, FACTS costs, voltage deviations, total power transfer capabilities, voltage stability, emission of generation units, system security, etc., are only a few examples of objective functions connected to the electric power system that can be optimized. The generated active powers, the voltage of the generation buses, the settings for the transformer taps, and the size of the FACTS devices are some of the system control variables that can be changed. To solve the optimal power flow problem, several traditional (deterministic) and modern (nondeterministic) heuristic optimization strategies have been put forth. Sensitivity analyses and gradient-based techniques are used in most traditional optimization strategies. Due to the nonlinear nature of optimal power flow problems, the classical approaches may become locked in local optimums, hence metaheuristic optimization techniques are frequently used to solve these issues. New methods have been developed to avoid these problems. In this review paper, metaheuristics and probabilistic methods proposed in literature will be analyzed and exposed. Furthermore, these methods allow load flow to perfectly fit new grid changes, such as DG penetration. Electricity in recent years, moved away from centralized production and increasingly towards DG. Therefore, it is easy to see that the current electricity grid is undergoing a period of great change and transformation. Traditional distribution grids are designed for “passive” operation and are characterized by a generally radial topology and unidirectional power flows towards the transformer. Therefore, the distribution grid is not designed to host significant amounts of distributed generation. From this knowledge, it is legitimate to think that much of this additional demand will be met with the help of DG, but only if the grid is ready, i.e., infrastructure upgrades are needed and are combined with the application of new technologies for monitoring and regulating the grid. The transition to the grid of the future, however, depends on quantifying how to optimize investments according to the maximum use of the current grid in terms of new RES and new installable loads. In this challenging context, the optimal load flow problem aims to solve the grids to show the energy distribution companies how best to invest money. The time-to-market strategy imposes a constraint on getting the fastest load flow result, which is also lead by real-time energy market regulation. This paper aims to give the reader an overview mainly of the LF and OPF methods found in recent literature, with a global focus on the best-fit method over grid topology as an innovation aspect. Within several methods deployed in the last half century, this paper will report on only the ones mentioned in at least several papers so that the most relevant papers will be mentioned. The paper will first take into account the load flow theory, and then focus on classical and new methods (probabilistic and metaheuristic) with a special analysis of specific grid topology-related applications.
2. Load Flow Problem Theory
The fundamental analysis in power systems is load flow analysis. It entails examining the grid from the standpoint of electricity flows. Loads and generators, we know, have time-varying diagrams. Load flow analysis is used to determine the nodal voltages and electricity flowing in the lines that connect these nodes. We evaluate the loads or generators at a certain time instant for this purpose. This moment will pass quickly (3–4 min). We consider a state to be a stationary condition if we observe a load that remains constant during such a time frame. Two stationary states can be thought of as two sequential instants (steady state operation). In these circumstances, we consider that the system is working.
The idea of load flow analysis is to find the voltage on each busbar and the power flows on the various lines, because we need to contain the voltage within certain limits, also not to overload the lines themselves. Consider, for example, busbar 2 in Figure 1. If we analyze it in more detail, we find the following diagram shown in Figure 2:
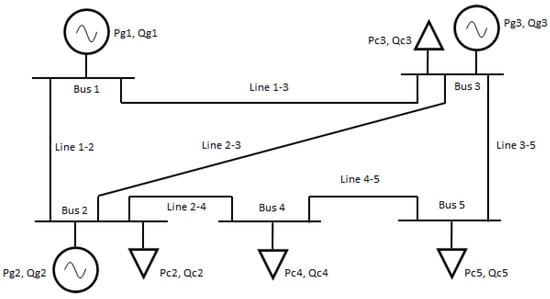
Figure 1.
Typical scheme of a load flow power grid.
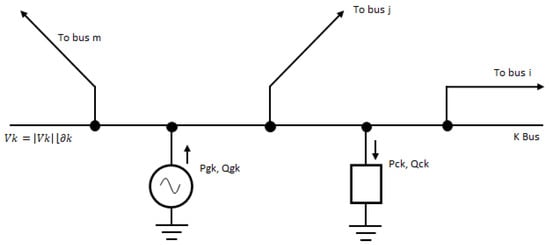
Figure 2.
Detail of k-bus of Figure 1 generic grid.
The Pk and Qk of the k busbar will be expressed in Equation (1):
where:
Considering the transmission lines equivalent model, then we get Figure 3:
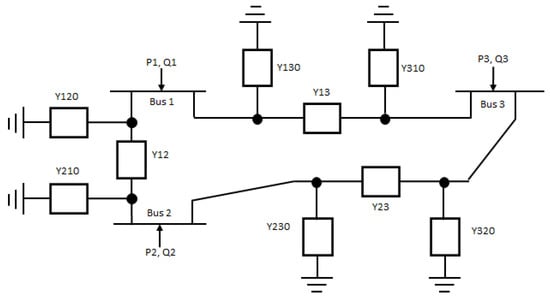
Figure 3.
A three bus power grid, considering complete lines model.
The bus admittance matrix (Ybus) can be written for simple inspection. The elements of the diagonal Yii are called self-admittances while the other elements Yij are called mutual admittances. Therefore, it is possible to write Equation (3) in compact form:
where the nodal voltages can be found solving linear algebraic equations in matrix form. Let us consider Equation (3), which can be expressed in a less compact form:
for each element Ik of the Ibus vector. The power at a given bus results in:
Substituting (4) in (5) we get:
with k = 1, 2, …, N nodes. Now, considering that:
substituting (6) in (7), we get:
That is, applying Euler’s equality in Equation (8):
We then have (9) which represent the power flow equations. These two equations expressed in P (active power) and Q (reactive power) tie together the active and reactive power of each bus to the module and the voltages of the buses via the admittances (self or mutual) of the grid.
These two equations are:
- Algebraic (no derivatives), since we are in stationary conditions.
- Nonlinear, due to the presence of trigonometric functions and nodal voltages.
To solve these equations, we must, therefore, make use of iterative numerical computation.
3. Principal Load Flow Methods: Clusters and Descriptions
Load flow methods essentially consist of an algorithm to iteratively solve nonlinear power flow Equation (9). According to the most recent review papers, load flow methods can be classified as conventional (also referred as classic) and non-conventional ones. Non-conventional ones are best projected in order to achieve optimal power flow problem solutions. Then, some methods can be better applied to certain grid topologies than others, thus, grids can be classified as classical unidirectional grids or RES penetrated grids (referred to as bidirectional grids due to the power inversion phenomenon). For the sake of completion, it is worthwhile mentioning that power flow problems can be solved in centralized and distributed/decentralized settings [1,2]. Then, typical grid topology is radial grids, linear grids, and rural grids. Now let us see how different methods work.
3.1. Classical Methods
Within classical methods we can find NR and GS method referenced in literature. Let us study how they work.
3.1.1. Newton—Raphson Method
Newton—Raphson’s method, also known as the method of tangents, is one of the methods for the approximate calculation of a solution to an equation of the form f(x) = 0. It is applied after determining an interval [a,b] that contains a single root. The method consists of substituting the curve y = f(x) for the tangent to the curve itself, starting from any point; for simplicity, one can start from one of the two points whose abscissa is the extreme of the interval [a,b] and take, as the approximate value of the root, the abscissa Xt of the point where the tangent intersects the x-axis within the interval [a,b]. Proceeding iteratively, it is shown that the recurrence relation of the method is:
which makes it possible to determine successive approximations of the root of the equation y = f(x) = 0. With the hypotheses posed, it is shown that the succession of Xn converges to the root rather quickly. In more detail, it is shown that if one is in an opportune neighbourhood of the solution, convergence will be quadratic, otherwise it will be linear (slower). In practice, given a permissible approximation tolerance of tau, the iterative procedure is terminated when the following condition is fulfilled:
Sometimes N-R may even fail to converge if one is looking for a solution that is too far away from the considered interval. In order to determine the interval in question in a more approximate but still effective manner, one usually precedes N-R with the bisection method to calculate the interval in which to operate.
Let us then consider solving the nonlinear equations of the LF problem. These equations express the relationship between Pk, Qk, and Vk. We can then write these equations in general form according to the more extended notation that takes into account all the nodes from 2 to N, without considering the balance node that we have assumed to be number 1:
The unknowns can also be made explicit according to the same notation:
Now, making an initial assumption of the solution (called start) equal to we can then expand the generic f(x) in Taylor series around x0, thus finding that:
By stopping the development at first order, we then solve for x and obtain:
Having a system of equations and implementing a method based on iterative calculation, the previous equation can be rewritten as:
where the J represents the Jacobian, defined as:
i represents the current number of iterations reached. The calculation stops when varies within the set tolerance limit and convergence is, therefore, reached. Now, the fact that it is necessary to calculate the inverse of the Jacobian is computationally disadvantageous, as it is a very expensive operation. Calculating an inverse matrix from an N × N, in fact, increases almost linearly with N. In addition, we will also have 2N − 1 equations to solve. Generally, one does not calculate the inverse of the Jacobian but resorts to other means. To this end, we consider the increment on x and y that each iteration produces as:
Therefore, the following equation is obtained in which the inverse of the Jacobian appears:
It can be rewritten as:
This, in essence, is a system that is in the form Ax = y and can be solved by the known methods of linear algebra. In fact, in this way we have linearized a nonlinear problem, i.e., from a set of nonlinear algebraic equations we have obtained a set of linear equations.
3.1.2. Gauss—Seidel Method
An alternative method to Newton—Raphson’s method is the Gauss—Seidel method. In numerical analysis, the Gauss—Seidel method is an iterative method, similar to the Jacobian method, for solving a linear system written in the matrix form Ax = b. Let us try to linearize the LF equations. To this end, we recall that:
We know that the k-th current Ik of the Ibus, written in a less compact form, will be equal to:
In extended form:
With k = 1, 2, …, N nodes. The complex power can be written as:
Thus, expressing the current as a function of Ik, we have:
Equalizing the two expressions in Ik we have:
The unknown is Vk, with k being the number of the node under consideration. We can rewrite the expression as:
Hence, finally:
with k = 1, 2, …, N nodes. This expression links Vk (Vkr + jVki) with the active and reactive power of the individual bus and is the solving equation underlying the Gauss—Seidel method.
This equation is:
- –
- algebraic (no derivatives) and
- –
- nonlinear.
It can be also solved numerically by iteration, considering Vk at the first member as the result of a (linear) calculation that sees Vk at the second member as the current one and Vk at the first member as that of the next iteration. In formula:
Let us, therefore, consider a network with a slack bus and only PQ buses; we will deal with the PV buses later. The solving equation obviously applies to the PQ buses only as the slack bus is not part of the LF calculations. Let us, therefore, see how to set up an iterative method. To start the first account, we can also make the initial flat start assumption here, i.e., all voltages of the various busbars equal 1 + j0 p.u. From this assumption, the nodal voltages (i + 1) are calculated with reference to the formula above. From the calculation in step 2, a more accurate estimate is obtained, and so on, until Vk(i + 1) − Vk(i) are less than a set tolerance. Therefore, to summarize, the steps of the algorithm are:
- the generation and absorption powers on each busbar are known, the total powers at each bus are calculated,
- the Ybus is created,
- the nodal voltages (also in polar coordinates if desired) are set to the flat start value, and
- the solving equation is solved iteratively until convergence below a set tolerance is achieved.
One computation aspect of the G—S method is that it has a rather slow convergence, as one has linearised the problem and the speed of convergence has the same order of magnitude as the number of busbars. This is a disadvantage in networks with hundreds of busbars.
It is possible, however, to speed up convergence, with an alpha-factor. This guarantees faster convergence from the case where alpha is unitary. The value of this parameter can vary between 1.5 and 1.7. However, G—S is poorly suited for networks with many known factors where, instead, N-R requires a fixed number of iterations approximately independent of the number of nodes.
3.2. About Optimal Power Flow
A power system optimization challenge is optimal power flow (OPF) [3,4,5,6,7,8,9,10,11,12,13]. Carpentier [14] first raised this issue in 1962. The objective of OPF is to identify a steady-state operating point that meets operating constraints and demands while minimizing the cost of power generation. A nonlinear programming (NLP) problem can be used to formulate the issue since some restrictions and potential objective functions are nonlinear. Kirchhoff’s voltage law (KVL), which describes the power flow in the transmission line as a nonlinear function of bus voltage and phase angle, contains limitations that are the major source of nonlinearity in the standard OPF polar formulation. The feasible region of the OPF issue is nonconvex due to the presence of nonlinear equality constraints [15], increasing the likelihood that local OPF solutions exist. However, one of the authors in the 1997 work [16] made the observation that OPF solutions are distinct in practice, which is still a widely held belief. Dommel and Tinney [17] offered the first solution to the OPF issue in 1968, and several others have subsequently been put forth. The authors of [18,19] provide an excellent summary of the literature on traditional optimization techniques applied to OPF during the past 30 years. If there is a local minimum, none of these methods will necessarily uncover the global minimum. The possibility that the OPF problem has local optimum states is a significant but poorly discussed issue in the literature. Both traditional local nonlinear programming and evolutionary techniques are included in a recent literature review [20] of OPF. Evolutionary algorithms are global optimization techniques that attempt to find global optima. Global techniques are much slower than the local ones so should only be used for problems where local optima may exist. The possibility of convergence to local solutions is cited by the authors of [21] as a significant shortcoming of classical optimization approaches used to tackle the OPF problem. However, none of these surveys mention any instances of local OPF optimums or provide an estimation of how frequently they occur in actual usage. Numerous approaches have been found to expand the OPF issue. For instance, risk-based OPF and security-constrained OPF address the issue of ensuring the network works securely. Nevertheless, if local optimum solutions exist for the original OPF issue, they should also exist for extensions, so in this paper we restrict attention to the standard OPF problem. The authors of [22] provide an intriguing semi-definite program (SDP) formulation of an OPF issue dual. They demonstrate that if there is no duality gap, a globally optimal solution to the OPF can be recovered from the SDP dual, and they provide a testable condition that ensures there is no duality gap after solving the SDP dual. However, it is not clear whether there will be a duality gap solely from the qualities of a general network, and it is unclear how frequently the strategy actually works in practice. In [23,24], sufficient requirements for the absence of a duality gap that solely depend on network features are provided. These are applicable to tree networks and lossless loop networks and call for set voltage magnitudes, restrictions on the angle difference across lines, and/or a great deal of freedom in the real and reactive power balance at buses. However, neither universal networks nor any of the examples in this paper satisfy these requirements. The SDP technique has some drawbacks, which are explored in [25]. Examples of modified IEEE test situations where the SDP recovery approach fails are presented in [26], and a branch and bound method that finds the global optimum in these cases is proposed. This technique makes use of the SDP formulation for the relaxations. However, there were no local OPF solutions in any of these circumstances.
3.3. Non-Classical Methods
In this paragraph, principals non-classical methods referred to in the literature will be presented.
3.3.1. Probabilistic Load Flow Methods
The deterministic load flow problem ignores uncertainties such as the variation of load requirements and the power oscillations brought on by renewable generation, which might be of utmost significance in the evaluation of distribution systems with or without DR penetration. It is necessary to use a different mathematical strategy to account for these uncertainties. The solutions up to this point have a probabilistic foundation—approach, fuzzy logic application, or interval analysis. The probabilistic load flow [12] was first proposed in 1974 [27], and it has since been improved and used in the study and design of power systems. To derive system states and power flows in terms of a density function and to incorporate system uncertainties in the result, inputs must be provided using their probability density function (or alternatively, the cumulative density function). The load uncertainty is typically not very high, and a normal distribution can be used to model it in most cases [9]. The expansion of renewable resources, however, brings with it additional difficulties. For instance, wind variability is quite large and cannot be modeled by a normal distribution. Either a numerical or an analytical method can be used to solve the probabilistic load flow. Below is an overview of the fundamental methods employed in the probabilistic load flow solution and how it is applied to distribution system analysis [10].
Numerical Solution Methods
Random number generation and random sampling are the two primary components of a Monte Carlo simulation approach. A probabilistic load flow based on this method basically entails repeatedly solving a deterministic power flow with inputs in various combinations while utilizing the nonlinear version of the load flow equations. Results from this approach are typically used as a reference to the results from other probabilistic load flow solutions to check their accuracy because the precise load flow equations are used. Due to the potential need for a high number of load flow solutions, this method’s principal drawback is the lengthy computation time that may be involved.
Analytical Solution Methods
The fundamental principle of the analytical approach is to perform algebraic operations on density functions of random input variables in order to derive density functions for random state variables and line flows. Input power variables might not be entirely independent of one another, and load flow equations are nonlinear, which make it challenging to solve probabilistic load flow equations. Several simulations are typically included to perform the probabilistic load flow using an analytical approach: power variables are completely independent or linearly coupled; normal distribution and discrete distribution are typically assumed for both load and generation; and network setup and parameter are constant. These assumptions are all made in the load flow equations. Different methods have been proposed to mitigate the error caused by the linearization of the load flow equations. Two typical solutions consist of using multilateralization or the quadratic probabilistic load flow. Point estimation methods can be included into the group of approximate methods. Since then, a number of works have addressed the shortcomings of the initial strategy, for instance, by utilizing correlated input variables or lowering the quantity of input random variables. Cumulants and Gram—Charlier expansion theory can be combined, as suggested in [12], to increase the effectiveness of a probabilistic load flow method. The fundamental benefit of utilizing Gram series is that the density function of any type of standardized variable may be expressed as the sum of weighted standard normal distributions at various derivative orders. The weights can be determined using several cumulant orders. It is possible to obtain cumulative density functions directly without integrating probability density functions. Although it has the drawback of requiring linearization, it can still be used to independent random variables. This method may have convergence issues for non-normal distributions; a less computationally intensive alternative is the Cornish—Fisher expansion.
3.3.2. Typical Grids Applications for Probabilistic Methods
The connection of generating and energy storage units to distribution systems presents several challenges for probabilistic calculations: wind forecast cannot be based on a normal distribution; there can be power generation interdependence between different DG units (e.g., correlated wind power generation) [11]; and the continuous and typically large variation of the power generation from DG may result in a large error if linearized load flow equations around the mean values are used. Due to the substantial correlation between generations from wind turbines in surrounding wind farms, modeling the interdependence of wind power generation is crucial (see [28,29]). The analytical probabilistic load flow method needs to incorporate theoretical expressions that take into consideration the relationship between stochastic generations and loads, as shown in [28]. A linearized version of the load flow equations was utilized in [30], one of the earliest papers on probabilistic load flow analyses in radial distribution systems [4] with stochastic wind generation. By including the adjustment of voltage and reactive power control devices, the authors improved the approach [31]. To account for uncertainties in time-varying loads, voltage regulators, switching capacitors, and network reconfiguration, Su [32] employed a single-phase version with the Monte Carlo method. The Monte Carlo approach and a single-phase distribution model were also applied in [28,33]. The authors of the first research examined the effects of stochastic wind generation, while the authors of the second presented the effects of solar generation. The influence of wind farms [6] was examined using a probabilistic three-phase load flow based on the Monte Carlo method in [34]. This article proposed a novel way for simulating induction generators that could take into consideration system imbalance. Distribution systems with load and generation uncertainties have also been studied using fuzzy set theory [35,36,37]. The topic of [38] was the application of the interval arithmetic technique to the load flow problem in distribution systems with uncertain input parameters. Distribution systems with energy storage units have been examined in very few studies, the test cases have been rather straightforward, and the major objective has not been to determine how energy storage affects voltages, power flows, and losses [39,40,41].
3.3.3. Metaheuristic Methods for OPF
In general, the exact method and approach method can be used to solve the optimization problem. The words meta and heuristic are the roots of the word metaheuristic [5]. Meta refers to a high-level methodology, whereas heuristics refers to the art of developing novel problem-solving techniques. A metaheuristic is a heuristic approach that does not depend on the nature of the problem. There are two types of metaheuristic methods: metaheuristics based on single-solution local searches and metaheuristics based on population data (random search). ACO, GA, and PSO are a few instances of metaheuristic techniques based on population. ACO, GA, and PSO are the three metaheuristic techniques used in this study.
Genetic Algorithm (GA)
The widely used stochastic optimization technique known as “genetic algorithms” (GA) draws its inspiration from the mechanics of genetics and natural selection as shown in Figure 4. They operate under the tenet of best-adapted individuals prevailing. GA was utilized by A-F. Attia et al. [42] to resolve the OPF issue. The IEEE-30 bus system has been used to create and implement the suggested solution. Results are evaluated in comparison to other techniques in the literature. The efficiency of the suggested strategy was demonstrated through comparison. Three optimization techniques, including GA, were employed by S. Kahourzade et al. [43] to address single- and multi-objective OPF problems. On the IEEE-30 bus system, the proposed technique has been developed and used.
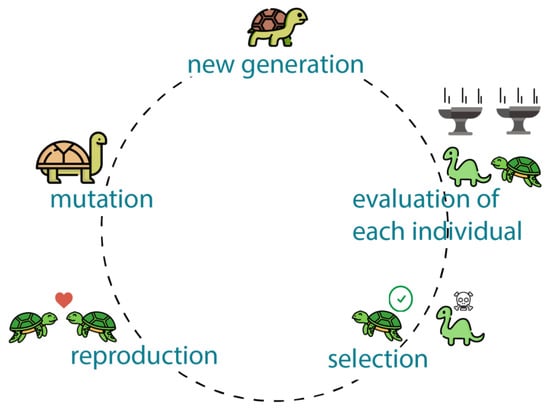
Figure 4.
Genetic Algorithm simple illustration.
Programming in Evolution (EP)
The focus of evolutionary programming (EP), a stochastic optimization, is on the behavioral relationships between parents and children [44]. Three optimization techniques, including EP, were employed by S. Kahourzade et al. [43] to address single- and multi-objective OPF problems. On the IEEE-30 bus system, the proposed technique has been developed and used. Results for the single- and multi-objective strategies were superior to those of other techniques. EP was employed by P. Somasundaram et al. [44] to address the OPF issue. The approach was created and used with the IEEE-30 bus system. The obtained results are contrasted with those obtained using the traditional security-constrained optimal power flow (SCOPF).
Particle Swarm Optimization (PSO)
Kennedy and Eberhart proposed the particle swarm optimization (OPF) technique in 1995 as an alternative to conventional genetic algorithms (GA). These algorithms were influenced by the organized movements of swarms of insects as shown in Figure 5. Animals move in groups to find food or to defend themselves from predators, according to observation. PSO was employed by N. Kalfallah et al. [45] to regulate reactive power in the western Algerian power system. Utilizing the approach has improved the voltage profile and decreased power losses. It also demonstrated how installing SCV devices can dramatically reduce power losses and keep voltages within safe ranges. Three optimization techniques, including PSO, were employed by S. Kahourzade et al. [44] to solve the single- and multi-objective OPF issue. On the IEEE-30 bus system, the proposed technique has been developed and used.
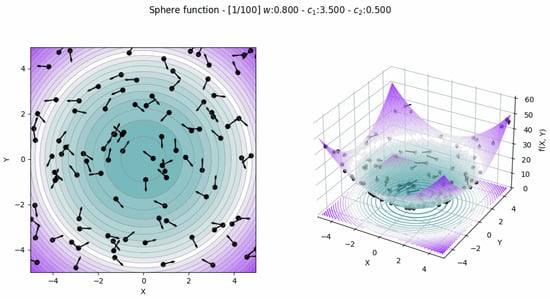
Figure 5.
PSO algorithm simple illustration.
Differential Evolution (DE)
The differential evolution (DE) method draws inspiration from GA and evolutionary tactics. Problems with continuous variables are addressed by it. DE was employed by M. Varadarajan and K.S. Swarup [46] to address the OPF issue. The technique’s performance was evaluated on the IEEE-14, 30, 57, and 118 bus systems, and its outcomes were contrasted with those of traditional approaches. It has been found that using the DE approach to solve OF problems with nonlinear objectives and constraints is a straightforward but effective technique. DE was employed by M. Varadarajan and K.S. Swarup [47] to address the OPF issue. The technique was evaluated using the IEEE-14, 30, and 118 bus systems, and the findings are then contrasted with those of a traditional method and, subsequently, with those of the PSO. It has been observed that results obtained with the DE method were more robust than those of PSO and sequential quadratic programming (SQP) algorithms.
Artificial Bee Colony (ABC)
The artificial bee colony is based on the unique manner in which bees communicate as shown in Figure 6. In order to find the best solutions to various optimization problems, the ABC algorithm does, in fact, imitate the foraging and dancing behaviors of honey-bees [48]. ABC was utilized by M. R. Adaryani and A. Karami [49] to solve a multi-objective problem. The method’s efficacy and validity were tested on the IEEE-9. 30 and 57 bus systems. Results have been compared with those obtained using other techniques described in the literature. The method can be used to solve a variety of problems on a wide scale, as evidenced by its effectiveness and the caliber of its outcomes. Chaotic ABC was utilized by K. Ayan et al. [48] to address the STSCOPF (security and transient stability constrained optimum power flow) problem. The IEEE-30 and 39 bus systems have been used to develop and implement its method. Results were compared to those found in the literature and demonstrated the validity and efficacy of the suggested method.
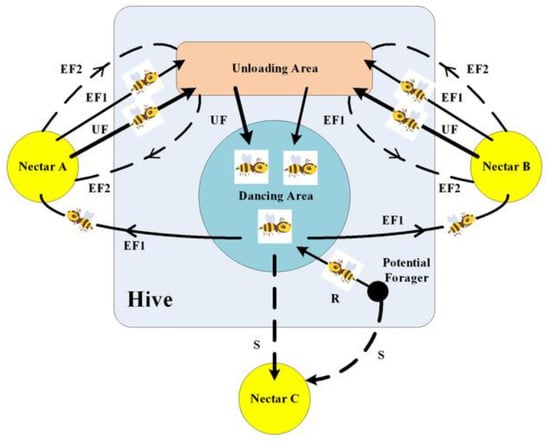
Figure 6.
ABC algorithm simple illustration.
Gravitational Search Algorithm (GSA)
The Newtonian theory of gravity served as the inspiration for the gravitational search algorithm (GSA) in optimization techniques [50] as shown in Figure 7. GSA was utilized by S. Duman et al. [51] to resolve OPF issues. The technique was created and examined on the IEEE-30 and 57 bus systems. Results from GSA are contrasted with those from other metaheuristic techniques that have been published in the literature. It has been noted that outcomes are robust, efficient, and high quality for resolving OPF issues. The allocation of the thyristor-controlled series compensator (TCSC) utilizing the congestion rent contribution methodology based on the location of the marginal price was solved by A. Sharma and S. K. Jain [52] using GSA. The technique was created and examined on the IEEE-30 and 57 bus systems. Other heuristics methods reported in the literature are used to compare GSA’s performance.
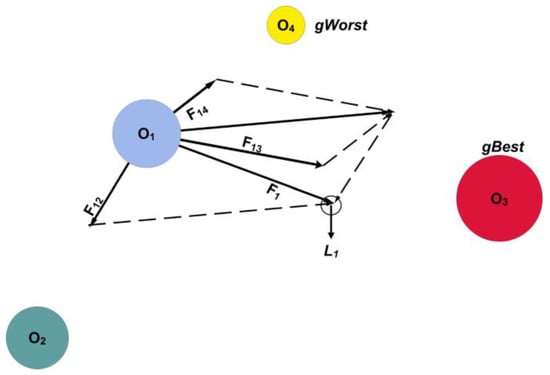
Figure 7.
GSA algorithm simple illustration.
Wolf Optimization Algorithm
Mirjalili et al. introduced the grey wolf optimizer (GWO) algorithm in 2014 [53]. The leadership structure and hunting strategy employed by grey wolves to capture their prey until it stops moving are mimicked by this algorithm. By mimicking the social behavior of grey wolves in their social life when seeking food, GWO is similar to other population-based metaheuristic algorithms; they adhere to hierarchy in the group. The hierarchy of grey wolves is divided into two levels as shown in Figure 8, with (alpha) symbolizing the group’s leaders and (beta), which assists alpha in making choices [54]. Delta and omega are the next levels; they are the lowest ranks in the group, and they must eat after every level. In actuality, these wolves hunt in packs and engage in a three-step process that includes chasing, encircling, and attacking. The method begins with a predetermined number of randomly positioned wolves. The hierarchy of grey wolves’ leadership can be simulated using four different wolf group types [55,56]. This hierarchy respects the social dominant degree in which the high class is named alpha (α) and is mostly responsible for making decisions about hunting and order the other wolves in the pack. The steps are reported below:
- Initializing the search agents.
- Assigning alpha, beta and gamma by fitness.
- Encircling the prey: represents the circular area around the best solution (prey).
- Hunting step: the encircling process comes to the second step involving hunting guided by the alpha wolf group.
- Attacking the prey.
- Steps 2 to 5 are then repeated until the maximum number of iterations is reached.
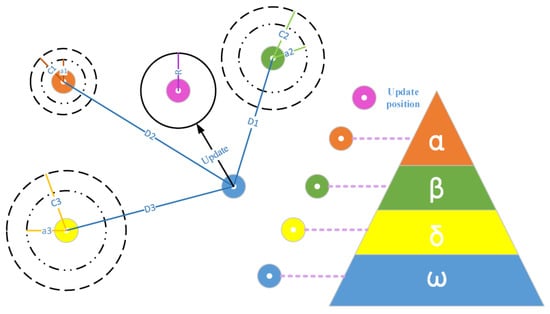
Figure 8.
Grey Wolf algorithm hierarchy simple illustration.
Cuckoo Optimization Algorithm
The cuckoo optimization algorithm (COA) is a metaheuristic algorithm that draws its inspiration from nature and the cuckoo family of birds [57]. The primary drivers behind the creation of this new evolutionary optimization algorithm were the unique lifestyle of these birds and their traits in egg laying and breeding as shown in Figure 9. It is a brand new evolutionary algorithm that works well for problems involving continuous nonlinear optimization. Like other evolutionary techniques, COA begins with a starting population. The cuckoo optimization algorithm’s foundation is the struggle to live among cuckoos [7]. Some of the cuckoos or their eggs may not survive the competition. The cuckoo groups that have survived travel to a more favorable environment where they begin to reproduce and lay eggs. The goal of the cuckoos’ survival strategy is to eventually unite them into one society with the highest profit margins. The COA algorithm’s capacity to resolve challenging, nonlinear, and nonconvex optimization problems has been demonstrated through the application to a variety of benchmark functions and a real-world scenario [58,59]. Faster convergence rates and a decrease in computing complexity are the COA’s major characteristics [60]. It is a population-based algorithm, just like other evolutionary algorithms. Within the boundaries of the control parameter, the initial population is created at random. Then, until a stopping requirement is achieved, the levy flight operator is performed on each person.
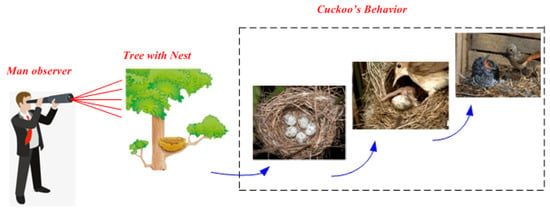
Figure 9.
Cuckoo algorithm simple illustration.
3.3.4. Application of Heuristic Methods on AC MV Grids
Heuristic methods answer the best way to expand AC medium-voltage distribution networks for rural applications [8,9]. By limiting the number of branches that are linked to a substation, the notion of a minimal spanning tree is applied to choose the best distribution feeder routes (mixed-integer linear programming formulation). The maximum anticipated current that is absorbed by the loads is computed in order to determine the lowest thermal bound of the conductor caliber for the selected feeder routes. Networks of rural, residential, commercial, and industrial grid areas are primarily grouped in metropolitan regions, and electrical distribution networks are a part of the power system responsible for supplying electrical services to these areas [61]. In order to reduce investment costs, these grids are often designed with a radial configuration [13]. However, this configuration causes these grids to create large power losses (between 6 and 18 percent in the case of Colombia, for example) [62]. Due to the dispersion of the loads and low power consumption, this situation is less promising when rural distribution networks are examined [63]. Given that electricity services are globally viewed as public services, the regulatory bodies in charge of managing the electricity market have given distribution companies benefits, such as tax breaks or the addition of new factors to the formula for calculating energy prices, to encourage the provision of electrical services to rural areas. The objective is to raise the standard of living in rural communities [62]. An example of a mixed integer nonlinear programming (MINLP) problem is the challenge of electrical distribution expansion planning that is optimal [64]. It entails making the best choices for distribution line routes, choosing the size (caliber) of conductors, locating and sizing existing and new substations, and calculating the operational expenses of the grid over the planning horizon [65,66]. The distribution system planning problem has been addressed by a number of optimization methodologies; the majority of these approaches concentrate on metropolitan network applications, some of which are briefly discussed here. In [64], a model with an explicit radiality restriction discusses the subject of optimal growth planning in distribution networks. The resulting MINLP model was solved in the A mathematical programming language (AMPL) environment using a test feeder of 54 buses. The authors did not compare the reported numerical results to other optimization method-ologies based on exact models or metaheuristics, and the optimization model does not include different caliber options, which reduces complexity due to a smaller size of the solution space. Nevertheless, the reported numerical results satisfy the planning requirements. The authors of [67] recommended utilizing a genetic algorithm and an ant-colony optimizer to create distribution networks for medium-voltage applications. The methodology is tested on a small test feeder with 10 nodes, accounting for different diameter sizes. To demonstrate the methodology’s efficacy, no comparison to precise or metaheuristic methodologies was undertaken. The authors of [68] describe the application of a genetic algorithm to the growth of medium-voltage distribution networks. Numerical results came from two test feeds with 13 and 30 buses, respectively. The grid topology has been set by the utility, which restricts the size of the solution space and transforms the original problem of planning distribution systems into a problem of choosing conductors in distribution networks in the most efficient manner. To design distribution networks taking into account a variety of objective functions, including investment costs, operating costs, and the amount of unsupplied energy, the authors introduced a multi-objective optimization model in [66]. A distribution network of 54 buses was utilized to numerically confirm the authors’ theory; although, they only used the single-phase equivalent of the network in their formulation and did not compare it to exact or metaheuristic approaches. The authors of [69] developed an optimization methodology for planning distribution networks using a three-phase description of the network by combining a genetic algorithm with the tabu search algorithm (TSA). The provided numerical results demonstrated the usefulness of the TSA approach in determining the set of calibers that must be assigned to the network after the grid topology was defined using a heuristic graph generator. [63] provides a thorough analysis of the distribution network expansion planning problem, including a discussion of several optimization approaches and models. The authors examined the integration of distributed generation and energy storage technologies in the context of the conventional issue of expansion planning. The validation of numbers in a 54-bus system shows that the variances in the various parts of the final solution plan and energy storage technologies, such as generators, were considered. Using the earlier optimization models simplifies the planning of the distribution system. This reduction decreases the complexity of the optimization issue for the assessment of the power flow problem [12] by ignoring possible load and impedance imbalances as well as loads with single-phase, two-phase, and three-phase connections, including X- and Y-connections. In order to go beyond the prior research that is currently available in the literature, we provide an easily implementable optimization technique to create rural distribution grids that is composed of three steps and that can be used to single-phase or three-phase distribution grids [70]. The first step handles the route selection problem by articulating the problem of least spanning tree (linear integer programming model) to reduce the total length of the conductors [71,72].
The grid topology identified in the first stage is used in the second phase to compute the predicted current in each distribution line route, allowing the initial conductor calibers to be determined. The third stage establishes a TSA with the calibers selected in the previous stage in order to determine the best grid calibers that minimize the costs of purchasing conductors and the costs of energy losses over the anticipated horizon [72]. The main advantage of this heuristic approach is that the initial solution for a rural distribution grid obtained by applying the first two stages can be regarded as the upper bound of the objective function, i.e., the maximum admissible grid costs, which implies that the TSA seeks to reduce this function by utilizing and exploring the solution space. The TSA, in conjunction with a three-phase power-flow technique, is used to determine the root-mean-square (RMS) of the current in lines and the voltages in nodes, as well as the operational costs associated with power losses across the planning horizon [73]. In Figure 10, it is than reported the structure of 30 bus typical grid with nodes labeled in numbers.
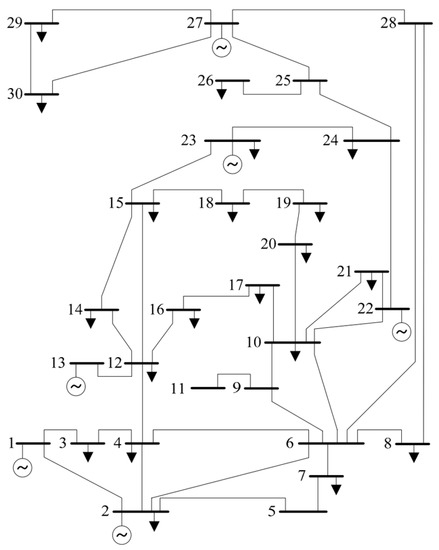
Figure 10.
IEEE typical 30 bus rural grid.
4. Conclusions
In recent years, centralized production of electricity has decreased and decentralized generation (DG) has increased. Thus, the current power system is going through a time of significant change and development. Traditional distribution grids have a usually radial layout, unidirectional power flows towards the transformer, and are designed for “passive” operation. As a result, a sizable percentage of dispersed power is not intended for the distribution grid. According to what has been revealed, it is reasonable to assume that DG will assist in meeting a large portion of this increased demand, but only if the grid is ready, which means infrastructure upgrades are required in addition to the use of new technology for grid monitoring and regulation. However, determining how to optimize investments in accordance with the present grid’s maximum utilization in terms of new RES and new installable loads is essential for the transition to the grid of the future. The optimal load flow problem seeks to resolve the grids in this difficult situation in order to instruct energy distribution businesses on how to make the greatest financial investments. Additionally, the time-to-market strategy places a restriction on obtaining the quickest load flow results, which is also driven by real-time energy market regulation. Several techniques have been presented in this review paper to show how much interest there is on this topic and what are the opportunities of research in this field. In our future work, we intend to investigate the development of a new load flow method called compensation admittance load flow (CALF) which aims to combine NR and GS advantages with a simple model of implementation. Furthermore, we intend to consider the possibility of developing more effective and efficient solution methods, relying on hybridization of metaheuristics, for optimal power flow [74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89].
Author Contributions
Conceptualization, B.-G.R. and F.R.-F.; methodology, B.-G.R.; formal analysis, B.-G.R.; investigation, B.-G.R.; resources, B.-G.R.; data curation, B.-G.R.; writing—original draft preparation, B.-G.R. and F.R.-F.; writing—review and editing, B.-G.R. and F.R.-F.; visualization, B.-G.R.; supervision, F.R.-F. and A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Scarabaggio, P.; Carli, R.; Dotoli, M. Noncooperative Equilibrium Seeking in Distributed Energy Systems Under AC Power Flow Nonlinear Constraints. IEEE Trans. Control Netw. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Yao, M.; Molzahn, D.K.; Mathieu, J.L. An Optimal Power-Flow Approach to Improve Power System Voltage Stability Using Demand Response. IEEE Trans. Control Netw. Syst. 2019, 6, 1015–1025. [Google Scholar] [CrossRef]
- Bukhsh, W.A.; Grothey, A.; McKinnon, K.I.M.; Trodden, P.A. Local Solutions of the Optimal Power Flow Problem. IEEE Trans. Power Syst. 2013, 28, 4780–4788. [Google Scholar] [CrossRef]
- Martinez, J.A.; Mahseredjian, J. Load flow calculations in distribution systems with distributed resources. A review. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar]
- Charles, P.; Mehazzem, F.; Soubdhan, T. A Review on Optimal Power Flow Problems: Conventional and Metaheuristic Solutions. In Proceedings of the 2nd International Conference on Smart Power & Internet Energy Systems, Bangkok, Thailand, 15–18 September 2020; pp. 1–6. [Google Scholar]
- Haddi, S.; Bouketir, O.; Bouketir, T. Improved Optimal Power Flow for a Power System Incorporating Wind Power Generation by Using Grey Wolf Optimizer Algorithm. Power Eng. Electr. Eng. 2018, 16, 471–488. [Google Scholar] [CrossRef]
- Ramamohana, M.R.; Naresh Babu, A.V. Optimal power flow using cuckoo optimization algorithm. IJAREEIE 2013, 2, 4213–4218. [Google Scholar]
- Montoya, O.D.; Serra, F.M.; De Angelo, C.H.; Chamorro, H.R.; Alvarado-Barrios, L. Heuristic Methodology for Planning AC Rural Medium-Voltage Distribution Grids. Energies 2021, 14, 5141. [Google Scholar] [CrossRef]
- Momoh, J.A. Review of Optimization Techniques for Renewable Energy Resources. In Proceedings of the 2014 IEEE Symposium on Power Electronics and Machines for Wind and Water Applications, Milwaukee, WI, USA, 24–26 July 2014; pp. 1–8. [Google Scholar]
- Martinez, J.A.; Mahseredjian, J. Load flow methods in Distribution Systems with Dispersed Generations: A brief review. In Proceedings of the 2015 1st Conference on Power, Dielectric and Energy Management at NERIST (ICPDEN), Arunachal Pradesh, India, 10–11 January 2015; pp. 1–4. [Google Scholar]
- Nusair, K.; Alhmoud, L. Application of Equilibrium Optimizer Algorithm for Optimal Power Flow with High Penetration of Renewable Energy. Energies 2020, 13, 6066. [Google Scholar] [CrossRef]
- Hossain, A.L.; Rokonuzzaman, M.; Amin, N.; Zhang, J.; Mishu, M.K.; Tan, W.-S.; Islam, M.R.; Roy, R.B. Probabilistic Load Flow–Based Optimal Placement and Sizing of Distributed Generators. In Proceedings of the 2019 4th International Conference on Electrical, Electronics, Communication, Computer Technologies and Optimization Techniques (ICEECCOT), Mysuru, India, 13–14 December 2019. [Google Scholar]
- Gulakhmadov, A.; Asanova, S.; Asanova, D.; Safaraliev, M.; Tavlintsev, A.; Lyukhanov, E.; Semenenko, S.; Odinaev, I. Power Flows and Losses Calculation in Radial Networks by Representing the Network Topology in the Hierarchical Structure Form. Energies 2022, 15, 765. [Google Scholar] [CrossRef]
- Carpentier, J. Contribution a l’etude du dispacting economique. Bull. Soc. Fr. Electr. 1962, 3, 431–447. [Google Scholar]
- Hiskens, I.A.; Davy, R.J. Exploring the power flow solution space boundary. IEEE Trans. Power Syst. 2001, 16, 389–395. [Google Scholar] [CrossRef]
- Momoh, J.A.; Koessler, R.; Bond, M.; Stott, B.; Sun, D.; Papalexopoulos, A.; Ristanovic, P. Challenges to optimal power flow. IEEE Trans. Power Syst. 1997, 12, 444–455. [Google Scholar] [CrossRef]
- Dommel, H.W.; Tinney, W.F. Optimal power flow solutions. IEEE Trans. Power Appar. Syst. 1968, PAS-87, 1866–1876. [Google Scholar] [CrossRef]
- Momoh, J.A.; Adapa, R.; El-Hawary, M.E. A review of selected optimal power flow literature to 1993. i. nonlinear and quadratic programming approaches. IEEE Trans. Power Syst. 1999, 14, 96–104. [Google Scholar] [CrossRef]
- Momoh, J.A.; El-Hawary, M.E.; Adapa, R. A review of selected optimal power flow literature to 1993. ii. newton, linear programming and interior point methods. IEEE Trans. Power Syst. 1999, 14, 105–111. [Google Scholar] [CrossRef]
- Qiu, Z.; Deconinck, G.; Belmans, R. A literature survey of optimal power flow problems in the electricity market context. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009. [Google Scholar]
- AlRashidi, M.; El-Hawary, M. Applications of computational intelligence techniques for solving the revived optimal power flow problem. Electr. Power Syst. Res. 2009, 79, 694–702. [Google Scholar] [CrossRef]
- Lavaei, J.; Low, S.H. Convexification of optimal power flow problem. In Proceedings of the 2010 48th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 29 September–1 October 2010. [Google Scholar]
- Zhang, B.; Tse, D. Geometry of injection regions of power networks. IEEE Trans. Power Syst. 2012, 28, 788–797. [Google Scholar] [CrossRef]
- Lavaei, J.; Tse, D.; Zhang, B. Geometry of power flows in tree networks. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Lesieutre, B.C.; Molzahn, D.K.; Borden, A.R.; DeMarco, C.L. Examining the limits of the application of semidefinite programming to power flow problems. In Proceedings of the 2011 49th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 28–30 September 2011. [Google Scholar]
- Gopalakrishnan, A.; Raghunathan, A.U.; Nikovski, D.; Biegler, L.T. Global optimization of optimal power flow using a branch & bound algorithm. In Proceedings of the 2012 50th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 1–5 October 2012. [Google Scholar]
- Borkowska, B. Probabilistic load flow. IEEE Trans. Power Appar. Syst. 1974, 93, 752–759. [Google Scholar] [CrossRef]
- Papaefthymiou, G.; Schavemaker, P.; van der Sluis, L.; Kling, W.; Kurowicka, D.; Cooke, R. Integration of stochastic generation in power systems. Int. J. Electr. Power Energy Syst. 2006, 28, 655–667. [Google Scholar] [CrossRef]
- Papaefthymiou, G.; Kurowicka, D. Using copulas for modeling stochastic dependence in power system uncertainty analysis. IEEE Trans. Power Syst. 2009, 24, 40–49. [Google Scholar] [CrossRef]
- Hatziargyriou, N.D.; Karakatsanis, T.S.; Papadopoulos, M. Probabilistic load flow in distribution systems containing dispersed wind power generation. IEEE Trans. Power Syst. 1993, 8, 159–165. [Google Scholar] [CrossRef]
- Hatziargyriou, N.D.; Karakatsanis, T.S. Distribution system voltage and reactive power control based on probabilistic load flow analysis. IEE Proc. Gener. Transm. Distrib. 1997, 144, 363–369. [Google Scholar] [CrossRef]
- Su, C.L. Distribution Probabilistic Load Flow Solution Considering Network Reconfiguration and Voltage Control Devices; PSCC: Liege, Belgium, 2005. [Google Scholar]
- Conti, S.; Raiti, S. Probabilistic load flow using Monte Carlo techniques for distribution networks with photovoltaic generators. Sol. Energy 2007, 81, 1473–1481. [Google Scholar] [CrossRef]
- Caramia, P.; Carpinelli, G.; Varilone, P.; Verde, P. Probabilistic three-phase load flow. Electr. Power Energy Syst. 1999, 21, 55–69. [Google Scholar] [CrossRef]
- Das, D.; Ghosh, S.; Srinivas, D.K. Fuzzy distribution load flow. Electr. Power Energy Syst. 1999, 27, 1215–1226. [Google Scholar]
- Bijwe, P.R.; Raju, G.K.V. Fuzzy distribution power flow for weakly meshed systems. IEEE Trans. Power Syst. 2006, 21, 1645–1652. [Google Scholar] [CrossRef]
- Kalesar, B.M.; Sei, A.R. Fuzzy load flow in balanced and unbalanced radial distribution systems incorporating composite load model. Electr. Power Energy Syst. 2010, 32, 17–23. [Google Scholar] [CrossRef]
- Das, B. Consideration of Input Parameter Uncertainties in Load Flow Solution of Three-Phase Unbalanced Radial Distribution System. IEEE Trans. Power Syst. 2006, 21, 1088–1095. [Google Scholar] [CrossRef]
- Korpaas, M.; Holen, A.T.; Hildrum, R. Operation and sizing of energy storage for wind power plants in a market system. Int. J. Electr. Power Energy Syst. 2003, 25, 599–606. [Google Scholar] [CrossRef]
- Klöckl, B.; Stricker, P.; Koeppel, G. On the properties of stochastic power sources in combination with local energy storage. In Proceedings of the Cigre Symposium on Power Systems with Dispersed Generation, Athens, Greece, 13–16 April 2005. [Google Scholar]
- Koeppel, G.; Korpaas, M. Using storage devices for compensating uncertainties caused by non-dispatchable generators. In Proceedings of the 9th PMAPS, Stockholm, Sweden, 11–15 June 2006. [Google Scholar]
- Attia, A.-F.; Al-Turki, Y.A.; Abusorrah, A.M. Optimal Power Flow Using Adapted Genetic Algorithm with Adjusting Population Size. Electr. Power Compon. Syst. 2012, 40, 1285–1299. [Google Scholar] [CrossRef]
- Kahourzade, S.; Mahmoudi, A.; Mokhlis, H.B. A comparative study of multi-objective optimal power based on particle swarm, evolutionary programming and genetic algorithm. Electr. Eng. 2015, 97, 1–12. [Google Scholar] [CrossRef]
- Somasundaram, P.; Kuppusamy, K.; Devi, R.P.K. Evolutionary programming based security constrained optimal power _ow. J. Electr. Power Syst. Res. 2004, 72, 137145. [Google Scholar] [CrossRef]
- Kalfallah, N.; Benzergua, F.; Cherki, I.; Chaker, A. Use of Genetic Algorithm and Particle Swarm Optimisation Methods for the Optimal Control of Reactive Power in western Algerian Power System. Energy Procedia 2015, 74, 265–272. [Google Scholar]
- Varadarajan, M.; Swarup, K.S. Differential evolutionary algorithm for optimal reactive power dispatch. Electr. Power Energy Syst. 2008, 81, 435–441. [Google Scholar] [CrossRef]
- Varadarajan, M.; Swarup, K.S. Differential evolution approach for optimal reactive power dispatch. Appl. Soft Comput. 2008, 8, 1549–1561. [Google Scholar] [CrossRef]
- Ayan, K.; Klç, U.; Barakl, B. Chaotic artificial bee colony algorithm based solution of security and transient stability constrained optimal power flow. Electr. Power Energy Syst. 2015, 64, 136–147. [Google Scholar] [CrossRef]
- Adaryani, M.R.; Karami, A. Artificial bee colony algorithm for solving multi-objective optimal power flow problem. Electr. Power Energy Syst. 2006, 53, 77–85. [Google Scholar]
- Rashedi, E.; Rashedi, E.; Nezamabadi, H. A comprehensive survey on gravitational search algorithm. Swarm Evol. Comput. 2018, 41, 141–158. [Google Scholar] [CrossRef]
- Duman, S.; Güvenç, U.; Sönmez, Y.; Yörükeren, N. Optimal power flow using gravitational search algorithm. Energy Convers. Manag. 2012, 59, 86–95. [Google Scholar] [CrossRef]
- Sharma, A.; Jain, S.K. Gravitational search assisted algorithm for TCSC placement for congestion control in deregulated power system. Electr. Power Syst. Res. 2019, 174, 113. [Google Scholar] [CrossRef]
- Mondal, S.; Bhattacharya, A.; Nee-Dey, S.H. Multi-objective economic emission load dispatch solution using gravitational search algorithm and considering wind power penetration. Int. J. Electr. Power Energy Syst. 2013, 44, 282–292. [Google Scholar] [CrossRef]
- El-Fergany, A.; Hasanien, H. Single and Multi-objective Optimal Power Flow Using Grey Wolf Optimizer and Differential Evolution Algorithms. Electr. Power Compon. Syst. 2015, 43, 1548–1559. [Google Scholar] [CrossRef]
- Mohamed, A.A.; El-Gaafary, A.M.; Mohamed, Y.S.; Hemeida, A.M. Multiobjective Modified Grey Wolf Optimizer for Optimal Power Flow. In Proceedings of the Eighteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016; pp. 982–990, ISBN 978-1-4673-9063-7. [Google Scholar] [CrossRef]
- Kapoor, S.; Zeya, I.; Singhal, C.; Nanda, S.J. A Grey Wolf Optimizer Based Automatic Clustering Algorithm for Satellite Image Segmentation. Procedia Comput. Sci. 2017, 115, 415–422. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing, NaBIC, Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Yang, X.S.; Deb, S. Engineering optimization by Cuckoo search. Int. J. Math. Modell. Numer. 2010, 1, 330–343. [Google Scholar]
- Rao, M.R.; Babu, A.N. Cuckoo Optimization Algorithm. Appl. Soft Comput. 2011, 11, 5508–5518. [Google Scholar]
- Abido, M.A. Optimal power flow using tabu search algorithm. Electr. Power Compon. Syst. 2002, 30, 469–483. [Google Scholar] [CrossRef]
- Picard, J.; Aguado, I.; Cobos, N.; Fuster-Roig, V.; Quijano-López, A. Electric Distribution System Planning Methodology Considering Distributed Energy Resources: A Contribution towards Real Smart Grid Deployment. Energies 2021, 14, 1924. [Google Scholar] [CrossRef]
- Riaño, F.; Cruz, J.; Montoya, O.; Chamorro, H.; Alvarado-Barrios, L. Reduction of Losses and Operating Costs in Distribution Networks Using a Genetic Algorithm and Mathematical Optimization. Electronics 2021, 10, 419. [Google Scholar] [CrossRef]
- Li, R.; Wang, W.; Chen, Z.; Jiang, J.; Zhang, W. A Review of Optimal Planning Active Distribution System: Models, Methods, and Future Researches. Energies 2017, 10, 1715. [Google Scholar] [CrossRef]
- Lavorato, M.; Franco, J.F.; Rider, M.J.; Romero, R. Imposing Radiality Constraints in Distribution System Optimization Problems. IEEE Trans. Power Syst. 2011, 27, 172–180. [Google Scholar] [CrossRef]
- Farrag, M. A new model for distribution system planning. Int. J. Electr. Power Energy Syst. 1999, 21, 523–531. [Google Scholar] [CrossRef]
- Mejía-Solanilla, A.M.; Hincapié-Isaza, R.A.; Gallego-Rendón, R.A. Optimal planning of distribution systems considering multipleobjectives: Investment cost, reliability and technical losses. Rev. Tecnura 2015, 19, 106. [Google Scholar]
- Dong, Y.F.; Gu, J.H.; Li, N.N.; Hou, X.D.; Yan, W.L. Combination of Genetic Algorithm and Ant Colony Algorithm for Distribution Network Planning. In Proceedings of the 2007 IEEE International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007. [Google Scholar]
- Kilyeni, S.; Barbulescu, C.; Simo, A.; Teslovan, R.; Oros, C. Genetic algorithm-based distribution network expansion planning. In Proceedings of the 2014 IEEE 49th International Universities Power Engineering Conference (UPEC), Cluj-Napoca, Romania, 2–5 September 2014. [Google Scholar]
- Montoya, O.D.; Grajales, A.; Hincapié, R.A.; Granada, M. A new approach to solve the distribution system planning problem considering automatic reclosers. Ing. Rev. Chil. Ing. 2017, 25, 415–429. [Google Scholar] [CrossRef]
- Montoya, O.D.; Giraldo, J.S.; Grisales-Noreña, L.F.; Chamorro, H.R.; Alvarado-Barrios, L. Accurate and Efficient Derivative-Free Three-Phase Power Flow Method for Unbalanced Distribution Networks. Computation 2021, 9, 61. [Google Scholar] [CrossRef]
- Lavorato, M.; Rider, M.J.; Garcia, A.V.; Romero, R. Distribution network planning using a constructive heuristic algorithm. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Montoya, O.; Grajales, A.; Hincapié, R. Optimal selection of conductors in distribution systems using tabu search algorithm. Ing. Rev. Chil. Ing. 2018, 26, 283–295. [Google Scholar]
- Mohamad, H.; Zalnidzham, W.I.F.W.; Salim, N.A.; Shahbudin, S.; Yasin, Z.M. Power system restoration in distribution network using minimum spanning tree—Kruskal’s algorithm. Indones. J. Electr. Eng. Comput. Sci. 2019, 16, 1–8. [Google Scholar] [CrossRef]
- Kumari, A.; Vaisakh, K. Ensuring expected security cost with flexible resources using modified DE algorithm based dynamic optimal power flow. Appl. Soft Comput. 2022, 124, 108991. [Google Scholar] [CrossRef]
- El-Sattar, S.A.; Kamel, S.; Ebeed, M.; Jurado, F. An improved version of salp swarm algorithm for solving optimal power flow problem. Soft Comput. 2021, 25, 4027–4052. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.; Mallipeddi, R.; Amaratunga, G.A. Optimal power flow solutions using differential evolution algorithm integrated with effective constraint handling techniques. Eng. Appl. Artif. Intell. 2018, 68, 81–100. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A.J. Multi-objective optimal power flow solutions using a constraint handling technique of evolutionary algorithms. Soft Comput. 2019, 24, 2999–3023. [Google Scholar] [CrossRef]
- Deng, Z.; Rotaru, M.D.; Sykulski, J.K. Kriging Assisted Surrogate Evolutionary Computation to Solve Optimal Power Flow Problems. IEEE Trans. Power Syst. 2019, 35, 831–839. [Google Scholar] [CrossRef]
- Chen, G.; Qian, J.; Zhang, Z.; Li, S. Application of modified pigeon-inspired optimization algorithm and constraint-objective sorting rule on multi-objective optimal power flow problem. Appl. Soft Comput. 2020, 92, 106321. [Google Scholar] [CrossRef]
- Kaur, M.; Narang, N. An integrated optimization technique for optimal power flow solution. Soft Comput. 2019, 24, 10865–10882. [Google Scholar] [CrossRef]
- Medina, M.A.; Das, S.; Coello, C.A.C.; Ramírez, J.M. Decomposition-based modern metaheuristic algorithms for multi-objective optimal power flow—A comparative study. Eng. Appl. Artif. Intell. 2014, 32, 10–20. [Google Scholar] [CrossRef]
- Pulluri, H.; Naresh, R.; Sharma, V. A solution network based on stud krill herd algorithm for optimal power flow problems. Soft Comput. 2016, 22, 159–176. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Akbel, M.; Duman, S. Optimization of Optimal Power Flow Problem Using Multi-Objective Manta Ray Foraging Optimizer. Appl. Soft Comput. 2021, 116, 108334. [Google Scholar] [CrossRef]
- Sörensen, K. Metaheuristics–The metaphor exposed. Int. Trans. Oper. Res. 2013, 22, 3–18. [Google Scholar] [CrossRef]
- Molina, D.; Poyatos, J.; Del Ser, J.; García, S.; Hussain, A.; Herrera, F. Comprehensive Taxonomies of Nature- and Bio-inspired Optimization: Inspiration Versus Algorithmic Behavior, Critical Analysis Recommendations. Cogn. Comput. 2020, 12, 897–939. [Google Scholar] [CrossRef]
- Blum, C.; Puchinger, J.; Raidl, G.R.; Roli, A. Hybrid metaheuristics in combinatorial optimization: A survey. Appl. Soft Comput. 2011, 11, 4135–4151. [Google Scholar] [CrossRef] [Green Version]
- D’Andreagiovanni, F.; Krolikowski, J.; Pulaj, J. A fast hybrid primal heuristic for multiband robust capacitated network design with multiple time periods. Appl. Soft Comput. 2015, 26, 497–507. [Google Scholar] [CrossRef]
- Maciel, O.; Valdivia, A.; Oliva, D.; Cuevas, E.; Zaldívar, D.; Pérez-Cisneros, M. A novel hybrid metaheuristic optimization method: Hypercube natural aggregation algorithm. Soft Comput. 2019, 24, 8823–8856. [Google Scholar] [CrossRef]
- Shilaja, C.; Ravi, K. Optimal Power Flow Using Hybrid DA-APSO Algorithm in Renewable Energy Resources. Energy Procedia 2017, 117, 1085–1092. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).