Abstract
In this article, a theoretical mathematical model of gas flow through a duct in the case of local mass and momentum sources and sinks is presented. The continuity equation and motion equation with one-dimensional, density-stable gas flows were used to create this model. The size of sources and sinks and their locations have an effect on the size of gas stream flows in the duct, gas energy losses, and the parameters of the mechanical source energy that is causing the flow. In the traditional approach to describing the gas flow in the duct, the concept of resistivity and the equivalent resistance of the conduit is used. In the case of flow in the duct with local mass and momentum sources and sinks, the transport resistance depends on a bigger number of parameters than the concept of specific resistance usage. The location and size of the source flux or mass and momentum sinks and the fan work (suction, blowing) were taken into account in the presented model. The model gives the opportunity to determine the mechanical energy losses and efficiency of gas transport in the duct.
1. Introduction
Many technological industries use gaseous-substance transport through ducts. Depending on how the duct’s components are connected, the duct can be tight or permeable. Ventilation and fluid mechanics use a concept involving the difficulty posed by a tight duct to the fully developed turbulent flow of a gaseous medium. Specific drag and equivalent drag are the terms used to identify this difficulty [1,2,3]. They are sufficient for the correct identification of this difficulty in most technical problems. Flow resistance in ducts or mine workings has been the subject of many studies in the literature [4,5,6,7]. In the ventilation of mines, the stability of air flows is particularly important, which determines the safety of employees [8]. Many studies also concern leaking ducts in both HVAC systems and mining [9,10,11]. However, some cases involve flows in a duct in which a local mass and momentum source or sink exists for the same gaseous medium. In these circumstances, the flow difficulty depends on more parameters than would be considered when using the term specific drag.
The advantage of the model is the determination of the optimal location of the sources of mass due to the transport efficiency in the duct. Transport efficiency is a function of many parameters (including the location of the source of mass, the mass flow rate of the local source of mass, and the diameter of the duct or fan direction). This allows the model to be used both for flow in ducts and in mine workings. The obtained solution of the mathematical model is characterized by a close mathematical relationship connecting transport efficiency, mass flow rate, and the relative location of the local source of mass.
The value of the specific drag of the duct is defined as [1,2,12,13]:
The duct drag can be also calculated using geometric duct parameters and duct flow parameters. If the flow difficulty in a duct is caused by the forces opposing motion encountered by the flowing medium with a finite viscosity and density due to duct roughness, then the following equation can be used [1,12,13,14]:
In some cases, it is necessary, or more convenient, to express the specific drag of the duct R* as [2]:
If the duct features an internal local source of gas mass, then the mass flow rate of gas varies in different sections of the duct. In such a case, the equivalent drag of the entire duct is not the sum of its sectional drags. The energy efficiency ef for the observed medium’s flow can be given by the following equation:
If the mass flow rate of fluid is the same along the entire length of the duct, then transport efficiency is easy to determine. In a duct with an internal source of mass sink, the mass flow rate of gas varies in different sections of the duct. Thus, it is enough to choose which mass flow rate should be used in the denominator of Formula (4). In the considered flow cases, the gas transport efficiency ratio is given by the following equation:
This paper investigates various locations and flow rates of the internal sources of gas mass and momentum. The incoming gas is considered to have the same density as the gas flowing through the duct due to a mechanical source of energy. For different momenta of the internal-source mass flow rate (or internal sink), we determined the flow rates of gas passing through the entire length of the duct, the losses of gas energy due to forces resisting motion in the duct, and the work done by the mechanical source of energy. Duct gas transport efficiencies were determined for the investigated cases.
2. Considered Flow Cases and Calculation Results
All the flow cases presented in this paper involve a one-dimensional, steady state of gas flow in the duct, of constant density along the entire flow path. Local sources of mass with the same densities and different velocities were considered. Additionally discussed were cases involving local mass sinks in various locations of the duct. For all the cases, we determined the factors affecting the gas flow difficulty and gas transport efficiency in the duct. The theoretical models for the flows investigated in this paper were developed using a continuity equation and an equation of motion. The one-dimensional continuity equation in the presence of a mass source is as follows [3,12,14,15]:
Each component of Equation (6) has a unit of kg/(m·s). The internal source of mass is a local source of mass located at a point with the coordinate x = xa: , whose mass flow rate as a function of time is , kg/s. It is assumed that the mass flow rate of such a source will be constant over time , which can be expressed as:
Equation (6) can be formulated as follows:
The equation of motion for a one-dimensional non-steady flow with mass and momentum coming from an internal source is written as [1,12,14]:
Assuming that the cross-sectional area of the duct is uniform along its length, i.e., that , and considering the following equations:
the equation of motion (9) can be written as follows:
Assuming a steady-state flow and density, , with the previously made assumption that , the continuity Equation (8) and the equation of motion (2), as provided below, form a system of equations that constitute the theoretical model of the cases investigated in this paper:
Equation (14) defines the duct’s equivalent drag per unit :
thus, the system of Equation (13) can be written as follows:
Further, in this paper, the theoretical model (15) will be adjusted to the investigated flow case involving an internal source of mass and momentum.
For the analyzed calculation cases, we assumed that the mass flow rate of the source or sink is many times lower than the mass flow rate of the gas flowing through a duct in which the mass source or sink is absent. The presented examples involve a duct with drag R* = 0.0165 (kg·m)−1, = 1.2 kg/m3, F = 50 m2. The approximation ratios of the cubic polynomial that describe the fan are a = −0.0000958, b = −0.010539, c = 15.59840, d = 1963.750. For the purposes of this paper, the reference value of the mass flow rate of gas flowing through the duct (no mass sources/sinks) is = 350.076 kg/s.
2.1. Case 1
This case involves the presence of a local source of gas mass located at a point with the coordinate , with mass efficiency that is constant over time. The incoming mass has no momentum, which means that its velocity is u = 0. Local mass sources can occur at different points of the duct. At one end of the duct, a fan is installed as a mechanical source of mechanical energy, working in one of the two modes: suction (Case 1a) or blowing (Case 1b). The mass source parameters are independent of the fan’s working mode, although this is a factor that affects the flow results. These cases are demonstrated in Figure 1.
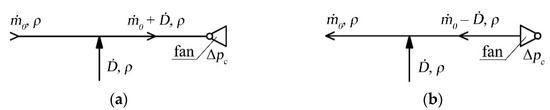
Figure 1.
Gas flow chart for Case 1 under consideration: (a) fan working in the suction mode, (b) fan working in the blowing mode.
After adjusting the model (15) to the conditions of Cases 1a and 1b, we obtained the theoretical model in the form of the following system of equations:
After integrating the system of Equation (16) along the path “x” but within a circuit closed by the external atmosphere, including , , and , the following was obtained:
The quantity (as well as the quantity ) in Formula (17) is the unit step function 1(x − xa), equal to 0 for x < xa and equal to 1 for x xa, [4]. As can be seen from (17), when (no source), the system of Equation (17) is expressed as:
Using (18), the equation of motion from the system of Equation (17) can be written as:
Formula (19) indicates that the local source () causes a lower head loss in the duct:
It can be stated that each local source of gas mass entering the duct, with a velocity of 0 and density equal to that of the gas flowing through the duct due to the mechanical source of mechanical energy, will result in decreased losses of mechanical energy due to forces opposing motion in the duct. This is independent of whether the fan (source of mechanical energy) works in the suction or blowing mode. For Cases 1a and 1b, it can be written that:
The fan working at the end of the duct has a characteristic curve that can be mathematically approximated with a cubic polynomial for the variable (kg/s), which is the mass flow rate of gas flowing through the fan (:
When the fan is working in the suction mode, as in Case 1a:
For Case 1a under consideration, the value can be calculated with the equation:
The following relationship exists for Case 1b:
Thus, the value can be calculated with the equation:
The gas transport efficiency in Cases 1a and 1b is given by the relationship (27):
Figure 2 illustrates the results of the numerical calculations of the mass flow rate of gas and depending on the point at which the source of mass is located for three gas flow rates (10, 30, 50 kg/s).
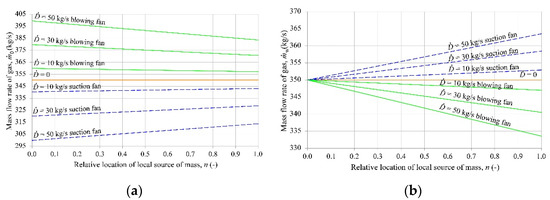
Figure 2.
Results of numerical calculations for (a) Case 1a, (b) Case 1b.
The orange color is used to mark the straight line corresponding to the reference value for , the green straight lines represent the fan working in the blowing mode, and the dotted lines apply to the fan working in the suction mode.
As shown in Figure 2a, when the fan is working in the blowing mode, the mass flow rate of gas at the duct entry is higher than in the absence of a local source of mass. When the fan is working in the suction mode, the local source of gas mass entering the duct causes the mass flow rate of gas at the duct entry to be lower than in the absence of a local source of mass. The mass flow rate of gas at the duct entry improves when the source of mass gas is located closer to the working suction fan.
As shown in Figure 2b, when the fan is working in the blowing mode, the source of gas mass causes the initial starting point of the fan to shift to the left on the fan’s characteristic curve. This is reflected in the decrease in the mass flow rate of gas flowing through the fan. The larger the flow rate of the local source of mass, the farther the fan’s operating point from the initial point. When the fan is working in the suction mode, the presence of a local source of gas mass causes the initial operating point of the fan to shift to the right on the fan’s characteristic curve. This entails an increase in the mass flow rate of gas flowing through the fan. If the gas source flow rate is the same, the shift of the operating point to the right in the characteristic curve is smaller than the corresponding shift of the operating point to the left in the case of the blowing mode. What this Figure also shows is that the location of the mass source has a varying effect on the fan’s operating point. When the fan is working in the blowing mode, the point of the local source that is closer to the end of the duct corresponds to the operating point farther left from the fan’s initial operating point. If the fan is working in the suction mode, the point of the local source of mass that is closer to the fan causes the operating point to shift farther to the right on the characteristic curve.
Figure 3 shows the duct gas transport efficiency in the presence of a local source of mass.
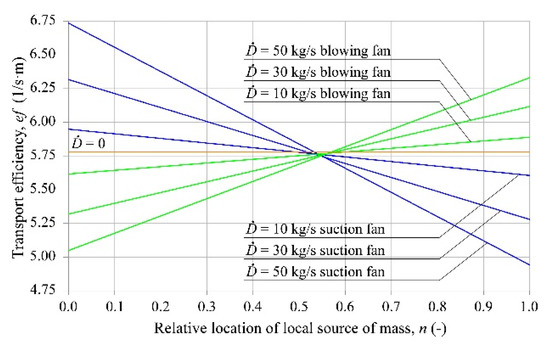
Figure 3.
Duct gas transport efficiency in the presence of a local source of mass.
As shown in Figure 3, the transport efficiency of a system in which the fan is working in the suction mode is lower than in a system whose fan is working in the absence of a local source of gas mass. The higher the mass flow rate, the lower the transport efficiency. When the fan is working in the blowing mode, higher gas mass flow rates are associated with higher transport efficiencies. In terms of energy, it is better when the local source of mass is closer to the duct entry.
2.2. Case 2
This case involves the presence of a local mass sink of gas located at a point with the coordinate xa, with mass efficiency that is constant over time. The mass leaving the duct (in contrast to Case 1) has a momentum, which means that this case involves a local mass and momentum sink. Local mass sources can occur at different points of the duct. The calculations below take this into account. At one end of the duct, a fan is installed as a mechanical source of mechanical energy, working in one of the two modes (as in Case 1): suction (Case 2a) or blowing (Case 2b). The sink of mass flow rate is independent of the thermal driving head created by the fan, although it is a factor affecting the resulting values . The value of momentum depends on the fan’s characteristic curve and the flow rate of mass leaving the duct. These cases are demonstrated in Figure 4.
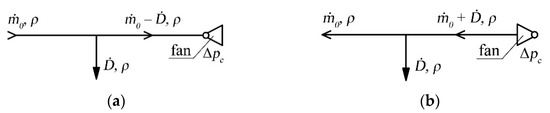
Figure 4.
Gas flow chart for Case 2 under consideration: (a) fan working in the suction mode, (b) fan working in the blowing mode.
After adjusting the system of Equation (15) to the parameters included in examples 2a and 2b, the following theoretical model is obtained:
After transformations, the following relationship is obtained:
As can be seen from (29), when (no source), then:
Using (30), it can be written that:
Formula (31) indicates that the local sink of mass and momentum might cause changes in the mechanical energy due to forces opposing motion in the duct. These changes can be lower or higher than losses of mechanical energy due to the absence of a local sink.
If:
which means that:
then:
If:
then:
For Cases 2a and 2b, it can be written that:
and:
When the fan is working in the suction mode, as in Case 2a, then:
And for Case 2a under consideration, the value can be calculated with the Equation:
For Case 2b under consideration, in which the fan is working in the blowing mode, the following relationship exists:
so for Case 2b, the value can be calculated with the Equation:
The gas transport efficiency is expressed by the relationship (43):
Figure 5 illustrates the results of the numerical calculations of the mass flow rate of gas and depending on the point at which the sink of mass is located for three gas flow rates (10, 30, 50 kg/s).
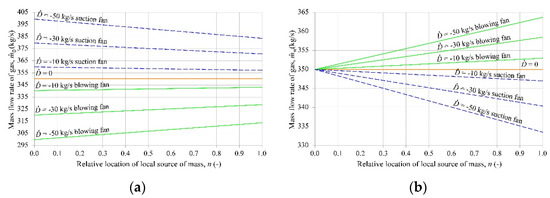
Figure 5.
Results of numerical calculations for (a) Case 2a, (b) Case 2b.
The straight lines in Figure 5 are to be interpreted in the same way as in Case 1.
As shown in Figure 5a, when the fan is working in the suction mode, the mass flow rate of gas at the duct entry is higher than in the absence of a local source of mass. When the fan is working in the blowing mode, the mass flow rate at the duct entry is lower than in the absence of a local mass sink. A gas mass sink that is located closer to the duct entry and its higher mass efficiency supported by the fan working in the suction mode has a positive effect on the mass flow rate of gas at the duct entry. As shown in Figure 5b, if the fan is working in the blowing mode, the mass flow rate of gas flowing through the fan is growing, and higher sinks give rise to higher mass flow rates. This means that the fan’s operating point shifts to the right from the initial operating point. When the fan is working in the suction mode, the operating point shifts to the left from the initial operating point.
Figure 6 shows the duct gas transport efficiency in the presence of a local sink of mass.
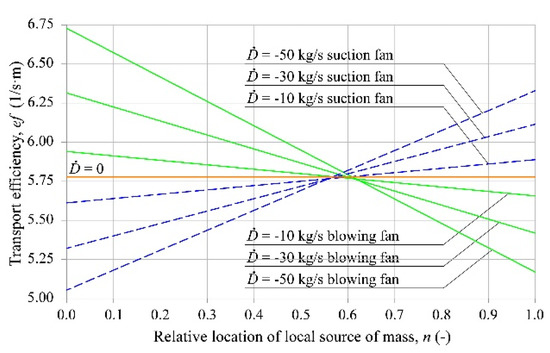
Figure 6.
Duct gas transport efficiency in the presence of a local sink of mass.
As shown in Figure 6, if the fan is working in the blowing mode and in the presence of a sink, the transport efficiency of the duct is better than in the absence of a sink (when the local sink is closer to the fan). The efficiency decreases as the mass flow rate of the gas sink increases, and as the sink location moves closer to the fan.
3. Conclusions
The gas transport in the duct can be disturbed by the presence of local mass and momentum sources or sinks. On the basis of theoretical models and calculation examples, it can be seen that the presence of a local inflow or outflow of gas has an effect on the mass stream size at the beginning of the duct and depends on the nature of the fan work at the end of the duct. For the gas supply and for the blowing fan, the mass stream increases at the beginning of the duct. In the case of the suction fan, this flow decreases. The gas outflow causes the opposite effect. Local inflow and outflow of gas have an influence on the mass stream of gas flowing through the fan. For the inflow and work of the suction fan, it can be seen the increase in the gas stream—and, in the case of the blowing fan, its decrease. For the local sink, the situation is similar. The location and size of the source or sink have an influence on the stream value.
The transport efficiency improves when its value is lower. This means that the forces opposing motion, associated with the flow of 1 kg/s of gas at the duct entry, are lower. It was shown that for local inflow, it is more advantageous to locate the source closer to the suction fan and further from the blowing fan. In the case of the local sink, the situation is the opposite.
In the presented models, the equal density of sources, sinks, and flowing gas in the duct was assumed. In mining and other technical cases, inflow sources and mass and momentum sinks may have different densities. This is a reason why future research will develop the model with the aim of inflow sources and mass and momentum sinks density.
Author Contributions
Conceptualization, B.P. and Z.K.; methodology, B.P. and Z.K.; software, B.P. and R.Ł.; validation, Z.K., R.Ł. and P.Ż.; formal analysis, P.Ż. and R.Ł.; investigation, B.P. and Z.K.; resources, B.P.; data curation, R.Ł. and P.Ż.; writing—original draft preparation, Z.K.; writing—review and editing, B.P.; visualization, R.Ł. and P.Ż.; supervision, Z.K.; project administration, Z.K.; funding acquisition, B.P. All authors have read and agreed to the published version of the manuscript.
Funding
The article was supported by the program “Excellence initiative—research university” for the AGH University of Science and Technology.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The results of the analysis are presented in the article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| hydraulic diameter of the duct, m | |
| internal source of mass flow, kg/(m·s) | |
| mass flow rate of local source of mass, kg/s | |
| energy efficiency for the observed medium’s flow, (m·s)−1 | |
| cross-sectional area of the duct, m2 | |
| gravity, m/s2 | |
| hydraulic gradient per unit (dimensionless) caused by the linear resistance of the duct, | |
| duct length, m | |
| mass flow rate of fluid, kg/s | |
| mass flow rate of gas entering the duct, the opposite end of which features a mechanical suction source (mass flow rate of gas leaving the duct, the opposite end of which features a mechanical suction source), kg/s | |
| mass flow rate of gas flowing through the fan, kg/s | |
| ratio of the drag of the duct section from its entry to the point where the local source of mass is located and the drag of the entire duct () | |
| absolute static pressure of the fluid, Pa | |
| cross-sectional circumference of the duct, m | |
| distributed drag per unit of the duct (a straight duct), kg/m8 | |
| specific drag, Ns2/m8 or kg/m7 | |
| R* | specific drag of the duct, 1/(kg·m) |
| duct’s equivalent drag per unit, kg/m8 | |
| flow velocity of incoming mass aligned with the mass flow direction in the duct, m/s | |
| volumetric flow rate of the flowing fluid, m3/s | |
| loss of mechanical energy (total head), N/m2 | |
| static-pressure drop at local resistance at a point with the coordinate , N/m2 | |
| x | distance, m |
| z | above-sea-level spot height of a given duct location, m |
| Greek symbols | |
| distributed-resistance coefficient of the duct, kg/m3 | |
| Dirac delta function distribution, 1/m | |
| total pressure increase for a working fan, N/m2 | |
| dimensionless distributed resistance coefficient of the duct, | |
| average gas velocity, m/s | |
| density, kg/m3 | |
| time, s | |
References
- Pawiński, J.; Roszkowski, J.; Strzemiński, J. Przewietrzanie Kopalń; Śląskie Wydawnictwo Techniczne: Katowice, Poland, 1995. [Google Scholar]
- Ptaszyński, B. Charakterystyka przepływowa przewodu transportującego różne media. In Proceedings of the 8 Szkoła Aerologii Górniczej. Sekcja Aerologii Górniczej: Nowoczesne Metody Zwalczania Zagrożeń Aerologicznych w Podziemnych Wyrobiskach Górniczych, Jaworze, Poland, 13–16 October 2015. [Google Scholar]
- Wacławik, J. Mechanika Płynów i Termodynamika; Wydawnictwo AGH: Kraków, Poland, 1993. [Google Scholar]
- Dziurzyński, W.; Krach, A.; Pałka, T. Airflow Sensitivity Assessment Based on Underground Mine Ventilation Systems Modeling. Energies 2017, 10, 1451. [Google Scholar] [CrossRef]
- Zmrhal, V.; Boháč, J. Pressure loss of flexible ventilation ducts for residential ventilation: Absolute roughness and compression effect. J. Build. Eng. 2021, 44, 103320. [Google Scholar] [CrossRef]
- Sleiti, A.K.; Zhai, J.; Idem, S. Computational fluid dynamics to predict duct fitting losses: Challenges and opportunities. HVAC&R Res. 2013, 19, 2–9. [Google Scholar] [CrossRef]
- Kodali, C.; Idem, S. Modeling flow and pressure distributions in multi-branch light-commercial duct systems. Sci. Technol. Built Environ. 2021, 27, 240–252. [Google Scholar] [CrossRef]
- Semin, M.A.; Levin, L.Y. Stability of air flows in mine ventilation networks. Process Saf. Environ. Prot. 2019, 124, 167–171. [Google Scholar] [CrossRef]
- Onder, M.; Cevik, E. Statistical model for the volume rate reaching the end of ventilation duct. Tunn. Undergr. Space Technol. 2008, 23, 179–184. [Google Scholar] [CrossRef]
- Auld, G. An estimation of fan performance for leaky ventilation ducts. Tunn. Undergr. Space Technol. 2004, 19, 539–549. [Google Scholar] [CrossRef]
- Akhtar, S.; Kumral, M.; Sasmito, A.P. Correlating variability of the leakage characteristics with the hydraulic performance of an auxiliary ventilation system. Build. Environ. 2017, 121, 200–214. [Google Scholar] [CrossRef]
- McPherson, M.J. Subsurface Ventilation and Environmental Engineering; Chapman&Hall: London, UK, 1992. [Google Scholar]
- Wacławik, J. Wentylacja Kopalń, Tom I, II; Wydawnictwo AGH: Krakow, Poland, 2010. [Google Scholar]
- Yamaguchi, H. Engineering Fluid Mechanics; Springer Netherlands: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Bergander, M.J. Fluid Mechanics Volume 1. Basic Principles; AGH University of Science and Technology Press: Krakow, Poland, 2010. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).