Do Factor Market Distortions and Carbon Dioxide Emissions Distort Energy Industry Chain Technical Efficiency? A Heterogeneous Stochastic Frontier Analysis
Abstract
1. Introduction
2. Literature Review
3. Methods
3.1. Research Model Design
3.1.1. Definition of Energy Industry Chain Technical Efficiency
3.1.2. Stochastic Frontier Analysis Model of Heterogeneity
3.2. Variables and Data Description
3.2.1. Input Variables
3.2.2. Output Variables
3.2.3. Core Variables
3.2.4. Control Variables
3.2.5. Data Description
4. Results
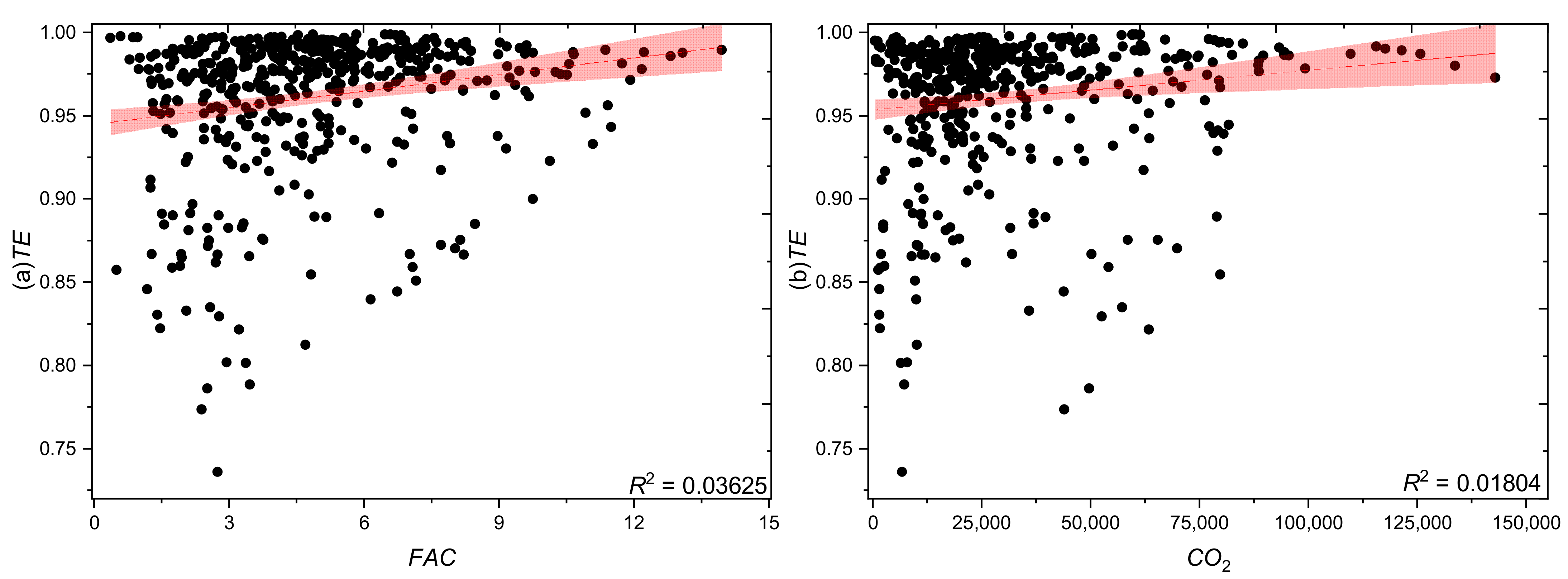
4.1. Analysis of Regression Results
4.2. The Evolution of Energy TE
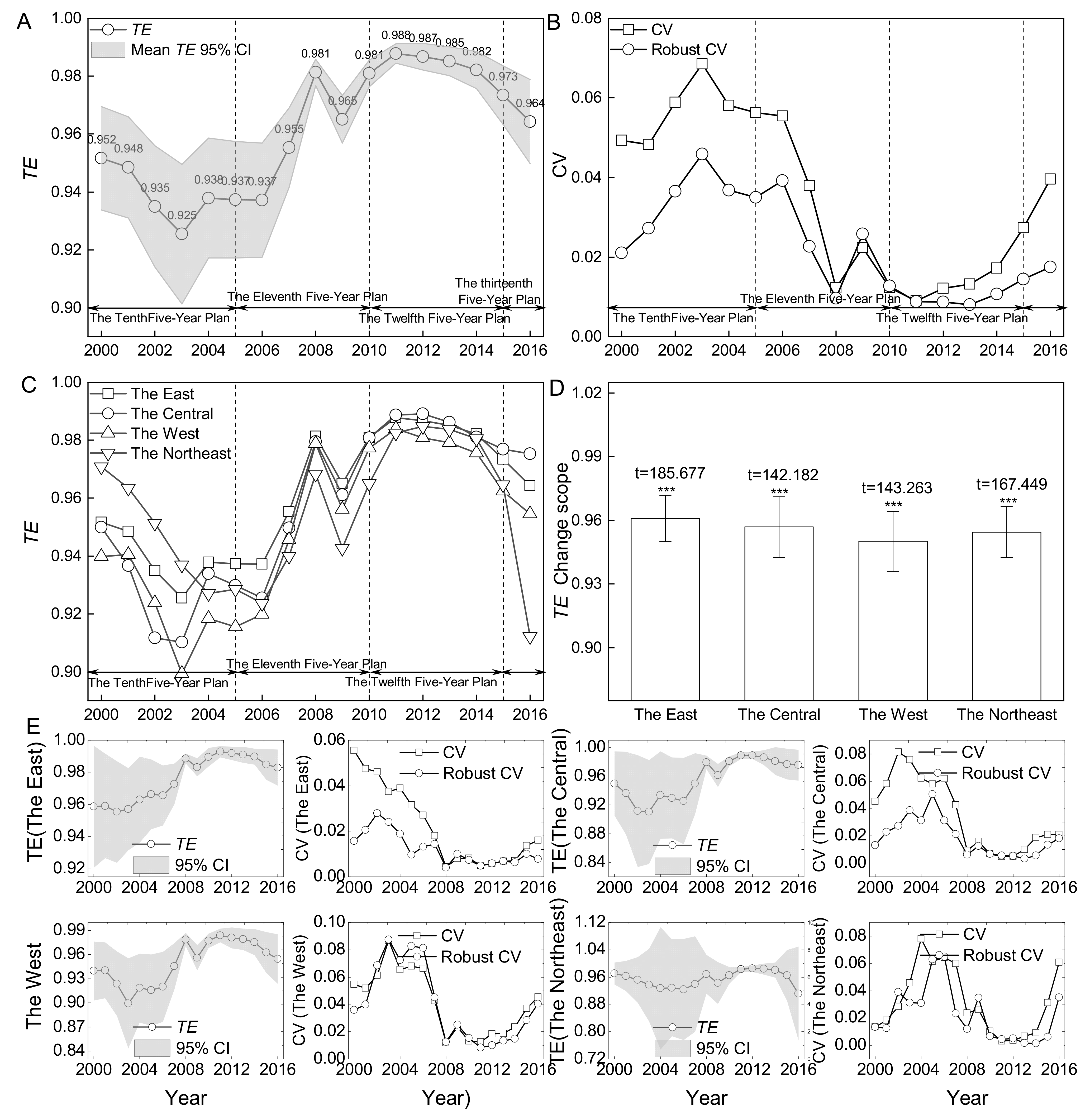
4.2.1. Overall Change
4.2.2. Time Trend Change
4.2.3. TE Changes in Provinces and Cities
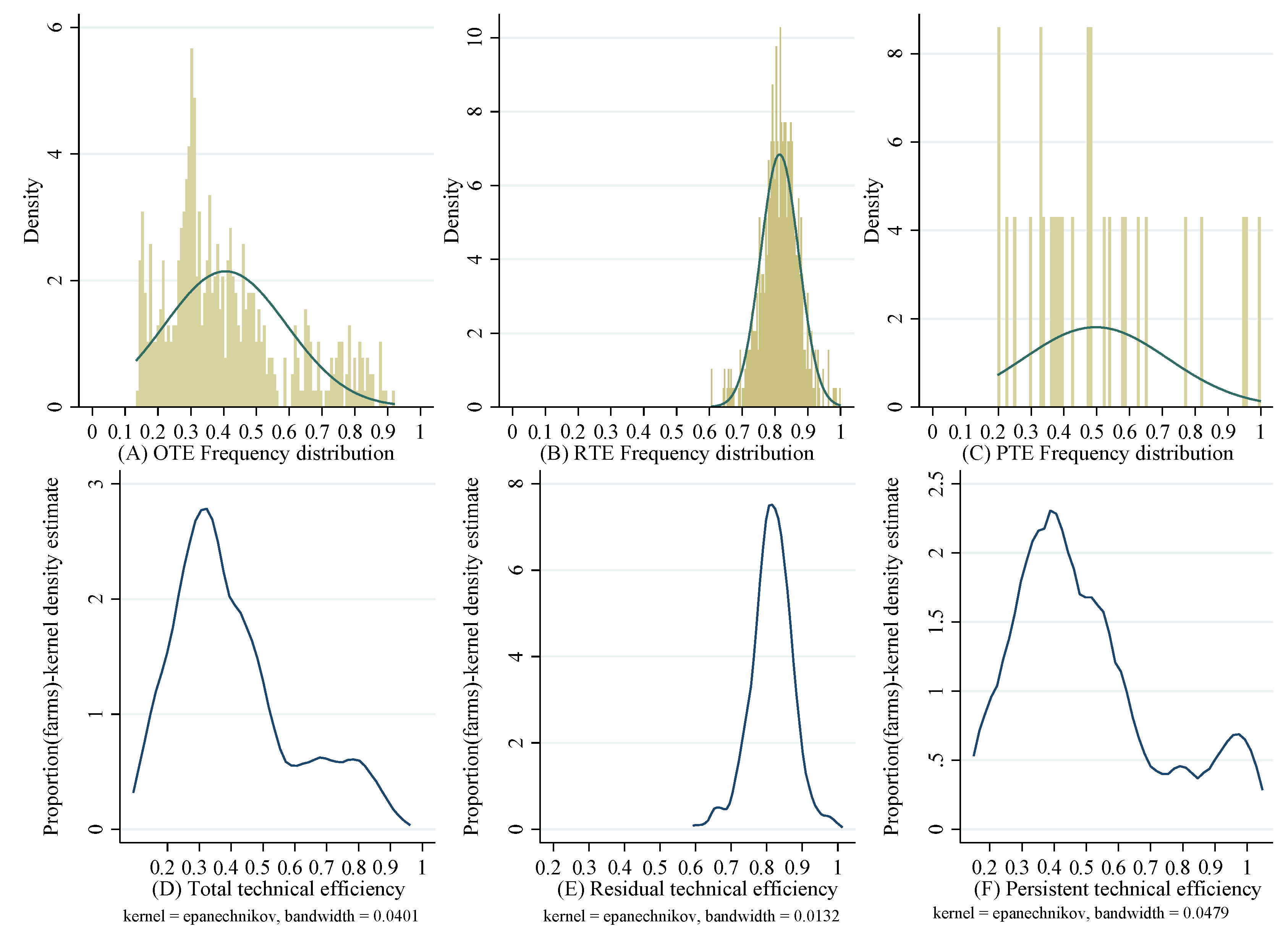
4.2.4. Energy Technical Efficiency Decomposition and Robustness Analysis
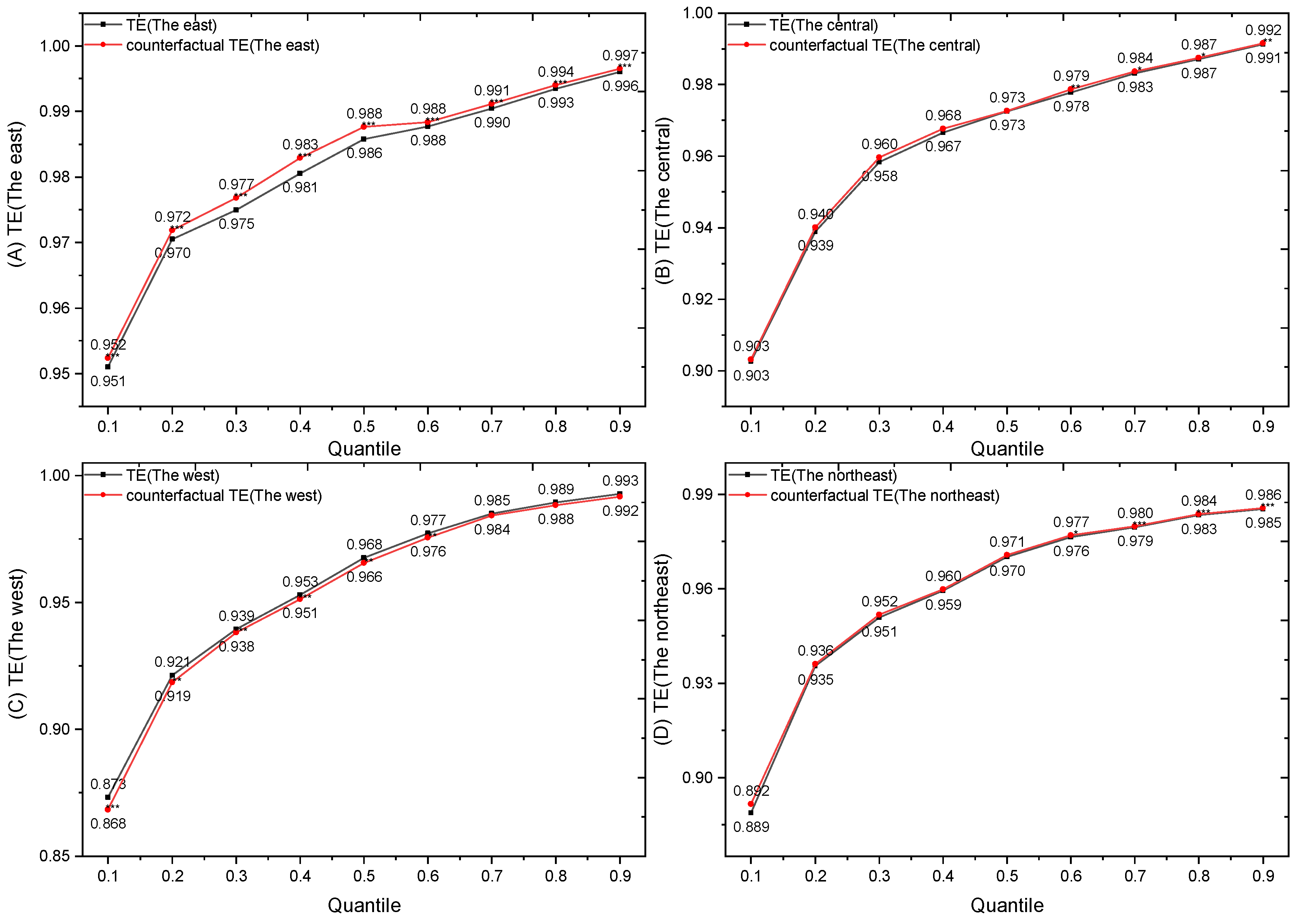
4.3. Counterfactual Analysis
4.3.1. Counterfactual Result
4.3.2. Counterfactual Test
5. Conclusions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gong, F.; Park, J.; Cao, Y. The impact of IT spillovers on technical efficiency: The role of IT intensity and supply chain relationships. Inf. Manag. 2022, 59, 103589. [Google Scholar] [CrossRef]
- Lin, B.; Du, K. The Energy Effect of Factor Market Distortion in China. Econ. Res. J. 2013, 48, 125–136. (In Chinese) [Google Scholar]
- Bányai, T. Real-Time Decision Making in First Mile and Last Mile Logistics: How Smart Scheduling Affects Energy Efficiency of Hyperconnected Supply Chain Solutions. Energies 2018, 11, 1833. [Google Scholar] [CrossRef]
- Cui, H.; Huang, Z.; Yüksel, S.; Dinçer, H. Analysis of the innovation strategies for green supply chain management in the energy industry using the QFD-based hybrid interval valued intuitionistic fuzzy decision approach. Renew. Sustain. Energy Rev. 2021, 143, 110844. [Google Scholar] [CrossRef]
- Marchi, B.; Zanoni, S. Supply Chain Management for Improved Energy Efficiency: Review and Opportunities. Energies 2017, 10, 1618. [Google Scholar] [CrossRef]
- Yang, B.; Liu, B.; Peng, J.; Liu, X. The impact of the embedded global value chain position on energy-biased technology progress: Evidence from chinas manufacturing. Technol. Soc. 2022, 71, 102065. [Google Scholar] [CrossRef]
- Yang, M.; Yang, F.; Sun, C. Factor market distortion correction, resource reallocation and potential productivity gains: An empirical study on China’s heavy industry sector. Energy Econ. 2018, 69, 270–279. [Google Scholar] [CrossRef]
- Peng, J.; Xiao, J.; Wen, L.; Zhang, L. Energy industry investment influences total factor productivity of energy exploitation: A biased technical change analysis. J. Clean. Prod. 2019, 237, 117847. [Google Scholar] [CrossRef]
- Peng, J.; Xiao, J.; Zhang, L.; Wang, T. The impact of China’s ‘Atmosphere Ten Articles’ policy on total factor productivity of energy exploitation: Empirical evidence using synthetic control methods. Resour. Policy 2020, 65, 101544. [Google Scholar] [CrossRef]
- Aminpour, S.; Irajpour, A.; Yazdani, M.; Mohtashami, A. The Design of a Multi-directional Network Chain Model Offering a Closed Loop in the Automotive Industry by Providing Energy and Time Efficiency Programs. Ind. Manag. J. 2020, 12, 319–343. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, Y.; Yuan, X.; Cao, D.; Zuo, J.; Gao, J. Addressing the efficiency of the core ecological industrial chain: A DEA approach. J. Clean. Prod. 2017, 156, 235–243. [Google Scholar] [CrossRef]
- Nunes, L.; Causer, T.; Ciolkosz, D. Biomass for energy: A review on supply chain management models. Renew. Sustain. Energy Rev. 2019, 120, 109658. [Google Scholar] [CrossRef]
- Dong, F.; An, X.; Li, C. Performance evaluation of wind power industry chain based on three-stage DEA. J. Renew. Sustain. Energy 2021, 13, 033313. [Google Scholar] [CrossRef]
- Farrell, M.J. The measurement of productive efficiency. J. R. Stat. Soc. Ser. A 1957, 120, 253–281. [Google Scholar] [CrossRef]
- Hoffmann, P. 2 groups discuss energy-efficiency in existing buildings national-institute-of-building-sciences and of-fice-of-technology-assessment. Archit. Rec. 1982, 170, 35. [Google Scholar]
- Bengtson, H.H. Small scale ethanol production from corn—Technology, energy efficiency and economics. Energy Agric. 1983, 2, 197–217. [Google Scholar] [CrossRef]
- Huang, H.; Ge, L.; Wang, M. Analysis to the total- factor energy efficiency of Chinese cities. Urban Probl. 2015, 53–60. (In Chinese) [Google Scholar] [CrossRef]
- Meng, C.; Chen, Y. China’s Inter-regional Energy Efficiency during the Period of 1995–2010: Descriptive Statistic and DEA Analysis Based on Provincial Panel Data. Financ. Trade Econ. 2012, 116–123. (In Chinese) [Google Scholar] [CrossRef]
- Chen, X. Research on the Difference of Energy Consumption Output Efficiency in China under Unexpected Output. Chin. J. Manag. Sci. 2019, 27, 191–198. (In Chinese) [Google Scholar] [CrossRef]
- Meng, Q.C.; Huang, W.D.; Rong, X.X. Energy Efficiency Calculation and Analysis on Potentials of Emissions Reduction under Haze Enironment. Chin. J. Manag. Sci. 2016, 24, 53–61. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Streimikiene, D.; Jusoh, A.; Khoshnoudi, M. A comprehensive review of data envelopment analysis (DEA) approach in energy efficiency. Renew. Sustain. Energy Rev. 2017, 70, 1298–1322. [Google Scholar] [CrossRef]
- Hu, J.L.; Honma, S. A Comparative Study of Energy Efficiency of OECD Countries: An Application of the Stochastic Frontier Analysis. Energy Procedia 2014, 61, 2280–2283. [Google Scholar] [CrossRef][Green Version]
- Haider, S.; Mishra, P.P. Does innovative capability enhance the energy efficiency of Indian Iron and Steel firms? A Bayesian stochastic frontier analysis. Energy Econ. 2021, 95, 105128. [Google Scholar] [CrossRef]
- Wei, C.; Shen, M. Energy efficiency and its influencing factors: An empirical Analysis based on DEA. Manag. World 2007, 66–76. [Google Scholar] [CrossRef]
- Mandal, S.K. Do undesirable output and environmental regulation matter in energy efficiency analysis? Evidence from Indian Cement Industry. Energy Policy 2010, 38, 6076–6083. [Google Scholar] [CrossRef]
- Bi, G.-B.; Song, W.; Zhou, P.; Liang, L. Does environmental regulation affect energy efficiency in China’s thermal power generation? Empirical evidence from a slacks-based DEA model. Energy Policy 2014, 66, 537–546. [Google Scholar] [CrossRef]
- Saeedi, H.; Behdani, B.; Wiegmans, B.; Zuidwijk, R. Assessing the technical efficiency of intermodal freight transport chains using a modified network DEA approach. Transp. Res. Part E Logist. Transp. Rev. 2019, 126, 66–86. [Google Scholar] [CrossRef]
- Ziętek-Kwaśniewska, K.; Zuba-Ciszewska, M.; Nucińska, J. Technical Efficiency of Cooperative and Non-Cooperative Dairies in Poland: Toward the First Link of the Supply Chain. Agriculture 2022, 12, 52. [Google Scholar] [CrossRef]
- Battese, G.E.; Coelli, T.J. Frontier production functions, technical efficiency and panel data: With application to paddy farmers in India. J. Prod. Anal. 1992, 3, 153–169. [Google Scholar] [CrossRef]
- Wei, C.; Zheng, X. A New Perspective on Energy Efficiency Enhancement: A Test Based on Market Segmentation. Soc. Sci. China 2017, 90–111. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2017&filename=ZSHK201710008&uniplatform=NZKPT&v=XNRKJcSwrZ70ljNrIyDM3QdbaFP0QDvMP_iVRcnlBArDT9r8n6VOrGlhvRja18Tf (accessed on 19 August 2022).
- Wang, H.-J.; Ho, C.-W. Estimating fixed-effect panel stochastic frontier models by model transformation. J. Econ. 2010, 157, 286–296. [Google Scholar] [CrossRef]
- Li, W.; Zhang, K. The Effects of Air Pollution on Enterprises’ Productivity: Evidence from Chinese Industrial Enterprises. Manag. World 2019, 35, 95–112, 119. (In Chinese) [Google Scholar] [CrossRef]
- Ito, K.; Zhang, S. Willingness to pay for clean air: Evidence from air purifier markets in China. J. Political Econ. 2020, 128, 1627–1672. [Google Scholar] [CrossRef]
- Fu, S.; Ma, Z.; Ni, B.; Peng, J.; Zhang, L.; Fu, Q. Research on the spatial differences of pollution-intensive industry transfer under the environmental regulation in China. Ecol. Indic. 2021, 129, 107921. [Google Scholar] [CrossRef]
- Chen, X. China’s provincial energy efficiency evaluation and improvement path under unexpected output. Southeast Acad. Res. 2018, 151–159. (In Chinese) [Google Scholar] [CrossRef]
- Greene, W. Reconsidering heterogeneity in panel data estimators of the stochastic frontier model. J. Econ. 2005, 126, 269–303. [Google Scholar] [CrossRef]
- Chernozhukov, V.; Fernández Val, I.; Melly, B. Inference on counterfactual distributions. Econometrica 2013, 81, 2205–2268. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.; Zhou, D. Measuring economy-wide energy efficiency performance: A parametric frontier approach. Appl. Energy 2012, 90, 196–200. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Heshmati, A. Efficiency Measurement in Swedish Dairy Farms: An Application of Rotating Panel Data, 1976–1988. Am. J. Agric. Econ. 1995, 77, 660–674. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Lien, G.; Hardaker, B. Technical efficiency in competing panel data models: A study of Norwegian grain farming. J. Prod. Anal. 2012, 41, 321–337. [Google Scholar] [CrossRef]
- Peng, J.; Xu, R.; Fu, L.; Yu, M.; Xu, Y.-D. The evolution pattern of green innovation efficiency of industrial enterprises in the Yangtze River Economic Belt. China Environ. Sci. 2019, 39, 4886–4900. [Google Scholar] [CrossRef]
- Sun, X.; Loh, L.; Chen, Z.; Zhou, X. Factor price distortion and ecological efficiency: The role of institutional quality. Environ. Sci. Pollut. Res. 2019, 27, 5293–5304. [Google Scholar] [CrossRef] [PubMed]
- Manevska-Tasevska, G.; Hansson, H.; Labajova, K. Impact of Management Practices on Persistent and Residual Technical Efficiency—A Study of Swedish pig Farming. Manag. Decis. Econ. 2016, 38, 890–905. [Google Scholar] [CrossRef]
- Agasisti, T.; Gralka, S. The transient and persistent efficiency of Italian and German universities: A stochastic frontier analysis. Appl. Econ. 2019, 51, 5012–5030. [Google Scholar] [CrossRef]
- Schmidt, P.; Sickles, R.C. Production Frontiers and Panel Data. J. Bus. Econ. Stat. 1984, 2, 367–374. [Google Scholar] [CrossRef]
- Kodde, D.A.; Palm, F.C. Wald criteria for jointly testing equality and inequality restrictions. Econom. J. Econom. Soc. 1986, 54, 1243–1248. [Google Scholar] [CrossRef]

| Variables | (Vars) | Unit | Obs | Mean | SD | Min | Max |
|---|---|---|---|---|---|---|---|
| regional GDP | GDP | 100 million yuan | 493 | 8.042 | 0.886 | 6 | 10 |
| labor | LAB | person | 493 | 7.552 | 0.836 | 6 | 9 |
| capital | CAP | 100 million yuan | 493 | 9.404 | 1.042 | 7 | 12 |
| energy consumption | ENE | bcm | 493 | 9.342 | 0.865 | 6 | 11 |
| labor squared | LABsq | / | 493 | 57.736 | 12.182 | 32 | 78 |
| capital squared | CAPsq | / | 493 | 89.512 | 19.402 | 44 | 138 |
| energy consumption squared | ENEsq | / | 493 | 88.026 | 15.637 | 37 | 124 |
| interaction between labor and capital | LABC | / | 493 | 71.600 | 14.020 | 37 | 103 |
| interaction between labor and energy consumption | LABE | / | 493 | 71.054 | 12.743 | 35 | 98 |
| interaction between capital and energy consumption | CAPE | / | 493 | 88.578 | 16.605 | 44 | 131 |
| factor market development degree score | FAC | / | 493 | 4.845 | 2.459 | 0 | 14 |
| regional CO2 emissions | CO2 | ton | 493 | 10.023 | 0.896 | 6 | 12 |
| average years of education | EDU | person | 493 | 2.123 | 0.126 | 2 | 3 |
| regional education expenditure | EDR | 100 million yuan | 493 | 14.562 | 1.154 | 11 | 17 |
| regional public financial expenditure | FIN | 100 milllion yuan | 493 | 16.398 | 1.091 | 13 | 19 |
| R&D expenditure | RD | 100 million yuan | 493 | 13.511 | 1.633 | 9 | 17 |
| district population | POP | person | 493 | 8.158 | 0.771 | 6 | 9 |
| total regional trade | TRA | 100 million yuan | 493 | 5.259 | 1.764 | 1 | 9 |
| Vars | GDP | LAB | CAP | ENE | FAC | CO2 | EDU | EDR | FIN | RD |
|---|---|---|---|---|---|---|---|---|---|---|
| GDP | 1 | 0.79 *** | 0.81 *** | 0.69 *** | 0.58 *** | 0.68 *** | 0.32 *** | 0.62 *** | 0.61 *** | 0.79 *** |
| LAB | 0.85 *** | 1 | 0.61 *** | 0.62 *** | 0.23 *** | 0.62 *** | −0.09 ** | 0.52 *** | 0.47 *** | 0.52 *** |
| CAP | 0.84 *** | 0.67 *** | 1 | 0.775 *** | 0.68 *** | 0.77 *** | 0.59 *** | 0.92 *** | 0.92 *** | 0.92 *** |
| ENE | 0.75 *** | 0.69 *** | 0.81 *** | 1 | 0.36 *** | 0.99 *** | 0.39 *** | 0.72 *** | 0.72 *** | 0.67 *** |
| FAC | 0.49 *** | 0.15 *** | 0.60 *** | 0.29 *** | 1 | 0.36 *** | 0.61 *** | 0.59 *** | 0.59 *** | 0.76 *** |
| CO2 | 0.76 *** | 0.69 *** | 0.79 *** | 0.99 *** | 0.28 *** | 1 | 0.39 *** | 0.71 *** | 0.71 *** | 0.66 *** |
| EDU | 0.36 *** | −0.05 | 0.57 *** | 0.36 *** | 0.66 *** | 0.34 *** | 1 | 0.57 *** | 0.61 *** | 0.67 *** |
| EDR | 0.68 *** | 0.57 *** | 0.93 *** | 0.76 *** | 0.52 *** | 0.75 *** | 0.55 *** | 1 | 0.99 *** | 0.85 *** |
| FIN | 0.65 *** | 0.53 *** | 0.92 *** | 0.75 *** | 0.53 *** | 0.74 *** | 0.58 *** | 0.99 *** | 1 | 0.85 *** |
| RD | 0.82 *** | 0.59 *** | 0.93 *** | 0.73 *** | 0.7 *** | 0.72 *** | 0.66 *** | 0.87 *** | 0.87 *** | 1 |
| POP | 0.85 *** | 0.99 *** | 0.64 *** | 0.69 *** | 0.13 ** | 0.7 *** | −0.05 | 0.53 *** | 0.49 *** | 0.55 *** |
| TRA | 0.82 *** | 0.48 *** | 0.84 *** | 0.63 *** | 0.74 *** | 0.62 *** | 0.66 *** | 0.74 *** | 0.73 *** | 0.87 *** |
| Function | Trans-Log | Cobb–Douglas | ||||||
|---|---|---|---|---|---|---|---|---|
| (1) OLS | (2) FE | (3) RE | (4) SFA | (5) SFA | (6) SFA | (7) SFA | (8) SFA | |
| LAB | −0.0043 | 1.261 *** | 0.872 ** | 1.129 *** | 0.876 *** | −0.0329 | −0.0326 | −0.0664 * |
| (0.381) | (0.309) | (0.371) | (0.348) | (0.290) | (0.0378) | (0.0405) | (0.0384) | |
| CAP | 2.430 *** | 0.602 *** | 0.770 *** | 0.616 *** | 0.424 *** | 0.106 *** | 0.0852 *** | 0.101 *** |
| (0.342) | (0.0765) | (0.112) | (0.0778) | (0.0700) | (0.00889) | (0.0102) | (0.00763) | |
| ENE | −0.474 | −0.232 *** | −0.244 ** | −0.223 *** | −0.187 *** | 0.214 *** | 0.188 *** | 0.179 *** |
| (0.340) | (0.0822) | (0.122) | (0.0826) | (0.0706) | (0.0131) | (0.0141) | (0.0110) | |
| LABsq | −0.120 *** | −0.134 *** | −0.102 *** | −0.123 *** | −0.101 *** | |||
| (0.0434) | (0.0260) | (0.0317) | (0.0291) | (0.0256) | ||||
| CAPsq | −0.0882 *** | −0.0479 *** | −0.0827 *** | −0.0502 *** | −0.0218 *** | |||
| (0.0336) | (0.00715) | (0.0101) | (0.00712) | (0.00841) | ||||
| ENEsq | −0.0180 | 0.0839 *** | 0.0730 *** | 0.0838 *** | 0.0915 *** | |||
| (0.0443) | (0.0109) | (0.0162) | (0.0108) | (0.0130) | ||||
| LABC | 0.0494 | 0.150 *** | 0.189 *** | 0.153 *** | 0.128 *** | |||
| (0.0571) | (0.0142) | (0.0200) | (0.0146) | (0.0159) | ||||
| LABE | 0.202 *** | −0.0607 *** | −0.0637 ** | −0.0633 *** | −0.0569 *** | |||
| (0.0647) | (0.0175) | (0.0258) | (0.0176) | (0.0173) | ||||
| CAPE | −0.0779 | −0.0765 *** | −0.0568 *** | −0.0756 *** | −0.0960 *** | |||
| (0.0617) | (0.0130) | (0.0194) | (0.0128) | (0.0185) | ||||
| Energy industrial chain technology efficiency loss function estimation | ||||||||
| FAC | 0.519 *** | 0.479 *** | ||||||
| (0.132) | (0.115) | |||||||
| CO2 | 2.246 *** | 1.470 *** | ||||||
| (0.402) | (0.283) | |||||||
| EDU | −1.541 | 2.874 ** | ||||||
| (2.221) | (1.430) | |||||||
| EDR | −2.961 ** | −0.575 | ||||||
| (1.150) | (0.937) | |||||||
| FIN | 0.764 | −0.830 | ||||||
| (1.011) | (0.881) | |||||||
| RD | 1.152 *** | 0.581 ** | ||||||
| (0.321) | (0.226) | |||||||
| POP | −0.764 ** | −0.479 | ||||||
| (0.383) | (0.301) | |||||||
| TRA | −1.510 *** | −1.498 *** | ||||||
| (0.307) | (0.278) | |||||||
| Cons | −4.947 *** | 0.0155 | −0.597 | 1.367 | −6.833 *** | 0.662 ** | (0.273) | 6.425 *** |
| (1.227) | (0.929) | (1.131) | (1.017) | (0.851) | (0.277) | (0.312) | (0.209) | |
| Obs | 493 | 493 | 493 | 493 | 493 | 493 | 493 | 493 |
| Region | Mean | S.D. | Mix | Q1 | Q3 | Max |
|---|---|---|---|---|---|---|
| The east | 0.961 | 0.029 | 0.8124 | 0.9727 | 0.9914 | 0.9985 |
| The central | 0.957 | 0.046 | 0.7735 | 0.9481 | 0.9847 | 0.9960 |
| The west | 0.950 | 0.049 | 0.7359 | 0.9329 | 0.9876 | 0.9974 |
| The northeast | 0.955 | 0.038 | 0.8444 | 0.9421 | 0.9810 | 0.9883 |
| Provinces | 2000 | 2005 | ① | 2006 | 2010 | ② | 2011 | 2015 | ③ | 2016 | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 0.812 | 0.885 | 0.854 | 0.900 | 0.977 | 0.954 | 0.988 | 0.988 | 0.988 | 0.989 | 0.931↑ |
| Tianjin | 0.946 | 0.975 | 0.941 | 0.965 | 0.977 | 0.971 | 0.983 | 0.952 | 0.973 | 0.943 | 0.959↓ |
| Hebei | 0.975 | 0.963 | 0.965 | 0.951 | 0.986 | 0.974 | 0.991 | 0.980 | 0.986 | 0.983 | 0.975↑ |
| Shanghai | 0.966 | 0.968 | 0.953 | 0.975 | 0.987 | 0.982 | 0.990 | 0.981 | 0.987 | 0.986 | 0.973↑ |
| Jiangsu | 0.976 | 0.977 | 0.973 | 0.973 | 0.995 | 0.987 | 0.996 | 0.994 | 0.995 | 0.993 | 0.985↑ |
| Zhejiang | 0.964 | 0.966 | 0.970 | 0.962 | 0.996 | 0.981 | 0.997 | 0.994 | 0.996 | 0.992 | 0.982↑ |
| Fujian | 0.991 | 0.978 | 0.986 | 0.978 | 0.996 | 0.986 | 0.997 | 0.989 | 0.995 | 0.981 | 0.988↓ |
| Shandong | 0.990 | 0.967 | 0.981 | 0.971 | 0.987 | 0.980 | 0.992 | 0.980 | 0.987 | 0.973 | 0.982↓ |
| Guangdong | 0.985 | 0.991 | 0.989 | 0.991 | 0.998 | 0.995 | 0.999 | 0.998 | 0.998 | 0.998 | 0.994↑ |
| Hainan | 0.982 | 0.995 | 0.988 | 0.991 | 0.996 | 0.992 | 0.997 | 0.995 | 0.996 | 0.992 | 0.992↑ |
| Shanxi | 0.867 | 0.835 | 0.821 | 0.822 | 0.977 | 0.915 | 0.986 | 0.939 | 0.964 | 0.939 | 0.897↑ |
| Anhui | 0.970 | 0.972 | 0.968 | 0.965 | 0.985 | 0.974 | 0.992 | 0.974 | 0.987 | 0.966 | 0.975↓ |
| Jiangxi | 0.973 | 0.958 | 0.963 | 0.967 | 0.991 | 0.982 | 0.996 | 0.994 | 0.995 | 0.993 | 0.980↑ |
| Henan | 0.981 | 0.979 | 0.974 | 0.968 | 0.976 | 0.975 | 0.984 | 0.992 | 0.989 | 0.993 | 0.980↑ |
| Hubei | 0.943 | 0.908 | 0.906 | 0.903 | 0.974 | 0.947 | 0.984 | 0.976 | 0.983 | 0.978 | 0.945↑ |
| Hunan | 0.967 | 0.926 | 0.941 | 0.930 | 0.983 | 0.964 | 0.990 | 0.987 | 0.990 | 0.984 | 0.965↑ |
| Inner Mongolia | 0.987 | 0.882 | 0.951 | 0.885 | 0.960 | 0.932 | 0.959 | 0.889 | 0.932 | 0.855 | 0.934↓ |
| Guangxi | 0.988 | 0.990 | 0.989 | 0.992 | 0.994 | 0.994 | 0.996 | 0.996 | 0.995 | 0.995 | 0.993↑ |
| Sichuan | 0.957 | 0.936 | 0.939 | 0.928 | 0.975 | 0.956 | 0.989 | 0.988 | 0.990 | 0.988 | 0.962↑ |
| Guizhou | 0.890 | 0.875 | 0.885 | 0.862 | 0.966 | 0.933 | 0.982 | 0.992 | 0.987 | 0.990 | 0.935↑ |
| Yunnan | 0.982 | 0.957 | 0.967 | 0.961 | 0.983 | 0.977 | 0.990 | 0.991 | 0.992 | 0.989 | 0.978↓ |
| Shaanxi | 0.897 | 0.938 | 0.892 | 0.943 | 0.968 | 0.958 | 0.983 | 0.930 | 0.966 | 0.923 | 0.935↑ |
| Gansu | 0.984 | 0.936 | 0.951 | 0.955 | 0.987 | 0.972 | 0.990 | 0.951 | 0.979 | 0.947 | 0.965↓ |
| Qinghai | 0.857 | 0.867 | 0.847 | 0.882 | 0.978 | 0.938 | 0.987 | 0.963 | 0.977 | 0.936 | 0.917↑ |
| Ningxia | 0.885 | 0.789 | 0.830 | 0.802 | 0.966 | 0.906 | 0.967 | 0.935 | 0.951 | 0.952 | 0.895↓ |
| Xinjiang | 0.972 | 0.987 | 0.978 | 0.988 | 0.997 | 0.992 | 0.997 | 0.989 | 0.995 | 0.972 | 0.987↑ |
| Liaoning | 0.959 | 0.867 | 0.905 | 0.859 | 0.957 | 0.910 | 0.980 | 0.984 | 0.984 | 0.870 | 0.928↓ |
| Jilin | 0.968 | 0.939 | 0.955 | 0.935 | 0.976 | 0.964 | 0.986 | 0.980 | 0.986 | 0.975 | 0.968↑ |
| Heilongjiang | 0.985 | 0.979 | 0.979 | 0.976 | 0.962 | 0.970 | 0.983 | 0.930 | 0.968 | 0.891 | 0.968↓ |
| The east | 0.952 | 0.937 | 0.939 | 0.937 | 0.981 | 0.964 | 0.988 | 0.973 | 0.983 | 0.964 | 0.961↑ |
| The central | 0.950 | 0.930 | 0.929 | 0.926 | 0.981 | 0.959 | 0.989 | 0.977 | 0.984 | 0.975 | 0.957↑ |
| The west | 0.940 | 0.916 | 0.923 | 0.920 | 0.977 | 0.956 | 0.984 | 0.962 | 0.976 | 0.955 | 0.950↑ |
| The northeast | 0.971 | 0.929 | 0.946 | 0.924 | 0.965 | 0.948 | 0.983 | 0.965 | 0.979 | 0.912 | 0.955↓ |
| Null-Hypothesis | The East | The Central | The West | The Northeast | ||||
|---|---|---|---|---|---|---|---|---|
| KS | CMS | KS | CMS | KS | CMS | KS | CMS | |
| Correct specification of the parametric 0 | 0.69 | 0.77 | 0.27 | 0.63 | 0.45 | 0.51 | 0.59 | 0.72 |
| Correct specification of the parametric 1 | 0.57 | 0.58 | 0.16 | 0.59 | 0.17 | 0.6 | 0.71 | 0.71 |
| Differences between the observable distributions | ||||||||
| No effect: QE(tau) = 0 | 0.00 | 0.00 | 0.16 | 0.08 | 0.00 | 0.00 | 0.00 | 0.00 |
| Constant effect: QE(tau) = QE(0.5) | 0.68 | 0.89 | 0.94 | 0.97 | 0.00 | 0.00 | 0.68 | 0.89 |
| Stochastic dominance: QE(tau) > 0 | 0.88 | 0.88 | 0.97 | 0.97 | 0.95 | 0.95 | 0.88 | 0.88 |
| Stochastic dominance: QE(tau) < 0 | 0.00 | 0.00 | 0.11 | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 |
| Effects of characteristics | ||||||||
| No effect: QE(tau) = 0 | 0.67 | 0.58 | 0.55 | 0.39 | 0.25 | 0.14 | 0.67 | 0.58 |
| Constant effect: QE(tau) = QE(0.5) | 0.92 | 0.92 | 0.67 | 0.73 | 0.46 | 0.59 | 0.92 | 0.92 |
| Stochastic dominance: QE(tau) > 0 | 0.50 | 0.27 | 0.43 | 0.32 | 0.89 | 0.89 | 0.50 | 0.27 |
| Stochastic dominance: QE(tau) < 0 | 0.93 | 0.93 | 0.96 | 0.96 | 0.19 | 0.08 | 0.93 | 0.93 |
| Effects of coefficients | ||||||||
| No effect: QE(tau) = 0 | 0.00 | 0.00 | 0.13 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 |
| Constant effect: QE(tau) = QE(0.5) | 0.68 | 0.86 | 0.83 | 0.95 | 0.00 | 0.00 | 0.68 | 0.86 |
| Stochastic dominance: QE(tau) > 0 | 0.86 | 0.86 | 0.96 | 0.96 | 0.91 | 0.95 | 0.86 | 0.86 |
| Stochastic dominance: QE(tau) < 0 | 0.00 | 0.00 | 0.08 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Peng, J.; Lu, X. Do Factor Market Distortions and Carbon Dioxide Emissions Distort Energy Industry Chain Technical Efficiency? A Heterogeneous Stochastic Frontier Analysis. Energies 2022, 15, 6154. https://doi.org/10.3390/en15176154
Lu H, Peng J, Lu X. Do Factor Market Distortions and Carbon Dioxide Emissions Distort Energy Industry Chain Technical Efficiency? A Heterogeneous Stochastic Frontier Analysis. Energies. 2022; 15(17):6154. https://doi.org/10.3390/en15176154
Chicago/Turabian StyleLu, Hengfan, Jiachao Peng, and Xiangyi Lu. 2022. "Do Factor Market Distortions and Carbon Dioxide Emissions Distort Energy Industry Chain Technical Efficiency? A Heterogeneous Stochastic Frontier Analysis" Energies 15, no. 17: 6154. https://doi.org/10.3390/en15176154
APA StyleLu, H., Peng, J., & Lu, X. (2022). Do Factor Market Distortions and Carbon Dioxide Emissions Distort Energy Industry Chain Technical Efficiency? A Heterogeneous Stochastic Frontier Analysis. Energies, 15(17), 6154. https://doi.org/10.3390/en15176154






