The Effect of Mining Remnants on Elastic Strain Energy Arising in the Tremor-Inducing Layer
Abstract
:1. Introduction
2. Materials and Methods
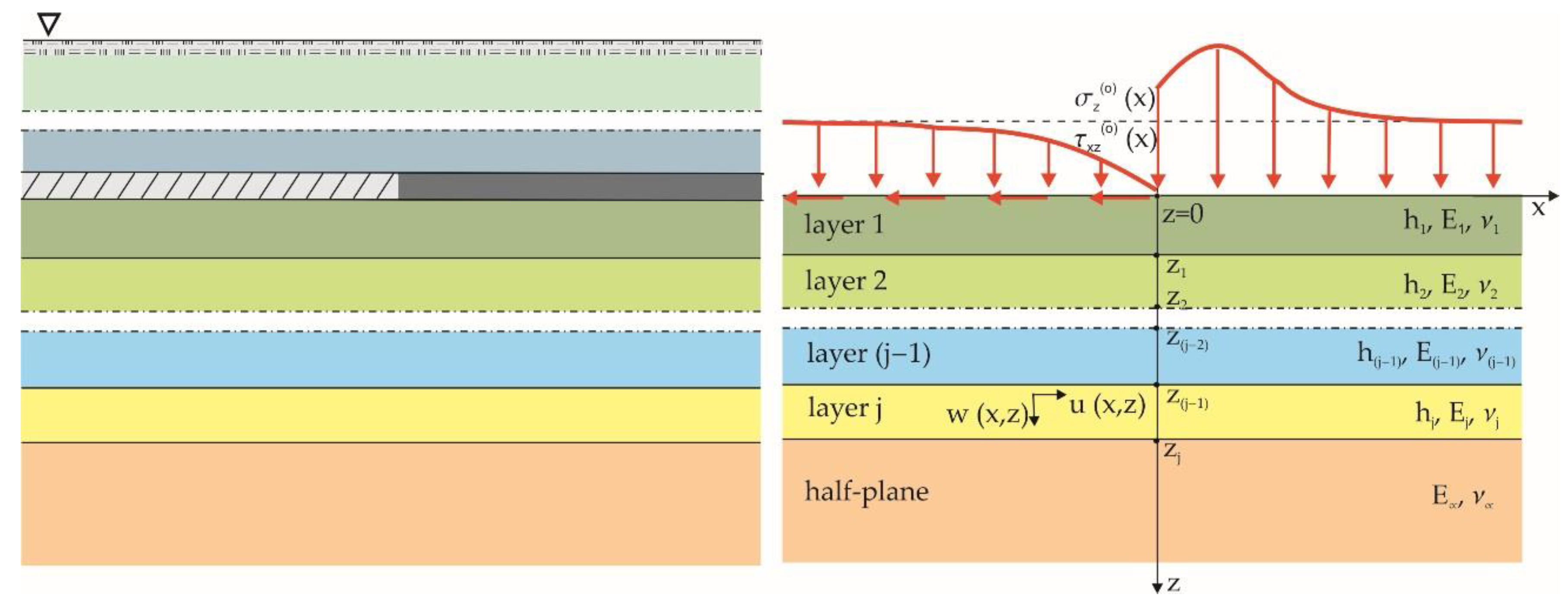
2.1. A Geomechanical Model of the Stratified Rock Mass
- -
- The specificity of the mining remnants is modeled by an appropriate distribution of stresses or displacements.
- -
- Due to the order of seam extraction (from top to bottom), the analysis of impacts of the mining remnants is focused on the bottom level rock strata.
- -
- Between the mining remnants and the studied level, zj−1, there are n layers (n = 1, 2, 3 … j) constituting homogeneous, isotropic and contained elastic bands with the following parameters: thickness (m), strain modulus (Pa), Poisson ratio (−).
- -
- Rock formations underlying the level zj are modeled by a homogeneous and isotropic elastic half-plane with the following strain parameters: (Pa, −).
- -
- Interactions between the contacting layers involve sliding (no friction and cohesion), cohesive and frictional effects.
- -
- The 2D state of stress is assumed.
- -
- Conditions at the level of the mining remnants, modeled accordingly by an appropriate distribution of stresses or displacements (mixed boundary conditions are also possible);
- -
- Conditions defining the interactions between the contacting layers, taking into account different contact variants: with no friction or involving cohesive and frictional effects.
2.2. Boundary Conditions
- -
- At the level of mining remnants: for z = 0
- -
- On the interface level: (j−1) and jth for z = zj
- Variant I—Cohesion force arising on the interface between the layers (the so-called “stitching” of layers)
- Variant II—No cohesion or friction forces acting on the interface between layers (so-called “slippage” effect)
- Variant III—Friction forces arising on the interface between layers
2.3. A System Modeling the Impact of Mining Remnants on a Multi-Layer Medium
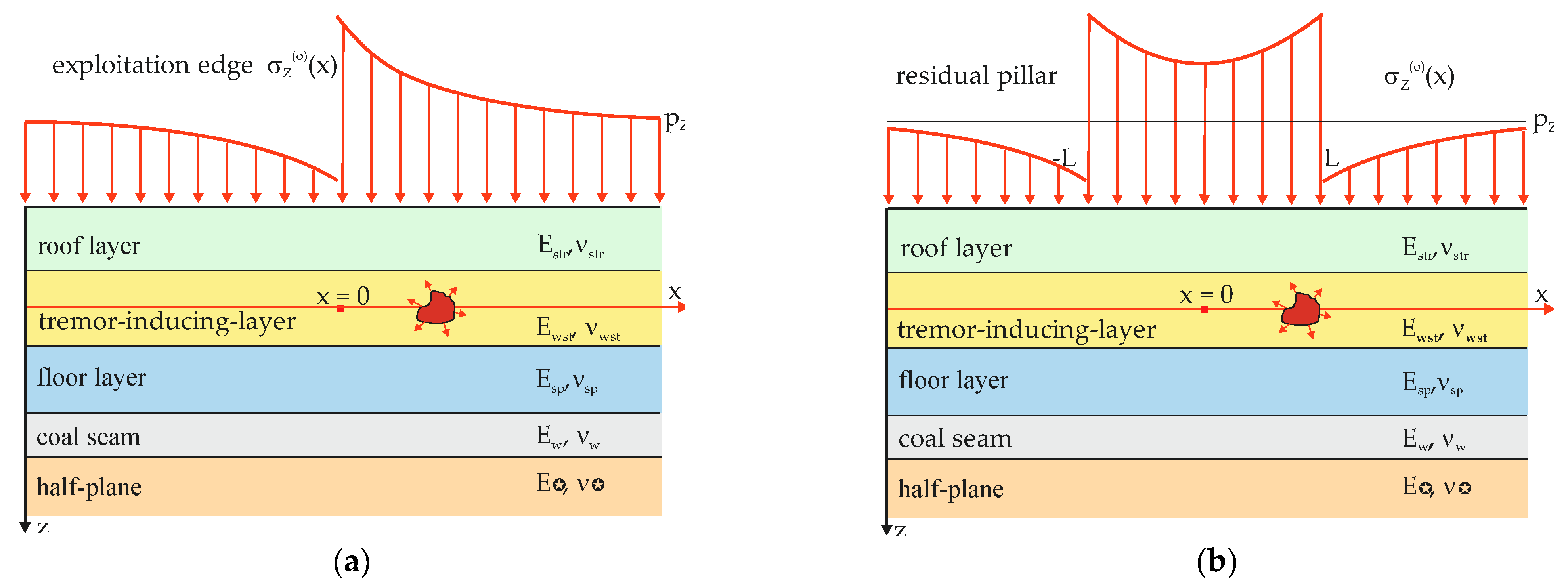
- -
- The mining remnants are modeled by an uneven distribution of additional vertical stresses, , corresponding to the conditions on the left exploitation edge or the residual pillar.
- -
- There are four layers between the mining remnants and the elastic half-plane, including the tremor-inducing layer and the seam.
- -
- The “stitching” or “slipping” effects occur on the interface between the layers.
- -
- In the case of the exploitation edge (Figure 4):
- -
- For goafs:
- -
- For undisturbed coal body:
- -
- In the case of a residual pillar (Figure 5):
- -
- For goafs:
- -
- For pillars:
- -
- For the exploitation edge:
- -
- For a residual pillar:
2.4. Variability of the Specific Strain Energy
3. Results and Discussion
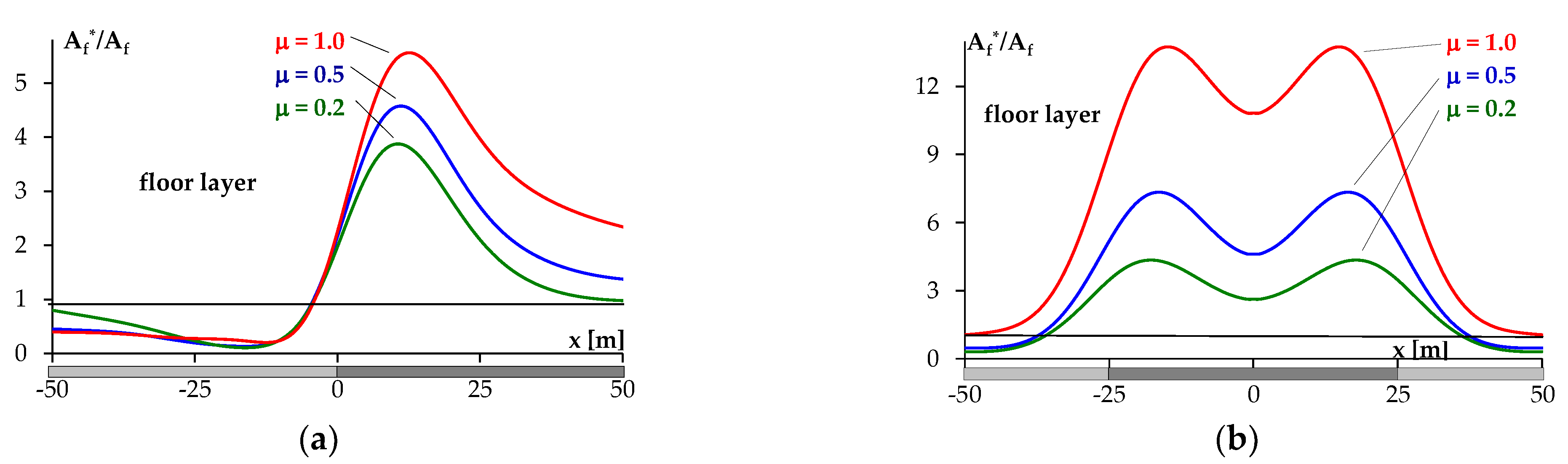
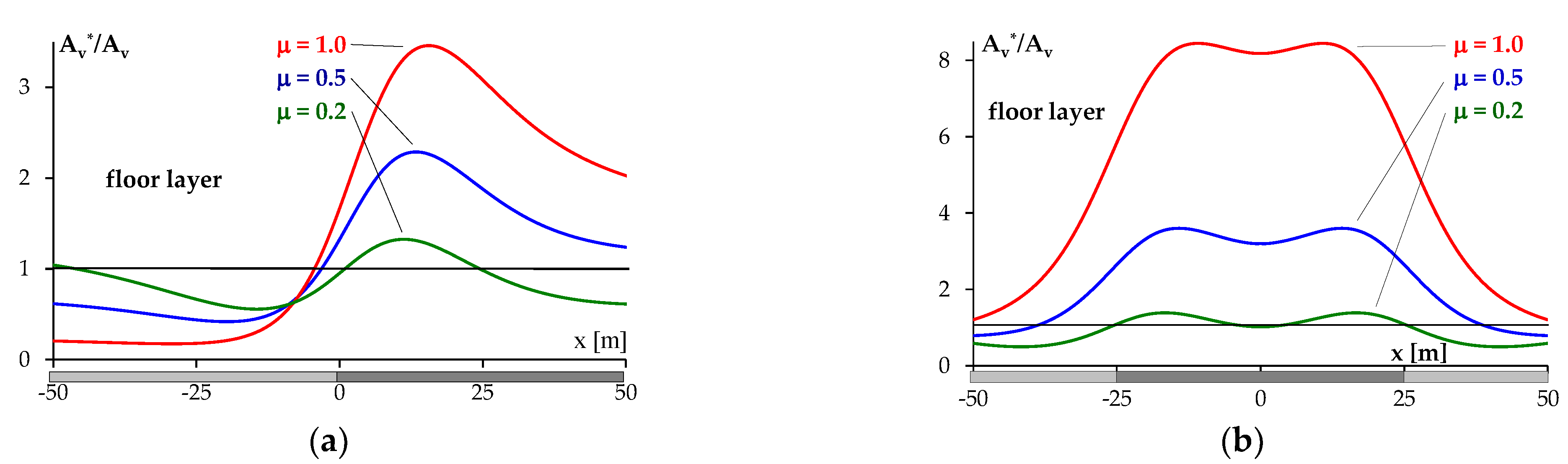
3.1. Development of Strain Energy Depending on the Strain Behavior of the Layers
- -
- μ = 1.0—the roof/floor layer is the least deformable/prone to deformation,
- -
- μ = 0.5—the roof/floor layer is less deformable,
- -
- μ = 0.2—the roof/floor layer is the most deformable.
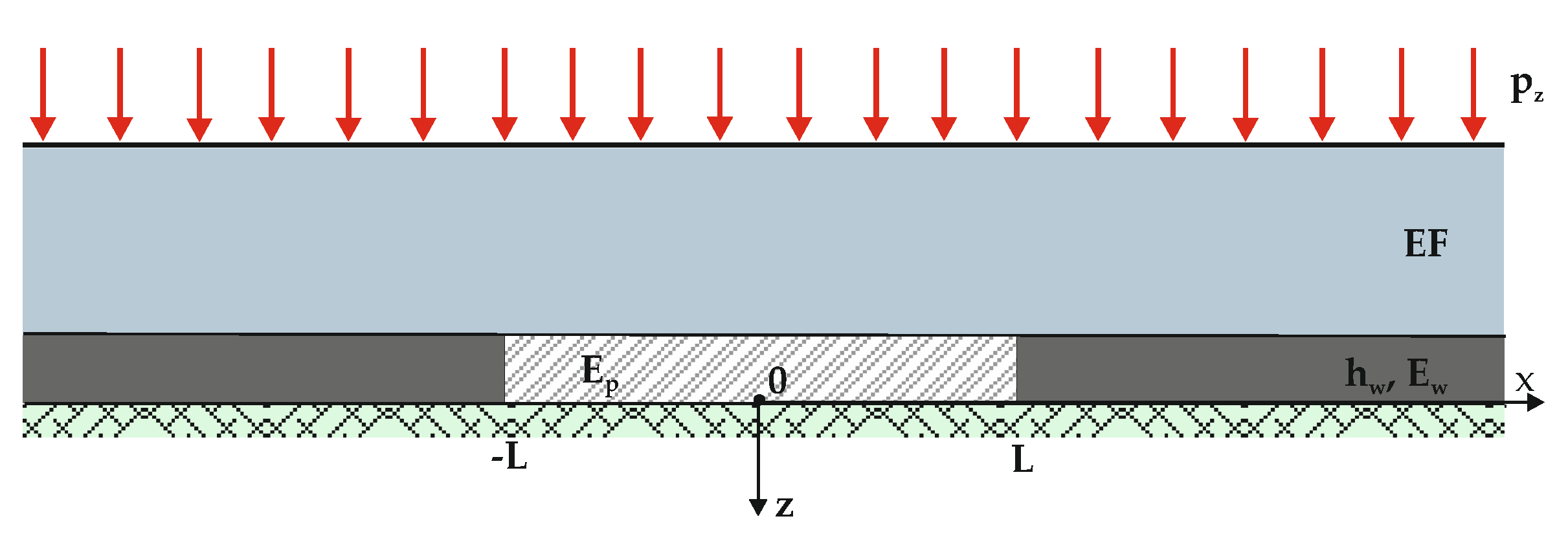
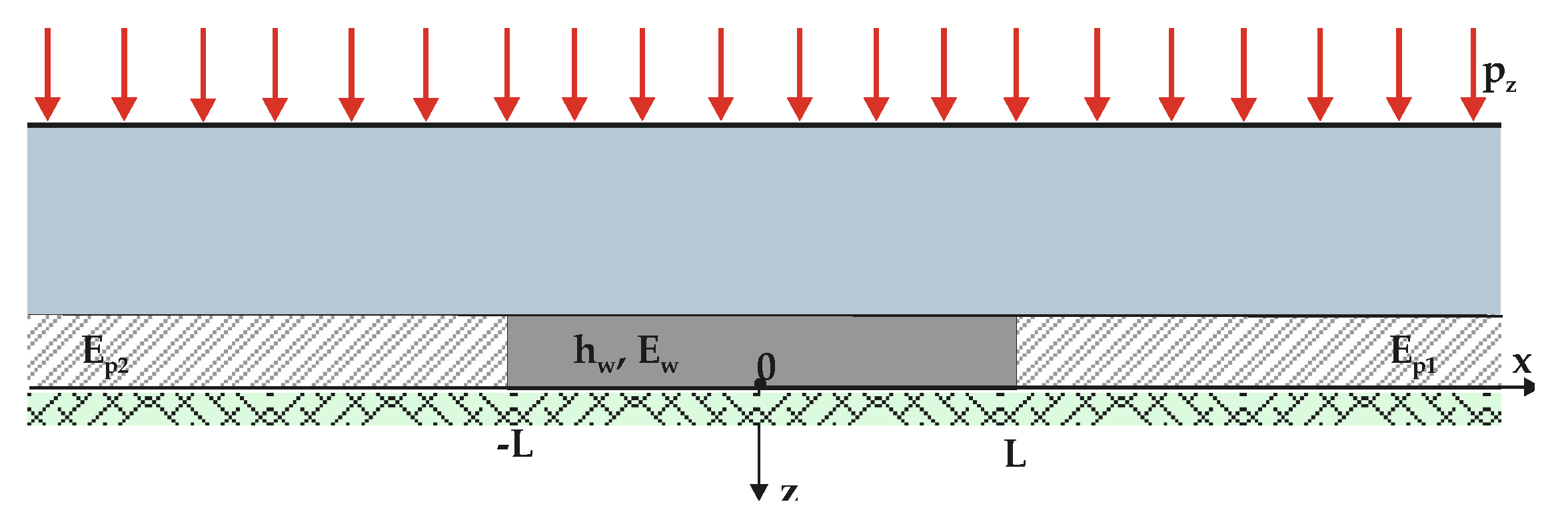
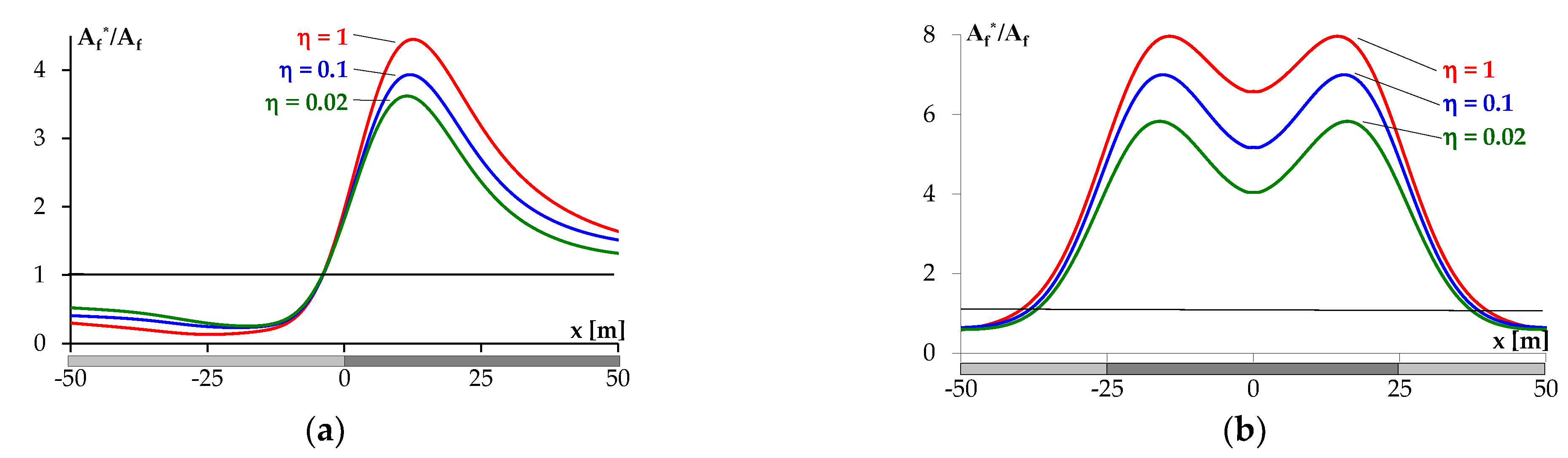
3.2. Buildup of Strain Energy Depending on the Method of Liquidation of the Goafs
- -
- η = 1—the seam has not been extracted,
- -
- η = 0.1—the seam has been extracted by the hydraulic filling method,
- -
- η = 0.02—the seam has been extracted after caving-in of the roof.
4. Conclusions
- -
- The impacts of previous mining operations lead to changes in the primary state of stress, revealed as non-uniform distributions of the total strain energy, being the sum of the volumetric and shear strain. In stress-relief zones, the secondary strain energy tends to decrease whilst in the elevated stress zones the strain energy increases.
- -
- The mining remnants can, under certain conditions, lead to exceeding the critical stress in the rock strata and, consequently may trigger rock failure. Specifically, the fracturing in tremor-inducing layers is likely to trigger the tremor occurrence.
- -
- Extraction of the underlying seam in the area affected by the tremor-inducing layer will reduce the risk of tremor occurrence in this layer and the magnitude of seismic energy of potential tremors. The risk level will be the lowest when the seam is mined following the caving-in of the roof beneath the tremor-inducing layer.
- -
- The strain properties of rock layers in the vicinity of the tremor-inducing layer will determine the tremor hazard level.
- -
- The risk will be the greatest where there are highly deformable formations between the mining remnants and the tremor-inducing layer. As these layers have high rigidity, the tremor-inducing layer is less likely to fracture, which limits the seismic energy of potential tremors.
- -
- In the case of formations underlying the burst-prone strata, the reverse is observed. High deformability of strata results in a decrease in the tremor hazard level as seismic activity of the tremor-inducing layer will be reduced.
- -
- The tremor hazard level can be reduced by adopting the roof control strategy involving caving-in, thus enhancing the deformability of the immediate roof layers, or by taking appropriate preventive measures (e.g., stress-relieving blasting, rock loosening watering) to cater for various types of fracturing. Therefore, the tremor hazard can be effectively reduced not only through stress-relieving blasting in the tremor-inducing layer, but also by de-stressing the underlying formations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Burtan, Z.; Chlebowski, D. Natural hazard conditions resulting in major accidents in the coal-mining sector in Poland. In Proceedings of the 25th World Mining Congress, Astana, Kazakhstan, 19–21 June 2018; pp. 62–71. [Google Scholar]
- State Mining Authority. Evaluation of Work Safety, Mine Rescue Systems and General Safety Features in Connection with Geological and Mining Activities in 2020 Katowice; State Mining Authority: Katowice, Poland, 2021. (In Polish) [Google Scholar]
- Dymek, F. State of stress and strain in rock strata on top of the seam being mined, in the light of the linear theory of elasticity. Arch. Min. Sci. 1961, 6, 283–314. (In Polish) [Google Scholar]
- Dymek, F. Applications of the elastic half-plane concept to solving problems of strata mechanics. J. AGH-UST 1963, 9, 17–55. (In Polish) [Google Scholar]
- Dymek, F. Selected 2D and 3D solutions for rheological media and their applications to strata mechanics. Arch. Min. Sci. 1973, 17, 123–144. (In Polish) [Google Scholar]
- Dymek, F. The state of stress and strain in the around a horizontal excavation. Arch. Min. Sci. 1973, 18, 413–419. (In Polish) [Google Scholar]
- Dymek, F. Selected boundary problems in theory of elasticity and visco-elasticity having relevance to rock strata mechanics. Arch. Min. Sci. 1974, 19, 117–142. (In Polish) [Google Scholar]
- Dymek, F.; Dymek, J.F. Selected solutions for a transversely isotropic medium and their applications in strata mechanics. J. AGH-UST 1985, 1, 73–93. (In Polish) [Google Scholar]
- Dymek, F.; Dymek, J.F. Solution of the state of strain and displacement for an elastic, transversely isotropic medium. J. AGH-UST 1987, 1, 5–16. (In Polish) [Google Scholar]
- Jóźkiewicz, S.; Kłeczek, Z. The impacts of the abandoned exploitation edge on mining conditions in overlying and underlying seams. J. AGH-UST 1972, 36, 29–38. (In Polish) [Google Scholar]
- Korman, S. The state of stress in rock strata underneath the seam being mined. Part I—Theoretical backgrounds. Arch. Min. Sci. 1957, II/3, 114–128. (In Polish) [Google Scholar]
- Golecki, J.; Jóźkiewicz, S. The impacts of underground mining operations on rock strata deformation in the light of the theory of elasticity. Przegląd. Górniczy. 1963, 19/6, 253–258. (In Polish) [Google Scholar]
- Gil, H. The state of stress and strain in an infinite elastic-plastic region and its applications in rock mechanics. Arch. Min. Sci. 1964, 9/1, 46–63. (In Polish) [Google Scholar]
- Gil, H. Stress and strain distribution in rock strata modelled as a visco-elastic medium. Arch. Min. Sci. 1965, 3/1, 16–29. (In Polish) [Google Scholar]
- Gil, H. Distribution of displacements in a horizontal section comprising loose and elastic medium caused by mixed boundary stress conditions. Arch. Min. Sci. 1966, XI/4, 377–385. (In Polish) [Google Scholar]
- Gil, H.; Czypionka, S. The impacts of exploitation Edge in discontinued mining operation on overlying and underlying seams. Przegląd Górniczy 1973, 5, 181–183. (In Polish) [Google Scholar]
- Gil, H.; Czypionka, S.; Krzyżowski, A. Determining the hazard zone when the working face is approaching the goafs left from previous mining operations and the existing egdes in overlying or underlying seams. J. Sil. Polytech. 1976, 70, 43–52. (In Polish) [Google Scholar]
- Gil, H. The Theory of strata Mechanics. In PWN Warszawa; Elsevier: Amsterdam, The Netherlands; Oxford, UK; New York, NY, USA; Tokyo, Japan, 1991. [Google Scholar]
- Gil, H.; Kraj, W. The distribution of displacements and stresses in rocks in an abandoned working face. Arch. Min. Sci. 1974, 19, 1. (In Polish) [Google Scholar]
- Chudek, M.; Stefański, L. Stress and strain in rock strata in the vicinity of longwall workings, mining remnants and protective pillars in underground mines. J. Sil. Polytech. 1985, 136, 401–412. (In Polish) [Google Scholar]
- Chudek, M.; Stefański, L. The impacts of underground mining on deformation of stratified rock mass. J. AGH-UST 1989, 145, 214–226. (In Polish) [Google Scholar]
- Szpetkowski, S. The course and activation values of seam mining operations. Arch. Min. Sci. 1979, 24/3, 313–336. (In Polish) [Google Scholar]
- Szpetkowski, S. Predicting the Impacts of Mining Operations on the Rock Strata and Ground Surface; Silesian Technical Publishers: Katowice, Poland, 1995. (In Polish) [Google Scholar]
- Kłeczek, Z.; Zorychta, A. The impacts of old excavations on the state of strain in burst-prone rock strata. J. Sil. Polytech. 1990, 185, 7–34. (In Polish) [Google Scholar]
- Zorychta, A.; Burtan, Z.; Chlebowski, D. The influence of the width of longwall gob on the value of stress under the edges of the exploitation area. In Proceedings of the Application of Computer Methods in Rock Mechanic—Proceedings of International Symposium on Application of Computer Methods in Rock Mechanics and Engineering (Volume 2), Xi’an, China, 24 May 1993. [Google Scholar]
- Chlebowski, D.; Burtan, Z.; Cieślik, J.; Zorychta, A. The state of stress and stress in the longwall face underneath the exploitation edge of previous mining activities. J. IGSMiE Pol. Akad. Nauk. 2017, 99, 159–170. (In Polish) [Google Scholar]
- Chlebowski, D.; Burtan, Z.; Zorychta, A. Evaluation of rockburst hazard under abandoned mine workings. Arch. Min. Sci. 2018, 63, 687–699. [Google Scholar]
- Zorychta, A.; Burtan, Z. The effects of stratified rock medium on development of the state of stress and rockburst hazard levels. Res. Pap. Cent. Min. Inst. 1998, 26, 119–132. (In Polish) [Google Scholar]
- Avierszyn, S.G. Rock Movements in Underground Mining; Ugletieichnizdat: Moskwa, Russia, 1947. (In Russian) [Google Scholar]
- Avierszyn, S.G. Rock Bursts; Ugletieichnizdat: Moskwa, Russia, 1955. (In Russian) [Google Scholar]
- Pietuchow, I.M. Rock Bumps in Coal Mines; Niedra: Moskwa, Russia, 1972. (In Russian) [Google Scholar]
- Pietuchow, I.M.; Linkow, A.M.; Sidorow, W.S.; Feldman, I.A. Theory of Protective Seams; Niedra: Moskwa, Russia, 1976. (In Russian) [Google Scholar]
- Everling, G. Application of Rock Mechanics in Deep Coal Mines. In Proceedings of the Third Congress ISRM, Washington, DC, USA, 1–7 September 1974. [Google Scholar]
- Salamon, M.D.G. Rock Mechanics of underground Excavation. In Proceedings of the Third Congress ISRM, Washington, DC, USA, 1–7 September 1974. [Google Scholar]
- Zhou, Y.; Haycocks, C. Designing for Upper Seam Stability in Multiple Seam Mining. In Proceedings of the Fifth Conference on Ground Control in Mining, Morgantown, Virginia, 11–13 June 1986. [Google Scholar]
- Alber, M.; Fritschen, R.; Bischoff, M.; Meier, T. Rock mechanical investigations of seismic events in a deep longwall coal mine. Int. J. Rock Mech. Min. Sci. 2009, 46, 408–420. [Google Scholar] [CrossRef]
- Singh, A.K.; Singh, R.; Maiti, J.; Kumar, R.; Mandal, P. Assessment of mining induced stress development over coal pillars during depillaring. Int. J. Rock Mech. Min. Sci. 2011, 48, 805–818. [Google Scholar] [CrossRef]
- Suchowerska, A.M.; Merifield, R.S.; Carter, J.P. Vertical stress changes in multi-seam mining under super-critical longwall panels. Int. J. Rock Mech. Min. Sci. 2013, 61, 306–320. [Google Scholar] [CrossRef]
- Haijun, J.; Shenggen, C.; Yun, Z.; Wang, C. Analytical solutions of hard roof’s bending moment, deflection and energy under the front abutment pressure before periodic weighting. Int. J. Min. Sci. Technol. 2016, 26, 175–181. [Google Scholar]
- Wang, W.; Jiang, T.; Wang, Z.; Ren, M. A analytical model for cover stress re-establishment in the goaf after longwall caving mining. J. S. Afr. Inst. Min. Metall. 2017, 117, 671–683. [Google Scholar] [CrossRef]
- Dong, X.; Karrech, A.; Basarir, H.; Elchalakani, M.; Qi, C. Analytical solution of energy redistribution in rectangular openings upon in-situ rock mass alteration. Int. J. Rock Mech. Min. Sci. 2018, 106, 74–83. [Google Scholar] [CrossRef]
- Zhang, Q.; Peng, C.H.; Liu, R.C.; Jiang, B.S.; Lu, M.M. Analytical solutions for the mechanical behaviors of a hard roof subjected to any form of front abutment pressures. Tunn. Undergr. Space Technol. 2019, 85, 128–139. [Google Scholar] [CrossRef]
- Feng, G.; Wang, P. Simulation of recovery of upper remnant coal pillar while mining the ultra-close lower panel using longwall top coal caving. Int. J. Min. Sci. Technol. 2020, 30, 55–61. [Google Scholar] [CrossRef]
- Wang, X.; Guan, K.; Yang, T.; Liu, X. Instability mechanism of pillar burst in asymmetric mining based on cusp catastrophe model. Rock Mech. Rock Eng. 2021, 54, 1463–1479. [Google Scholar] [CrossRef]
- Maleki, H. Coal pillar mechanics of violent failure in U.S. Mines. Int. J. Min. Sci. Technol. 2017, 27, 387–392. [Google Scholar] [CrossRef]
- Li, Z.; Dou, L.; Cai, W.; Wang, G.; He, J.; Gong, S.; Ding, Y. Investigation and analysis of the rock burst mechanism induced within fault-pillars. Int. J. Rock Mech. Min. Sci. 2014, 70, 192–200. [Google Scholar] [CrossRef]
- Tulu, I.B.; Esterhuizen, G.S.; Klemetti, T.; Murphy, M.M.; Sumner, J.; Sloan, M. A case study of multi-seam coal mine entry stability analysis with strength reduction method. Int. J. Min. Sci. Technol. 2016, 26, 193–198. [Google Scholar] [CrossRef]
- Klemetti, T.M.; Sears, M.M.; Tulu, I.B. Design concerns of room and pillar retreat panels. Int. J. Min. Sci. Technol. 2017, 27, 29–35. [Google Scholar] [CrossRef]
- Zhang, P.; Tulu, B.; Sears, M.M.; Trackemas, J. Geotechnical considerations for concurrent pillar recovery in close-distance multiple seams. Int. J. Min. Sci. Technol. 2018, 28, 7–21. [Google Scholar] [CrossRef]
- Salamon, M.D.G. An Introductory Mathematical Analysis of the Movements and Stresses Induced by Mining in Stratified Rocks; King’s College: London, UK; University of Durham, Department of Mining: Durham, UK, 1961. [Google Scholar]
- Salamon, M.D.G. Elastic analysis of displacements and stresses induced by the mining of seam or reef de-posits, Part I. J. S. Afr. Inst. Min. Metall. 1963, 64, 128–149. [Google Scholar]
- Salamon, M.D.G. Deformation of stratified rock masses: A laminated model. SAIMM—J. South. Afr. Inst. Min. Metall. 1991, 91, 9–25. [Google Scholar]
- Burtan, Z. Geomechanical model of stratified rock mass. Yearb. AGH-UST 2010, 34, 33–42. (In Polish) [Google Scholar]
- Burtan, Z. Geomechanical model of a transversely isotropic medium as a simplified model of stratified rock mass. Yearbook AGH-UST 2011, 35, 13–22. (In Polish) [Google Scholar]
- Salamon, M.D.G. Elastic moduli of a stratified rock mass. Int. J. Rock Mech. Sci. 1968, 5, 519–527. [Google Scholar] [CrossRef]
- Wardle, L.J.; Gerrard, C.M. The “equivalent” anisotropic properties of layered rock and soil masses. Rock Mech. 1972, 4, 155–175. [Google Scholar] [CrossRef]
- Jiang, X.; Shuchun, L.; Guangzhi, Y. Nonlinear Deformation and Damage Characteristics of Rock under Cyclic Loading; Science Press: Beijing, China, 2012. [Google Scholar]
- Chudek, M. Rockbursts in stratified rock strata. J. Sil. Polytech. 1990, 185, 81–117. (In Polish) [Google Scholar]
- Shou, K. A two-dimensional displacement discontinuity method for multilayered elastic media. Int. J. Rock Mech. Min. Sci. 1997, 288, 3–4. [Google Scholar] [CrossRef]
- Zhou, N.; Liu, H.; Zhang, J.; Yan, H. Study on rock burst event disaster and prevention mechanisms of hard roof. Adv. Civ. Eng. 2019, 1, 6910139. [Google Scholar] [CrossRef]
- Zhang, C.; Canbulat, I.; Tahmasebinia, F.; Vardar, O.; Saydam, S. Analysis of a potential coalburst phenomenon in different strata layers in underground coal mines. In Deep Mining 2017: Proceedings of the Eighth International Conference on Deep and High Stress Mining; Wesseloo, J., Ed.; Australian Centre for Geomechanics: Perth, Australia, 2017; pp. 413–422. [Google Scholar]
- Ju, Y.; Wang, Y.; Su, C.; Zhang, D.; Ren, Z. Numerical analysis of the dynamic evolution of mining-induced stresses and fractures in multi-layered rock strata using continuum-based discrete element methods. Int. J. Rock Mech. Min. Sci. 2019, 113, 191–210. [Google Scholar] [CrossRef]
- Zhengyi, T.; Jiazhen, L.; Meng, W.; Kang, W.; Zhupeng, J.; Caiwang, T. Fracture Mechanism in Overlying Strata during Longwall Mining. Shock. Vib. 2021, 2021, 4764732. [Google Scholar]
- Ji, S.; He, H.; Karlovšek, J. Application of superposition method to study the mechanical behaviour of overlying strata in longwall mining. Int. J. Rock Mech. Min. Sci. 2021, 146, 104874. [Google Scholar] [CrossRef]
- Pan, C.; Xia, B.; Zuo, Y.; Yu, B.; Ou, C. Mechanism and control technology of strong ground pressure behavior induced by high-position hard roofs in extra-thick coal seam mining. Int. J. Min. Sci. Technol. 2022, 33, 499–511. [Google Scholar] [CrossRef]
- Shen, B.; King, A.; Guo, H. Displacement, stress and seismicity in roadway roofs during mining-induced failure. Int. J. Rock Mech. Min. Sci. 2008, 45, 672–688. [Google Scholar] [CrossRef]
- Marcak, H. Seismicity in mines due to roof layer bending. Arch. Min. Sci. 2012, 57, 229–250. [Google Scholar]
- Fan, J.; Dou, L.; He, H.; Du, T.; Zhang, S.; Gui, B.; Sun, X. Directional hydraulic fracturing to control hard-roof rockburst in coal mines. Int. J. Min. Sci. Technol. 2012, 22, 177–181. [Google Scholar] [CrossRef]
- Bräuner, G. Rockbursts in Coal Mines and Their Prevention; Routledge: London, UK, 2017. [Google Scholar]
- Huang, B.; Liu, J.; Zhang, Q. The reasonable breaking location of overhanging hard roof for directional hydraulic fracturing to control strong strata behaviors of gob-side entry. Int. J. Rock Mech. Min. Sci. 2018, 103, 1–11. [Google Scholar] [CrossRef]
- Tahmasebinia, F.; Zhang, C.; Canbulat, I.; Sepasgozar, S.; Saydam, S. A Novel Damage Model for Strata Layers and Coal Mass. Energies 2020, 13, 1928. [Google Scholar] [CrossRef]
- Burzyński, W. Studies on Stress Hypotheses; Academy of Technical Sciences: Lviv, Ukraine, 1928. (In Polish) [Google Scholar]
- Burzyński, W. Teoretyczne podstawy hipotez wytężenia, Czasopismo Techniczne, 47, 1929, 1–41; (English translation available): Theoretical foundations of stress hypotheses of material effort. Engng. Trans. 2008, 56, 269–305. [Google Scholar]
- Fudzii, T.; Dzako, M. Mechanics of Cracking of Composite Materials; Mir: Moskwa, Russia, 1982. (In Russian) [Google Scholar]
- Możarowski, W.W.; Starżinski, W.E. Applied Mechanics of Stratified Composite Materials; Nauka i Technika: Mińsk, Belarus, 1988. (In Russian) [Google Scholar]
- Pobiedria, B.E. Mechanics of Composite Materials; Izd. Moskowskowo Uniwiersitieta: Moskwa, Russia, 1984. (In Russian) [Google Scholar]
- Sneddon, I.N. Fourier Transforms; McGraw-Hill: New York, NY, USA, 1951. [Google Scholar]
- Sneddon, I.N. Integral Transformation Method in Mixed Boundary Problems in the Classical Theory of Elasticity; Polish Academy of Sciences: Warsaw, Poland, 1974. (In Polish) [Google Scholar]
- Kłeczek, Z. Mining Geomechanics; Silesian Technical Publishers: Katowice, Poland, 1994. (In Polish) [Google Scholar]



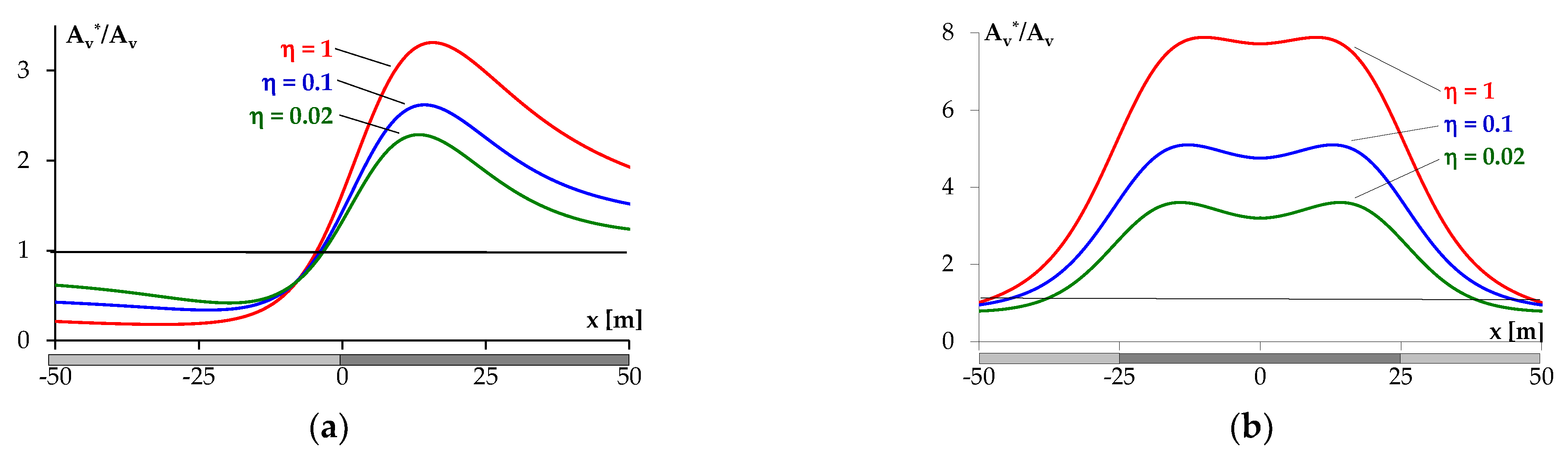
| Rock Type | Strain Modulus E × 109 (Pa) | Poisson Ratio ν (−) |
|---|---|---|
| Sandstone | 6.8–29.6 | 0.22–0.27 |
| Sandy shale | 9.6–17.6 | 0.22–0.27 |
| Illite shale | 7.3–16.8 | 0.22–0.27 |
| Hard coal | 1.2–6.5 | 0.27–0.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burtan, Z.; Chlebowski, D. The Effect of Mining Remnants on Elastic Strain Energy Arising in the Tremor-Inducing Layer. Energies 2022, 15, 6031. https://doi.org/10.3390/en15166031
Burtan Z, Chlebowski D. The Effect of Mining Remnants on Elastic Strain Energy Arising in the Tremor-Inducing Layer. Energies. 2022; 15(16):6031. https://doi.org/10.3390/en15166031
Chicago/Turabian StyleBurtan, Zbigniew, and Dariusz Chlebowski. 2022. "The Effect of Mining Remnants on Elastic Strain Energy Arising in the Tremor-Inducing Layer" Energies 15, no. 16: 6031. https://doi.org/10.3390/en15166031
APA StyleBurtan, Z., & Chlebowski, D. (2022). The Effect of Mining Remnants on Elastic Strain Energy Arising in the Tremor-Inducing Layer. Energies, 15(16), 6031. https://doi.org/10.3390/en15166031






