Rate Transient Behavior of Wells Intercepting Non-Uniform Fractures in a Layered Tight Gas Reservoir
Abstract
:1. Introduction
2. Methodology
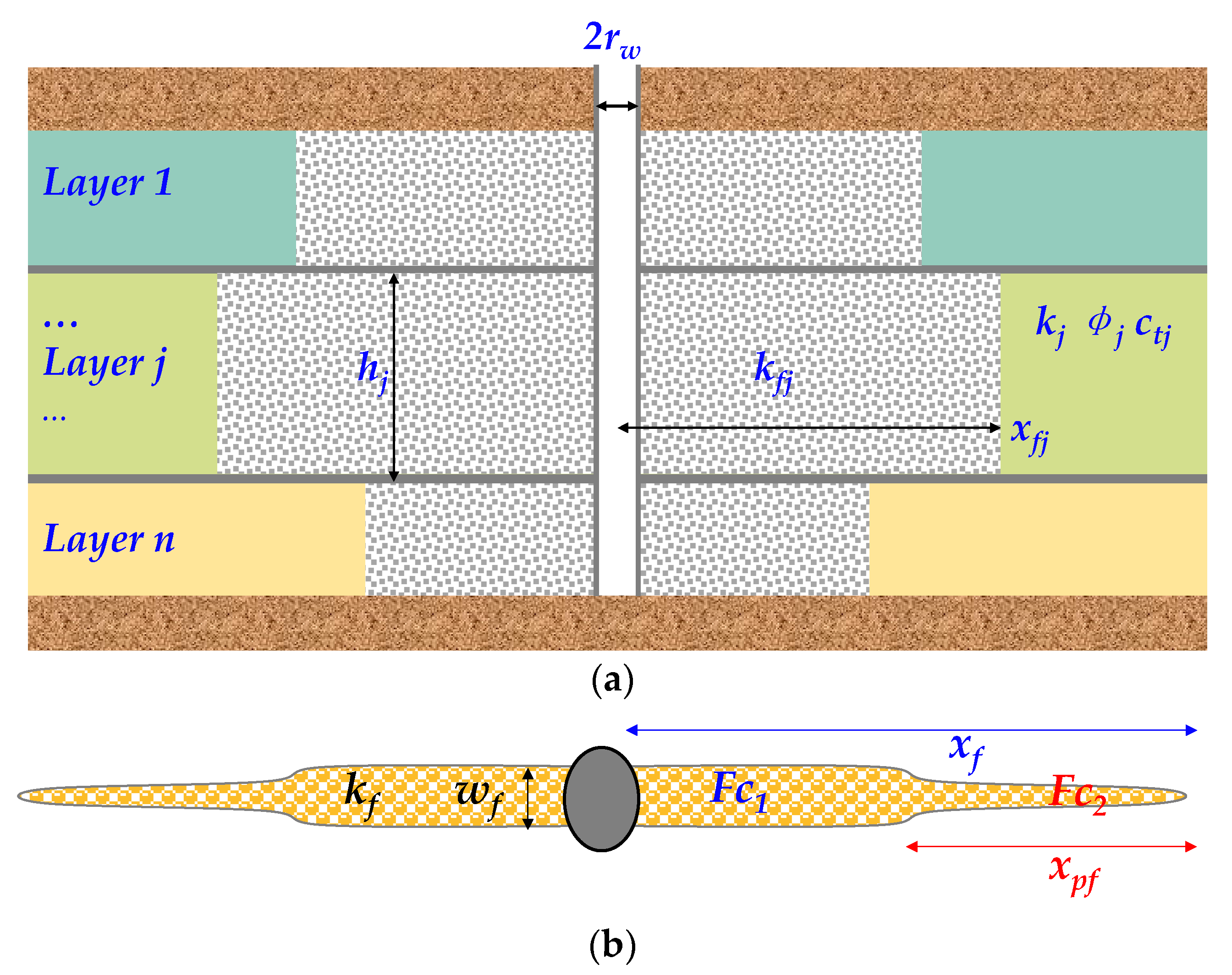
2.1. Physical Model
- (1)
- An MLVF commingled production well is located in a tight gas reservoir. Each layer has an individual constant thickness (hj), and vertical fracture length (xfj);
- (2)
- Any layer is penetrated by an MLVF commingled production well with height (ht) and radius (rw). The formation parameters belonging to any layer are different, such as the formation permeability (kj), formation porosity (φj), and reservoir total compressibility (ctj);
- (3)
- The formation porosity is filled with natural gas with constant viscosity (μ). The isothermal volume factor (B) is a constant value. The pressure (pj) and flow rate (qj) belonging to any layer are different due to the commingled production;
- (4)
- As shown in Figure 1b, the fracture width (wf) and fracture conductivity (Fc) is decreased from the wellbore to the toe of the fracture. In detail, the nearby fracture has higher conductivity (FC1) and more width than the further fracture. The further fracture has poor conductivity (FC2) and a smaller fracture length (xpf);
- (5)
- The gravity and temperature effects are ignored.
2.2. Mathematical Model
3. Result and Discussion
3.1. Solution Validation
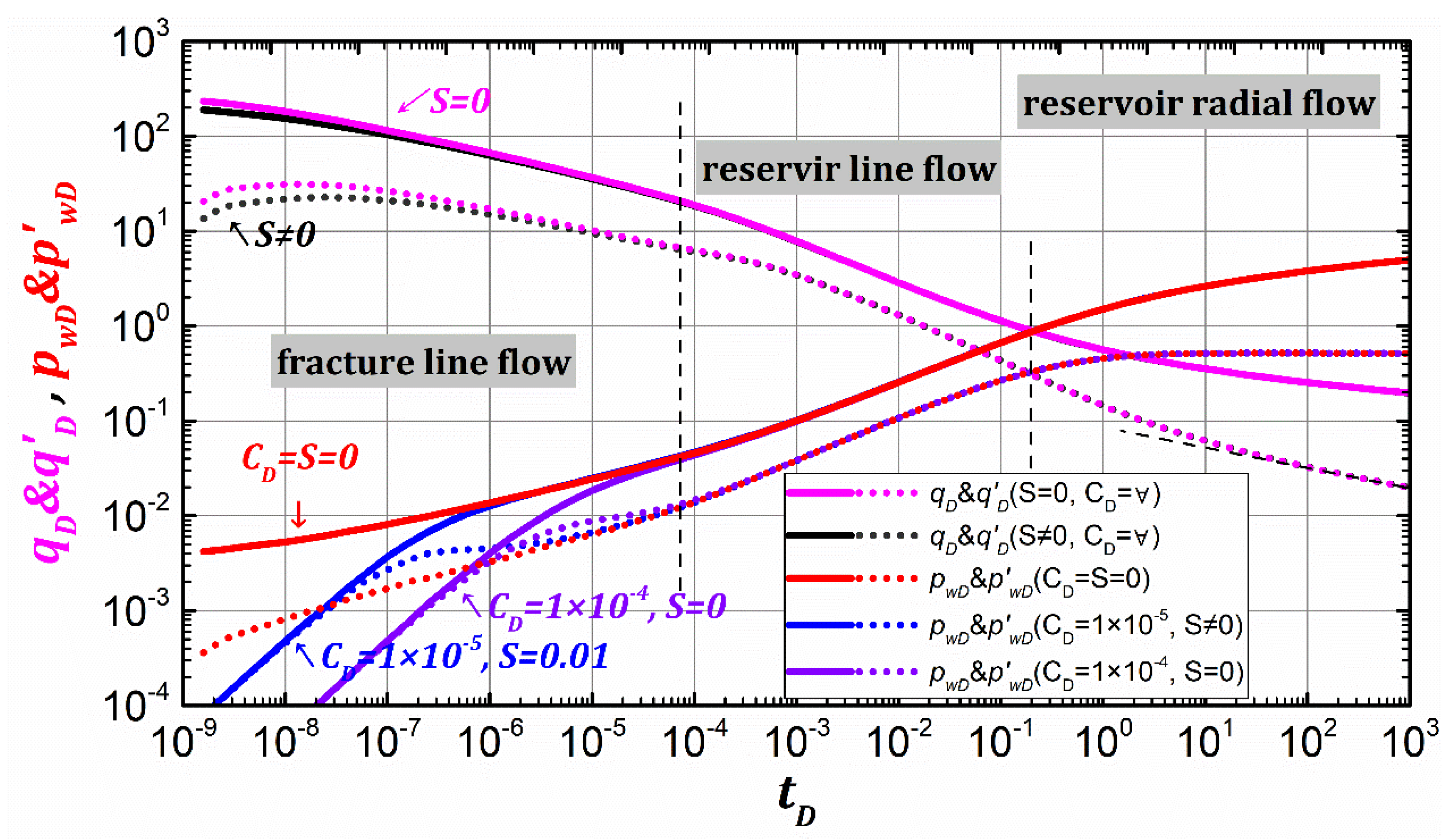
3.2. Combined Type Curve
3.3. Sensitivity Analysis
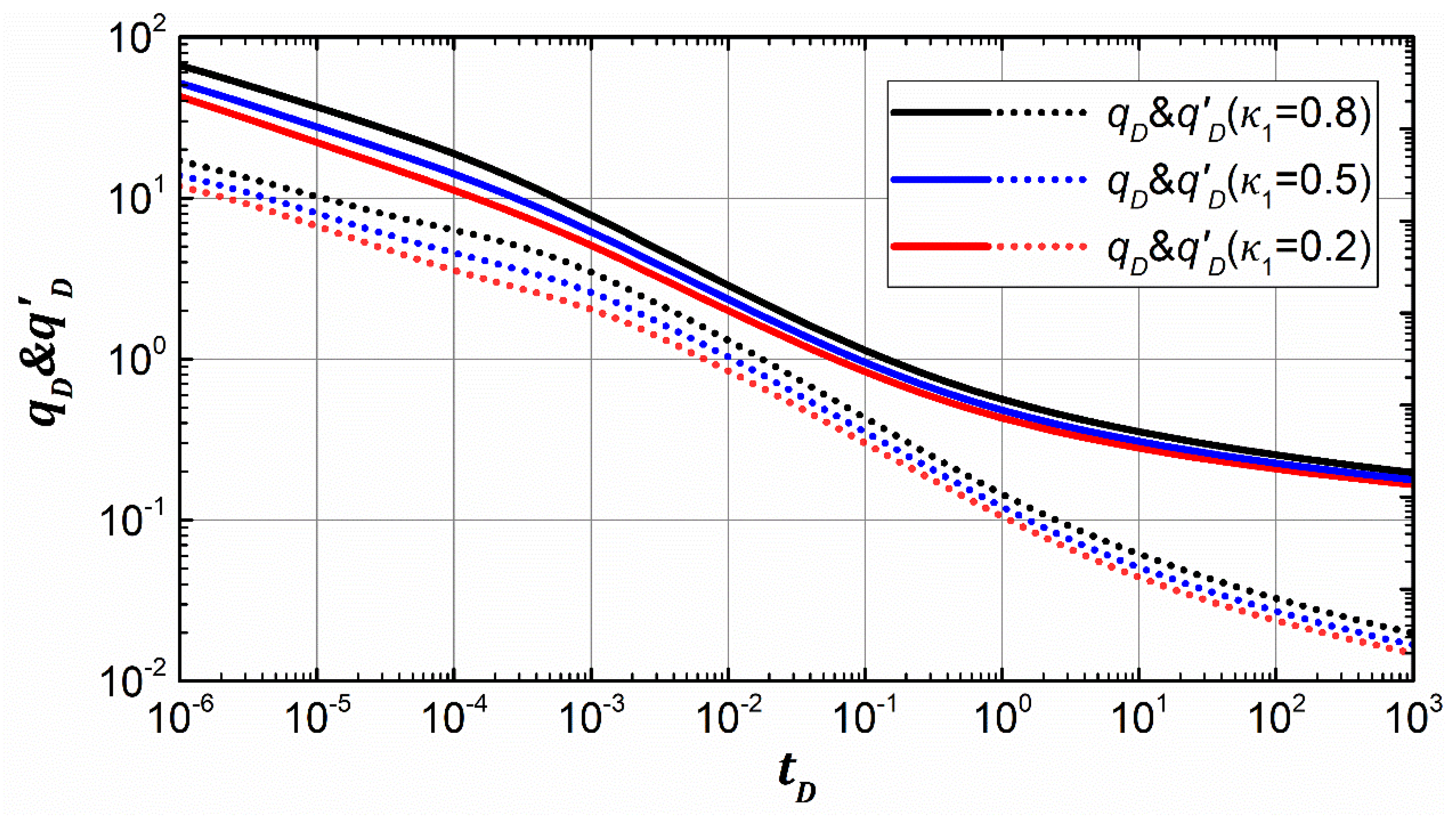
3.3.1. Formation Transmissibility
3.3.2. Formation Storability
3.3.3. Fracture Length
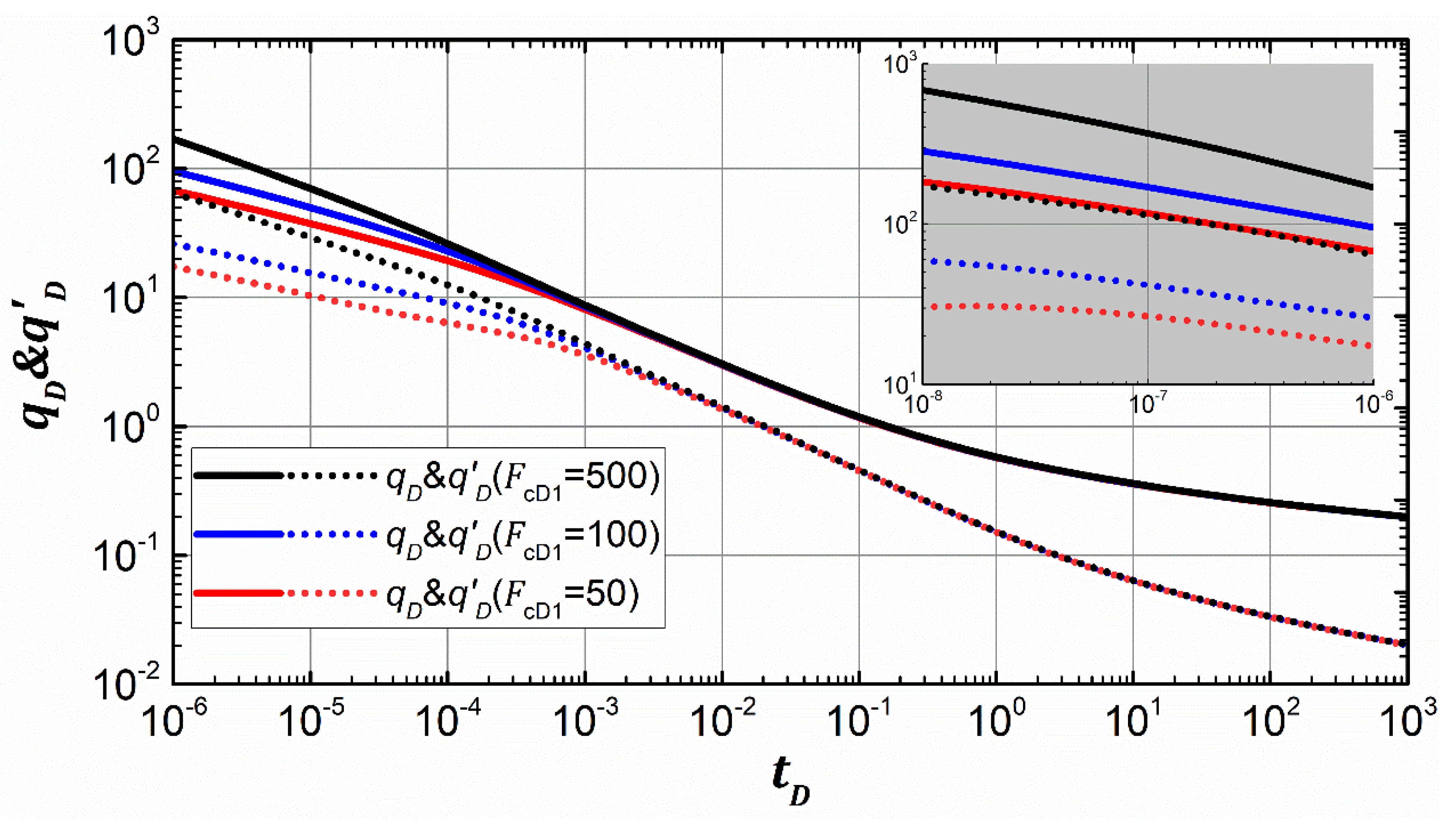
3.3.4. Fracture Conductivity
3.3.5. Fracture Extension
4. Conclusions
- (1)
- The rate transient behavior can be divided into three stages: the early stage, with −1/4 linear decreasing feature, the difference between rate and rate derivative is log4; the middle stage, with −1/2 linear decreasing feature, the difference between rate and rate derivative is log2; the later stage, the rate derivative curve is linearly decreasing.
- (2)
- The rate transient response is different from the pressure transient response, and wellbore storage has no effect on the rate transient behavior. On the other hand, the formation skin affects only the very early stages of rate transient behavior and the overall effect is not very large. Therefore, wellbore storage and formation skin do not need special consideration in the production decline analysis of multi-layer fractured vertical wells in tight gas reservoirs.
- (3)
- Reservoir transmissibility has an impact on the whole rate transient stage, and the storability mainly affects the middle stage of the rate transient response. As the formation transmissibility and storability increase, the combined RTA type curve moves upward, showing higher production and the influence of formation transmissibility is obviously larger than that of formation storability.
- (4)
- Fracture length has an impact on the whole rate transient stage, and fracture conductivity and fracture extension of high conductivity mainly affect the early stage of the transient rate. The longer the fracture length, the greater the fracture conductivity, the longer fracture extension of the high conductivity fracture, the higher the combined RTA curve, and the higher the production.
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
Nomenclature
| B | Isothermal volume factor, m3/m3 |
| C | Wellbore storage factor, m3/Pa |
| cf | Formation compressibility, Pa−1 |
| cg | Gag compressibility, Pa−1 |
| ct | Total compressibility, Pa−1 |
| FC | Fracture conductivity |
| h | Thickness, m |
| k | Permeability m2 |
| K0 | Bessel function |
| n | Number of layers, positive integer |
| p | Pressure, Pa |
| pi | Initial formation pressure, Pa |
| pw | Bottom-hole pressure, Pa |
| q | Flow rate, m3/s |
| Q | Well production, m3/d |
| Rp | Fracture extension ratio |
| S | Skin factor |
| t | Real production time, s |
| u | Laplace variable |
| wf | Fracture width, m |
| x | X-axis distance, m |
| y | Y-axis distance, m |
| z | Gas compression factor |
| α | Fracture length ratio, fraction |
| μ | Viscosity of the fluid, Pa·s |
| φ | Porosity, fraction |
| κ | Transmissibility ratio, fraction |
| ω | Storability ratio, fraction |
| *D | Dimensionless parameters |
| *f | Fracture parameters |
| *j | Layer j |
| *’ | Derivate of parameters |
Appendix A. Reservoir Flow Model
| Parameters | Definition | Parameters | Definition |
|---|---|---|---|
| Dimensionless pressure | Dimensionless time | ||
| Dimensionless rate | Dimensionless fracture length | ||
| Dimensionless transmissibility factor | Dimensionless storability factor | ||
| Dimensionless wellbore storage | Dimensionless fracture conductivity | ||
| Dimensionless distance | Dimensionless fracture extension |
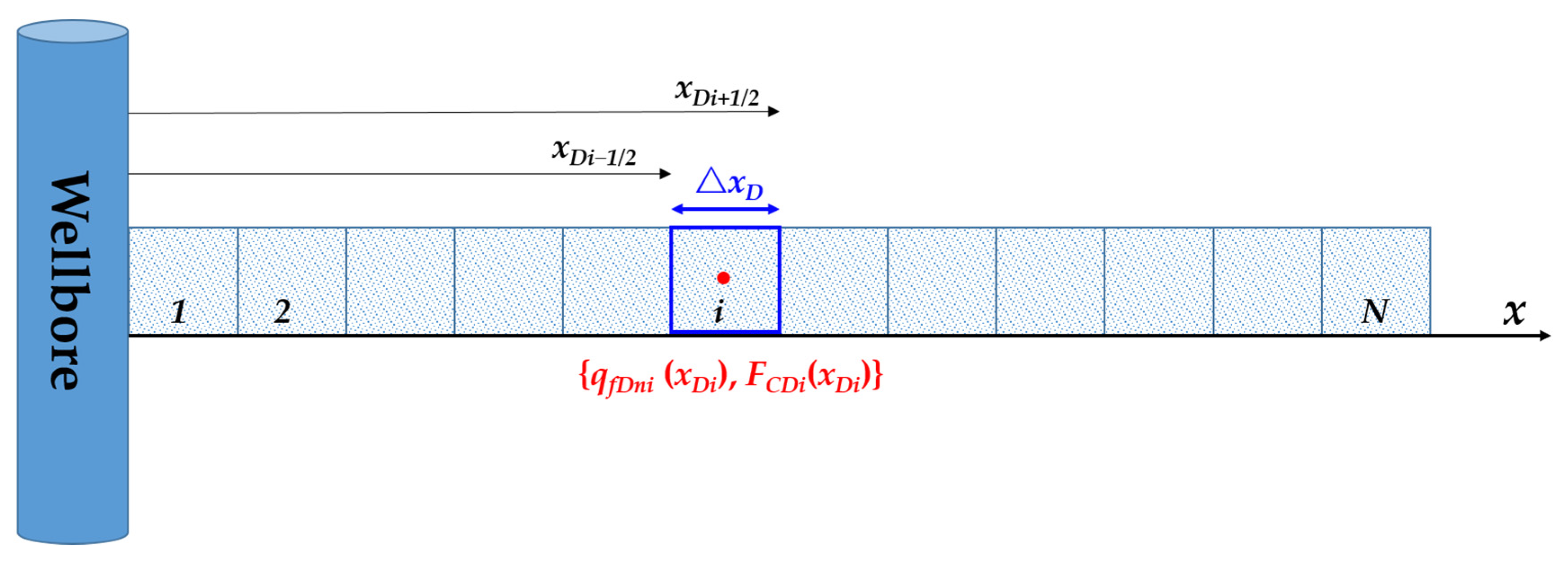
Appendix B. Fracture Flow Model
Appendix C. Solution of the Model
References
- Denney, D. Challenges of Tight and Shale-Gas Production in China. J. Pet. Technol. 2013, 65, 153–156. [Google Scholar] [CrossRef]
- Sahin, A. Unconventional Natural Gas Potential in Saudi Arabia. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 10 March 2013. [Google Scholar] [CrossRef]
- McLennan, J.D.; Green, S.J.; Bai, M. Proppant Placement during Tight Gas Shale Stimulation: Literature Review and Speculation. In Proceedings of the 42nd U.S. Rock Mechanics Symposium (USRMS), San Francisco, CA, USA, 29 June–2 July 2008. [Google Scholar]
- Haghshenas, A.; Hamedpour, M. Well Performance Analysis in Shale/Tight Gas Reservoirs: Case Study Review. In Proceedings of the SPE Conference at Oman Petroleum & Energy Show, Muscat, Oman, 21–23 March 2022. [Google Scholar] [CrossRef]
- Muskat, M. The flow of homogeneous fluids through porous media. Soil Sci. 1938, 46, 169. Available online: https://blasingame.engr.tamu.edu/z_zCourse_Archive/P620_18C/P620_zReference/PDF_Txt_Msk_Flw_Fld_(1946).pdf (accessed on 12 July 2022). [CrossRef]
- Gringarten, A.C.; Ramey, H.J., Jr. The Use of Source and Green’s Functions in Solving Unsteady-Flow Problems in Reservoirs. Soc. Pet. Eng. J. 1973, 13, 285–296. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramey, H.J., Jr.; Raghavan, R. Unsteady-State Pressure Distributions Created by a Well with a Single Infinite-Conductivity Vertical Fracture. Soc. Pet. Eng. J. 1974, 14, 347–360. [Google Scholar] [CrossRef] [Green Version]
- Cinco-Ley, H.; Samaniego, V.F.; Dominguez, N. Transient pressure analysis for a well with finite conductivity fracture. Soc. Pet. Eng. AIME J. 1978, 18, 253–269. [Google Scholar] [CrossRef] [Green Version]
- Cinco-Ley, H.; Fernando, S.V. Transient Pressure Analysis for Fractured Wells. J. Pet. Technol. 1981, 33, 1749–1766. [Google Scholar] [CrossRef]
- Cinco-Ley, H.; Meng, H.Z. Pressure Transient Analysis of Wells With Finite Conductivity Vertical Fractures in Double Porosity Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 2–5 October 1988. [Google Scholar] [CrossRef]
- Wei, C.; Cheng, S.; Tu, K.; An, X.; Qu, D.; Zeng, F.; Wu, D. A hybrid analytic solution for a well with a finite-conductivity vertical fracture. J. Pet. Sci. Eng. 2020, 188, 106900. [Google Scholar] [CrossRef]
- Luo, L.; Cheng, S.; Lee, J. Characterization of refracture orientation in poorly propped fractured wells by pressure transient analysis: Model, pitfall, and application. J. Nat. Gas Sci. Eng. 2020, 79, 103332. [Google Scholar] [CrossRef]
- Dou, X.; Hong, S.; Tao, Z.; Lu, J.; Xing, G. Transient Pressure and Rate Behavior of a Vertically Refractured Well in a Shale Gas Reservoir. Energies 2022, 15, 4345. [Google Scholar] [CrossRef]
- He, Y.; Cheng, S.; Rui, Z.; Qin, J.; Fu, L.; Shi, J.; Wang, Y.; Li, D.; Patil, S.; Yu, H.; et al. An Improved Rate-Transient Analysis Model of Multi-Fractured Horizontal Wells with Non-Uniform Hydraulic Fracture Properties. Energies 2018, 11, 393. [Google Scholar] [CrossRef] [Green Version]
- Zhao, K.; Du, P. A new production prediction model for multistage fractured horizontal well in tight oil reservoirs. Adv. Geo-Energy Res. 2020, 4, 152–161. [Google Scholar] [CrossRef]
- Xu, G.; Yin, H.; Yuan, H.; Xing, C. Decline curve analysis for multiple-fractured horizontal wells in tight oil reservoirs. Adv. Geo-Energy Res. 2020, 4, 296–304. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, S.; Zhu, C.; Luo, L. A numerical model to evaluate formation properties through pressure-transient analysis with alternate polymer flooding. Adv. Geo-Energy Res. 2019, 3, 94–103. [Google Scholar] [CrossRef]
- Wei, C.; Liu, Y.; Deng, Y.; Cheng, S.; Hassanzadeh, H. Analytical well-test model for hydraulicly fractured wells with multiwell interference in double porosity gas reservoirs. J. Nat. Gas Sci. Eng. 2022, 103, 104624. [Google Scholar] [CrossRef]
- Sun, B.; Shi, W.; Zhang, R.; Cheng, S.; Zhang, C.; Di, S.; Cui, N. Transient Behavior of Vertical Commingled Well in Vertical Non-Uniform Boundary Radii Reservoir. Energies 2020, 13, 2305. [Google Scholar] [CrossRef]
- Shi, W.; Yao, Y.; Cheng, S.; Shi, Z. Pressure transient analysis of acid fracturing stimulated well in multilayered fractured carbonate reservoirs: A field case in Western Sichuan Basin, China. J. Pet. Sci. Eng. 2019, 184, 106462. [Google Scholar] [CrossRef]
- Van Everdingen, A.F.; Hurst, W. The Application of the Laplace Transformation to Flow Problems in Reservoirs. J. Pet. Technol. 1949, 1, 305–324. [Google Scholar] [CrossRef]
- Stehfest, H. Numerical inversion of Laplace transforms. Commun. ACM 1970, 13, 624. [Google Scholar] [CrossRef]




| Hydraulic Fracturing Type | Net Pay (m) | Porosity (%) | Permeability (10−3 μm2) | Gas Saturation (%) | Absolute Open Flow (104 m3/d) |
|---|---|---|---|---|---|
| 4 layers | 11.2 | 10.9 | 0.63 | 66.8 | 9.01 |
| 2 layers | 10.1 | 11.4 | 0.77 | 71.9 | 6.11 |
| Commingled fracturing | 9.9 | 10.9 | 0.65 | 73.3 | 5.27 |
| Dimensionless Parameters | Value | ||
|---|---|---|---|
| Type Curve | Sensitivity Analysis | ||
| Wellbore | Dimensionless wellbore storage (CD) | 1 × 10−5 | / |
| Formation | Skin factor (S) | 0.01 | / |
| Permeability ratio (κ) | 0.5 | 0.2, 0.5, 0.8 | |
| Storability ratio (ω) | 0.5 | 0.3, 0.5, 0.7 | |
| Fracture | Dimensionless fracture length (α) | 0.5 | 0.1, 0.3, 0.5, 0.7, 0.9 |
| Dimensionless fracture conductivity (FCD) | 50 | 50, 100, 500 | |
| Dimensionless fracture extension (RD) | 0.5 | 0.1, 0.3, 0.5, 0.7, 0.9 | |
| Transient Behavior Stages | Combined Type Curves Feature | |
|---|---|---|
| PTA | RTA | |
| Wellbore storage | M = 1, dp = 0 | / |
| Skin transient | / | / |
| Fracture line flow | m = 1/4, dp = log4 | m = −1/4, dq = log4 |
| Reservoir line flow | m = 1/2, dp = log2 | m = −1/2, dq = log2 |
| Reservoir radial flow | p’wD = 0.5 | m = tanθ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Cheng, S.; Wang, Y.; Chen, G.; Yan, K.; Ma, Y. Rate Transient Behavior of Wells Intercepting Non-Uniform Fractures in a Layered Tight Gas Reservoir. Energies 2022, 15, 5705. https://doi.org/10.3390/en15155705
Zhang C, Cheng S, Wang Y, Chen G, Yan K, Ma Y. Rate Transient Behavior of Wells Intercepting Non-Uniform Fractures in a Layered Tight Gas Reservoir. Energies. 2022; 15(15):5705. https://doi.org/10.3390/en15155705
Chicago/Turabian StyleZhang, Chengwei, Shiqing Cheng, Yang Wang, Gang Chen, Ke Yan, and Yongda Ma. 2022. "Rate Transient Behavior of Wells Intercepting Non-Uniform Fractures in a Layered Tight Gas Reservoir" Energies 15, no. 15: 5705. https://doi.org/10.3390/en15155705
APA StyleZhang, C., Cheng, S., Wang, Y., Chen, G., Yan, K., & Ma, Y. (2022). Rate Transient Behavior of Wells Intercepting Non-Uniform Fractures in a Layered Tight Gas Reservoir. Energies, 15(15), 5705. https://doi.org/10.3390/en15155705








