Local Heat Transfer Dynamics in the In-Line Tube Bundle under Asymmetrical Pulsating Flow
Abstract
:1. Introduction
2. Mathematical Model
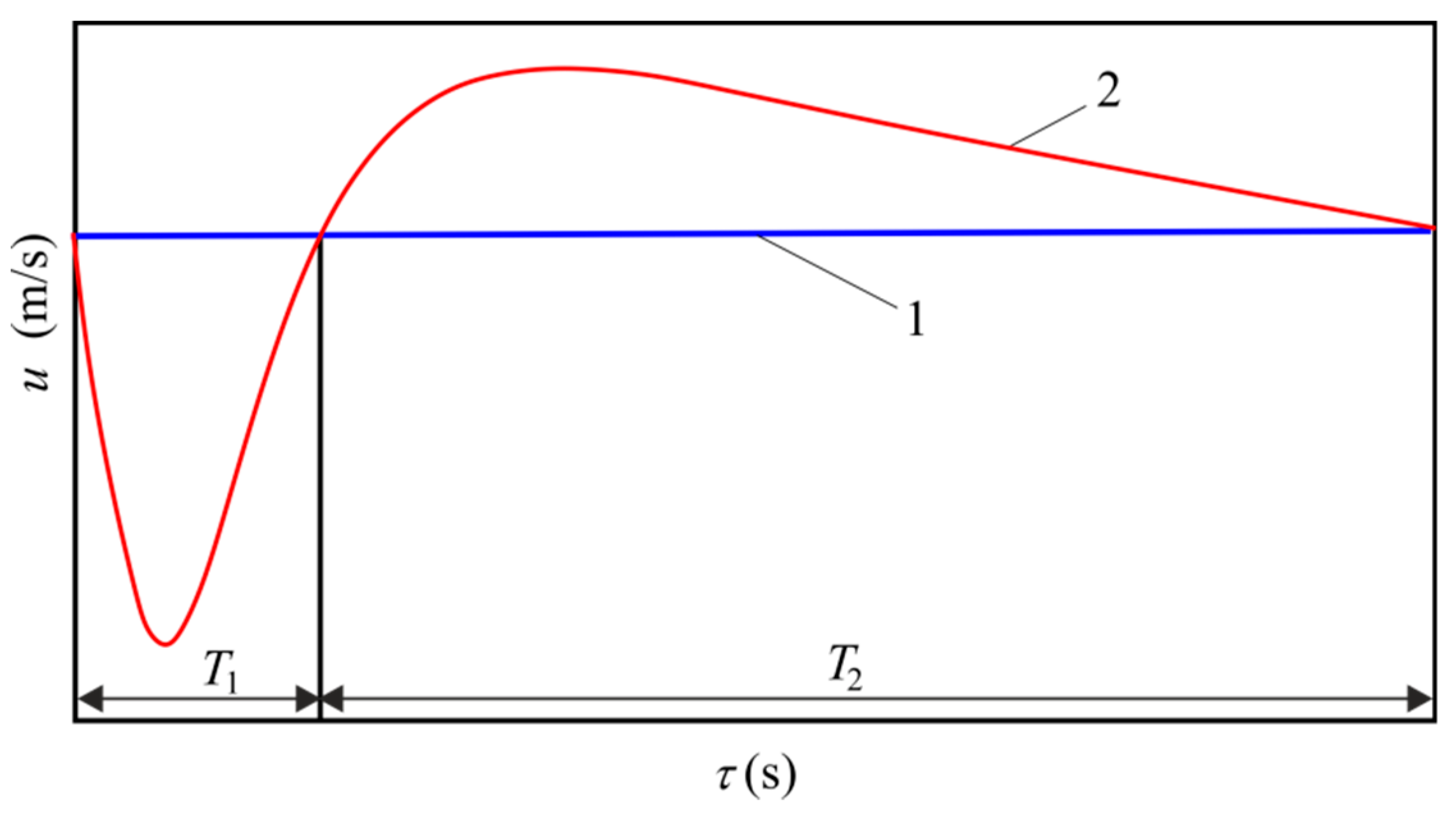
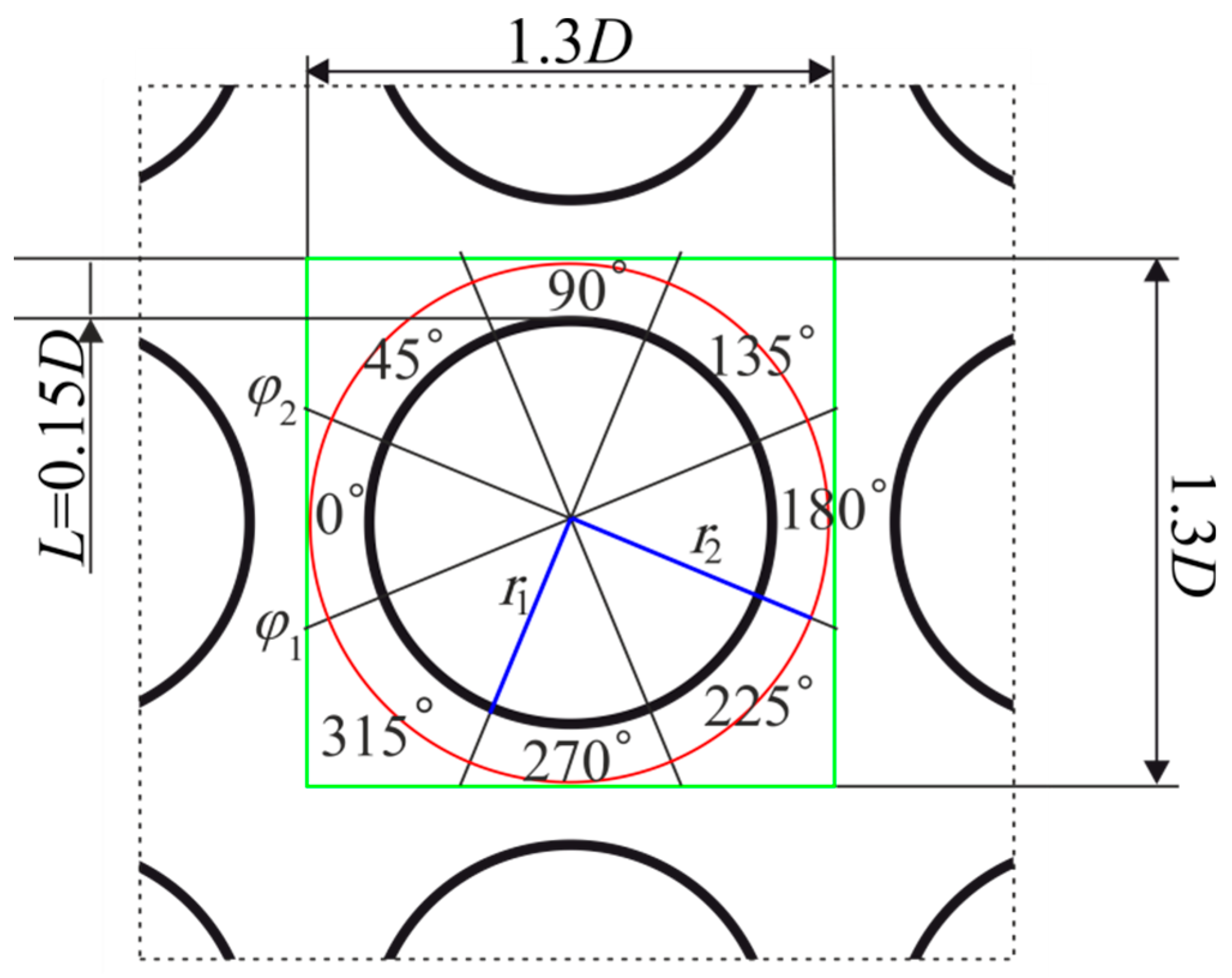
2.1. Computational Domain and Boundary Conditions
2.2. Modeling Approach
2.3. Methodology for Evaluating Results of Simulation
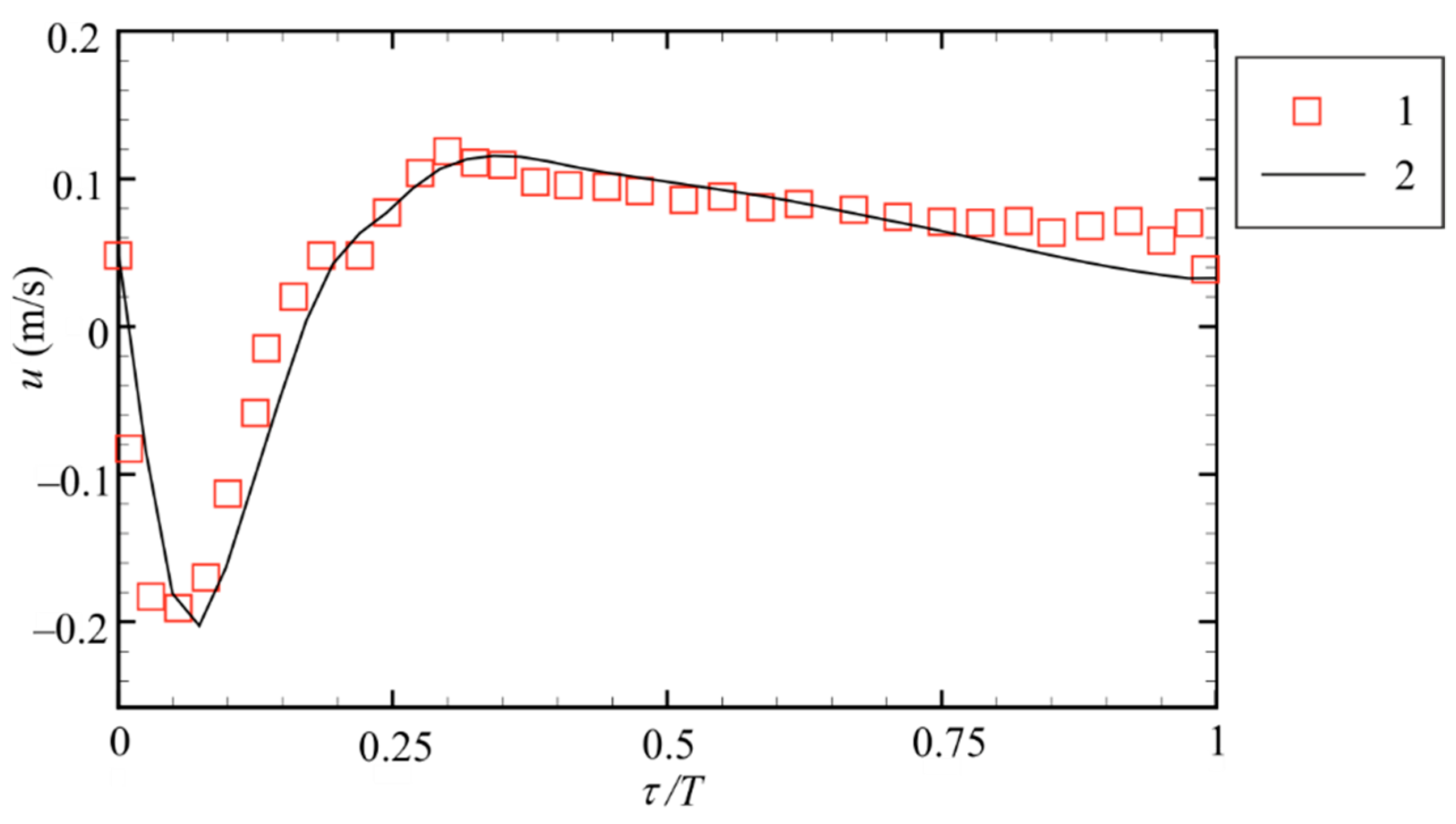
2.4. Model Verification
3. Results and Discussion
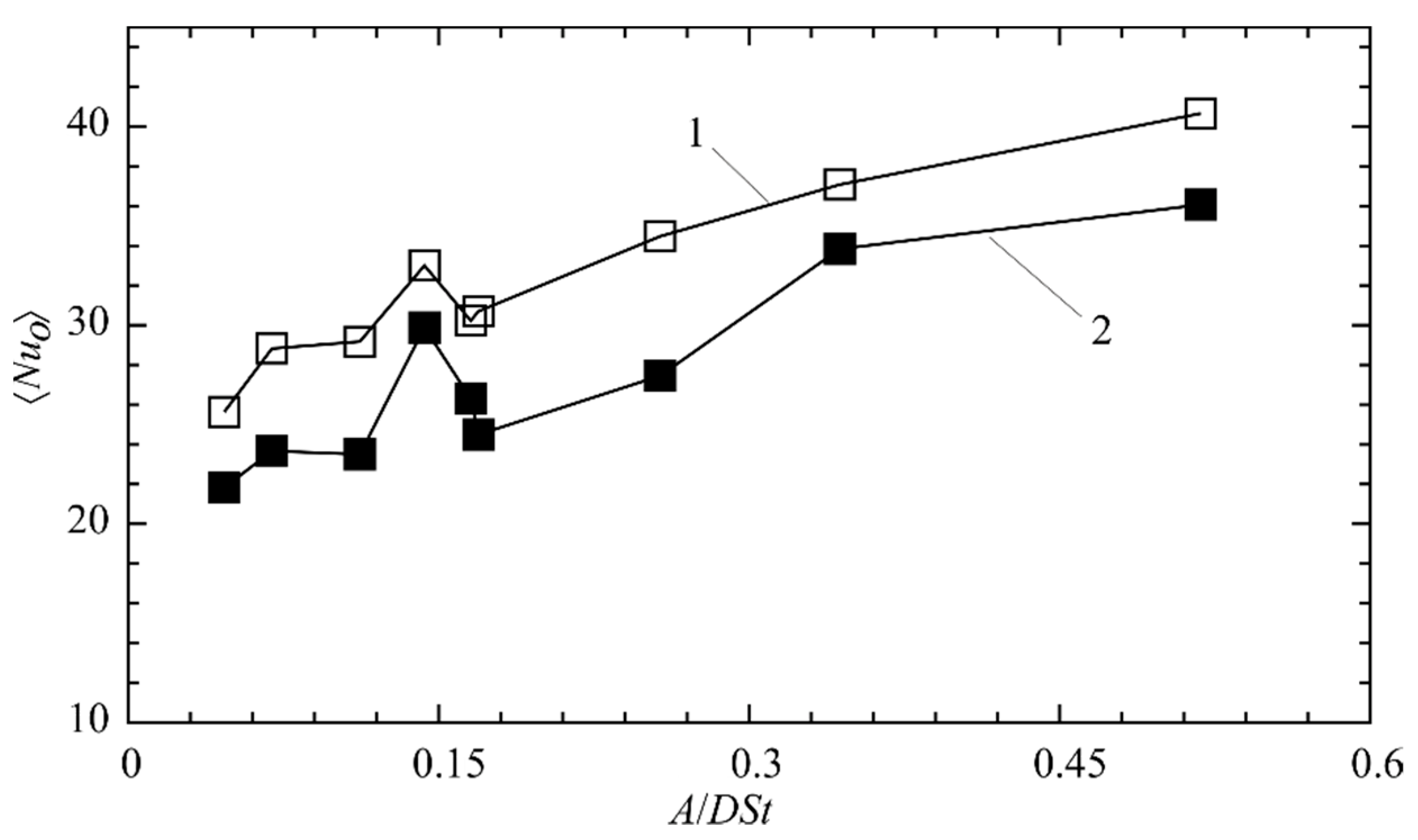
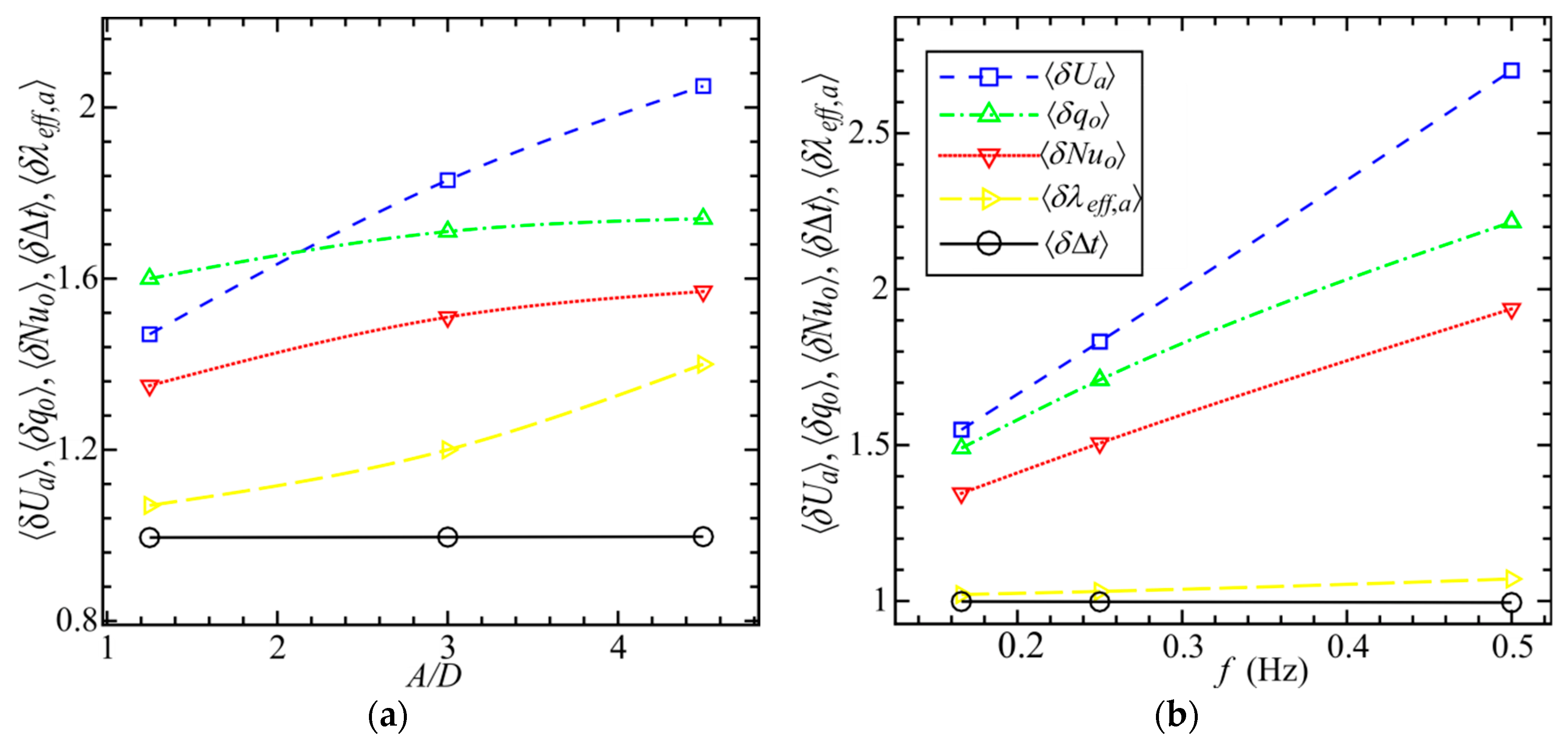
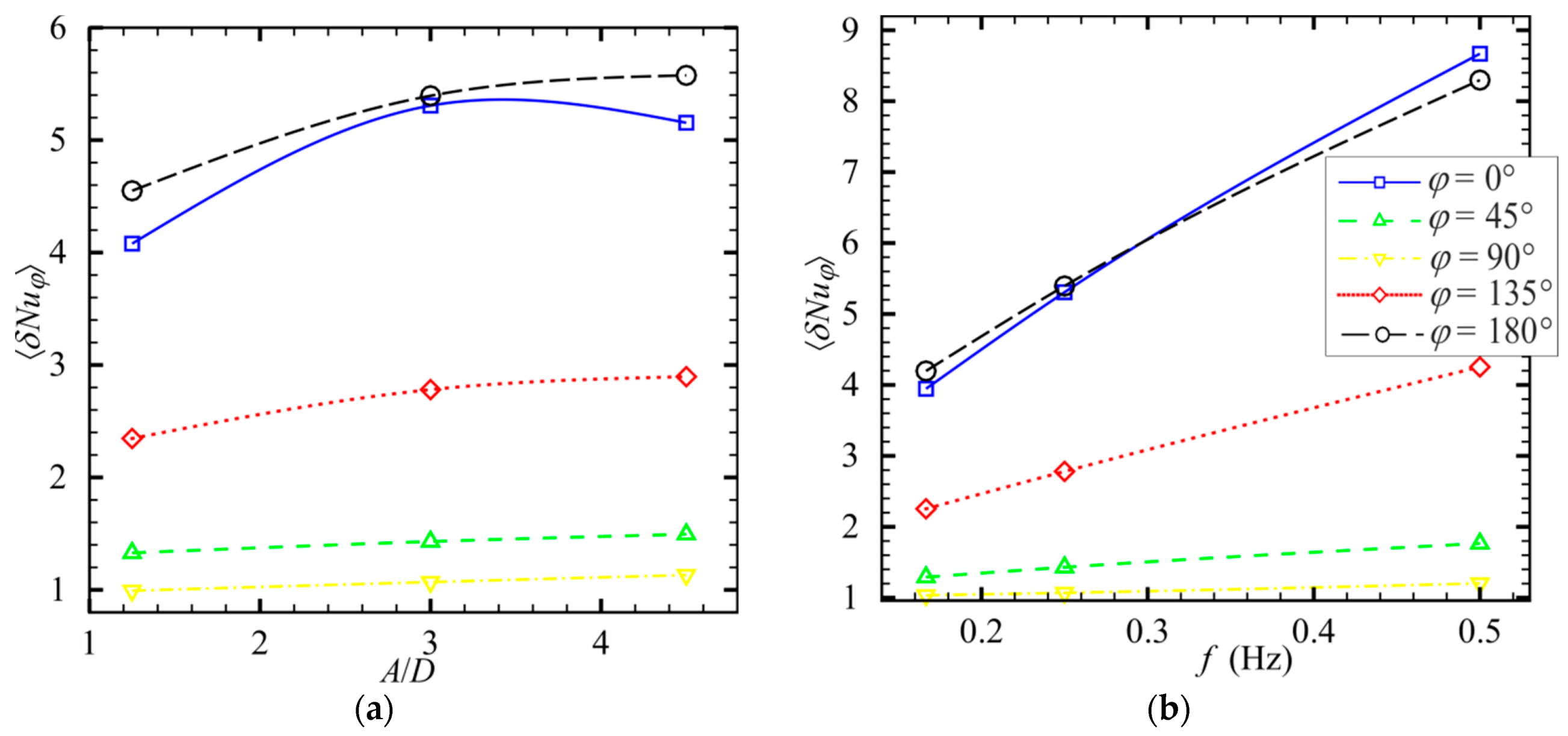
3.1. Effect of Amplitude and Frequency of Pulsations on the Flow and Heat Transfer Characteristics
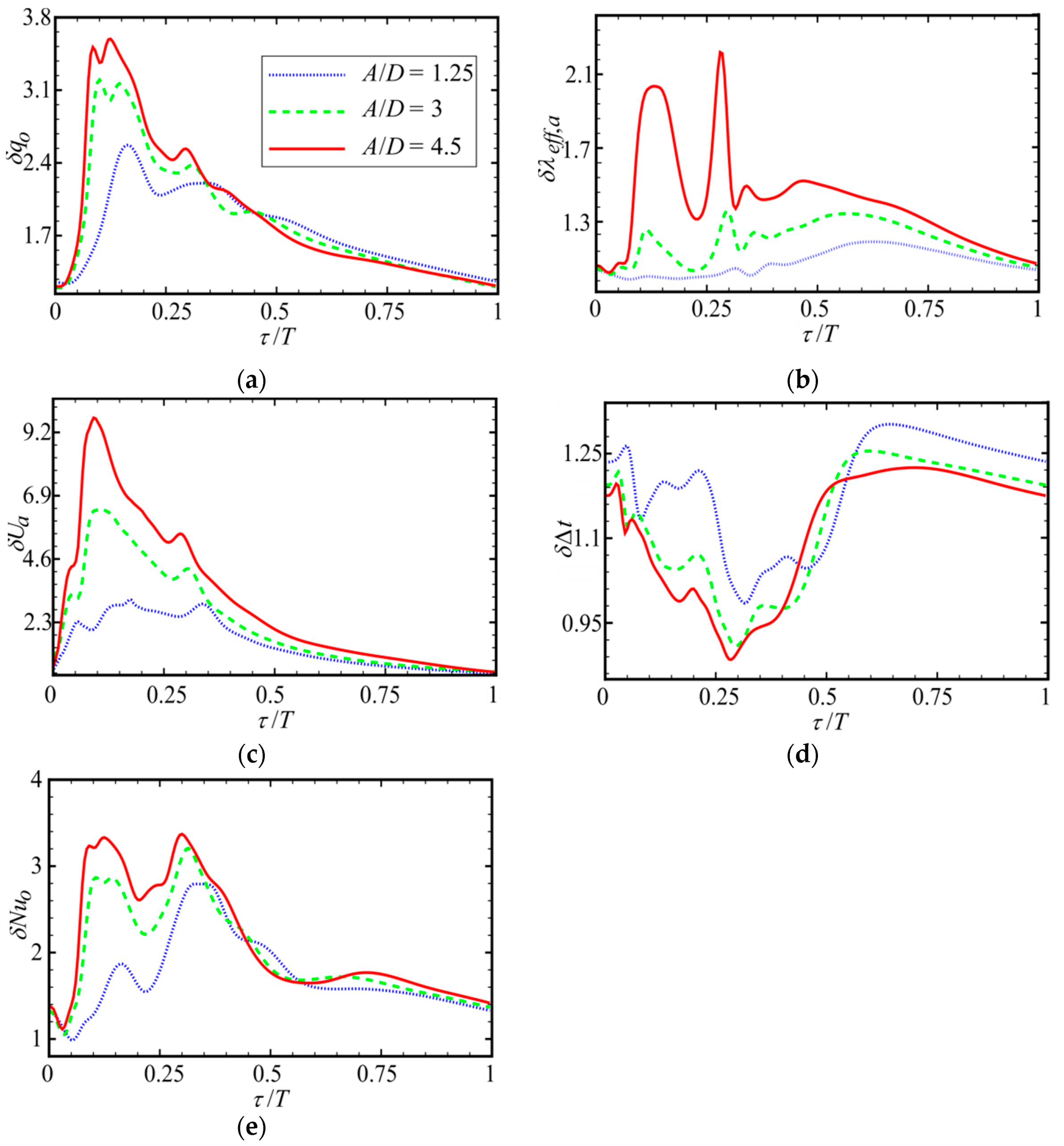
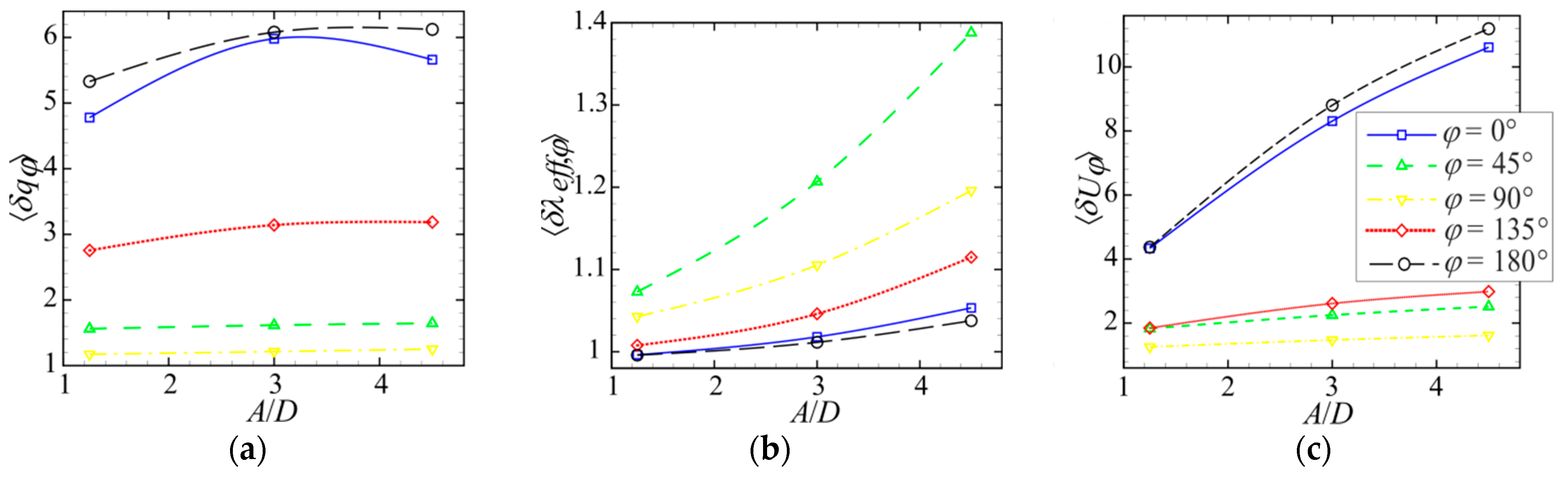
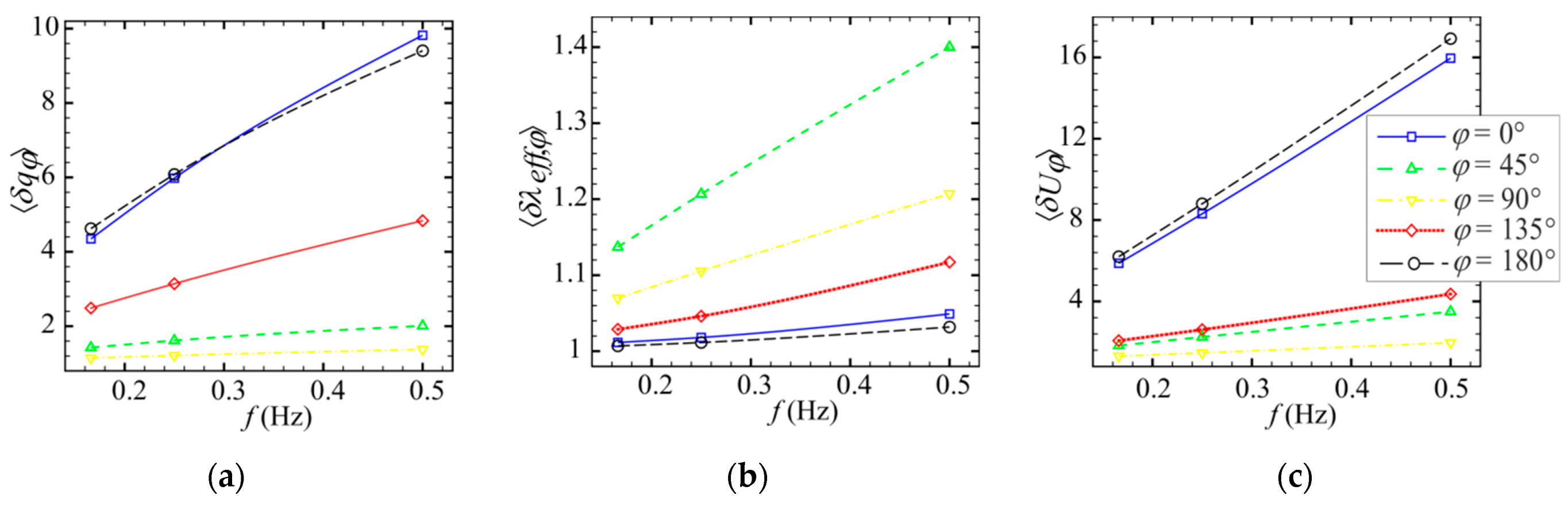
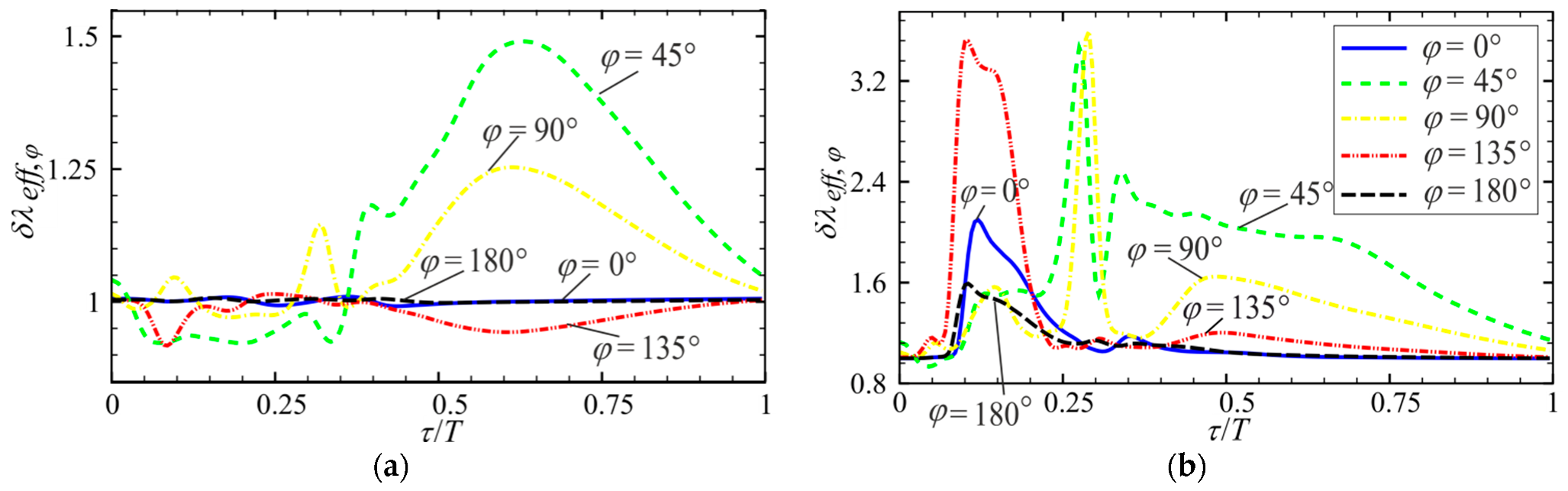
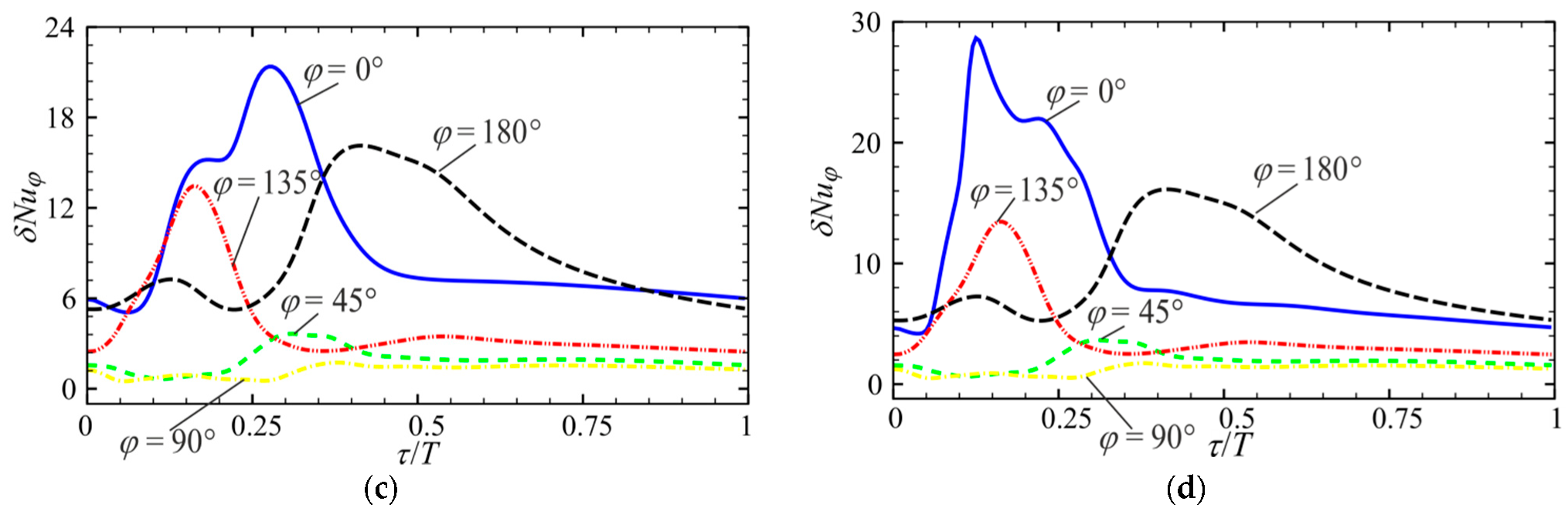
3.2. Effect of Amplitude and Frequency of Pulsations on Local Flow Characteristics and Heat Transfer
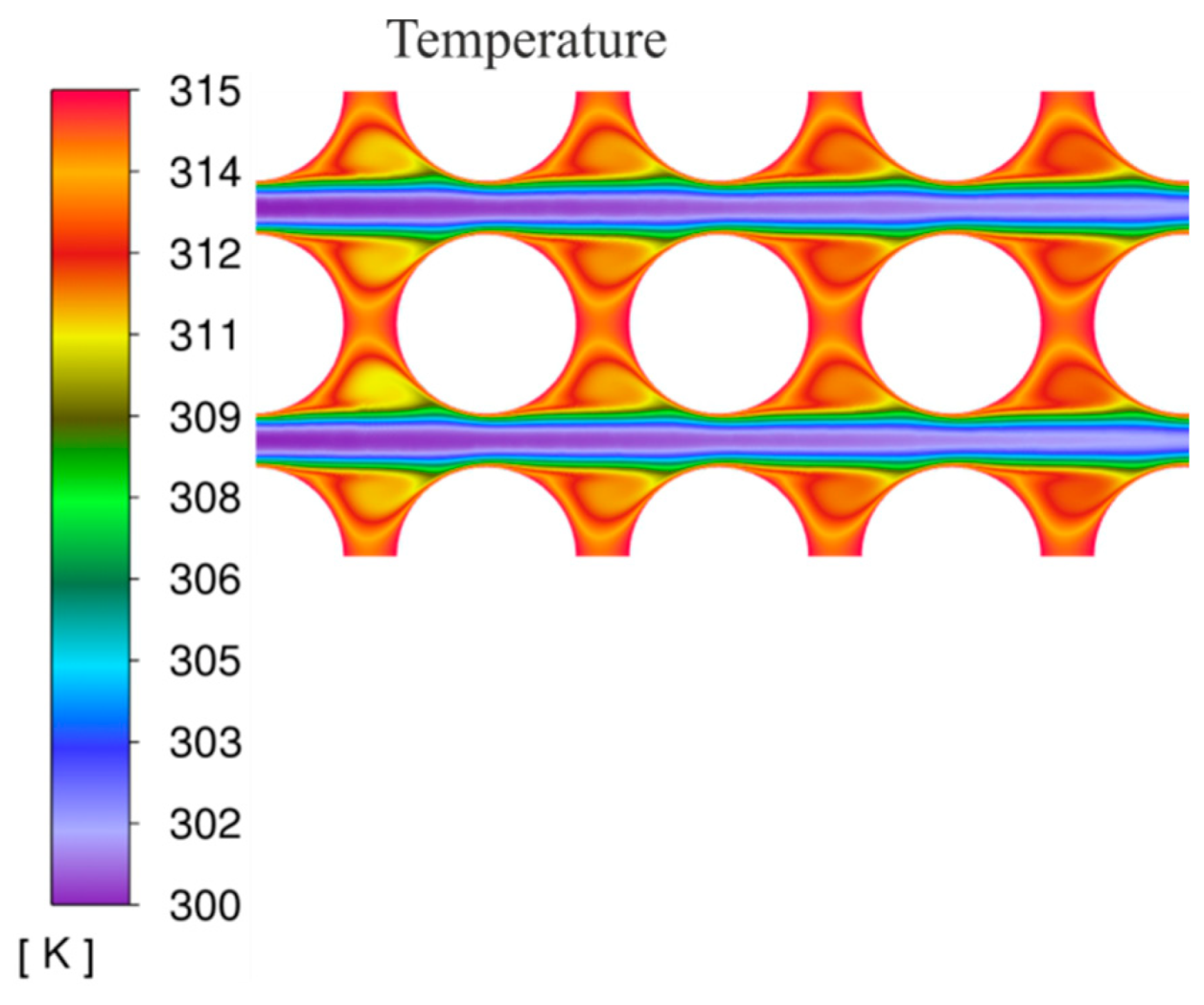
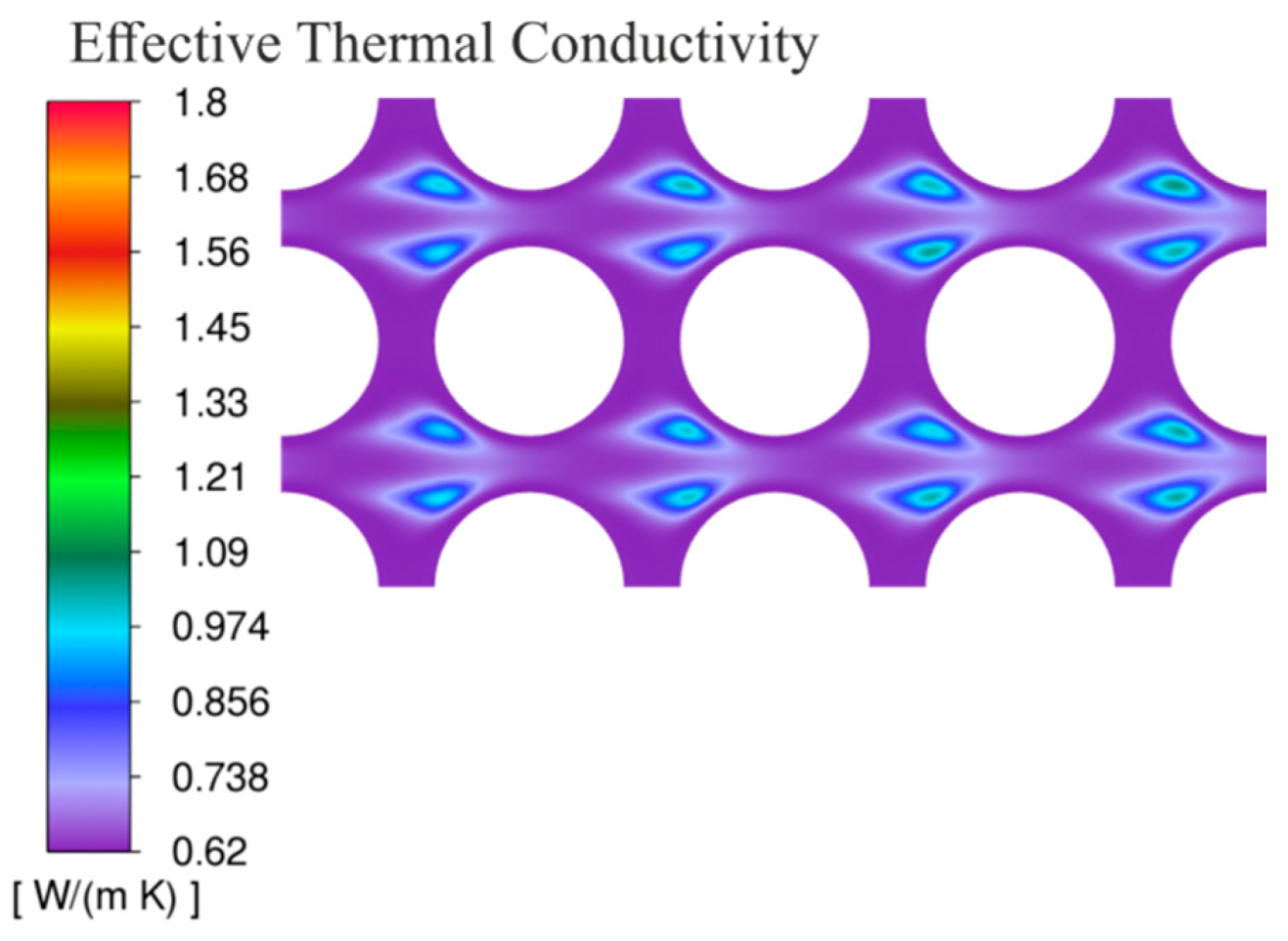
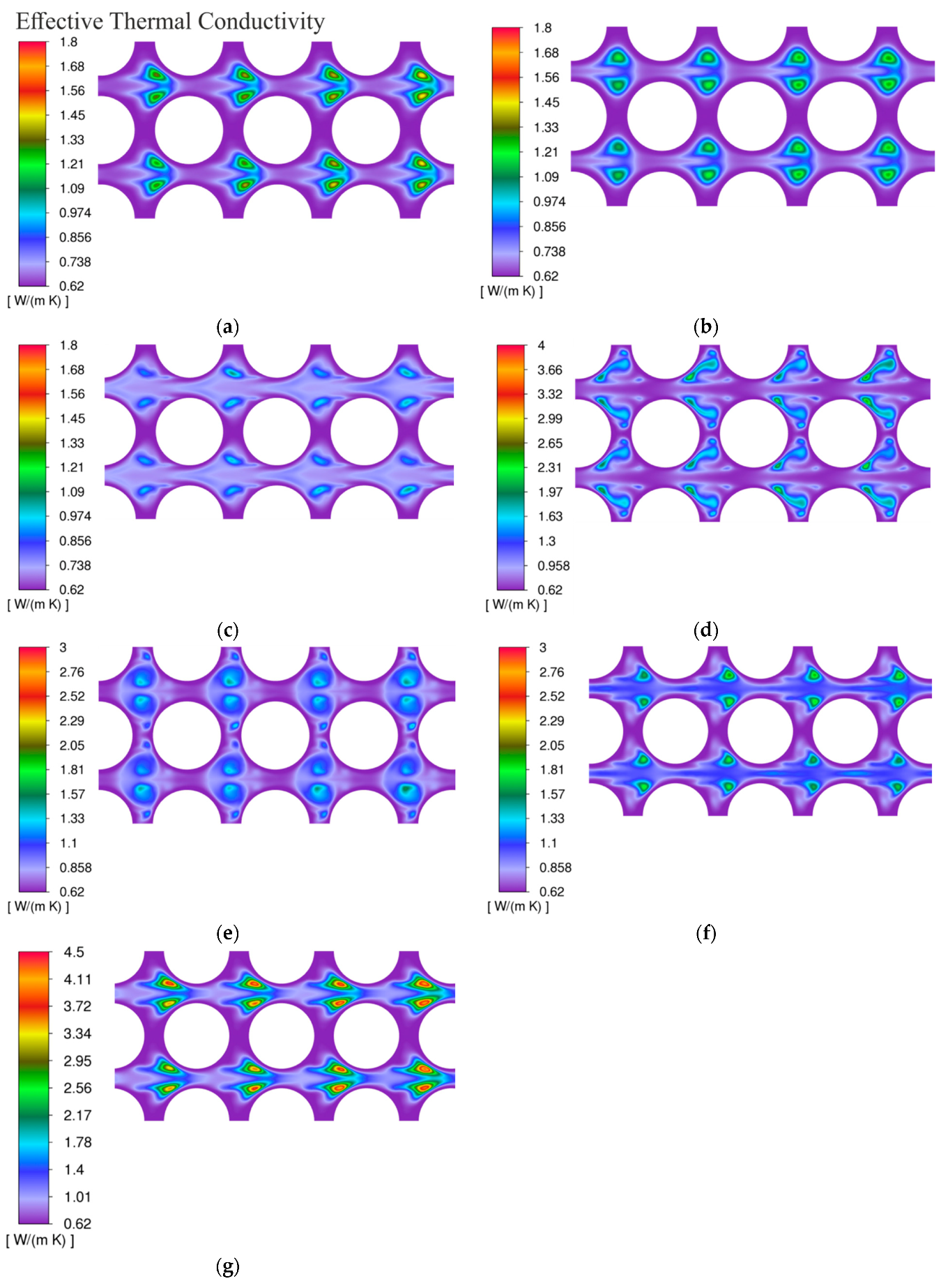
3.3. Contour Plots of Temperature, Effective Thermal Conductivity, and Plots of the Velocity Vector
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | Dimensional amplitude of pulsation, m |
| A/D | Dimensionless relative amplitude of pulsation |
| D | Diameter of the tubes in tube bundle, m |
| Dj | Diameter of the hydraulic model elements, m |
| f | Frequency of pulsation, Hz |
| F(φ,r) | Area of the sector around the cylinder in the tube bundle, m2 |
| g | Gravity acceleration, m s−2 |
| H | Pressure in the hydraulic model elements, mH2O |
| Hh | Pressure on the surface of the liquid in the hydraulic accumulator, mH2O |
| Hp.c. | Pressure on the surface of the liquid in the pulsation chamber, mH2O |
| k | Hydraulic resistance coefficient of the hydraulic model elements |
| l | Length of the hydraulic model elements, m |
| Nu | Nusselt number |
| P | Pressure, Pa |
| q | Heat flux, W m−2 |
| Q | Volumetric flow rate in the hydraulic model elements, m3 s−1 |
| Re | Reynolds numbers |
| rmin/D | Minimum cell size in the near-wall region |
| S | Area of the hydraulic model elements, m2 |
| s/D | Relative transverse and longitudinal pitch of tube bundle |
| Sh0 | Hole area at the bottom of the hydraulic accumulator, m2 |
| Sp.c.0 | Hole area at the bottom of the pulsation chamber, m2 |
| St | Strouhal number |
| tf | Flow temperature at the inlet of the tube bundle, °C |
| ts | Temperature around central cylinder in the fifth row of the tube bundle, °C |
| tw | Tube bundle wall temperature, °C |
| u | Flow velocity at inlet of the tube bundle, m s−1 |
| U | Velocity around central cylinder in the fifth row of the tube bundle, m s−1 |
| Ux,y | Velocity components, m s−1 |
| ymax/D | Maximum mesh size related to the tube diameter |
| z1 | Liquid level in the hydraulic accumulator, m |
| z2 | Liquid level in the pulsation chamber, m |
| T | Period of the pulsation, s |
| T1 | First half-period of the pulsation, s |
| T2 | Second half-period of the pulsation, s |
| x | x-coordinate |
| y | y-coordinate |
| Greek symbols | |
| η | Kinematic viscosity, m2 s−1 |
| λ | Thermal conductivity, W m−1 K−1 |
| λeff | Effective thermal conductivity, W m−1 K−1 |
| λturb | Turbulent thermal conductivity, W m−1 K−1 |
| τ | Time, s |
| τ1 | Start time of the pulsation period, s |
| τ2 | End time of the pulsation period, s |
| Δt | Temperature difference, °C |
| Subscripts | |
| st | Steady flow |
| p | Pulsating flow |
| o | Averaged value over the surface of the cylinder wall in the tube bundle |
| a | Averaged value over the annular area around the cylinder in the tube bundle |
| φ | Averaged value depending on the azimuth angle |
| δ | Enhancement factor |
| Notations | |
| 〈 〉 | Averaged value over one period of the pulsation |
References
- Bergles, A.E.; Manglik, R.M. Current progress and new developments in enhanced heat and mass transfer. J. Enhanc. Heat Transf. 2013, 20, 1–15. [Google Scholar] [CrossRef]
- Alam, T.; Kim, M.-H. A comprehensive review on single phase heat transfer enhancement techniques in heat exchanger applications. Renew. Sustain. Energy Rev. 2018, 81, 813–839. [Google Scholar] [CrossRef]
- Wang, W.; Shuai, Y.; Li, B.; Li, B.; Lee, K.-S. Enhanced heat transfer performance for multi-tube heat exchangers with various tube arrangements. Int. J. Heat Mass Transf. 2021, 168, 120905. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Ahn, H.S. A comprehensive review on micro/nanoscale surface modification techniques for heat transfer enhancement in heat exchanger. Int. J. Heat Mass Transf. 2021, 178, 121601. [Google Scholar] [CrossRef]
- Maradiya, C.; Vadher, J.; Agarwal, R. The heat transfer enhancement techniques and their Thermal Performance Factor. Beni-Suef Univ. J. Basic Appl. Sci. 2018, 7, 1–21. [Google Scholar] [CrossRef]
- Li, X.; Zhu, D.; Sun, J.; Mo, X.; Liu, S. Heat transfer and pressure drop for twisted oval tube bundles with staggered layout in crossflow of air. Appl. Therm. Eng. 2019, 148, 1092–1098. [Google Scholar] [CrossRef]
- Khalatov, A.A.; Kovalenko, G.V.; Meiris, A.Z. Heat Transfer in Air Flow Across a Single-Row Bundle of Tubes With Spiral Grooves. J. Eng. Phys. Thermophys. 2018, 91, 64–71. [Google Scholar] [CrossRef]
- Pongsoi, P.; Pikulkajorn, S.; Wongwises, S. Effect of fin pitches on the optimum heat transfer performance of crimped spiral fin-and-tube heat exchangers. Int. J. Heat Mass Transf. 2012, 55, 6555–6566. [Google Scholar] [CrossRef]
- Mavridou, S.G.; Konstandinidis, E.; Bouris, D.G. Experimental evaluation of pairs of inline tubes of different size as components for heat exchanger tube bundles. Int. J. Heat Mass Transf. 2015, 90, 280–290. [Google Scholar] [CrossRef]
- Wangnipparnto, S.; Tiansuwan, J.; Kiatsiriroat, T.; Wang, C.C. Performance analysis of thermosyphon heat exchanger under electric field. Energy Convers. Manag. 2003, 44, 1163–1175. [Google Scholar] [CrossRef]
- Cheng, L.; Luan, T.; Du, W.; Xu, M. Heat transfer enhancement by flow-induced vibration in heat exchangers. Int. J. Heat Mass Transf. 2009, 52, 1053–1057. [Google Scholar] [CrossRef]
- Jeng, T.-M.; Tzeng, S.-C.; Xu, R. Heat transfer characteristics of a rotating cylinder with a lateral air impinging jet. Int. J. Heat Mass Transf. 2014, 70, 235–249. [Google Scholar] [CrossRef]
- Cheng, P.; Zhao, T.S. Heat transfer in oscillatory flows. Annu. Rev. Heat Transf. 1998, 9, 359–420. [Google Scholar] [CrossRef]
- Herman, C. The impact of flow oscillations on convective heat transfer. Annu. Rev. Heat Transf. 2000, 11, 495–561. [Google Scholar] [CrossRef]
- Elshafei, E.A.M.; Safwat Mohamed, M.; Mansour, H.; Sakr, M. Experimental study of heat transfer in pulsating turbulent flow in a pipe. Int. J. Heat Fluid Flow 2008, 29, 1029–1038. [Google Scholar] [CrossRef]
- Olayiwola, B.; Walzel, P. Cross-flow transport and heat transfer enhancement in laminar pulsed flow. Chem. Eng. Processing Process Intensif. 2008, 47, 929–937. [Google Scholar] [CrossRef]
- Kikuchi, Y.; Suzuki, H.; Kitagawa, M.; Ikeya, K.-I. Effect of Pulsating Strouhal Number on Heat Transfer around a Heated Cylinder in Pulsating Cross-Flow. JSME Int. J. Ser. B 2000, 43, 250–257. [Google Scholar] [CrossRef] [Green Version]
- Fu, W.-S.; Tong, B.-H. Numerical investigation of heat transfer from a heated oscillating cylinder in a cross flow. Int. J. Heat Mass Transf. 2002, 45, 3033–3043. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, G.; Guo, W.; Dong, C. Lattice Boltzmann simulation to laminar pulsating flow past a circular cylinder with constant temperature. Heat Mass Transf. 2017, 53, 2975–2986. [Google Scholar] [CrossRef]
- Ji, T.H.; Kim, S.Y.; Hyun, J.M. Experiments on heat transfer enhancement from a heated square cylinder in a pulsating channel flow. Int. J. Heat Mass Transf. 2008, 51, 1130–1138. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, W.; Dong, H.; Thakur, A.K.; Yang, B.; Zhao, W. Numerical analysis of heat transfer enhancement of fluid past an oscillating circular cylinder in laminar flow regime. Prog. Nucl. Energy 2021, 139, 103853. [Google Scholar] [CrossRef]
- Mikheev, N.I.; Molochnikov, V.M.; Mikheev, A.N.; Dushina, O.A. Hydrodynamics and heat transfer of pulsating flow around a cylinder. Int. J. Heat Mass Transf. 2017, 109, 254–265. [Google Scholar] [CrossRef]
- Molochnikov, V.M.; Mikheev, N.I.; Mikheev, A.N.; Paereliy, A.A. Heat transfer from a cylinder in pulsating cross-flow. Thermophys. Aeromech. 2017, 24, 569–575. [Google Scholar] [CrossRef]
- Molochnikov, V.M.; Mikheev, A.N.; Aslaev, A.K.; Dushina, O.A.; Paereliy, A.A. Heat transfer of a tube bundle in a pulsating flow. Thermophys. Aeromech. 2019, 26, 547–559. [Google Scholar] [CrossRef]
- Molochnikov, V.M.; Mikheev, A.N.; Aslaev, A.K.; Goltsman, A.E.; Paereliy, A.A. Flow structure between the tubes and heat transfer of a tube bundle in pulsating flow. J. Phys. Conf. Ser. 2018, 1105, 012024. [Google Scholar] [CrossRef]
- Liang, C.L.; Papadakis, G. Study of the effect of flow pulsation on the flow field and heat transfer over an inline cylinder array using LES. Eng. Turbul. Model. Exp. 2005, 6, 813–822. [Google Scholar] [CrossRef]
- Wu, Z.; You, S.; Zhang, H.; Zheng, W. Experimental investigation on heat transfer characteristics of staggered tube bundle heat exchanger immersed in oscillating flow. Int. J. Heat Mass Transf. 2020, 148, 119125. [Google Scholar] [CrossRef]
- Chen, S.; Huang, Q.; Liang, M.; Chen, H.; Chen, L.; Hou, Y. Numerical study on the heat transfer characteristics of oscillating flow in cryogenic regenerators. Cryogenics 2018, 96, 99–107. [Google Scholar] [CrossRef]
- Mulcahey, T.I.; Pathak, M.G.; Ghiaasiaan, S.M. The effect of flow pulsation on drag and heat transfer in an array of heated square cylinders. Int. J. Therm. Sci. 2013, 64, 105–120. [Google Scholar] [CrossRef]
- Balabani, S.; Yianneskis, M. An experimental study of the mean flow and turbulence structure of cross-flow over tube bundles. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 1996, 210, 317–331. [Google Scholar] [CrossRef]
- Shah, R.K.; Sekulić, D.P. Fundamentals of Heat Exchanger Design; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Zhukauskas, A.A.; Ulinskas, R. Heat Transfer in Banks of Tubes in Crossflow of fluid; Mintis: Vilnius, Lithuania, 1968; p. 200. (In Russian) [Google Scholar]
- Zukauskas, A. Heat Transfer from Tubes in Crossflow. Adv. Heat Transf. 1972, 18, 87–159. [Google Scholar]
- Ye, Q.; Zhang, Y.; Wei, J. A comprehensive review of pulsating flow on heat transfer enhancement. Appl. Therm. Eng. 2021, 196, 117275. [Google Scholar] [CrossRef]
- Sung, H.J.; Hwang, K.S.; Hyun, J.M. Experimental-study on mass-transfer from a circular-cylinder in pulsating flow. Int. J. Heat Mass Transf. 1994, 37, 2203–2210. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Hong, J.-L.; Aung, W. Numerical prediction of lock-on effect on convective heat transfer from a transversely oscillating circular cylinder. Int. J. Heat Mass Transf. 1997, 40, 1825–1834. [Google Scholar] [CrossRef]
- Konstantinidis, E.; Balabani, S.; Yianneskis, M. Relationship Between Vortex Shedding Lock-On and Heat Transfer. Chem. Eng. Res. Des. 2003, 81, 695–699. [Google Scholar] [CrossRef]
- Perwaiz, J.; Base, T.E. Heat-transfer from a cylinder and finned tube in a pulsating cross-flow. Exp. Therm. Fluid Sci. 1992, 5, 506–512. [Google Scholar] [CrossRef]
- Ilyin, V.K.; Sabitov, L.S.; Haibullina, A.I.; Hayrullin, A.R.; IOP. Factors influencing on the thermal flow with the cross-section of the corridor tube bundle in low-frequency non-symmetric pulsations. IOP Conf. Ser. Mater. Sci. Eng. 2017, 240, 012026. [Google Scholar] [CrossRef]
- Abramov, A.G.; Levchenya, A.M.; Smirnov, E.M.; Smirnov, P.E. Numerical simulation of liquid metal turbulent heat transfer from an inline tube bundle in cross-flow. St. Petersburg Polytech. Univ. J. Phys. Math. 2015, 1, 356–363. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, N.G.; Kirillov, A.I.; Smirnov, E.M.; Ris, V.V. Numerical Modeling of Buoyancy-Induced Fluid Flow and Heat Transfer in a Staggered Tube Bank. In Proceedings of the 2010 14th International Heat Transfer Conference, Washington, DC, USA, 8–13 August 2010; pp. 545–551. [Google Scholar]
- Hajbullina, A.; Hajrullin, A.; Il’in, V. Heat transfer in the flow channel in tube bundle corridor type under imposed on the flow liquid of upstream low-frequency asymmetrical pulsations. Power Eng. Res. Equip. Technol. 2016, 18, 56–67. (In Russian) [Google Scholar] [CrossRef]
- Larock, B.E.; Jeppson, R.W.; Watters, G.Z. Hydraulics of Pipeline Systems; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flow. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; p. 439. [Google Scholar]
- Wang, Y.Q.; Jackson, P.L. Turbulence Modeling Applied to Flow Through a Staggered Tube Bundle. J. Thermophys. Heat Transf. 2010, 24, 534–543. [Google Scholar] [CrossRef]
- Kim, S.-M.; Ghiaasiaan, S.M. Numerical Modeling of Laminar Pulsating Flow in Porous Media. J. Fluids Eng. 2009, 131, 041203. [Google Scholar] [CrossRef]
- Haibullina, A.I. Improving the Efficiency of Heat Exchangers due to Low-Frequency Flow Pulsations. Ph.D. Thesis, Kazan State Power Engineering University, Kazan, Russia, 2017. (In Russian). [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haibullina, A.; Khairullin, A.; Balzamov, D.; Ilyin, V.; Bronskaya, V.; Khairullina, L. Local Heat Transfer Dynamics in the In-Line Tube Bundle under Asymmetrical Pulsating Flow. Energies 2022, 15, 5571. https://doi.org/10.3390/en15155571
Haibullina A, Khairullin A, Balzamov D, Ilyin V, Bronskaya V, Khairullina L. Local Heat Transfer Dynamics in the In-Line Tube Bundle under Asymmetrical Pulsating Flow. Energies. 2022; 15(15):5571. https://doi.org/10.3390/en15155571
Chicago/Turabian StyleHaibullina, Aigul, Aidar Khairullin, Denis Balzamov, Vladimir Ilyin, Veronika Bronskaya, and Liliya Khairullina. 2022. "Local Heat Transfer Dynamics in the In-Line Tube Bundle under Asymmetrical Pulsating Flow" Energies 15, no. 15: 5571. https://doi.org/10.3390/en15155571
APA StyleHaibullina, A., Khairullin, A., Balzamov, D., Ilyin, V., Bronskaya, V., & Khairullina, L. (2022). Local Heat Transfer Dynamics in the In-Line Tube Bundle under Asymmetrical Pulsating Flow. Energies, 15(15), 5571. https://doi.org/10.3390/en15155571





