Influence of Height–Diameter Ratio on Rock Compressive Failure Characteristics and Damage Evolution Law
Abstract
:1. Introduction
2. Test Materials and Test Methods
3. Analysis of Test Results
3.1. Mechanical Characteristics of Sandstones with Different Height-to-Diameter Ratios
3.1.1. Influence of Height–Diameter Ratio Change on Sandstone Strength
3.1.2. Influence of Height–Diameter Ratio Change on Sandstone Deformation
3.1.3. Influence of Height–Diameter Ratio Change on Sandstone Fracture Morphology
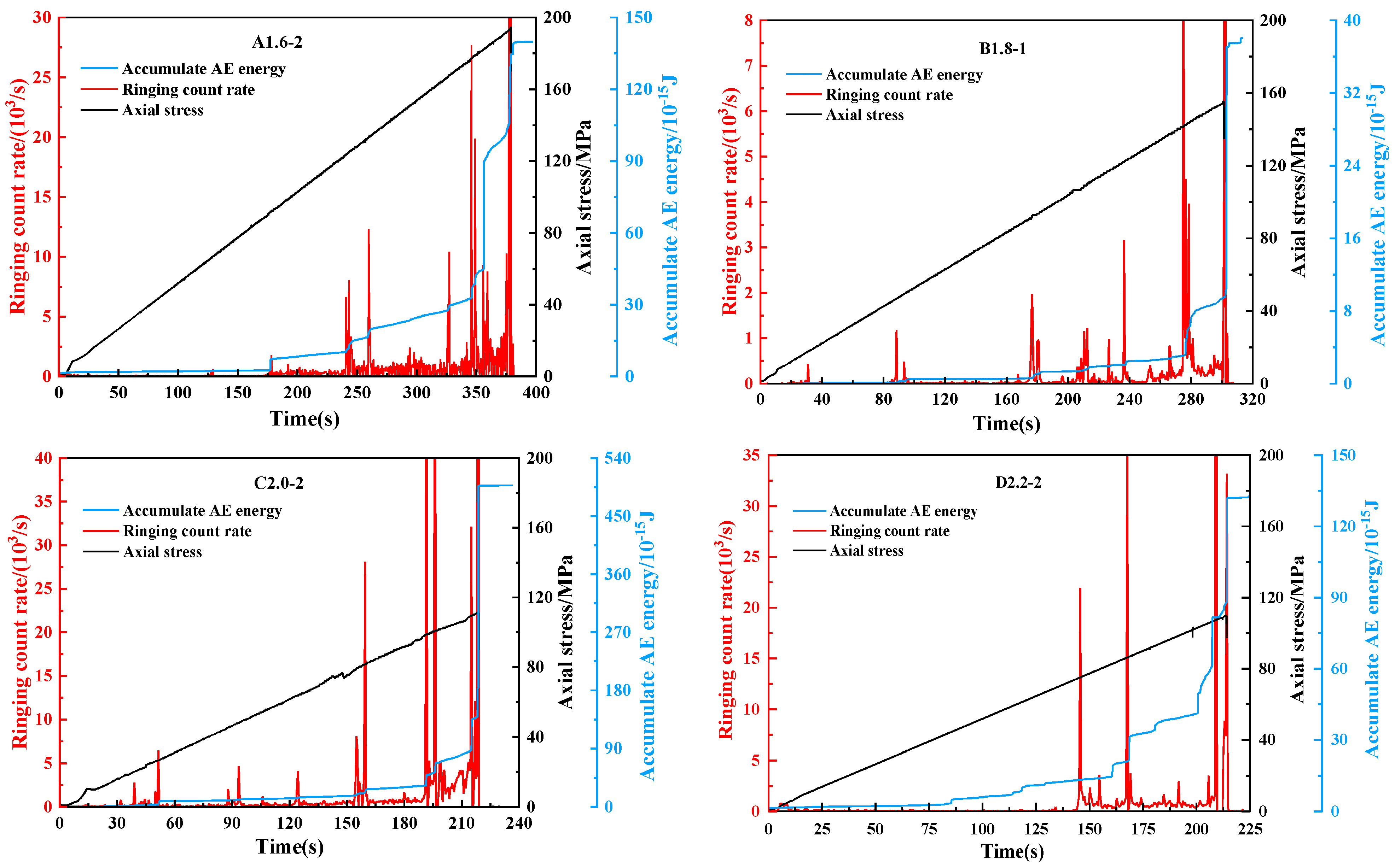
3.2. Acoustic Emission Evolution Law of Rock Samples with Different Height–Diameter Ratios
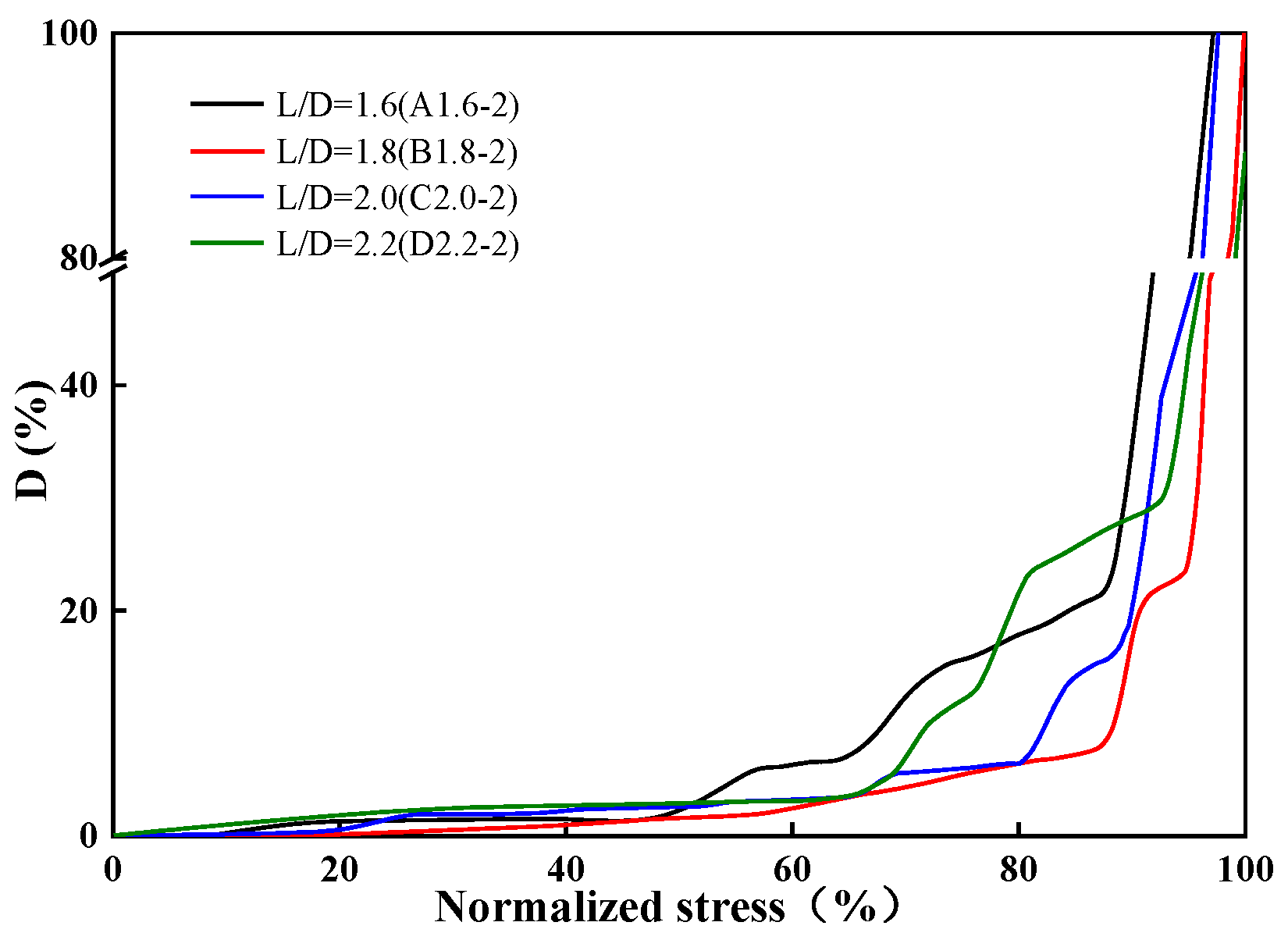
3.3. Analysis of Damage Evolution in Sandstones with Different Height-to-Diameter Ratios
4. Discussion
5. Conclusions
- (1)
- With the increase in the height–diameter ratio, the rock strength shows a nonlinear downward trend. The smaller the height–diameter ratio, the greater the influence of the end face effect, so the higher the strength. However, beyond a certain height–diameter ratio, the influence range of the end face effect becomes smaller, and the decreasing trend of the peak strength becomes slower due to the influence of the primary defects in the test piece.
- (2)
- With the increase in the height–diameter ratio, the peak strain of the specimen shows a trend of decreasing first and then increasing, and it is relatively stable near L/D = 2, indicating that with the increase in rock size, the deformation is not only related to the end face friction effect, but also related to the number of primary cracks in the rock is related.
- (3)
- The smaller the height–diameter ratio is, the more serious the rock damage is. As the height–diameter ratio increases, the damage form gradually transitions from conical to oblique shear failure.
- (4)
- With the increase in the height–diameter ratio, the rising phase of the acoustic emission signal is short before the fracture, and the destruction is more concentrated. The accumulated energy increased steadily in the early stage. After entering the unstable damage stage, the internal crack of the specimen develops and penetrates with the dissipation of energy, and the accumulated energy increases sharply during the instability failure. Therefore, the occurrence of rock damage can be predicted through the mutation of acoustic emission signals.
- (5)
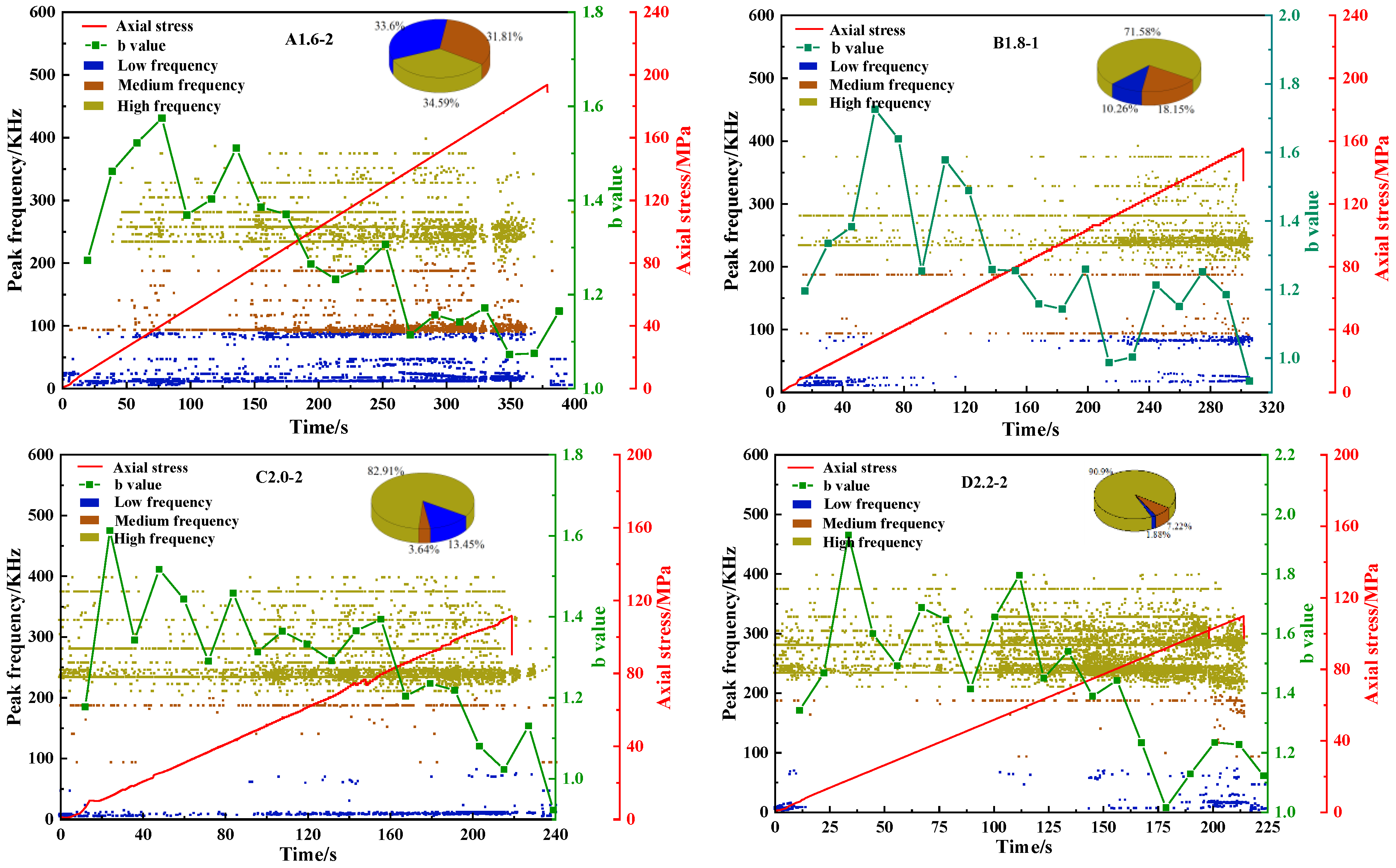
- With the increase in the height–diameter ratio, the overall level of acoustic emission b value showed an upward trend, the proportion of high-frequency signals gradually increased, the proportion of low-frequency signals gradually decreased, and the tiny cracks in the rock developed more densely.
- (6)
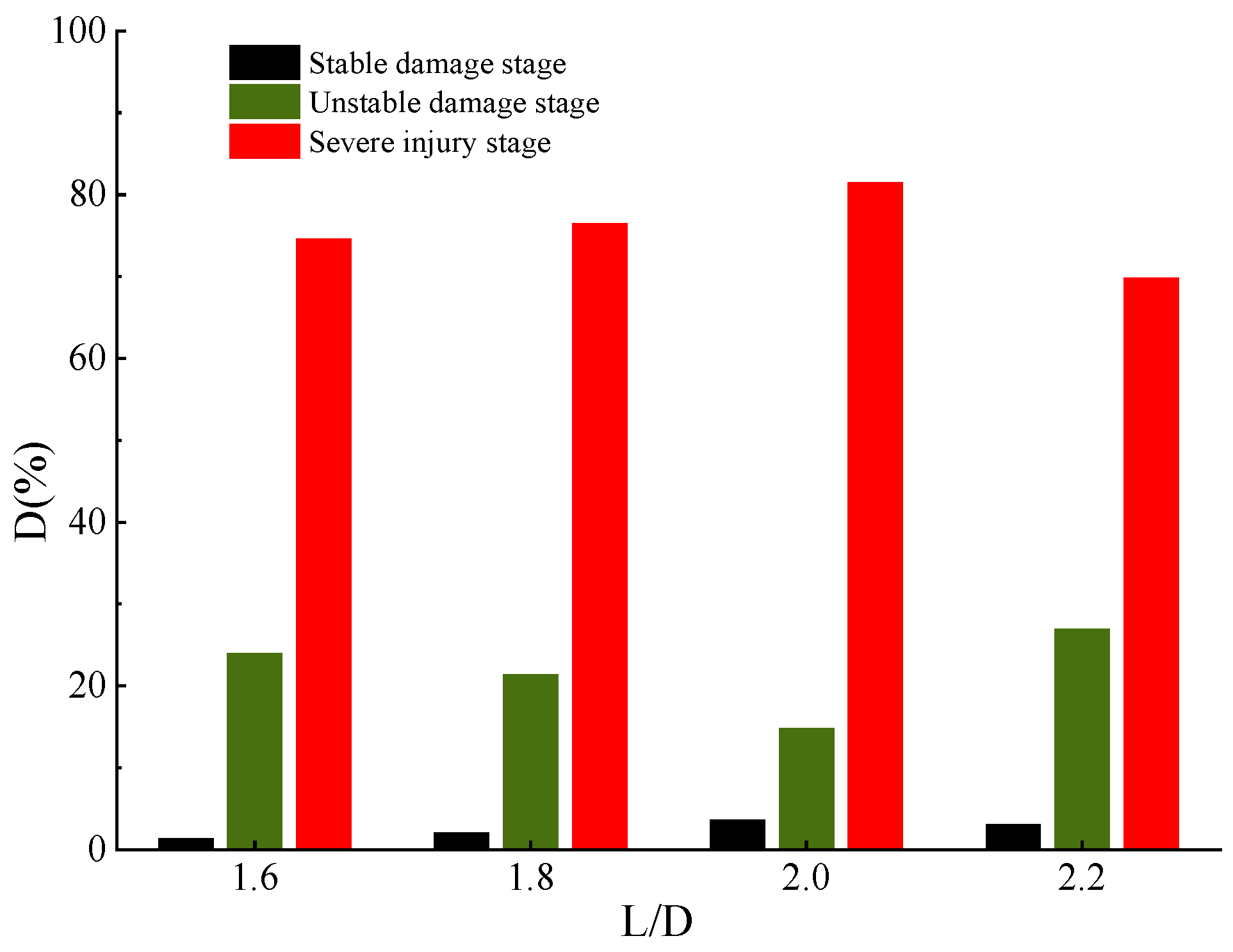
- The value of the rock damage curve is small in the stable damage stage. With the increase in the height–diameter ratio, the damage in the unstable damage stage shows a trend of first decreasing and then increasing. When L/D = 2, it reaches the minimum value, and the value in the severe damage stage is higher as a whole, which has the greatest impact on the damage of the specimen, and the damage is relatively concentrated.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, X.; Huai, Z.; Li, X.B.; Gong, F.Q. Fracture patterns induced by deep underground excavation based on a crack propagation model. J. China Coal Soc. 2019, 44, 1378–1390. [Google Scholar]
- Yan, P.; Lu, W.B.; Chen, M.; Zhou, C.B. Effect of initial geo-stress dynamic unloading during tunnel excavation. Chin. J. Geotech. Eng. 2009, 31, 1888–1894. [Google Scholar]
- You, M.Q.; Zou, Y.F. Discussion on heterogeneity of rock material and size effect on specimen strength. Chin. J. Rock Mech. Eng. 2000, 19, 391–395. [Google Scholar]
- Yang, S.Q.; Su, C.D.; Xu, W.Y. Experimental and theoretical study on size effect of rock materials. Eng. Mech. 2005, 22, 112–118. [Google Scholar] [CrossRef]
- Yang, S.Q.; Xu, W.Y.; Su, C.D. Study on statistical damage constitutive model of rock considering scale effect. Chin. J. Rock Mech. Eng. 2005, 24, 4484–4490. [Google Scholar]
- Komurlu, E. Loading rate conditions and specimen size effect on strength and deformability of rock materials under uniaxial compression. Int. J. Geo Eng. 2018, 9, 17. [Google Scholar] [CrossRef]
- Shi, Y.K.; Ma, Y.H.; Yin, Y.C. Research on size effect affected to seam bump-prone test results. Coal Sci. Technol. 2014, 42, 23–26. [Google Scholar]
- Yilmaz, Y.; Eun, J.; Panahi, S.S.; Mousavi, M.S. Effects of height-to-diameter ratio (H/D) for specimens with various water contents on unconfined compressive strength of a clayey soil. Eng. Geol. 2019, 257, 105136. [Google Scholar] [CrossRef]
- Zhao, G.M.; Liu, Z.X.; Meng, X.R.; Zhang, R.F.; Kao, S.M.; Qi, M.J. Energy accumulation and dissipation test and analysis method of height-diameter ratio sandstone. J. China Coal Soc. 2022, 47, 1110–1121. [Google Scholar]
- Ling, Z.Z.; Zhang, Y.B.; Tang, S.B.; Li, L.C.; Tang, C.A. Size effect of rock messes and associated representative element properties. Chin. J. Rock Mech. Eng. 2013, 32, 1157–1166. [Google Scholar]
- Tuncay, E.; Hasancebi, N. The effect of length to diameter ratio test specimens on the uniaxial compressive strength of rock. Bull. Eng. Geol. Environ. 2009, 68, 491–497. [Google Scholar] [CrossRef]
- Tuncay, E.; Özcan, N.T.; Kalender, A. An approach to predict the length-to-diameter ratio of a rock core specimen for uniaxial compression tests. Bull. Eng. Geol. Environ. 2019, 78, 5467–5482. [Google Scholar] [CrossRef]
- Zhu, Z.D.; Zhang., A.J.; Xing, F.D.; Xu, W.Y. Experimental study on correlation between compressive strength of rocks and sample size. J. Hohai Univ. Sci. Technol. 2004, 32, 42–45. [Google Scholar]
- Darlington, W.J.; Ranjith, P.G.; Choi, S.K. The effect of specimen size on strength and other properties in laboratory testing of rock and rock-like cementitious brittle materials. Rock Mech. Rock Eng. 2011, 44, 513–529. [Google Scholar] [CrossRef]
- Liu, C.Y.; Zhao, G.M.; Xu, W.S.; Meng, X.R.; Huang, S.J.; Zhou, J.; Wang, Y.K. Experimental investigation on failure process and Spatio-temporal evolution of rockburst in granite with a prefabricated circular hole. J. Cent. South Univ. 2020, 27, 2930–2944. [Google Scholar] [CrossRef]
- Liu, C.Y.; Zhao, G.M.; XU, W.S.; Meng, X.R. Experimental study on rockburst and its spatio-temporal evolution criterion in high stress roadway. J. China Coal Soc. 2020, 45, 998–1008. [Google Scholar]
- Wen, Z.J.; Huang, J.; Jiang, Y.J.; Zuo, Y.J.; Zhu, Z.W.; Xiao, P. Development and experiment of a coupled static-dynamic cyclic loading test system. J. Cent. South Univ. Sci. Technol. 2021, 52, 2817–2827. [Google Scholar]
- Wang, Q.Y.; Zhu, W.C.; Liu, H.L.; Niu, L.L.; Li, R.F. Size effect of long-term strength of sandstone under uniaxial compression. Rock Soil Mech. 2016, 37, 981–990. [Google Scholar]
- Ling, C.Y.; Li, X.; Zhang, H.; Li, S.D.; Hao, J.M.; Ma, C.F. Research on size effect of uniaxial compression properties of granite under medium and low strain rates. Chin. J. Rock Mech. Eng. 2013, 32, 528–536. [Google Scholar]
- Tatiana, D.; Martin, B.; Petra, D.; Renáta, A. Influence of specimen size and shape on the uniaxial compressive strength values of selected Western Carpathians rocks. Environ. Earth Sci. 2022, 81, 247. [Google Scholar]
- Jiang, J.J.; Deng, Z.G.; Ouyang, Z.H.; Zhang, N.B.; Wang, Y.; Zhang, G.H. Study on Precursory Characteristics of Acoustic Emission of Instable Failure Coal Body with Different Sizes. Saf. Coal Mines 2017, 48, 37–40. [Google Scholar]
- Hong, L.; Li, X.B.; Ma, C.D.; Yin, S.B.; Ye, Z.Y.; Liao, G.Y. Study on size effect of rock dynamic strength and strain rate sensitivity. Chin. J. Rock Mech. Eng. 2008, 27, 526–533. [Google Scholar]
- Meng, Q.B.; Han, L.J.; Pu., H.; Li, H.; Wen, S.Y.; Li, H. Experimental study on the effect of size effect and strain rate on rock mechanical properties. J. China Univ. Min. Technol. 2016, 45, 233–243. [Google Scholar]
- Qi, C.Z.; Wang, M.Y.; Bai, J.P.; Li, K.R. Mechanism underlying dynamic size effect on rock mass strength. Int. J. Impact Eng. 2014, 68, 1–7. [Google Scholar] [CrossRef]
- Pankov, I.; Asanov, V.; Beltyukov, N. Mechanism of Scale Effect in Saliferous Rock under Compression. Procedia Eng. 2017, 191, 918–924. [Google Scholar] [CrossRef]
- Li, G.C.; Sun, C.L.; He, J.T.; Sun, Y.T.; Dong, Y.X.; Zhao, H.S. Macro and meso scalesimulation study of the strength-weakening property of soft mudstone affected by water. J. China Univ. Min. Technol. 2019, 48, 935–942. [Google Scholar]
- Liu, B.S.; Zhang, J.S.; Du, Q.Z.; Tu, J.F. Size effect in rock shear strength. Chin. J. Rock Mech. Eng. 1998, 17, 611–614. [Google Scholar]
- Sun, C.; Liu, F.; Jiang, M.J.; Chen, H. Discrete element numerical simulation of size effect and end restraint of rock compressive strength. Chin. J. Rock Mech. Eng. 2014, 33 (Suppl. S2), 3421–3428. [Google Scholar]
- Li, S.L.; Liu, G.J.; Jia, R.F.; Xue, F.; Wang, K.Y. Study on friction effect and damage evolution of end face in uniaxial compression test. J. Min. Strat. Control Eng. 2021, 3, 99–108. [Google Scholar]
- Peng, J.; Wong, L.N.Y.; The, C.I. A re-examination of slenderness ratio effect on rock strength Insights from DEM grain-based modelling. Eng. Geol. 2018, 246, 245–254. [Google Scholar] [CrossRef]
- Chen, J.C.; Chemenda, A.I. Numerical simulation of true 3D rock tests with classical and new three invariant constitutive models focusing on the end effects. Arab. J. Sci. Eng. 2020, 45, 9367–9378. [Google Scholar] [CrossRef]
- Liu, G.; Xiao, F.K.; Qin, T. Rock mechanics characteristics and acoustic emission rule under small-size effect. Chin. J. Rock Mech. Eng. 2018, 37 (Suppl. S2), 3905–3917. [Google Scholar]
- You, M.Q.; Hua, A.Z. Damage in the form of rock specimens under uniaxial compression and the carrying of reduce. Chin. J. Rock Mech. Eng. 1998, 17, 292–296. [Google Scholar]
- Gong, F.Q.; Luo, Y.; Li, X.B.; Si, X.F.; Tao, M. Experimental simulation investigation on rockburst induced by spalling failure in deep circular tunnels. Tunn. Undergr. Space Technol. 2018, 81, 413–427. [Google Scholar] [CrossRef]
- Miao, J.L.; He, M.C.; Li, D.J.; Zeng, F.J.; Zhang, Q. Acoustic emission characteristics of granite under strain rockburst test and its macro-fracture mechanism. Chin. J. Rock Mech. Eng. 2009, 28, 1593–1603. [Google Scholar]
- Dong, L.J.; Zhang, Y.H.; Sun, D.Y.; Chen, Y.C.; Tang, Z. Stage characteristics of acoustic emission and identification of unstable crack state for granite fractures. Chin. J. Rock Mech. Eng. 2022, 41, 120–131. [Google Scholar]
- Jia, X.N. Experimental Study on Acoustic Emission Eigen Frequency Spectrum Features of Strain Bursts. Ph.D. Thesis, China University of Mining and Technology, Beijing, China, 2013. [Google Scholar]
- Cai, M.; Kaiser, P.K.; Morioka, H.; Minami, M.; Maejima, T.; Tasaka, Y.; Kurose, H. FLAC/PFC coupled numerical simulation of AE in large-scale underground excavations. Int. J. Rock Mech. Min. Sci. 2007, 44, 550–564. [Google Scholar] [CrossRef]
- Martin, C.D.; Maybee, W.G. The strength of hard-rock pillars. Int. J. Rock Mech. Min. Sci. 2000, 37, 1239–1246. [Google Scholar] [CrossRef]
- Qi, H.G.; Yu, J.H. Rationality and comprehensive unloading technology of deep high stress section coal pillars. J. China Coal Soc. 2018, 43, 3257–3264. [Google Scholar]

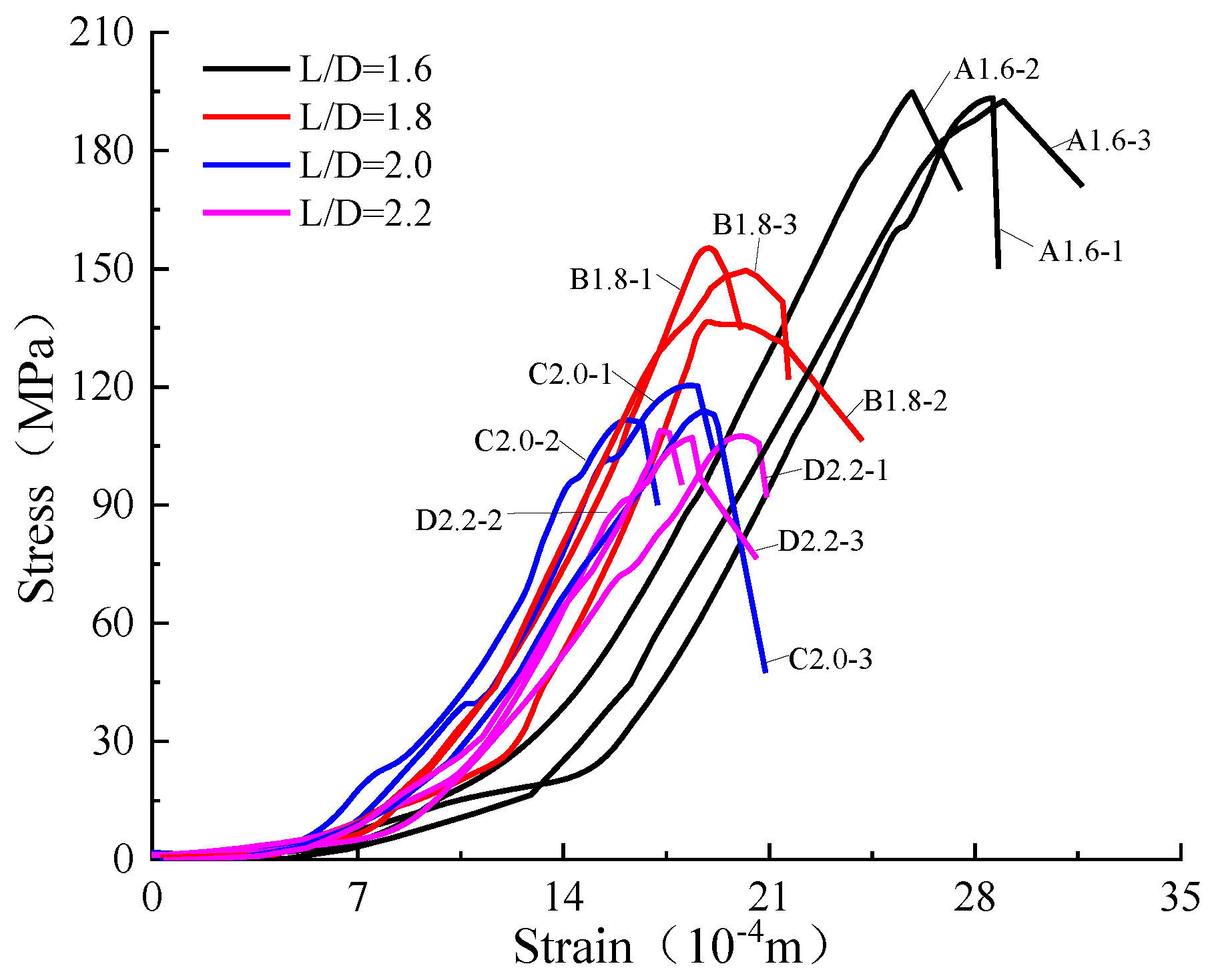

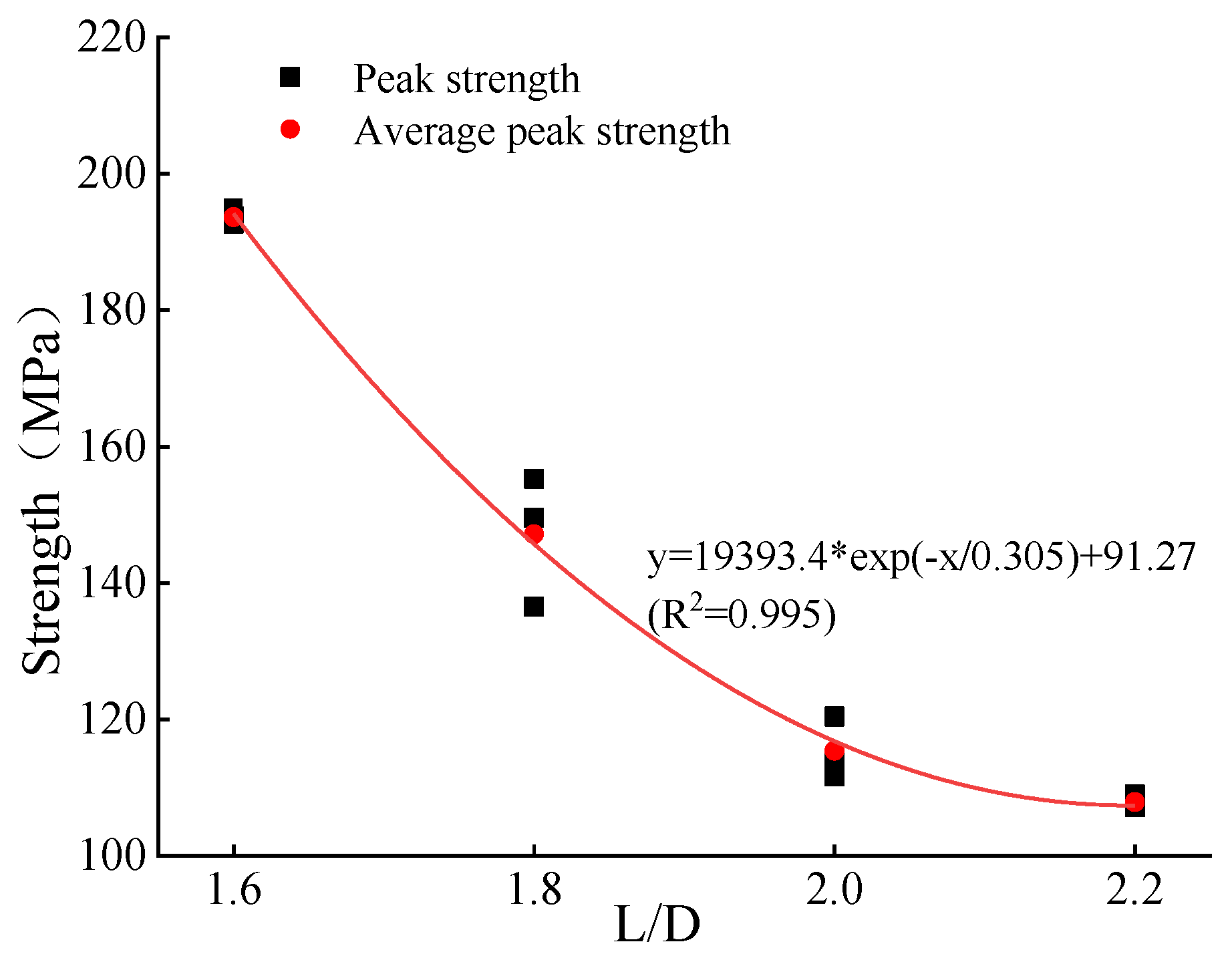
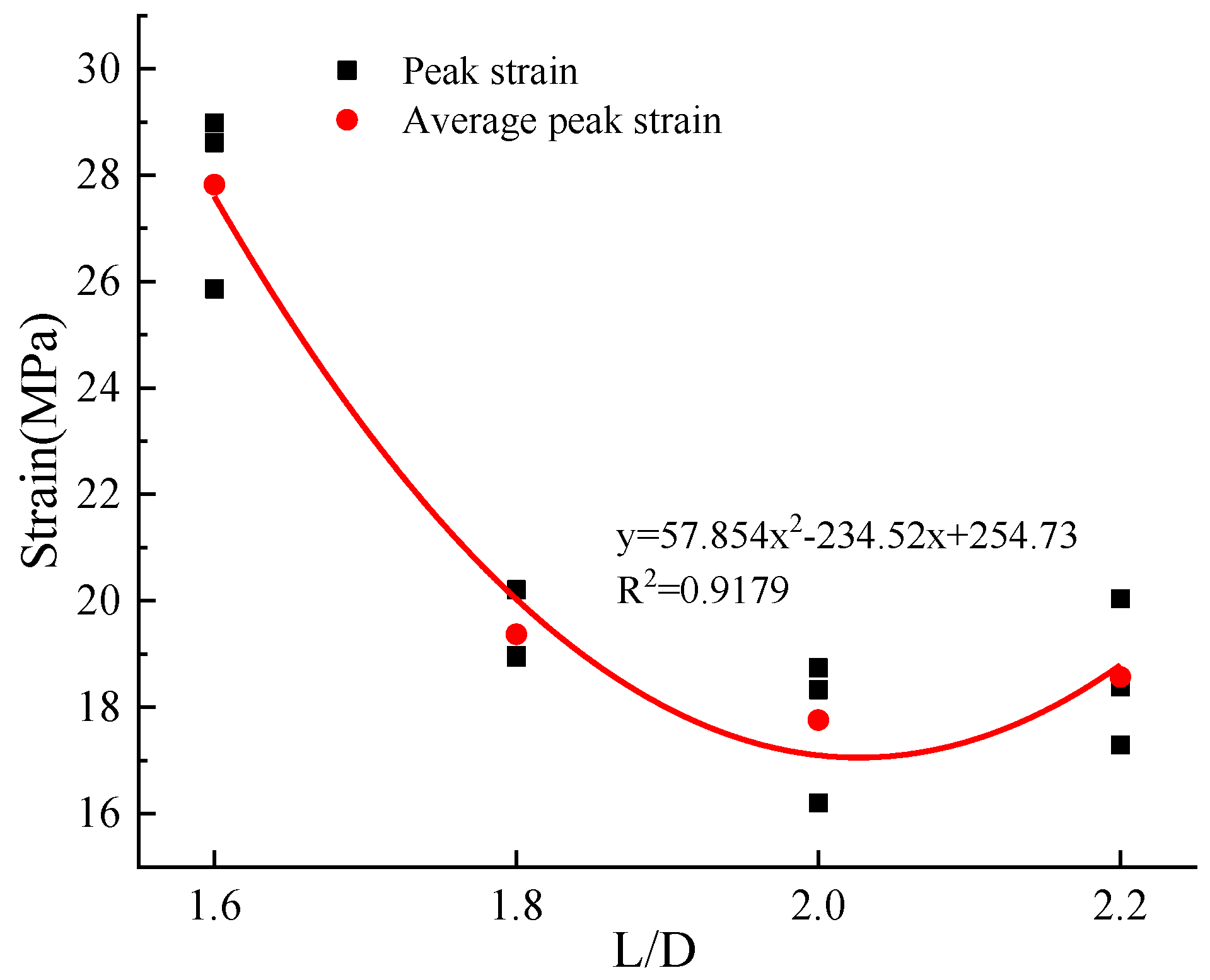

| Sample Number | Sample Diameter × Height (mm × mm) | Sample Cross-Sectional Area (mm2) | Peak Strength (MPa) | Peak Strain (10−4 m) | Elastic Modulus (GPa) |
|---|---|---|---|---|---|
| A1.6-1 | 50.26 × 80.88 | 1983.97 | 193.38 | 28.61 | 14.82 |
| A1.6-2 | 50.28 × 81.05 | 1985.55 | 194.89 | 25.86 | 14.54 |
| A1.6-3 | 50.39 × 79.58 | 1994.24 | 192.67 | 28.98 | 13.14 |
| B1.8-1 | 50.25 × 90.77 | 1983.18 | 155.26 | 18.94 | 15.27 |
| B1.8-2 | 50.32 × 89.65 | 1988.71 | 136.53 | 18.97 | 16.13 |
| B1.8-3 | 50.11 × 91.18 | 1972.14 | 149.56 | 20.21 | 15.40 |
| C2.0-1 | 50.20 × 99.88 | 1979.23 | 120.39 | 18.33 | 15.74 |
| C2.0-2 | 50.15 × 100.97 | 1975.29 | 111.66 | 16.20 | 13.73 |
| C2.0-3 | 50.30 × 99.58 | 1987.13 | 114.02 | 18.74 | 13.11 |
| D2.2-1 | 50.07 × 111.32 | 1968.99 | 107.49 | 20.04 | 10.80 |
| D2.2-2 | 50.15 × 109.64 | 1975.29 | 108.93 | 17.29 | 14.67 |
| D2.2-3 | 50.16 × 112.12 | 1976.08 | 107.12 | 18.38 | 12.81 |
| Mesoscopic Parameters | Take Value |
|---|---|
| Particle radius (mm) | 0.23~0.299 |
| Damping ratio | 0.7 |
| Porosity | 0.15 |
| Particle density (kg·m−3) | 2661 |
| Particle Contact Modulus (GPa) | 1 × 109 |
| Bonded internal friction angle (°) | 45 |
| Friction coefficient between particles | 0.5 |
| Normal contact stiffness (MPa) | 85.217 |
| Tangential Contact Stiffness (MPa) | 71.014 |
| Normal to Tangential Stiffness Ratio | 1.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, M.; Zhao, G.; Xu, W.; Cheng, X.; Liu, C.; Liu, Z.; Zhu, S.; Wu, X. Influence of Height–Diameter Ratio on Rock Compressive Failure Characteristics and Damage Evolution Law. Energies 2022, 15, 5557. https://doi.org/10.3390/en15155557
Qi M, Zhao G, Xu W, Cheng X, Liu C, Liu Z, Zhu S, Wu X. Influence of Height–Diameter Ratio on Rock Compressive Failure Characteristics and Damage Evolution Law. Energies. 2022; 15(15):5557. https://doi.org/10.3390/en15155557
Chicago/Turabian StyleQi, Minjie, Guangming Zhao, Wensong Xu, Xiang Cheng, Chongyan Liu, Zhixi Liu, Shikui Zhu, and Xukun Wu. 2022. "Influence of Height–Diameter Ratio on Rock Compressive Failure Characteristics and Damage Evolution Law" Energies 15, no. 15: 5557. https://doi.org/10.3390/en15155557
APA StyleQi, M., Zhao, G., Xu, W., Cheng, X., Liu, C., Liu, Z., Zhu, S., & Wu, X. (2022). Influence of Height–Diameter Ratio on Rock Compressive Failure Characteristics and Damage Evolution Law. Energies, 15(15), 5557. https://doi.org/10.3390/en15155557






