Multicriteria Decision Aiding for Planning Renewable Power Production at Moroccan Airports
Abstract
:1. Introduction
- Consolidating the governance of sustainable development;
- Succeeding in the transition towards a green economy;
- Improving the management and development of natural resources and strengthening biodiversity conservation;
- Accelerating the implementation of the national climate change policy;
- Giving particular attention to sensitive areas;
- Promoting human development and reducing social and territorial inequalities;
- Promoting a culture of sustainable development.
- Noise abatement;
- Emission reduction and air quality;
- Energy use;
- Water use;
- Waste management and materials;
- Water pollution reduction;
- Biodiversity preservation and land use.
2. SMAA—Multicriteria Analysis Method
2.1. Basic SMAA Method
- The acceptability indexai. This describes how widely an alternative can be accepted as being best (most preferred). It is computed as the share of different (stochastic) weights that make the alternative xi most preferred. In the group decision making context, we can think of the applied weight distribution to represent the preferences of different DMs (and possible other stakeholders). With this interpretation, the acceptability index can be interpreted as the share of DMs that prefer alternative xi. Inefficient alternatives are never most preferred, which is indicated by the zero acceptability index;
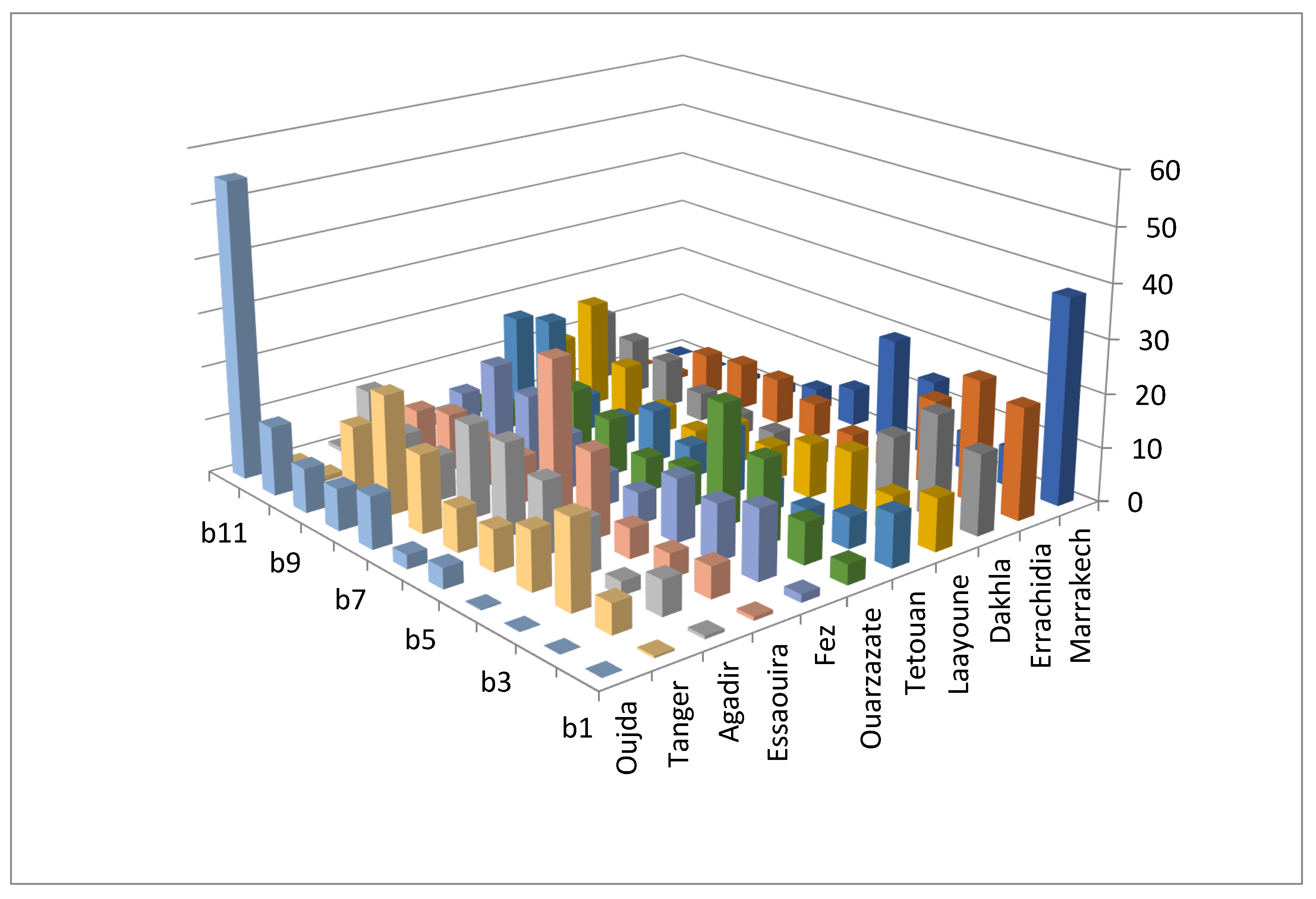
- The rank acceptability index . This is a generalization of the acceptability index for each rank r ∈ {1, …, m}. It describes how widely an alternative obtains rank r. Obviously, = ai. Rank acceptability indices are useful for a more holistic evaluation of all alternatives. In particular, in the problem setting of finding one or a few best alternatives, often no alternatives are clearly superior in terms of the (first rank) acceptability index. In these cases, it makes sense to study the entire rank acceptability profile of each alternative. Good compromise alternatives are those receiving high rank acceptability indices for the top ranks and low indices for the worst ranks. A good way to visualize the rank acceptability indices is to draw them as a 3-dimensional column chart where alternatives (xi) are on one axis, the ranks (r) are on the other axis, and the height of the column is ;
- The pairwise winning indexcik. This describes how widely, considering the stochastic weight distribution, one alternative is better than another. Technically, the pairwise winning index is the probability that alternative i is better than k. Because the pairwise winning index is computed entirely based on the two alternatives, it is not subject to the rank reversal problem. This means that adding or removing other alternatives or changing criteria measurements of other alternatives does not affect the pairwise winning index. The pairwise winning indices can also be used to form a stochastic ranking of the alternatives. This will be described in more detail in Section 2.2;
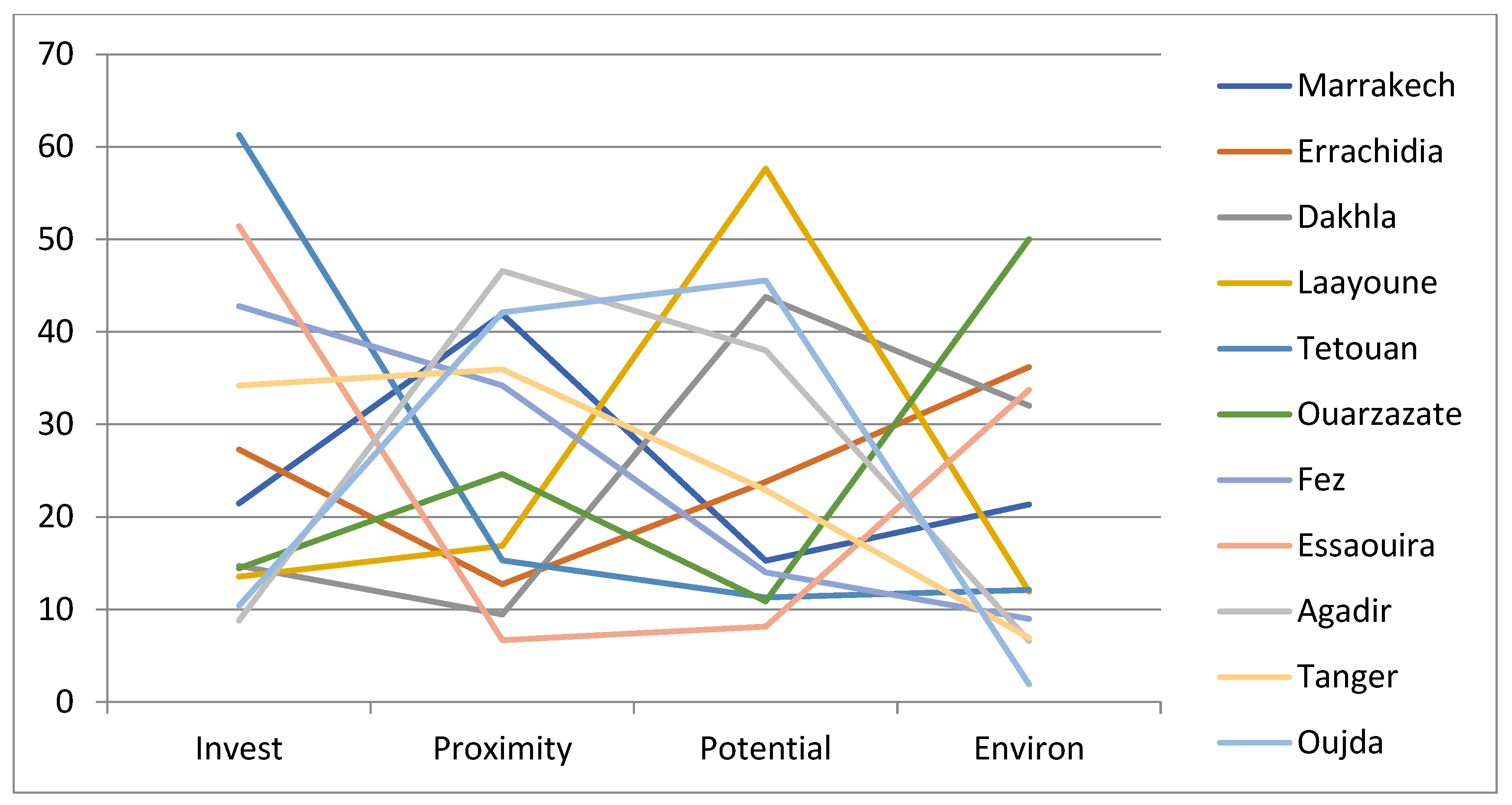
- The central weight vector . This describes what kinds of weights are favourable for the alternative xi, i.e., to make it the most preferable. The central weights can be presented to the DMs in order to help them understand how different weights correspond to different choices. The central weights are undefined for inefficient alternatives. Central weights can be visualized, e.g., by a two-dimensional line chart where alternatives are represented by lines of different colours, the horizontal axis contains the criteria, and the vertical axis contains the weights;
- The confidence factor . This is the probability that an alternative is the most preferred if its central weight vector is selected. The confidence factors measure if the criteria measurements are accurate enough to discern the alternatives reliably. A low confidence factor together with a low acceptability index indicates that an alternative is unlikely the most preferred and can be eliminated when seeking one best alternative.
2.2. Ranking Based on Pairwise Winning Indices
2.3. Implementations of SMAA
3. Problem Description
4. Multicriteria Analysis
4.1. Preliminary Analysis
4.2. First SMAA Model
- Investment cost reflects the cost per MW for wind and solar plants at each respective location; this also includes the land cost, which is higher near larger cities. Investment costs are represented here as dimensionless numbers on a 100-point scale, where 100 is worst and corresponds to the highest costs. Investment costs were evaluated by the Regional Investment Centre of Morocco, which is a public governmental organization;
- Proximity of the production sites to the grid. This criterion measures how well the grid can respond to the transfer needs of renewable power at the location. Proximity was evaluated by a group of ONDA experts on an ordinal scale, i.e., the experts placed the alternatives on different rank levels from the best (1) to the worst (7);
- Potential to market the renewable energy. Potential is related to the zone of economic influence of the airport. Potential is represented here by dimensionless numbers on a 1000-point scale, where 1000 is best and 0 is the worst. Potential was evaluated by the Regional Investment Centre of Morocco;
- Environmental impacts at different locations. Aircraft noise and pollution are typical environmental impacts in air transport. Renewable energy production does not affect the noise and pollution. However, these impacts must still be assessed because it is difficult to develop an airport into a sustainable airport if the noise and pollution levels are high. A group of ONDA experts evaluated the environmental impacts of the alternatives on an ordinal scale in consensus after deliberation. As a result, the experts placed the alternatives on different rank levels from the best (1) to the worst (4).
- Marrakech is the choice if Proximity is emphasized somewhat more than the other criteria, but overall, the weight distribution is still quite balanced (21%, 42%, 15%, 21%);
- Errachidia is most preferred with emphasis on Environ (36%) and a low weight on Proximity (12%);
- Dakhla is favoured by emphasizing Potential (44%) and Environ (32%);
- Tetouan is the choice if Invest (61%) is the most important.
4.3. Second SMAA Model
4.4. Third SMAA Model
5. Discussion
- (1)
- Compute the transitive closure of preference relation in order to identify cyclically dependent strong components of the preference relation. Then, form a partial ranking by assigning the same rank to the cyclically dependent subsets of alternatives;
- (2)
- If a complete ranking is needed, apply the Ranked Pairs procedure for ranking the cyclically winning subsets of alternatives. The Ranked Pairs method considers the pairwise winning indices in strength order, breaking cycles at the weakest pairwise winning indices.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Morocco 2017. Stratégie Nationale de Développement Durable 2017–2030, RAPPORT FINAL. Available online: https://www.greengrowthknowledge.org/sites/default/files/downloads/policy-database/Morocco_Sustainable_Development_Strategy.pdf (accessed on 12 July 2022).
- Nfaoui, H.; Sayigh, A. Sustainability in Energy and Buildings: Research Advances, Special Edition—Mediterranean Green Energy Forum 2013 (MGEF-13); Future Technology Press: Shoreham-by-Sea, UK, 2013; Volume 2, pp. 36–43. Available online: https://nimbusvault.net/publications/koala/sebra (accessed on 12 July 2022).
- Azzioui, A.; Bouhamidi, M.H.; Mouadine, M.; Ettarid, M. Towards a more reliable evaluation of the Morocco’s solar resource. AIP Conf. Proc. 2019, 2126, 190003. [Google Scholar] [CrossRef]
- Afrik21. MOROCCO: Ranked Second Worldwide in Climate Change Control. Afrik 21. Green Economy and Sustainable Growth in Africa, 30 April 2020. Available online: https://www.afrik21.africa/en/morocco-ranked-second-worldwide-in-climate-change-control/ (accessed on 19 May 2022).
- Germanwatch. 2020. Available online: https://www.germanwatch.org/en/indices (accessed on 12 July 2022).
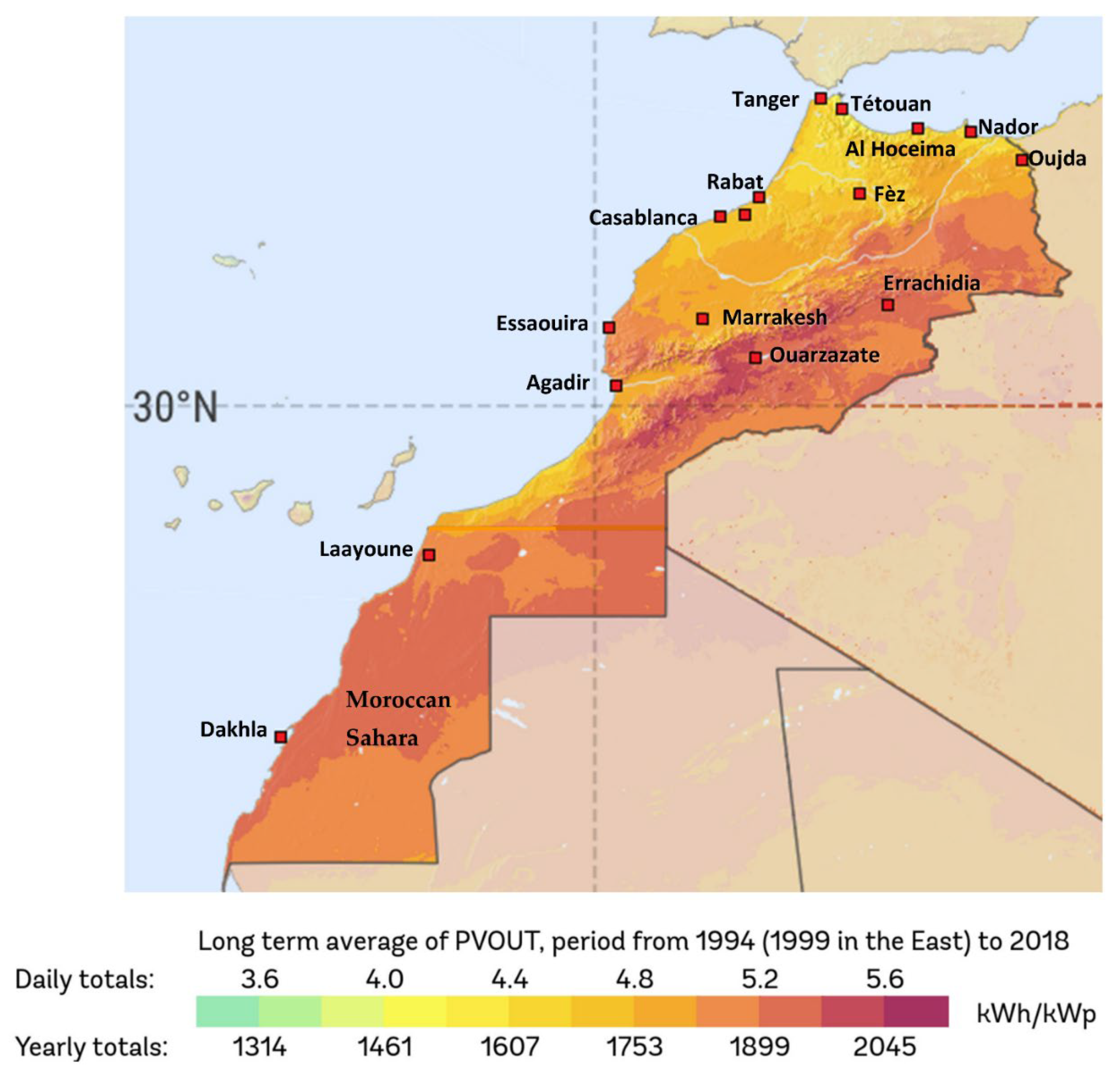
- World Bank. World Bank Group Global Solar Atlas. 2020. Available online: https://globalsolaratlas.info (accessed on 12 July 2022).
- Kılkış, Ş.; Kılkış, Ş. Benchmarking airports based on a sustainability ranking index. J. Clean. Prod. 2016, 130, 248–259. [Google Scholar] [CrossRef]
- Chao, C.C.; Lirn, T.C.; Lin, H.C. Indicators and evaluation model for analyzing environmental protection performance of airports. J. Air Transp. Manag. 2017, 63, 61–70. [Google Scholar] [CrossRef]
- Boussauw, K.; Vanoutrive, T. Flying Green from a Carbon Neutral Airport: The Case of Brussels. Sustainability 2019, 11, 2102. [Google Scholar] [CrossRef] [Green Version]
- Boca Santa, S.L.; Ribeiro, J.M.P.; Mazon, G.; Schneider, J.; Barcelose, R.L.; Osório de Andrade Guerra, J.B.S. A Green Airport model: Proposition based on social and environmental management systems. Sustain. Cities Soc. 2020, 59, 102160. [Google Scholar] [CrossRef]
- Ferrulli, P. Green Airport Design Evaluation (GrADE)—Methods and tools improving infrastructure planning. Transp. Res. Procedia 2016, 14, 3781–3790. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.C.; Tsai, W.H.; Yang, C.H.; Lin, Y.Z. An MCDM approach for selecting green aviation fleet program management strategies under multi-resource limitations. J. Air Transp. Manag. 2018, 68, 76–85. [Google Scholar] [CrossRef]
- Kumar, A.; Aswin, A.; Gupta, H. Evaluating green performance of the airports using hybrid BWM and VIKOR methodology. Tour. Manag. 2020, 76, 103941. [Google Scholar] [CrossRef]
- Wu, D.; Qi, H. Evaluating the economic and ecological impact for small and medium airport subsidies in China. J. Clean. Prod. 2021, 281, 124811. [Google Scholar] [CrossRef]
- Kucukvar, M.; Alawi, K.A.; Abdella, G.M.; Bulak, M.E.; Onat, N.C.; Bulu, M.; Yalçıntaş, M. A frontier-based managerial approach for relative sustainability performance assessment of the world’s airports. Sustain. Dev. 2022, 29, 89–107. [Google Scholar] [CrossRef]
- Kaya, S.K.; Erginel, N. Futuristic airport: A sustainable airport design by integrating hesitant fuzzy SWARA and hesitant fuzzy sustainable quality function deployment. J. Clean. Prod. 2020, 275, 123880. [Google Scholar] [CrossRef]
- Nikoloudis, C.; Aravossis, K.; Strantzali, E.; Chrysanthopoulos, N. A novel multicriteria methodology for evaluating urban development. J. Clean. Prod. 2020, 263, 120796. [Google Scholar] [CrossRef]
- Broniewicz, E.; Ogrodnik, K. A Comparative Evaluation of Multi-Criteria Analysis Methods for Sustainable Transport. Energies 2021, 14, 5100. [Google Scholar] [CrossRef]
- Pinto, G.; Abdollahi, E.; Cappozoli, A.; Savoldi, L.; Lahdelma, R. Optimization and Multicriteria Evaluation of Carbon-neutral Technologies for District Heating. Energies 2019, 12, 1653. [Google Scholar] [CrossRef] [Green Version]
- Bandaru, S.H.; Becerra, V.; Khanna, S.; Espargilliere, H.; Torres Sevilla, L.; Radulovic, J.; Hutchinson, D.; Khusainov, R. A General Framework for Multi-Criteria Based Feasibility Studies for Solar Energy Projects: Application to a Real-World Solar Farm. Energies 2021, 14, 2204. [Google Scholar] [CrossRef]
- Vagiona, D.G. Comparative Multicriteria Analysis Methods for Ranking Sites for Solar Farm Deployment: A Case Study in Greece. Energies 2021, 14, 8371. [Google Scholar] [CrossRef]
- Tsagkari, M.; Roca, J.; Stephanides, P. Sustainability of local renewable energy projects: A comprehensive framework and an empirical analysis on two islands. Sustain. Dev. 2022, 1–14. [Google Scholar] [CrossRef]
- Alhammad, A.; Sun, Q.; Tao, Y. Optimal Solar Plant Site Identification Using GIS and Remote Sensing: Framework and Case Study. Energies 2022, 15, 312. [Google Scholar] [CrossRef]
- Lahdelma, R.; Salminen, P. SMAA-2: Stochastic multicriteria acceptability analysis for group decision making. Oper. Res. 2001, 49, 444–454. [Google Scholar] [CrossRef]
- Salminen, P.; Hokkanen, J.; Lahdelma, R. Comparing multicriteria methods in the context of environmental problems. Eur. J. Oper. Res. 1998, 104, 485–496. [Google Scholar] [CrossRef]
- Sałabun, W.; Watróbski, J.; Shekhovtsov, A. Are MCDA Methods Benchmarkable? A Comparative Study of TOPSIS, VIKOR, COPRAS, and PROMETHEE II Methods. Symmetry 2020, 12, 1549. [Google Scholar] [CrossRef]
- Paradowski, B.; Salabun, W. Are the results of MCDA methods reliable? Selection of materials for Thermal Energy Storage. Procedia Comput. Sci. 2021, 192, 1313–1322. [Google Scholar] [CrossRef]
- Cinelli, M.; Kadziński, M.; Miebs, G.; Gonzalez, M.; Słowiński, R. Recommending multiple criteria decision analysis methods with a new taxonomy-based decision support system. Eur. J. Oper. Res. 2022, 302, 633–651. [Google Scholar] [CrossRef]
- Tervonen, T.; Lahdelma, R. Implementing stochastic multicriteria acceptability analysis. Eur. J. Oper. Res. 2007, 178, 500–513. [Google Scholar] [CrossRef] [Green Version]
- Menou, A.; Benallou, A.; Lahdelma, R.; Salminen, P. Decision support for centralizing cargo at a Moroccan airport hub using stochastic multicriteria acceptability analysis. Eur. J. Oper. Res. 2010, 204, 621–629. [Google Scholar] [CrossRef]
- Tervonen, T.; Figueira, J. A survey on stochastic multicriteria acceptability analysis methods. J. Multi-Criteria Decis. Anal. 2008, 15, 1–14. [Google Scholar] [CrossRef]
- Lahdelma, R.; Salminen, P. Stochastic multicriteria acceptability analysis (SMAA). In Trends in Multiple Criteria Decision Analysis; Ehrgott, M., Figueira, J.R., Greco, S., Eds.; International Series in Operations Research and Management Science; Springer: Berlin, Germany, 2010; Volume 142. [Google Scholar]
- Pelissari, R.; Oliveira, M.C.; Ben Amor, S.; Kandakoglu, A.; Helleno, A.L. SMAA methods and their applications: A literature review and future research directions. Ann. Oper. Res. 2019, 293, 433–493. [Google Scholar] [CrossRef]
- Lahdelma, R.; Hokkanen, J.; Salminen, P. SMAA—Stochastic multiobjective acceptability analysis. Eur. J. Oper. Res. 1998, 106, 137–143. [Google Scholar] [CrossRef]
- Lahdelma, R.; Salminen, P. The shape of the utility or value function in stochastic multicriteria acceptability analysis. OR Spectr. 2012, 34, 785–802. [Google Scholar] [CrossRef]
- Lahdelma, R.; Miettinen, K.; Salminen, P. Ordinal criteria in stochastic multicriteria acceptability analysis (SMAA). Eur. J. Oper. Res. 2003, 147, 117–127. [Google Scholar] [CrossRef]
- Montes, I.; Rademaker, M.; Pérez-Fernández, R.; de Baets, B. A correspondence between voting procedures and stochastic orderings. Eur. J. Oper. Res. 2020, 285, 977–987. [Google Scholar] [CrossRef]
- Kahn, A.B. Topological sorting of large networks. Commun. ACM 1962, 5, 558–562. [Google Scholar] [CrossRef]
- Condorcet, M. An essay on the application of probability theory to plurality decision making: An election between three candidates. In The Political Theory of Concordet; Sommerlad, F., McLean, I., Eds.; University of Oxford: Oxford, UK, 1989. [Google Scholar]
- Nuutila, E. Efficient Transitive Closure Computation in Large Digraphs. Ph.D. Thesis, Helsinki University of Technology, Helsinki, Finland, 1995; 124p. [Google Scholar]
- Tideman, T.N. Independence of clones as a criterion for voting rules. Soc. Choice Welf. 1987, 4, 185–206. [Google Scholar] [CrossRef]
- Nurmi, H. Comparing Voting Systems; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Tervonen, T. SMAA.fi—Open Source Decision Aiding Software for Real-Life Applications. 2009. Available online: http://smaa.fi/jsmaa (accessed on 19 July 2022).
- Ortega, S.; Manana, M. Energy Research in Airports: A Review. Energies 2016, 9, 349. [Google Scholar] [CrossRef] [Green Version]
- Akyüz, M.K.; Kafali, H.; Altuntaş, Ö. An analysis on energy performance indicator and GWP at Airports: A case study. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 43, 2402–2418. [Google Scholar] [CrossRef]
- World Bank. World Bank Group Global Wind Atlas. 2020. Available online: https://globalwindatlas.info (accessed on 12 July 2022).
- Lahdelma, R.; Makkonen, S.; Salminen, P. Two ways to handle dependent uncertainties in multi-criteria decision problems. Omega 2009, 37, 79–92. [Google Scholar] [CrossRef]

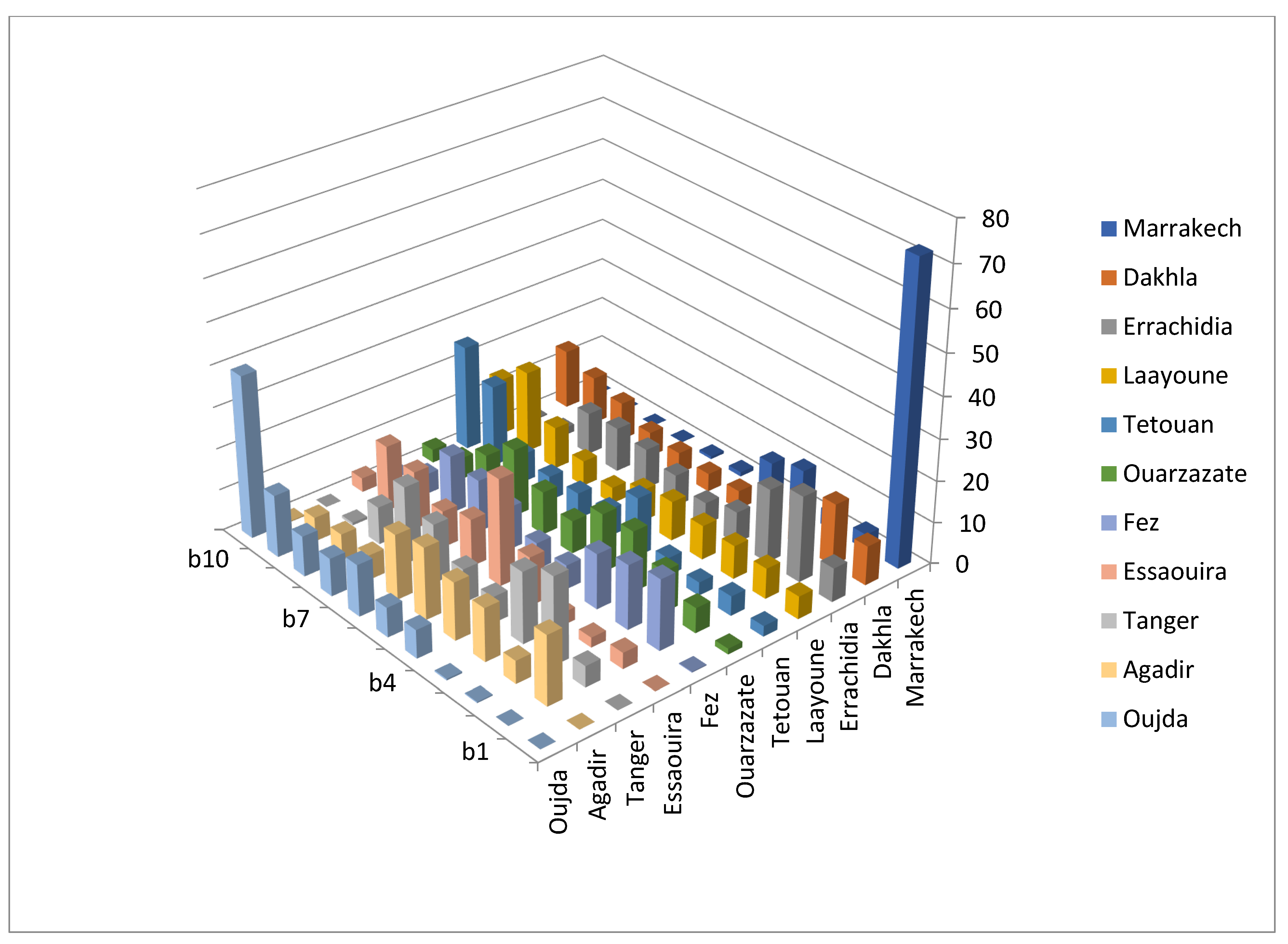

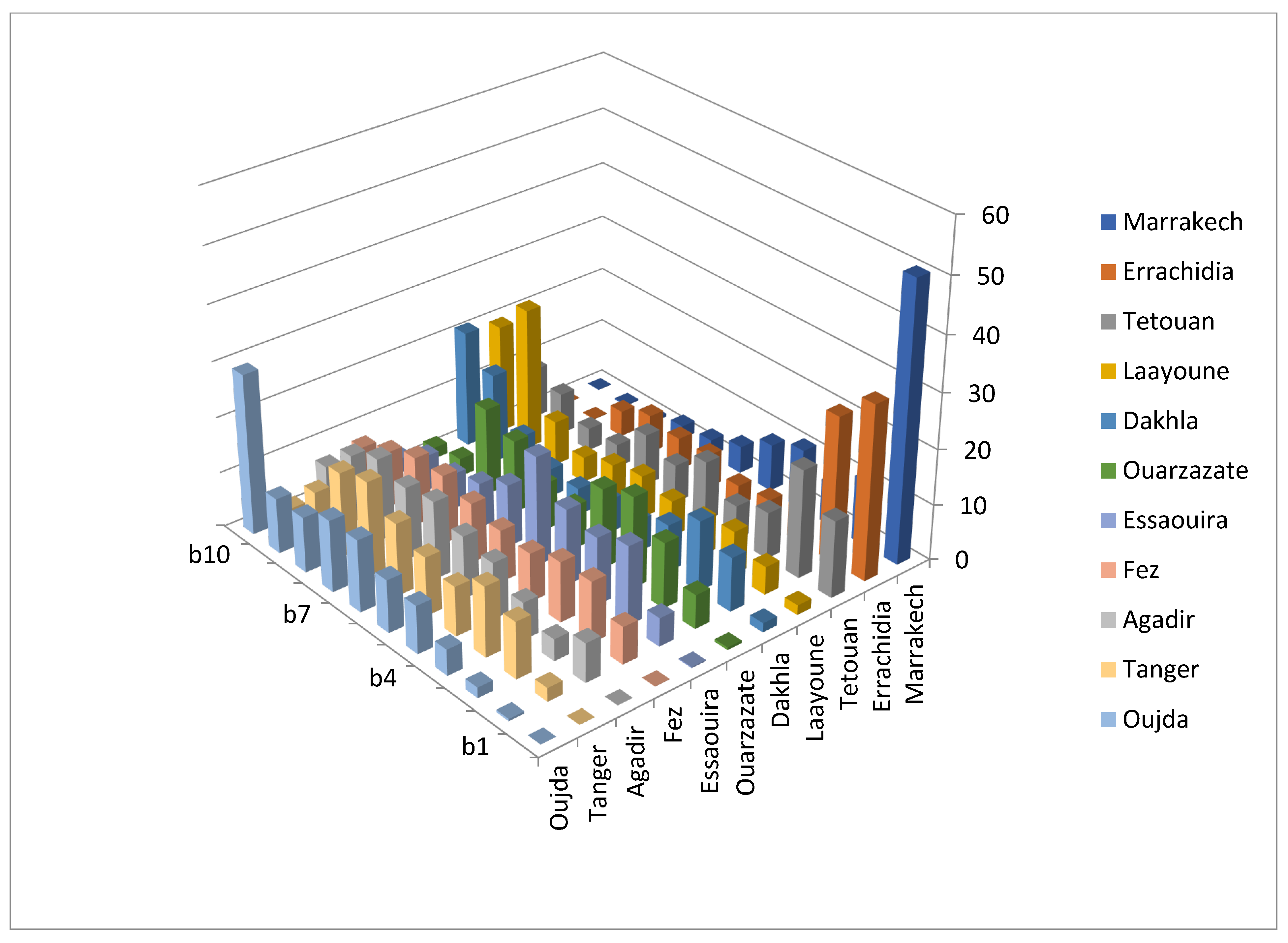

| Airport | PAX (Pass./a) | Electric Power Demand (MWh) | EPI (kWh/PAX) | Annual Solar Radiation (kWh/m2) at Optimal Angle | Average Wind Speed (m/s) 100 m Altitude |
|---|---|---|---|---|---|
| Agadir | 2,011,718 | 3542 | 1.76 | 2268 | 5.23 |
| Al Hoceima | 92,121 | 591 | 6.42 | 2034 | 4.48 |
| Casablanca | 10,306,293 | 23,166 | 2.25 | 2142 | 5.10 |
| Dakhla | 257,411 | 446 | 1.73 | 2339 | 9.87 |
| Errachidia | 53,366 | 325 | 6.09 | 2422 | 5.73 |
| Essaouira | 120,435 | 568 | 4.72 | 2315 | 6.83 |
| Fez | 1,419,566 | 3028 | 2.13 | 2139 | 4.00 |
| Laayoune | 255,610 | 488 | 1.91 | 2350 | 4.00 |
| Marrakech | 6,422,292 | 11,492 | 1.79 | 2271 | 3.09 |
| Nador | 772,371 | 1231 | 1.59 | 2092 | 4.32 |
| Ouarzazate | 136,007 | 456 | 3.35 | 2482 | 4.24 |
| Oujda | 702,631 | 2894 | 4.12 | 2148 | 4.74 |
| Rabat | 1,100,846 | 3205 | 2.91 | 2114 | 4.24 |
| Tanger | 1,359,364 | 2934 | 2.16 | 2110 | 7.49 |
| Tetouan | 39,982 | 272 | 6.80 | 1960 | 6.68 |
| Airport | Practical Potential for Renewable Energy Production | Connectivity with Wind Power | Connectivity with Solar Power | Connectivity with National Power Grid |
|---|---|---|---|---|
| Agadir | XXX | XX | XXX | XXX |
| Al Hoceima | X | - | X | XX |
| Casablanca | XXX | X | X | XXX |
| Dakhla | X | XXX | XXX | XX |
| Errachidia | X | - | XXX | XX |
| Essaouira | XX | XXX | X | XXX |
| Fès | XX | XX | X | XXX |
| Laayoune | XX | XX | XXX | XX |
| Marrakesh | XXX | - | XXX | XXX |
| Nador | XX | X | X | XX |
| Ouarzazate | X | - | XXX | XX |
| Oujda | XX | - | XX | XXX |
| Rabat | XXX | - | - | XXX |
| Tanger | XXX | XXX | X | XXX |
| Tétouan | XX | XXX | X | XXX |
| First SMAA | Invest | Proximity | Potential | Environ | ||
| Second SMAA | Invest | Proximity | Potential | Environ | Elec | |
| Third SMAA | Invest | Proximity | Potential | Environ | Elec | EPI |
| Airport | Min | Min | Max | Min | Max | Max |
| Agadir | 70 | 2 | 300 | 3 | 3542 | 1.76 |
| Dakhla | 85 | 7 | 900 | 1 | 446 | 1.73 |
| Errachidia | 75 | 6 | 800 | 1 | 325 | 6.09 |
| Essaouira | 55 | 4 | 200 | 2 | 568 | 4.72 |
| Fez | 50 | 2 | 150 | 3 | 3028 | 2.13 |
| Laayoune | 90 | 6 | 940 | 2 | 488 | 1.91 |
| Marrakesh | 60 | 1 | 200 | 2 | 11,492 | 1.79 |
| Ouarzazate | 80 | 5 | 500 | 1 | 456 | 3.36 |
| Oujda | 75 | 4 | 400 | 4 | 2894 | 4.12 |
| Tanger | 55 | 2 | 200 | 3 | 2934 | 2.16 |
| Tetouan | 35 | 3 | 50 | 3 | 272 | 6.81 |
| Uncertainty | ±5 | ordinal | ±25 | ordinal | ±10% | ±14% |
| Alt | Marrakech | Errachidia | Dakhla | Ouarzazate | Tanger | Fez | Essaouira | Laayoune | Agadir | Tetouan | Oujda |
| Marrakech | 0 | 51 | 56 | 60 | 92 | 90 | 89 | 66 | 92 | 85 | 95 |
| Errachidia | 49 | 0 | 75 | 75 | 64 | 63 | 68 | 81 | 68 | 66 | 89 |
| Dakhla | 44 | 25 | 0 | 52 | 57 | 57 | 58 | 63 | 61 | 59 | 80 |
| Ouarzazate | 40 | 25 | 48 | 0 | 58 | 58 | 63 | 61 | 62 | 62 | 88 |
| Tanger | 8 | 36 | 43 | 42 | 0 | 56 | 53 | 49 | 59 | 65 | 90 |
| Fez | 10 | 37 | 43 | 42 | 44 | 0 | 52 | 49 | 57 | 67 | 88 |
| Essaouira | 11 | 32 | 42 | 37 | 47 | 48 | 0 | 52 | 53 | 56 | 87 |
| Laayoune | 34 | 19 | 37 | 39 | 51 | 51 | 48 | 0 | 54 | 54 | 80 |
| Agadir | 8 | 32 | 39 | 38 | 41 | 43 | 47 | 46 | 0 | 58 | 93 |
| Tetouan | 15 | 34 | 41 | 38 | 35 | 33 | 44 | 46 | 42 | 0 | 81 |
| Oujda | 5 | 11 | 20 | 12 | 10 | 12 | 13 | 20 | 7 | 19 | 0 |
| Alt | Marrakech | Errachidia | Agadir | Tanger | Fez | Dakhla | Ouarzazate | Essaouira | Laayoune | Tetouan | Oujda |
| Marrakech | 0 | 77 | 99 | 99 | 98 | 78 | 85 | 99 | 85 | 97 | 99 |
| Errachidia | 23 | 0 | 56 | 55 | 54 | 72 | 74 | 67 | 79 | 66 | 80 |
| Agadir | 1 | 44 | 0 | 56 | 53 | 49.7 | 53 | 67 | 57 | 77 | 96 |
| Tanger | 1 | 45 | 44 | 0 | 49 | 50.2 | 53 | 70 | 57 | 83 | 90 |
| Fez | 2 | 46 | 47 | 50.6 | 0 | 50.7 | 53 | 70 | 58 | 87 | 88 |
| Dakhla | 22 | 28 | 50.3 | 49.8 | 49 | 0 | 52 | 58 | 63 | 60 | 72 |
| Ouarzazate | 15 | 26 | 47 | 47 | 47 | 48 | 0 | 62 | 61 | 63 | 75 |
| Essaouira | 1 | 33 | 33 | 30 | 30 | 42 | 38 | 0 | 52 | 59 | 72 |
| Laayoune | 15 | 21 | 43 | 43 | 42 | 37 | 39 | 48 | 0 | 55 | 69 |
| Tetouan | 3 | 34 | 23 | 17 | 13 | 40 | 37 | 41 | 45 | 0 | 66 |
| Oujda | 1 | 20 | 4 | 10 | 12 | 28 | 25 | 28 | 31 | 34 | 0 |
| Alt | Marrakech | Errachidia | Tetouan | Essaouira | Ouarzazate | Tanger | Fez | Dakhla | Agadir | Laayoune | Oujda |
| Marrakech | 0 | 58 | 74 | 82 | 77 | 98 | 97 | 78 | 99 | 84 | 93 |
| Errachidia | 42 | 0 | 62 | 76 | 90 | 73 | 72 | 96 | 75 | 96 | 87 |
| Tetouan | 26 | 38 | 0 | 64 | 58 | 65 | 65 | 61 | 65 | 67 | 82 |
| Essaouira | 18 | 24 | 36 | 0 | 53 | 59.1 | 59 | 61 | 61 | 69 | 77 |
| Ouarzazate | 23 | 10 | 42 | 47 | 0 | 56.8 | 56 | 67 | 60 | 74 | 69 |
| Tanger | 2 | 27 | 35 | 40.9 | 43.2 | 0 | 51 | 52 | 59 | 59 | 70 |
| Fez | 3 | 28 | 35 | 41 | 44 | 49 | 0 | 53 | 58 | 59 | 70 |
| Dakhla | 22 | 4 | 39 | 39 | 33 | 48 | 47 | 0 | 50 | 59 | 58 |
| Agadir | 1 | 25 | 35 | 39 | 40 | 41 | 42 | 50 | 0 | 56 | 68 |
| Laayoune | 16 | 4 | 33 | 31 | 26 | 41 | 41 | 41 | 44 | 0 | 54 |
| Oujda | 7 | 13 | 18 | 23 | 31 | 30 | 30 | 42 | 32 | 46 | 0 |
| Airport Rankings | First Model | Second Model | Third Model |
|---|---|---|---|
| Marrakesh | 1 | 1 | 1 |
| Errachidia | 2 | 2 | 2 |
| Tetouan | 10 | 10 | 3 |
| Essaouira | 5–8 (7) | 8 | 4 |
| Ouarzazate | 4 | 7 | 5 |
| Tanger | 5–8 (5) | 3–6 (4) | 6 |
| Fez | 5–8 (6) | 3–6 (5) | 7 |
| Dakhla | 3 | 3–6 (6) | 8 |
| Agadir | 9 | 3–6 (3) | 9 |
| Laayoune | 5–8 (8) | 9 | 10 |
| Oujda | 11 | 11 | 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menou, A.; Lahdelma, R.; Salminen, P. Multicriteria Decision Aiding for Planning Renewable Power Production at Moroccan Airports. Energies 2022, 15, 5271. https://doi.org/10.3390/en15145271
Menou A, Lahdelma R, Salminen P. Multicriteria Decision Aiding for Planning Renewable Power Production at Moroccan Airports. Energies. 2022; 15(14):5271. https://doi.org/10.3390/en15145271
Chicago/Turabian StyleMenou, Abdellah, Risto Lahdelma, and Pekka Salminen. 2022. "Multicriteria Decision Aiding for Planning Renewable Power Production at Moroccan Airports" Energies 15, no. 14: 5271. https://doi.org/10.3390/en15145271
APA StyleMenou, A., Lahdelma, R., & Salminen, P. (2022). Multicriteria Decision Aiding for Planning Renewable Power Production at Moroccan Airports. Energies, 15(14), 5271. https://doi.org/10.3390/en15145271






