Artificial Electric Field Algorithm-Pattern Search for Many-Criteria Networks Reconfiguration Considering Power Quality and Energy Not Supplied
Abstract
1. Introduction
- Network automation based on optimal reconfiguration;
- Network reconfiguration with many-criteria decision-making optimization;
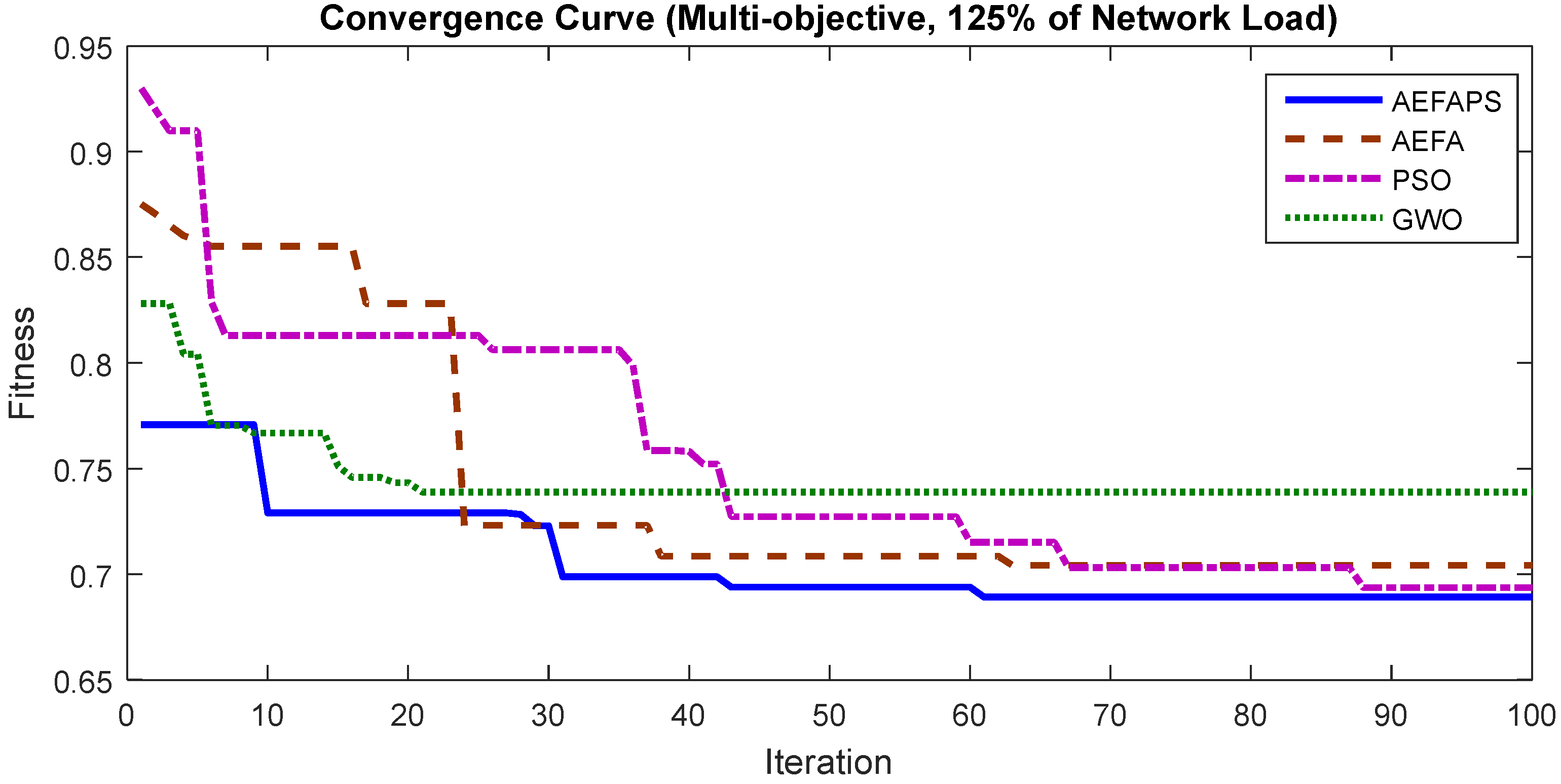
- Using artificial electric field algorithm-pattern search (AEFAPS) for problem-solving;
- Using pattern search in the suggested algorithm to improve global and local searches;
- Superiority of AEFAPS compared with conventional AEFA, GWO, and PSO methods.
2. Problem Formulation
2.1. Objective Function
2.1.1. Power Losses
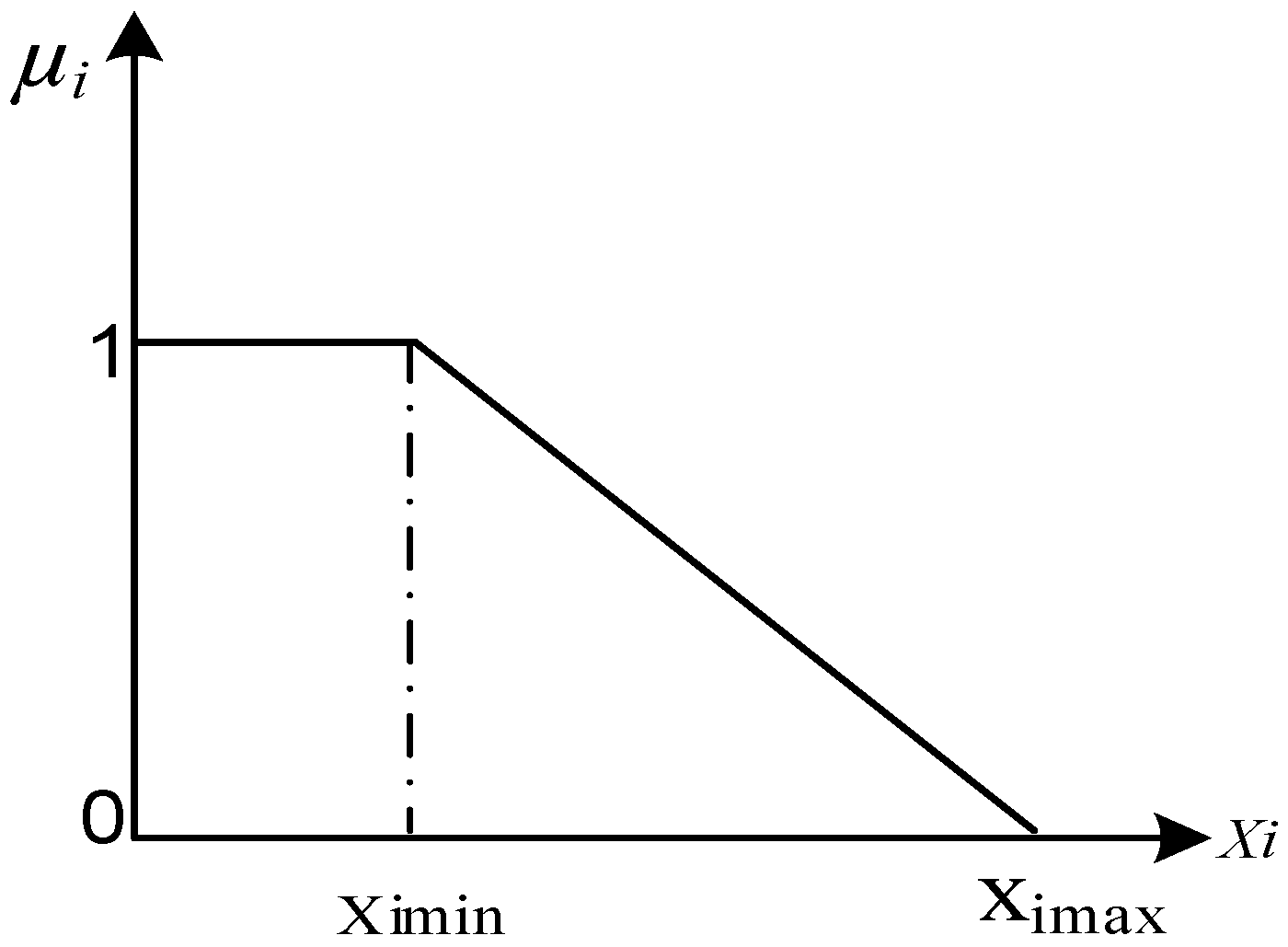
2.1.2. Voltage Sag
2.1.3. Voltage Unbalance
2.1.4. Reliability
2.2. Constraints
- Power balance
- Voltage constraint
- Lines constraint
- Voltage unbalance constraint
- Voltage sag constraint
- Network radiality
2.3. Many-Criteria Decision-Making Optimization
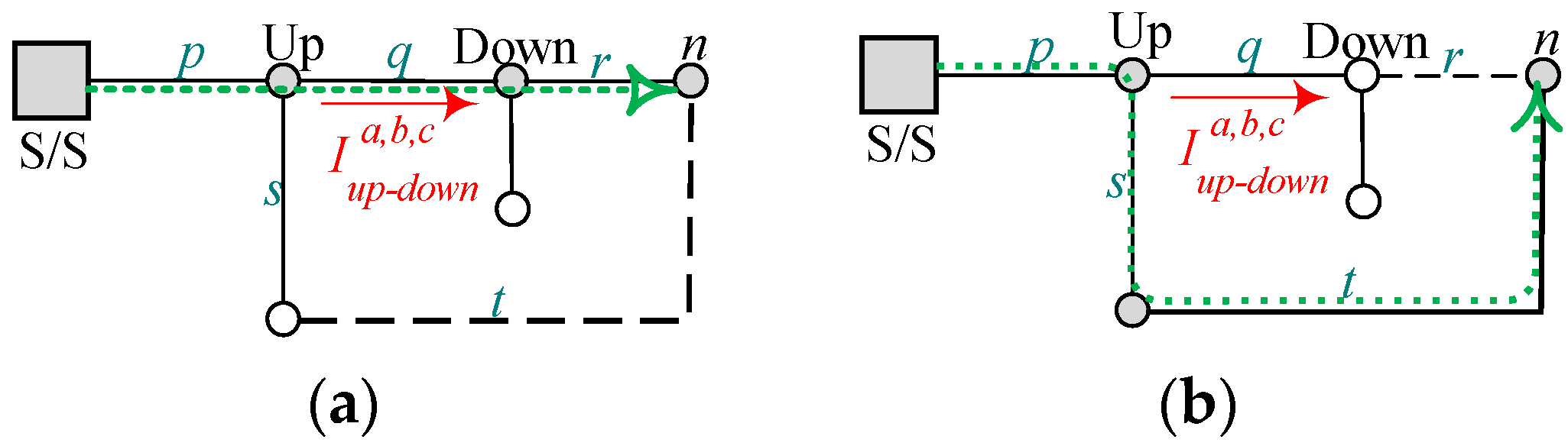
3. Power Flow and Branch Exchange Method
4. Proposed Optimizer
4.1. Overview of AEFA
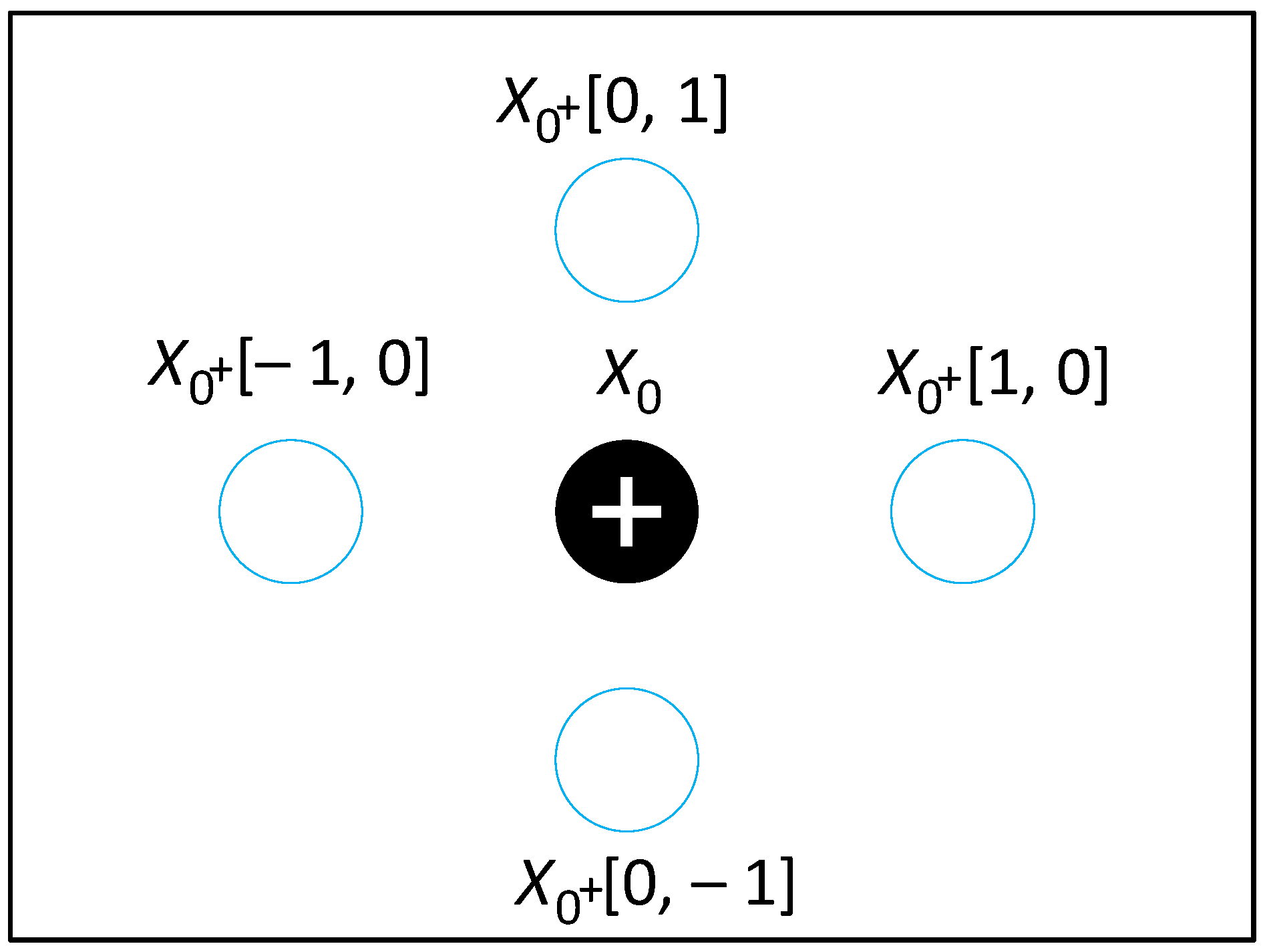
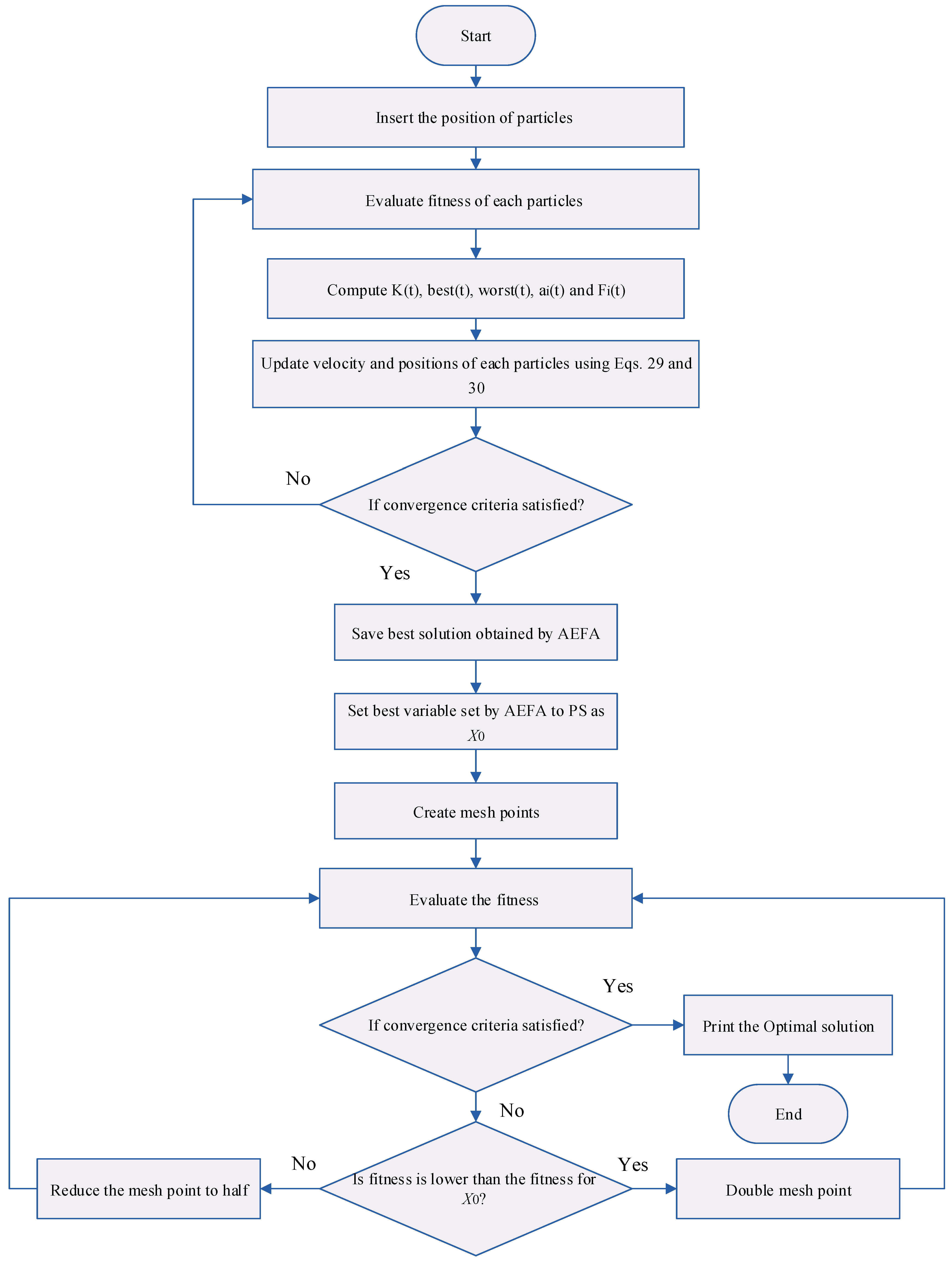
4.2. Overview of AEFAPS
- (a)
- The size of the mesh is lowering its defined value.
- (b)
- The iteration number reaches the predetermined value.
- (c)
- The distance between points determined in a desirable selection and the point determined in the following desirable selection is lower than the allowable value.
- (d)
- Changing the fitness from a desirable selection to another successful selection is lower than the allowable value.
4.3. The AEFAPS Method Implementation
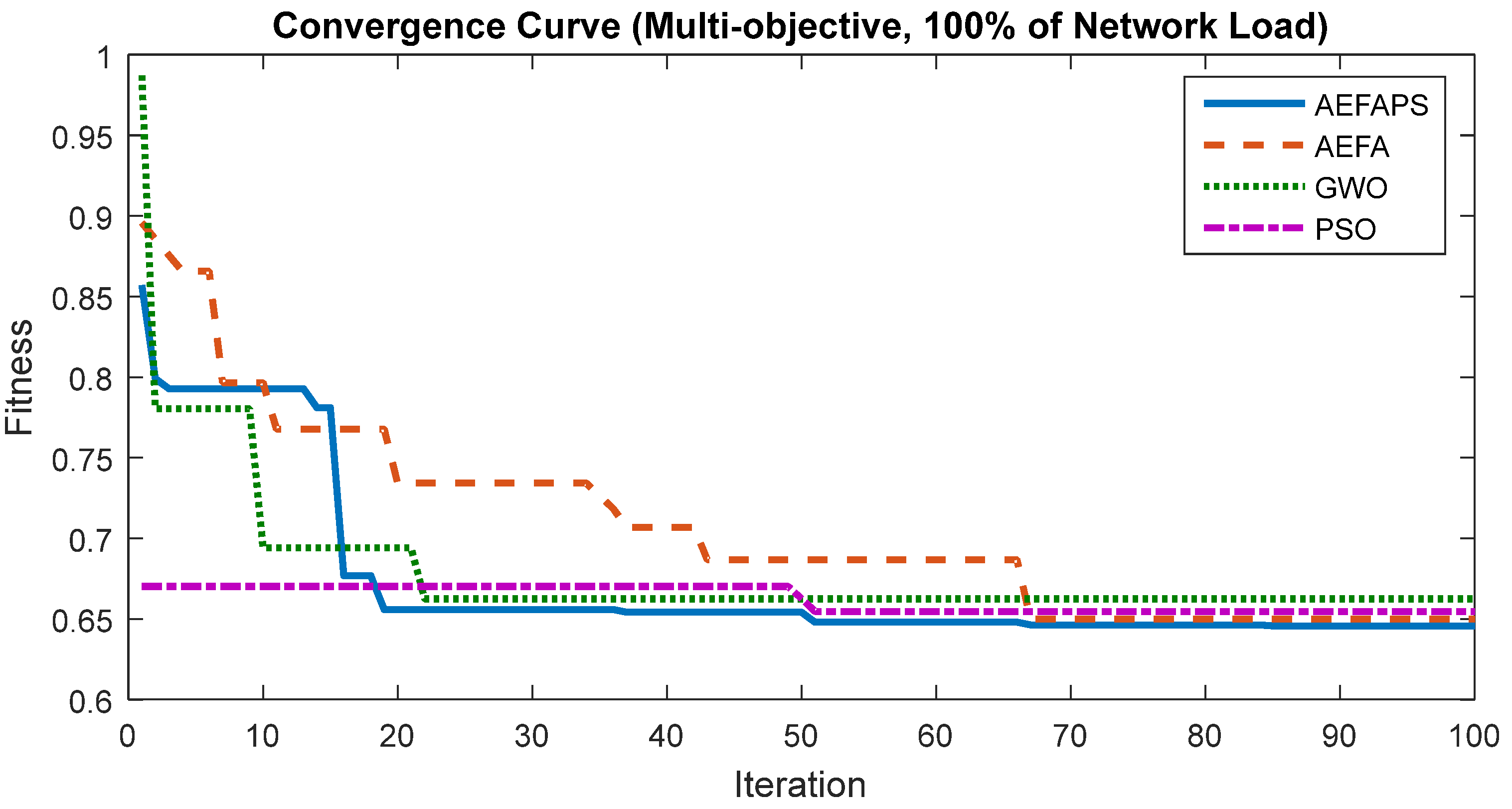
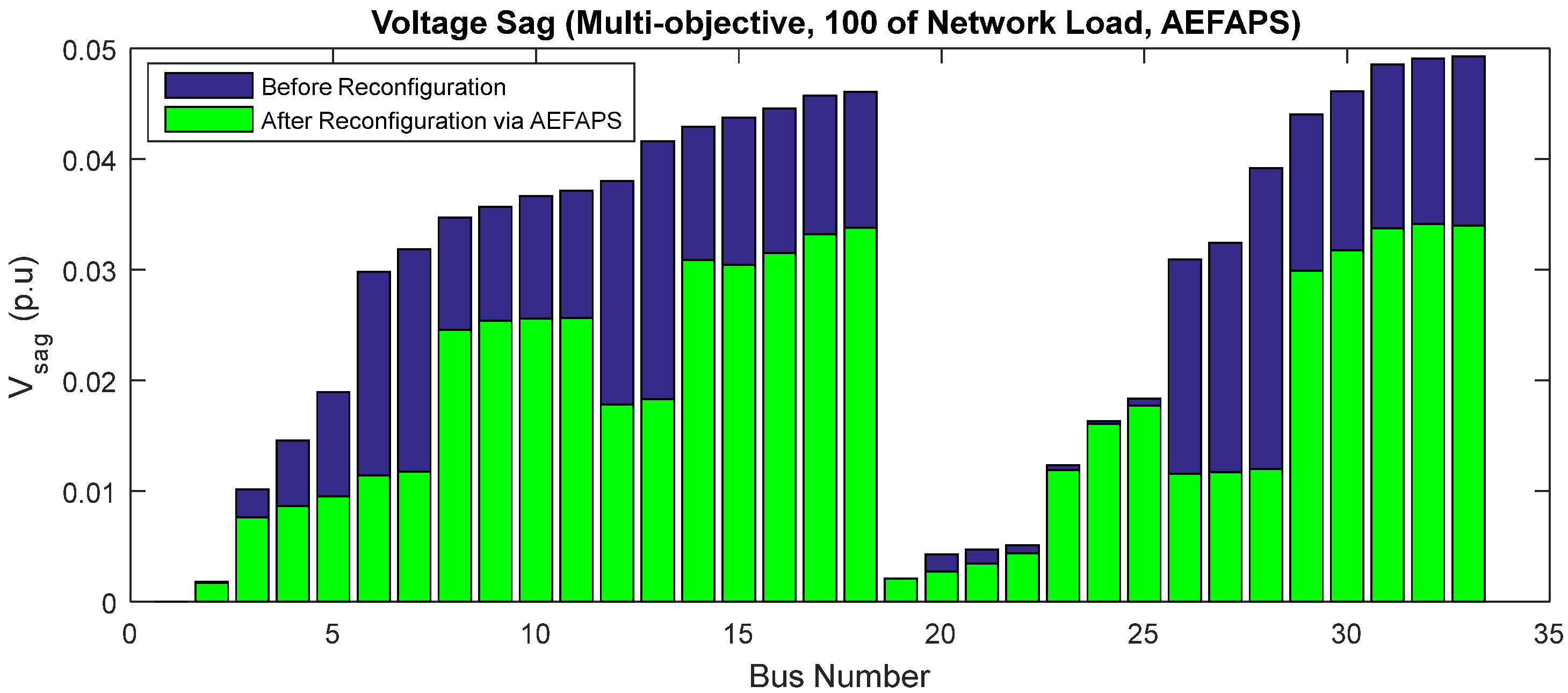
5. Results and Discussion
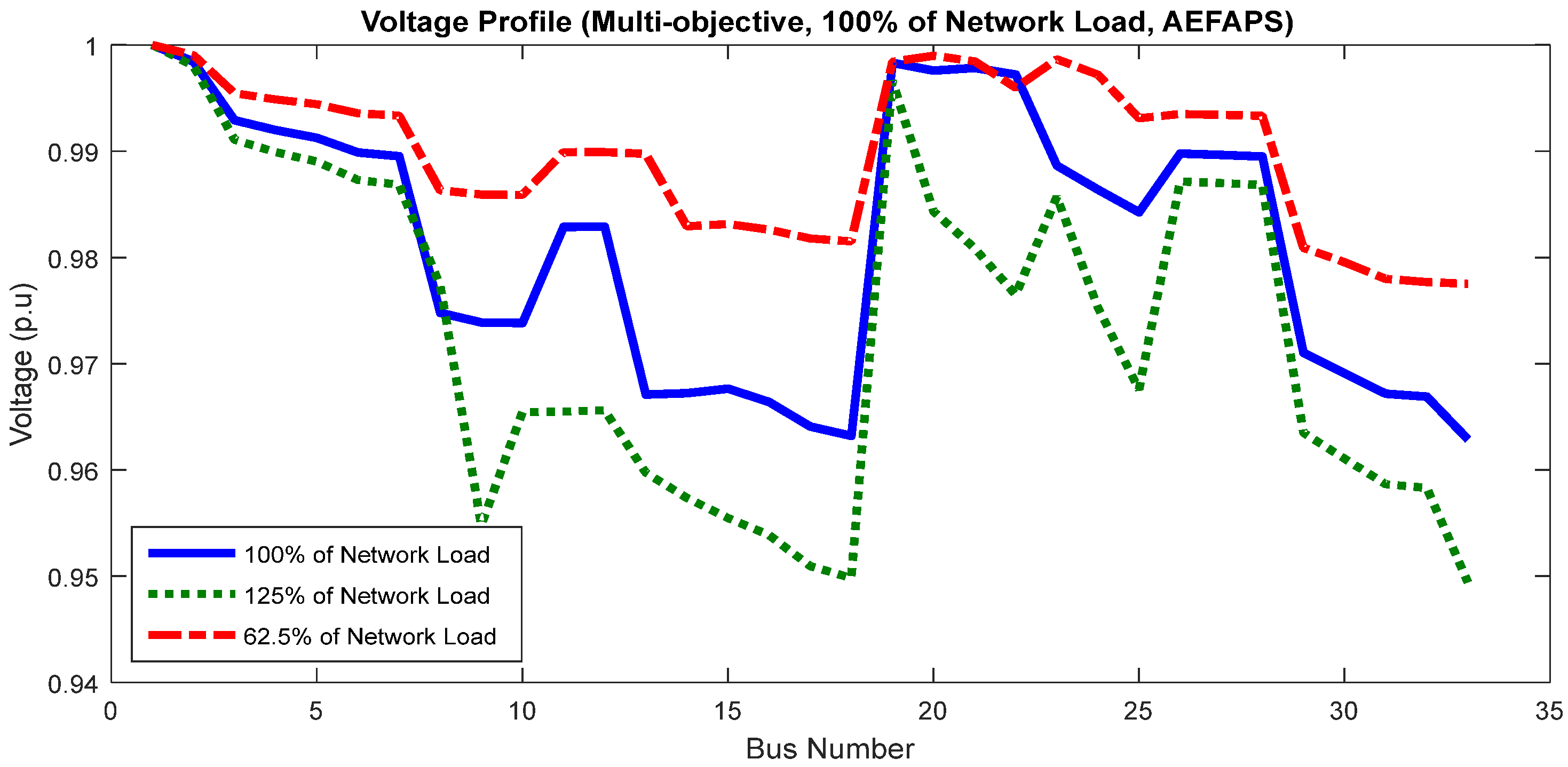
5.1. Results of Unbalanced 33-Bus Network
5.1.1. Effect of Load Increasing
5.1.2. Effect of Load Decreasing
5.1.3. Comparison of the Effect of Load Variations
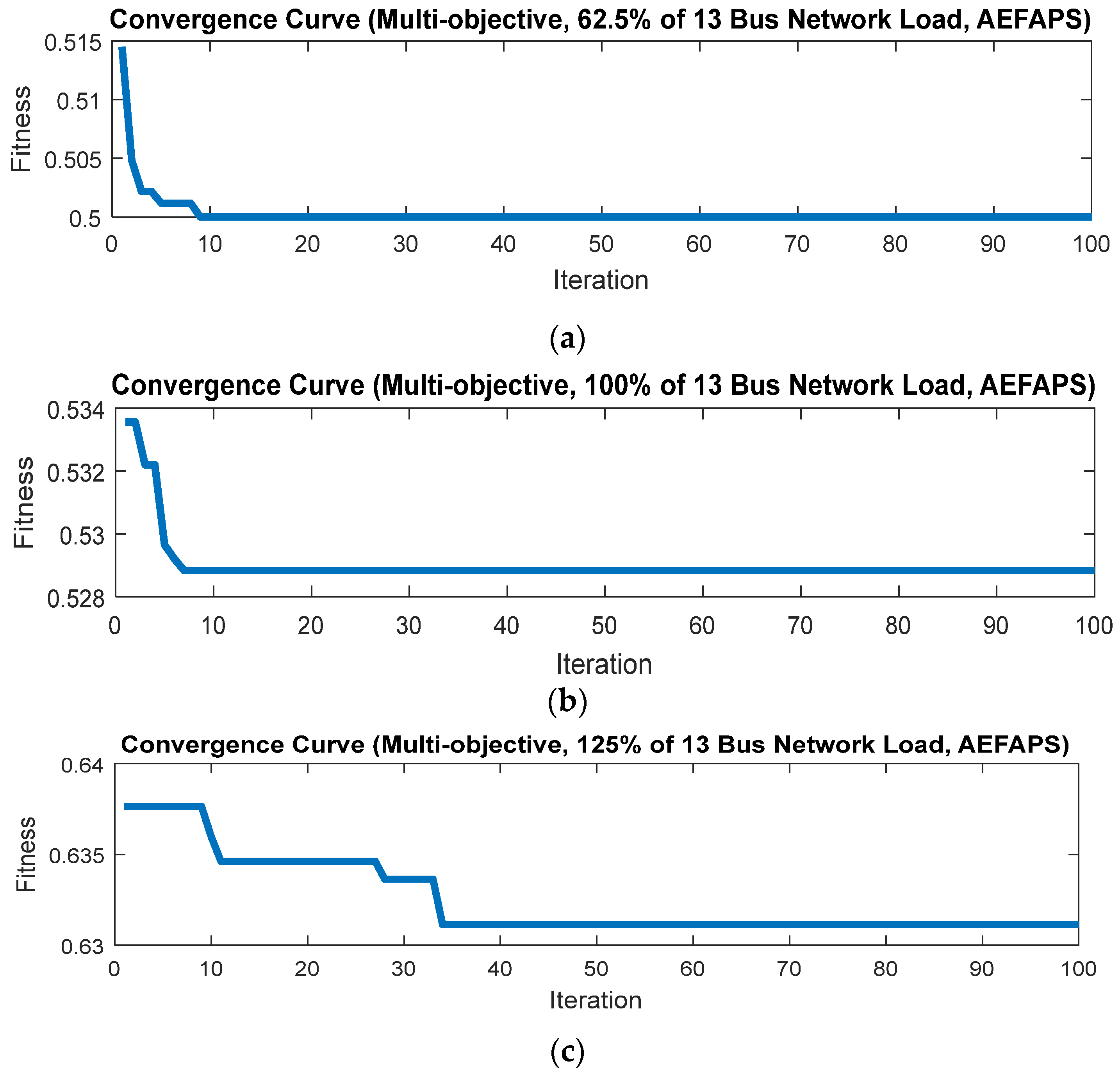
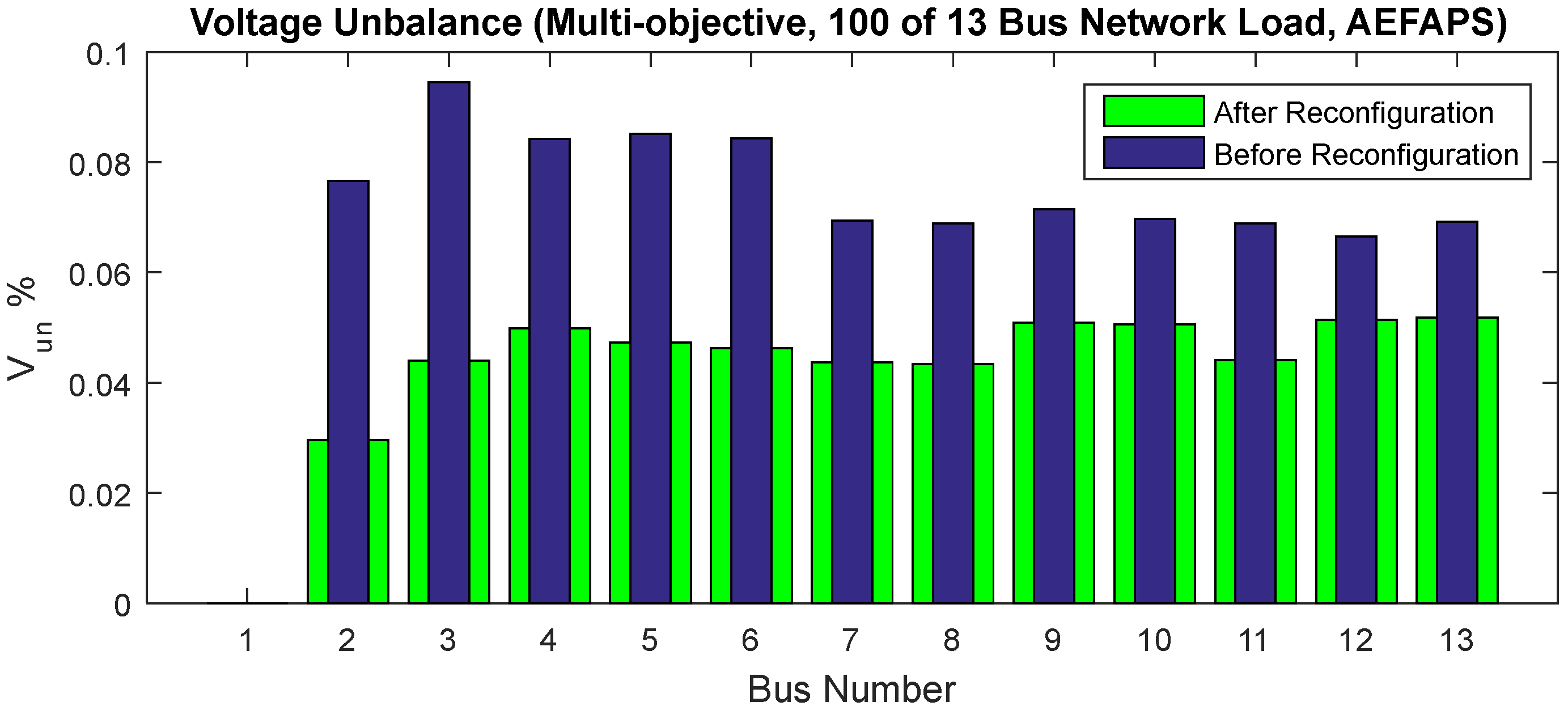
5.2. Results of Unbalanced 13-Bus Network
5.3. Comparison the Results with Previous Studies
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Power loss | |
| Ohmic resistance of the k-th line | |
| Reactance of the k-th line | |
| Voltage of bus i | |
| Voltage of bus j | |
| Current of the k-th line | |
| Bus voltage i in the condition of the fault in bus j | |
| Average voltage sag | |
| Fault current for a fault at bus p | |
| Admittance matrix with fault | |
| S-impedance of bus p | |
| Pre-fault voltage at bus p | |
| Negative sequence voltage of bus i | |
| Positive sequence voltage of bus i | |
| Average of voltage unbalance | |
| Energy not supplied | |
| Average of active power at load point i | |
| Unavailability of load point i | |
| Line outage rate | |
| Average outage time of load point i | |
| Minimum voltage | |
| Maximum voltage | |
| Maximum allowable current | |
| Maximum voltage unbalance | |
| Minimum voltage sag | |
| Index matrix | |
| Membership function of loss | |
| Membership function of ENS | |
| Membership function of voltage unbalance | |
| Membership function of voltage sag | |
| Voltage of each phase of the bus | |
| Branch impedance of each phase of the bus | |
| Current of the line between up and down buses | |
| Best fitness position achieved by any particle i | |
| Pbest | Optimal fitness |
| Qi | Charged particles of i |
| Qj | Charged particles of j |
| K | Constant of Coulomb |
| Rij | Euclidean distance among two charged particles, i and j |
| N | Number of particles |
| Velocity of the charged particle | |
| Initial point | |
| AEFAPS | Artificial electric field algorithm-pattern search |
| AEFA | Artificial electric field algorithm |
| PS | Pattern search |
| ENS | Energy not supplied |
| PSO | Particle swarm optimization |
| GWO | Grey wolf optimizer |
| DG | Distributed generation |
| ACO | Ant colony optimization |
| TS | Taboo search |
| ACSA | Adaptive cuckoo search algorithm |
| CSA | Cuckoo search algorithm |
| BA | Bat algorithm |
| FA | Firefly algorithm |
| GA | Genetic algorithm |
References
- Naderipour, A.; Abdul-Malek, Z.; Vahid, M.Z.; Seifabad, Z.M.; Hajivand, M.; Arabi-Nowdeh, S. Optimal, Reliable and Cost-Effective Framework of Photovoltaic-Wind-Battery Energy System Design Considering Outage Concept Using Grey Wolf Optimizer Algorithm—Case Study for Iran. IEEE Access 2019, 7, 182611–182623. [Google Scholar] [CrossRef]
- Moghaddam, M.J.H.; Kalam, A.; Shi, J.; Nowdeh, S.A.; Gandoman, F.H.; Ahmadi, A. A New Model for Reconfiguration and Distributed Generation Allocation in Distribution Network Considering Power Quality Indices and Network Losses. IEEE Syst. J. 2020, 14, 3530–3538. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdullah, A.; Marzbali, M.H.; Nowdeh, S.A. An improved corona-virus herd immunity optimizer algorithm for network reconfiguration based on fuzzy multi-criteria approach. Expert Syst. Appl. 2021, 187, 115914. [Google Scholar] [CrossRef] [PubMed]
- Shaheen, A.; Elsayed, A.; El-Sehiemy, R.A.; Abdelaziz, A.Y. Equilibrium optimization algorithm for network reconfiguration and distributed generation allocation in power systems. Appl. Soft Comput. 2020, 98, 106867. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdul-Malek, Z.; Nowdeh, S.A.; Ramachandaramurthy, V.K.; Kalam, A.; Guerrero, J. Optimal allocation for combined heat and power system with respect to maximum allowable capacity for reduced losses and improved voltage profile and reliability of microgrids considering loading condition. Energy 2020, 196, 117124. [Google Scholar] [CrossRef]
- Aziz, T.; Lin, Z.; Waseem, M.; Liu, S. Review on optimization methodologies in transmission network reconfiguration of power systems for grid resilience. Int. Trans. Electr. Energy Syst. 2020, 31, e12704. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdul-Malek, Z.; Ramachandaramurthy, V.K.; Kalam, A.; Miveh, M.R. Hierarchical control strategy for a three-phase 4-wire microgrid under unbalanced and nonlinear load conditions. ISA Trans. 2019, 94, 352–369. [Google Scholar] [CrossRef]
- Moghaddam, M.J.H.; Kalam, A.; Nowdeh, S.A.; Ahmadi, A.; Babanezhad, M.; Saha, S. Optimal sizing and energy management of stand-alone hybrid photovoltaic/wind system based on hydrogen storage considering LOEE and LOLE reliability indices using flower pollination algorithm. Renew. Energy 2018, 135, 1412–1434. [Google Scholar] [CrossRef]
- Hadidian-Moghaddam, M.J.; Nowdeh, S.A.; Bigdeli, M. Optimal sizing of a stand-alone hybrid photovoltaic/wind system using new grey wolf optimizer considering reliability. J. Renew. Sustain. Energy 2016, 8, 035903. [Google Scholar] [CrossRef]
- Gerez, C.; Costa, E.C.M.; Filho, A.J.S. Distribution Network Reconfiguration Considering Voltage and Current Unbalance Indexes and Variable Demand Solved through a Selective Bio-Inspired Metaheuristic. Energies 2022, 15, 1686. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Elsayed, A.M.; El-Sehiemy, R.A.; Kamel, S.; Ghoneim, S.S.M. A modified marine predators optimization algorithm for simultaneous network reconfiguration and distributed generator allocation in distribution systems under different loading conditions. Eng. Optim. 2021, 54, 687–708. [Google Scholar] [CrossRef]
- Shaheen, A.; Elsayed, A.; Ginidi, A.; El-Sehiemy, R.; Elattar, E. A heap-based algorithm with deeper exploitative feature for optimal allocations of distributed generations with feeder reconfiguration in power distribution networks. Knowl.-Based Syst. 2022, 241, 108269. [Google Scholar] [CrossRef]
- Ch, Y.; Goswami, S.; Chatterjee, D. Effect of network reconfiguration on power quality of distribution system. Int. J. Electr. Power Energy Syst. 2016, 83, 87–95. [Google Scholar] [CrossRef]
- Mazza, A.; Chicco, G.; Russo, A.; Virjoghe, E.O. Multi-Objective Distribution Network Reconfiguration Based on Pareto Front Ranking. Intell. Ind. Syst. 2016, 2, 287–302. [Google Scholar] [CrossRef][Green Version]
- Su, C.-T.; Chang, C.-F.; Chiou, J.-P. Distribution network reconfiguration for loss reduction by ant colony search algorithm. Electr. Power Syst. Res. 2005, 75, 190–199. [Google Scholar] [CrossRef]
- Abdelaziz, A.; Mohamed, F.; Mekhamer, S.; Badr, M. Distribution system reconfiguration using a modified Tabu Search algorithm. Electr. Power Syst. Res. 2010, 80, 943–953. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Truong, A.V.; Phung, T.A. A novel method based on adaptive cuckoo search for optimal network reconfiguration and distributed generation allocation in distribution network. Int. J. Electr. Power Energy Syst. 2016, 78, 801–815. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Truong, A.V. Distribution network reconfiguration for power loss minimization and voltage profile improvement using cuckoo search algorithm. Int. J. Electr. Power Energy Syst. 2015, 68, 233–242. [Google Scholar] [CrossRef]
- Diaaeldin, I.M.; Aleem, S.H.E.A.; El-Rafei, A.; Abdelaziz, A.Y.; Zobaa, A.F. Enhancement of Hosting Capacity with Soft Open Points and Distribution System Reconfiguration: Multi-Objective Bilevel Stochastic Optimization. Energies 2020, 13, 5446. [Google Scholar] [CrossRef]
- Lotfipour, A.; Afrakhte, H. A discrete Teaching–Learning-Based Optimization algorithm to solve distribution system reconfiguration in presence of distributed generation. Int. J. Electr. Power Energy Syst. 2016, 82, 264–273. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Niknam, T. Multi-objective stochastic Distribution Feeder Reconfiguration from the reliability point of view. Energy 2014, 64, 342–354. [Google Scholar] [CrossRef]
- Shareef, H.; Ibrahim, A.A.; Salman, N.; Mohamed, A.; Ai, W.L. Power quality and reliability enhancement in distribution systems via optimum network reconfiguration by using quantum firefly algorithm. Int. J. Electr. Power Energy Syst. 2014, 58, 160–169. [Google Scholar] [CrossRef]
- Shariatkhah, M.-H.; Haghifam, M.-R.; Salehi, J.; Moser, A. Duration based reconfiguration of electric distribution networks using dynamic programming and harmony search algorithm. Int. J. Electr. Power Energy Syst. 2012, 41, 1–10. [Google Scholar] [CrossRef]
- Rajaram, R.; Kumar, K.S.; Rajasekar, N. Power system reconfiguration in a radial distribution network for reducing losses and to improve voltage profile using modified plant growth simulation algorithm with Distributed Generation (DG). Energy Rep. 2015, 1, 116–122. [Google Scholar] [CrossRef]
- Jafar-Nowdeh, A.; Babanezhad, M.; Arabi-Nowdeh, S.; Naderipour, A.; Kamyab, H.; Abdul-Malek, Z.; Ramachandaramurthy, V.K. Meta-heuristic matrix moth–flame algorithm for optimal reconfiguration of distribution networks and placement of solar and wind renewable sources considering reliability. Environ. Technol. Innov. 2020, 20, 101118. [Google Scholar] [CrossRef]
- Anita; Yadav, A. AEFA: Artificial electric field algorithm for global optimization. Swarm Evol. Comput. 2019, 48, 93–108. [Google Scholar] [CrossRef]
- Li, W.-M.; Jiang, Z.-H.; Wang, T.-L.; Zhu, H.-P. Optimization method based on Generalized Pattern Search Algorithm to identify bridge parameters indirectly by a passing vehicle. J. Sound Vib. 2014, 333, 364–380. [Google Scholar] [CrossRef]
- Wu, M.; Li, K.; Kwong, S.; Zhang, Q. Evolutionary Many-Objective Optimization Based on Adversarial Decomposition. IEEE Trans. Cybern. 2018, 50, 753–764. [Google Scholar] [CrossRef]
- Shi, Y. Particle swarm optimization: Developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No. 01TH8546), Seoul, Korea, 27–30 May 2001; Volume 1, pp. 81–86. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Gunther, E.; Mebta, H. A survey of distribution system power quality-preliminary results. IEEE Trans. Power Deliv. 1995, 10, 322–329. [Google Scholar] [CrossRef]
- Nowdeh, S.A.; Davoudkhani, I.F.; Moghaddam, M.H.; Najmi, E.S.; Abdelaziz, A.Y.; Ahmadi, A.; Razavi, S.; Gandoman, F.H. Fuzzy multi-objective placement of renewable energy sources in distribution system with objective of loss reduction and reliability improvement using a novel hybrid method. Appl. Soft Comput. 2019, 77, 761–779. [Google Scholar] [CrossRef]
- Swarnkar, A.; Gupta, N.; Niazi, K. Adapted ant colony optimization for efficient reconfiguration of balanced and unbalanced distribution systems for loss minimization. Swarm Evol. Comput. 2011, 1, 129–137. [Google Scholar] [CrossRef]
- Mirhoseini, S.H.; Hosseini, S.M.; Ghanbari, M.; Gandomkar, M. Multi-objective Reconfiguration of Distribution Network Using a Heuristic Modified Ant Colony Optimization Algorithm. Modeling Simul. Electr. Electron. Eng. 2015, 1, 23–33. [Google Scholar] [CrossRef]
- Kasaei, M.J.; Nikoukar, J. DG allocation with consideration of costs and losses in distribution networks using ant colony algorithm. Majlesi J. Electr. Eng. 2016, 10, 51–56. [Google Scholar]
- Wu, Y.-K.; Lee, C.-Y.; Liu, L.-C.; Tsai, S.-H. Study of Reconfiguration for the Distribution System With Distributed Generators. IEEE Trans. Power Deliv. 2010, 25, 1678–1685. [Google Scholar] [CrossRef]
- Taher, S.A.; Karimi, M.H. Optimal reconfiguration and DG allocation in balanced and unbalanced distribution systems. Ain Shams Eng. J. 2014, 5, 735–749. [Google Scholar] [CrossRef]
- El Ela, A.A.; Allam, S.; Shatla, M. Maximal optimal benefits of distributed generation using genetic algorithms. Electr. Power Syst. Res. 2010, 80, 869–877. [Google Scholar] [CrossRef]




| Ref. | Power Loss | Voltage Sag | Voltage Unbalance | ENS | Multi-Objective | Unbalanced Network | Improved/Hybrid Algorithm | Research Gap |
|---|---|---|---|---|---|---|---|---|
| [10] | ✓ | ✕ | ✓ | ✕ | ✓ | ✓ | ✓ | Not considering the power quality and reliability indices |
| [4] | ✓ | ✕ | ✕ | ✕ | ✓ | ✕ | ✓ | Not evaluating the power quality and reliability indices |
| [11] | ✓ | ✕ | ✕ | ✕ | ✓ | ✕ | ✓ | Without the power quality and reliability indices |
| [12] | ✓ | ✕ | ✕ | ✕ | ✓ | ✕ | ✕ | Not studying the power quality and reliability indices |
| [13] | ✓ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | Not incorporating power quality and reliability indices |
| [14] | ✓ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | Without the power quality indices |
| [15] | ✓ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | Without the power quality and reliability indices |
| [16] | ✓ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | Not investigating the power quality and reliability indices |
| [17] | ✓ | ✕ | ✕ | ✕ | ✓ | ✕ | ✓ | Without the power quality and reliability indices |
| [18] | ✓ | ✕ | ✕ | ✕ | ✓ | ✕ | ✕ | Not considering the power quality and reliability indices |
| [19] | ✓ | ✕ | ✕ | ✕ | ✓ | ✕ | ✕ | Without the power quality and reliability indices |
| [20] | ✓ | ✕ | ✕ | ✕ | ✓ | ✕ | ✓ | Without studying the power quality and reliability indices |
| [21] | ✓ | ✕ | ✕ | ✕ | ✓ | ✕ | ✕ | Without the power quality and reliability indices |
| [22] | ✓ | ✕ | ✓ | ✓ | ✓ | ✕ | ✕ | Not considering the voltage sag and unbalanced network |
| [23] | ✓ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | Not considering the power quality and reliability indices |
| [24] | ✓ | ✕ | ✕ | ✕ | ✓ | ✕ | ✕ | Without the power quality and reliability indices |
| This paper | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Considering power quality, reliability, unbalanced network, and hybrid algorithm |
| ENS (kWh) | Vun (%) | Vsag (p.u) | Loss (kW) | Item |
|---|---|---|---|---|
| 7.43 | 4.92 | 0.9566 | 207.44 | Value |
| Item | Initial | Method | Min Loss | Min Vsag | Min Vun | Min ENS | Many-Criteria |
|---|---|---|---|---|---|---|---|
| Solution | 33, 34, 35, 36, 37 | AEFAPS | 7, 9, 14, 32, 37 | 9, 14, 28, 32, 33 | 7, 12, 21, 27, 32 | 7, 9, 14, 16, 28 | 7, 11, 13, 28, 32 |
| AEFA | 7, 10, 28, 32, 34 | 7, 10, 13, 17, 28 | 6, 8, 10, 28, 30 | 7, 10, 14, 16, 27 | 8, 14, 28, 32, 33 | ||
| PSO | 7, 14, 21, 28, 32 | 7, 10, 14, 17, 28 | 11, 12, 20, 28, 30 | 13, 16, 20, 21, 28 | 8, 13, 28, 32, 33 | ||
| GWO | 9, 14, 28, 31, 33 | 9, 14, 17, 28, 33 | 12, 20, 21, 28, 30 | 13, 16, 21, 28, 33 | 7, 14, 21, 28, 32 | ||
| Loss (kW) | 207.44 | AEFAPS | 142.85 | 147.61 | 167.96 | 158.17 | 146.96 |
| AEFA | 147.59 | 172.64 | 207.73 | 165.11 | 148.51 | ||
| PSO | 148.19 | 153.12 | 204.02 | 186.87 | 150.57 | ||
| GWO | 147.54 | 154.14 | 203.38 | 179.69 | 153.19 | ||
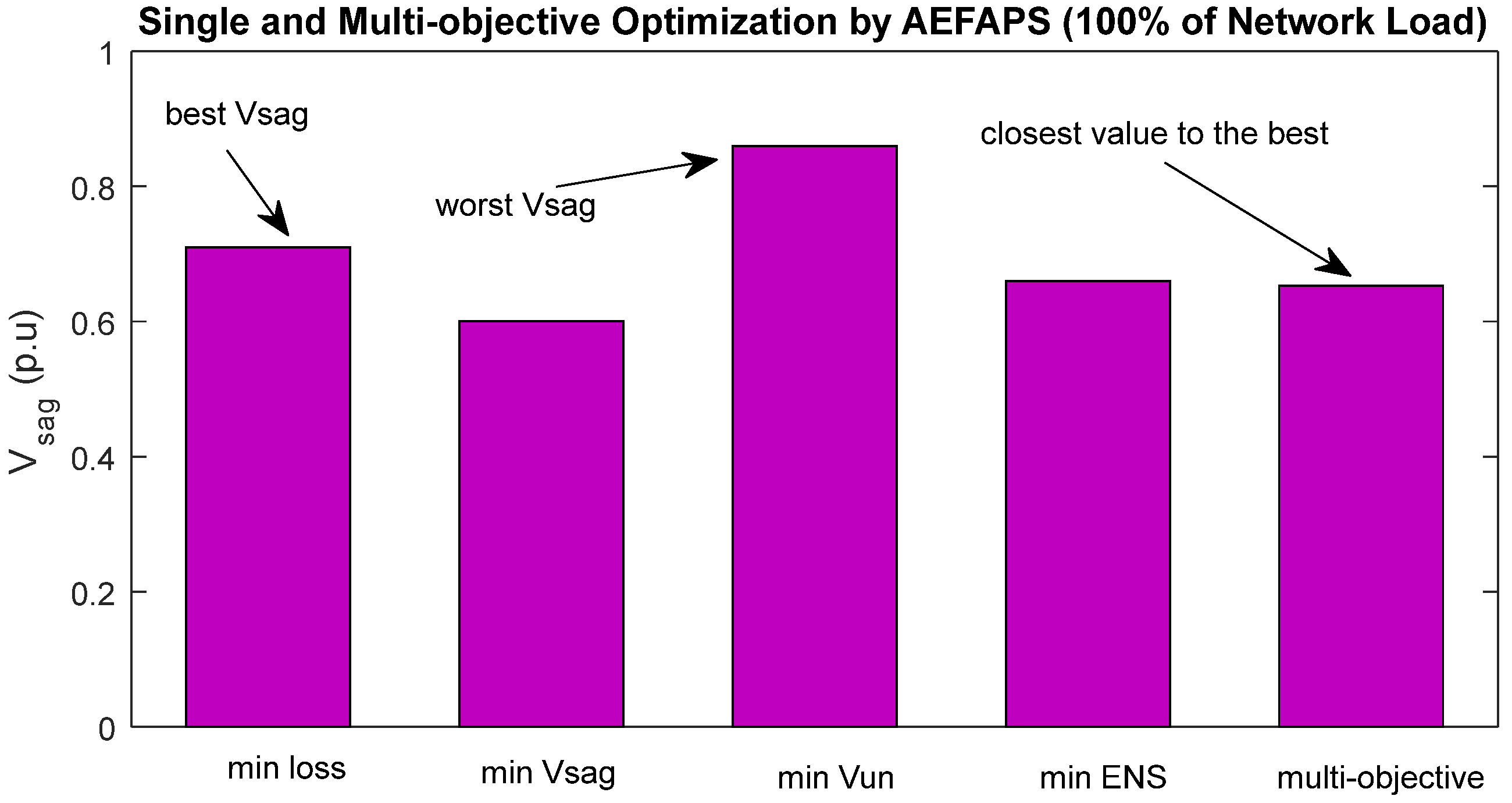
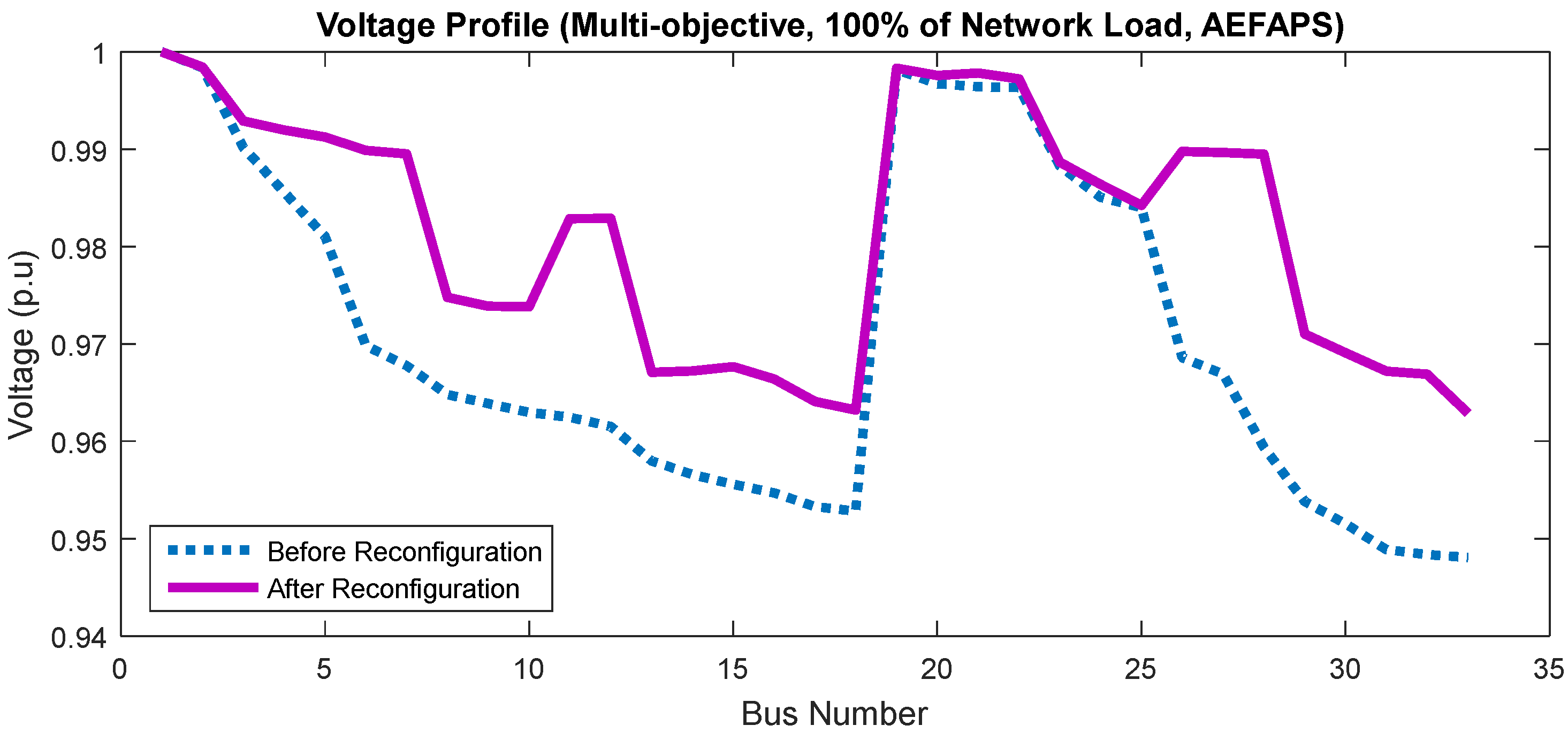
| Vsag (p.u) | 0.9566 | AEFAPS | 0.71 | 0.60 | 0.86 | 0.66 | 0.653 |
| AEFA | 0.665 | 0.626 | 0.963 | 0.727 | 0.667 | ||
| PSO | 0.713 | 0.615 | 1.014 | 0.823 | 0.684 | ||
| GWO | 0.644 | 0.617 | 1.014 | 0.778 | 0.713 | ||
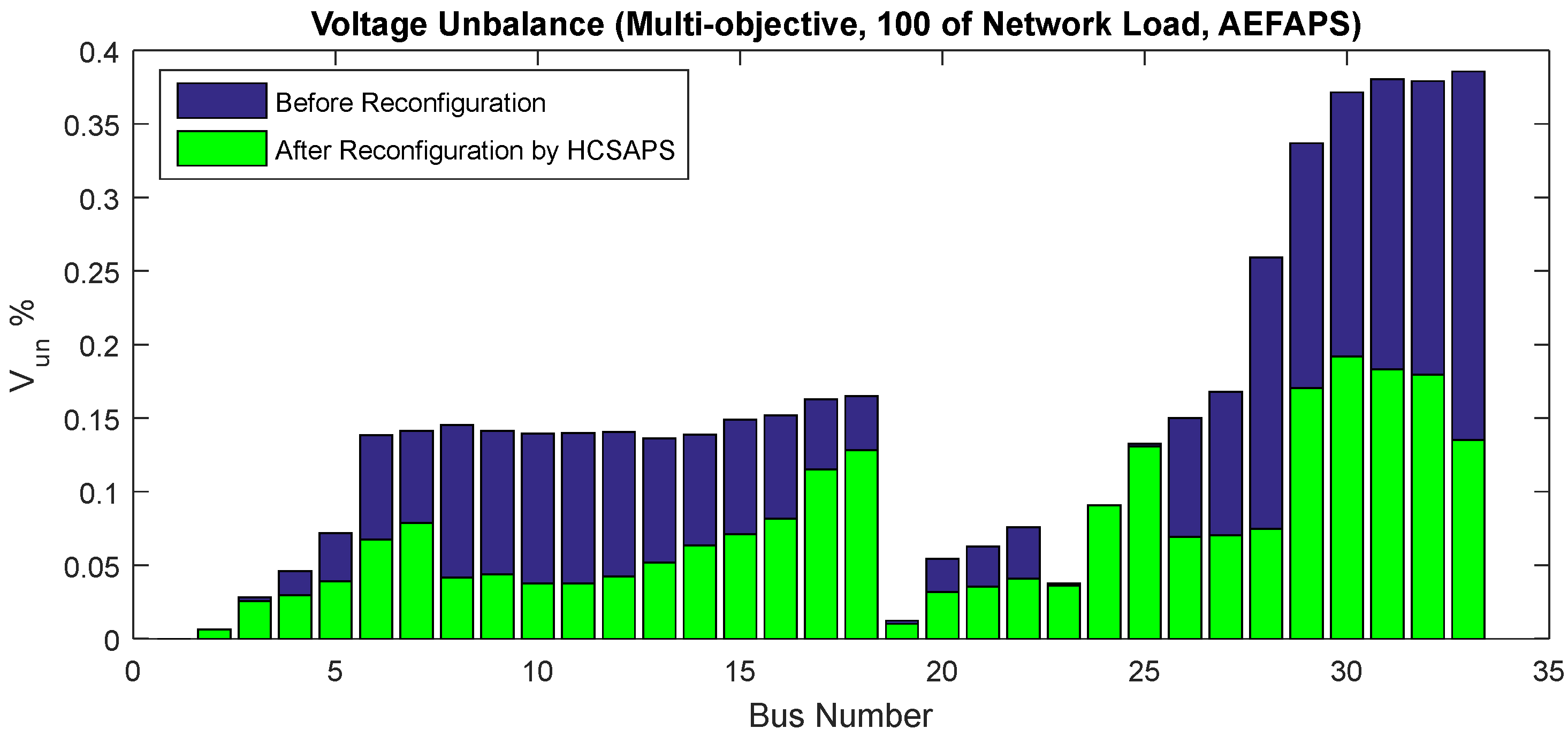
| Vun (%) | 4.922 | AEFAPS | 3.73 | 4.06 | 2.05 | 3.78 | 2.42 |
| AEFA | 3.79 | 7.17 | 2.11 | 3.71 | 2.47 | ||
| PSO | 2.41 | 3.62 | 2.24 | 4.37 | 2.42 | ||
| GWO | 3.84 | 4.28 | 2.21 | 4.09 | 2.42 | ||
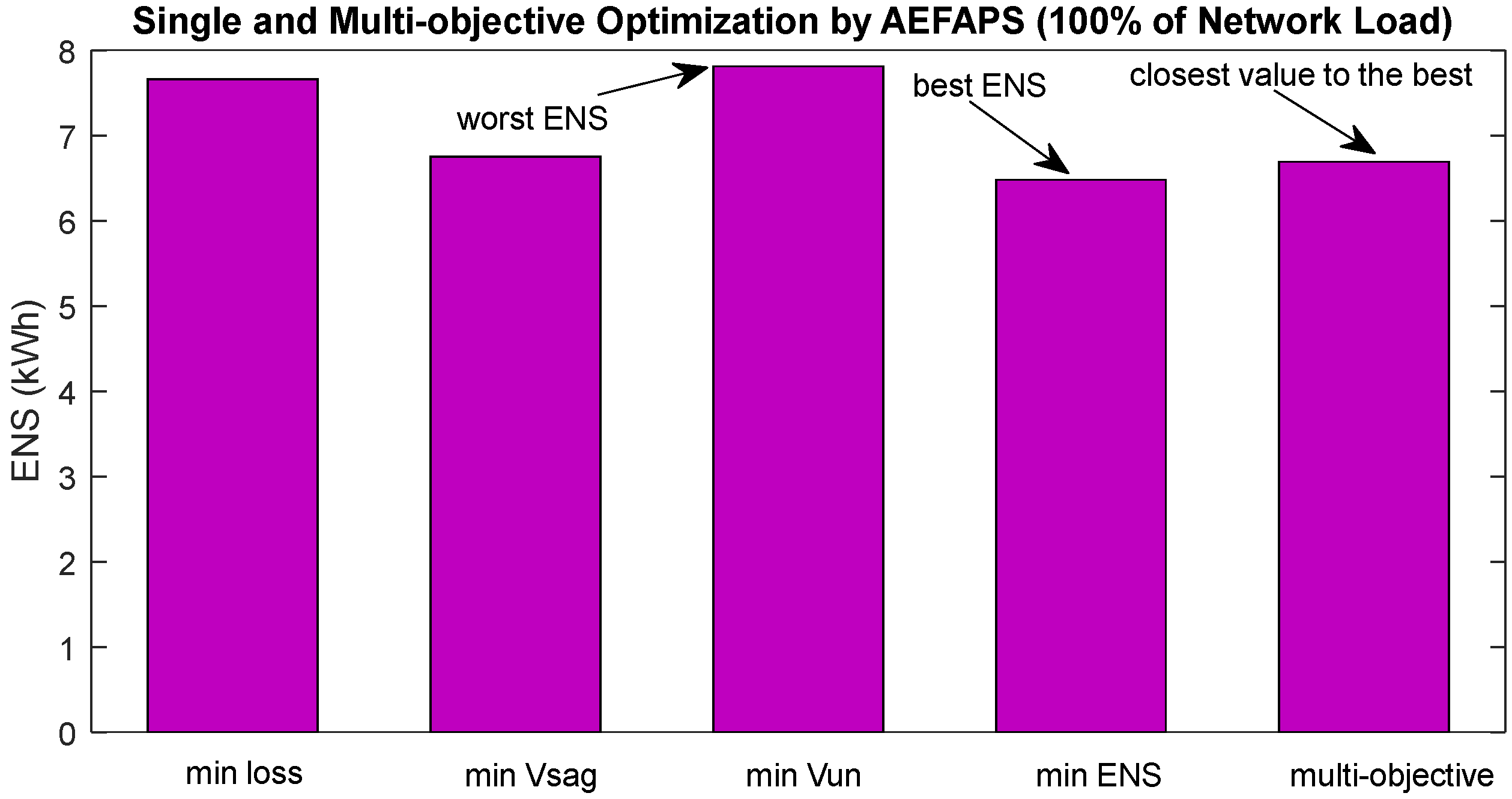
| ENS (MWh/year) | 7.432 | AEFAPS | 6.71 | 6.75 | 7.81 | 6.48 | 6.69 |
| AEFA | 8.08 | 8.34 | 7.85 | 6.51 | 6.90 | ||
| PSO | 7.25 | 6.557 | 7.50 | 6.60 | 7.02 | ||
| GWO | 6.93 | 6.35 | 7.51 | 6.51 | 7.25 |
| Item | Initial | Method | Min Loss | Min Vsag | Min Vun | Min ENS | Many-Criteria |
|---|---|---|---|---|---|---|---|
| Solution | 33, 34, 35, 36, 37 | AEFAPS | 7, 9, 14, 32, 37 | 7, 10, 14, 17, 28 | 7, 12, 21, 27, 32 | 10, 13, 16, 28, 33 | 7, 10, 28, 32, 34 |
| AEFA | 9, 7, 14, 28, 31 | 7, 9, 14, 17, 28 | 6, 8, 12, 28, 30 | 7, 10, 14, 16, 28 | 8, 14, 28, 32, 33 | ||
| PSO | 7, 14, 17, 21, 28 | 9, 14, 17, 28, 33 | 11, 12, 20, 28, 30 | 7, 9, 14, 16, 28 | 8, 14, 28, 32, 33 | ||
| GWO | 7, 10, 17, 14, 28 | 7, 11, 17, 28, 34 | 7, 12, 21, 27, 32 | 7, 9, 14, 16, 28 | 7, 10, 13, 17, 28 | ||
| Loss (kW) | 331.19 | AEFAPS | 226.38 | 236.92 | 302.25 | 259.63 | 232.98 |
| AEFA | 229.18 | 237.09 | 300.76 | 243.10 | 240.88 | ||
| PSO | 239.36 | 244.65 | 324.54 | 243.45 | 241.46 | ||
| GWO | 236.92 | 239.29 | 251.22 | 243.45 | 239.10 | ||
| Vsag (p.u) | 1.209 | AEFAPS | 0.839 | 0.775 | 1.270 | 0.838 | 0.833 |
| AEFA | 0.859 | 0.777 | 1.264 | 0.798 | 0.894 | ||
| PSO | 0.866 | 0.778 | 1.283 | 0.801 | 0.841 | ||
| GWO | 0.775 | 0.795 | 0.945 | 0.801 | 0.838 | ||
| Vun (%) | 6.341 | AEFAPS | 4.939 | 4.613 | 2.446 | 4.449 | 2.932 |
| AEFA | 3.982 | 4.746 | 2.524 | 4.649 | 2.943 | ||
| PSO | 5.137 | 5.454 | 2.839 | 4.806 | 3.156 | ||
| GWO | 4.613 | 4.458 | 2.624 | 4.806 | 4.329 | ||
| ENS (MWh/year) | 9.291 | AEFAPS | 9.090 | 8.196 | 10.143 | 7.881 | 8.074 |
| AEFA | 9.098 | 8.174 | 10.517 | 8.128 | 8.666 | ||
| PSO | 8.731 | 7.943 | 9.394 | 8.107 | 8.630 | ||
| GWO | 8.196 | 8.245 | 9.015 | 8.107 | 8.156 |
| Item | Initial | Method | Min Loss | Min Vsag | Min Vun | Min ENS | Many-Criteria |
|---|---|---|---|---|---|---|---|
| Solution | 33, 34, 35, 36, 37 | AEFAPS | 7, 9, 14, 32, 37 | 7, 9, 14, 28, 36 | 6, 8, 10, 28, 30 | 10, 13, 16, 28, 33 | 7, 10, 13, 28, 36 |
| AEFA | 7, 10, 14, 36, 37 | 7, 9, 12, 17, 28 | 6, 8, 9, 27, 30 | 11, 13, 17, 25, 33 | 8, 14, 28, 32, 33 | ||
| PSO | 7, 11, 28, 32, 34 | 7, 14, 17, 21, 28 | 7, 8, 10, 12, 27 | 11, 12, 16, 20, 28 | 7, 13, 21, 28, 32 | ||
| GWO | 7, 10, 14, 17, 28 | 7, 10, 14, 17, 28 | 12, 21, 27, 30, 33 | 7, 11, 14, 16, 28 | 7, 10, 13, 17, 28 | ||
| Loss (kW) | 331.19 | AEFAPS | 54.66 | 56.49 | 71.31 | 62.30 | 56.35 |
| AEFA | 55.72 | 57.90 | 71.32 | 65.64 | 57.01 | ||
| PSO | 56.12 | 59.97 | 79.67 | 71.61 | 58.85 | ||
| GWO | 57.06 | 57.06 | 73.45 | 58.44 | 57.57 | ||
| Vsag (p.u) | 1.209 | AEFAPS | 0.407 | 0.378 | 0.613 | 0.409 | 0.389 |
| AEFA | 0.408 | 0.392 | 0.619 | 0.449 | 0.424 | ||
| PSO | 0.404 | 0.425 | 0.610 | 0.512 | 0.444 | ||
| GWO | 0.381 | 0.381 | 0.585 | 0.393 | 0.388 | ||
| Vun (%) | 6.341 | AEFAPS | 2.358 | 1.926 | 1.161 | 2.109 | 1.513 |
| AEFA | 2.415 | 2.165 | 1.213 | 1.982 | 1.504 | ||
| PSO | 1.522 | 2.441 | 1.933 | 2.665 | 1.330 | ||
| GWO | 2.207 | 2.207 | 1.218 | 2.172 | 2.069 | ||
| ENS (MWh/year) | 9.291 | AEFAPS | 4.545 | 4.273 | 5.071 | 3.940 | 4.214 |
| AEFA | 4.491 | 4.148 | 5.101 | 4.046 | 4.372 | ||
| PSO | 4.302 | 4.365 | 4.367 | 4.121 | 4.501 | ||
| GWO | 4.098 | 4.098 | 4.641 | 4.079 | 4.128 |
| Item | Solution | Loss (Kw) | Vsag (p.u) | Vun (%) | ENS (kWh) |
|---|---|---|---|---|---|
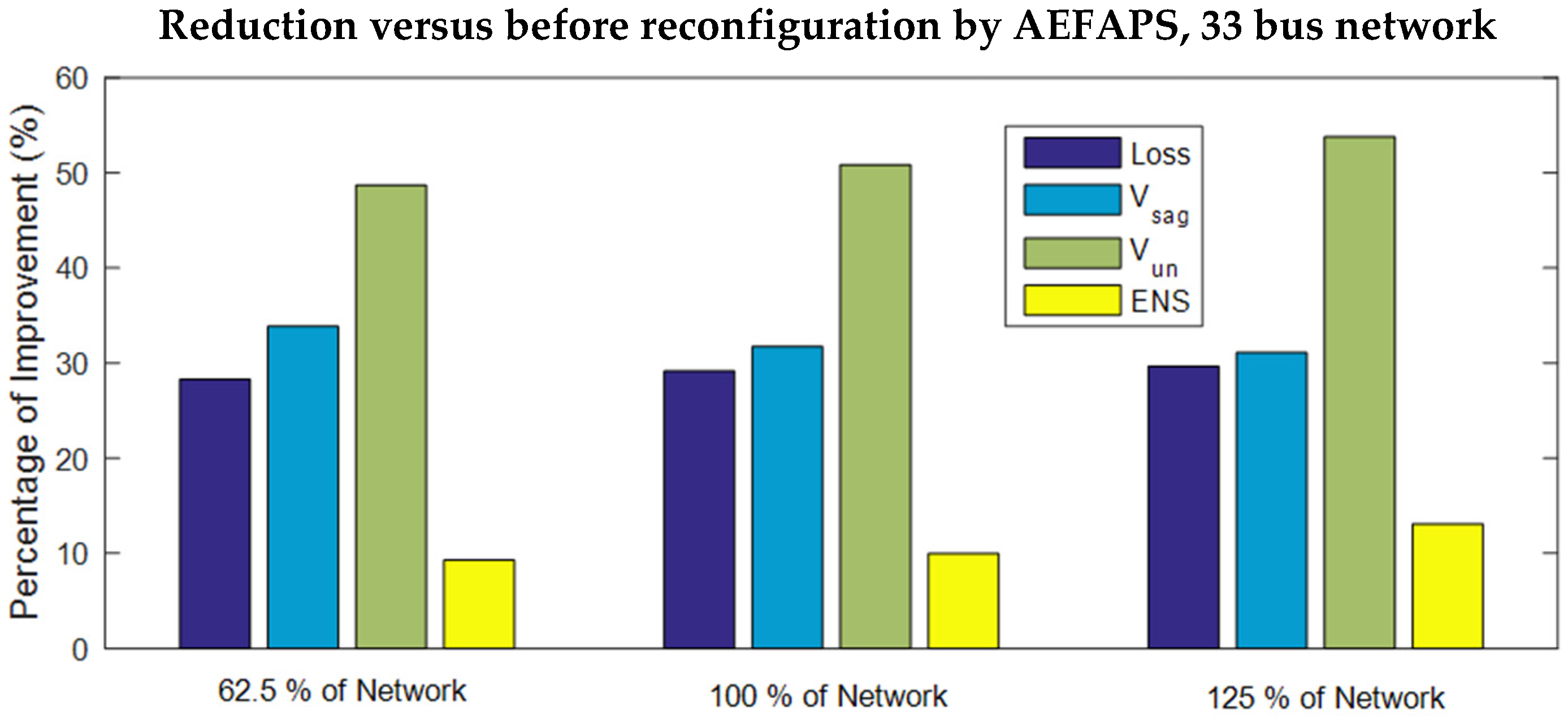
| 62.5% | 7, 10, 13, 28, 36 | 56.35 28.29% | 0.389 33.84% | 1.513 48.67% | 4.214 9.27% |
| 100% | 7, 10, 13, 28, 36 | 146.96 29.15% | 0.653 31.73% | 2.42 50.83% | 6.69 9.98% |
| 125% | 7, 10, 28, 32, 34 | 232.98 29.65% | 0.833 31.10% | 2.932 53.76% | 8.074 13.09% |
| Item | Solution | Loss (kW) | Vsag (p.u) | Vun (%) | ENS (kWh) |
|---|---|---|---|---|---|
| Initial | 13,14,15,16,17 | 175.58 | 0.980 | 0.81 | 4.346 |
| 100% of Network Load | 6,8,9,10,14 | 127.51 | 0.31 | 0.552 | 1.860 |
| Item | Solution | Loss (kW) | Vsag (p.u) | Vun (%) | ENS (kWh) |
|---|---|---|---|---|---|
| Initial | 13,14,15,16,17 | 191.67 | 1.204 | 1.142 | 5.433 |
| 62.5% of Network Load | 6,8,9,11,14 | 143.48 | 0.49 | 0.740 | 2.505 |
| Item | Solution | Loss (kW) | Vsag (p.u) | Vun (%) | ENS (kWh) |
|---|---|---|---|---|---|
| Initial | 13,14,15,16,17 | 191.67 | 1.204 | 1.142 | 5.433 |
| 125% of Network Load | 6,8,9,11,14 | 143.48 | 0.49 | 0.740 | 2.505 |
| Item | Open Switches | Loss (kW) |
|---|---|---|
| AEFAPS | 7, 9, 14, 32, 37 | 142.85 |
| AEFA | 7, 10, 28, 32, 34 | 147.59 |
| PSO | 7, 14, 21, 28, 32 | 153.19 |
| GWO | 9, 14, 28, 31, 33 | 147.54 |
| AACO [33] | 7, 9, 14, 28, 32 | 143.87 |
| MINLP [13] | 7, 9, 14, 28, 36 | 144.49 |
| Item | Open Switches | Loss (kW) |
|---|---|---|
| AEFAPS (unbalanced) | 7, 9, 14, 16, 28 | 6.48 |
| AEFAPS (balanced) | 7, 9, 11, 28, 36 | 6.21 |
| AEFA (unbalanced) | 7, 10, 14, 16, 27 | 6.51 |
| PSO (unbalanced) | 13, 16, 20, 21, 28 | 6.60 |
| GWO (unbalanced) | 13, 16, 21, 28, 33 | 6.51 |
| MACO (balanced) [34] | 7, 11, 14, 36, 37 | 6.446 |
| Item | Open Switches | Loss (kW) |
|---|---|---|
| AEFAPS (unbalanced) | 7, 9, 14, 32, 37 | 142.85 |
| AEFAPS (balanced) | 7, 9, 14, 32, 37 | 139.55 |
| ACS (balanced) | 7, 9, 14, 28, 32 | 139.98 |
| AACO (balanced) [35] | 7, 9, 14, 28, 32 | 139.98 |
| MINLP (balanced) [36] | 7, 9, 14, 32, 37 | 139.55 |
| CSA (balanced) [37] | 7, 9, 14, 32, 37 | 139.84 |
| RGA (balanced) [18] | 7, 9, 14, 32, 37 | 139.84 |
| GA (balanced) [38] | 7, 9, 14, 32, 37 | 139.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alanazi, A.; Alanazi, M. Artificial Electric Field Algorithm-Pattern Search for Many-Criteria Networks Reconfiguration Considering Power Quality and Energy Not Supplied. Energies 2022, 15, 5269. https://doi.org/10.3390/en15145269
Alanazi A, Alanazi M. Artificial Electric Field Algorithm-Pattern Search for Many-Criteria Networks Reconfiguration Considering Power Quality and Energy Not Supplied. Energies. 2022; 15(14):5269. https://doi.org/10.3390/en15145269
Chicago/Turabian StyleAlanazi, Abdulaziz, and Mohana Alanazi. 2022. "Artificial Electric Field Algorithm-Pattern Search for Many-Criteria Networks Reconfiguration Considering Power Quality and Energy Not Supplied" Energies 15, no. 14: 5269. https://doi.org/10.3390/en15145269
APA StyleAlanazi, A., & Alanazi, M. (2022). Artificial Electric Field Algorithm-Pattern Search for Many-Criteria Networks Reconfiguration Considering Power Quality and Energy Not Supplied. Energies, 15(14), 5269. https://doi.org/10.3390/en15145269








