A Review of Proxy Modeling Highlighting Applications for Reservoir Engineering
Abstract
:1. Introduction
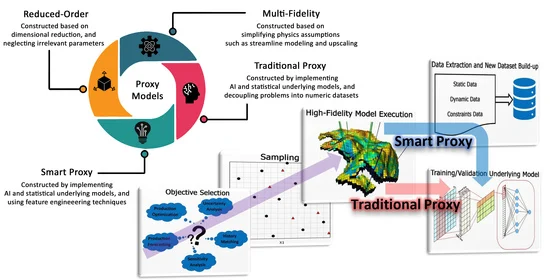
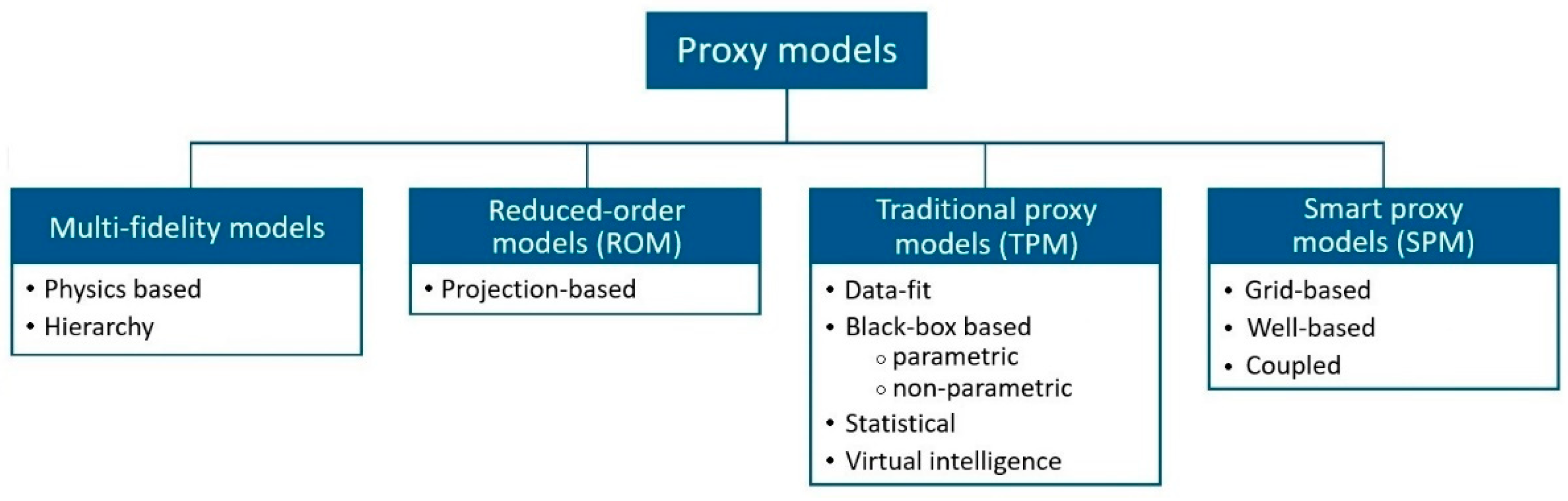
2. Proxy Modeling Classification
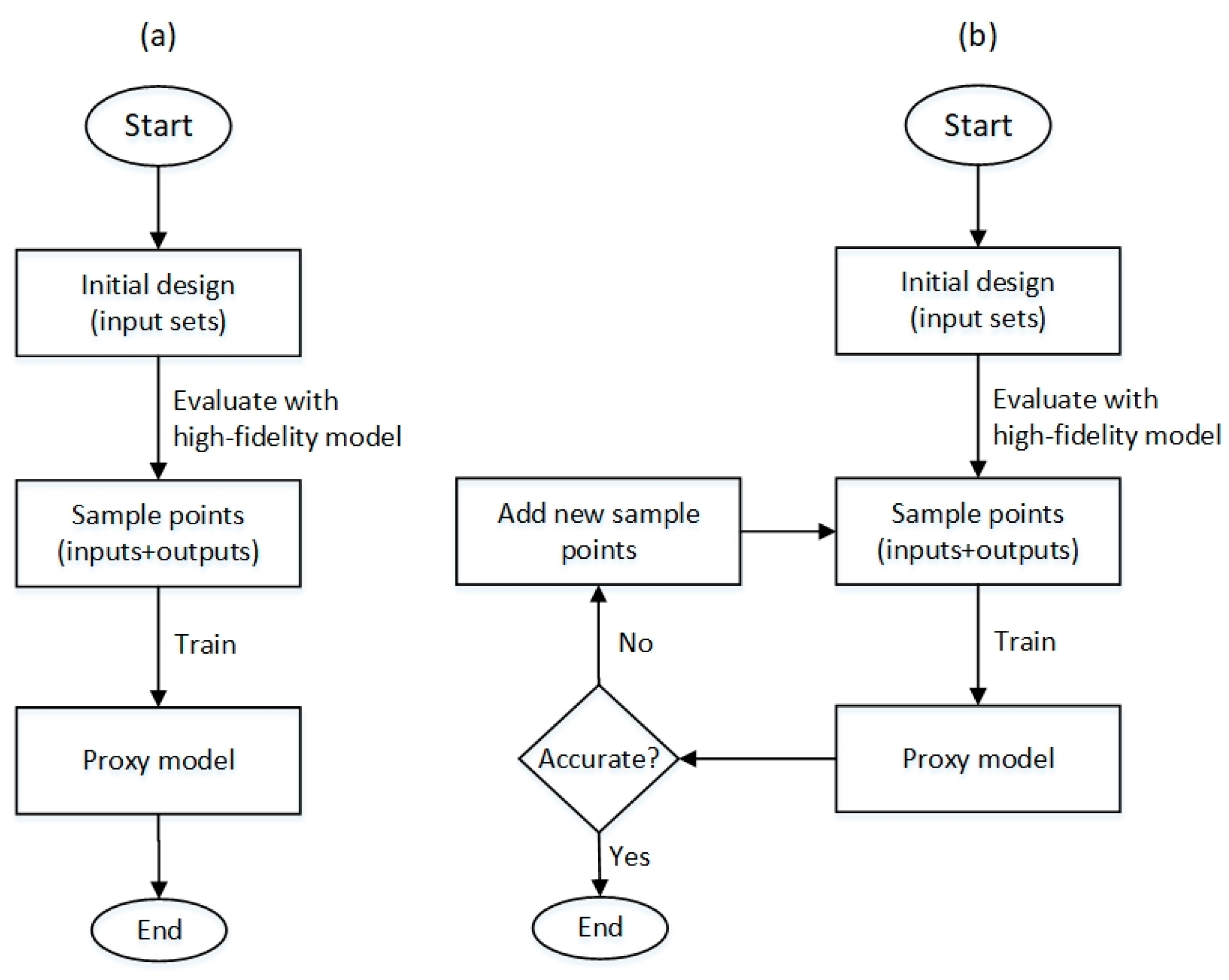
3. Methodology
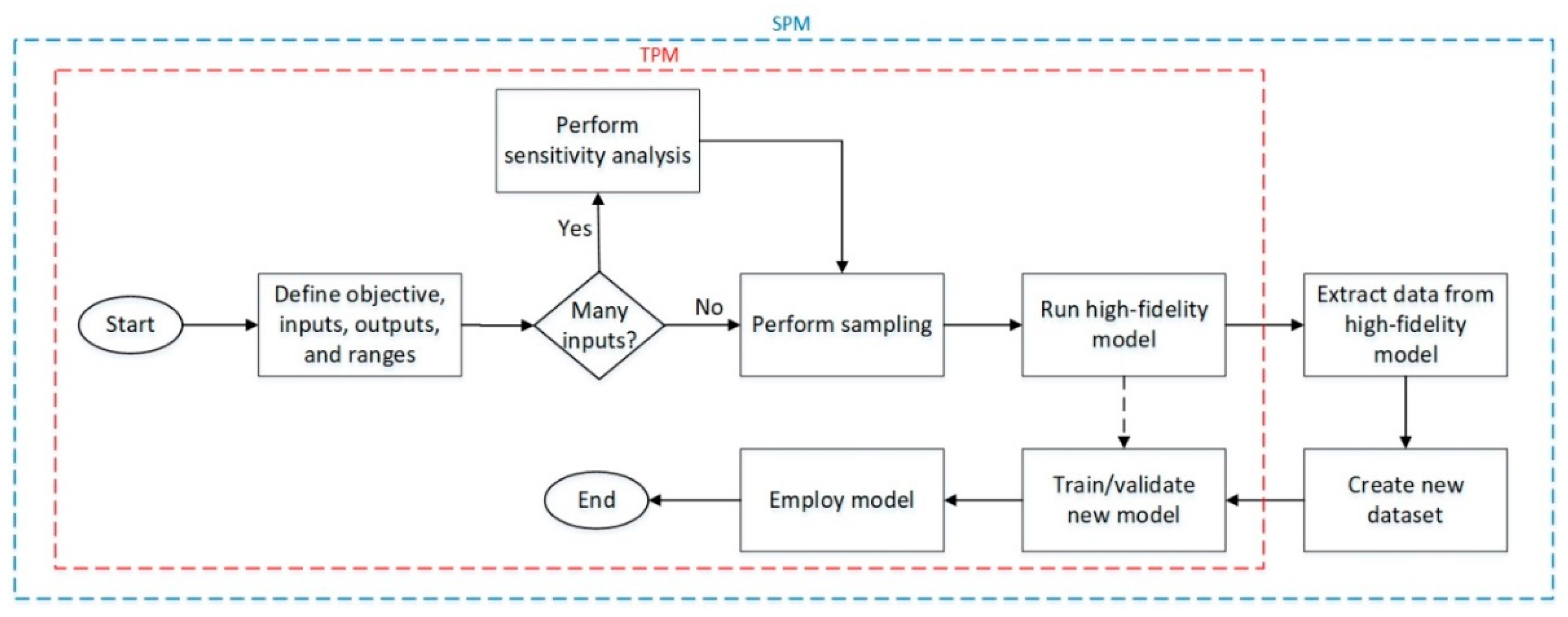
3.1. Sensitivity Analysis (SA)
3.2. Sampling
3.3. Popular Models for PM Construction
3.3.1. Polynomial Regression (PR)
3.3.2. Kriging (KG)
3.3.3. Multivariate Adaptive Regression Splines (MARS)
3.3.4. Artificial Neural Networks (ANN)
3.3.5. Radial Basis Function (RBF)
3.3.6. Support Vector Regression (SVR)
3.3.7. Genetic Programming (GP)
3.3.8. Random Forest (RF)
3.3.9. Extreme Gradient Boosting (XGboost)
3.3.10. Polynomial Chaos Expansion (PCE)
3.4. Optimization
4. Application of Proxy Models in the Oil and Gas Industry
4.1. Multi-Fidelity Models (MFM)
4.2. Reduced-Order Models (ROM)
4.3. Traditional Proxy Models (TPM)
4.4. Smart Proxy Models (SPM)
| Ref. | Subject | Sampling Technique | Underlying Model | Optimizer | Class |
| Kovscek and Wang [125] | Uncertainty quantification in a carbon dioxide storage case | - | Streamlines | - | MFM |
| Tanaka et al. [123] | Production optimization in waterflooding | - | Streamlines | GA | MFM |
| Wang and Kovscek [126] | History matching in a heterogeneous reservoir | - | Streamlines | - | MFM |
| Tang et al. [195] | Investigating the effects of the permeability heterogeneity and well completion in near-wellbore region | - | Streamlines | - | MFM |
| Kam et al. [128] | Three-phase history matching | - | Streamlines | GA | MFM |
| Taware et al. [130] | Well placement optimization in a mature carbonate field | - | Streamlines | - | MFM |
| Allam et al. [134] | History matching | - | Upscaling | - | MFM |
| Yang et al. [136] | Multiphase uncertainty quantification and history matching | - | Upscaling | - | MFM |
| Holanda et al. [141] | Reservoir characterization and history matching | - | CRM | - | MFM |
| Artun [142] | Characterizing interwell reservoir connectivity | - | CRM | - | MFM |
| Cardoso and Durlofsky [150] | Production optimization in waterflooding | - | TPWL/POD | Gradient-based | ROM |
| Xiao et al. [152] | History matching | Smolyak sparse [196] | TPWL/POD | Gradient-based | ROM |
| Rousset et al. [154] | Production prediction of SAGD operation | - | TPWL/POD | - | ROM |
| He and Durlofsky [155] | Compositional simulation of the reservoir | - | TPWL/POD | - | ROM |
| Gildin et al. [156] | Simulation of flow in heterogeneous porous media | - | DEIM/POD | - | ROM |
| Li et al. [158] | Compressible gas flow in porous media | - | DEIM/POD | - | ROM |
| Alghareeb and Williams [160] | Production optimization in waterflooding | - | DEIM/POD | - | ROM |
| Al-Mudhafar [100] | Production optimization in cyclic CO2 flooding | - | PR, MARS, RF | - | TPM |
| Golzari et al. [167] | Production optimization in three different cases to increase recovery and net present value (NPV) | Adaptive LHS | ANN | GA | TPM |
| Amiri Kolajoobi et al. [168] | Uncertainty quantification and determination of cumulative oil production | LHS | ANN | - | TPM |
| Peng and Gupta [169] | Uncertainty quantification in a fluvial reservoir | Factorial | PR | - | TPM |
| Zubarev [170] | History matching and production optimization | LHS | PR, KG, ANN | GA | TPM |
| Guo et al. [171] | History matching in a channelized reservoir | Random selection | SVR | Distributed Gauss–Newton [197] | TPM |
| Avansi [172] | Field development planning | BBD | PR | - | TPM |
| Ligero et al. [173] | Risk assessment in economic and technical parameters on an offshore field | Factorial | PR | - | TPM |
| Risso et al. [174] | Assessment of risk curves for uncertainties in the reservoir | BBD, CCD | PR | - | TPM |
| Ghassemzadeh and Charkhi [175] | Gas lift optimization to maximize recovery and NPV | - | ANN | GA | TPM |
| Ebrahimi and E. Khamehchi [109] | Gas lift optimization in NGL process | LHS | SVR | PSO, GA | TPM |
| Zangl et al. [176] | Gas storage management and optimization for pressure | Factorial | ANN | GA | TPM |
| Artun et al. [177] | Screening and optimization of cyclic pressure pulsing in naturally fractured reservoirs | - | ANN | GA | TPM |
| Gu et al. [180] | Waterflooding optimization in terms of watercut | - | XGboost | DE | TPM |
| Chen et al. [181] | Waterflooding optimization in terms of recovery and NPV | LHS | KG | DE | TPM |
| Ogbeiwi et al. [182] | Optimization of water injection rate and oil production rate in waterflooding | BBD | PR | GA | TPM |
| Bruyelle and Guérillot [183] | Waterflooding optimization in terms of well parameters | BBD | ANN | Covariance matrix adaptation evolution strategy [198] | TPM |
| Bruyelle and Guérillot [184] | Well placement optimization to maximize recovery and NPV | BBD | ANN | Covariance matrix adaptation evolution strategy | TPM |
| Hassani et al. [185] | Optimization of the horizontal well placement | Optimal, LHS | PR, RBF | GA | TPM |
| Nwachukwu et al. [186] | Injector well placement optimization to maximize recovery and NPV | Random selection | XGboost | - | TPM |
| Aydin et al. [187] | Monitoring of a geothermal reservoir temperature and pressure from wellhead data | - | ANN | - | TPM |
| Wang et al. [188] | Well control optimization to maximize recovery and NPV | LHS | SVR | Non-dominated sorting GA-II [199] | TPM |
| Simonov et al. [200] | Production optimization in a miscible flooding case | LHS | RF | MC | TPM |
| Redouane et al. [201] | Well placement optimization to maximize recovery | LHS, Sobol, Halton | ANFIS [202] | GA | TPM |
| Fedutenko et al. [189] | Production prediction of SAGD operation | LHS | PR, KG, RBF | - | TPM |
| Al-Mudhafar and Rao [190] | Recovery evaluation in CO2-GAGD operation | LHS | PR, MARS, GBM | - | TPM |
| Jaber et al. [191] | Recovery evaluation in miscible CO2-WAG flooding | BBD | PR | - | TPM |
| Agada et al. [192] | Recovery and net gas utilization factor optimization of a CO2-WAG operation in a fractured reservoir | BBD | PCE | GA | TPM |
| Elsheikh et al. [203] | Watercut determination in waterflooding cases | Nested sampling, MCMC | PCE | - | TPM |
| Yu et al. [204] | History matching and production forecasting | Hammersley [205] | GP | - | TPM |
| Kalla and White [206] | Optimization of a gas well with water conning | OAS | PR | - | TPM |
| Ibiam et al. [193] | Sensitivity analysis and polymer flooding optimization | LHS | PR | PSO | TPM |
| Kim and Durlofsky [207] | History matching and well-by-well oil and water flow rate prediction in waterflooding | Random selection | RNN | PSO | TPM |
| Kim and Durlofsky [208] | Predicting NPV with time-varying BHP | Uniform distribution | RNN | PSO | TPM |
| Kim et al. [209] | Multi-well placement optimization | Uniform distribution | CNN | PSO | TPM |
| Haghshenas et al. [20] | Evaluating the effect of injection rates on oil saturation using the grid-based SPM | LHS | ANN | - | SPM |
| Alenezi and Mohaghegh [194] | Evaluating the effect of injection rates on oil saturation and pressure using the grid-based SPM | Random selection | ANN | - | SPM |
| Amini and Mohaghegh [21] | Gas injection monitoring in porous media using the grid-based SPM | - | ANN | Gradient descent | SPM |
| Gholami et al. [18] | WAG monitoring and production optimization using the grid-based and well-based SPMs | LHS | ANN | - | SPM |
| He et al. [19] | History matching using well-based SPM | LHS | ANN | DE | SPM |
| Shahkarami et al. [22] | History matching using well-based SPM | LHS | ANN | - | SPM |
| Ng et al. [23] | Production optimization in a fractured reservoir | - | ANN | PSO | SPM |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACO | ant colony optimization |
| ANFIS | adaptive neuro fuzzy inference system |
| ANN | artificial neural networks |
| BBD | box–Behnken design |
| BHP | bottom hole pressure |
| CCD | central composite design |
| CNN | convolutional neural networks |
| CRM | capacitance-resistance modeling |
| DE | differential evolution |
| DEIM | discrete empirical interpolation method |
| GA | genetic algorithm |
| GAGD | gas-assisted gravity drainage |
| GBM | gradient boosting machine |
| GP | genetic programming |
| GSA | global sensitivity analysis |
| KG | kriging |
| LHS | Latin hypercube sampling |
| LSA | local sensitivity analysis |
| MARS | multivariate adaptive regression splines |
| MC | Monte Carlo |
| MCMC | Markov chain Monte Carlo |
| MFM | multi-fidelity model |
| NPV | net present value |
| OAS | orthogonal array sampling |
| PBD | Plackett–Burman design |
| PCE | polynomial chaos expansion |
| PM | proxy model |
| POD | proper orthogonal decompositions |
| PR | polynomial regression |
| PSO | particle swarm optimization |
| RBF | radial basis functions |
| ReLU | rectified linear unit |
| RF | random forest |
| RNN | recurrent neural networks |
| ROM | reduced-order model |
| RSM | response surface model |
| SA | sensitivity analysis |
| SAGD | steam-assisted gravity drainage |
| SBO | surrogate-model-based optimization |
| SPM | smart proxy model |
| SVM | support vector machine |
| SVR | support vector regression |
| TPM | traditional proxy model |
| TPWL | trajectory-piecewise linear |
| WAG | water alternating gas |
| XGboost | extreme gradient boosting |
References
- Larson, M. Numerical Modeling. In Encyclopedia of Coastal Science; Schwartz, M.L., Ed.; Springer: Dordrecht, The Netherlands, 2005; pp. 730–733. ISBN 978-1-4020-3880-8. [Google Scholar]
- Carmo, J.S.A.d. Physical Modelling vs. Numerical Modelling: Complementarity and Learning. Preprints 2020. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M. Introduction to Numerical Methods. In Computational Methods for Fluid Dynamics; Ferziger, J.H., Perić, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 21–37. ISBN 978-3-642-56026-2. [Google Scholar]
- Koziel, S.; Leifsson, L. Surrogate-Based Modeling and Optimization: Applications in Engineering; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-7550-7. [Google Scholar]
- Avansi, G.; Rios, V.; Schiozer, D. Numerical Tuning in Reservoir Simulation: It Is Worth the Effort in Practical Petroleum Applications. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 59. [Google Scholar] [CrossRef]
- Available online: http://www.webofknowledge.com/ (accessed on 14 August 2021).
- Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008; ISBN 978-0-470-77080-1. [Google Scholar]
- Ahmed, M.; Qin, N. Surrogate-Based Aerodynamic Design Optimization: Use of Surrogates in Aerodynamic Design Optimization. In Proceedings of the International Conference on Aerospace Sciences and Aviation Technology, Cairo, Egypt, 9–11 April 2009; Volume 13, pp. 1–26. [Google Scholar]
- Eldred, M.; Dunlavy, D. Formulations for Surrogate-Based Optimization with Data Fit, Multifidelity, and Reduced-Order Models. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006. [Google Scholar]
- Panjalizadeh, H.; Alizadeh, N.; Mashhadi, H. A Workflow for Risk Analysis and Optimization of Steam Flooding Scenario Using Static and Dynamic Proxy Models. J. Pet. Sci. Eng. 2014, 121, 78–86. [Google Scholar] [CrossRef]
- Mohaghegh, S.D. Data-Driven Analytics for the Geological Storage of CO2; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2018; ISBN 978-1-315-28081-3. [Google Scholar]
- Bartz-Beielstein, T.; Zaefferer, M. Model-Based Methods for Continuous and Discrete Global Optimization. Appl. Soft Comput. 2017, 55, 154–167. [Google Scholar] [CrossRef] [Green Version]
- Barton, R.R.; Meckesheimer, M. Chapter 18—Metamodel-Based Simulation Optimization. In Handbooks in Operations Research and Management Science; Henderson, S.G., Nelson, B.L., Eds.; Simulation; Elsevier: Amsterdam, The Netherlands, 2006; Volume 13, pp. 535–574. [Google Scholar]
- Jaber, A.K.; Al-Jawad, S.N.; Alhuraishawy, A.K. A Review of Proxy Modeling Applications in Numerical Reservoir Simulation. Arab. J. Geosci. 2019, 12, 701. [Google Scholar] [CrossRef]
- Yondo, R.; Andrés, E.; Valero, E. A Review on Design of Experiments and Surrogate Models in Aircraft Real-Time and Many-Query Aerodynamic Analyses. Prog. Aerosp. Sci. 2018, 96, 23–61. [Google Scholar] [CrossRef]
- Giselle Fernández-Godino, M.; Park, C.; Kim, N.H.; Haftka, R.T. Issues in Deciding Whether to Use Multifidelity Surrogates. AIAA J. 2019, 57, 2039–2054. [Google Scholar] [CrossRef]
- Thenon, A.; Gervais, V.; Ravalec, M.L. Multi-Fidelity Meta-Modeling for Reservoir Engineering—Application to History Matching. Comput. Geosci. 2016, 20, 1231–1250. [Google Scholar] [CrossRef]
- Gholami, V.; Mohaghegh, S.D.; Maysami, M. Smart Proxy Modeling of SACROC CO2-EOR. Fluids 2019, 4, 85. [Google Scholar] [CrossRef] [Green Version]
- He, Q.; Mohaghegh, S.D.; Liu, Z. Reservoir Simulation Using Smart Proxy in SACROC Unit—Case Study; OnePetro: Canton, OH, USA, 2016. [Google Scholar]
- Haghshenas, Y.; Emami Niri, M.; Amini, S.; Amiri Kolajoobi, R. Developing Grid-Based Smart Proxy Model to Evaluate Various Water Flooding Injection Scenarios. Pet. Sci. Technol. 2020, 38, 870–881. [Google Scholar] [CrossRef]
- Amini, S.; Mohaghegh, S. Application of Machine Learning and Artificial Intelligence in Proxy Modeling for Fluid Flow in Porous Media. Fluids 2019, 4, 126. [Google Scholar] [CrossRef] [Green Version]
- Shahkarami, A.; Mohaghegh, S.D.; Gholami, V.; Haghighat, S.A. Artificial Intelligence (AI) Assisted History Matching; OnePetro: Denver, CO, USA, 2014. [Google Scholar]
- Ng, C.S.W.; Jahanbani Ghahfarokhi, A.; Nait Amar, M.; Torsæter, O. Smart Proxy Modeling of a Fractured Reservoir Model for Production Optimization: Implementation of Metaheuristic Algorithm and Probabilistic Application. Nat. Resour. Res. 2021, 30, 2431–2462. [Google Scholar] [CrossRef]
- Benner, P.; Gugercin, S.; Willcox, K. A Survey of Projection-Based Model Reduction Methods for Parametric Dynamical Systems. SIAM Rev. 2015, 57, 483–531. [Google Scholar] [CrossRef]
- Arridge, S.R.; Kaipio, J.P.; Kolehmainen, V.; Schweiger, M.; Somersalo, E.; Tarvainen, T.; Vauhkonen, M. Approximation Errors and Model Reduction with an Application in Optical Diffusion Tomography. Inverse. Probl. 2006, 22, 175–195. [Google Scholar] [CrossRef] [Green Version]
- March, A.; Willcox, K. Provably Convergent Multifidelity Optimization Algorithm Not Requiring High-Fidelity Derivatives. AIAA J. 2012, 50, 1079–1089. [Google Scholar] [CrossRef] [Green Version]
- Cozad, A.; Sahinidis, N.V.; Miller, D.C. Learning Surrogate Models for Simulation-Based Optimization. AIChE J. 2014, 60, 2211–2227. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the Dynamics of Coherent Structures Part I: Coherent Structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Rewienski, M.J. A Trajectory Piecewise-Linear Approach to Model Order Reduction of Nonlinear Dynamical Systems. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1975. Available online: https://dspace.mit.edu/handle/1721.1/28273 (accessed on 28 August 2021).
- Chaturantabut, S.; Sorensen, D.C. Nonlinear Model Reduction via Discrete Empirical Interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Wan, X.; Pekny, J.F.; Reklaitis, G.V. Simulation-Based Optimization with Surrogate Models—Application to Supply Chain Management. Comput. Chem. Eng. 2005, 29, 1317–1328. [Google Scholar] [CrossRef]
- Amsallem, D.; Hetmaniuk, U. A Posteriori Error Estimators for Linear Reduced-Order Models Using Krylov-Based Integrators. Int. J. Numer. Methods Eng. 2015, 102, 1238–1261. [Google Scholar] [CrossRef]
- Rouhani, S.; Myers, D.E. Problems in Space-Time Kriging of Geohydrological Data. Math. Geol. 1990, 22, 611–623. [Google Scholar] [CrossRef]
- Lazzeri, F. Machine Learning for Time Series Forecasting with Python; Wiley: Hoboken, NJ, USA, 2020; ISBN 2020947403. [Google Scholar]
- Mohaghegh, S.D.; Abdulla, F.; Abdou, M.; Gaskari, R.; Maysami, M. Smart Proxy: An Innovative Reservoir Management Tool. In Case Study of a Giant Mature Oilfield in the UAE; OnePetro: Abu Dhabi, United Arab Emirates, 2015. [Google Scholar]
- Amini, S.; Mohaghegh, S.D.; Gaskari, R.; Bromhal, G. Uncertainty Analysis of a CO2 Sequestration Project Using Surrogate Reservoir Modeling Technique; OnePetro: Bakersfield, CA, USA, 2012. [Google Scholar]
- Mohaghegh, S.D.; Hafez, H.H.; Gaskari, R.; Haajizadeh, M.; Kenawy, M. Uncertainty Analysis of a Giant Oil Field in the Middle East Using Surrogate Reservoir Model; OnePetro: Abu Dhabi, United Arab Emirates, 2006. [Google Scholar]
- Mohaghegh, S.D.; Amini, S.; Gholami, V.; Gaskari, R.; Bromhal, G. Grid-Based Surrogate Reservoir Modeling (SRM) for Fast Track Analysis of Numerical Reservoir Simulation Models at the Grid Block Level; OnePetro: Bakersfield, CA, USA, 2012. [Google Scholar]
- Henao, C.A.; Maravelias, C.T. Surrogate-Based Process Synthesis. In Computer Aided Chemical Engineering; Pierucci, S., Ferraris, G.B., Eds.; 20 European Symposium on Computer Aided Process Engineering; Elsevier: Amsterdam, The Netherlands, 2010; Volume 28, pp. 1129–1134. [Google Scholar]
- Hoops, S.; Hontecillas, R.; Abedi, V.; Leber, A.; Philipson, C.; Carbo, A.; Bassaganya-Riera, J. Chapter 5—Ordinary Differential Equations (ODEs) Based Modeling. In Computational Immunology; Bassaganya-Riera, J., Ed.; Academic Press: Cambridge, MA, USA, 2016; pp. 63–78. ISBN 978-0-12-803697-6. [Google Scholar]
- Simske, S. Chapter 5—Sensitivity Analysis and Big System Engineering. In Meta-Analytics; Simske, S., Ed.; Morgan Kaufmann: San Francisco, CA, USA, 2019; pp. 187–201. ISBN 978-0-12-814623-1. [Google Scholar]
- Van Steenkiste, T.; van der Herten, J.; Couckuyt, I.; Dhaene, T. Data-Efficient Sensitivity Analysis with Surrogate Modeling. In Uncertainty Modeling for Engineering Applications; Canavero, F., Ed.; PoliTO Springer Series; Springer: Cham, Switzerland, 2019; pp. 55–69. ISBN 978-3-030-04870-9. [Google Scholar]
- Amini, S.; Mohaghegh, S.D.; Gaskari, R.; Bromhal, G.S. Pattern Recognition and Data-Driven Analytics for Fast and Accurate Replication of Complex Numerical Reservoir Models at the Grid Block Level; OnePetro: Utrecht, The Netherlands, 2014. [Google Scholar]
- Anand, A.; Agrawal, M.; Bhatt, N.; Ram, M. Chapter 11—Software Patch Scheduling Policy Incorporating Functional Safety Standards. In Advances in System Reliability Engineering; Ram, M., Davim, J.P., Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 267–279. ISBN 978-0-12-815906-4. [Google Scholar]
- Hou, Z.; Lu, W.; Chen, M. Surrogate-Based Sensitivity Analysis and Uncertainty Analysis for DNAPL-Contaminated Aquifer Remediation. J. Water Resour. Plan. Manag. 2016, 142, 04016043. [Google Scholar] [CrossRef]
- Iooss, B.; Lemaître, P. A Review on Global Sensitivity Analysis Methods. In Uncertainty Management in Simulation-Optimization of Complex Systems: Algorithms and Applications; Dellino, G., Meloni, C., Eds.; Operations Research/Computer Science Interfaces Series; Springer: Boston, MA, USA, 2015; pp. 101–122. ISBN 978-1-4899-7547-8. [Google Scholar]
- Chaudhry, A.A.; Buchwald, J.; Nagel, T. Local and Global Spatio-Temporal Sensitivity Analysis of Thermal Consolidation around a Point Heat Source. Int. J. Rock Mech. Min. Sci. 2021, 139, 104662. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P. How to Avoid a Perfunctory Sensitivity Analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Ye, M.; Hill, M.C. Chapter 10—Global Sensitivity Analysis for Uncertain Parameters, Models, and Scenarios. In Sensitivity Analysis in Earth Observation Modelling; Petropoulos, G.P., Srivastava, P.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 177–210. ISBN 978-0-12-803011-0. [Google Scholar]
- Razmyan, S.; Hosseinzadeh Lotfi, F. An Application of Monte-Carlo-Based Sensitivity Analysis on the Overlap in Discriminant Analysis. J. Appl. Math. 2012, 2012, 315868. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity Estimates for Nonlinear Mathematical Models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Song, X.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; Xu, C. Global Sensitivity Analysis in Hydrological Modeling: Review of Concepts, Methods, Theoretical Framework, and Applications. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef] [Green Version]
- Bhosekar, A.; Ierapetritou, M. Advances in Surrogate Based Modeling, Feasibility Analysis, and Optimization: A Review. Comput. Chem. Eng. 2018, 108, 250–267. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Information Science and Statistics; Springer: New York, NY, USA, 2006; ISBN 978-0-387-31073-2. [Google Scholar]
- Crombecq, K. Surrogate Modeling of Computer Experiments with Sequential Experimental Design. Ph.D. Thesis, Ghent University, Antwerp, Belgium, 2011. [Google Scholar]
- Pronzato, L.; Müller, W.G. Design of Computer Experiments: Space Filling and Beyond. Stat. Comput. 2012, 22, 681–701. [Google Scholar] [CrossRef]
- Garud, S.S.; Karimi, I.A.; Kraft, M. Design of Computer Experiments: A Review. Comput. Chem. Eng. 2017, 106, 71–95. [Google Scholar] [CrossRef]
- Choi, Y.; Song, D.; Yoon, S.; Koo, J. Comparison of Factorial and Latin Hypercube Sampling Designs for Meta-Models of Building Heating and Cooling Loads. Energies 2021, 14, 512. [Google Scholar] [CrossRef]
- Natoli, C. Classical Designs: Fractional Factorial Designs; Scientific Test and Analysis Techniques Center of Excellence (STAT COE): Hobson, OH, USA, 2018. [Google Scholar]
- Humbird, D.; Fei, Q. Chapter 20—Scale-up Considerations for Biofuels. In Biotechnology for Biofuel Production and Optimization; Eckert, C.A., Trinh, C.T., Eds.; Elsevier: Amsterdam, The Netherland, 2016; pp. 513–537. ISBN 978-0-444-63475-7. [Google Scholar]
- Hajjar, Z.; Kazemeini, M.; Rashidi, A.; Soltanali, S. Optimizing Parameters Affecting Synthesis of a Novel Co–Mo/GO Catalyst in a Naphtha HDS Reaction Utilizing D-Optimal Experimental Design Method. J. Taiwan Inst. Chem. Eng. 2017, 78, 566–575. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Viana, F.A.C.; Venter, G.; Balabanov, V. An Algorithm for Fast Optimal Latin Hypercube Design of Experiments. Int. J. Numer. Methods Eng. 2010, 82, 135–156. [Google Scholar] [CrossRef] [Green Version]
- Hedayat, A.S.; Sloane, N.J.A.; Stufken, J. Orthogonal Arrays: Theory and Applications; Springer Series in Statistics; Springer: New York, NY, USA, 1999; ISBN 978-0-387-98766-8. [Google Scholar]
- Eason, J.; Cremaschi, S. Adaptive Sequential Sampling for Surrogate Model Generation with Artificial Neural Networks. Comput. Chem. Eng. 2014, 68, 220–232. [Google Scholar] [CrossRef]
- Provost, F.; Jensen, D.; Oates, T. Efficient Progressive Sampling. In Proceedings of the Fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 15–18 August 1999; Association for Computing Machinery: New York, NY, USA, 1999; pp. 23–32. [Google Scholar]
- Gamerman, D.; Lopes, H.F. Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006; ISBN 978-1-58488-587-0. [Google Scholar]
- Sobol, I.M. On the Distribution of Points in a Cube and the Approximate Evaluation of Integrals. USSR Comput. Math. Math. Phys. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Halton, J.H. On the Efficiency of Certain Quasi-Random Sequences of Points in Evaluating Multi-Dimensional Integrals. Numer. Math. 1960, 2, 84–90. [Google Scholar] [CrossRef]
- Cheng, J.; Druzdzel, M.J. Computational Investigation of Low-Discrepancy Sequences in Simulation Algorithms for Bayesian Networks. arXiv 2013, arXiv:1301.3841. [Google Scholar]
- Qian, P.Z.G. Nested Latin Hypercube Designs. Biometrika 2009, 96, 957–970. [Google Scholar] [CrossRef] [Green Version]
- Rennen, G.; Husslage, B.; Van Dam, E.R.; Den Hertog, D. Nested Maximin Latin Hypercube Designs. Struct. Multidisc. Optim. 2010, 41, 371–395. [Google Scholar] [CrossRef] [Green Version]
- Xiong, F.; Xiong, Y.; Chen, W.; Yang, S. Optimizing Latin Hypercube Design for Sequential Sampling of Computer Experiments. Eng. Optim. 2009, 41, 793–810. [Google Scholar] [CrossRef]
- Barton, R.R. Metamodels for Simulation Input-Output Relations. In Proceedings of the 24th Conference on Winter Simulation, WSC 1992, Arlington, VA, USA, 13–16 December 1992; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 1992; pp. 289–299. [Google Scholar]
- van Beers, W.C.M.; Kleijnen, J.P.C. Kriging Interpolation in Simulation: A Survey. In Proceedings of the 2004 Winter Simulation Conference, Washington, DC, USA, 5–8 December 2004; Volume 1, p. 121. [Google Scholar]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and Analysis of Computer Experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Sasena, M.J. Flexibility and Efficiency Enhancements for Constrained Global Design Optimization with Kriging Approximations. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2002. [Google Scholar]
- Sacks, J.; Schiller, S.B.; Welch, W.J. Designs for Computer Experiments. Technometrics 1989, 31, 41–47. [Google Scholar] [CrossRef]
- Simpson, T.W.; Poplinski, J.D.; Koch, P.N.; Allen, J.K. Metamodels for Computer-Based Engineering Design: Survey and Recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef] [Green Version]
- McBride, K.; Sundmacher, K. Overview of Surrogate Modeling in Chemical Process Engineering. Chem. Ing. Tech. 2019, 91, 228–239. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Quirós, E.; Felicísimo, Á.M.; Cuartero, A. Testing Multivariate Adaptive Regression Splines (MARS) as a Method of Land Cover Classification of TERRA-ASTER Satellite Images. Sensors 2009, 9, 9011–9028. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T.C. Multivariate Adaptive Regression Splines and Neural Network Models for Prediction of Pile Drivability. Geosci. Front. 2016, 7, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Van Nguyen, N.; Lee, J.-W.; Tyan, M.; Kim, S. Repetitively Enhanced Neural Networks Method for Complex Engineering Design Optimisation Problems. Aeronaut. J. 2015, 119, 1253–1270. [Google Scholar] [CrossRef]
- Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation Functions: Comparison of Trends in Practice and Research for Deep Learning. arXiv 2018, arXiv:1811.03378. [Google Scholar]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-Art in Artificial Neural Network Applications: A Survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, S.-C.; Le, T.-H. Chapter 8—Convolutional Neural Network Architectures. In Principles and Labs for Deep Learning; Huang, S.-C., Le, T.-H., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 201–217. ISBN 978-0-323-90198-7. [Google Scholar]
- Haykin, S.O. Neural Networks and Learning Machines, 3rd ed.; Pearson: New York, NY, USA, 2009. [Google Scholar]
- Chen, S.; Cowan, C.F.N.; Grant, P.M. Orthogonal Least Squares Learning Algorithm for Radial Basis Function Networks. IEEE Trans. Neural Netw. 1991, 2, 302–309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vapnik, V. The Nature of Statistical Learning Theory. In Information Science and Statistics, 2nd ed.; Springer: New York, NY, USA, 2000; ISBN 978-0-387-98780-4. [Google Scholar]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support Vector Regression Machines. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA; Mozer, M.C., Jordan, M., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1997; Volume 9. [Google Scholar]
- Awad, M.; Khanna, R. Support Vector Regression. In Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Awad, M., Khanna, R., Eds.; Apress: Berkeley, CA, USA, 2015; pp. 67–80. ISBN 978-1-4302-5990-9. [Google Scholar]
- Koza, J.R. Genetic Programming as a Means for Programming Computers by Natural Selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Liao, Y.; Wang, J.; Meng, B.; Li, X. Integration of GP and GA for Mapping Population Distribution. Int. J. Geogr. Inf. Sci. 2010, 24, 47–67. [Google Scholar] [CrossRef]
- Raymond, C.; Chen, Q.; Xue, B.; Zhang, M. Genetic Programming with Rademacher Complexity for Symbolic Regression. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 2657–2664. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Ho, T.K. The Random Subspace Method for Constructing Decision Forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef] [Green Version]
- Storlie, C.B.; Swiler, L.P.; Helton, J.C.; Sallaberry, C.J. Implementation and Evaluation of Nonparametric Regression Procedures for Sensitivity Analysis of Computationally Demanding Models. Reliab. Eng. Syst. Saf. 2009, 94, 1735–1763. [Google Scholar] [CrossRef]
- Al-Mudhafar, W.J. Polynomial and Nonparametric Regressions for Efficient Predictive Proxy Metamodeling: Application through the CO2-EOR in Shale Oil Reservoirs. J. Nat. Gas Sci. Eng. 2019, 72, 103038. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A Comparative Analysis of XGBoost. Artif Intell Rev 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Zhong, R.; Johnson, R.; Chen, Z. Generating Pseudo Density Log from Drilling and Logging-While-Drilling Data Using Extreme Gradient Boosting (XGBoost). Int. J. Coal Geol. 2020, 220, 103416. [Google Scholar] [CrossRef]
- Wiener, N. The Homogeneous Chaos. Am. J. Math. 1938, 60, 897–936. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, Z.; Hu, J.; Hu, Y. Surrogate Modeling of High-Dimensional Problems via Data-Driven Polynomial Chaos Expansions and Sparse Partial Least Square. Comput. Methods Appl. Mech. Eng. 2020, 364, 112906. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener–Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Jain, T.; Patel, R.G.; Trivedi, J. Application of Polynomial Chaos Theory as an Accurate and Computationally Efficient Proxy Model for Heterogeneous Steam-Assisted Gravity Drainage Reservoirs. Energy Sci. Eng. 2017, 5, 270–289. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, A.; Khamehchi, E. Developing a Novel Workflow for Natural Gas Lift Optimization Using Advanced Support Vector Machine. J. Nat. Gas Sci. Eng. 2016, 28, 626–638. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. In Complex Adaptive Systems; A Bradford Book: Cambridge, MA, USA, 1992; ISBN 978-0-262-08213-6. [Google Scholar]
- Erdinc, O.; Uzunoglu, M. Optimum Design of Hybrid Renewable Energy Systems: Overview of Different Approaches. Renew. Sustain. Energy Rev. 2012, 16, 1412–1425. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. In Readings in Computer Vision; Fischler, M.A., Firschein, O., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1987; pp. 606–615. ISBN 978-0-08-051581-6. [Google Scholar]
- Mukhairez, H.H.A.; Maghari, A.Y.A. Performance Comparison of Simulated Annealing, GA and ACO Applied to TSP. IJICR 2015, 6, 647–654. [Google Scholar] [CrossRef]
- Qin, J.; Ni, L.; Shi, F. Combined Simulated Annealing Algorithm for the Discrete Facility Location Problem. Sci. World J. 2012, 2012, e576392. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant System: Optimization by a Colony of Cooperating Agents. IEEE Trans. Syst. Man Cybern. B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Natural Computing Series; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 978-3-540-20950-8. [Google Scholar]
- Kachitvichyanukul, V. Comparison of Three Evolutionary Algorithms: GA, PSO, and DE. Ind. Eng. Manag. Syst. 2012, 11, 215–223. [Google Scholar] [CrossRef] [Green Version]
- dos Santos Amorim, E.P.; Xavier, C.R.; Campos, R.S.; dos Santos, R.W. Comparison between Genetic Algorithms and Differential Evolution for Solving the History Matching Problem. In Proceedings of the Computational Science and Its Applications–ICCSA 2012, Salvador de Bahia, Brazil, 18–21 June 2012; Murgante, B., Gervasi, O., Misra, S., Nedjah, N., Rocha, A.M.A.C., Taniar, D., Apduhan, B.O., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 635–648. [Google Scholar]
- Slowik, A.; Kwasnicka, H. Evolutionary Algorithms and Their Applications to Engineering Problems. Neural Comput Applic 2020, 32, 12363–12379. [Google Scholar] [CrossRef] [Green Version]
- Georgioudakis, M.; Plevris, V. A Comparative Study of Differential Evolution Variants in Constrained Structural Optimization. Front. Built Environ. 2020, 6, 102. [Google Scholar] [CrossRef]
- Batycky, R.P.; Blunt, M.J.; Thiele, M.R. A 3D Field-Scale Streamline-Based Reservoir Simulator. SPE Reserv. Eng. 1997, 12, 246–254. [Google Scholar] [CrossRef]
- Tanaka, S.; Onishi, T.; Kam, D.; Dehghani, K.; Wen, X.-H. Application of Combined Streamline Based Reduced-Physics Surrogate and Response Surface Method for Field Development Optimization; OnePetro: Dhahran, Saudi Arabia, 2020. [Google Scholar]
- Thiele, M.R.; Batycky, R.P. Water Injection Optimization Using a Streamline-Based Workflow; OnePetro: Denver, CO, USA, 2003. [Google Scholar]
- Kovscek, A.R.; Wang, Y. Geologic Storage of Carbon Dioxide and Enhanced Oil Recovery. I. Uncertainty Quantification Employing a Streamline Based Proxy for Reservoir Flow Simulation. Energy Convers. Manag. 2005, 46, 1920–1940. [Google Scholar] [CrossRef]
- Wang, Y.; Kovscek, A.R. Streamline Approach for History Matching Production Data. SPE J. 2000, 5, 353–362. [Google Scholar] [CrossRef] [Green Version]
- Stenerud, V.R.; Kippe, V.; Lie, K.-A.; Datta-Gupta, A. Adaptive Multiscale Streamline Simulation and Inversion for High-Resolution Geomodels. SPE J. 2008, 13, 99–111. [Google Scholar] [CrossRef]
- Kam, D.; Han, J.; Datta-Gupta, A. Streamline-Based History Matching of Bottomhole Pressure and Three-Phase Production Data Using a Multiscale Approach. J. Pet. Sci. Eng. 2017, 154, 217–233. [Google Scholar] [CrossRef]
- Milliken, W.J.; Emanuel, A.S.; Chakravarty, A. Applications of 3D Streamline Simulation to Assist History Matching. SPE Reserv. Eval. Eng. 2001, 4, 502–508. [Google Scholar] [CrossRef]
- Taware, S.; Park, H.-Y.; Datta-Gupta, A.; Bhattacharya, S.; Tomar, A.K.; Kumar, M.; Rao, H.S. Well Placement Optimization in a Mature Carbonate Waterflood Using Streamline-Based Quality Maps; OnePetro: Mumbai, India, 2012. [Google Scholar]
- Thiele, M.R.; Batycky, R.P.; Blunt, M.J.; Orr, F.M., Jr. Simulating Flow in Heterogeneous Systems Using Streamtubes and Streamlines. SPE Reserv. Eng. 1996, 11, 5–12. [Google Scholar] [CrossRef]
- Datta-Gupta, A.; King, M.J. Streamline Simulation: Theory and Practice; Society of Petroleum Engineers: London, UK, 2007; ISBN 978-1-55563-111-6. [Google Scholar]
- Bardy, G.; Biver, P.; Caumon, G.; Renard, P. Oil Production Uncertainty Assessment by Predicting Reservoir Production Curves and Confidence Intervals from Arbitrary Proxy Responses. J. Pet. Sci. Eng. 2019, 176, 116–125. [Google Scholar] [CrossRef] [Green Version]
- Allam, F.A.; El-Banbi, A.H.; Bustami, S.S.; Saada, T.H.; Fahmy, I.I. History Match Tuning through Different Upscaling Algorithms; OnePetro: Houston, TX, USA, 2004. [Google Scholar]
- Li, H.; Durlofsky, L.J. Upscaling for Compositional Reservoir Simulation. SPE J. 2016, 21, 0873–0887. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, X.; Wu, X.-H.; Bi, L. Multiphase Upscaling Using Approximation Techniques; OnePetro: The Woodlands, TX, USA, 2013. [Google Scholar]
- Rios, V.S.; Santos, L.O.S.; Quadros, F.B.; Schiozer, D.J. New Upscaling Technique for Compositional Reservoir Simulations of Miscible Gas Injection. J. Pet. Sci. Eng. 2019, 175, 389–406. [Google Scholar] [CrossRef]
- Bruce, W.A. An Electrical Device for Analyzing Oil-Reservoir Behavior. Trans. AIME 1943, 151, 112–124. [Google Scholar] [CrossRef]
- Yousef, A.A.; Gentil, P.H.; Jensen, J.L.; Lake, L.W. A Capacitance Model to Infer Interwell Connectivity from Production and Injection Rate Fluctuations. SPE Reserv. Eval. Eng. 2006, 9, 630–646. [Google Scholar] [CrossRef]
- Almarri, M.; Prakasa, B.; Muradov, K.; Davies, D. Identification and Characterization of Thermally Induced Fractures Using Modern Analytical Techniques; OnePetro: Dammam, Saudi Arabia, 2017. [Google Scholar]
- de Holanda, R.W.; Gildin, E.; Jensen, J.L.; Lake, L.W.; Kabir, C.S. A State-of-the-Art Literature Review on Capacitance Resistance Models for Reservoir Characterization and Performance Forecasting. Energies 2018, 11, 3368. [Google Scholar] [CrossRef] [Green Version]
- Artun, E. Characterizing Reservoir Connectivity and Forecasting Waterflood Performance Using Data-Driven and Reduced-Physics Models; OnePetro: Anchorage, AK, USA, 2016. [Google Scholar]
- Wilson, K.C.; Durlofsky, L.J. Computational Optimization of Shale Resource Development Using Reduced-Physics Surrogate Models; OnePetro: Bakersfield, CA, USA, 2012. [Google Scholar]
- Chatterjee, A. An Introduction to the Proper Orthogonal Decomposition. Curr. Sci. 2000, 78, 808–817. [Google Scholar]
- Markovinović, R.; Jansen, J.D. Accelerating Iterative Solution Methods Using Reduced-Order Models as Solution Predictors. Int. J. Numer. Methods Eng. 2006, 68, 525–541. [Google Scholar] [CrossRef]
- Cardoso, M.A.; Durlofsky, L.J.; Sarma, P. Development and Application of Reduced-Order Modeling Procedures for Subsurface Flow Simulation. Int. J. Numer. Methods Eng. 2009, 77, 1322–1350. [Google Scholar] [CrossRef]
- van Doren, J.F.M.; Markovinović, R.; Jansen, J.-D. Reduced-Order Optimal Control of Water Flooding Using Proper Orthogonal Decomposition. Comput. Geosci. 2006, 10, 137–158. [Google Scholar] [CrossRef]
- Sun, X.; Xu, M. Optimal Control of Water Flooding Reservoir Using Proper Orthogonal Decomposition. J. Comput. Appl. Math. 2017, 320, 120–137. [Google Scholar] [CrossRef]
- Kaleta, M.P.; Hanea, R.G.; Heemink, A.W.; Jansen, J.-D. Model-Reduced Gradient-Based History Matching. Comput Geosci 2011, 15, 135–153. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, M.A.A.; Durlofsky, L.J.J. Use of Reduced-Order Modeling Procedures for Production Optimization. SPE J. 2009, 15, 426–435. [Google Scholar] [CrossRef]
- Cardoso, M.A. Reduced-Order Models for Reservoir Simulation; OnePetro: New Orleans, LA, USA, 2009. [Google Scholar]
- Xiao, C.; Leeuwenburgh, O.; Lin, H.X.; Heemink, A. Non-Intrusive Subdomain POD-TPWL for Reservoir History Matching. Comput. Geosci. 2019, 23, 537–565. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Sarma, P.; Durlofsky, L.J. Reduced-Order Flow Modeling and Geological Parameterization for Ensemble-Based Data Assimilation. Comput. Geosci. 2013, 55, 54–69. [Google Scholar] [CrossRef]
- Rousset, M.A.H.; Huang, C.K.; Klie, H.; Durlofsky, L.J. Reduced-Order Modeling for Thermal Recovery Processes. Comput. Geosci. 2014, 18, 401–415. [Google Scholar] [CrossRef]
- He, J.; Durlofsky, L.J. Reduced-Order Modeling for Compositional Simulation Using Trajectory Piecewise Linearization; OnePetro: The Woodlands, TX, USA, 2013. [Google Scholar]
- Gildin, E.; Ghasemi, M.; Romanovskay, A.; Efendiev, Y. Nonlinear Complexity Reduction for Fast Simulation of Flow in Heterogeneous Porous Media; OnePetro: The Woodlands, TX, USA, 2013. [Google Scholar]
- Klie, H. Unlocking Fast Reservoir Predictions via Non-Intrusive Reduced Order Models; OnePetro: The Woodlands, TX, USA, 2013. [Google Scholar]
- Li, J.; Fan, X.; Wang, Y.; Yu, B.; Sun, S.; Sun, D. A POD-DEIM Reduced Model for Compressible Gas Reservoir Flow Based on the Peng-Robinson Equation of State. J. Nat. Gas Sci. Eng. 2020, 79, 103367. [Google Scholar] [CrossRef]
- Ghommem, M.; Gildin, E.; Ghasemi, M. Complexity Reduction of Multiphase Flows in Heterogeneous Porous Media. SPE J. 2016, 21, 144–151. [Google Scholar] [CrossRef] [Green Version]
- Alghareeb, Z.M.; Williams, J.R. Optimum Decision-Making in Reservoir Managment Using Reduced-Order Models; OnePetro: New Orleans, LA, USA, 2013. [Google Scholar]
- Yoon, S.; Alghareeb, Z.M.; Williams, J.R. Hyper-Reduced-Order Models for Subsurface Flow Simulation. SPE J. 2016, 21, 2128–2140. [Google Scholar] [CrossRef]
- Peherstorfer, B.; Butnaru, D.; Willcox, K.; Bungartz, H.-J. Localized Discrete Empirical Interpolation Method. SIAM J. Sci. Comput. 2014, 36, A168–A192. [Google Scholar] [CrossRef]
- Trehan, S.; Durlofsky, L.J. Trajectory Piecewise Quadratic Reduced-Order Model for Subsurface Flow, with Application to PDE-Constrained Optimization. J. Comput. Phys. 2016, 326, 446–473. [Google Scholar] [CrossRef]
- Sidhu, H.S.; Narasingam, A.; Siddhamshetty, P.; Kwon, J.S.-I. Model Order Reduction of Nonlinear Parabolic PDE Systems with Moving Boundaries Using Sparse Proper Orthogonal Decomposition: Application to Hydraulic Fracturing. Comput. Chem. Eng. 2018, 112, 92–100. [Google Scholar] [CrossRef] [Green Version]
- Suwartadi, E. Gradient-Based Methods for Production Optimization of Oil Reservoirs. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2012. [Google Scholar]
- He, J. Reduced-Order Modeling for Oil-Water and Compositional Systems, with Application to Data Assimilation and Production Optimization. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2013. [Google Scholar]
- Golzari, A.; Haghighat Sefat, M.; Jamshidi, S. Development of an Adaptive Surrogate Model for Production Optimization. J. Pet. Sci. Eng. 2015, 133, 677–688. [Google Scholar] [CrossRef]
- Amiri Kolajoobi, R.; Haddadpour, H.; Emami Niri, M. Investigating the Capability of Data-Driven Proxy Models as Solution for Reservoir Geological Uncertainty Quantification. J. Pet. Sci. Eng. 2021, 205, 108860. [Google Scholar] [CrossRef]
- Peng, C.Y.; Gupta, R. Experimental Design in Deterministic Modelling: Assessing Significant Uncertainties; OnePetro: Jakarta, Indonesia, 2003. [Google Scholar]
- Zubarev, D.I. Pros and Cons of Applying Proxy-Models as a Substitute for Full Reservoir Simulations; OnePetro: New Orleans, LA, USA, 2009. [Google Scholar]
- Guo, Z.; Chen, C.; Gao, G.; Vink, J. Applying Support Vector Regression to Reduce the Effect of Numerical Noise and Enhance the Performance of History Matching; OnePetro: San Antonio, TX, USA, 2017. [Google Scholar]
- Avansi, G.D. Use of Proxy Models in the Selection of Production Strategy and Economic Evaluation of Petroleum Fields; OnePetro: New Orleans, LA, USA, 4 October 2009. [Google Scholar]
- Ligero, E.L.; Madeira, M.G.; Schiozer, D.J. Comparison of Techniques for Risk Analysis Applied to Petroleum-Field Development; OnePetro: Rio de Janeiro, Brazil, 2005. [Google Scholar]
- Risso, F.V.A.; Risso, F.F.; Schiozer, D.J. Risk Assessment of Oil Fields Using Proxy Models: A Case Study. J. Can. Pet. Technol. 2008, 47, 9–14. [Google Scholar] [CrossRef]
- Ghassemzadeh, S.; Charkhi, A.H. Optimization of Integrated Production System Using Advanced Proxy Based Models: A New Approach. J. Nat. Gas Sci. Eng. 2016, 35, 89–96. [Google Scholar] [CrossRef]
- Zangl, G.; Giovannoli, M.; Stundner, M. Application of Artificial Intelligence in Gas Storage Management; OnePetro: Vienna, Austria, 2006. [Google Scholar]
- Artun, E.; Ertekin, T.; Watson, R.; Al-Wadhahi, M. Development of Universal Proxy Models for Screening and Optimization of Cyclic Pressure Pulsing in Naturally Fractured Reservoirs. J. Nat. Gas Sci. Eng. 2011, 3, 667–686. [Google Scholar] [CrossRef]
- Sprunger, C.; Muther, T.; Syed, F.I.; Dahaghi, A.K.; Neghabhan, S. State of the Art Progress in Hydraulic Fracture Modeling Using AI/ML Techniques. Model. Earth Syst. Environ. 2022, 8, 1–13. [Google Scholar] [CrossRef]
- Syed, F.I.; AlShamsi, A.; Dahaghi, A.K.; Neghabhan, S. Application of ML & AI to Model Petrophysical and Geomechanical Properties of Shale Reservoirs—A Systematic Literature Review. Petroleum 2022, 8, 158–166. [Google Scholar] [CrossRef]
- Gu, J.; Liu, W.; Zhang, K.; Zhai, L.; Zhang, Y.; Chen, F. Reservoir Production Optimization Based on Surrograte Model and Differential Evolution Algorithm. J. Pet. Sci. Eng. 2021, 205, 108879. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, K.; Xue, X.; Zhang, L.; Yao, J.; Sun, H.; Fan, L.; Yang, Y. Surrogate-Assisted Evolutionary Algorithm with Dimensionality Reduction Method for Water Flooding Production Optimization. J. Pet. Sci. Eng. 2020, 185, 106633. [Google Scholar] [CrossRef]
- Ogbeiwi, P.; Stephen, K.D.; Arinkoola, A.O. Robust Optimisation of Water Flooding Using an Experimental Design-Based Surrogate Model: A Case Study of a Niger-Delta Oil Reservoir. J. Pet. Sci. Eng. 2020, 195, 107824. [Google Scholar] [CrossRef]
- Bruyelle, J.; Guérillot, D. Optimization of Waterflooding Strategy Using Artificial Neural Networks; OnePetro: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- Bruyelle, J.; Guérillot, D. Well Placement Optimization with an Artificial Intelligence Method Applied to Brugge Field; OnePetro: Dubai, United Arab Emirates, 2019. [Google Scholar]
- Hassani, H.; Sarkheil, H.; Foroud, T.; Karimpooli, S. A Proxy Modeling Approach to Optimization Horizontal Well Placement; OnePetro: San Francisco, CA, USA, 2011. [Google Scholar]
- Nwachukwu, A.; Jeong, H.; Pyrcz, M.; Lake, L.W. Fast Evaluation of Well Placements in Heterogeneous Reservoir Models Using Machine Learning. J. Pet. Sci. Eng. 2018, 163, 463–475. [Google Scholar] [CrossRef]
- Aydin, H.; Akin, S.; Senturk, E. A Proxy Model for Determining Reservoir Pressure and Temperature for Geothermal Wells. Geothermics 2020, 88, 101916. [Google Scholar] [CrossRef]
- Wang, L.; Li, Z.; Adenutsi, C.D.; Zhang, L.; Lai, F.; Wang, K. A Novel Multi-Objective Optimization Method for Well Control Parameters Based on PSO-LSSVR Proxy Model and NSGA-II Algorithm. J. Pet. Sci. Eng. 2021, 196, 107964. [Google Scholar] [CrossRef]
- Fedutenko, E.; Yang, C.; Card, C.; Nghiem, L.X. Time-Dependent Proxy Modeling of SAGD Process; OnePetro: Calgary, AB, Canada, 11 June 2013. [Google Scholar]
- Al-Mudhafar, W.J.; Rao, D.N. Proxy-Based Metamodeling Optimization of the Gas-Assisted Gravity Drainage GAGD Process in Heterogeneous Sandstone Reservoirs; OnePetro: Bakersfield, CA, USA, 2017. [Google Scholar]
- Jaber, A.K.; Awang, M.B.; Lenn, C.P. Box-Behnken Design for Assessment Proxy Model of Miscible CO2-WAG in Heterogeneous Clastic Reservoir. J. Nat. Gas Sci. Eng. 2017, 40, 236–248. [Google Scholar] [CrossRef]
- Agada, S.; Geiger, S.; Elsheikh, A.; Oladyshkin, S. Data-Driven Surrogates for Rapid Simulation and Optimization of WAG Injection in Fractured Carbonate Reservoirs. Pet. Geosci. 2017, 23, 270–283. [Google Scholar] [CrossRef]
- Ibiam, E.; Geiger, S.; Demyanov, V.; Arnold, D. Optimization of Polymer Flooding in a Heterogeneous Reservoir Considering Geological and History Matching Uncertainties. SPE Reserv. Eval. Eng. 2021, 24, 19–36. [Google Scholar] [CrossRef]
- Alenezi, F.; Mohaghegh, S. A Data-Driven Smart Proxy Model for a Comprehensive Reservoir Simulation. In Proceedings of the 2016 4th Saudi International Conference on Information Technology (Big Data Analysis) (KACSTIT), Riyadh, Saudi Arabia, 6–9 November 2016; pp. 1–6. [Google Scholar]
- Tang, X.; James, L.A.; Johansen, T.E. A New Streamline Model for Near-Well Flow Validated with Radial Flow Experiments. Comput. Geosci. 2018, 22, 363–388. [Google Scholar] [CrossRef]
- Smolyak, S.A. Quadrature and Interpolation Formulas for Tensor Products of Certain Classes of Functions. Sov. Math. Dokl. 1963, 4, 240–243. [Google Scholar]
- Gao, G.; Vink, J.C.; Chen, C.; Tarrahi, M.; El Khamra, Y. Uncertainty Quantification for History Matching Problems with Multiple Best Matches Using a Distributed Gauss-Newton Method; OnePetro: Dubai, United Arab Emirates, 2016. [Google Scholar]
- Hansen, N.; Ostermeier, A. Completely Derandomized Self-Adaptation in Evolution Strategies. EVolume Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. EVolume Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Simonov, M.; Shubin, A.; Penigin, A.; Perets, D.; Belonogov, E.; Margarit, A. Optimization of Oil Field Development Using a Surrogate Model: Case of Miscible Gas Injection; OnePetro: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- Redouane, K.; Zeraibi, N.; Nait Amar, M. Automated Optimization of Well Placement via Adaptive Space-Filling Surrogate Modelling and Evolutionary Algorithm; OnePetro: Abu Dhabi, United Arab Emirates, 2018. [Google Scholar]
- Jang, J.-S.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Hoteit, I.; Wheeler, M.F. Efficient Bayesian Inference of Subsurface Flow Models Using Nested Sampling and Sparse Polynomial Chaos Surrogates. Comput. Methods Appl. Mech. Eng. 2014, 269, 515–537. [Google Scholar] [CrossRef]
- Yu, T.; Wilkinson, D.; Castellini, A. Constructing Reservoir Flow Simulator Proxies Using Genetic Programming for History Matching and Production Forecast Uncertainty Analysis. J. Artif. EVolume Appl. 2007, 2008, e263108. [Google Scholar] [CrossRef] [Green Version]
- Hammersley, J.M. Monte Carlo Methods for Solving Multivariable Problems. Ann. New York Acad. Sci. 1960, 86, 844–874. [Google Scholar] [CrossRef]
- Kalla, S.; White, C.D. Efficient Design of Reservoir Simulation Studies for Development and Optimization; OnePetro: Dallas, TX, USA, 2005. [Google Scholar]
- Kim, Y.D.; Durlofsky, L.J. Convolutional-Recurrent Neural Network Proxy for Robust Optimization and Closed-Loop Reservoir Management. arXiv 2022, arXiv:2203.07524. [Google Scholar]
- Kim, Y.D.; Durlofsky, L.J. A Recurrent Neural Network–Based Proxy Model for Well-Control Optimization with Nonlinear Output Constraints. SPE J. 2021, 26, 1837–1857. [Google Scholar] [CrossRef]
- Kim, J.; Yang, H.; Choe, J. Robust Optimization of the Locations and Types of Multiple Wells Using CNN Based Proxy Models. J. Pet. Sci. Eng. 2020, 193, 107424. [Google Scholar] [CrossRef]

| Modeling Technique | Advantages | Disadvantages |
|---|---|---|
| PR |
| |
| KG |
| |
| MARS |
|
|
| ANN |
|
|
| RBF |
|
|
| SVR |
|
|
| GP |
|
|
| RF |
|
|
| XGBoost |
|
|
| PCE |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahrami, P.; Sahari Moghaddam, F.; James, L.A. A Review of Proxy Modeling Highlighting Applications for Reservoir Engineering. Energies 2022, 15, 5247. https://doi.org/10.3390/en15145247
Bahrami P, Sahari Moghaddam F, James LA. A Review of Proxy Modeling Highlighting Applications for Reservoir Engineering. Energies. 2022; 15(14):5247. https://doi.org/10.3390/en15145247
Chicago/Turabian StyleBahrami, Peyman, Farzan Sahari Moghaddam, and Lesley A. James. 2022. "A Review of Proxy Modeling Highlighting Applications for Reservoir Engineering" Energies 15, no. 14: 5247. https://doi.org/10.3390/en15145247
APA StyleBahrami, P., Sahari Moghaddam, F., & James, L. A. (2022). A Review of Proxy Modeling Highlighting Applications for Reservoir Engineering. Energies, 15(14), 5247. https://doi.org/10.3390/en15145247