Abstract
Clean energy liquid oxygen is more and more widely used in aerospace, but the research on the thermodynamic characteristics of liquid oxygen is still less. In this paper, a method for correcting the local saturated vapor pressure by thermodynamic effect is proposed, so we establish the Zwart modified cavitation model considering the thermodynamic characteristics. We choose the turbine pump inducer as the research object, and select liquid water and liquid oxygen at different temperatures as the fluid medium. Based on two different Zwart cavitation models, the cavitation flow characteristics of liquid water at different temperatures of 298 K, 320 K and 350 K are numerically simulated and analyzed, and the cavitation flow characteristics of liquid oxygen at different temperatures of 85 K, 90 K and 95 K are also numerically simulated and analyzed. According to the analysis of the simulation results, for liquid water at the temperature of 298–350 K, since the change range of its thermophysical parameters is very small, the inhibition of cavitation is not obvious, and the thermodynamic characteristics are not significant. For liquid oxygen, the cavitation effect is obvious at different temperatures. When the temperature increases gradually, the thermodynamic effect of liquid oxygen becomes more obvious, which can effectively inhibit the cavitation phenomenon of the inducer in the steady-state cavitation flow.
1. Introduction
The development of a high thrust liquid rocket engine pursues a high specific impulse and high thrust mass ratio, which makes the rotating speed of turbine pump higher and higher, and the fault problem of turbine pump caused by cavitation becomes more and more prominent. The installation of an inducer with high anti cavitation performance in front of a high-speed turbine pump has become the key technology to ensure the superior anti-cavitation performance of a turbine pump [1,2]. Green and clean energy, such as liquid hydrogen and liquid oxygen, is often used as the propellant of a high thrust oxyhydrogen engine. Its physical parameters are very sensitive to the temperature changes. When cavitation occurs, it shows a very strong thermodynamic effect [3].
Cavitation refers to the phenomenon that a fluid forms a gas-filled or steam-filled cavity under the influence of tensile stress generated by a local pressure lower than its saturated steam pressure [4]. When the static pressure in the flow locally drops to the vapor pressure of the liquid due to excess, a cavity filled with steam will be generated. Therefore, some fluid will evaporate and generate a two-phase flow in a small area of the flow field. When the static pressure transmitted downstream exceeds the steam pressure again, it will suddenly condense. When cavitation occurs, a cavity will grow in the liquid, so the latent heat required for evaporation can only be provided by the liquid around the cavity. Therefore, the liquid near the interface of the cavity is cooled, and the temperature in the cavity is lower than the temperature of the fluid, which means that the cavitation phenomenon is very sensitive to the temperature of the liquid. The liquid absorbs its own vaporization latent heat during the vaporization process, resulting in the temperature difference between the bubble and the surrounding liquid, which is lower than the temperature of the external liquid. According to Brennen [5], with the increase of the liquid temperature, the growth of cavitation is easy to be inhibited, which is called the thermodynamic effect. For low-temperature media such as liquid hydrogen and liquid oxygen [6], the cavitation mechanism is extremely complex due to their sensitive physical properties
Due to the lack of low-temperature medium cavitation test verification, most of the exploration of cavitation models still use the low-temperature experimental data made by Hord [7,8,9] in the 1970s. Although the commonly used cavitation models have good applicability in a normal temperature water cavitation flow, most of them are isothermal cavitation models developed based on experience, which cannot accurately predict the cavitation characteristics of low-temperature and high-temperature media with strong thermodynamic effects. As for the research on a cavitation model considering a thermodynamic effect, domestic and foreign scholars mainly modify the existing cavitation model and develop a cavitation model suitable for fluids with obvious thermodynamic effects. At present, the commonly used Merkle model [10], Singhal model [11], Schnerr-Sauer model [12] and Zwart model [13] are mostly two-phase mass transport equations based on the Rayleigh-Plesset cavitation dynamic equation, which are relatively mature cavitation models applied in numerical simulations. Goncalvès et al. [14] proposed a uniform single fluid cavitation model considering the thermal effect. Through numerical calculations, the overall performance of the inducer can be well-estimated when non-cavitation and cavitation occur. Ji et al. [15] modified the Singhal cavitation model and found that the modified cavitation model can better match the test results. Xu et al. [16] proposed a modified Merkle cavitation model to simulate the cavitation suppression of the inducer in heat-sensitive fluid. The results show that the cavitation performance of the inducer in liquid nitrogen is better than that in water.
The problem of low-temperature fluid cavitation has attracted extensive attention recently, and it is also one of the difficulties in cavitation research. In terms of numerical simulation research, considering the influence of the thermodynamic effect on the cavitation flow, the cavitation model needs to be improved and continue to carry out more in-depth research and master the flow characteristics of low-temperature fluid cavitation. Tseng et al. [17] carried out the numerical calculation of the cavitation thermal effect by modifying the cavitation model and combining the filtering method and obtained the calculation results, which are in good agreement with the experimental values. Li [18] modified the Zwart cavitation model on the basis of the turbulence model and proposed four cavitation models considering the thermodynamic effects. The numerical simulation of high-temperature water flow around hydrofoil and NACA0015 airfoils shows that the evaporation and condensation coefficients of 10 and 0.002 are in good agreement with the experimental results.
At present, clean energy liquid oxygen as propellants is widely used in aerospace, but there is little research on the low-temperature characteristics of liquid oxygen. Since the experimental requirements of cryogenic liquid oxygen in a liquid rocket engine are very high, and the experimental conditions and equipment are difficult to achieve, and an effective numerical simulation is selected for the analysis. The main purpose of this paper is to focus on the analysis of the thermodynamic characteristics of liquid water and liquid oxygen. The turbine pump inducer is selected as the three-dimensional model, and a cavitation model considering the thermodynamic effects is modified based on the Zwart cavitation model. The numerical simulation of the cavitation characteristics of water and low-temperature liquid oxygen in the inducer is carried out at different temperatures. Thus, the influence of the thermodynamic effects of liquid water and low-temperature liquid oxygen on the induced wheel cavitation is studied. Since cryogenic fluids are widely used in aerospace and other fields, the strategic significance of exploring their thermal effect cavitation mechanism is self-evident. Therefore, it is of great value and significance to explore the effect of the steady-state cavitation heat effect of low-temperature fluid on the internal flow field at different temperatures.
2. Numerical Calculation Method
2.1. Basic Governing Equation
The essence of the cavitation phenomenon studied in this paper is the problem of a gas–liquid two-phase flow. The law of the gas–liquid two-phase flow is much more complex than that of a single-phase flow [4]. Therefore, the homogeneous flow model with high accuracy for the bubble flow and mist flow is selected, in which the gas–liquid two-phase mixture is regarded as a uniform medium, and the density formula and viscosity formula of the mixture are as follows:
where represents the density of the mixture, represents the volume fraction, represents the viscosity of the mixture, the subscript represents the mixture and the subscript represents the vapor phase and liquid phase, respectively.
There are three basic governing equations [5] as follows:
Continuity equation:
Momentum equation:
Energy equation:
where and subscripts represent the coordinate axis, represents the velocity vector, represents the pressure, represents the temperature and represents the enthalpy, specifically , represents the specific heat, represents the mixed thermal conductivity, represents the turbulent thermal conductivity, represents the gas–liquid mass transfer source term, which includes evaporation source term and condensation source term, represents the latent heat and the subscript represents turbulence.
2.2. The Turbulence Model
In this paper, the turbulence model [19] is selected. The model is an empirical model with high economy, stability and calculation accuracy, which is suitable for turbulent flow with a high Reynolds number. The model mainly includes two equations. The first equation is equation as follows:
The second equation is the equation as follows:
where and represent the turbulent kinetic energy generation terms, which are caused by buoyancy; they can be ignored in this numerical simulation. is caused by viscous force, , , and are constants, and the empirical parameters in the model are , , and .
where is the turbulent eddy viscosity, is a dimensionless constant and the value is .
2.3. Zwart Cavitation Model
The most widely used Zwart cavitation model is adopted here [13]. The Rayleigh-Plesset equation [5] is adopted for the cavitation dynamic equation, as shown below:
where is the bubble radius, is the saturation pressure, is the far-field pressure, is the liquid density and is the tension coefficient between the liquid and the surrounding bubbles.
In the Zwart cavitation model, without considering the influence of the thermodynamic effect, the vaporization and condensation rate can be expressed.
When , in the evaporation state, the fluid changes from a liquid state to vapor state:
When , in the condensed state, the fluid changes from a vapor state to liquid state:
where represents the average radius of the bubbles, the default value is m, represents the volume fraction of the cavitation nucleons, the default value is , represents the coefficient of the condensing phase and represents the coefficient of the evaporating phase.
2.4. Thermodynamic Modified Zwart Cavitation Model
In recent years, the thermodynamic effect correction method developed is to correct the saturated vapor pressure in the cavitation process from the essence of the thermal inhibition effect, which is suitable for all cavitation models. Therefore, the thermodynamic effect correction method based on the B-factor theory is selected to correct the Zwart isothermal cavitation model in this paper.
In the process of the cavitating flow, due to the vaporization of the liquid, it is necessary to absorb its own latent heat of vaporization. Cavitation can reduce the temperature of cavitating bubbles and its surrounding liquid, which appears as a temperature difference with the outside world. According to the two-phase heat balance equation proposed by Ruggeri and Moore [20]:
where represents the latent heat of vaporization.
The B-factor is as follows:
According to the properties of ideal gas, Franc [21] and others proposed that the size of the B-factor can be approximately characterized by the volume fraction. The specific expression is as follows:
where represents the hole thickness, and represents the reference characteristic speed. Therefore, the temperature difference obtained from the latent heat absorbed by vaporization is:
The pressure change of the fluid medium caused by the temperature difference is:
The saturated vapor pressure of the fluid medium will change with the change of the temperature. It is a univariate function with temperature as the independent variable. In order to avoid the influence of the coefficients in the polynomial fitting on the accuracy of the results, the three parameters from the Antoine [22] formula applicable to most pure substances is adopted as follows:
where represents the current fluid temperature, and its unit is Celsius. When setting the simulation parameters, the default temperature unit is Kelvin. The specific formula is as follows:
where the unit of saturated vapor pressure is mmHg, Since the unit of saturated vapor pressure in Formulas (21) and (22) is mmHg, not Pa, we need to convert the unit. The specific formula is as follows:
where hg = 133.32236842105 Pa; that is, 1 mm Hg equals 133.32236842105 Pa. In Table 1, the constants A, B and C for calculating the vapor pressure of liquid oxygen at different temperatures are given.

Table 1.
Correlation constants of liquid water and liquid oxygen for the Antoine formula.
According to the data in Table 1, the formula of saturated vapor pressure of the liquid oxygen is:
According to the data in Table 1, the formula of saturated vapor pressure of the liquid water is:
The influence of turbulent kinetic energy [11] of the fluid medium on the saturated vapor pressure can be expressed as:
Therefore, the thermodynamic effect modified Zwart cavitation model is:
When , in the evaporation state, the fluid changes from a liquid state to vapor state:
When , in the condensed state, the fluid changes from a vapor state to liquid state:
2.5. Three Blades Inducer Model of Turbopump
As shown in Figure 1, it can been seen that the front view and side view of the three blades inducer model selected in this paper. As shown in Figure 2, in order to facilitate the operation and focus on analyzing the cavitation phenomenon of the inducer, the whole fluid domain is simplified. Therefore, the fluid domain of the inducer is set as a cylinder, in which the inducer is located.

Figure 1.
The model of three blades inducer. (a) Front view; (b) Side view.

Figure 2.
Simplified schematic diagram of the induction rotation domain, inlet and outlet.
In this paper, the three-dimensional model of the inducer is divided into hexahedral structured meshes with good quality and controllability. Firstly, the mesh block generation technology is used to establish the corresponding mesh topology for the fluid domain of the model and the inducer, and then, the hexahedral meshes are divided on this basis. The whole inducer basin grid is a hexahedral structured grid, and the inlet section and outlet section are meshed by ICEM CFD. The mesh quality is above 0.7. The inducer area grid is divided by a turbo grid, and the grid at the inducer blade, hub and other wall surfaces is encrypted. Figure 3a is the meshing diagram of the three blades inducer and Figure 3b is the meshing diagram of the fluid domain.

Figure 3.
Meshing diagram of the three blades inducer and fluid domain. (a) Mesh of inducer; (b) Mesh of fluid domain.
2.6. The Boundary Condition
The setting of boundary conditions is very important, and it is a steady analysis in the numerical simulation. It is necessary to set relevant working condition parameters and the flow direction. Table 2 shows the relevant parameters of the numerical calculations.

Table 2.
The relevant parameters of the numerical calculations.
The boundary conditions of the numerical simulation experiment in this paper are set as follows:
- The mass flow inlet and pressure outlet are adopted. This setting makes the model easier to converge;
- The initial liquid volume fraction at the inlet of the fluid domain is 1, and the initial gas volume fraction is 0;
- The wall of the fluid domain is set without slipping, the heat transfer mode is adiabatic and the wall roughness is smooth;
- The interface model of the contact surface between the stationary domain and rotating domain is a general connection, and the phase transition/mixing model is a frozen rotor; since it only involves the analysis of the cavitation flow characteristics in the steady state, different boundary conditions need to be set. In a steady-state flow, first select the steady state, the convergence accuracy is 1 × 10−4 of the default setting and the number of iterations is 100;
- The empirical constants of the condensation and evaporation phases of liquid water are the default: and ; the empirical constants [23,24] of the condensation and evaporation phases of liquid oxygen are corrected as and .
2.7. Grid Independence Verification
The working condition data of liquid water and liquid oxygen are shown in Table 3.

Table 3.
Working condition data of liquid water and liquid oxygen.
In this selection, five kinds of grids are preliminarily calculated, and a set of appropriate grids are selected according to the calculation conditions and needs.
The head coefficient is selected to evaluate the number of grids, and the specific expression is shown in the formula. As shown in Figure 4, when the number of grids increases, the head coefficient gradually tends to be stable. Considering the reasonable demand for the computer performance and computing time, three million grids are selected.

Figure 4.
Variation of the head coefficient with the number of grids.
2.8. Verification of Numerical Calculation Method
In order to verify the feasibility of the numerical calculation method, the two different Zwart cavitation models are used to numerically simulate the mediums of liquid water and liquid oxygen. The actual calculation efficiency of liquid water and liquid oxygen is compared with the working condition efficiency, as shown in Table 4. The specific expression of efficiency formula is shown in Equation (30). Compared with the working efficiency of liquid water, the actual efficiency calculation result of the Zwart isothermal cavitation model is 0.679, and the error is 5.69%. The actual efficiency calculation result of Zwart modified cavitation model is 0.745, and the error is 3.47%. Compared with the working efficiency of liquid oxygen, the actual efficiency calculation result of the Zwart isothermal cavitation model is 0.685, and the error is 4.86%. The actual efficiency calculation result of the Zwart modified cavitation model is 0.735, and the error is 1.67%.

Table 4.
Comparison of the cavitation efficiency of liquid water and liquid oxygen in different models.
3. Results and Discussion
3.1. Analysis of Steady-State Cavitation Characteristics of Liquid Water at Different Temperatures
For elaborating the differences of the thermodynamic effects of liquid water at three different temperatures, the cavitation flow characteristics in the Zwart isothermal cavitation model and Zwart modified cavitation model are studied. The physical parameters of liquid water at different temperatures are shown in Table 5. Three kinds of liquid water with different temperatures of 298 K, 320 K and 350 K are selected as the fluid medium to simulate the cavitation flow characteristics under steady-state conditions in the inducer. The cavitation characteristics of liquid water are mainly analyzed from the aspects of pressure distribution characteristics, temperature distribution characteristics, cavitation morphology and gas volume fraction.

Table 5.
Relevant parameters of liquid water in a saturated state.
3.1.1. Temperature Characteristic Analysis
In order to more directly and clearly describe the change of the temperature characteristics, the temperature difference of the fluid medium in the cavitating flow of the inducer during a steady flow is selected. Temperature is a manifestation of thermal energy. During the flow process, the local pressure of the liquid is lower than the local saturated vapor pressure, and vaporization occurs. Liquid vaporization absorbs the latent heat of vaporization, and a temperature difference is formed between the gas and liquid.
As shown in Figure 5, when the temperature of liquid water from 298 K to 320 K to 350 K, the increase of temperature difference for the Zwart isothermal cavitation model increases from 0.363 K to 0.843 K. For the Zwart modified cavitation model, the increase of temperature difference increases from 0.071 K to 0.221 K. Therefore, for the liquid water at the temperature of 298–350 K, the temperature hardly changes, indicating that the liquid water has no inhibition on cavitation, and the thermodynamic characteristics of the liquid water can be ignored.
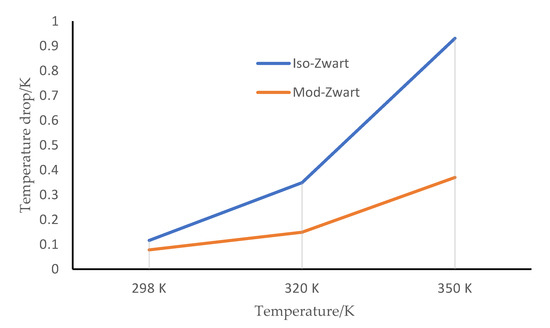
Figure 5.
Temperature difference distribution of liquid water in different cavitation models at three different temperatures.
When the liquid water is at the same temperature, the temperature difference in the Zwart modified cavitation model is always lower. For two different Zwart cavitation models, with the continuous increase of the temperature of the liquid water, the corresponding temperature difference shows the same law—that is, the temperature difference increases. At the same time, the temperature difference also increases gradually. The set value of the saturated vapor pressure is always a fixed value, but in fact, the saturated vapor pressure will increase. When the temperature rises, the set value of the saturated vapor pressure of liquid water remains unchanged so more heat can be absorbed, and the temperature difference will gradually increase.
3.1.2. Pressure Characteristic Analysis
When the liquid water temperature increases at 298 K, 320 K and 350 K, the Zwart modified cavitation model considering the thermodynamic effect and the default Zwart isothermal cavitation model are selected to simulate the pressure distribution of the cavitation flow field of the inducer of the turbopump. Define a pressure-related parameter differential pressure . Since the relative pressure of the inlet pressure and outlet pressure set in this simulation is atmospheric pressure and 2.0 MPa, the value of the differential pressure is based on the relative pressure. The value and distribution of the differential pressure of liquid water at different temperatures are calculated by simulation.
As shown in Figure 6 and Figure 7, in the two different Zwart cavitation models, the change of the differential pressure presents a similar change law. When the temperature increases from 298 K to 320 K to 350 K, the pressure at the head of the inducer is the largest when z = 0.01 m, the pressure difference decreases at z = 0.03 m and z = 0.05 m and the pressure at the tail of the inducer also tends towards a stable value. As the temperature increases from 298 K to 320 K to 350 K, the greater gradient of the saturated vapor pressure of liquid water with the temperature—that is, the higher sensitivity. It is not difficult to find from Figure 7 that, in the Zwart modified cavitation model with a thermodynamic effect, the pressure difference of the corresponding flow field is greater with the increase of the temperature. The saturated steam pressure in the corresponding cavitation area decreases more with the increase of the temperature, which is caused by the different sensitivity of the saturated steam pressure to the temperature difference due to the thermophysical properties of water at different temperatures.
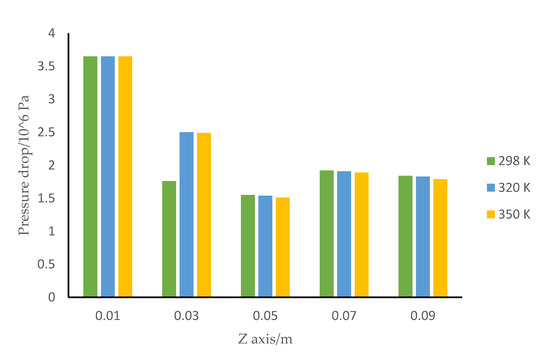
Figure 6.
Pressure difference distribution of liquid water at three different temperatures in the Zwart isothermal cavitation model.

Figure 7.
Pressure difference distribution of liquid water at three different temperatures in the Zwart modified cavitation model.
3.1.3. Cavitation and Bubble Characteristic Analysis
In the process of cavitation, the corresponding saturated vapor pressure also decreases with the decrease of the temperature, which affects the length and shape of cavitation. Figure 8 is a cross-sectional cloud diagram of cavitation morphology simulated by water at different temperatures in two different Zwart models.

Figure 8.
Cross-sectional cloud diagram of the liquid water vapor volume fraction of two different Zwart models at three temperatures. (a) Iso-Zwart T = 298 K; (b) Iso-Zwart T = 320 K; (c) Iso-Zwart T = 350 K; (d) Mod-Zwart T = 298 K; (e) Mod-Zwart T = 320 K; (f) Mod-Zwart T = 350 K.
As shown in Figure 8, the section at the second hub of the inducer (i.e., z = 0.03 m, which is the most obvious cavitation phenomenon) is selected for analysis. In the Zwart isothermal cavitation model, when the temperature increases gradually from 298 K to 320 K to 350 K, the area of cavitation increases gradually, there is no cavitation phenomenon at the rim and the peak area also expands gradually. Compared with the two different Zwart models, it can be found that, after adding the thermodynamic effect, the corresponding cavitation region and cavitation peak at the same temperature decrease correspondingly, and the changes of the cavitation region and cavitation peak become more obvious with the increase of the temperature. Combined with Figure 8 and Figure 9, it can be found that, for liquid water, the higher the temperature is, the more obvious the thermodynamic effect is.
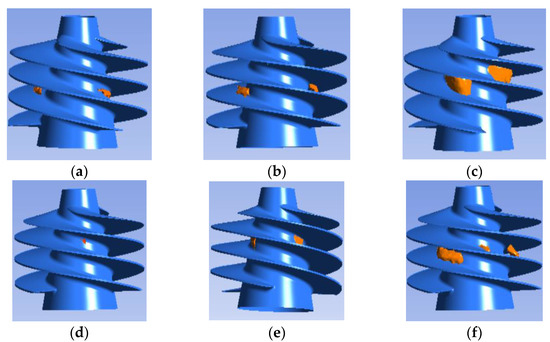
Figure 9.
Iso-surface cloud diagram of the liquid water vapor volume fraction of two different Zwart models at three temperatures; (a) Iso-Zwart T = 298 K; (b) Iso-Zwart T = 320 K; (c) Iso-Zwart T = 350 K; (d) Mod-Zwart T = 298 K; (e) Mod-Zwart T = 320 K; (f) Mod-Zwart T = 350 K.
As shown in Figure 9, it is a cloud diagram when the gas volume fraction iso-surface of the inducer is 0.9. It can be found that the cavitation area occurs near the hub and between the second and third turns of the inducer helix. Compared with Figure 8, for liquid water at the same temperature, after considering the thermodynamic effect, the volume fraction of the vapor phase decreases, the change gradient decreases, the intersection interface between the vapor and liquid becomes blurred and the bubble length shortens. However, this change is relatively weak at low temperatures. Comparing the two different Zwart models, when analyzing the changes in bubble morphology and vapor volume fraction of liquid water at 298 K, 320 K and 350 K, it can be found that the vapor volume fraction and cavitation level increase slightly.
3.2. Analysis of Steady-State Cavitation Characteristics of Liquid Oxygen at Different Temperatures
Considering the thermodynamic effect of liquid oxygen, the flow field becomes more complex in the cavitation flow. The physical parameters of liquid oxygen at different temperatures are shown in Table 6. In order to explore the cavitation flow characteristics of liquid oxygen, this section selects the Zwart cavitation model with a thermodynamic effect. Considering the thermodynamic effect, the cavitation flow characteristics of a liquid oxygen medium at three different temperatures of 86 K, 90 K and 95 K are analyzed.

Table 6.
Relevant parameters of liquid oxygen in a saturated state.
3.2.1. Temperature Characteristic Analysis
In order to analyze the difference of the cavitation characteristics of liquid oxygen, under the condition of a Zwart-modified cavitation model considering the thermodynamic effect, the temperature distribution differences of liquid oxygen at different temperatures in the cavitation flow state of the inducer are compared and analyzed. The temperature difference is , in which represents the initial temperature of the incoming flow, and is the current temperature.
As shown in Figure 10, the change of liquid oxygen temperature difference shows a similar law under three different temperatures of 86 K, 90 K and 95 K. Compared with Figure 10, it can be found that the temperature difference is the largest at 0.03 m in the z-axis direction of the inducer, because the cavitation effect is the most obvious here, and the most energy is required. Comparing the maximum temperature difference produced by liquid oxygen at different temperatures, it can be found that, when the liquid oxygen temperature increases from 86 K to 90 K to 95 K, the corresponding maximum temperature difference also increases. Since the physical parameters of liquid oxygen are sensitive to the change of temperature, the temperature difference corresponding to different thermal inhibition effects is almost the same. In the study of water cavitation characteristics, considering the poor sensitivity of water physical parameters to the temperature, in order to show the differences of the water thermodynamic effects at different temperatures, the selected water temperatures differ greatly. Therefore, the temperature difference distribution diagram shows the cavitation characteristics that the temperature difference decreases significantly with the increase of the temperature.

Figure 10.
Temperature difference distribution of three liquid oxygen temperatures in the Zwart-modified cavitation model.
3.2.2. Pressure Characteristic Analysis
As shown in Figure 11, the pressure distribution comparison diagram of liquid oxygen under three different temperatures of 86 K, 90 K and 95 k is simulated in the Zwart modified cavitation model. This section selects the change of the pressure-related parameter pressure difference to analyze the pressure change characteristics of liquid oxygen in the steady-state cavitation flow.

Figure 11.
Pressure difference distribution of liquid oxygen at three different temperatures in the Zwart modified cavitation model.
When the temperature increases from 86 K to 90 K to 95 K, the same variation law of differential pressure appears in the axial direction of the inducer. From Z = 0.01 M to Z = 0.05 m, the differential pressure first decreases greatly, then increases slightly from z = 0.05 m to Z = 0.07, and the differential pressure tends to be stable at the tail of the inducer. Compared with Figure 11, it can be seen that, after considering the thermodynamic effect, at the same position of the inducer, when the temperature difference changes the most, the corresponding pressure difference change is also at the maximum value. Compared to the pressure difference changes of liquid oxygen at three different temperatures in the Zwart modified cavitation model, when the temperature increases, the pressure difference decreases, which indicates that the liquid low-temperature medium liquid oxygen shows a stronger thermodynamic effect with the increase in the temperature.
3.2.3. Cavitation and Bubble Characteristic Analysis
As shown in Figure 12, at three different temperatures of 86 K, 90 K and 95 k, the cross-sectional cloud diagram of the liquid oxygen vapor phase volume fraction distribution simulated under two different Zwart models is adopted.

Figure 12.
Cross-sectional cloud diagram of the liquid oxygen vapor volume fraction of two different Zwart models at three temperatures. (a) Iso-Zwart T = 86 K; (b) Iso-Zwart T = 90 K; (c) Iso-Zwart T = 95 K; (d) Mod-Zwart T = 86 K; (e) Mod-Zwart T = 90 K; (f) Mod-Zwart T = 95 K.
As shown in Figure 13, it is the cloud diagram of the liquid oxygen vapor volume fraction iso-surface (equivalent number is 0.5) simulated under the conditions of two different Zwart models at three different temperatures of 86 K, 90 K and 95 k.

Figure 13.
Iso-surface cloud diagram of the liquid oxygen vapor volume fraction of two different Zwart models at three temperatures; (a) Iso-Zwart T = 86 K; (b) Iso-Zwart T = 90 K; (c) Iso-Zwart T = 95 K; (d) Mod-Zwart T = 86 K; (e) Mod-Zwart T = 90 K; (f) Mod-Zwart T = 95 K.
Combined with Figure 12 and Figure 13, it can be seen that, under three different temperatures, the calculation results of liquid oxygen in two different Zwart models with a thermodynamic effect are quite different. It can be found that the temperature difference increases with the increase of the liquid oxygen temperature, showing the characteristics of the enhanced thermodynamic effect. Meanwhile, the regional distribution of liquid oxygen cavitation is uneven, the cavitation level near the wheel hub is deep, and the cavitation level near the wheel rim is shallow. Compared with the Zwart isothermal cavitation model, in the Zwart modified cavitation model, according to the simulation results, compared with Figure 10, the saturated vapor pressure is reduced due to a certain degree of temperature difference during low-temperature liquid oxygen cavitation, and the cavitation area in liquid oxygen is relatively reduced at three different temperatures. With the increase of the temperature, the cavitation area is less. This means that the thermodynamic characteristics of cryogenic liquid oxygen have a significant effect on the suppression of cavitation. It is quite different from the calculation results of the Zwart isothermal cavitation model. The cavitation area of liquid oxygen with a higher temperature is significantly larger than that of liquid nitrogen with a lower temperature, the change gradient of the gas volume fraction is larger and the gas–liquid interface is clearer, which means that, in the same type of medium, the higher the temperature, the stronger the thermodynamic effect and the more obvious effect of inhibiting cavitation. The analysis shows that the Zwart modified cavitation model can reflect the influence of the thermodynamic effect of low-temperature medium liquid oxygen on cavitation.
Combined with Figure 14 and Figure 15, at 0.02 m in the z-axis direction, it can be found that, when the temperature of the cryogenic liquid oxygen gradually increases from 86 K to 95 k, the vapor volume fraction also decreases from 0.12 to 0.04 in the Zwart isothermal cavitation model and from 0.05 to 0.01 in the Zwart isothermal cavitation model. At 0.03 m, the vapor volume fraction reaches the maximum, indicating that the cavitation here is the most serious. At 86 K, 90 K and 95 k, the vapor volume fraction peaks in the Zwart isothermal cavitation model are 0.89, 0.85 and 0.8, respectively, and the vapor volume fraction peaks in the Zwart modified cavitation model are 0.71, 0.6 and 0.32, respectively. It is not difficult to find that the latter is much smaller than the former, which means that the thermodynamic characteristics of cryogenic liquid oxygen can play a certain role in inhibiting cavitation. At 0.04 m, the vapor fraction decreases. At 86 K, 90 K and 95 K, compared with the Zwart isothermal cavitation model, the vapor volume fraction in the Zwart modified cavitation model decreases sharply, which indicates that the cavitation is greatly suppressed.
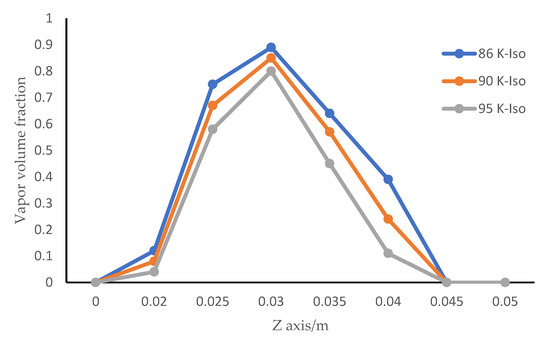
Figure 14.
Volume fraction distribution of liquid oxygen in the inducer in the Zwart isothermal cavitation model.

Figure 15.
Volume fraction distribution of liquid oxygen in the inducer in the Zwart modified. cavitation model.
Combined with the above analysis, when the fluid enters the head of the inducer from the inlet, the velocity does not change. However, due to the high-speed rotation of the inducer, the velocity of the fluid flowing through the inducer will also increase sharply, and the velocity of the fluid at the center of the blade will reach the maximum. At the same time, according to the Bernoulli equation, as the fluid velocity increases, the local static pressure of the fluid will decrease, and the local static pressure of the fluid at the center of the blade will decrease to the minimum. Cavitation occurs in the area where the local static pressure of the fluid is lower than the saturated vapor pressure of the fluid, so cavitation is accumulated in the center of the blade. It can be concluded that the thermodynamic effect has a great impact on liquid oxygen cavitation, and the existence of a thermodynamic effect effectively inhibits the development of cavitation in the inducer. When the temperature is higher, the thermodynamic effect is more significant, which shows that the influence of the thermodynamic effect must be considered in the simulation of the cavitation flow in low-temperature media such as liquid oxygen. We know that cavitation is a dynamic process of the gas–liquid two-phase flow. The thermophysical properties of liquid water are relatively stable, and the sensitivity of saturated vapor pressure to temperature change is not high. In the process of cavitation, less heat is required for vaporization, and the temperature change is small. The thermodynamic effect on cavitation is not relatively obvious. The variation gradient of saturated vapor pressure of low-temperature liquid oxygen with the temperature is much larger than that of water at a normal temperature, and it is highly sensitive to temperature changes. At the same time, the thermal conductivity of low-temperature fluid is lower than that of water. In the process of cavitation, more heat is required for vaporization, resulting in greater temperature changes, and its thermodynamic effect is more significant.
4. Conclusions
In order to study the thermodynamic characteristics of liquid oxygen in the inducer of a turbopump, a method considering the thermodynamic characteristics is proposed, and the original Zwart cavitation model is modified. Based on the two different Zwart models, liquid water and liquid oxygen media are used to simulate the steady-state cavitation flow characteristics. Through the research of this paper, the conclusions are as follows:
- The thermodynamic term of the Zwart isothermal cavitation model is modified, mainly considering the influence of the saturated vapor pressure, adding a turbulent kinetic energy term and considering the temperature difference in the cavitation region improved by the B-factor theory. For liquid oxygen in low-temperature medium, the empirical system of an evaporation term and condensation phase is modified.
- For liquid water, when the temperature increases, the liquid water cavitation deepens and the cavitation area becomes wider and bigger, but the position of the cavitation remains unchanged. In the Zwart modified cavitation model, the cavitation level of liquid water will be reduced. This shows that, when the cavitation is serious, the liquid absorbs more gasification latent heat from the cavitation area, and the saturated vapor pressure decreases, so the cavitation is inhibited to a certain extent. When the temperature of liquid water is high, it can show more obvious thermodynamic characteristics.
- For liquid oxygen, when the temperature increases, the temperature difference of liquid oxygen increases, the pressure difference also increases and the corresponding cavitation shape changes more obviously in the larger vapor volume fraction. It can be found that the Zwart modified cavitation model can reflect the thermodynamic effect of liquid oxygen on cavitation. The thermodynamic characteristics of liquid oxygen at different temperatures are obvious, but the higher temperature and more significant cavitation characteristics will inhibit the process of cavitation. Compared with liquid water, the temperature difference characteristics, pressure difference characteristics and cavitation of liquid oxygen change more significantly, which further verifies the thermodynamic characteristics of low-temperature medium liquid oxygen.
Author Contributions
Conceptualization, G.S. and Y.W.; methodology, G.S. and Y.W.; validation, G.S.; investigation, G.S.; data curation, G.S.; writing—original draft preparation, G.S.; writing—review and editing, Y.W. and S.L.; supervision, Y.W. and S.L.; project administration, S.L. and funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 11802168 and No. 52075310), Grand Joint Projects of Shanghai University (No. 202131) and the Key Technologies R&D Program of Henan Province (No. 222102220024).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim, D.; Sung, H.; Choi, C.; Kim, J. Cavitation instabilities of an inducer in a cryogenic pump. Acta Astronaut. 2017, 132, 19–24. [Google Scholar] [CrossRef]
- Utturkar, Y.; Wu, J.; Wang, G.; Shyy, W. Recent progress in modeling of cryogenic cavitation for liquid rocket propulsion. Progress Aerosp. Sci. 2005, 41, 558–608. [Google Scholar] [CrossRef]
- Long, X.; Liu, Q.; Ji, B.; Lu, Y. Numerical investigation of two typical cavitation shedding dynamics flow in liquid hydrogen with thermodynamic effects. Int. J. Heat Mass Transf. 2017, 109, 879–893. [Google Scholar] [CrossRef]
- Brennen, C.E. Cavitation and Bubble Dynamics; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Brennen, C.E. Hydrodynamics of Pumps; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Chen, T.; Chen, H.; Liang, W.; Huang, B.; Xiang, L. Experimental investigation of liquid nitrogen cavitating flows in converging-diverging nozzle with special emphasis on thermal transition. Int. J. Heat Mass Transf. 2019, 132, 618–630. [Google Scholar] [CrossRef]
- Hord, J.; Anderson, L.M.; Hall, W.J. Cavitation in Liquid Cryogens I—Venturi; NASA Contractor Report, NASA CR-2045; NASA: Washington, DC, USA, 1972. [Google Scholar]
- Hord, J. Cavitation in Liquid Cryogens II—Hydrofoil; NASA Contractor Report, NASA CR-2156; NASA: Washington, DC, USA, 1973. [Google Scholar]
- Hord, J. Cavitation in Liquid Cryogens III—Ogives; NASA Contractor Report, NASA CR-2242; NASA: Washington, DC, USA, 1973. [Google Scholar]
- Merkle, C.L.; Feng, J.; Buelow, P.E.O. Computational modeling of dynamics of sheet cavitation. In Proceedings of the 3rd International Symposium on Cavitation, Grenoble, France, 7–10 April 1998. [Google Scholar]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical basis and validation of the full cavitation model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the Fifth International Conference on Multiphase Flow, Yokohama, Japan, 30 May–3 June 2004. [Google Scholar]
- Goncalvès, E.; Fortes Patella, R.; Rolland, J.; Pouffary, B.; Challier, G. Thermodynamic effect on a cavitating inducer in liquid hydrogen. J. Fluids Eng. 2010, 132, 111305. [Google Scholar] [CrossRef]
- Ji, B.; Luo, X.W.; Wu, Y.L.; Zhang, Y.; Xu, H.Y. Simulation of high temperature water cavitation considering thermodynamic effect. Tsinghua Univ. J. Nat. Sci. 2010, 50, 262–265. [Google Scholar]
- Xu, B.; Feng, J.; Shen, X.; Zhang, D.; Zhang, W. Numerical investigation of cavitation suppression in an inducer for water and liquid nitrogen with emphasis on thermodynamic effect. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 212. [Google Scholar] [CrossRef]
- Tseng, C.; Shyy, W. Modeling for isothermal and cryogenic cavitation. Int. J. Heat Mass Transf. 2010, 53, 513–525. [Google Scholar] [CrossRef]
- Li, W.Q. Study on Cavitation Mechanism of Engine Cooling Water Pump under Thermodynamic Effect; Jiangsu University: Zhenjiang, China, 2016. [Google Scholar]
- Franc, J.P.; Rebattet, C.; Coulon, A. An Experimental investigation of thermal effects in a cavitating inducer. In Proceedings of the Fifth International Symposium on Cavitation (Cav2003), Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Ruggeri, R.S.; Moore, R.D. Method of Prediction of Pump Cavitation Performance for Various Liquids, Liquid Temperatures and Rotation Speeds; NASA Technical Note, NASA TN D-5292; NASA: Washington, DC, USA, 1969. [Google Scholar]
- Franc, J.P.; Janson, E.; Morel, P.; Rebattet, C.; Riondet, M. Visualizations of leading edge cavitation in an inducer at different temperatures. In Proceedings of the Fourth International Symposium on Cavitation, Pasadena, NL, Canada, 20–23 June 2001; Volume 1, pp. 24–130. [Google Scholar]
- Sonntag, R.E.; Borgnakke, C.; Wylen, G.J. Fundamentals of Thermodynamics; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Tani, N.; Yanabushi, N.; Tsujimoto, Y. Influence of flow coefficient and flow structure on rotational cavitation in inducer. J. Fluids Eng. 2012, 134, 021302. [Google Scholar] [CrossRef]
- Yu, A.; Tang, Q.; Zhou, D. Entropy production analysis in thermodynamic cavitating flow with the consideration of local compressibility. Int. J. Heat Mass Transf. 2020, 153, 119604. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).