Next Article in Journal
Review of Gas Engine Heat Pumps
Previous Article in Journal
How to Improve an Offshore Wind Station
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 15
Issue 13
10.3390/en15134872
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Numerical Modeling of Horizontal Axis Wind Turbine: Aerodynamic Performances Improvement Using an Efficient Passive Flow Control System

by
Riyadh Belamadi
1,*,
Abdelhakim Settar
2,
Khaled Chetehouna
2 and
Adrian Ilinca
3
1
Laboratoire de Technologies des Systèmes Energétiques (LTSE), Annaba Higher School of Industrial Technology, Annaba 23000, Algeria
2
INSA Centre Val de Loire, Université Orléans, PRISME EA 4229, F-18020 Bourges, France
3
Wind Energy Research Laboratory, University of Québec at Rimouski, 300, Allée des Ursulines, C.P. 3300, Rimouski, QC G5L 3A1, Canada
*
Author to whom correspondence should be addressed.
Energies 2022, 15(13), 4872; https://doi.org/10.3390/en15134872
Submission received: 2 June 2022 / Revised: 26 June 2022 / Accepted: 29 June 2022 / Published: 2 July 2022
Browse Figures
Versions Notes

Abstract

:
In this paper, we explore the improvement of the aerodynamic characteristics of wind turbine blades under stall conditions using passive flow control with slots. The National Renewable Energy Laboratory (NREL) Phase II rotor, for which detailed simulations and experimental data are available, served as a baseline for assessing the flow control system effects. The position and configuration of the slot used as a flow control system were determined using CFD analysis. The 3D-RANS equations are solved with ANSYS FLUENT using the k-ω SST turbulence closure model. The pressure coefficient for different wind speeds for the baseline configuration is compared to the available experimental data. The comparison shows that CFD results were better for the attached flow. The current work consists of a 3-D CFD modeling of a rotating blade equipped with different flow control systems: single-slot (S-S) and two-slots (T-S). The computation provides a better understanding of the influence of these flow control devices on the performance of wind turbine blades, the control of boundary layer separation, and the rotation effect. These control systems increase the power output by over 60% at high wind speeds with large separated boundary layer regions. For the configuration with the control system, the slot has shown its ability to delay the boundary layer separation. However, the improved aerodynamic performance has been proven for medium and high angles of attack where the flow is generally in the stall condition. The addition of the second slot changed the flow behavior, and an improvement was observed compared to the single slot configuration. The results are helpful for the design and development of a new generation of wind turbine blades.

1. Introduction

The flow separation and boundary layer control are methods aimed at improving an airfoil’s aerodynamic performance, increasing the wind turbine’s efficiency. In addition, these methods can adjust the wind turbine’s aerodynamic load and output power under varying wind speeds and ensure the generator’s safety [1].
The design of actuators is guided by the physical principles of the phenomenon to be controlled. Thus, it is possible to delay or prevent separation by exploiting various properties of the separated or about to be separated boundary layer. The boundary layer can exist under two different flow regimes, laminar and turbulent. The fluid layers slide over each other in the laminar flow without exchanging energy and mass between the neighboring layers. Therefore, the shear developed by the velocity gradient is entirely due to viscosity. Therefore, the laminar boundary layers can withstand only very small unfavorable pressure gradients before the flow separation occurs. On the other hand, in a turbulent flow, fluctuations of the axial velocity and the perpendicular velocity to the flow direction result in a significant transfer of momentum between the neighboring layers. This allows for overcoming larger unfavorable pressure gradients due to the continuous momentum transfer in the near-wall zone [2]. Overall, flow separation control techniques can be divided into two categories based on energy expenditure [3]:
(1) The active flow separation control requires additional energy for the boundary layer control, such as boundary layer blowing and suction [4,5,6,7] and synthetic jets [8,9,10], which can operate in two ways: (i) in an open-loop where the injection or suction of fluid is independent of the state or conditions of the flow such as wind speed and angle of attack (along the wingspan); (ii) in closed-loop, where the information is obtained from the sensors to control the rate of fluid injection/aspiration or to disable the control system in operating conditions where the flow is attached. Here we must mention that the open-loop or closed-loop methods are applicable for all active control methods [11], plasma actuators [12], and so on.
(2) Passive control techniques that do not require auxiliary power or a control loop, such as slot [13], multi-element airfoil [14,15,16], leading-edge slat [1,17], Gurney flap [18,19,20], self-activated flaps [21], vortex generator [22,23,24], stall strips [25,26], and other airfoil configurations that can delay or even eliminate dynamic stall.
Handley Page [27] and Lachmann [15,28] initially introduced the slotted and multi-element airfoils, but the first thorough and systematic study of these elements was performed by Weick and Shortal [29]. Weick and Shortal examined various combinations of slots and various slot locations to identify the optimal aerodynamic configuration. For an un-flapped airfoil, their study shows that the most effective position for a single slot is near the leading edge. However, when the slot is moved aft, the effectiveness decreases.
Multiple slots are generally relatively ineffective unless they include a slot near the leading-edge [29,30]. The leading-edge slot was firstly used in aircraft to delay the boundary layer separation at a low relative speed [16]. The particularity of this technique is to energize (adding kinetic energy) the boundary layer by augmenting the flow in the gap between the main body and slat [31], creating either large vortices or multiple smaller vortices, leading to separation delay of the main airfoil boundary layer. The hydrokinetic and wind turbines with leading-edge airfoil-slat were numerically and experimentally investigated by Yavuz et al. [32,33]. Their results showed that the stall angle of attack increased by 8°, and the maximum lift coefficient increased by 191.7%.
Akhter and Omar [10] noted a shift in the separation point from 47% to 0.67% chord for the slat configuration. They also noted that the geometric parameters and slat position relative to the blade are essential for performance enhancement. In addition, the circulation around the leading edge slat reduces the sharp increase in the flow velocity over the main airfoil body, thus regulating the flow separations and causing an improved pressure recovery [34].
Similarly, the use of a micro-cylinder was investigated for aerodynamic performance enhancement and flow separation control. Shi et al. [35] used an oscillating micro-cylinder at the leading edge and recorded an increase of 88.21% in lift/drag ratio at optimum oscillation mode. Furthermore, setting a micro-cylinder with a 1 mm diameter at the blade leading edge can improve torque under light stall conditions for 10 m/s free flow velocity [36].
Luo et al. [37] performed a parametric numerical study using Reynolds averaged Navier-Stokes calculation combined with delayed detached eddy simulation on a NACA0012 airfoil equipped with a micro-cylinder. The position of the micro-cylinder was at x/c = 0.02 based on a hypothesis that flow separation is impossible to control further downstream. They concluded that aerodynamic performances are highly sensitive to the spacing between the cylinder and suction surface.
A hybrid Reynolds averaged Navier–Stokes/Large-Eddy-Simulation turbulence technique was adopted by Liggett et al. [38] to study an oscillating flapped airfoil to determine the influence of modeling the gap on the performance and acoustic signature of the airfoil. Their results are compared with the experimental data to confirm the validity of the computational approach. They examined both attached and separated oscillating flows. The flow physics within the gap is important for the airfoil performance when a stall occurs and when acoustic signatures are required.
Two-dimensional RANS equations are common for CFD analysis of specific studies related to airfoil flow control. For example, Ramzi and Abed Errahmane [39] studied the effect of slot geometry on a cascade of the highly loaded axial compressor. Based on their 2-D analysis, results showed a maximum reduction of 28% of the loss ratio and an increase of 5° in the flow deflection angle.
To increase the power production of a modern multi-MW rotor [40], a two-dimensional CFD optimization approach was adopted by Gaunaa et al. [41], where the effects of using slots were quantified. The results indicate that the slats boost the aerodynamic performance of the inner part of rotors, and the effects may be better if the slats and the main rotor blade are designed simultaneously.
Standish [42] performed an extensive 2-D computational study to examine the influence of tab height and tab location on the upper and lower surfaces of the S809 and GU25-5(11)8 airfoils. His results show that the optimal tab height was in the order of the boundary layer thickness. Furthermore, the optimal location was at approximately 95% of the chord in terms of lift versus drag.
Buhl et al. [43] used 2-D calculation to investigate trailing-edge flaps of a 5 MW upwind reference turbine without changing its lift coefficient. Their analysis indicates that the potential of using trailing-edge flaps to reduce fluctuating loads is significant.
From the above works, the 2-D approach does not give a full insight into the complex 3-D flow phenomena around the wind turbine blade. For example, both rotation and radial flow components present in the rotor have a major effect on the lift and drag characteristics of the blade compared to a 2-D airfoil [44]. In 3-D rotor flows, two main factors are generally involved: (i) the Coriolis force, which acts in the direction of the chord as a favorable pressure gradient and tends to delay the separation of the boundary layer; (ii) the centrifugal forces, which produce a pumping effect in the spanwise direction.
Using a viscous-inviscid interaction model, the 3-D equations of the boundary layer on a rotating surface are solved numerically by Sørensen [45]. His results show a significant difference between the lift coefficients calculated for 2-D and 3-D cases.
Du and Selig [46] approached the resolution of the 3-D equations of the incompressible stationary boundary layer. Their analysis indicated that the delay in separation depends slightly on the effect of the pressure and mainly on the acceleration of the boundary layer flow, i.e., on the Coriolis forces. The two rotation effects become smaller going outwards, according to [47,48].
Hu and his colleagues [49] carried out a study on separation delay for wind turbines. The complex flow fields are simulated using CFD based on the 2-D stationery and 3-D rotation conditions. Their computation results show that rotation affects the pressure distribution on the surface, which can increase the 3-D stall-delay on Horizontal Axis Wind Turbines (HAWT).
This list is far from being exhaustive. Flow control methods, in all their forms, are widely used in the turbomachinery field, especially those with high aerodynamic loading (high-pressure ratio). For example, Cravero et al. [50] carried out a CFD simulation to study the effect of the ported shroud on the radial compressor stage under different operating conditions. Moreover, it develops some criteria to detect the limiting mass flow rate compared to a compressor without this device. Here, at the design rotational speed, an increase of 11% of the surge margin has been detected. Gabriel et al. [51] experimentally studied the effect of an active control to improve the stability of an axial compressor stage CME2 operating at 3200 rpm. It is an air injection system (continuous and pulsed) composed of 20 injectors that work independently of each other. Their results show that the control system improved the compressor operating range by decreasing the stalling mass flow rate and increasing the pressure rise for a given operating point.
The current work consists of a 3-D CFD modeling of a rotating blade equipped with different flow control systems: single-slot (S-S) and two-slots (T-S). The computation provides a better understanding of the influence of these flow control devices on the performance of wind turbine blades. The results are helpful for the development of a new generation of wind turbine blades. Several issues have been addressed, including the control of boundary layer separation and the rotation effect with the control system. The increase in the power output reaches over 60% at high wind speeds with large separated boundary layer regions.

2. Methodology

2.1. Experimental Data

In this subsection, turbine geometry considered during numerical computations is detailed. The National Renewable Energy Laboratory (NREL) Phase II rotor (Table 1) is chosen to conduct simulations and validation cases based on the experimental data [52]. The blades of the considered rotor are non-twisted and non-tapered with a constant cord of 0.4572 m. It consists of a HAWT rotor composed of three small blades with a 5.029 m radius mounted on a downwind machine [53]. NREL S809 airfoil series is used, except for the root. The airfoil thickness is t/c = 43% at 14.4% span and falls linearly to t/c = 20.95% at 30% span, while outboard of 30%, thickness is steady at that value (Figure 1). The nominal rotation speed is 72 rpm, the tip pitch equals 12°, and the cone angle is 3°.

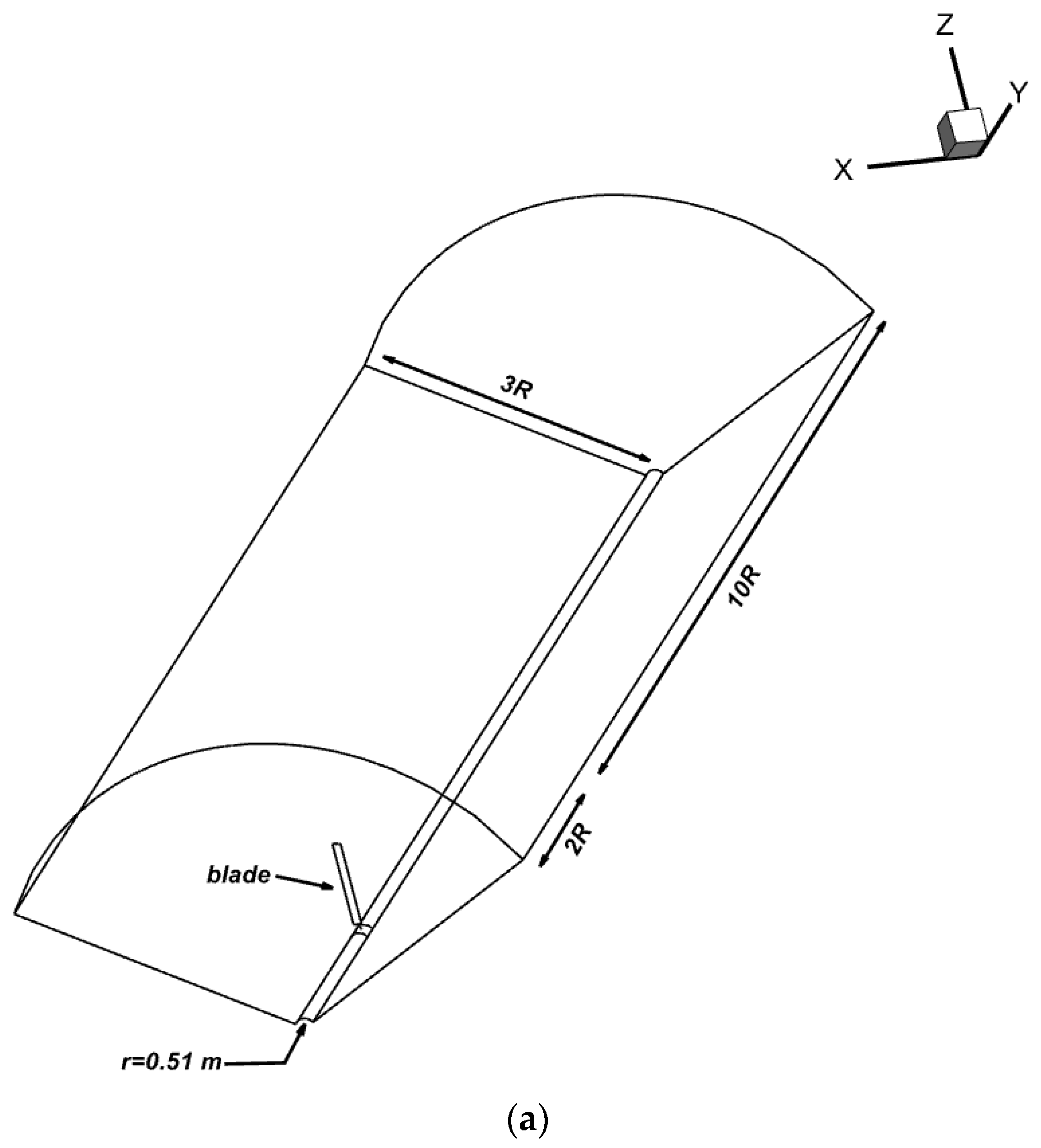
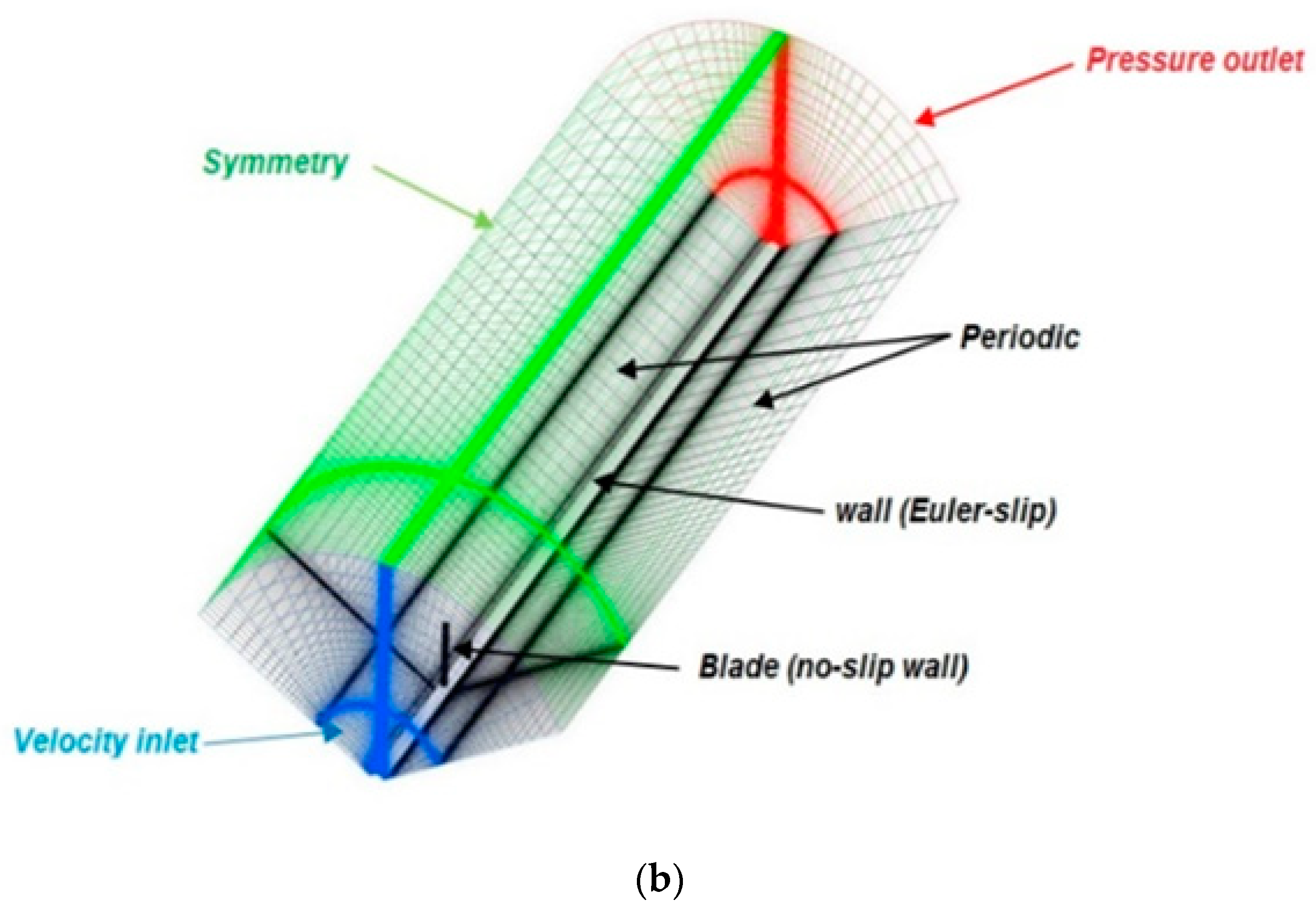
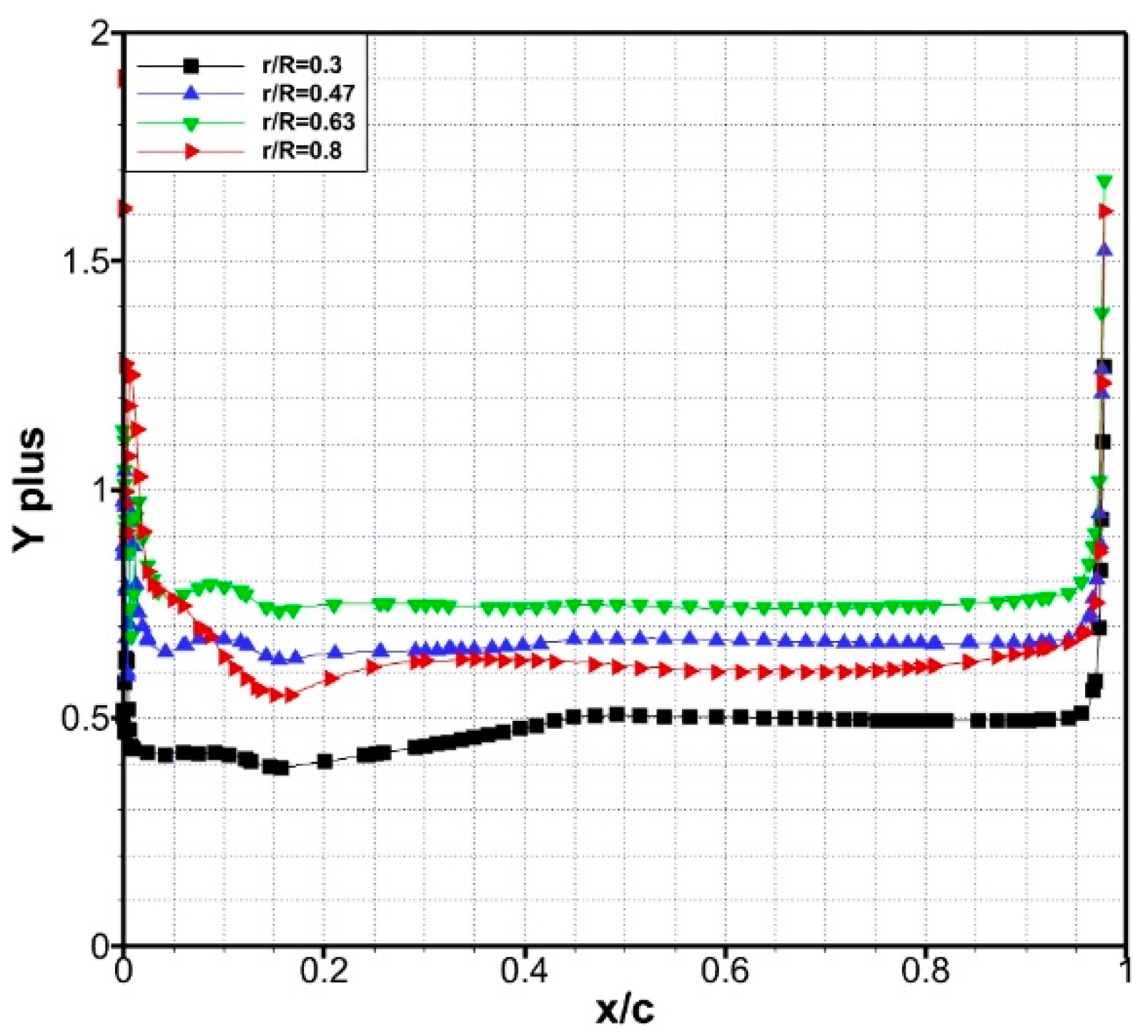
2.2. Boundary Conditions and Computational Mesh

Figure 2a,b depicts the computational domain, including boundary conditions and the mesh grid. Only one blade is treated for the computational domain, and a periodic condition is applied at 120°. The wind turbine tower and nacelle and the ground impact were ignored. The computational domain is surrounded by a small inner cylinder where the Euler condition was applied and an outer cylinder with a symmetry boundary condition. To eliminate far-field effects, the domain radius length equals three times the rotor diameter (3R). The inlet was placed at 2R upstream of the blade, where a uniform wind speed was assumed as the velocity inlet boundary condition (Table 2). In addition, turbulence conditions are characterized by a fixed turbulent intensity and viscosity ratio. The pressure outlet boundary condition was applied at 10R downstream of the rotor.
A structured C-type mesh was considered, which allows for better capture of the leading-edge curvature and of the airfoil. Figure 2b and Figure 3 show the hexahedral mesh distribution on the studied domain. The mesh density is nearly 2.8 million cells (for the baseline configuration), with 280 cells on the blade surface in the chordwise direction, 50 cells in the spanwise direction, and 6339 cells on the tip surface. The thickness of the first cell to the wall was kept at 2 × 10−5 m so that the y+ value is less than 1 for most of the blade surface (Figure 4), which is appropriate for k-ω with SST correction model.

2.3. Numerical Method

An incompressible steady Navier–Stokes solver is used to predict the aerodynamics proprieties of the different configurations. For the case of the rotating rotor, ANSYS Fluent provides us with several choices. The one used in the present study is called Single Moving Reference Frame (SRF) [54].
The pressure-based discretization scheme with a SIM-PLE algorithm was applied. A second-order upwind discretization scheme is used for all variables, i.e., pressure, momentum, and turbulence equations. To decrease the scaled residual below the value of 10−5, the convergence criterion and the under-relaxation factors were manipulated. The static pressure and torque were considered for each run to evaluate the solution convergence.
Since this work concentrates on flow control, large separation areas are anticipated, so the turbulence model would probably have a noticeable impact on the numerical solution. Therefore, the three-dimensional steady-state RANS equations with the closure turbulence model k-ω SST are first performed on the baseline configuration.
In the present work, and for simplification reasons, the influence of the mast and the nacelle on the rotor’s aerodynamics are neglected. This greatly simplifies the geometric complexity of the flow problem, and this simplification also avoids interference between the blades and the tower and nacelle.

3. Results

In this section, the computation results on the investigated blade are presented. The numerical results are first compared with the measured and computed data from [52,55]: (i) pressure coefficient (Cp) at different spanwise and wind speeds as well as the mechanical power production; (ii) the effect of rotation on the flow control system is investigated.

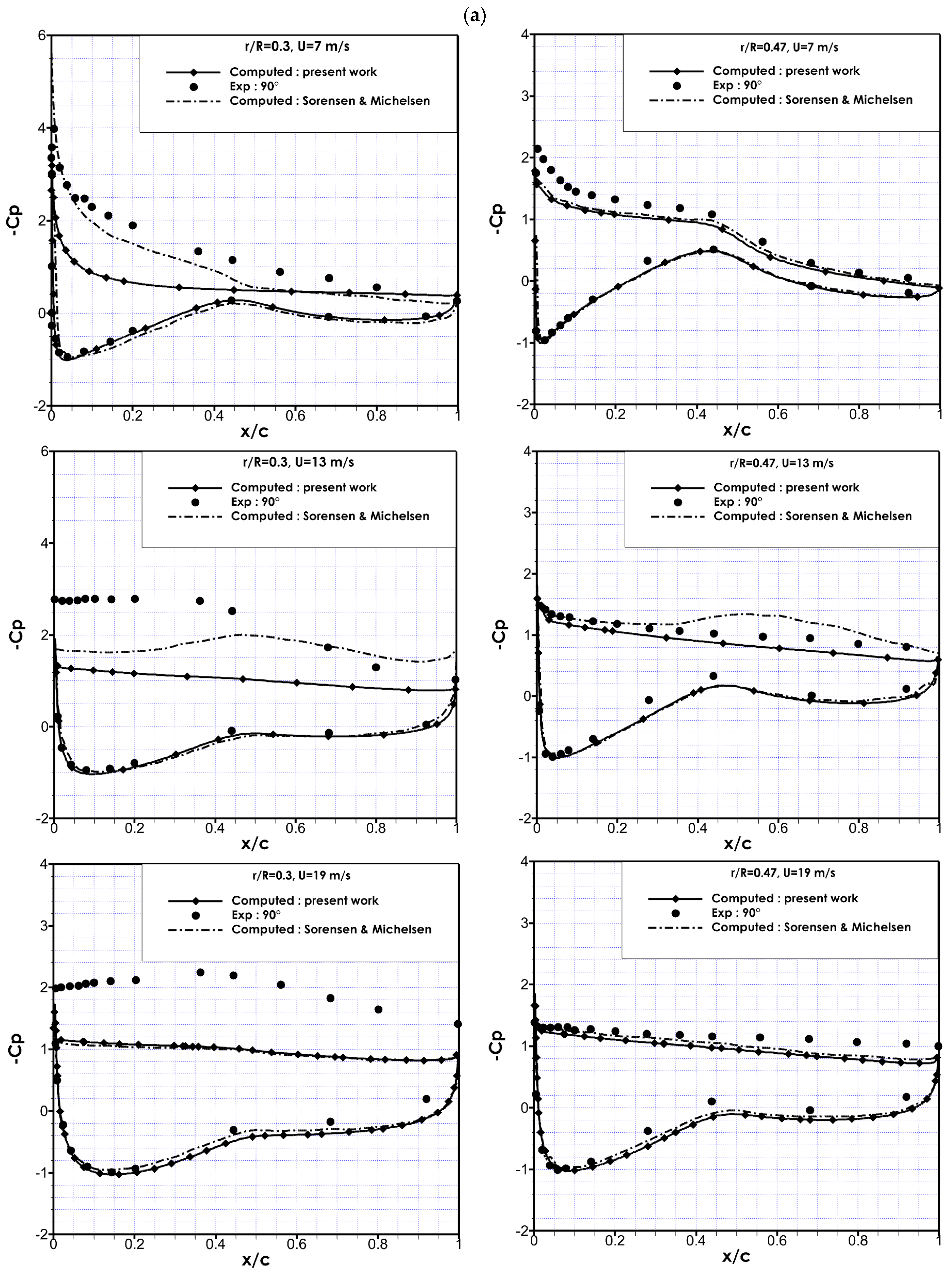
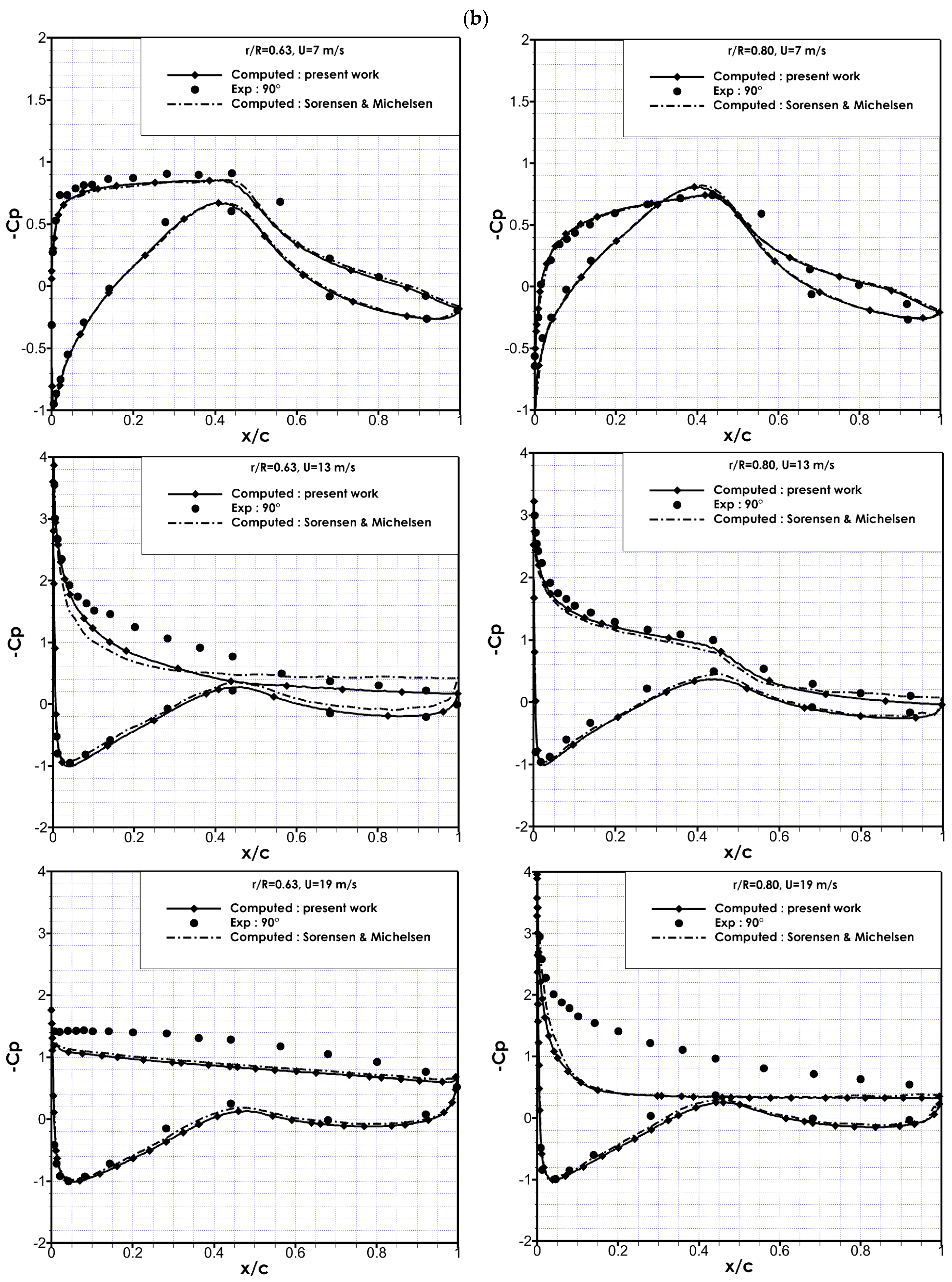
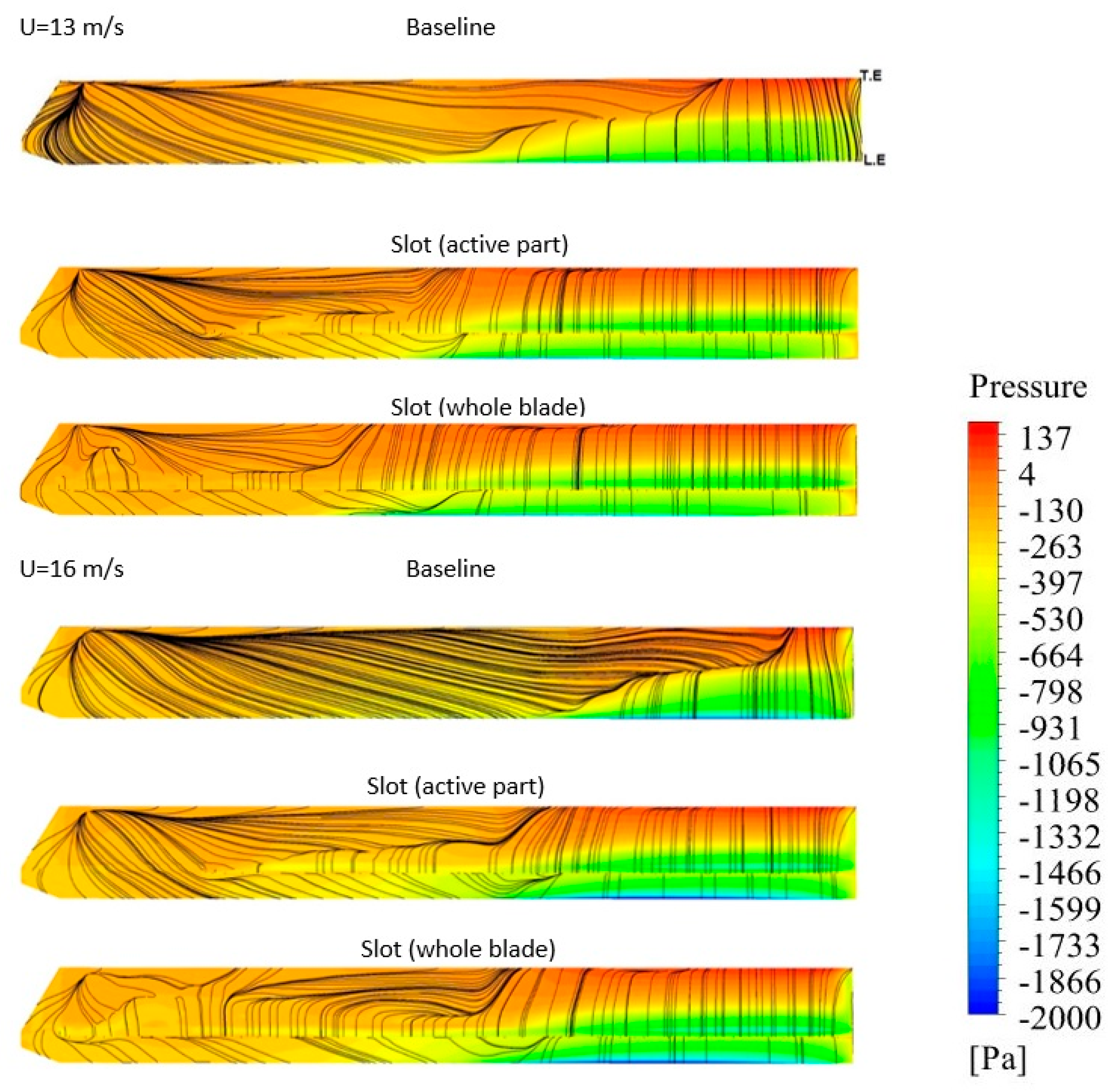
3.1. Pressure Distribution

The accuracy of the computed Cp against the corresponding experimental (the measurement is taken at the position 90° before the tower passage) and computed values [53,56] are verified at the four spanwise examined stations (r/R) for three different wind speeds. Figure 5a depicts the comparison of Cp for r/R = 0.3 and r/R = 0.47 for wind speeds of 7 m s−1, 13 m s−1, and 19 m s−1. Figure 5b presents Cp at r/R = 0.63 and r/R = 0.80 for the same wind speeds.
For the wind speed of 7 m s−1, the computed pressure distribution agrees with the measured ones. At these conditions, the computed angle of attack is 18.86° at r/R = 0.30, and 8.10°, 3.77°, and 1.20° at r/R = 0.47, 0.63 and 0.80, respectively. The agreement is very good for the upper and lower surface for the small AoA (near the blade’s tip), where the flow is wholly attached. However, as we approach the blade’s root, the AoA increases, and the flow is separated, leading to the agreement’s deterioration.
Significant deviations were observed for wind speeds of 13 m s−1 and 19 m s−1, and the agreement is generally worse for the upper side of the entire blade span. These discrepancies are proportional to AoA (Table 3). Therefore, the best agreement was seen near the blade’s tip, at lower AoA compared to the other sections (Figure 5).

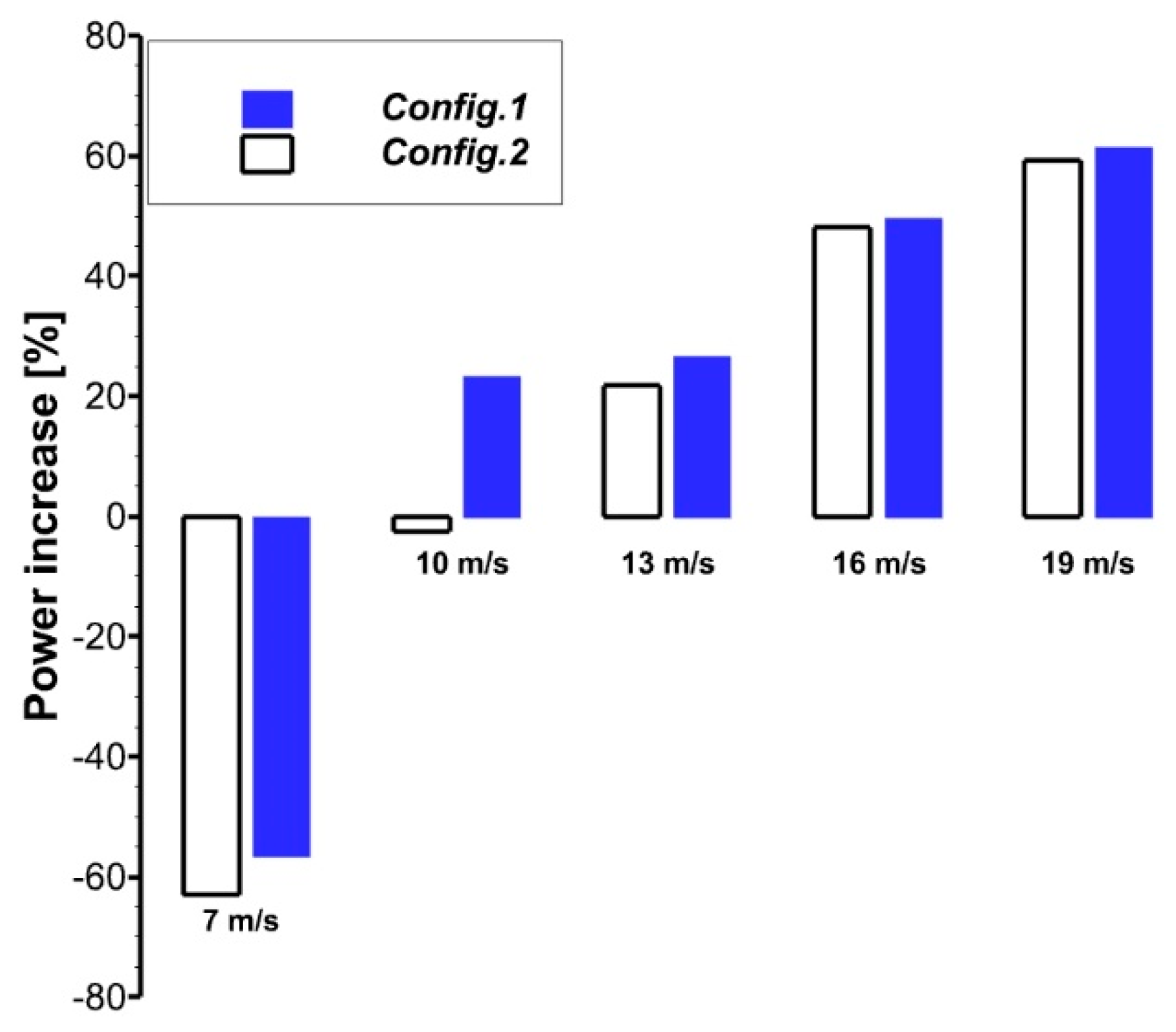
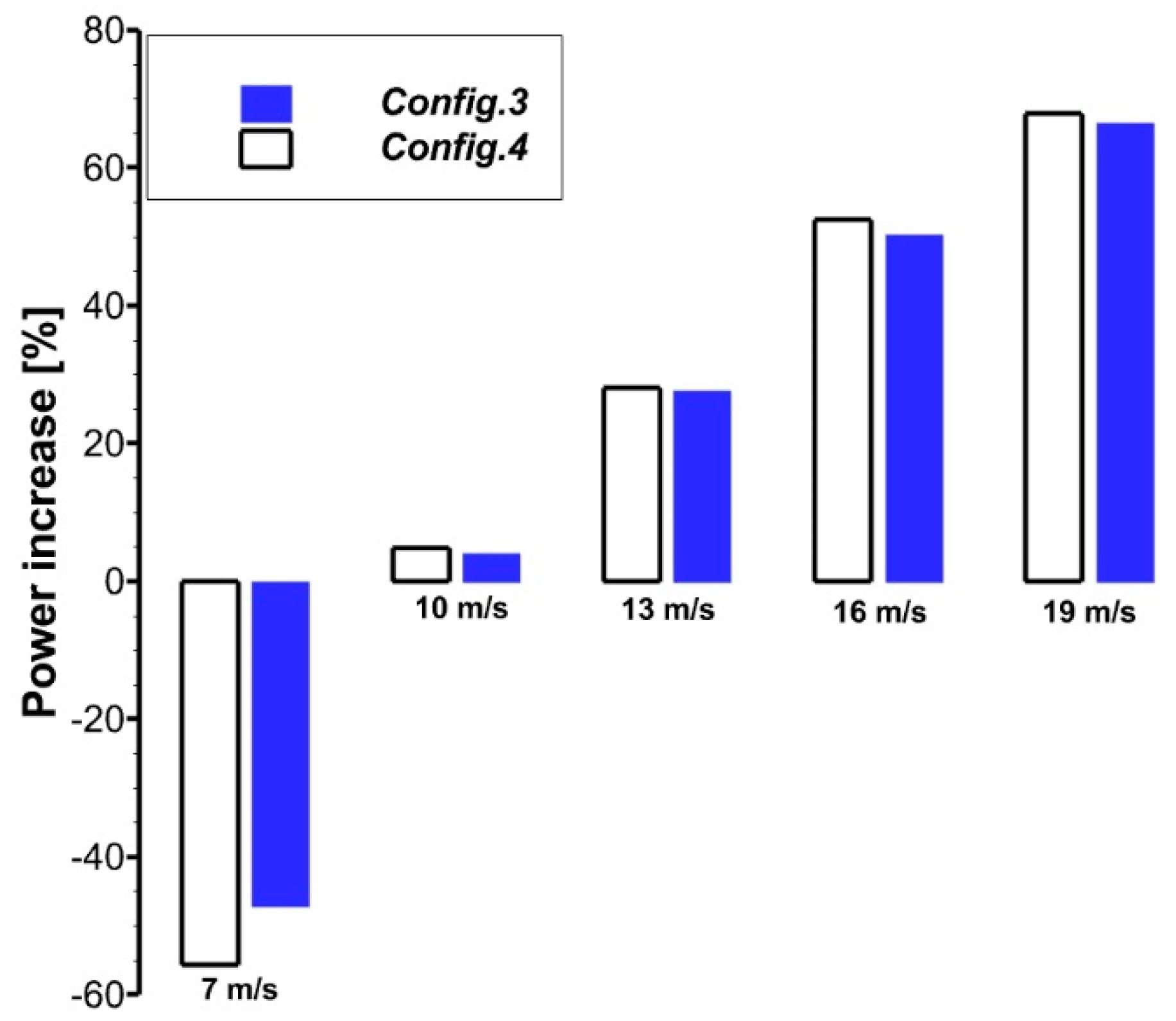
3.2. Power Production

A comparison between computed and measured power production for different wind speeds is illustrated in Table 4 at a wind speed of 7 m/s. The agreement is quite good, with an error of 4.33%. As the wind speed increases, the difference between the calculated and measured power production increases, where a maximum value of deviation (17.36%) is observed at a wind speed of 19 m/s.

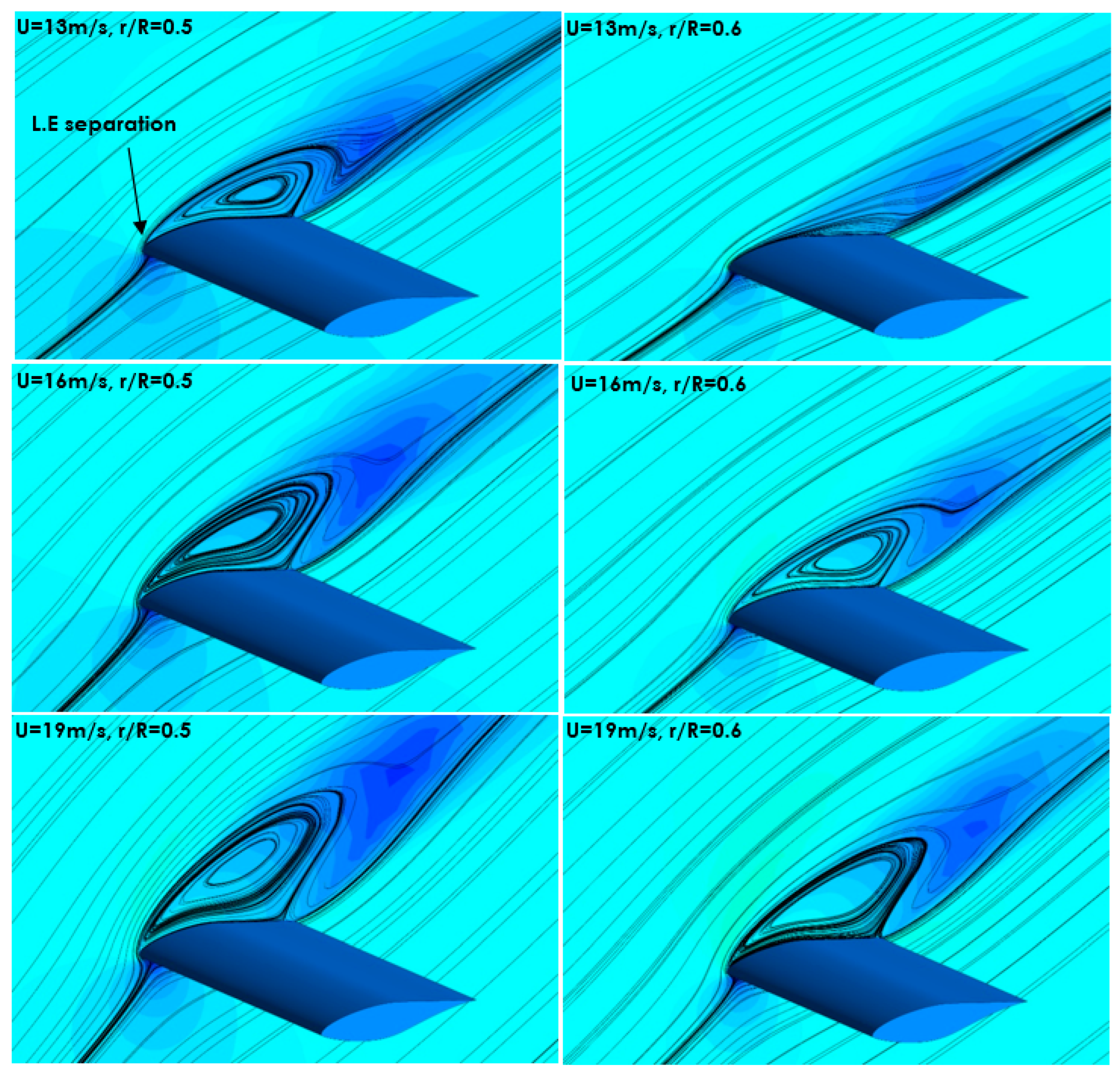
3.3. Effect of Rotation on the Control System

The aerodynamic characteristics of the blade are considerably affected by rotation (the Coriolis and Centrifugal forces). The aim here is to improve the efficiency of the wind turbine by applying a control system. In this subsection, four different configurations of the flow control system (Table 5) are compared in terms of power generated by the rotating blade. The first configuration consists of a Single-Slot (S-S) control system (Figure 6) applied over the whole blade span (outboard of r/R = 0.144), as shown in Figure 7a. The second one is applied in the active part of the blade, as shown in Figure 7b. The third and fourth configurations consist of Two-Slots, where a second small slot has been added to the S-S control system configuration as given in Figure 7c. All configurations are investigated from the overall point of view and then compared with the baseline configuration to determine the influence of rotation on the control system and then assess the blade performances.
As illustrated in Figure 7c, a hexahedral mesh of 8400 cells was generated for the first slot and 4000 for the second slot. It gives an overall cell number of approximately 3.7 million for configuration 1 and 4.6 million for configuration 4. The k-ω SST turbulence model with the appropriate wall modeling approach has been used for all steady-RANS simulations.

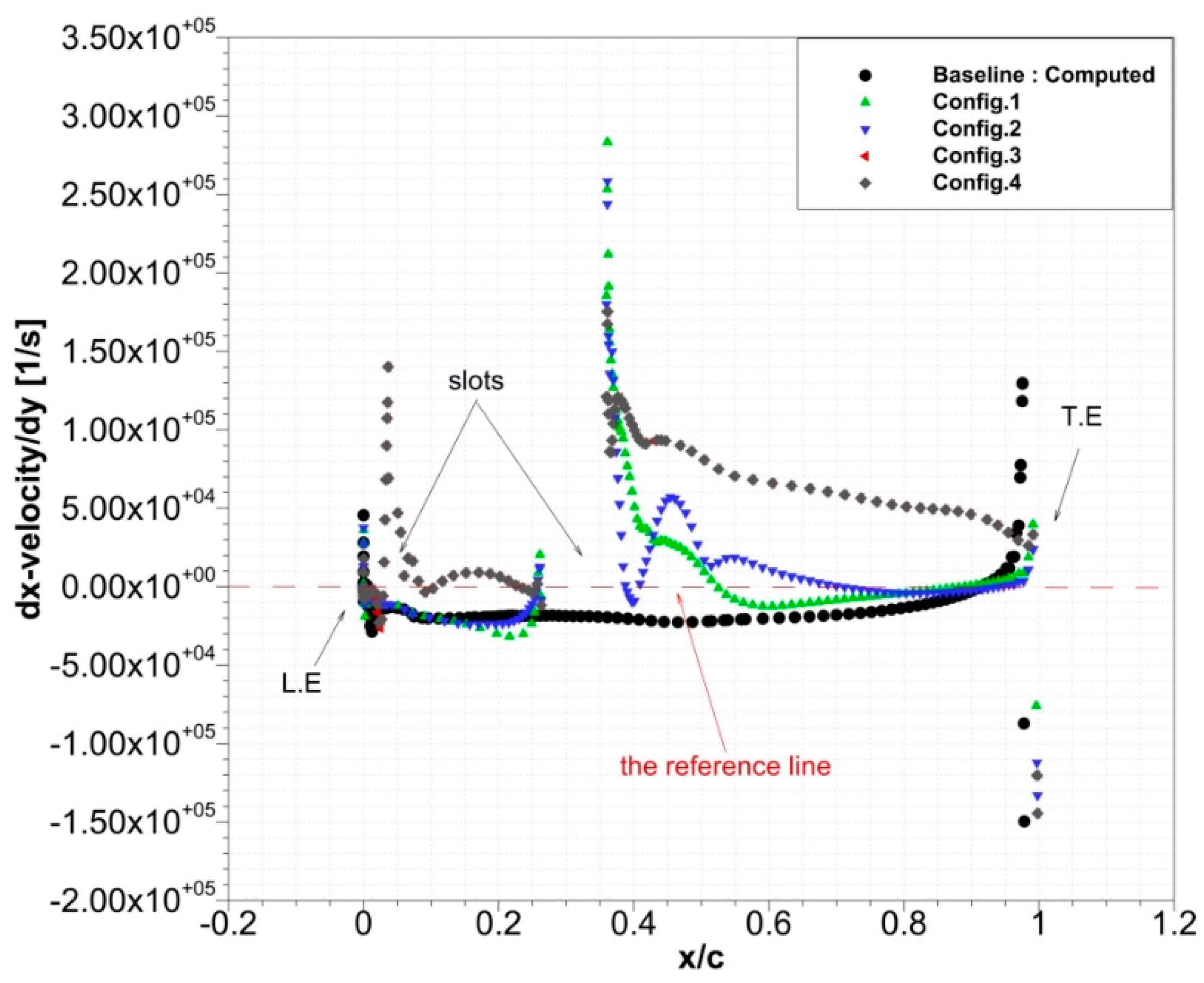
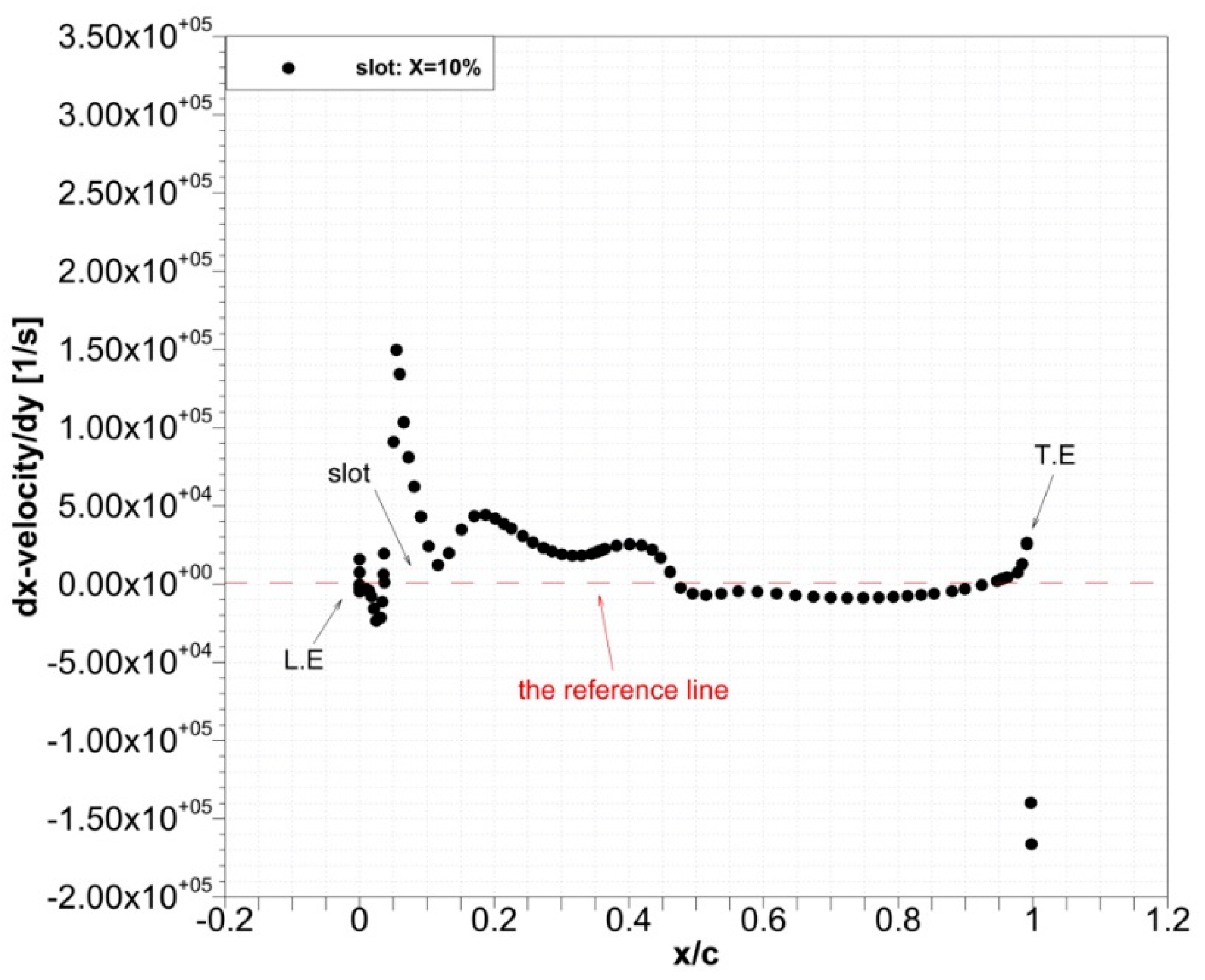
3.3.1. Applying a Single-Slot

The best position of the slot depends on the boundary layer separation position. Therefore, for the control system to adequately delay boundary layer separation and improve aerodynamic performance, the optimum position of the slot location must be just upstream of the separation point. More details are available in reference [13]. However, for a 3-D rotating flow, the angle of attack (the point of separation of the boundary layer) varies along with the blade’s spanwise position for the same wind speed (Table 3). Therefore, determining the exact optimal slot location for all the blade sections is not practical in terms of design. Based on this, the adopted approach to determine the slot position uses the mid-span section (r/R = 0.5) at the wind speed of 10 m s−1.
The geometric characteristics of the control system (see Figure 6) are a slot position at X = 30% (chord length) and a slope of ψ = −60° (y-axis direction). The converged section of the slot Y1/Y2 = 3, and Coanda radius Rc = 102 mm. The results of power increase of configurations 1 and 2, compared with baseline configuration (without flow control system), are shown in Figure 8 for different wind speeds: U∞ = 7 m s−1, 10 m s−1, 13 m s−1, 16 m s−1, and 19 m s−1. It corresponds to different flow situations: design condition, stall condition, and post-stall condition.
The comparison shows that both configurations exceed the baseline for wind speeds over 10 m s−1. At U∞ = 7 m s−1, there is a significant power decrease for configurations 1 (−56.46%) and 2 (−62.95%) compared to the baseline. For U∞ = 10 m s−1, a power increase of 23.27% for configuration 1 was obtained compared with the baseline. However, the performance of configuration 2 is still below the baseline. At U∞ = 13 m s−1, the power of both configurations exceeds that of the baseline. The increases are 26.62% and 21.88% for configurations 1 and 2, respectively. The maximum increase in the power compared with the baseline reaches 61.48% for configuration 1 at 19 m s−1.
The comparison of the S-S (single slot) configurations with baseline shows that the slot’s presence does not improve the aerodynamic performance of the blade at lower wind speeds. However, the control system’s efficiency is clearly enhanced for high wind speeds (stall and post-stall). As seen in Figure 8, the rate of power increase for configuration 1 is always exceeding the one for configuration 2. However, this difference decreases as the wind speed increases, i.e., the slightest difference is observed for the speed of 19 m/s, at 2.25%. Furthermore, the inboard region of the blade is characterized by the large separation of the boundary layer, which can occur over the entire upper surface of the blade for high wind speeds (see Figure 9). Therefore, the addition of momentum in this region can influence the behavior of the flow in the outboard region and improve the blade’s performance.
Figure 9 illustrates the streamlines colored by the static pressure on the upper side of the blade for the two configurations with control slots and the baseline. At U∞ = 13 m s−1, we observe that the flow is separated on most of the upper surface of the baseline configuration, except for the area near the blade tip. For the same wind speed, the boundary layer separation was almost eliminated in the active part for configuration 1. The controlled area is slightly larger than for configuration 2, which confirms the discussion below. At U∞ = 16 m s−1, the separation zone is larger for the baseline and the controlled configurations. The control system effect is almost the same for both configurations in the outboard region, which performed almost the same streamlined behavior. However, as the wind speed increases, the separated surface of the baseline configuration is enlarged. On the other hand, the control system shows its capacity to delay or even eliminate the boundary layer separation for high wind speeds.
To better analyze the control effect on the boundary layer separation for 3-D rotation flow, we visualize the XY plane’s streamlines at two locations, namely r/R = 0.5 and r/R = 0.6. A comparative view of the velocity distribution of the baseline configuration and with the S-S control system is illustrated in Figure 10 and Figure 11, respectively, for different wind speeds. At r/R = 0.5, the boundary layer separation is delayed for configuration 1, and the flow is almost attached downstream of the slot for U∞ = 13 m s−1 (Figure 11). For configuration 2, at the same location, the flow is well delayed except upstream of the slot where we observe the appearance of a small vortex, not seen in configuration 1. On the other hand, the control system eliminates the boundary layer separation at r/R = 0.6 for the two configurations compared with the baseline. For U∞ = 16 m s−1, the control system changes the flow behavior considerably at r/R = 0.5. However, the upstream vortex in configuration 1 is smaller than in configuration 2. At r/R = 0.6, the flow is well controlled for both configurations compared to baseline.
As mentioned above, the separation position of the boundary layer is related to the angle of attack, and the slot must be located just upstream of the separation point to have a positive (optimal) effect. As the angle of attack varies with blade spanwise position and the wind speed, using a single slot at the same location along the spanwise has a variable effect, i.e., positive or negative, depending on the slot location and spanwise position.
According to Figure 12, the main observation is that the slot has no positive effect when it is located in the middle of the separation zone, and the separation zone of the boundary layer remains almost the same or even enlarged. It is because the fluid passing through the slot does not have sufficient kinetic energy to re-energize the inner region of the boundary layer. The effect is quite the opposite of the desired one. Vortices are observed upstream of the slot for configuration 1, compared with configuration 2, for which no control is applied at this location.

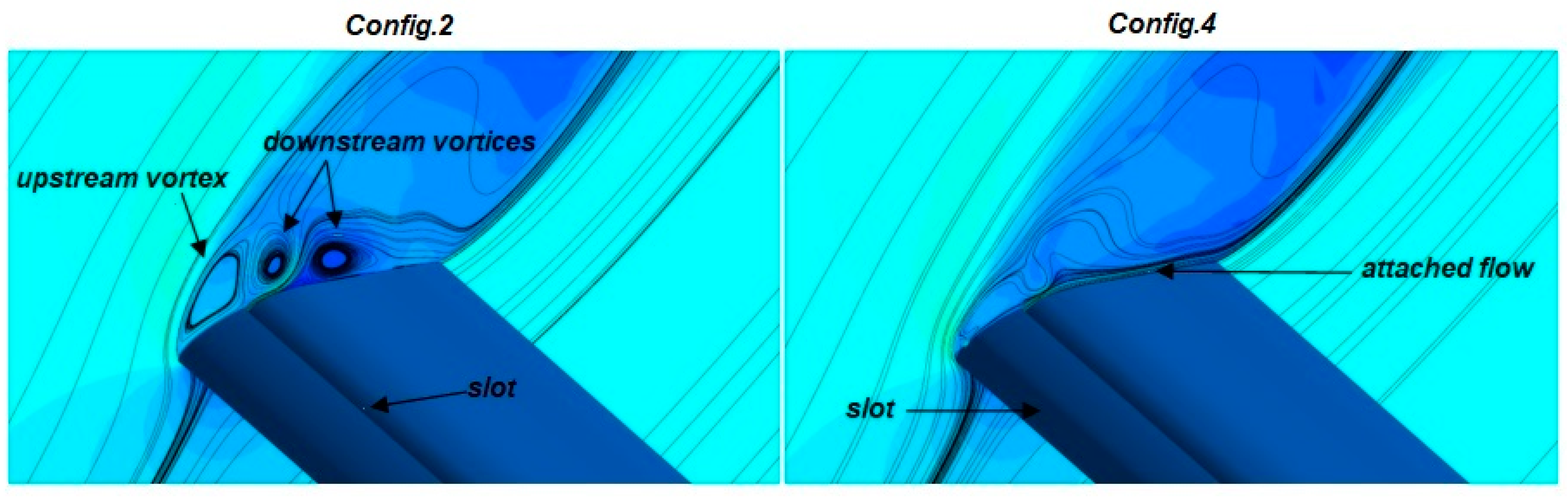
3.3.2. Two-Slots Control System Configurations

In this section, to improve the control system, we investigate the effect of adding a second slot (Two-Slots (T-S) control system configuration) close to the leading-edge while keeping the same characteristics of the first slot (S-S configuration). The second slot is located at X = 10% of the chordwise with a converged section Y1/Y2 = 2.6 and a slope ψ = −70° (see Figure 13). The power increase for configurations 3 and 4 compared with baseline are shown in Figure 14 for different wind speeds: U∞ = 7 m s−1, 10 m s−1, 13 m s−1, 16 m s−1, and 19 m s−1.
Again, we observe a deterioration of the power output at U∞ = 7 m s−1. The second slot leads to a significant decrease in power by −65.25% and −74.39% for configurations 3 and 4, respectively, compared with the baseline. We observe a slight power increase of approximately 2.35% for both configurations at 10 m s−1 wind speed. The increase is more significant for U∞ = 13 m s−1 at approximately 23%. Noticeably, the power increases significantly as the wind speed increases, as seen for U∞ = 16 m s−1 and U∞ = 19 m s−1. The highest increase is observed at U∞ = 19 m s−1, at 62.60% for configuration 3 and 63.38% for configuration 4.
To determine the best configuration, we compare the streamlines and the velocity distribution of S-S and T-S configurations at U∞ = 19 m s−1 wind speed (Figure 15) for two different planes r/R = 0.5 and 0.6. The main observation is the positive effect of adding the second slot. The flow behavior is considerably improved compared with S-S configurations and the baseline. At r/R = 0.5, the separation zone of the S-S configuration is more significant than for the T-S configuration. As a result, the downstream boundary layer separation (downstream relative to the slot location X2 = 30%) for the T-S configuration is delayed. For configuration 4, the upstream vortices completely disappear compared with the S-S configuration. At r/R = 0.6 plane, the separation is eliminated. The T-S configuration has proven its ability to improve the control system compared with the baseline and the S-S configuration.
Knowing that the kinetic energy in the region of the favorable pressure gradient is dissipated by internal viscous friction, it becomes insufficient to overcome too much strong overpressure, which leads to the boundary layer separation [56]. The role of the slot is then to re-energize the dead fluid zone where the particles’ movement near the wall is slowed down or even possibly stopped. However, the separation zone still exists, even with improved aerodynamic performance for the S-S configuration (see Figure 16). The size of the separation zone depends on the blade section and the wind speed (angle of attack). The reasons for boundary layer separation even with the S-S control system are:
(i)
The fluid passing through the slot does not have sufficient kinetic energy to re-energize the dead fluid zone;
(ii)
The location of the slot in the middle of the separation zone and the upstream vortex (relative to the slot location X2 = 30%) affects the downstream flow (main flow).
Figure 16 and Figure 17 show that the upstream vortex is almost eliminated by adding the first slot at the leading edge. In addition, this leading-edge slot has a positive effect even downstream of the second slot by keeping the boundary layer attached.
This section compares the boundary layer separation for the four configurations (two S-S and two T-S configurations) with the baseline. We used the derivative in the direction normal to the wall of the relative flow velocity on the blade in the x-direction as a criterion to detect separation. If this derivative is positive, the boundary layer is attached. If it is negative, the boundary layer is detached. Figure 17 illustrates this derivative’s distribution on the blade’s upper side at r/R = 0.5 and wind-speed U∞ = 19 m s−1. The negative values below the reference line represent separated flow, while positive values above the reference line represent the attached flow.
At 0 ≤ x / c < 0.3 , the flow is completely detached for configurations 1 and 2. The difference in static pressure between the lower and upper sides of the blade leads to an acceleration of the flow through the slot, which will renew the exhausted fluid layers from the friction effect and the strong pressure gradient. Consequently, the downstream flow is reattached to the wall. However, the main flow remains attached only over a distance of x/c = 0.4 to 0.5 and x/c = 0.4 at 0.75 for configurations 1 and 2, respectively. After that, the boundary layer separates again as the energization of the boundary layer is insufficient to counter the friction effects and adverse pressure gradient.
When adding a slot near the leading edge (configurations 3 and 4), we noticed a positive value of the relative velocity derivative (Figure 17) in the zone between the two slots ( 0.1 ≤ x / c < 0.2 ). The leading edge slot also affects the flow downstream of the downstream slot, where we observe that the main flow remains attached over the entire upper surface. It means that the first slot (X = 10%) is well-positioned with respect to the separation line, which gives positive values upstream of the downstream slot (X = 30%). As the first slot (X = 10%) is insufficient to re-energize the main flow to remain attached to the entire upper surface (Figure 18), the second, downstream, is essential to accelerate the flow and strengthen the boundary layer attachment.
In general, the configurations with a single slot, whatever the position, show lower performance than those with two slots, for which the flow remains attached over most of the upper side of the blade.

4. Conclusions

The current work consists of a 3-D CFD modeling of a rotating blade equipped with different flow control systems: single-slot (S-S) and two-slots (T-S). The computation provides a better understanding of the influence of these flow control devices on the performance of wind turbine blades. The results are helpful for the development of a new generation of wind turbine blades. Several issues have been addressed, including the control of boundary layer separation and the rotation effect with the control system. The results of the calculations were entirely satisfactory, and, in our opinion, they can represent a sound basis for future work in the wind turbine field. The most significant results are summarized below.
The capacity of the CFD-RANS method for calculating aerodynamic performance and loads on wind turbine blades has been demonstrated. While the agreement with the experimental data was better for the attached flow and close to the nominal conditions, the tool is suitable for designing blades equipped with control systems. In addition, the turbulence model k-ω SST with the advanced wall modeling approach used in this work has given good results even at relatively high angles of attack.
The presence of the slot has shown its ability to delay the boundary layer separation in the 3-D flow of the rotary blade. However, the improvement in aerodynamic performance has been proven only for medium and high wind speeds ( 10   m s − 1 ≤ U ∞ ), when the boundary layer is generally separated. Low wind speed (low angle of attack) makes it not effective to use slots for flow control (which is the main limitation), as the wind turbine power output is reduced. Therefore, it is necessary to design a blade with variable geometry that operates with slots only at higher wind speed, i.e., angle of attack. This can be done with a system opening or closing the slot according to wind speed. Indeed, at high angles of attack, the slot will significantly increase the overall performance of the rotor and the energy efficiency of wind turbines. The addition of a second slot near the leading edge further improves the power output and the flow behavior compared with the single slot configuration.
We noticed that the control system has no positive effect on the inboard region of the rotor due to the large separation on the entire upper surface. Therefore, we suggest applying a hybrid approach using two different control methods:
(i)
A first method (active or passive) for the inboard region of the rotor that does not depend on the separation point of the boundary layer. In fact, in this region (up to 30 to 40% of the blade span), the separation begins from the leading edge. However, applying a control method that must be located just upstream of the separation point will not be effective in this case;
(ii)
A second control method with two slots is applied for the middle span and the outboard region.

Author Contributions

Methodology, A.S. and A.I.; Supervision, K.C.; Writing—original draft, R.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

This research is a result of the PRFU project A11N01EP230220220001 funded in Algeria by La Direction Générale de la Recherche Scientifique et du Développement Technologique (DGRSDT).

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

AoAAngle of Attack
SSTShear Stress Transport
RANSReynolds-averaged Navier–Stokes
CFDComputational Fluid Dynamics
RDiameter
CpPressure coefficient
L.ELeading edge
T.ETrailing edge
S.SSuction side
P.SPressure side
S-SSingle slot
T-STwo slots
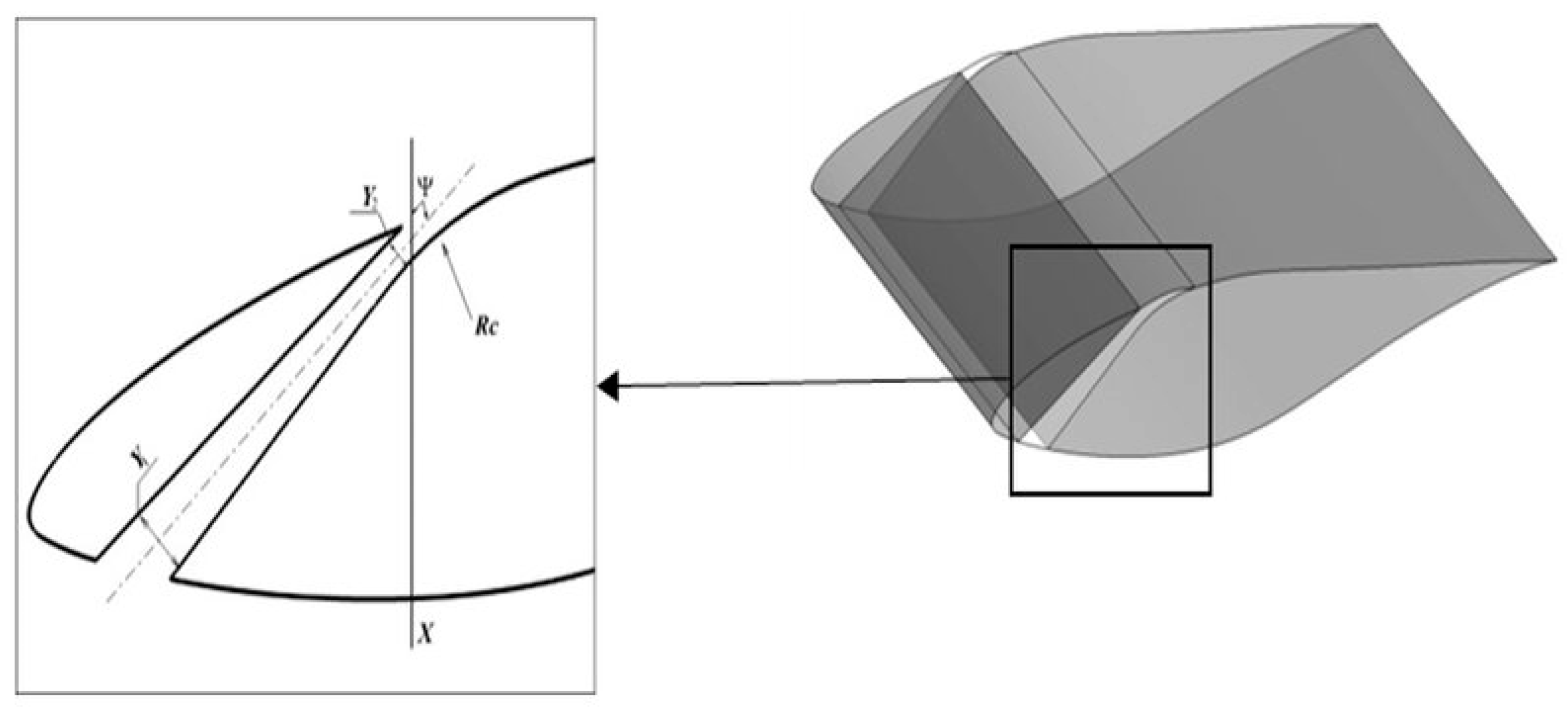
XSlot location
YSlot width
ψSlot slope
RcCoanda radius

References

  1. Wang, Y.; Li, G.; Luo, D.; Huang, D. Influence of microcylinder with different vibration laws on the flow control effect of a horizontal axis wind turbine. Wind Energy 2019, 22, 1800–1824. [Google Scholar] [CrossRef]
  2. El-Hak, M.G.; Pollard, A.; Bonnet, J.P. Flow Control, Fundamentals and Practices; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
  3. Kral, L.D. Active flow control technology. ASME Fluids Eng. Technol. Brief 2000, 53, 1–28. [Google Scholar]
  4. Prandtl, L. Ueber Fluessigkeitsbewegungen bei sehr Kleiner Reibung. 3; International Mathematical Congress: Heidelberg, Germany, 1904; p. 7. [Google Scholar]
  5. Bobonea, A. Unsteady computational simulation for active aerodynamic control of a horizontal axis wind turbine. AIP Conf. Proc. 2012, 1479, 1623–1626. [Google Scholar]
  6. Hosseini, S.S.; van Dam, C.P.; Pandya, S.A. Aerodynamic Load Control for Multi-Element Airfoils Using Surface-Normal Trailing-Edge Blowing. J. Aircr. 2019, 56, 1668–1676. [Google Scholar] [CrossRef]
  7. Rezaeiha, A.; Montazeri, H.; Blocken, B. Active flow control for power enhancement of vertical axis wind turbines: Leading-edge slot suction. Energy 2019, 189, 116131. [Google Scholar] [CrossRef]
  8. Luo, D.H.; Sun, X.J.; Huang, D.G.; Wu, G.Q. Flow control effectiveness of synthetic jet on a stalled airfoil. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 2106–2114. [Google Scholar] [CrossRef]
  9. Yen, J.; Ahmed, N.A. Enhancing vertical axis wind turbine by dynamic stall control using synthetic jets. J. Wind Eng. Ind. Aerodyn. 2013, 114, 12–17. [Google Scholar] [CrossRef]
  10. Akhter, M.Z.; Omar, F.K. Review of Flow-Control Devices for Wind-Turbine Performance Enhancement. Energies 2021, 14, 1268. [Google Scholar] [CrossRef]
  11. Brunton, S.L.; Noack, B.R. Closed-Loop Turbulence Control: Progress and Challenges. Appl. Mech. Rev. 2015, 67, 050801. [Google Scholar] [CrossRef]
  12. Guoqiang, L.; Weiguo, Z.; Yubiao, J.; Pengyu, Y. Experimental investigation of dynamic stall flow control for wind turbine airfoils using a plasma actuator. Energy 2019, 185, 90–101. [Google Scholar] [CrossRef]
  13. Belamadi, R.; Djemili, A.; Ilinca, A.; Mdouki, R. Aerodyanmic performance analysis of slotted airfoil for application 482 to wind turbine blades. J. Wind Eng. Ind. Aerodyn. 2016, 151, 79–99. [Google Scholar] [CrossRef]
  14. Handley, P.F. Wing and Similar Member of Aircraft. U.S. Patent 1353666, 21 September 2021. [Google Scholar]
  15. Houghton, E.L.; Carpenter, P.W. Aerodynamics for Engineering Students; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
  16. Ragheb, A.M.; Selig, M.S. Multielement Airfoils for Wind Turbines. In Wind Energy Engineering; Elsevier: Amsterdam, The Netherlands, 2017; pp. 203–219. [Google Scholar]
  17. Van Dam, C.P. The aerodynamic design of multi-element high-lift systems for transport airplanes. Prog. Aerosp. Sci. 2002, 38, 101–144. [Google Scholar] [CrossRef] [Green Version]
  18. Kentfield, J.A.C. Theoretically and experimentally obtained performances of Gurney-flap equipped wind turbines. In Proceedings of the Energy-Sources Technology Conference, New Orleans, LA, USA, 23–26 January 1994; pp. 31–40. [Google Scholar]
  19. Zhang, Y.; Ramdoss, V.; Saleem, Z.; Wang, X.; Schepers, G.; Ferreira, C. Effects of root Gurney flaps on the aerodynamic performance of a horizontal axis wind turbine. Energy 2019, 187, 11595. [Google Scholar] [CrossRef]
  20. Fernandez-Gamiz, U.; Errasti, I.; Zulueta, E.; Guede, J.M.L.; Boyano, A. Computational characterization of a Gurney flap on a DU91 (2) W250 airfoil. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2020; p. 01053. [Google Scholar]
  21. Meyer, R.; Hage, W.; Bechert, D.W.; Schatz, M.; Knacke, T.; Thiele, F. Separation Control by Self-Activated Movable Flaps. AIAA J. 2007, 45, 191–199. [Google Scholar] [CrossRef]
  22. Taylor, H.D. The Elimination of Diffuser Separation by Vortex Generators; United Air Craft Corporation Report No.R-4012-3; United Air Craft Corporation: Moscow, Russia, 1947. [Google Scholar]
  23. Wetzel, K.K.; Farokhi, S. Influence of Vortex Generators on NREL S807 Airfoil Aerodynamic Characteristics and Wind Turbine Performance. Wind Eng. 1995, 19, 157–165. [Google Scholar]
  24. Shan, H.; Jiang, L.; Liu, C.; Love, M.; Maines, B. Numerical study of passive and active flow separation control over a NACA0012 airfoil. Comput. Fluids 2008, 37, 975–992. [Google Scholar] [CrossRef]
  25. Zahle, F.; Sørensen, N.N.; Johansen, J. CFD Study of a NACA 63-415 Aerofoil Fitted with Stall Strips; Risø-R-1370; Risø National Laboratory, Pitney Bowes Management Services: Roskilde, Denmark, 2002. [Google Scholar]
  26. Timmer, W.A.; Van Rooij, R.P.J.O.M. Summary of the Delft University wind turbine dedicated airfoils. J. Sol. Energy Eng. 2003, 125, 488–496. [Google Scholar] [CrossRef]
  27. Handley, P.F. Wing and Similar Member of Aircraft. U.S. Patent 1,414,200, 24 October 1922. [Google Scholar]
  28. Lachmann, C.; Wieslsberger, C.; Katzmayr, R.; Kirste, L. Experiments with Slotted Wings; National Advisory Committee for Aeronautics: Washington, DC, USA, 1921. [Google Scholar]
  29. Weick, F.E.; Shortal, J.A. The Effect of Multiple Fixed Slots and a Trailing-Edge Flap on the Lift and Drag of a Clark Y Airfoil; NACA Report No.427; NASA: Washington, DC, USA, 1933; p. 6. [Google Scholar]
  30. Abbott, I.H.; von Doenhoff, A.E. Theory of Wing Sections; Dover Publications: Mineola, NY, USA, 1958. [Google Scholar]
  31. Rumsey, C.L.; Ying, S.X. Prediction of high lift: Review of present CFD capability. Prog. Aerosp. Sci. 2002, 38, 145–180. [Google Scholar] [CrossRef]
  32. Yavuz, T.; Koc, E.; Kaynak, B. Hydrodynamics performance of hydrofoil-slat arrangements in 3D analysis. Energy Convers. Manag. 2013, 75, 44–50. [Google Scholar] [CrossRef]
  33. Yavuz, T.; Koç, E.; Kılkış, B.; Erol, Ö.; Balas, C.; Aydemir, T. Performance analysis of the airfoil-slat arrangements for hydro and wind 542 turbine applications. Renew. Energy 2015, 74, 414–421. [Google Scholar] [CrossRef]
  34. Ullah, T.; Javed, A.; Abdullah, A.; Ali, M.; Uddin, E. Computational evaluation of an optimum leading-edge slat deflection angle for dynamic stall control in a novel urban-scale vertical axis wind turbine for low wind speed operation. Sustain. Energy Technol. Assess. 2020, 40, 100748. [Google Scholar] [CrossRef]
  35. Shi, X.; Sun, J.; Zhong, S.; Huang, D. Flow control of a stalled S809 airfoil using an oscillating micro-cylinder at different angles of attack. Renew. Energy 2021, 175, 405–414. [Google Scholar] [CrossRef]
  36. Wang, Y.; Li, G.; Shen, S.; Huang, D.; Zheng, Z. Investigation on aerodynamic performance of horizontal axis wind turbine by setting micro-cylinder in front of the blade leading edge. Energy 2018, 143, 1107–1124. [Google Scholar] [CrossRef]
  37. Luo, D.; Huang, D.; Sun, X. Passive flow control of a stalled airfoil using a microcylinder. J. Wind Eng. Ind. Aerodyn. 2017, 170, 256–273. [Google Scholar] [CrossRef]
  38. Liggett, N.; Smith, M.J. The physics of modeling unsteady flaps with gaps. J. Fluids Struct. 2013, 38, 255–272. [Google Scholar] [CrossRef]
  39. Ramzi, M.; AbedErrahmane, G. Passive control via slotted blading in a compressor cascade at stall condition. J. Appl. Fluid Mech. 2013, 6, 571–580. [Google Scholar]
  40. Bak, C.; Bitsche, R.; Yde, A.; Kim, T.; Hasen, M.H.; Zahle, F.; Gaunaa, M.; Wedel Heinen, J.J.; Behrens, T. Light rotor. In Proceedings of the 10MW Reference Wind Turbine EWEA Conference, Copenhagen, Denmark, 16–19 April 2012. [Google Scholar]
  41. Gaunaa, M.; Zahle, F.; Sørensen, N.N.; Bak, C. Quantification of the Effects of Using Slats on the Inner Part of a 10 MW Rotor. In Proceedings of the European Wind Energy Conference & Exhibition, EWEA, Copenhagen, Denmark, 16–19 April 2012. [Google Scholar]
  42. Standish, K.J. Aerodynamic Analysis of Blunt Trailing Edge Airfoils & A Microtab-Based Load Control System. Master’s Thesis, University of California, Davis, CA, USA, December 2003. [Google Scholar]
  43. Buhl, T.; Andersen, P.B.; Barlas, T.K. 2D Numerical Comparison of Trailing Edge Flaps up Wind WP1B3; Risoe-R No. 1628(EN); Risø National Laboratory, Forskningscenter Risoe: Roskilde, Denmark, 2007. [Google Scholar]
  44. Harris, F.D. Preliminary study of radial flow effects on rotor blades. J. Am. Helicopter Soc. 1966, 11, 1–21. [Google Scholar] [CrossRef]
  45. Sørensen, J.N. Prediction of the three-dimensional stall on wind turbine blade using three-level, viscous-inviscid interaction model. In Proceedings of the EWEC 86, Rome, Italy, 7–9 October 1986; pp. 429–435. [Google Scholar]
  46. Du, Z.; Selig, M.S. The effect of rotation on the boundary layer of a wind turbine blade. Renew. Energy 2000, 20, 167–181. [Google Scholar] [CrossRef]
  47. Shen, W.Z.; Sørensen, J.N. Quasi-3D Navier-Stokes model for a rotating airfoil. J. Comput. Phys. 1999, 150, 518–548. [Google Scholar] [CrossRef]
  48. Chaviaropoulos, P.K.; Hansen, M.O.L. Three-dimensional and rotational effects on wind turbine blades by means of a quasi-3D Navier-Stokes solver. J. Fluid Eng. 2000, 122, 330–336. [Google Scholar] [CrossRef]
  49. Hu, D.; Hua, O.; Du, Z. A study on stall-delay for horizontal axis wind turbine. Renew. Energy 2006, 31, 821–836. [Google Scholar] [CrossRef]
  50. Cravero, C.; Leutcha, P.J.; Marsano, D. Simulation and Modeling of Ported Shroud Effects on Radial Compressor Stage Stability Limits. Energies 2022, 15, 2571. [Google Scholar] [CrossRef]
  51. Margalida, G.; Joseph, P.; Roussette, O.; Dazin, A. Active flow control in an axial compressor for stability improvement: On the effect of flow control on stall inception. Exp. Fluids 2021, 62, 12. [Google Scholar] [CrossRef]
  52. Butterfield, C.P.; Musial, W.P.; Simms, D.A. Combined Experiment Final Report—Phase II; NREL TP-422-4807; National Renewable Energy Laboratory: Golden, CO, USA, 1992. [Google Scholar]
  53. Burton TSharpe DJenkins, N.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons Ltd.: Chichester, UK, 2001. [Google Scholar]
  54. ANSYS Inc. Ansysfluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2010. [Google Scholar]
  55. Sorensen, N.N.; Michelsen, J.A. Aerodynamic predictions for the unsteady aerodynamics experiment phase-ii rotor at the national renewable energy laboratory. In Proceedings of the 2000 ASME Wind Energy Symposium, Reno, NV, USA, 10–13 January 2000. AIAA-2000-0037. [Google Scholar]
  56. Maskell, E.C. Flow Separation in Three-Dimension; Royal Aircraft Establishment: Farnborough, UK, 1955. [Google Scholar]
Energies 15 04872 g001 550
Figure 1. NREL phase ii rotor.
Figure 1. NREL phase ii rotor.
Energies 15 04872 g001
Energies 15 04872 g002a 550Energies 15 04872 g002b 550
Figure 2. (a) Computational domain and (b) grid and boundary conditions.
Figure 2. (a) Computational domain and (b) grid and boundary conditions.
Energies 15 04872 g002aEnergies 15 04872 g002b
Energies 15 04872 g003 550
Figure 3. Zoom view on the mesh details.
Figure 3. Zoom view on the mesh details.
Energies 15 04872 g003
Energies 15 04872 g004 550
Figure 4. Y plus over the suction side at different spanwise sections for a wind speed of 19 m s−1.
Figure 4. Y plus over the suction side at different spanwise sections for a wind speed of 19 m s−1.
Energies 15 04872 g004
Energies 15 04872 g005a 550Energies 15 04872 g005b 550
Figure 5. Experimental and computed pressure coefficient at different spanwise sections and wind speeds of 7 m s−1, 13 m s−1, and 19 m s−1 for NREL Phase II [52,55]: (a) r/R = 0.30 and r/R = 0.47, (b) r/R = 0.63 and r/R = 0.80.
Figure 5. Experimental and computed pressure coefficient at different spanwise sections and wind speeds of 7 m s−1, 13 m s−1, and 19 m s−1 for NREL Phase II [52,55]: (a) r/R = 0.30 and r/R = 0.47, (b) r/R = 0.63 and r/R = 0.80.
Energies 15 04872 g005aEnergies 15 04872 g005b
Energies 15 04872 g006 550
Figure 6. The geometric characteristics of the slot.
Figure 6. The geometric characteristics of the slot.
Energies 15 04872 g006
Energies 15 04872 g007 550
Figure 7. Geometric characteristics and mesh of the slot(s). (a) Configuration 1; (b) Configuration 2; (c) Configurations 3 and 4.
Figure 7. Geometric characteristics and mesh of the slot(s). (a) Configuration 1; (b) Configuration 2; (c) Configurations 3 and 4.
Energies 15 04872 g007
Energies 15 04872 g008 550
Figure 8. Power increase of configurations 1 and 2 compared to baseline.
Figure 8. Power increase of configurations 1 and 2 compared to baseline.
Energies 15 04872 g008
Energies 15 04872 g009 550
Figure 9. Comparative view of the streamlines on the upper surface of the blade, comparison between configuration 1 (whole blade), configuration 2 (active part), and the baseline (top).
Figure 9. Comparative view of the streamlines on the upper surface of the blade, comparison between configuration 1 (whole blade), configuration 2 (active part), and the baseline (top).
Energies 15 04872 g009
Energies 15 04872 g010 550
Figure 10. Streamlines and velocity distributions for baseline configuration at r/R = 0.5 and r/R = 0.6 for windspeeds U∞ = 13 m s−1, 16 m s−1, and 19 m s−1.
Figure 10. Streamlines and velocity distributions for baseline configuration at r/R = 0.5 and r/R = 0.6 for windspeeds U∞ = 13 m s−1, 16 m s−1, and 19 m s−1.
Energies 15 04872 g010
Energies 15 04872 g011 550
Figure 11. Streamlines and velocity distributions for configurations 1 and 2 compared to baseline at r/R = 0.5 and r/R = 0.6 for windspeeds U∞ = 13 m s−1 and 16 m s−1.
Figure 11. Streamlines and velocity distributions for configurations 1 and 2 compared to baseline at r/R = 0.5 and r/R = 0.6 for windspeeds U∞ = 13 m s−1 and 16 m s−1.
Energies 15 04872 g011
Energies 15 04872 g012 550
Figure 12. Comparative view of streamlines and velocity distributions for configurations 1 and 2 at r/R = 0.2 and U∞ = 16 m s−1.
Figure 12. Comparative view of streamlines and velocity distributions for configurations 1 and 2 at r/R = 0.2 and U∞ = 16 m s−1.
Energies 15 04872 g012
Energies 15 04872 g013 550
Figure 13. Second slot geometric characteristics.
Figure 13. Second slot geometric characteristics.
Energies 15 04872 g013
Energies 15 04872 g014 550
Figure 14. Power increase for configurations 3 and 4 compared to baseline.
Figure 14. Power increase for configurations 3 and 4 compared to baseline.
Energies 15 04872 g014
Energies 15 04872 g015 550
Figure 15. Streamlines and velocity distributions for configurations 1 to 4 compared to baseline at r/R = 0.5 and r/R = 0.6 for wind speed U∞ = 19 m s−1.
Figure 15. Streamlines and velocity distributions for configurations 1 to 4 compared to baseline at r/R = 0.5 and r/R = 0.6 for wind speed U∞ = 19 m s−1.
Energies 15 04872 g015
Energies 15 04872 g016 550
Figure 16. Zoom view on velocity distributions for configurations 2 and 4 at r/R = 0.5 for U∞ = 19 m s−1.
Figure 16. Zoom view on velocity distributions for configurations 2 and 4 at r/R = 0.5 for U∞ = 19 m s−1.
Energies 15 04872 g016
Energies 15 04872 g017 550
Figure 17. The distribution of the relative velocity derivative in the normal direction to the upper side of the blade for S-S, T-S, and baseline configurations, r/R = 0.5 and wind-speed U ∞ = 19 m s−1.
Figure 17. The distribution of the relative velocity derivative in the normal direction to the upper side of the blade for S-S, T-S, and baseline configurations, r/R = 0.5 and wind-speed U ∞ = 19 m s−1.
Energies 15 04872 g017
Energies 15 04872 g018 550
Figure 18. The distribution of the relative velocity derivative in the normal direction to the upper side of the blade for S-S configuration, r/R = 0.5 and wind-speed U ∞ = 19 m s−1.
Figure 18. The distribution of the relative velocity derivative in the normal direction to the upper side of the blade for S-S configuration, r/R = 0.5 and wind-speed U ∞ = 19 m s−1.
Energies 15 04872 g018
Table
Table 1. Rotor description.
Table 1. Rotor description.
Number of blades3
Rotor diameter10.06 m
RPM72 rpm
Rotor locationDownwind
Root extension0.723 m
Pitch angle12°
Blade profile S809
Twist angle0°
Table
Table 2. Boundary conditions.
Table 2. Boundary conditions.
Boundary ConditionsPosition
Velocity inlet 2R upstream of the blade
symmetryOuter cylinder at 3R
Wall (no-slip) blade
Wall (Euler-slip) Inner   cylinder   at   r = 0.51   m
PeriodicAt 120°
Pressure outlet2R downstream of the blade
Table
Table 3. The values of the angle of attack at different blade sections.
Table 3. The values of the angle of attack at different blade sections.
Computed AoA [°]
Section r/R7 m s−113 m s−119 m s−1
0.318.8633.9945.46
0.478.1022.0433.59
0.633.7715.5225.55
0.801.209.4019.27
Table
Table 4. Comparison of measured and computed power production.
Table 4. Comparison of measured and computed power production.
Wind SpeedMeasured Power [kW]Computed Power [kW]Error %
72.542.434.33
1312.9712.354.78
1918.6015.3717.36
Table
Table 5. Studied configurations.
Table 5. Studied configurations.
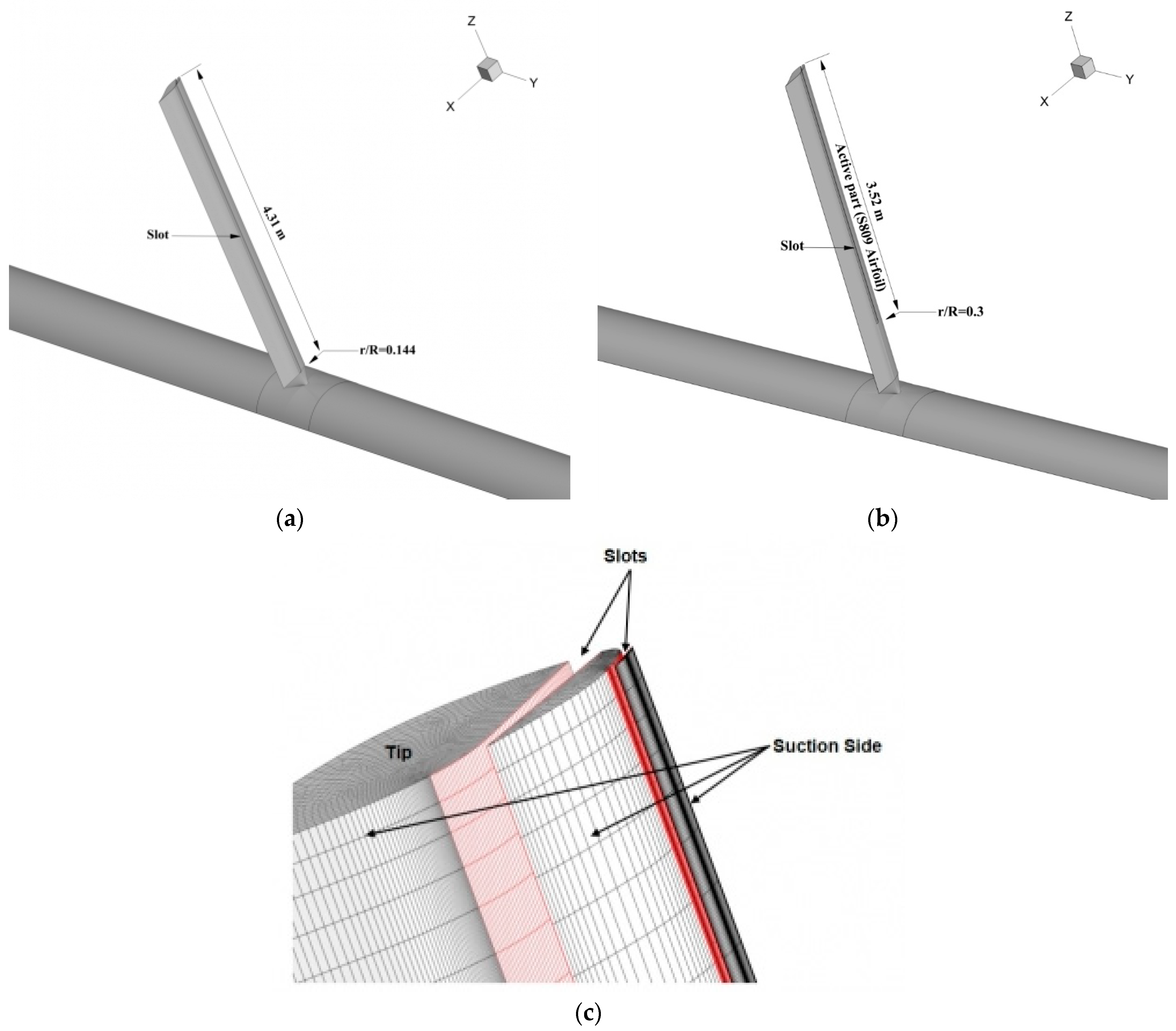
Configuration 1Single-slot from r/R = 0.144 to blade tip (whole blade)
Configuration 2Single-slot from r/R = 1.509 to blade tip (active part)
Configuration 3Two-slots from r/R = 1.509 to blade tip (active part)
Configuration 4Two-slots slot from r/R = 0.144 to blade tip (whole blade)
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Belamadi, R.; Settar, A.; Chetehouna, K.; Ilinca, A. Numerical Modeling of Horizontal Axis Wind Turbine: Aerodynamic Performances Improvement Using an Efficient Passive Flow Control System. Energies 2022, 15, 4872. https://doi.org/10.3390/en15134872

AMA Style

Belamadi R, Settar A, Chetehouna K, Ilinca A. Numerical Modeling of Horizontal Axis Wind Turbine: Aerodynamic Performances Improvement Using an Efficient Passive Flow Control System. Energies. 2022; 15(13):4872. https://doi.org/10.3390/en15134872

Chicago/Turabian Style

Belamadi, Riyadh, Abdelhakim Settar, Khaled Chetehouna, and Adrian Ilinca. 2022. "Numerical Modeling of Horizontal Axis Wind Turbine: Aerodynamic Performances Improvement Using an Efficient Passive Flow Control System" Energies 15, no. 13: 4872. https://doi.org/10.3390/en15134872

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop