Non-Stationary Random Medium Parameter Estimation of Petrophysical Parameters Driven by Seismic Data
Abstract
:1. Introduction
2. Methods
2.1. Mathematical Characterization of Random Medium
2.2. Estimation Principles of Stationary Random Medium Parameters for Petrophysical Parameters
2.3. Estimation Process of Non-Stationary Random Medium Parameters
3. Numerical Examples
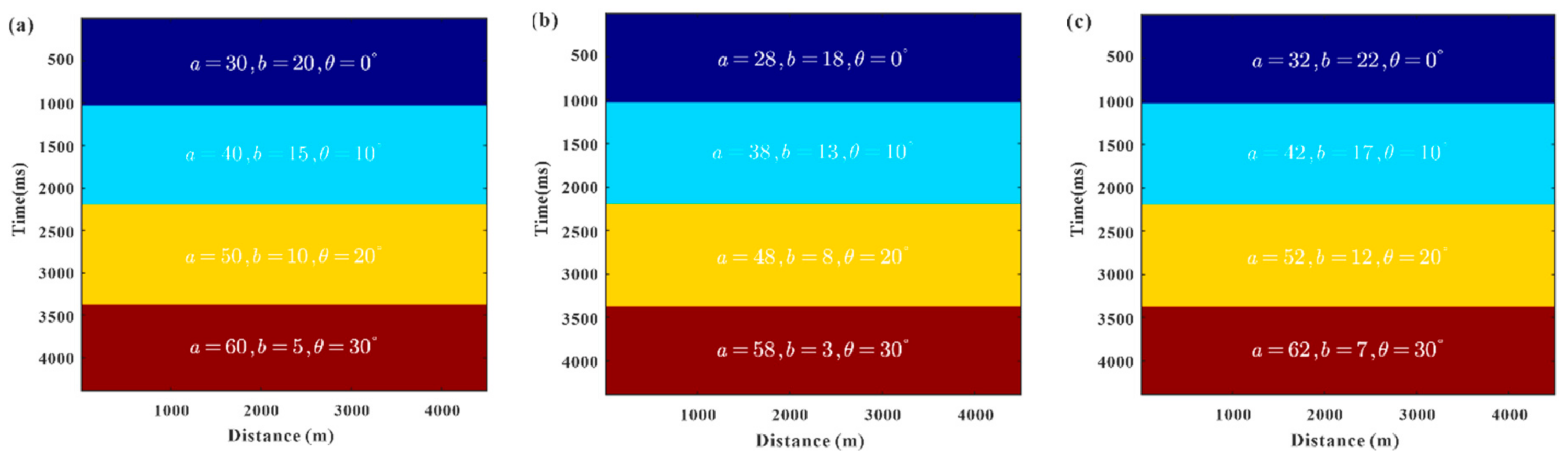
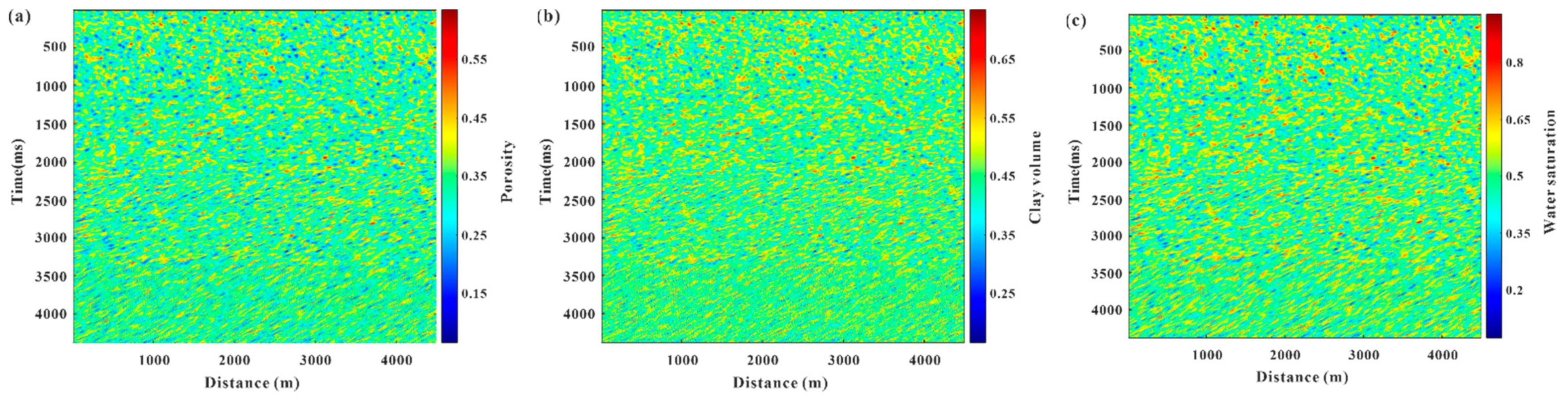
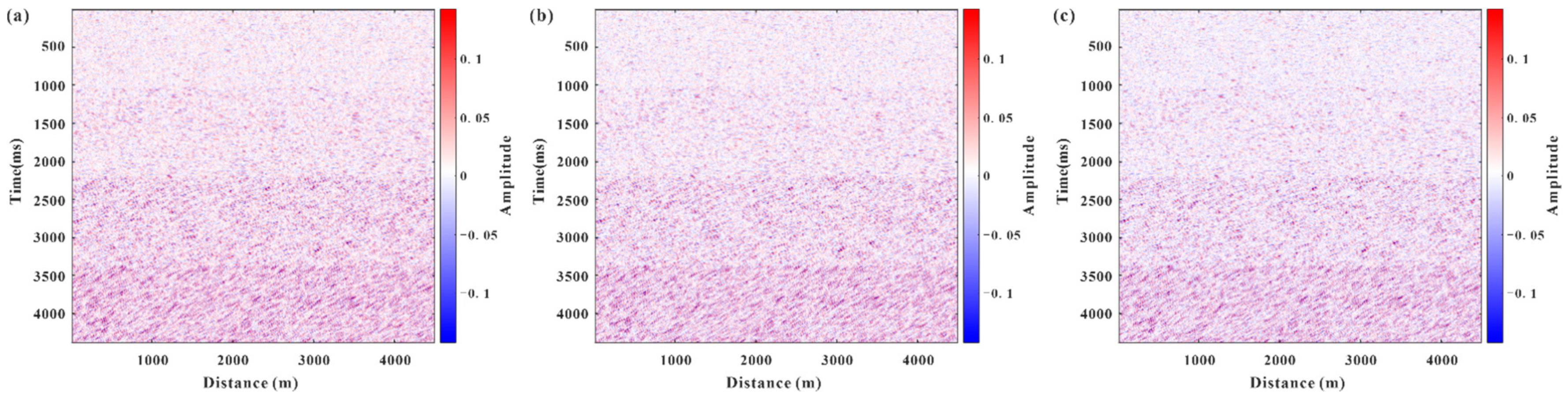
3.1. Autocorrelation Parameter Estimation of Four-Layer Model
3.2. Autocorrelation Parameter Estimation of Marmousi2 Model
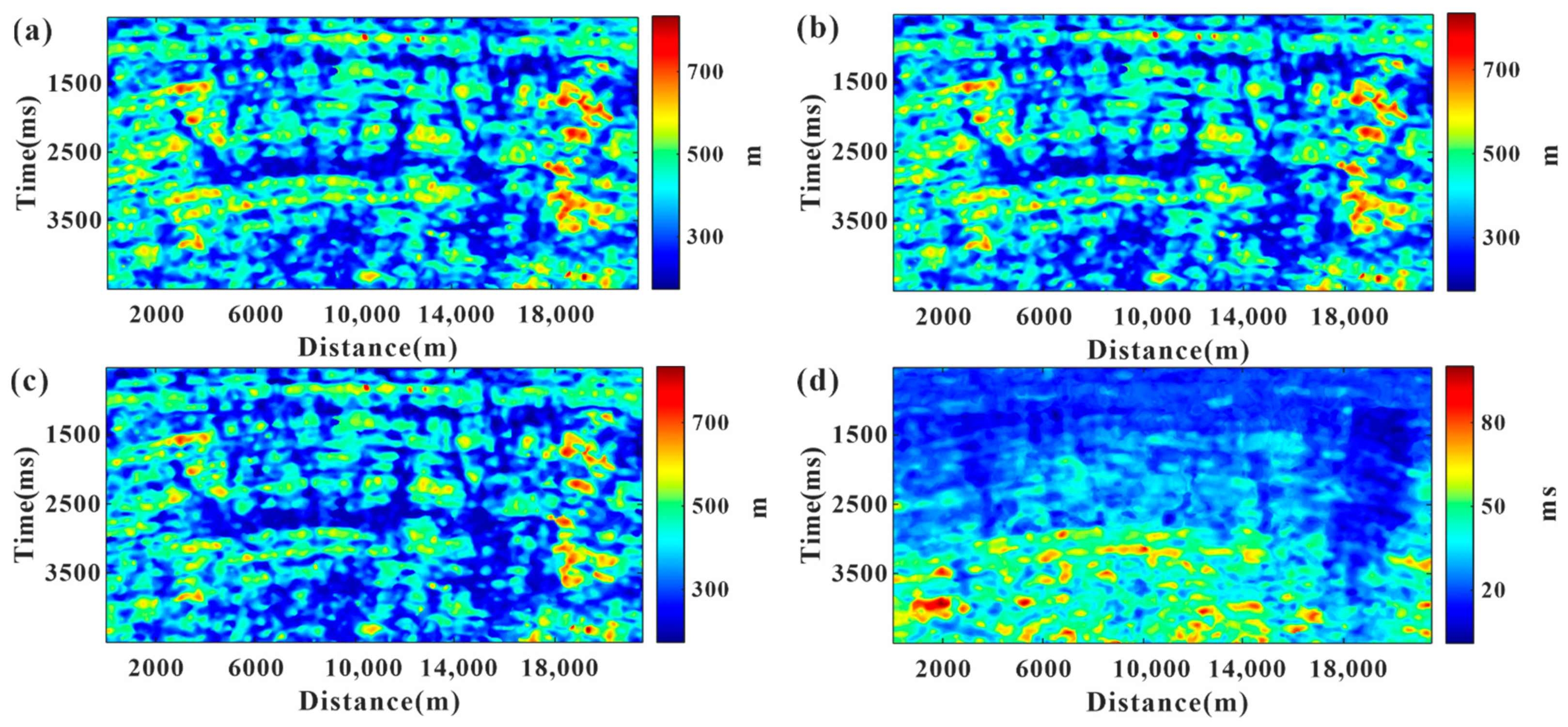
4. Field Data Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Aki, K. Analysis of the seismic coda of local earthquakes as scattered waves. J. Geophys. Res. 1969, 74, 615–631. [Google Scholar] [CrossRef]
- Ikelle, L.; Yung, S.; Daube, F. 2-D random media with ellipsoidal autocorrelation functions. Geophysics 1993, 58, 1359–1372. [Google Scholar] [CrossRef]
- Levander, A.; England, R.W.; Smith, S.K.; Hobbs, R.W.; Goff, J.A.; Holliger, K. Stochastic characterization and seismic response of upper and middle crustal rocks based on the Lewisian gneiss complex, Scotland. Geophys. J. Int. 1994, 119, 243–259. [Google Scholar] [CrossRef] [Green Version]
- Hurich, C.A.; Kocurko, A. Statistical approaches to interpretation of seismic reflection data. Tectonophysics 2000, 329, 251–267. [Google Scholar] [CrossRef]
- Gu, Y.; Zhu, P.M.; Li, H.; Li, X.Y. Stationary random medium parameter estimation of two-dimensional post-stack seismic data. Chin. J. Geophys. 2014, 57, 2291–2301. [Google Scholar]
- Gibson, B.S. Analysis of lateral coherency in wide-angle seismic images of heterogeneous targets. J. Geophys. Res. Solid Earth 1991, 96, 10261–10273. [Google Scholar] [CrossRef]
- Poppeliers, C. Estimating vertical stochastic scale parameters from seismic reflection data: Deconvolution with non-white reflectivity. Geophys. J. Int. 2007, 168, 769–778. [Google Scholar] [CrossRef] [Green Version]
- Saito, T.; Sato, H.; Ohtake, M. Envelope broadening of spherically outgoing waves in three-dimensional random media having power law spectra. J. Geophys. Res. Solid Earth 2002, 107, ESE-3. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Wang, S.; Tang, G.; Li, J.; Sun, C. Stochastic parameter estimation of heterogeneity from crosswell seismic data based on the Monte Carlo radiative transfer theory. J. Geophys. Eng. 2017, 14, 621–633. [Google Scholar] [CrossRef]
- Carpentier, S.F.A.; Roy-Chowdhury, K. Conservation of lateral stochastic structure of a medium in its simulated seismic response. J. Geophys. Res. Solid Earth 2009, 114, B10. [Google Scholar] [CrossRef] [Green Version]
- Irving, J.; Knight, R.; Holliger, K. Estimation of the lateral correlation structure of subsurface water content from surface-based ground-penetrating radar reflection images. Water Resour. Res. 2009, 45, 1–14. [Google Scholar] [CrossRef]
- Scholer, M.; Irving, J.; Holliger, K. Estimation of the correlation structure of crustal velocity heterogeneity from seismic reflection data. Geophys. J. Int. 2010, 183, 1408–1428. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y. Numerical Modeling and Parameter Estimation for 3D Non-Stationary Random Medium. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2013. [Google Scholar]
- Jeulin, D. Dead Leaves Models: From Space Tessellations to Random Functions; Springer: Cham, Switzerland, 2021; Volume 53, pp. 329–418. [Google Scholar]
- Bakulin, A.; Grechka, V.; Tsvankin, I. Estimation of fracture parameters from reflection seismic data—Part II: Fractured models with orthorhombic symmetry. Geophysics 2000, 65, 1803–1817. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Xu, Y.; Zeng, Z.; Li, J.; Zhang, D. Simulation of Martian Near-Surface Structure and Imaging of Future GPR Data from Mars. IEEE Trans. Geosci. Remote Sens. 2021, 21, 1–11. [Google Scholar] [CrossRef]
- Yan, F.; Han, D.H. Accuracy and sensitivity analysis on seismic anisotropy parameter estimation. J. Geophys. Eng. 2018, 15, 539–553. [Google Scholar] [CrossRef] [Green Version]
- Carpentier, S.F.A.; Roy-Chowdhury, K.; Hurich, C.A. Mapping correlation lengths of lower crustal heterogeneities together with their maximum-likelihood uncertainties. Tectonophysics 2011, 508, 117–130. [Google Scholar] [CrossRef]
- Yang, X.W.; Zhu, P.M. Stochastic seismic inversion based on an improved local gradual deformation method. Comput. Geosci. 2017, 109, 75–86. [Google Scholar] [CrossRef]
- Yang, X.W.; Mao, N.B.; Zhu, P.M.; Xiao, D. Two-level uncertainty assessment in stochastic seismic inversion based on the gradual deformation method. Geophysics 2020, 85, M33–M42. [Google Scholar] [CrossRef]
- Fan, Y.; Lu, Q.T.; Feng, J.; Zhang, J.; Luo, S.Y. Estimation of lateral correlation length from deep seismic reflection profile based on stochastic model. Acta Geophys. 2021, 69, 1297–1312. [Google Scholar]
- Wang, B.L.; Lin, Y.; Zhang, G.Z.; Yin, X.Y.; Zhao, C. Prestack seismic stochastic inversion based on statistical characteristic parameters. Appl. Geophys. 2021, 18, 63–74. [Google Scholar]
- Litwiniszyn, J. Application of the equation of stochastic processes to spatial problems of mechanics of some types of bodies. Bull. L’Academie Pol. Des. Sci. 1956, 4, 91–95. [Google Scholar]
- Xi, X.; Yao, Y. Simulations of Random Medium Model and Intermixed Random Medium. J. China Univ. Geosci. 2002, 27, 67–71. [Google Scholar]
- Xi, X.; Yao, Y. 2-D random media and wave equation forward modeling. Oil Geophys. Prospect. 2001, 36, 546–552. [Google Scholar]
- Xi, X.; Yao, Y. Non-stationary random medium model. Oil Geophys. Prospect. 2005, 40, 71–75. [Google Scholar]
- Yin, X.Y.; Cui, W.; Zong, Z.Y.; Liu, X.J. Petrophysical property inversion of reservoirs based on elastic impedance. Chin. J. Geophys. 2014, 57, 4132–4140. [Google Scholar]
- Zhang, J.J.; Yin, X.Y.; Zhang, G.Z.; Gu, Y.P.; Fan, X.G. Prediction method of physical parameters based on linearized rock physics inversion. Pet. Explor. Dev. 2020, 47, 59–67. [Google Scholar] [CrossRef]
- Grana, D. Bayesian linearized rock-physics inversion. Geophysics 2016, 81, D625–D641. [Google Scholar] [CrossRef]
- Connolly, P. Elastic impedance. Lead. Edge 1999, 18, 438–452. [Google Scholar] [CrossRef]
- Martin, G.S.; Wiley, R.; Marfurt, K.J. Marmousi2: An elastic upgrade for Marmousi. Lead. Edge 2006, 25, 156–166. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Zhang, G.; Huang, M.; Wang, B.; Chen, S. Non-Stationary Random Medium Parameter Estimation of Petrophysical Parameters Driven by Seismic Data. Energies 2022, 15, 4849. https://doi.org/10.3390/en15134849
Lin Y, Zhang G, Huang M, Wang B, Chen S. Non-Stationary Random Medium Parameter Estimation of Petrophysical Parameters Driven by Seismic Data. Energies. 2022; 15(13):4849. https://doi.org/10.3390/en15134849
Chicago/Turabian StyleLin, Ying, Guangzhi Zhang, Minmin Huang, Baoli Wang, and Siyuan Chen. 2022. "Non-Stationary Random Medium Parameter Estimation of Petrophysical Parameters Driven by Seismic Data" Energies 15, no. 13: 4849. https://doi.org/10.3390/en15134849
APA StyleLin, Y., Zhang, G., Huang, M., Wang, B., & Chen, S. (2022). Non-Stationary Random Medium Parameter Estimation of Petrophysical Parameters Driven by Seismic Data. Energies, 15(13), 4849. https://doi.org/10.3390/en15134849





