Abstract
The importance of the optimization principle implementation in ensuring the radiation protection of NPP personnel was emphasized. The potential of route optimization in reducing the dose load of the personnel of nuclear power plants and other nuclear facilities is shown. The paper considers the main directions of the authors’ development of the theory and algorithms of route optimization of work in inhomogeneous radiation fields during maintenance, repair, modernization, dismantling of NPP equipment, and elimination of the radiation accident consequences. The results of the computational experiments that were carried out with the “Uran” supercomputer of the IMM UB RAS for the checking of the developed algorithms are presented. The article provides an overview of the developed methods of route optimization of work using the dynamic programming method, including consideration of the constraints in the form of precedence conditions, which means the requirement to perform certain tasks only after the completion of others. Dijkstra’s method was used to solve the “dosimetrist’s problem”, where the optimal route for the dosimetrist’s movement is being constructed, including obstacles bypassing and visiting specified points in the room where it is necessary to perform work to determine the radiation environment characteristics such as measuring the radiation dose rate, taking samples, etc. The routing of movements with the non-additive aggregation of costs is considered. The content of the problem is shown on the example of the radiation accident consequences eliminating on a locality, where, as a result of radioactive fragments scattering, a system of emitting elements appears, which must be deactivated, i.e., dismantled or screened. This task must be carried out in consecutive cycles with a definite threshold level of personnel exposure per shift. A characteristic feature is the dependence of cost functions (here, dosimetric cost) on the list of tasks: only sources that have not been dismantled yet continue emitting at the moment. Precedence conditions are also possible.
1. Introduction
The optimization principle is of great practical importance for ensuring the radiation safety of personnel at all stages of the life cycle of operating and especially newly designed NPPs.
In 2007, the ICRP issued recommendations that combine and complement the previous ones [1]. The recommendations reemphasize and further reinforce the importance of the optimization of radiation protection, thereby disseminating the successful experience of putting this requirement into practice, presently in planned exposure situations too.
Close attention should be paid to the optimization of radiation protection in all possible areas, including the route optimization of work in nonuniform radiation fields [2].
The inhomogeneity of the radiation dose rate at different points in the premises determines the dependence of dose costs on the choice of the personnel movement trajectory. The shortest path in length does not mean the minimum radiation dose [3,4].
Since the beginning of the 2000s, a team of scientists from the Ural Federal University and the Institute of Mathematics and Mechanics of the Ural Branch of the Russian Academy of Sciences has been developing the theory and methods for the route optimization of personnel dose loads. During this time, we have developed a theoretical justification, have obtained new world-class scientific results in the field of route optimization of work, have built computational algorithms for solving a number of applied problems of route optimization in the nuclear power industry (Figure 1), and have performed computational experiments, including the “Uran” supercomputer of the IMM UB RAS assisted experiments [5].
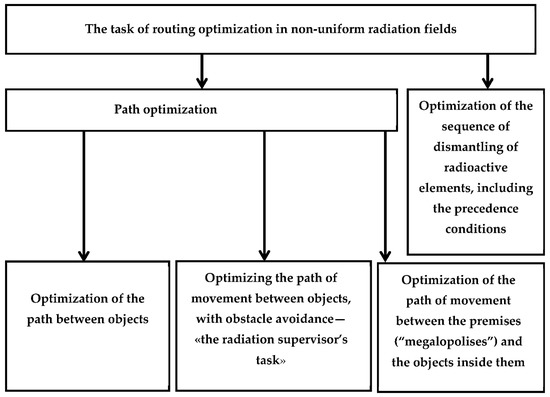
Figure 1.
Variants of route optimization problems in inhomogeneous radiation fields.
The basis used was the classical traveling salesman problem (TSP). The interpretation of this problem for the nuclear power industry was given in [6]. The classical formulation of the traveling salesman problem is given, for example, in [7]. Note that the traveling salesman problem is one of the most popular discrete optimization problems. There are N cities. The salesman leaves one of the cities that is the base and must visit all the remaining (N − 1) cities. It is required to choose from N! possible routes the route of the smallest length. In the problems under consideration, the length is replaced by the minimum total effective dose of radiation. Later, generalizations of the traveling salesman problem appeared, considering the precedence conditions (the precedence constrained TSP) [8,9,10,11,12]. The variant of the dynamic programming method (DPM) developed for these problems differs in that it does not use the entire array of values of the Bellman function [13,14].
A feature of applied engineering problems are restrictions, for example, “precedence conditions”, requiring certain tasks to be performed after others. These restrictions hinder the use of standard methods of discrete optimization such as the branch and bound method [15,16]. But it is possible to use the restrictions to reduce the enumeration in the computational implementation of exact solution methods. It was possible to achieve this goal without a loss of quality on the basis of previously developed and very non-standard methods. Theoretical materials, which allowed to set in an exact form the mathematical formulations of the considered engineering problems in the nuclear power industry, are detailed in the second part of the monograph [17].
Let there be N objects that need to be visited and work to be done there. We shall designate α(k) the permutation of N numbers 1,2,…,N, which specifies the objects visiting order. The following expression determines the total radiation dose for a given order of objects visiting α:
where is the dose rate, is the time spent by personnel in the i-th isodose area, and is the radiation dose received when moving from object i to j.
In (1), the value , which specifies the total radiation dose when working on an object, does not depend on the order of the objects visiting. When minimizing the functional (1) with respect to α, only the “transit component” is minimized
In the problem of reducing the radiation dose during dismantling, the minimized functional depended not only on the “transit component”, but also on the dose received during dismantling operations.
2. The Traveling Salesman Problem
We fix the initial point (base), which we give the index 0. We use the index to designate the final state obtained by choosing a route in the form of a permutation in , and so we fix the beginning and end of the process.
We consider the matrix of costs to be given. We call the visiting points “cities” and identify them with indices from . If and , then is interpreted as the cost of moving i⟶j. Routes are permutations in , i.e., the ordered sets (i1,…..iN), where ; the values of it are pairwise different. The choice of a route defines a chain of movements
which starts from the base and ends in the “city” number iN. In this case the link (it,it+1), where , is estimated by the cost ; the initial move costs .
0 ⟶ i1 ⟶ … ⟶ iN,
We consider an N-dimensional vector with non-negative components k1, …, kN to be given. The cost of the route (3) is the sum
Let us consider cost (4) minimization by rational choice of route (3). The total number of routes is N!; it increases rapidly with N, which makes it difficult to enumerate the options. We consider “cities” to be points of a two- or three-dimensional metric space. Then we can take the distance as Euclidean, which, from the point of view of (4), corresponds to the problem of minimizing the length of the broken line (Figure 2).
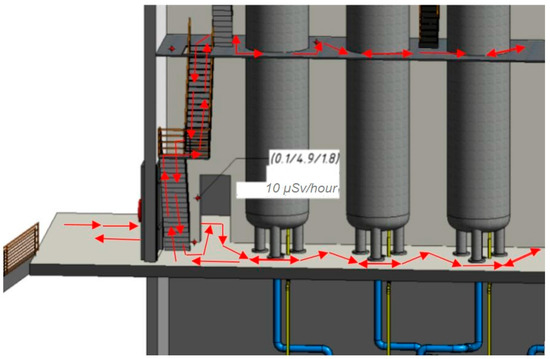
Figure 2.
An example of solving the problem of movement on a plane and in three-dimensional space (3D model of the volume compensator room of the VVER-210 reactor plant).
For metric versions of the TSP, many approximate algorithms have been developed that allow us to solve high-dimensional problems with a given accuracy level (optimal algorithms determine the extremum exactly but work well only for small N). When solving high-dimensional problems, it is necessary to apply a variety of heuristics. The structure of heuristics can be formed on the basis of theoretical constructions corresponding to optimal methods. Here we can note the Bellman equations in DPM.
The remarkable property of dependency
is that it can be built over the layers corresponding to each work with “lists” of fixed cardinality, using the following rule: if , and K, , is a non-empty “list”, then
(i,K) ⟶ v(i,K)
Expression (6) is the Bellman equation, which determines the evolution of the extrema of “partial” or shortened variants of the TSP; wherein
We can determine the entire dependence (5), including the global extremum of the main problem with the help of (6) and (7) and the boundary condition
Knowing dependence (4) makes it easy to build the optimal route. From (6), (7) we have the equality
We choose from the minimum condition (8):
We move to the “city” number i1, while having a “list”
of unfulfilled tasks. Returning to (6), we obtain the equality
Considering (10), we choose i2 from the minimum condition:
Using (9), we obtain the equality
Further constructions are similar and lead to the implementation of a route
for which the chain of equalities
is true.
In (11) it is assumed that N ≥ 3. Despite the simplicity of the formulation, the above-mentioned TSP model can be applied to solving some variants of the problem related to radiation safety.
3. Routing Problem with Restrictions and Dependence of Cost Functions on the List of Tasks
The process of moving between points , where N is a given natural number (N > 2), starts from the initial point . The sequence of visits may vary
where the indices , 1 ≤ ≤ N, are pairwise distinct and subject to restrictions in the form of precedence conditions: such a pair of indices p, q can be given,
that for numbers k and l,
realizing p and q in the form
the inequality k < l holds. This corresponds to the presentation of points with indices p and q as the “sender” and “receiver” of the cargo, i.e., “sender” must be visited before “receiver”.
1 ≤ p ≤ N, 1 ≤ q ≤ N,
1 ≤ k ≤ N, 1 ≤ l ≤ N,
Let us consider the case when at the j-th step (0 ≤ j ≤ N − 1) the cost function depends on the entire list of indices , which corresponds to tasks not completed at the moment of the j-th move, i.e., . In this case, a person is exposed to radiation from non-dismantled elements.
In the case when we dismantle N objects in the sequence α(1), α(2), …, α(N), where α is a permutation of indices from (1,) , the total radiation dose will be calculated by the following formula:
Here is the radiation dose rate created by the object number α(i); tα(i) is the dismantling time of the object number α(i). Note that in the case under consideration, the radiation dose when moving between objects is not taken into consideration. For example, the travel time between objects is quite short.
Let us consider, as an example, the simplest variant of the problem related to finding the optimal variant of the sequence for four objects. Table 1 gives the dismantling time and the created dose rate for each object [18].

Table 1.
The dismantling time and dose rates for the objects.
As mentioned above, there are N! variants of admissible routes in the optimization problem. For this simplest example (four objects in a room), there are 24 acceptable routes (Figure 3). Two of them turned out to be the optimal routes (dismantling sequences), where total radiation dose was minimal:
2 ⟶ 1 ⟶4 ⟶ 3, 1 ⟶ 2 ⟶ 4 ⟶ 3.
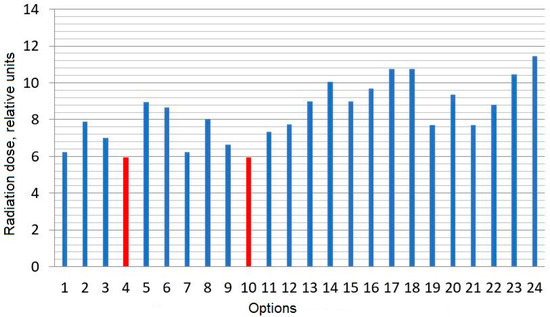
Figure 3.
Exposure dose for personnel with possible options of the sequence of dismantling of four radioactive objects in the room. Minimal options are marked with red.
Figure 4 graphically shows the effect of radiation fields created by radioactive objects in the process of dismantling, according to the option 2 ⟶ 1 ⟶ 4 ⟶ 3.
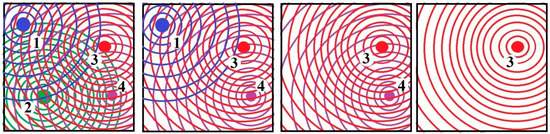
Figure 4.
Diagram of the effects of radiation fields created by the objects in the room during dismantling in the sequence 2 ⟶ 1 ⟶ 4 ⟶ 3.
The example does not consider the “transit component”. If its contribution is significant, then the Expression (13) should be supplemented with (2).
4. Dismantling of Radioactive Objects
The problem of route optimization when performing the dismantling of radiation hazardous equipment makes it possible to find the minimum value of the total radiation dose when performing the necessary work in inhomogeneous radiation fields [19,20,21].
Let us consider the case of radioactive objects dismantling as the route develops. At the time of the next movement, only non-dismantled objects cause irradiation. When moving from “city” i to “city” j (where we carry out dismantling), we have a “list” , of unfulfilled tasks; besides and . Therefore, the impact of sources on a person making the movement i⟶j, where , and i ≠ j, should be estimated by a non-negative number , which characterizes integrally the impact of sources with numbers from the “list” K. There must be a volumetric matrix with coefficients to use them in (6) as individual dose costs. Each movement has unique list of tasks that depends on the route. The list of tasks is unique for each movement and depends on the route. If in addition (see (5))
is a route (permutation of indices from ), then the cost (6) of route (14) should be replaced by
The problem under consideration turns to minimizing the value (15) by the enumeration of all possible routes (14). It replaces the classical TSP.
Extremum is the smallest value of all values (15) for the enumeration of possible routes (14). The solution of the main problem comes in determining and finding the optimal route.
To find the extremum , a procedure based on DPM was used, with a feature related to the dependence of the cost matrix on the list of tasks.
Along with the main one, we consider shortened route problems, which are defined similarly to the common traveling salesman problem. We assign each partial route a cost
in the case of n ≥ 2; for n = 1, the route (reduced to the index i1) is estimated by the value
For n ≥ 2, we denote by v(I, K) the smallest value (14) in the enumeration of all (partial) routes ; for n = 1, we identify v(i, K) with value (17).
If and K = ∅, then we assume that v(i, K) = v(i, ∅) = . Thus, an array of possible values v(i, K) is defined, and K is some “list” of jobs, i.e., . Herewith, it is obvious that
Thus, the Bellman function is introduced, whose behavior is characterized by the following equation (Bellman equation): if K is a non-empty “list” (i.e., K is a non-empty subset of ), and , then
Expression (19) is similar to Equation (6) but differs in the use of a “volumetric” cost matrix. Based on (19), we can construct an optimal route, keeping in mind the following rule: if we are “located” in a “city” number and , , there is some non-empty list tasks to be performed, then the choice of the next task from the list , i.e., j ∈ , should be performed in such a way that
As j, one should choose the solution of the problem
Problem (20) is first solved for i = 0, = ; then, after finding i1 = j, consider variant (20), for which i = i1 and =\{i1}. The subsequent operations for constructing the optimal route are similar.
5. Constraints in the Form of Precedence Conditions
In real conditions, the dismantling of radioactive equipment cannot be carried out in an arbitrary sequence, for example, the dismantling of objects located on different floors or in the interior of the main hall. In this regard, it became necessary to consider the precedence conditions when constructing the route. The variant of the dynamic programming method created for this made it possible to reduce the number of possible routes and, as a result, to reduce the amount of calculations [22,23].
Let us apply the developed algorithm for a system of 18 dismantled blocks (Figure 5). The precedence condition “1–2” means that the object No. 2 can only be dismantled after the object No. 1. Therefore, routes with “invalid” back hops are excluded from consideration [18].
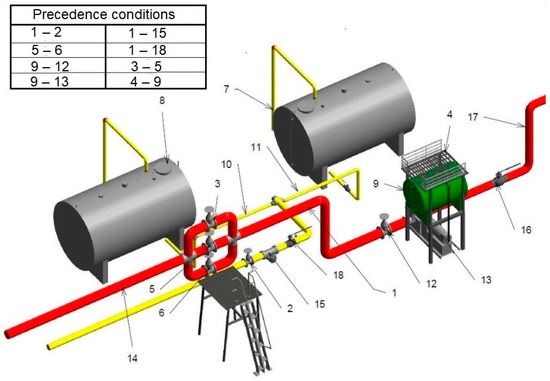
Figure 5.
Model of the dismantled system of 18 radioactive objects.
The results of the computational experiment showed that, for this example, the dose costs of the optimal dismantling sequence is less than the maximum value (the costs of the most unfavorable sequence) by 28.7% with the precedence conditions and by 46.7% in the absence of precedence conditions.
6. The Dosimetrist Problem
The dosimetrist problem was formulated in order to optimize the route of the dosimetrist when performing measurements while analyzing the pilot operation of the subsystem for the automated processing of data from non-routine measurements of the radiation situation at power units No. 1 and No. 2 of the Beloyarsk NPP [24,25]. It developed the optimal route construction algorithm for a dosimetrist that visits certain points to determine the parameters of the radiation situation, i.e., measure the dose rate, take samples, etc. To determine the cost functions, considering the avoidance of obstacles, Dijkstra’s method of finding the shortest path in the graph was used. Detailed results of the research are presented in the article “Reducing the exposure dose by optimizing the route of personnel movement with visiting the specified points taking into account the avoidance of obstacles” (Tashlykov O.L., Grigoryev A.M., Kropachev Yu.A.), which is included in this Special Issue on “Nuclear Engineering and Technology”, as well as in publications [26,27].
7. The Problem of Movement Routing with Non-Additive Cost Aggregation
The problem of routing movements with the non-additive aggregation of costs, or rather, a generalized version of the well-known bottleneck problem, is another area of the research. When setting, it is allowed to choose the initial state (process base) within a given set, which is not necessarily finite. It is assumed that the cost functions can depend on the list of tasks that have not been completed at the moment; there are also precedence conditions. Statements of this kind can arise in a wide variety of engineering applications. The majority of research in the field of solving the TSP refers to the “additive” version, where the costs of moving between “cities” are summed up. The formulation under consideration contains significant differences from the CC not only quantitatively, but also qualitatively [28,29].
Let us provide some meaningful statement focused on applications related to the dismantling of radiation-hazardous equipment or the cleanup of a territory contaminated as a result of an accident from radiation-hazardous objects. In this case, we mean the task of eliminating the consequences of a radiation accident on the ground, when a system of radiating elements arises from the spread of radioactive fragments [30].
Let, in a certain area, there be N points of radiation-hazardous objects that need to be dismantled (“turned off”), and the contaminated area should be decontaminated (Figure 6) [31]. On the first day, workers dismantle the first facility, receiving a dose from all existing facilities. On the second day, the next object is dismantled. Every day, work begins at the place where work was completed the day before. The dismantled object ceases to be a source of radiation. On the Nth day, the last object is dismantled. Each worker receives a daily dose of radiation, which should not exceed the established one. It is necessary to determine the order of dismantling with the minimum daily dose of radiation.
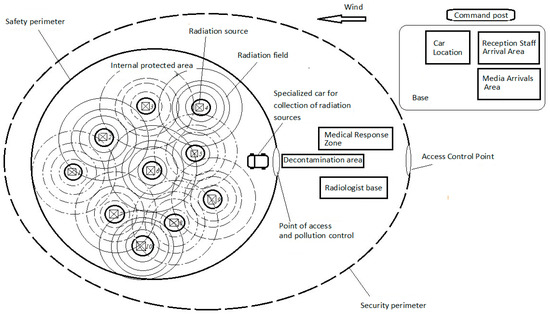
Figure 6.
Scheme of emergency response zone.
We use a variant of the “bottlenecks” problem (non-additive quality criterion). Let the order of visiting objects α be given (the route of visiting N “cities”). Each radioactive object is located inside the corresponding “city”. The entry and exit points of the “city” will be denoted by a two-dimensional vector , with coordinates , the first coordinate is the entry point to , and the second is the exit point. In essence, these are the points through which we can approach the i-th source of radiation. The maximum value of the dose along the route α is
The first term defines the “transit” dose received when moving from the α(k − 1) object to the α(k) object, and the second is the radiation dose during the dismantling of the α(k) object.
It is required to determine the procedure for performing one-day cycles of work in order to “eliminate” radioactive objects in a dangerous area α, in which the maximum daily dose will take the smallest value. This problem can be formulated as
where D is defined as a set of all admissible routes α and the entry–exit points corresponding to these routes in “cities”. A variant of dynamic programming has been created for the problem, considering the precedence conditions.
8. Conclusions
The heterogeneity of radiation fields in the radiation-hazardous zone determines a significant potential for minimizing dose costs through the route optimization of work: finding the optimal route for personnel movement or the optimal sequence for the dismantling of radioactive equipment. For problems related to the dismantling of radioactive equipment, new theoretical results were obtained on exact and approximate methods for solving route problems with a complicated criterion, including internal work and explicit dependencies on the list of currently unfulfilled tasks.
In the process of solving the problem, it was possible to use a set of constraints in the form of precedence conditions, which were traditionally considered difficult for the optimization method. The constraints were applied to overcome computational difficulties, since on this basis it was possible to actually reduce the dimension of the problem without a loss of quality.
Author Contributions
Conceptualization, O.L.T. and A.N.S.; methodology, A.G.C.; software, A.A.C.; validation, O.L.T. and A.N.S.; formal analysis, A.G.C.; investigation, A.G.C., O.L.T. and A.N.S.; writing—original draft preparation, A.N.S.; writing—review and editing, O.L.T. and A.N.S.; visualization, O.L.T.; supervision, A.G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Valentin, J. (Ed.) The 2007 Recommendations of the International Commission on Radiological Protection; ICRP Publication No. 103; The International Commission on Radiological Protection: Ottawa, ON, USA, 2007; Volume 37, pp. 2–4. [Google Scholar]
- Mikhailova, A.; Tashlykov, O. The ways of implementation of the optimization principle in the personnel radiological protection. Phys. Atom. Nucl. 2020, 83, 1718–1726. [Google Scholar] [CrossRef]
- Tashlykov, O.L.; Sesekin, A.N.; Scheklein, S.E.; Chentsov, A.G. Route optimization methods for radiation hazardous work. Safety, efficiency and economics of nuclear energy. In Proceedings of the Seventh International Scientific and Technical Conference, Moscow, Russia, 26–27 May 2010; p. 1530156. [Google Scholar]
- Tashlykov, O.L.; Sesekin, A.N.; Scheklein, S.E.; Balushkin, F.A.; Chentsov, A.G.; Khomyakov, A.P. Mathematical Simulation Methods Capability for Solution of the Personnel Irradiation Decrease Problem. Radiat. Saf. Issues 2009, 4, 47–57. [Google Scholar]
- Grigoryev, A.M.; Tashlykov, O.L. Solving a routing optimization of works in radiation fields with using a supercomputer. AIP Conf. Proc. 2015, 2018, 020028. [Google Scholar]
- Sesekin, A.N.; Tashlykov, O.L.; Scheklein, S.E.; Kuklin, M.Y.; Chentsov, A.G.; Kadnikov, A.A. Using of dynamic programming method for optimization trajectory workers’ movement at emission of rays threat zone with the purpose of minimization radiation processing. Izv. Vuzov. Yad. Energ. 2006, 2, 41–48. [Google Scholar]
- Gutin, G.; Punnen, A.P. The Traveling Salesman Problem and Its Variations; Springer: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Bellman, R. Dynamic Programming Treatment of the Travelling Salesman Problem. J. Assoc. Comput. Mach. 1962, 9, 61–63. [Google Scholar] [CrossRef]
- Kubo, M.; Kasugai, H. The precedence constrained traveling salesman problem. J. Oper. Res. Soc. Jpn. 1991, 34, 152–172. [Google Scholar] [CrossRef][Green Version]
- Salii, Y. Revisiting Dynamic Programming for Precedence-Constrained Traveling Salesman Problem and Its Time-Dependent Generalization. Eur. J. Oper. Res. 2017, 4, 32–42. [Google Scholar] [CrossRef]
- Balas, E. New classes of efficiently solvable generalized Traveling Salesman Problems. Ann. Oper. Res. 1999, 86, 529–558. [Google Scholar] [CrossRef]
- Khachai, M.Y.; Neznakhina, E.D. Approximation Schemes for the Generalized Traveling Salesman Problem. Proc. Steklov Inst. Math. 2017, 299 (Suppl. S1), 97–105. [Google Scholar] [CrossRef]
- Chentsov, A.G.; Sesekin, A.N.; Shcheklein, A.N.; Tashlykov, O.L. On One Modification of Traveling Salesman Problem Oriented on Application in Atomic Engineering. AIP Conf. Proc. 2010, 1293, 197–202. [Google Scholar]
- Sesekin, A.N.; Tashlykov, O.L.; Shcheklein, S.Y.; Chentsov, A.G. Route optimization in the removal of radiation hazards. WIT Trans. Ecol. Environ. 2014, 190, 919–926. [Google Scholar]
- Kalantari, B.; Hill, A.V.; Arora, S.R. An algorithm for the traveling salesman problem with pickup and delivery customers. Eur. J. Oper. Res. 1985, 22, 377–386. [Google Scholar] [CrossRef]
- Cook, W.J. Pursuit of the Traveling Salesman: Mathematics at the Limits of Computation; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Korobkin, V.V.; Sesekin, A.N.; Tashlykov, O.L.; Chentsov, A.G. Routing Methods and Their Applications in Improving the Efficiency and Safety of Operating Nuclear Power Plants; Novye Tekhnologii: Moscow, Russia, 2012; 234p. [Google Scholar]
- Tashlykov, O.L. NPP: Life Extension and Decommissioning: A Textbook; Publishing House of the Ural University: Ekaterinburg, Russia, 2020; 216p. [Google Scholar]
- Nosov, Y.V.; Rovneiko, A.V.; Tashlykov, O.L.; Shcheklein, S.E. Decommissioning Features of BN-350, -600 Fast Reactors. At. Energy 2019, 125, 219–223. [Google Scholar] [CrossRef]
- Tashlykov, O.L.; Sesekin, A.N.; Scheklein, S.E.; Chentsov, A.G. Development of the optimal algorithms of the NPP decommissioning using the methods of mathematical simulation. Izv. Vuzov. Yad. Energ. 2009, 2, 115–120. [Google Scholar]
- Balushkin, F.A.; Sesekin, A.N.; Tashlykov, O.L.; Cheblokov, I.B.; Shcheklein, S.E.; Chentsov, A.G. Use of dynamic programming method to optimize the dismantling of NPP units under decommissioning to minimize radiation exposure. Izv. Vuzov. Yad. Energ. 2009, 4, 169–176. [Google Scholar]
- Chentsov, A.G. Extreme Problems of Routing and Tasks Distribution. In Reguljarnaja i Haoticheskajadinamika; NIC: Moscow, Russia, 2008. (In Russian) [Google Scholar]
- Chentsov, A.A.; Chentsov, A.G. Dynamic programming method in the generalized courier problem. J. Comput. Syst. Sci. Int. 2008, 47, 464–474. [Google Scholar] [CrossRef]
- Kropachev, Y.A.; Tashlykov, O.L.; Sesekin, A.N.; Shcheklein, S.E.; Khomyakov, A.P. The automated data processing subsystem for unscheduled measurements of radiological environment. Nucl. Radiat. Saf. 2019, 93, 26–35. [Google Scholar]
- Kropachev, Y.A.; Tashlykov, O.L.; Shcheklein, S.E. Optimization of radiation protection at the stage of nuclear power plant units decommissioning. Izv. Vuzov. Yad. Energ. 2019, 1, 119–130. [Google Scholar]
- Grigoryev, A.M.; Tashlykov, O.L.; Popel, A.A.; Kropachev, Y.A. Determination of radiation field parameters for the problems of routing optimization based on interpolation with radial basis functions. AIP Conf. Proc. 2020, 2313, 020007. [Google Scholar]
- Grigoryev, A.M.; Tashlykov, O.L. Route optimization during works in non-stationary radiation fields with obstacles. AIP Conf. Proc. 2019, 2174, 020216. [Google Scholar]
- Chentsov, A.A.; Chentsov, A.G.; Sesekin, A.N.; Tashlykov, O.L. Application of a generalized bottleneck routing problem to the task of adhering to acceptable doses of radiation during the dismantling of radiation hazardous objects. IFAC PapersOnLine 2019, 52, 2656–2661. [Google Scholar] [CrossRef]
- Chentsov, A.G.; Chentsov, A.A.; Sesekin, A.N. Problems of Movement Routing with Non-Additive Cost Aggregation; IAEA: Moscow, Russia, 2020. (In Russian) [Google Scholar]
- General Instructions for Assessing and Responding to Radiological Emergencies; IAEA-TECDOC-1162; IAEA: Vienna, Austria, 2004; 204p.
- Tashlykov, O.L.; Sesekin, A.N.; Shcheklein, S.E. Route Optimization Methods for Response to Radiological Emergency Situations. IOP Conf. Ser. Mater. Sci. Eng. 2020, 972, 012004. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).