Time-Series Forecasting of a CO2-EOR and CO2 Storage Project Using a Data-Driven Approach
Abstract
:1. Introduction
2. Literature Review
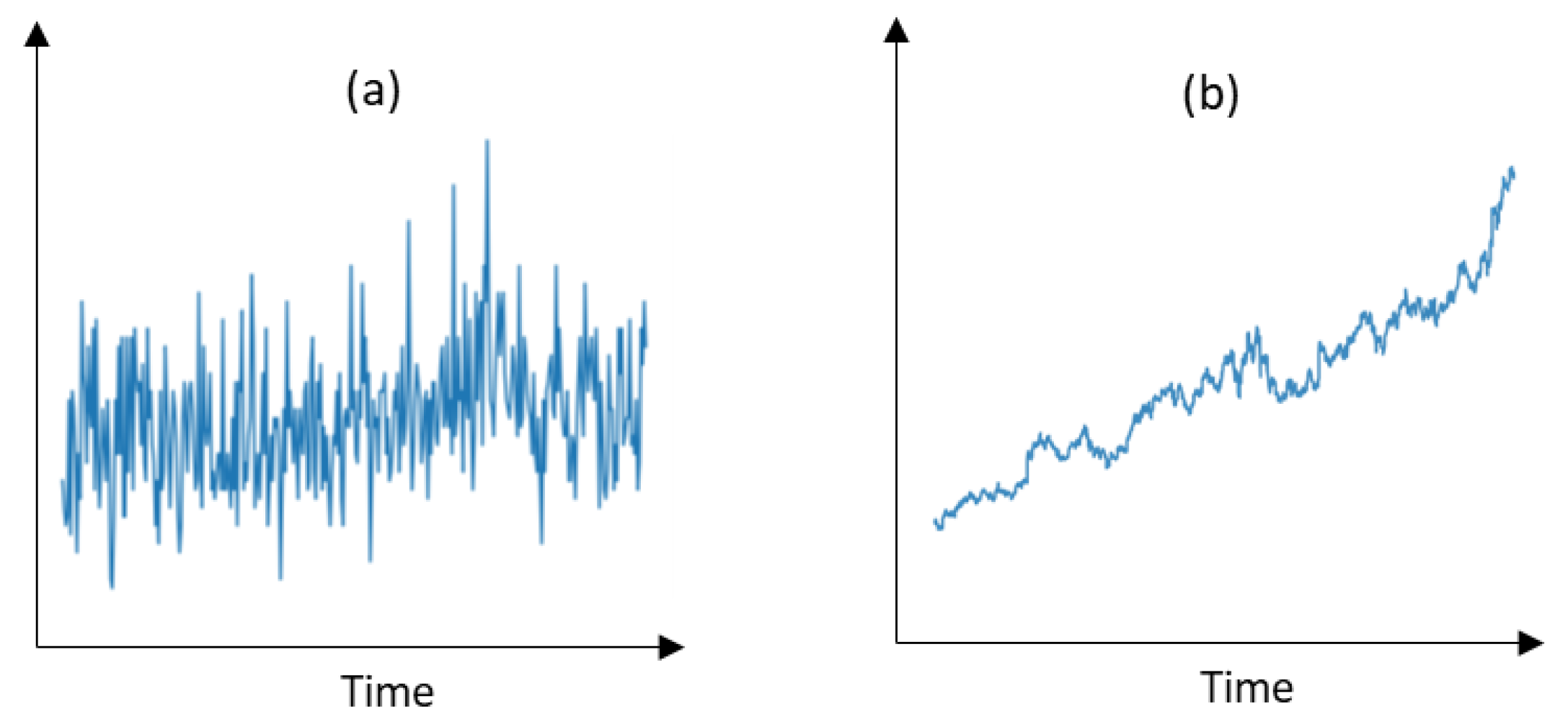
2.1. Time Series
2.2. Data-Driven Models
2.2.1. Autoregressive (AR)
2.2.2. Multilayer Perceptron (MLP)
2.2.3. Long Short-Term Memory (LSTM) Network
3. Methods
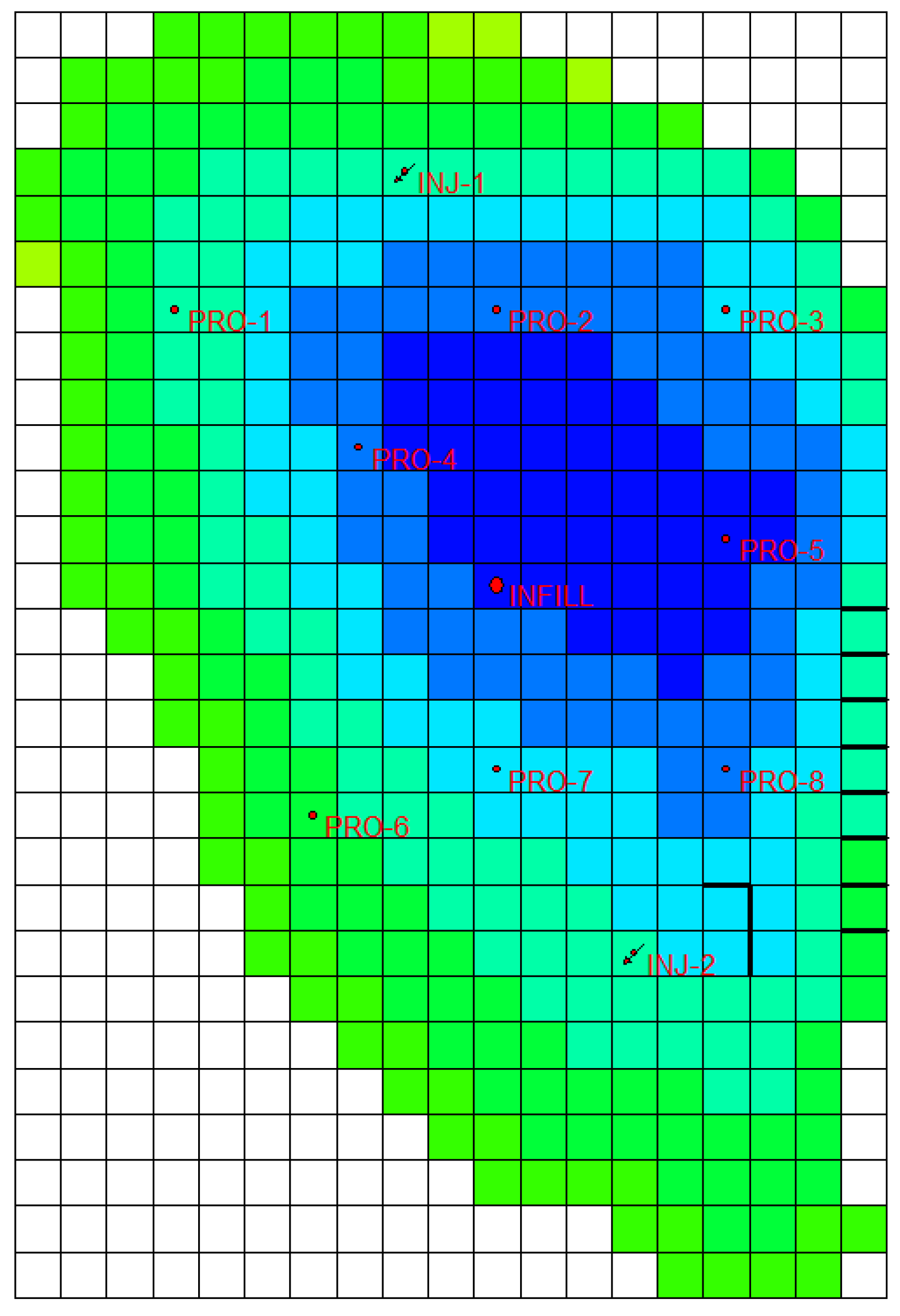
3.1. Reservoir Model
3.2. Data
3.2.1. Features
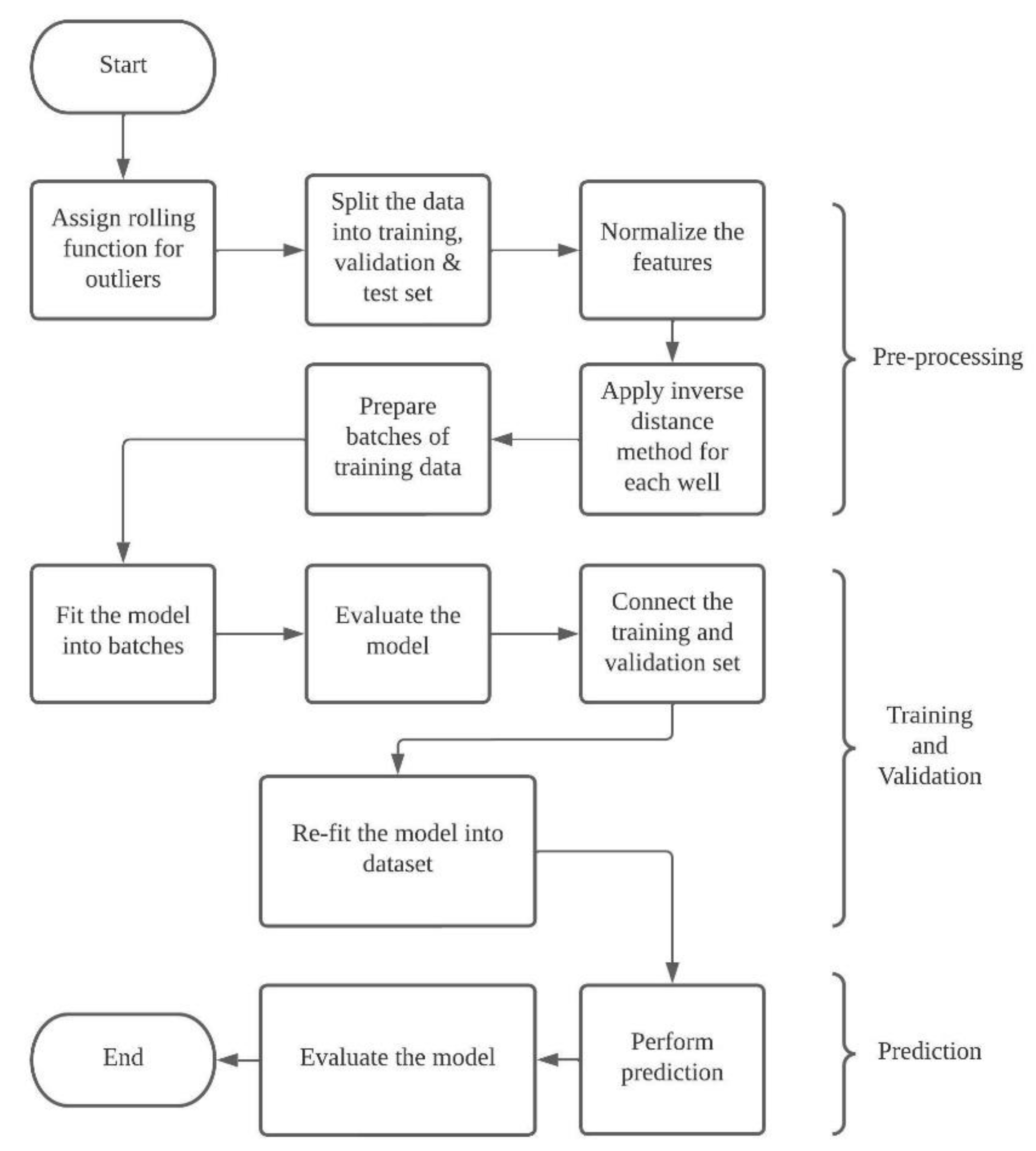
3.2.2. Preprocessing
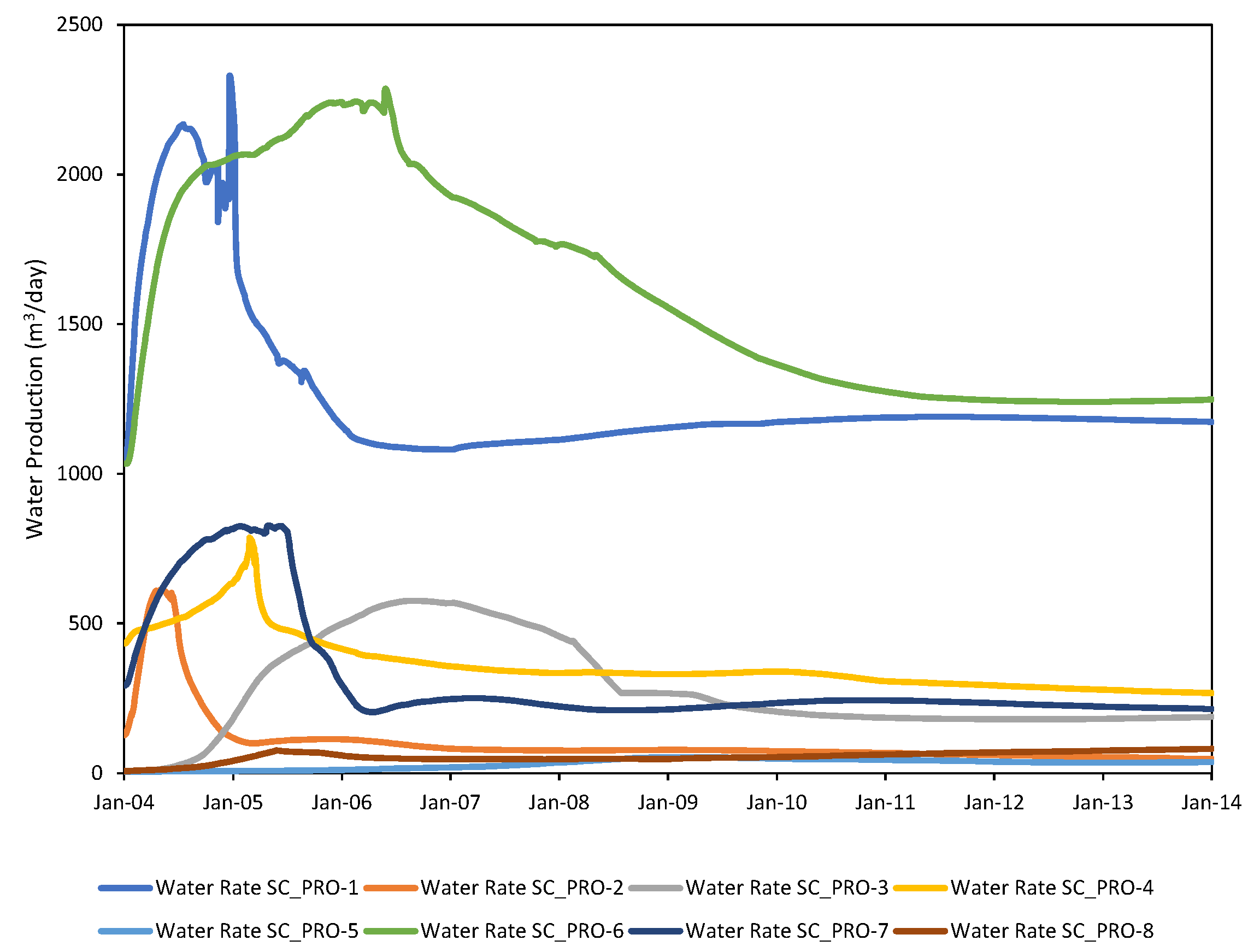
3.2.3. Exploratory Data Analysis (EDA)
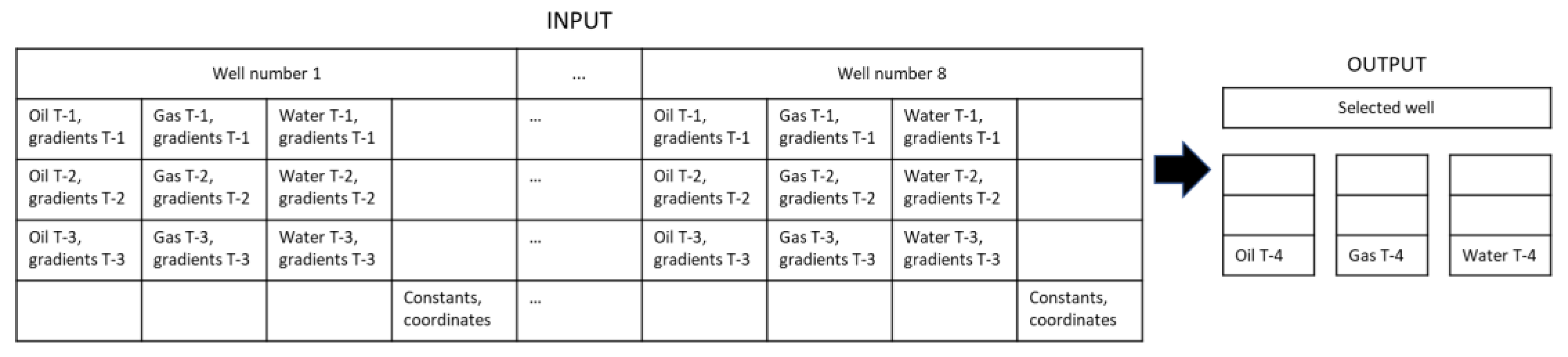
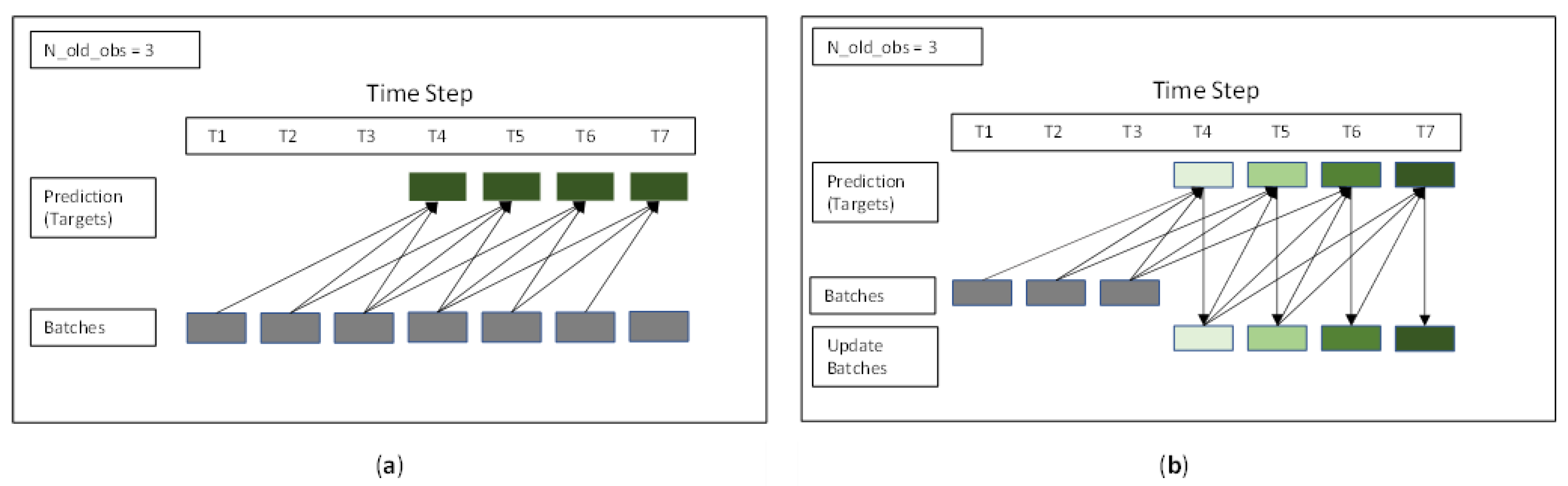
3.3. Problem Formulation
3.4. Model Development
3.5. Model Evaluation and Prediction
3.6. Model Optimization
4. Results and Discussions
4.1. Model Optimization
4.2. Existing Well Prediction
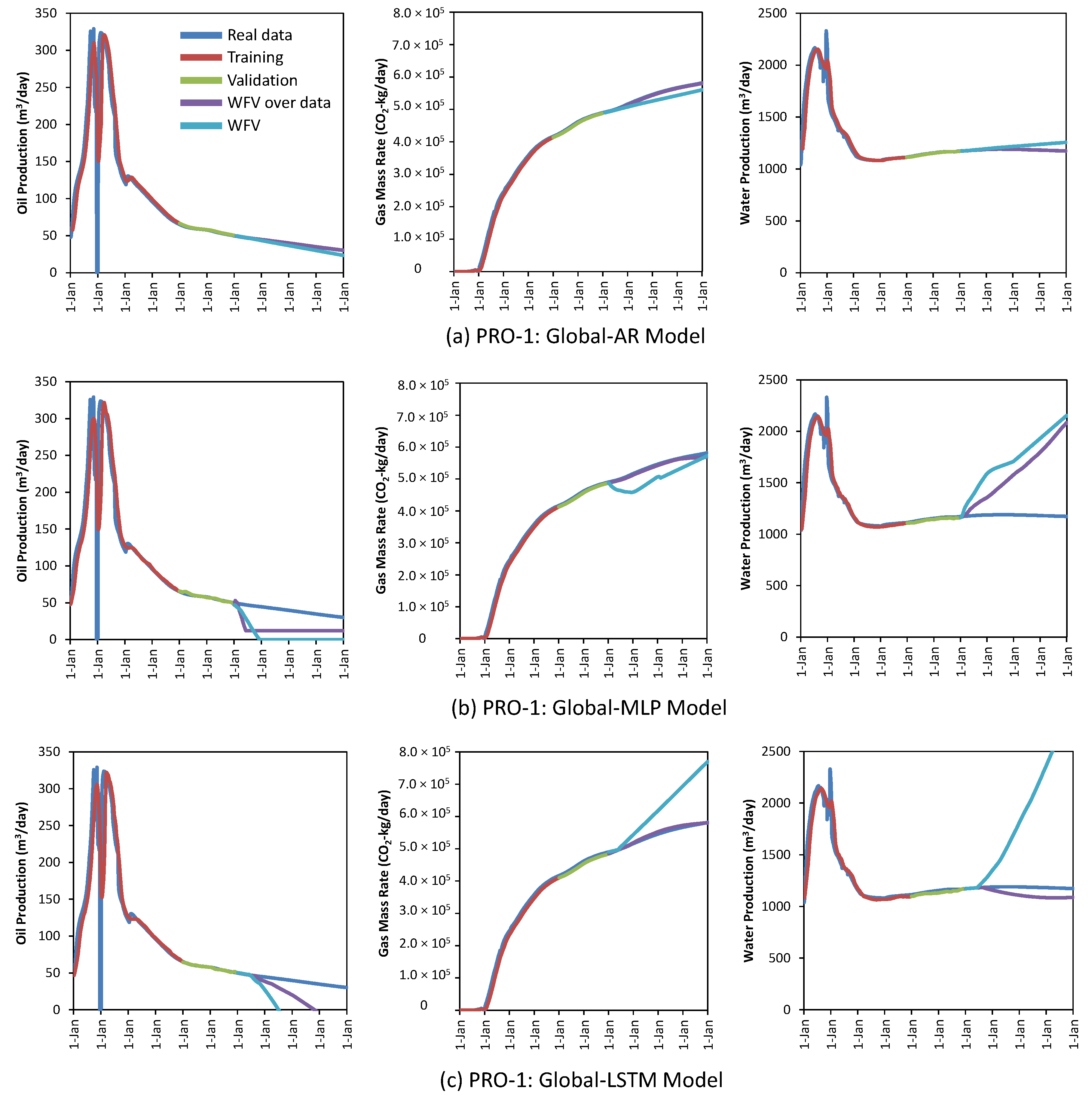
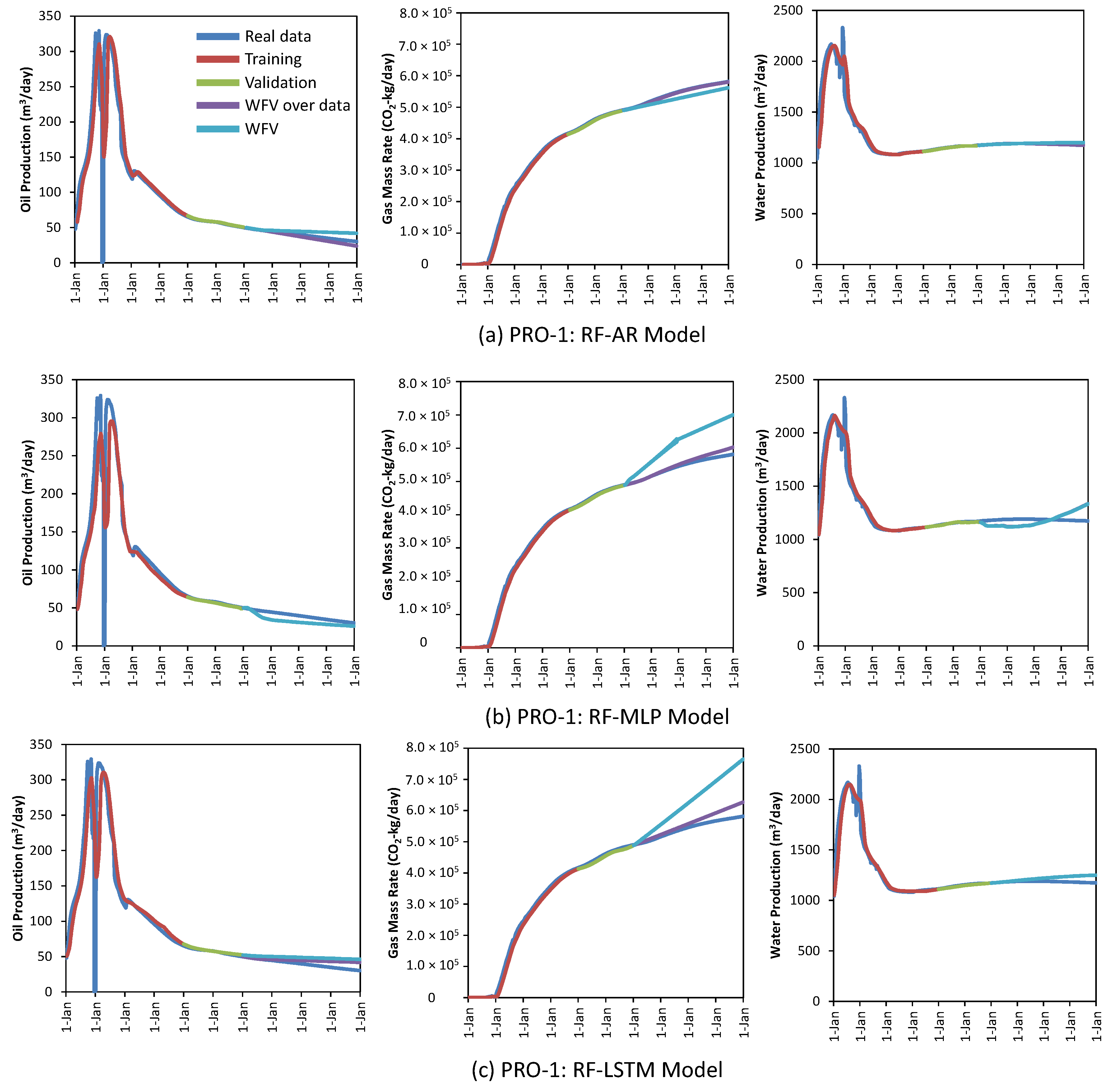
4.2.1. Global Model
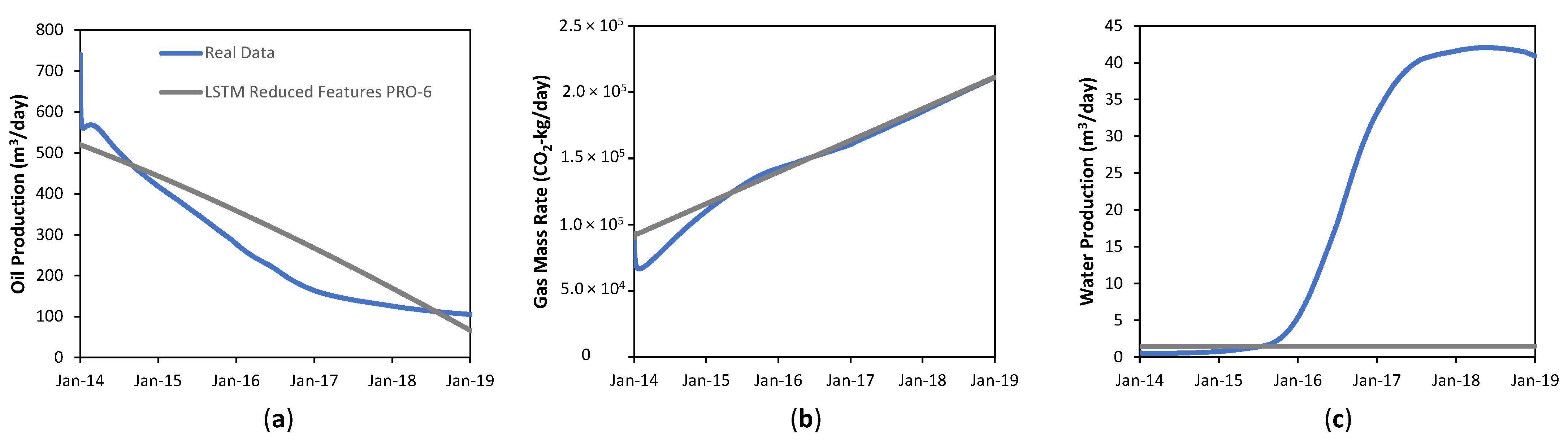
4.2.2. Reduced Feature Model
4.2.3. Comparing Global Model vs. Reduced Feature Model
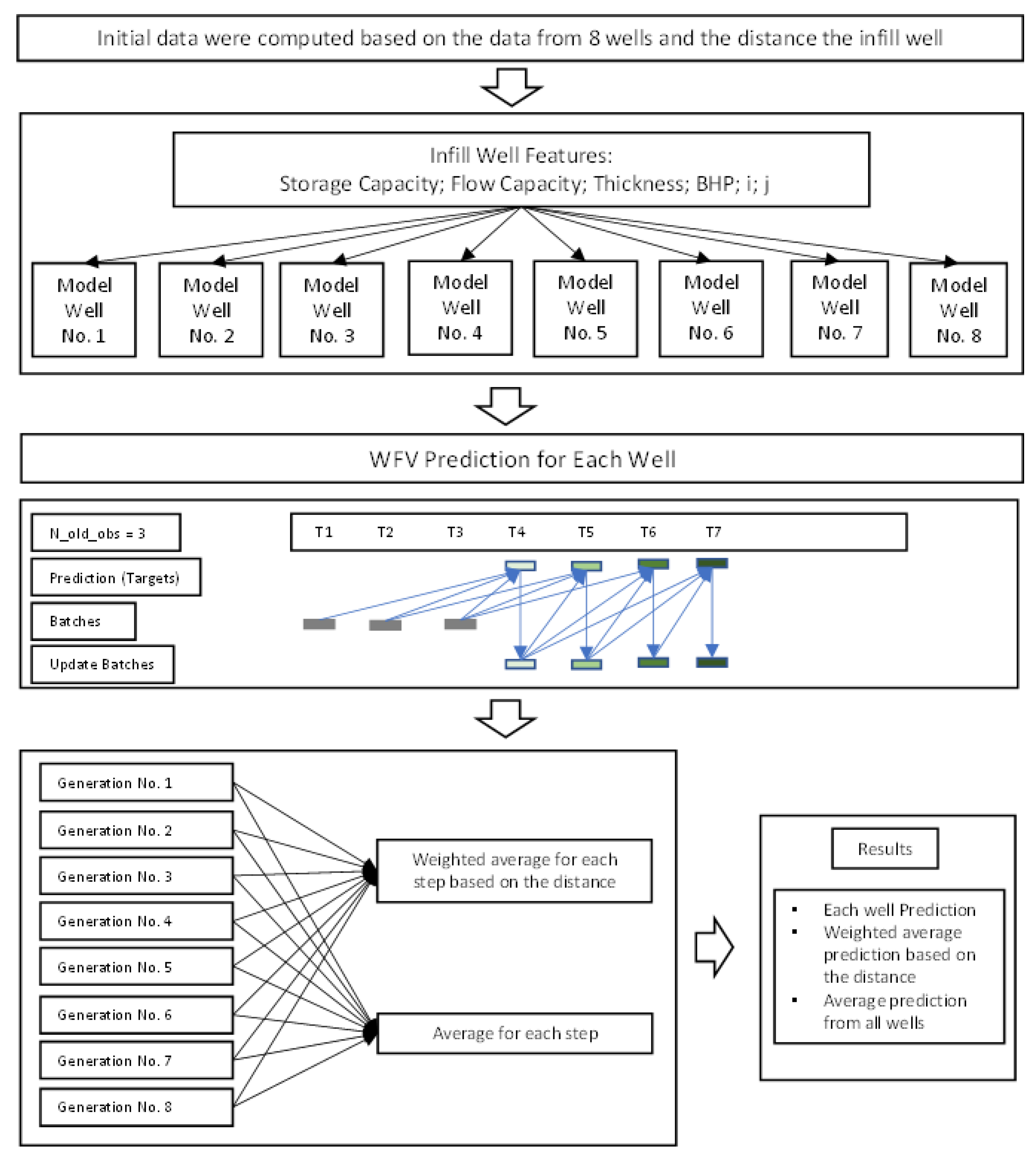
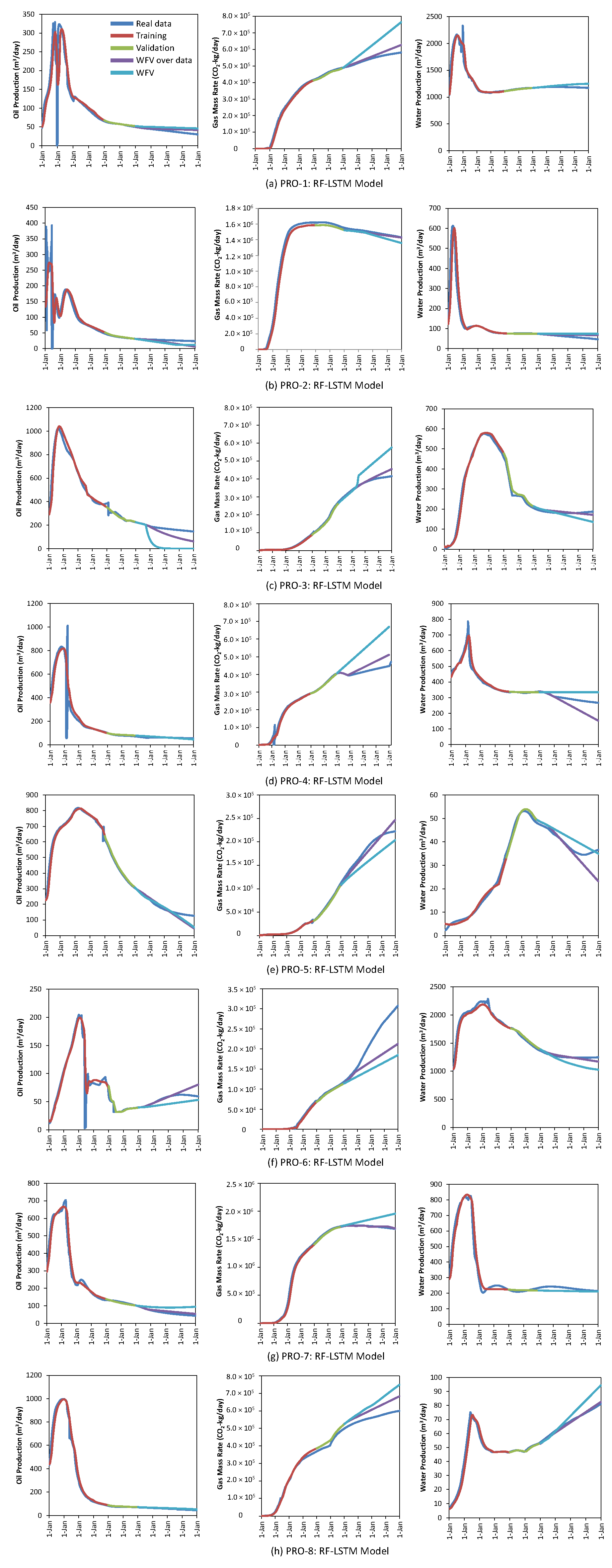
4.3. Future Infill Well Forecasting
5. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allen, M.; Babiker, M.; Chen, Y.; de Coninck, H.; Connors, S.; van Diemen, R.; Dube, O.P.; Ebi, K.L.; Engelbrecht, F.; Ferrat, M.; et al. Technical Summary: Global Warming of 1.5° C. An IPCC Special Report on the Impacts of Global Warming of 1.5° C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2019. [Google Scholar]
- Orr, F.M., Jr. Storage of Carbon Dioxide in Geologic Formations. J. Petrol. Technol. 2004, 56, 90–97. [Google Scholar] [CrossRef]
- Tadjer, A.; Hong, A.; Bratvold, R.B. Machine Learning Based Decline Curve Analysis for Short-Term Oil Production Forecast. Energy Explor. Exploit. 2021, 39, 1747–1769. [Google Scholar] [CrossRef]
- Werneck, R.d.O.; Prates, R.; Moura, R.; Gonçalves, M.M.; Castro, M.; Soriano-Vargas, A.; Ribeiro Mendes Júnior, P.; Hossain, M.M.; Zampieri, M.F.; Ferreira, A.; et al. Data-Driven Deep-Learning Forecasting for Oil Production and Pressure. J. Petrol. Sci. Eng. 2022, 210, 109937. [Google Scholar] [CrossRef]
- Negash, B.M.; Yaw, A.D. Artificial Neural Network Based Production Forecasting for a Hydrocarbon Reservoir Under Water Injection. Petrol. Explor. Dev. 2020, 47, 383–392. [Google Scholar] [CrossRef]
- Khan, H.; Louis, C. An Artificial Intelligence Neural Networks Driven Approach to Forecast Production in Unconventional Reservoirs–Comparative Analysis with Decline Curve. In Proceedings of the IPTC—International Petroleum Technology Conference, Virtual, 23 March–1 April 2021. [Google Scholar]
- Yu, Y.; Liu, S.; Liu, Y.; Bao, Y.; Zhang, L.; Dong, Y. Data-Driven Proxy Model for Forecasting of Cumulative Oil Production During the Steam-Assisted Gravity Drainage Process. ACS Omega 2021, 6, 11497–11509. [Google Scholar] [CrossRef]
- Le Van, S.; Chon, B.H. Evaluating the Critical Performances of a CO2–Enhanced Oil Recovery Process Using Artificial Neural Network Models. J. Petrol. Sci. Eng. 2017, 157, 207–222. [Google Scholar] [CrossRef]
- Al-Shabandar, R.; Jaddoa, A.; Liatsis, P.; Hussain, A.J. A Deep Gated Recurrent Neural Network for Petroleum Production Forecasting. Mach. Learn. Appl. 2021, 3, 100013. [Google Scholar] [CrossRef]
- Song, X.; Liu, Y.; Xue, L.; Wang, J.; Zhang, J.; Wang, J.; Jiang, L.; Cheng, Z.; Cheng, Z. Time-Series Well Performance Prediction Based on Long Short-Term Memory (LSTM) Neural Network Model. J. Petrol. Sci. Eng. 2020, 186, 106682. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, H.; Kong, X.; Shen, L.; Jia, Y. Machine Learning-Based Production Prediction Model and Its Application in Duvernay Formation. Energies 2021, 14, 5509. [Google Scholar] [CrossRef]
- AlRassas, A.M.; Al-Qaness, M.A.; Ewees, A.A.; Ren, S.; Sun, R.; Pan, L.; Abd Elaziz, M. Advance Artificial Time Series Forecasting Model for Oil Production Using Neuro Fuzzy-Based Slime Mould Algorithm. J. Petrol. Explor. Prod. Technol. 2021, 12, 383–395. [Google Scholar] [CrossRef]
- Dama, F.; Sinoquet, C. Time Series Analysis and Modeling to Forecast: A Survey. arXiv 2021, arXiv:2104.00164. [Google Scholar]
- Tariq, H.; Hanif, M.K.; Sarwar, M.U.; Bari, S.; Sarfraz, M.S.; Oskouei, R.J. Employing Deep Learning and Time Series Analysis to Tackle the Accuracy and Robustness of the Forecasting Problem. Sec. Commun. Netw. 2021, 2021, 5587511. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Jennings, C.L.; Kulahci, M. Introduction to Time Series Analysis and Forecasting; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Lara-Benítez, P.; Carranza-García, M.; Riquelme, J.C. An Experimental Review on Deep Learning Architectures for Time Series Forecasting. Int. J. Neural Syst. 2021, 31, 2130001. [Google Scholar] [CrossRef] [PubMed]
- Torres, J.F.; Hadjout, D.; Sebaa, A.; Martínez-Álvarez, F.; Troncoso, A. Deep Learning for Time Series Forecasting: A Survey. Big Data 2021, 9, 3–21. [Google Scholar] [CrossRef]
- Elsayed, S.; Thyssens, D.; Rashed, A.; Jomaa, H.S.; Schmidt-Thieme, L. Do We Really Need Deep Learning Models for Time Series Forecasting? arXiv 2021, arXiv:2101.02118. [Google Scholar]
- Wan, R.; Mei, S.; Wang, J.; Liu, M.; Yang, F. Multivariate Temporal Convolutional Network: A Deep Neural Networks Approach for Multivariate Time Series Forecasting. Electronics 2019, 8, 876. [Google Scholar] [CrossRef] [Green Version]
- Binkowski, M.; Marti, G.; Donnat, P. Autoregressive Convolutional Neural Networks for Asynchronous Time Series. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Dorffner, G. Neural networks for time series processing. Neural Netw. World 1996, 6, 447–468. [Google Scholar]
- Brownlee, J. Deep Learning for Time Series Forecasting: Predict the Future with MLPs, CNNs and LSTMs in Python; Machine Learning Mastery: San Juan, PR, USA, 2018. [Google Scholar]
- Sezer, O.B.; Gudelek, M.U.; Ozbayoglu, A.M. Financial Time Series Forecasting with Deep Learning: A Systematic Literature Review: 2005–2019. Appl. Soft Comput. 2020, 90, 106181. [Google Scholar] [CrossRef] [Green Version]
- Kulga, B.; Artun, E.; Ertekin, T. Development of a Data-Driven Forecasting Tool for Hydraulically Fractured, Horizontal Wells in Tight-Gas Sands. Comput. Geosci. 2017, 103, 99–110. [Google Scholar] [CrossRef]
- Kovscek, A.R.; Cakici, M.D. Geologic Storage of Carbon Dioxide and Enhanced Oil Recovery. II. Cooptimization of Storage and Recovery. Energy Convers. Manag. 2005, 46, 1941–1956. [Google Scholar] [CrossRef]
- Lyons, J.; Nasrabadi, H. Well Placement Optimization Under Time-Dependent Uncertainty Using an Ensemble Kalman Filter and a Genetic Algorithm. J. Petrol. Sci. Eng. 2013, 109, 70–79. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, L.; Yang, H.-Q.; Zhang, L.; Yao, Y.-P. Machine Learning for Pore-Water Pressure Time-Series Prediction: Application of Recurrent Neural Networks. Geosci. Front. 2021, 12, 453–467. [Google Scholar] [CrossRef]
- Johnson, C.R.; Greenkorn, R.A.; Woods, E.G. Pulse-Testing: A New Method for Describing Reservoir Flow Properties between Wells. J. Petrol. Technol. 1966, 18, 1599–1604. [Google Scholar] [CrossRef]
- Abedini, M.; Nasseri, M. Inverse Distance Weighted Revisited. In Proceedings of the 4th APHW Conference, Beijing, China, 4 November 2008. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer Feedforward Networks Are Universal Approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Abdullayeva, F.; Imamverdiyev, Y. Development of Oil Production Forecasting Method Based on Deep Learning. Stat. Optim. Inf. Comput. 2019, 7, 826–839. [Google Scholar] [CrossRef] [Green Version]




| Parameter | Value | Unit |
|---|---|---|
| Pressure at reference depth | 28,300 | kPa |
| Bottomhole flowing pressure | 19,810 | kPa |
| Pressure Fracture | 42,450 | kPa |
| Reservoir temperature at reference depth | 110 | °C |
| Free water level | 2395 | m |
| Free oil level | 2355 | m |
| Initial water saturation | 0.2 | fraction |
| Initial oil saturation (oil zone) | 0.8 | fraction |
| Initial oil saturation (gas cap) | 0.3 | fraction |
| Initial gas saturation (gas cap) | 0.5 | fraction |
| Reference depth | 2355 | m |
| Perforated Layer | |||
|---|---|---|---|
| Well | 1 | 3 | 5 |
| PRO-1 | ● | ||
| PRO-2 | ● | ||
| PRO-3 | ● | ● | ● |
| PRO-4 | ● | ||
| PRO-5 | ● | ● | |
| PRO-6 | ● | ● | ● |
| PRO-7 | ● | ● | ● |
| PRO-8 | ● | ● | |
| INFILL | ● | ||
| Well | Avg. Porosity | Avg. Permeability (mD) | Storage Capacity (m) | Flow Capacity (mD-m) | Avg. Fm Thickness (m) | BHP (kPa) | i | j |
|---|---|---|---|---|---|---|---|---|
| PRO-1 | 0.43 | 988.0 | 1.462 | 3359.2 | 3.40 | 20,500 | 4 | 22 |
| PRO-2 | 0.43 | 804.0 | 1.634 | 3055.2 | 3.80 | 19,100 | 11 | 22 |
| PRO-3 | 0.43 | 690.3 | 1.658 | 2551.9 | 3.90 | 20,000 | 16 | 22 |
| PRO-4 | 0.42 | 963.0 | 1.932 | 4429.8 | 4.60 | 18,700 | 8 | 19 |
| PRO-5 | 0.32 | 370.0 | 1.632 | 1887.0 | 5.10 | 19,800 | 16 | 17 |
| PRO-6 | 0.40 | 897.7 | 1.956 | 4375.6 | 4.93 | 20,800 | 7 | 11 |
| PRO-7 | 0.34 | 536.0 | 1.298 | 1961.8 | 3.97 | 20,100 | 11 | 12 |
| PRO-8 | 0.24 | 370.0 | 0.784 | 1231.7 | 3.65 | 19,500 | 16 | 12 |
| INFILL | 0.41 | 906.0 | 2.132 | 4711.2 | 5.2 | 20,000 | 11 | 16 |
| Hyperparameters | Data Driven Model | Description | Range |
|---|---|---|---|
| Hidden layers | MLP/LSTM | It determines the depth of the neural network. | [4, 5, 6, 7, 8] |
| Dropout | MLP/LSTM | It eliminates certain connections between neurons in each iteration. It is used to prevent overfitting. | [0.01, 0.001, 0.0001] |
| L1/L2 Regularization | MLP/LSTM | It prevents overfitting, stopping weights that are too high so that the model does not depend on a single feature. | [0.0001, 0.00001, 0.000001, 0.0000001, 0.00000001] |
| Units | MLP/LSTM | It determines the level of knowledge that is extracted by each layer. It is highly dependent on the size of the data used. | [128, 256, 512, 1024] |
| N_old_obs | AR | The number of observations used for the model. | [15, 20, 25, 30] |
| Mod_update | AR | The number of observations after which the updated model should be generated. | [25, 50, 100, 200, 400] |
| W_model_init | AR | The ratio for the initial model to the updated model to be taken into consideration. | [0.00, 0.5, 1.00] |
| Model | Parameter | Global Model | Reduced Feature Model | ||
|---|---|---|---|---|---|
| Oil | Gas | Water | |||
| AR | Factor for inverse distance | 20 | 20 | 20 | 20 |
| Number of previous observations | 30 | 30 | 30 | 25 | |
| Optimizers | Least square | Least square | Least square | Least square | |
| Ratio for initial/update model | 0.0:1.0 | 0.0:1.0 | 1.0:0.0 | 0.0:1.0 | |
| No. of observations to update model | 50 | 25 | 200 | 25 | |
| MLP | Factor for inverse distance | 20 | 20 | 20 | 20 |
| Number of previous observations | 5 | 5 | 5 | 5 | |
| Optimizers | Adam | Adam | Adam | Adam | |
| Activation function | ReLU | ReLU | ReLU | ReLU | |
| No. of hidden layers | 8 | 8 | 4 | 8 | |
| No. of units | 1024 | 512 | 1024 | 256 | |
| Dropout | 0.01 | 0.01 | 0.0001 | 0.0001 | |
| Kernel regularizator | L1 | L1 | L1 | L1 | |
| Kernel regularizator rate | 0.000001 | 0.00000001 | 0.0000001 | 0.0000001 | |
| Activity regularizator | L2 | L2 | L2 | L2 | |
| Activity regularizator rate | 0.00001 | 0.0001 | 0.0000001 | 0.00001 | |
| LSTM | Factor for inverse distance | 20 | 20 | 20 | 20 |
| Number of previous observations | 5 | 5 | 5 | 5 | |
| Optimizers | Adam | Adam | Adam | Adam | |
| Activation function | ReLU | ReLU | ReLU | ReLU | |
| No. of hidden layers | 6 | 7 | 8 | 8 | |
| No. of units | 1024 | 256 | 512 | 512 | |
| Dropout | 0.01 | 0.001 | 0.0001 | 0.001 | |
| Kernel regularizator | L1 | L1 | L1 | L1 | |
| Kernel regularizator rate | 0.0001 | 0.0001 | 0.0000001 | 0.000001 | |
| Activity regularizator | L2 | L2 | L2 | L2 | |
| Activity regularizator rate | 0.00000001 | 0.0000001 | 0.0000001 | 0.000001 | |
| WFV over Data | WFV | |||||
|---|---|---|---|---|---|---|
| Model | Oil Rate | Gas Mass Rate (CO2) | Water Rate | Oil Rate | Gas Mass Rate (CO2) | Water Rate |
| AR—Global | 1.16% | 0.68% | 1.80% | 13.37% | 9.93% | 14.13% |
| AR—Reduced Feature | 1.88% | 0.58% | 0.50% | 15.20% | 8.13% | 11.67% |
| MLP—Global | 133.60% | 6.95% | 75.19% | 95.60% | 16.23% | 104.47% |
| MLP—Reduced Feature | 34.59% | 5.54% | 38.51% | 33.47% | 15.15% | 38.78% |
| LSTM—Global | 41.46% | 3.86% | 31.25% | 142.96% | 15.38% | 72.19% |
| LSTM—Reduced Feature | 14.84% | 5.63% | 7.15% | 28.87% | 12.06% | 10.05% |
| WFV over Data (Days) | WFV (Days) | |||||
|---|---|---|---|---|---|---|
| Model | Oil Rate | Gas Mass Rate (CO2) | Water Rate | Oil Rate | Gas Mass Rate (CO2) | Water Rate |
| AR—Global | 1430 | 1430 | 1343 | 918 | 378 | 856 |
| AR—Reduced Feature | 1430 | 1430 | 1435 | 860 | 452 | 633 |
| MLP—Global | 346 | 333 | 84 | 346 | 13 | 83 |
| MLP—Reduced Feature | 209 | 425 | 30 | 150 | 44 | 18 |
| LSTM—Global | 180 | 269 | 261 | 158 | 177 | 172 |
| LSTM—Reduced Feature | 269 | 284 | 278 | 176 | 187 | 183 |
| WFV over Data (Days) | WFV (Days) | |||||
|---|---|---|---|---|---|---|
| Model | Oil Rate | Gas Mass Rate (CO2) | Water Rate | Oil Rate | Gas Mass Rate (CO2) | Water Rate |
| AR—Global | 0 | 0 | 0 | 424 | 242 | 503 |
| AR—Reduced Feature | 0 | 0 | 243 | 442 | 260 | 495 |
| MLP—Global | 253 | 466 | 39 | 184 | 53 | 26 |
| MLP—Reduced Feature | 518 | 457 | 210 | 518 | 12 | 211 |
| LSTM—Global | 12 | 10 | 11 | 13 | 12 | 12 |
| LSTM—Reduced Feature | 7 | 9 | 9 | 13 | 11 | 15 |
| Time Series | MAPE | % Shape Difference |
|---|---|---|
| Oil Rate | 28% | 28% |
| Gas Mass Rate (CO2) | 5% | 6% |
| Water Rate | 98% | 17% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iskandar, U.P.; Kurihara, M. Time-Series Forecasting of a CO2-EOR and CO2 Storage Project Using a Data-Driven Approach. Energies 2022, 15, 4768. https://doi.org/10.3390/en15134768
Iskandar UP, Kurihara M. Time-Series Forecasting of a CO2-EOR and CO2 Storage Project Using a Data-Driven Approach. Energies. 2022; 15(13):4768. https://doi.org/10.3390/en15134768
Chicago/Turabian StyleIskandar, Utomo Pratama, and Masanori Kurihara. 2022. "Time-Series Forecasting of a CO2-EOR and CO2 Storage Project Using a Data-Driven Approach" Energies 15, no. 13: 4768. https://doi.org/10.3390/en15134768
APA StyleIskandar, U. P., & Kurihara, M. (2022). Time-Series Forecasting of a CO2-EOR and CO2 Storage Project Using a Data-Driven Approach. Energies, 15(13), 4768. https://doi.org/10.3390/en15134768





