Power Transformer Diagnosis Based on Dissolved Gases Analysis and Copula Function
Abstract
:1. Introduction
2. Copula Function and Common Factor Analysis
2.1. Copula Function
2.2. Common Factor Analysis
3. Copula Function Selection and Parameter Fitting
3.1. Bayesian Estimation of θ
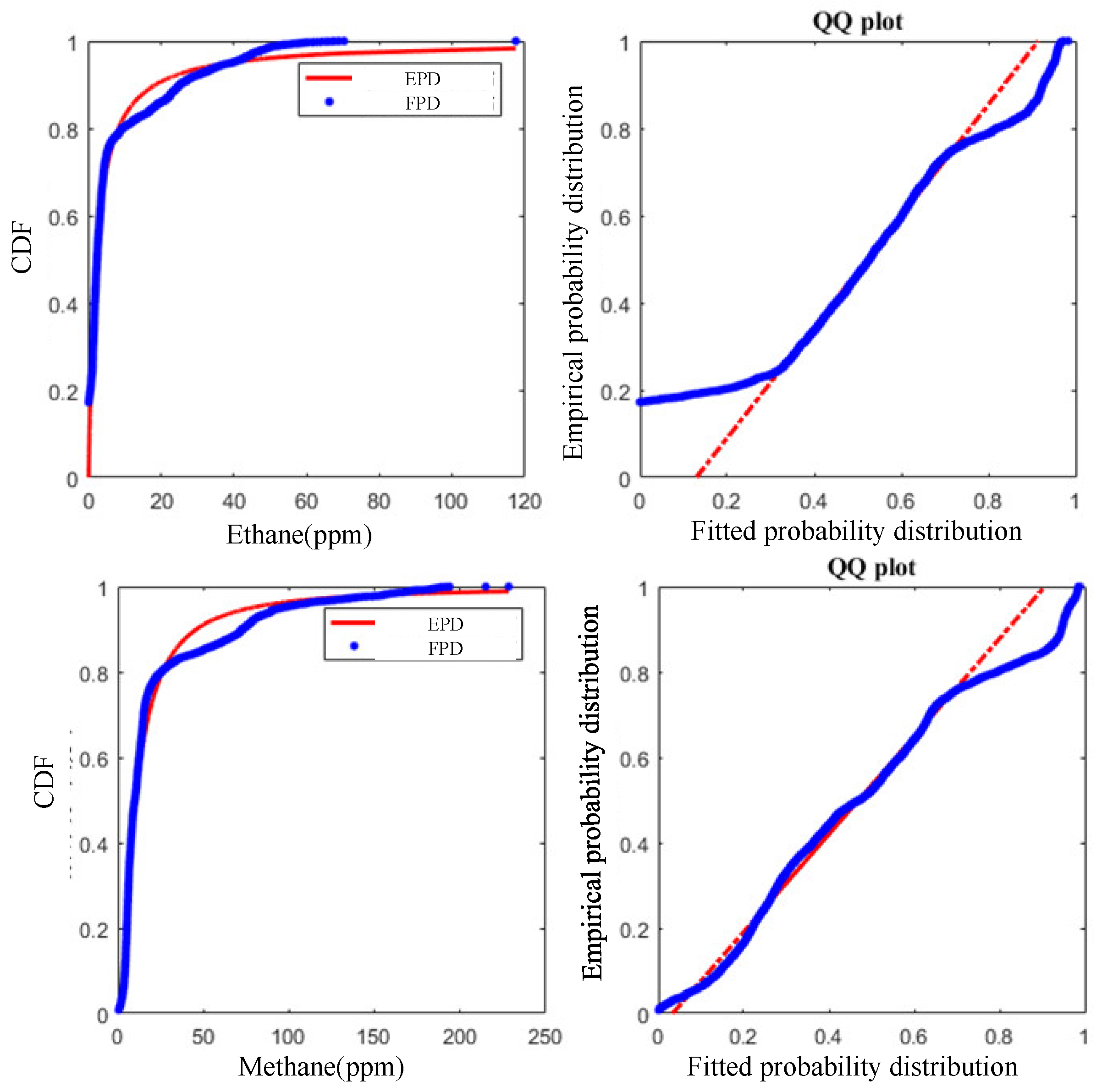
3.2. Goodness of Fitting
4. Study Cases
4.1. Factor Analysis of Dissolved Gas in Oil
4.2. Marginal Distribution Fitting
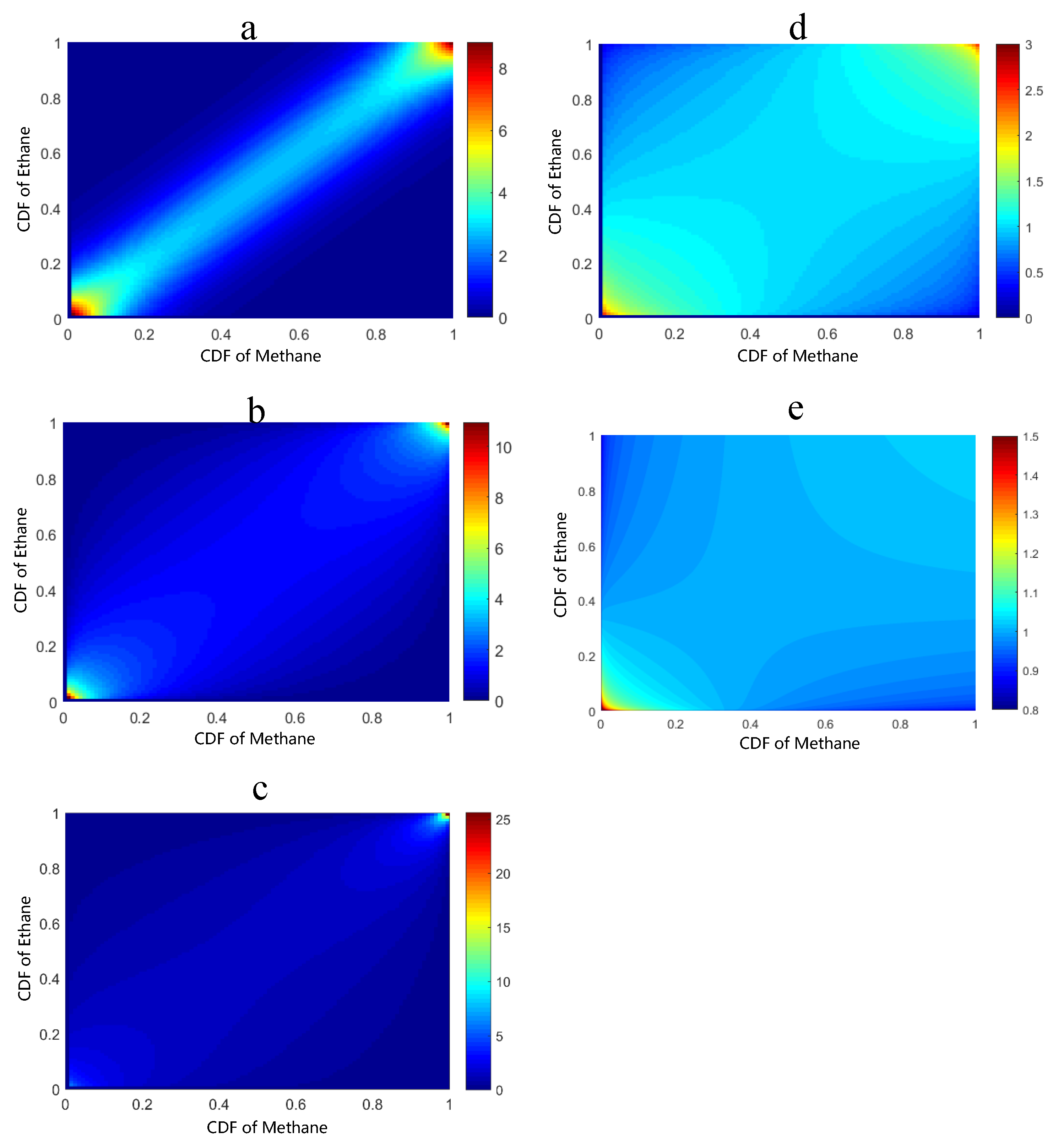
4.3. Copula Function Selection and Fitting
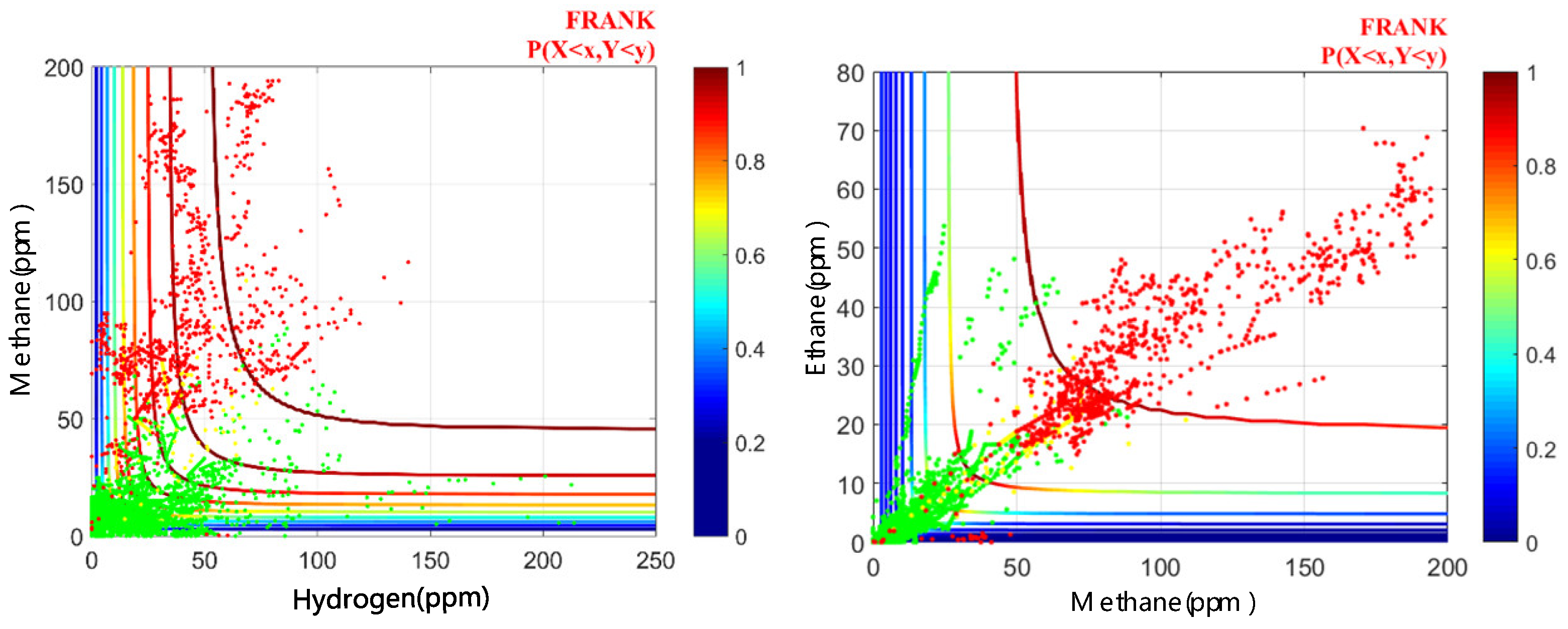
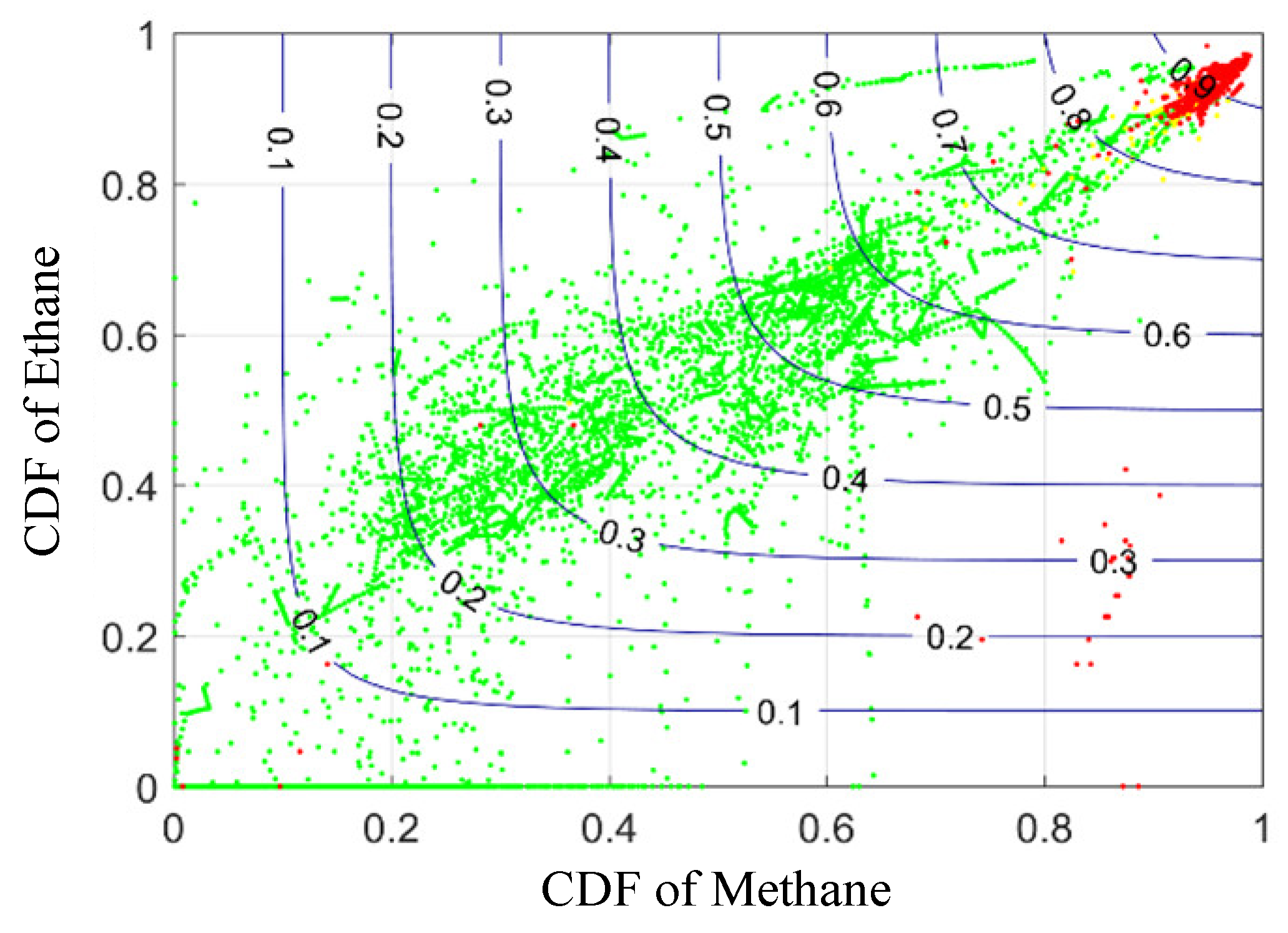
4.4. Transformer Status Diagnosis of Power Transformer
5. Conclusions
- (1)
- Compared with other combinations of fault characteristic gases, the copula function CDF boundary whose marginal variable is hydrocarbon gas can separate the transformer healthy and faulty status, and the joint probability of the dissolved gas in oil is correlated with the transformer healthy or defective status.
- (2)
- When the CDF result of the dissolved gas in the oil in the copula function is close to 0.8, the fluctuation of its gas concentration leads to a sharp change in the probability that the data diagnosis results are defective or healthy.
- (3)
- Based on the correlation between the joint probability of dissolved gas in the oil and the transformer state (healthy or defective), the nearest neighbor algorithm can be used to evaluate the correlation between the data of the unknown state and the known state data in the copula function, and thus the unknown data state can be evaluated.
- (4)
- The binary copula function selected in this paper has a low degree of freedom and avoids deep network training. The copula function is used to separate the correlation structure between the marginal distribution and random variables, which simplifies the multivariate probability modeling process and is beneficial to field applications and implementation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Symbols and Acronyms
| AIC | Akaike information criterion |
| BIC | Bayesian information criterion |
| CDF | cumulative distribution probability |
| DGA | dissolved gas analysis |
| KMO | Kaiser–Meyer–Olkin |
| NSE | Nash coefficient |
| RMSE | root mean square error |
| THC | total hydrocarbons |
| k | the sample size |
| R | correlation matrix |
| Q | anti-image correlation matrix |
References
- Mahmoudi, N.; Samimi, M.H.; Mohseni, H. Experiences with transformer diagnosis by DGA: Case studies. IET Gener. Transm. Distrib. 2019, 13, 5431–5439. [Google Scholar] [CrossRef]
- Ghoneim, S.S.; Taha, I.B. A new approach of DGA interpretation technique for transformer fault diagnosis. Int. J. Electr. Power Energy Syst. 2016, 81, 265–274. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, R.; Chen, M.; Wang, W.; Zhang, C. Dynamic Fault Prediction of Power Transformers Based on Hidden Markov Model of Dissolved Gases Analysis. IEEE Trans. Power Deliv. 2019, 34, 1393–1400. [Google Scholar] [CrossRef]
- Kim, S.-W.; Kim, S.-J.; Seo, H.-D.; Jung, J.-R.; Yang, H.-J.; Duval, M. New methods of DGA diagnosis using IEC TC 10 and related databases Part 1: Application of gas-ratio combinations. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 685–690. [Google Scholar] [CrossRef]
- Li, S.; Wu, G.; Gao, B.; Hao, C.; Xin, D.; Yin, X. Interpretation of DGA for transformer fault diagnosis with complementary SaE-ELM and arctangent transform. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 586–595. [Google Scholar] [CrossRef]
- Yang, D.; Qin, J.; Pang, Y.; Huang, T. A novel double-stacked autoencoder for power transformers DGA signals with an imbalanced data structure. IEEE Trans. Ind. Electron. 2021, 69, 1977–1987. [Google Scholar] [CrossRef]
- Malik, H.; Mishra, S. Application of Gene Expression Programming (GEP) in Power Transformers Fault Diagnosis Using DGA. IEEE Trans. Ind. Appl. 2016, 52, 4556–4565. [Google Scholar] [CrossRef]
- Taha, I.B.M.; Ibrahim, S.; Mansour, D.-E.A. Power Transformer Fault Diagnosis Based on DGA Using a Convolutional Neural Network with Noise in Measurements. IEEE Access 2021, 9, 111162–111170. [Google Scholar] [CrossRef]
- Chatterjee, K.; Dawn, S.; Jadoun, V.K.; Jarial, R. Novel prediction-reliability based graphical DGA technique using multi-layer perceptron network & gas ratio combination algorithm. IET Sci. Meas. Technol. 2019, 13, 836–842. [Google Scholar] [CrossRef]
- Ghoneim, S.S.M.; Taha, I.B.M.; Elkalashy, N.I. Integrated ANN-based proactive fault diagnostic scheme for power transformers using dissolved gas analysis. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1838–1845. [Google Scholar] [CrossRef]
- Illias, H.A.; Chai, X.R. Hybrid modified evolutionary particle swarm optimisation-time varying acceleration coefficient-artificial neural network for power transformer fault diagnosis. Measurement 2016, 90, 94–102. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, H.; Zhang, Y.; Li, X.; Fang, J.; Liu, Y.; Liao, C.; Li, Y.; Zhao, J. Dissolved Gases Forecasting Based on Wavelet Least Squares Support Vector Regression and Imperialist Competition Algorithm for Assessing Incipient Faults of Transformer Polymer Insulation. Polymers 2019, 11, 85. [Google Scholar] [CrossRef] [Green Version]
- Benmahamed, Y.; Kherif, O.; Teguar, M.; Boubakeur, A.; Ghoneim, S. Accuracy Improvement of Transformer Faults Diagnostic Based on DGA Data Using SVM-BA Classifier. Energies 2021, 14, 2970. [Google Scholar] [CrossRef]
- Huang, Y.-C.; Sun, H.-C. Dissolved gas analysis of mineral oil for power transformer fault diagnosis using fuzzy logic. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 974–981. [Google Scholar] [CrossRef]
- Bhalla, D.; Bansal, R.K.; Gupta, H.O. Integrating AI based DGA fault diagnosis using Dempster–Shafer Theory. Int. J. Electr. Power Energy Syst. 2013, 48, 31–38. [Google Scholar] [CrossRef]
- Islam, S.M.; Wu, T.; Ledwich, G. A novel fuzzy logic approach to transformer fault diagnosis. IEEE Trans. Dielectr. Electr. Insul. 2000, 7, 177–186. [Google Scholar] [CrossRef]
- Gouda, O.E.; El-Hoshy, S.H.; El-Tamaly, H.H. Proposed heptagon graph for DGA interpretation of oil transformers. IET Gener. Transm. Distrib. 2018, 12, 490–498. [Google Scholar] [CrossRef]
- Alghamdi, A.S.; Muhamad, N.A.; Suleiman, A.A. DGA Interpretation of Oil Filled Transformer Condition Diagnosis. Trans. Electr. Electron. Mater. 2012, 13, 229–232. [Google Scholar] [CrossRef] [Green Version]
- Illias, H.A.; Chai, X.R.; Abu Bakar, A.H.; Mokhlis, H. Transformer Incipient Fault Prediction Using Combined Artificial Neural Network and Various Particle Swarm Optimisation Techniques. PLoS ONE 2015, 10, e0129363. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Ma, Y.; Jia, Q.; Su, Y. Development of a Bayesian-copula-based frequency analysis method for hydrological risk assessment—The Naryn River in Central Asia. J. Hydrol. 2020, 580, 124349. [Google Scholar] [CrossRef]
- Dehghani, E.; Ranjbar, S.; Atashafrooz, M.; Negarestani, H.; Mosavi, A.; Kovacs, L. Introducing Copula as a Novel Statistical Method in Psychological Analysis. Int. J. Environ. Res. Public Health 2021, 18, 7972. [Google Scholar] [CrossRef] [PubMed]
- Morteza, A.; Amirmazlaghani, M. A Novel Gaussian-Copula modeling for image despeckling in the shearlet do-main. Signal Processing 2022, 192, 108340. [Google Scholar] [CrossRef]
- Paul, D.; Goswami, A.K. Copula based bivariate modelling of DGA and breakdown voltage in high voltage transformers and reactors. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1763–1770. [Google Scholar] [CrossRef]



| Dissolved Gases | Common Factor Loading #1 | Common Factor Loading #2 |
|---|---|---|
| H2 | 0.271 | 0.460 |
| CH4 | 0.916 | 0.301 |
| C2H6 | 0.993 | 0.085 |
| C2H4 | 0.774 | 0.602 |
| C2H2 | 0.088 | 0.746 |
| THC (total hydrocarbons) | 0.886 | 0.457 |
| Copula Function Type | RMSE | NSE | Parameters of Fitting |
|---|---|---|---|
| Gaussian | 1.1549 | 0.9767 | 0.8301 |
| T | 0.9455 | 0.9844 | 0.9001, 7.8203 |
| Frank | 0.7690 | 0.9897 | 15.9219 |
| Clayton | 1.8818 | 0.9382 | 1.3189 |
| Gumbel | 0.9886 | 0.9826 | 3.6969 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhu, H.; Li, B.; Wu, R.; Jiang, J. Power Transformer Diagnosis Based on Dissolved Gases Analysis and Copula Function. Energies 2022, 15, 4192. https://doi.org/10.3390/en15124192
Zhang X, Zhu H, Li B, Wu R, Jiang J. Power Transformer Diagnosis Based on Dissolved Gases Analysis and Copula Function. Energies. 2022; 15(12):4192. https://doi.org/10.3390/en15124192
Chicago/Turabian StyleZhang, Xiaoqin, Hongbin Zhu, Bo Li, Ruihan Wu, and Jun Jiang. 2022. "Power Transformer Diagnosis Based on Dissolved Gases Analysis and Copula Function" Energies 15, no. 12: 4192. https://doi.org/10.3390/en15124192
APA StyleZhang, X., Zhu, H., Li, B., Wu, R., & Jiang, J. (2022). Power Transformer Diagnosis Based on Dissolved Gases Analysis and Copula Function. Energies, 15(12), 4192. https://doi.org/10.3390/en15124192






