Oblique Detonation Wave Control with O3 and H2O2 Sensitization in Hypersonic Flow
Abstract
:1. Introduction
2. Numerical Method
2.1. Computational Domain
2.2. Boundary and Initial Conditions
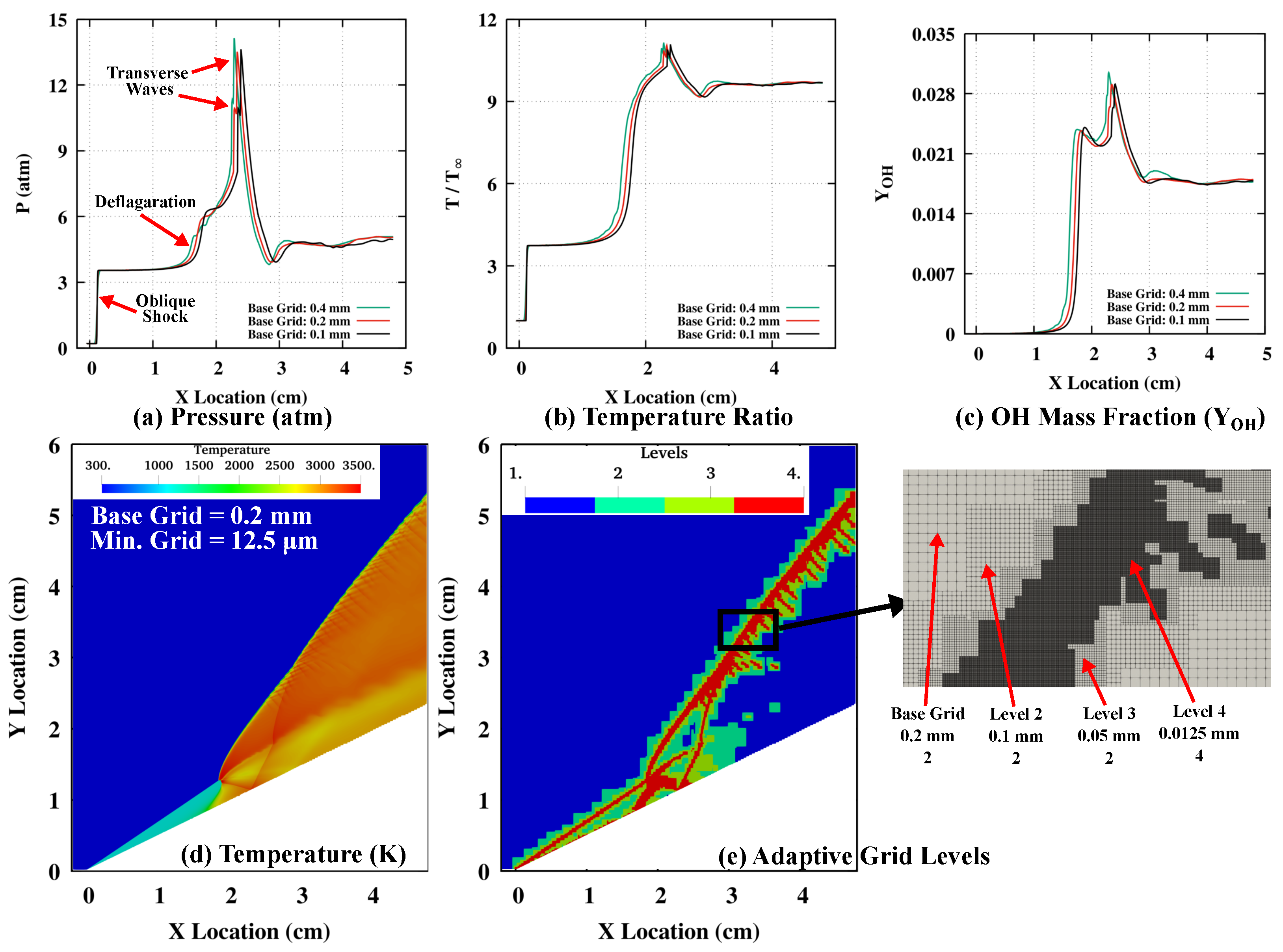
2.3. Grid Independence
3. Results and Discussions
3.1. ODW Formation with No Additives
3.2. Effect of and Addition at Mach 7
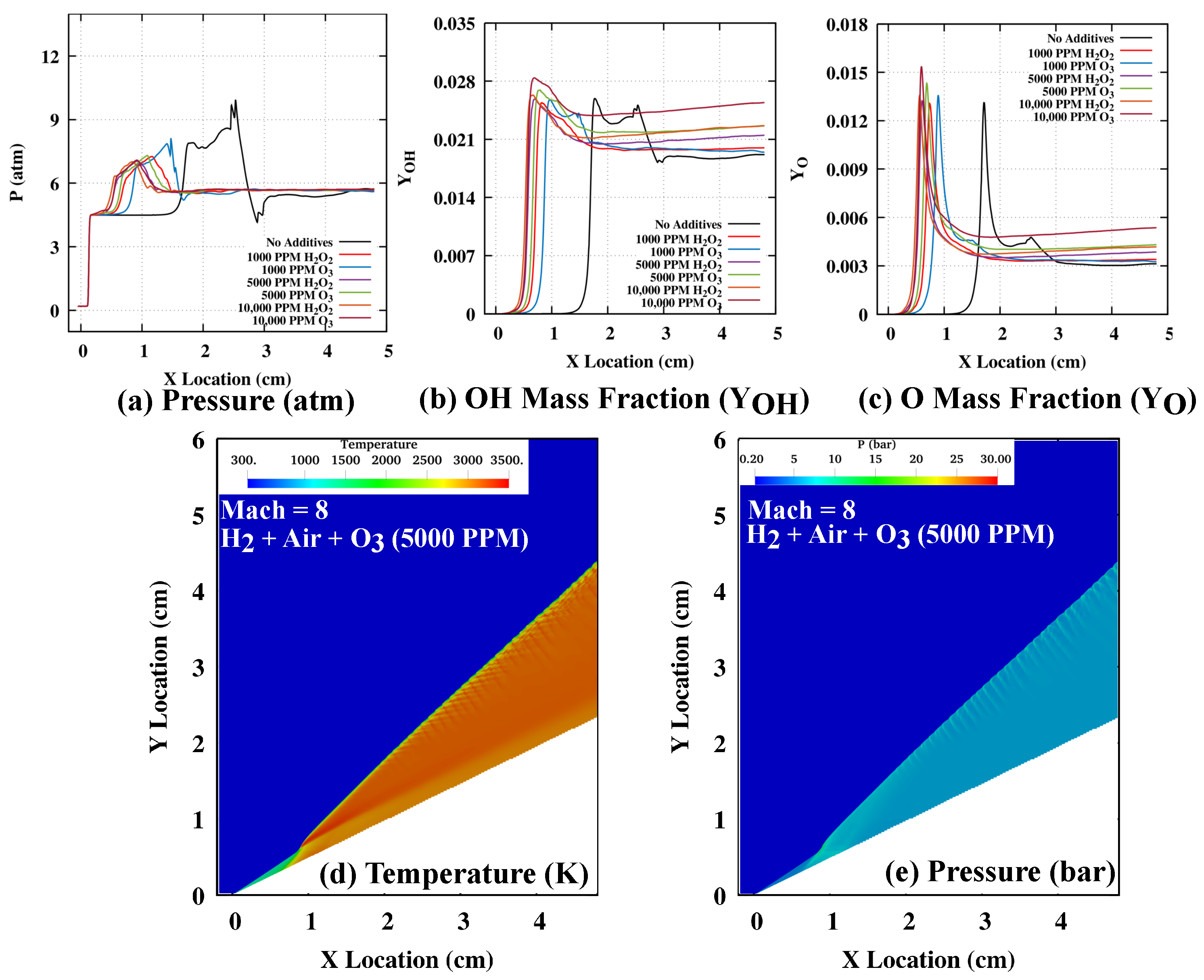
3.3. Effect of and Addition at Mach 8
3.4. Effect of and Addition at Mach 9
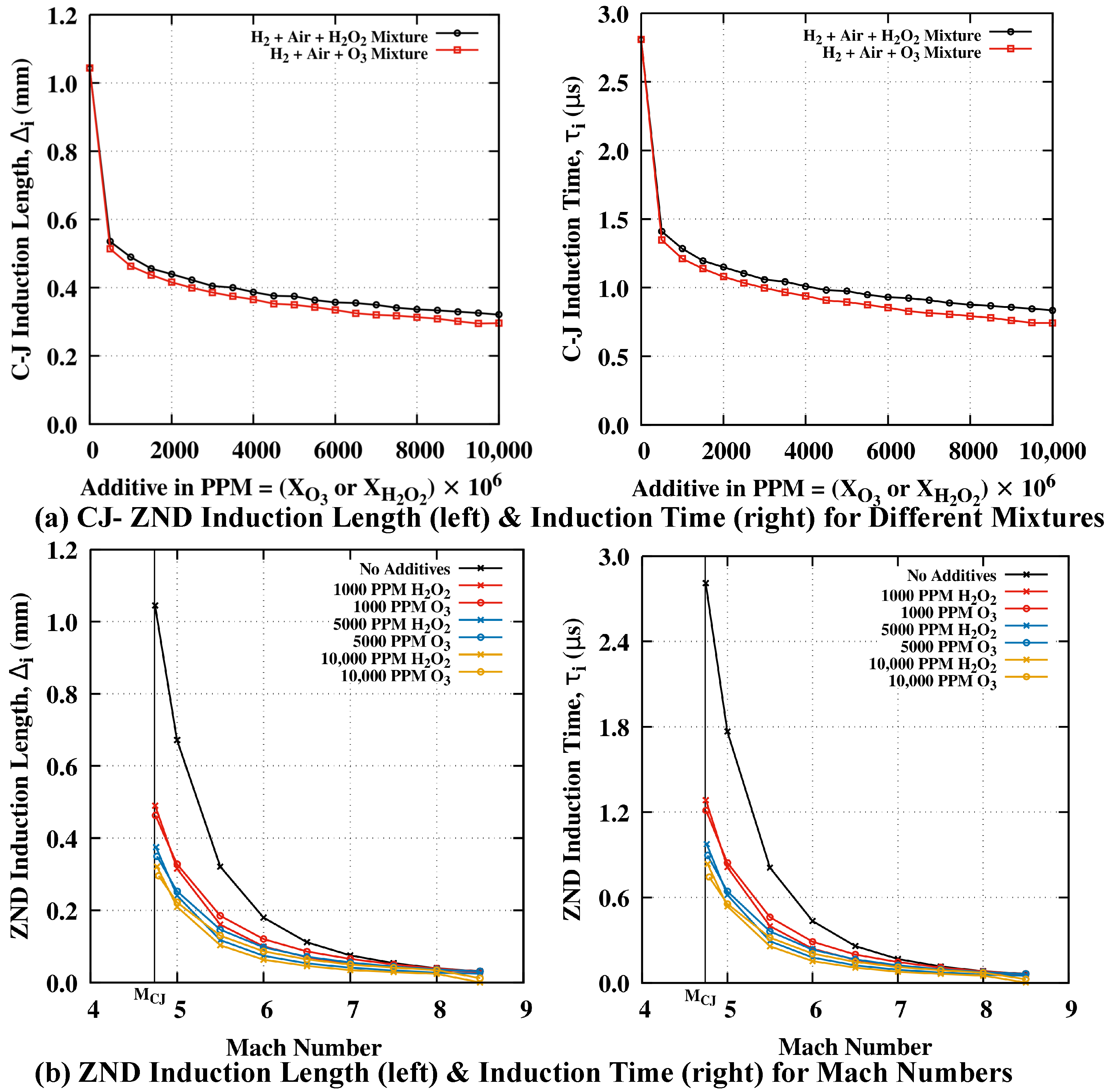
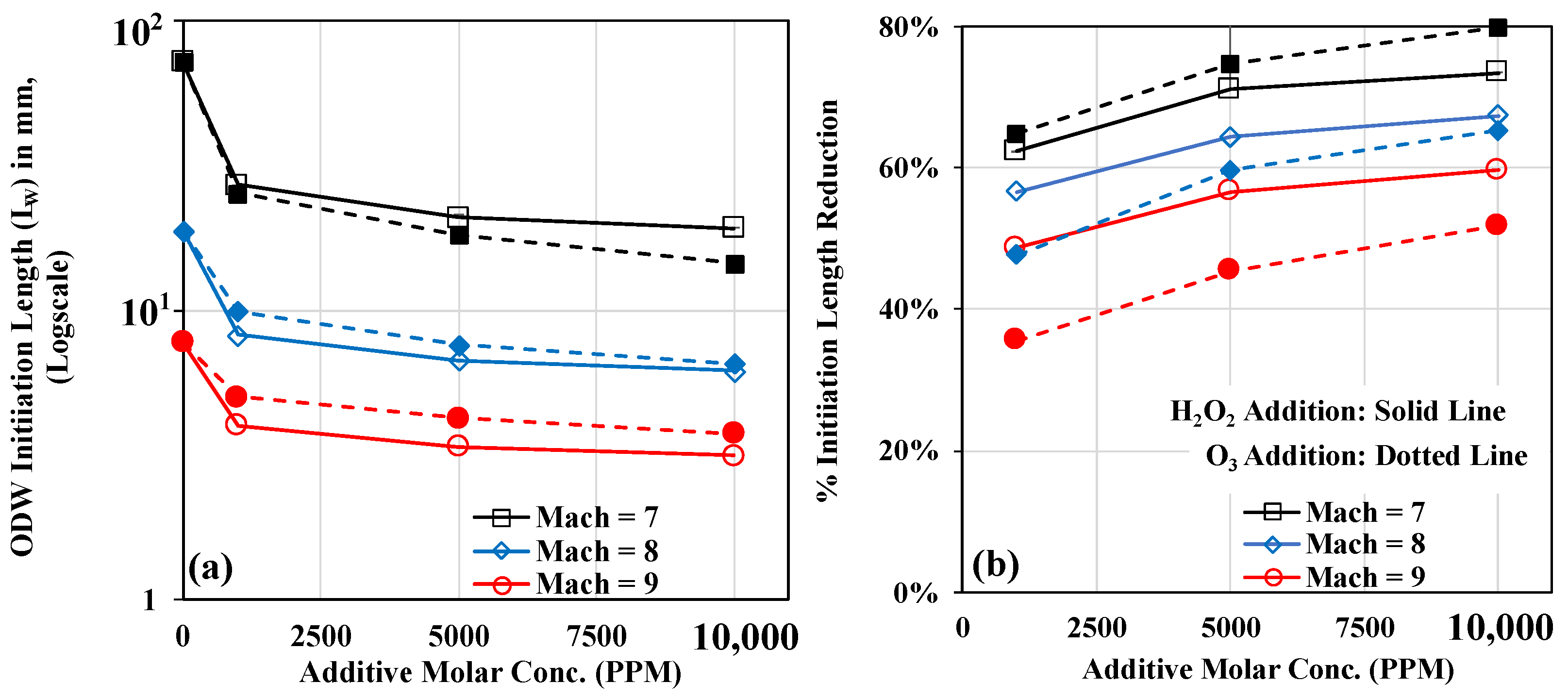
3.5. Effect on ODW Initiation Length
4. Conclusions
- The mixing of and from a small amount, 1000 PPM, to a moderate amount, 10,000 PPM, can effectively reduce the initiation lengths of an oblique shock to oblique detonation wave transition at all Mach numbers studied.
- At Mach 7, the reduction in initiation length is up to 80% with and addition during the abrupt transition. The addition has been found to be more effective in comparison to the addition for low Mach number abrupt transition conditions, and it can be utilized to increase lower operating flight speeds for ODWE.
- At Mach 8, the moderate abrupt OSW to ODW transition can be modified to a smoother transition by adding a small amount of and . Furthermore, addition has been found to be more effective in reducing the initiation length in comparison to the same amount of addition for Mach 8 and 9 during smooth ODW transitions.
- The Mach number dependence of the compressed region in the initiation zone behind the oblique was responsible for the different performances of and addition for initiation length reduction. decomposition was dominated regarding the initiation length reduction at a relatively lower Mach number, while formation from was dominant at higher Mach numbers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, J.H.S. The Detonation Phenomenon, 1st ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Kailasanath, K. Review of Propulsion Applications of Detonation Waves. AIAA J. 2000, 38, 1698–1708. [Google Scholar] [CrossRef]
- Wolanski, P. Detonative propulsion. Proc. Combust. Inst. 2013, 34, 125–158. [Google Scholar] [CrossRef]
- Viguier, C.; da Silva, L.F.F.; Desbordes, D.; Deshaies, B. Onset of oblique detonation waves: Comparison between experimental and numerical results for hydrogen-air mixtures. Symp. (Int.) Combust. 1996, 26, 3023–3031. [Google Scholar] [CrossRef]
- Pratt, D.T.; Humphrey, J.W.; Glenn, D.E. Morphology of standing oblique detonation waves. J. Propuls. Power 1991, 7, 837–845. [Google Scholar] [CrossRef]
- Powers, J.M.; Stewart, D.S. Approximate solutions for oblique detonations in the hypersonic limit. AIAA J. 1992, 30, 726–736. [Google Scholar] [CrossRef]
- Wang, A.F.; Zhao, W.; Jiang, Z.L. The criterion of the existence or inexistence of transverse shock wave at wedge supported oblique detonation wave. Acta Mech. Sin. 2011, 27, 611–619. [Google Scholar] [CrossRef] [Green Version]
- Verreault, J.; Higgins, A.J. Initiation of detonation by conical projectiles. Proc. Combust. Inst. 2011, 33, 2311–2318. [Google Scholar] [CrossRef]
- Rosato, D.A.; Thornton, M.; Sosa, J.; Bachman, C.; Goodwin, G.B.; Ahmed, K.A. Stabilized detonation for hypersonic propulsion. Proc. Natl. Acad. Sci. USA 2021, 118, e2102244118. [Google Scholar] [CrossRef] [PubMed]
- Silva, F.D.; Deshaies, B. Stabilization of an oblique detonation wave by a wedge: A parametric numerical study. Combust. Flame 2000, 121, 152–166. [Google Scholar] [CrossRef]
- Teng, H.; Zhang, Y.; Jiang, Z. Numerical investigation on the induction zone structure of the oblique detonation waves. Comput. Fluids 2014, 95, 127–131. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Yang, P.; Teng, H.; Ng, H.D.; Wen, C. Transition Between Different Initiation Structures of Wedge-Induced Oblique Detonations. AIAA J. 2018, 56, 4016–4023. [Google Scholar] [CrossRef]
- Teng, H.; Ng, H.D.; Jiang, Z. Initiation characteristics of wedge induced oblique detonation waves in a stoichiometric hydrogen air mixture. Proc. Combust. Inst. 2017, 36, 2735–2742. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Li, H.; Xiang, G.; Peng, S. Initiation characteristics of oblique detonation waves from a finite wedge under argon dilution. Chin. J. Aeronaut. 2021, 34, 81–90. [Google Scholar] [CrossRef]
- Miao, S.; Zhou, J.; Lin, Z.; Cai, X.; Liu, S. Numerical Study on Thermodynamic Efficiency and Stability of Oblique Detonation Waves. AIAA J. 2018, 56, 3112–3122. [Google Scholar] [CrossRef]
- Magzumov, A.E.; Kirillov, I.A.; Rusanov, V.D. Effect of small additives of ozone and hydrogen peroxide on the induction-zone length of hydrogen-air mixtures in a one-dimensional model of a detonation wave. Combust. Explos. Shock Waves 1998, 34, 338–341. [Google Scholar] [CrossRef]
- Crane, J.; Shi, X.; Singh, A.V.; Tao, Y.; Wang, H. Isolating the effect of induction length on detonation structure: Hydrogen–oxygen detonation promoted by ozone. Combust. Flame 2019, 200, 44–52. [Google Scholar] [CrossRef]
- Kumar, D.S.; Ivin, K.; Singh, A.V. Sensitizing gaseous detonations for hydrogen/ethylene-air mixtures using ozone and H2O2 as dopants for application in rotating detonation engines. Proc. Combust. Inst. 2021, 38, 3825–3834. [Google Scholar] [CrossRef]
- Qin, Q.; Zhang, X. Nitrogen dilution effects on the local detachment of the oblique detonation wave in the 2H2-O2 mixture. Int. J. Hydrogen Energy 2021, 46, 6873–6884. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, Y.; Ng, H.D.; Teng, H. Numerical investigation on the initiation of oblique detonation waves in stoichiometric acetylene–oxygen mixtures with high argon dilution. Combust. Flame 2019, 204, 391–396. [Google Scholar] [CrossRef]
- Maeda, S.; Inada, R.; Kasahara, J.; Matsuo, A. Visualization of the non-steady state oblique detonation wave phenomena around hypersonic spherical projectile. Proc. Combust. Inst. 2011, 33, 2343–2349. [Google Scholar] [CrossRef] [Green Version]
- Viguier, C.; Gourara, A.; Desbordes, D. Three-dimensional structure of stabilization of oblique detonation wave in hypersonic flow. Symp. (Int.) Combust. 1998, 27, 2207–2214. [Google Scholar] [CrossRef]
- Sosa, J.; Rosato, D.A.; Goodwin, G.B.; Bachman, C.L.; Oran, E.S.; Ahmed, K.A. Controlled detonation initiation in hypersonic flow. Proc. Combust. Inst. 2021, 38, 3513–3520. [Google Scholar] [CrossRef]
- Li, C.; Kailasanath, K.; Oran, E.S. Detonation structures behind oblique shocks. Phys. Fluids 1994, 6, 1600–1611. [Google Scholar] [CrossRef]
- Li, C.; Kailasanath, K.; Oran, E. Effects of boundary layers on oblique-detonation structures. In Proceedings of the 31st Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1993; AIAA: Reston, VI, USA, 1993. Chapter AIAA-93-0450. p. 13. [Google Scholar] [CrossRef]
- Oran, E.S.; Weber, J.W.; Stefaniw, E.I.; Lefebvre, M.H.; Anderson, J.D. A Numerical Study of a Two-Dimensional H2-O2-Ar Detonation Using a Detailed Chemical Reaction Model. Combust. Flame 1998, 113, 147–163. [Google Scholar] [CrossRef]
- Deiterding, R. Parallel Adaptive Simulation of Multi-Dimensional Detonation Structures. Ph.D. Thesis, Brandenburgische Technische Universitat Cottbus, Cottbus, Germany, 2003. [Google Scholar]
- Deiterding, R. High-Resolution Numerical Simulation and Analysis of Mach Reflection Structures in Detonation Waves in Low-Pressure H2–O2–Ar Mixtures: A Summary of Results Obtained with the Adaptive Mesh Refinement Framework AMROC. J. Combust. 2011, 2011, 738969. [Google Scholar] [CrossRef] [Green Version]
- Deiterding, R. A parallel adaptive method for simulating shock-induced combustion with detailed chemical kinetics in complex domains. Comput. Struct. 2009, 87, 769–783. [Google Scholar] [CrossRef] [Green Version]
- Harmon, P.; Vashishtha, A.; Callaghan, D.; Nolan, C.; Deiterding, R. Study of Direct Gas Injection into stagnation zone of Blunt Nose at Hypersonic Flow. In Proceedings of the AIAA Propulsion and Energy 2021 Forum, Virtual, 9–11 August 2021; AIAA: Reston, VI, USA, 2021. Chapter Session. p. 3529. [Google Scholar] [CrossRef]
- Vashishtha, A.; Callaghan, D.; Nolan, C.; Deiterding, R. Numerical Investigation of Detonation Propagation Through Small Orifice Holes. Trans. Aerosp. Res. 2021, 2021, 17–33. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Xiao, B.; Yan, Z.; Wang, C. Hysteresis phenomenon of the oblique detonation wave. Combust. Flame 2018, 192, 170–179. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, B.; Wang, L.; Wang, C. Numerical Study of Disturbance Resistance of Oblique Detonation Waves. Int. J. Aerosp. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Huang, Y.; Luan, Z.; Li, Z.; Ji, H.; You, Y. Study on the flow characteristics in the non-detonation reaction zones of wedge-induced oblique detonation transitions. Aerosp. Sci. Technol. 2022, 120, 107282. [Google Scholar] [CrossRef]
- Westbrook, C.K. Chemical kinetics of hydrocarbon oxidation in gaseous detonations. Combust. Flame 1982, 46, 191–210. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, X.; Ju, Y. Kinetic studies of ozone assisted low temperature oxidation of dimethyl ether in a flow reactor using molecular-beam mass spectrometry. Combust. Flame 2016, 173, 187–194. [Google Scholar] [CrossRef]
- Atkins, C.W.C.; Deiterding, R. Modelling Hypersonic Flows in Thermochemical Nonequilibrium Using Adaptive Mesh Refinement. In Proceedings of the 7th European Conference on Computational Fluid Dynamics, Glasgow, UK, 11–15 June 2018; pp. 672–683. Available online: https://eprints.soton.ac.uk/420989/ (accessed on 2 April 2022).
- Scoggins, J.B.; Leroy, V.; Bellas-Chatzigeorgis, G.; Dias, B.; Magin, T.E. Mutation++: MUlticomponent Thermodynamic And Transport properties for IONized gases in C++. SoftwareX 2020, 12, 100575. [Google Scholar] [CrossRef]
- Shi, L.; Shen, H.; Zhang, P.; Zhang, D.; Wen, C. Assessment of Vibrational Non-Equilibrium Effect on Detonation Cell Size. Combust. Sci. Technol. 2017, 189, 841–853. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.Y.; Kim, D.W.; Jeung, I.S.; Ma, F.; Yang, V. Cell-like structure of unstable oblique detonation wave from high-resolution numerical simulation. Proc. Combust. Inst. 2007, 31, 2473–2480. [Google Scholar] [CrossRef]
- Verreault, J.; Higgins, A.J.; Stowe, R.A. Formation of transverse waves in oblique detonations. Proc. Combust. Inst. 2013, 34, 1913–1920. [Google Scholar] [CrossRef]
- Browne, S.; Ziegler, J.; Bitter, N.; Schmidt, B.; Lawson, J.; Shepherd, J.E. SDToolbox: Numerical Tools for Shock and Detonation Wave Modeling. In Technical Report GALCIT Technical Report FM2018.001; Revised January 2021; Explosion Dynamics Laboratory: Livermore, CA, USA, 2018. [Google Scholar]
- Goodwin, D.G.; Speth, R.L.; Moffat, H.K.; Weber, B.W. Cantera: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes. Version 2.5.1. 2021. Available online: https://www.cantera.org (accessed on 2 April 2022). [CrossRef]
- Zhang, Z.; Wen, C.; Yuan, C.; Liu, Y.; Han, G.; Wang, C.; Jiang, Z. An experimental study of formation of stabilized oblique detonation waves in a combustor. Combust. Flame 2022, 237, 111868. [Google Scholar] [CrossRef]





| Description | Value |
|---|---|
| Freestream Mach Number () | 7, 8, 9 |
| Freestream Speed () | 2.8–3.6 km/s |
| Freestream Pressure () | 20 kPa |
| Freestream Temperature () | 300 K |
| -Air Equivalence Ratio () | 1.0 |
| Deflection Angle () | 26.0° |
| (No Additive) | 4.75 |
| CJ Speed | 1940.09 m/s (No Additive) |
| 1921.37 m/s (10,000 PPM ) | |
| 1943.28 mm (10,000 PPM ) | |
| CJ-ZND Induction Length | 1.04 mm (No Additive) |
| 0.32 mm (10,000 PPM ) | |
| 0.29 mm (10,000 PPM ) |
| Mach Number | Theoretical ODW Angle | Numerical ODW Angle |
|---|---|---|
| Mach = 7 | 47.7° | 47.1° |
| Mach = 8 | 42.5° | 44.9° |
| Mach = 9 | 39.2° | 38.9° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vashishtha, A.; Panigrahy, S.; Campi, D.; Callaghan, D.; Nolan, C.; Deiterding, R. Oblique Detonation Wave Control with O3 and H2O2 Sensitization in Hypersonic Flow. Energies 2022, 15, 4140. https://doi.org/10.3390/en15114140
Vashishtha A, Panigrahy S, Campi D, Callaghan D, Nolan C, Deiterding R. Oblique Detonation Wave Control with O3 and H2O2 Sensitization in Hypersonic Flow. Energies. 2022; 15(11):4140. https://doi.org/10.3390/en15114140
Chicago/Turabian StyleVashishtha, Ashish, Snehasish Panigrahy, Dino Campi, Dean Callaghan, Cathal Nolan, and Ralf Deiterding. 2022. "Oblique Detonation Wave Control with O3 and H2O2 Sensitization in Hypersonic Flow" Energies 15, no. 11: 4140. https://doi.org/10.3390/en15114140
APA StyleVashishtha, A., Panigrahy, S., Campi, D., Callaghan, D., Nolan, C., & Deiterding, R. (2022). Oblique Detonation Wave Control with O3 and H2O2 Sensitization in Hypersonic Flow. Energies, 15(11), 4140. https://doi.org/10.3390/en15114140







