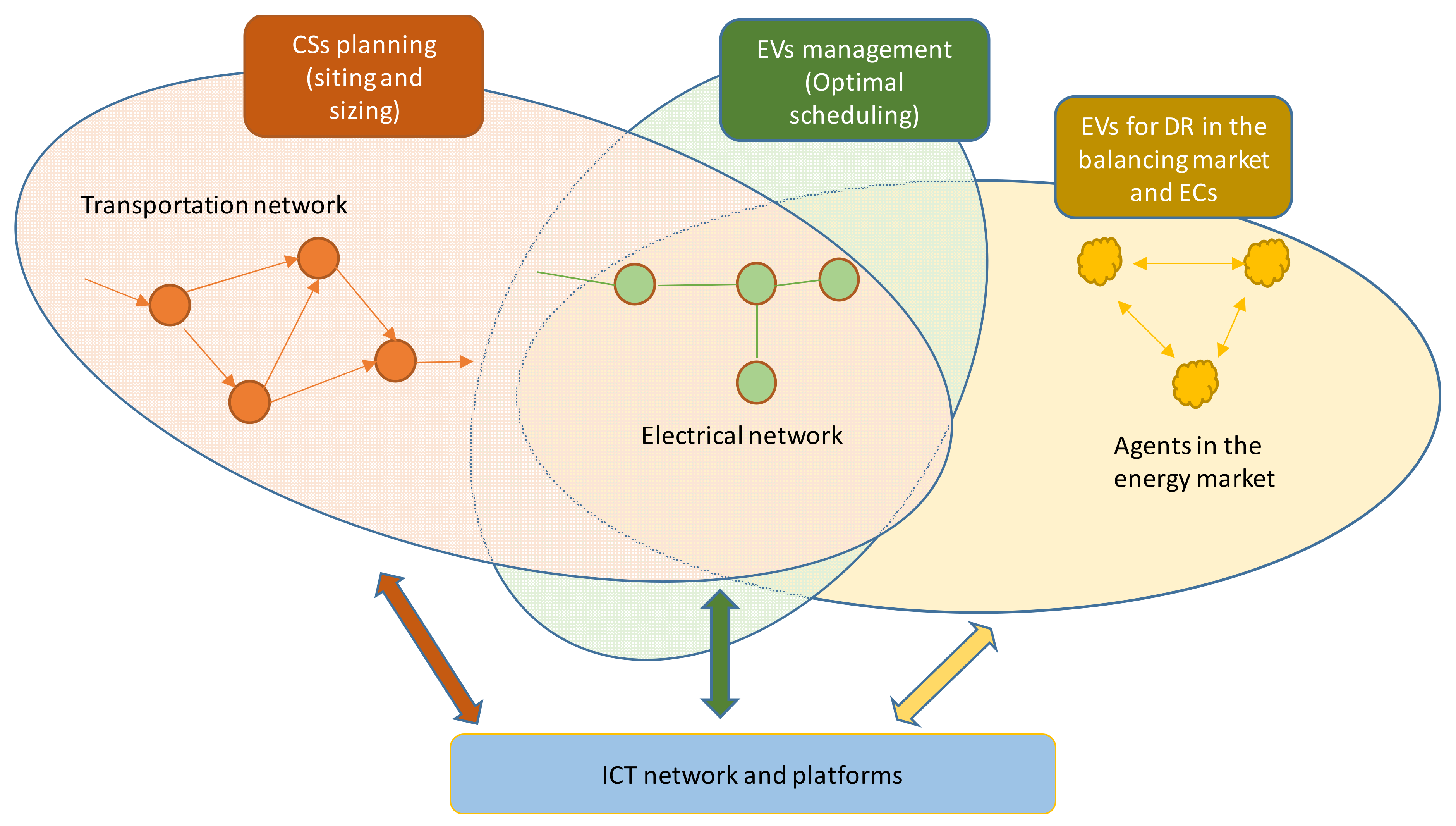
Towards the Integration of Sustainable Transportation and Smart Grids: A Review on Electric Vehicles’ Management
Abstract
:1. Introduction
- -
- Siting and sizing of CSs (i.e., planning), taking into account traffic, electrical grid, available software tools, and transportation networks;
- -
- Optimal management of EVs’ schedule in smart grids, polygeneration microgrids, buildings, etc.;
- -
- Routing and charging of vehicles that transport goods and people;
- -
- Integration of EVs in the energy market for demand response purposes.
2. EVs’ Optimal Scheduling in a Smart Grid
- -
- First of all, local private areas (microgrids, buildings, sustainable districts that own EVs) are considered, in which EVs are part of overall energy management. Within this framework, particular attention was devoted to the advantages and disadvantages of V2G services;
- -
- Then, attention was focused on public areas (i.e., charging parks) and public transportation (electrical buses, car-sharing);
- -
- Finally, it was discussed how optimization models can be used in practice using ICT platforms.
3. Charging Station Planning
- -
- Attention is firstly dedicated to existing review papers related to the optimal planning of charging stations, highlighting the main challenges;
- -
- Then, optimization problems that include coupled transportation and power networks are described;
- -
- Finally, the role of GIS (Geographic Information System) tools is highlighted.
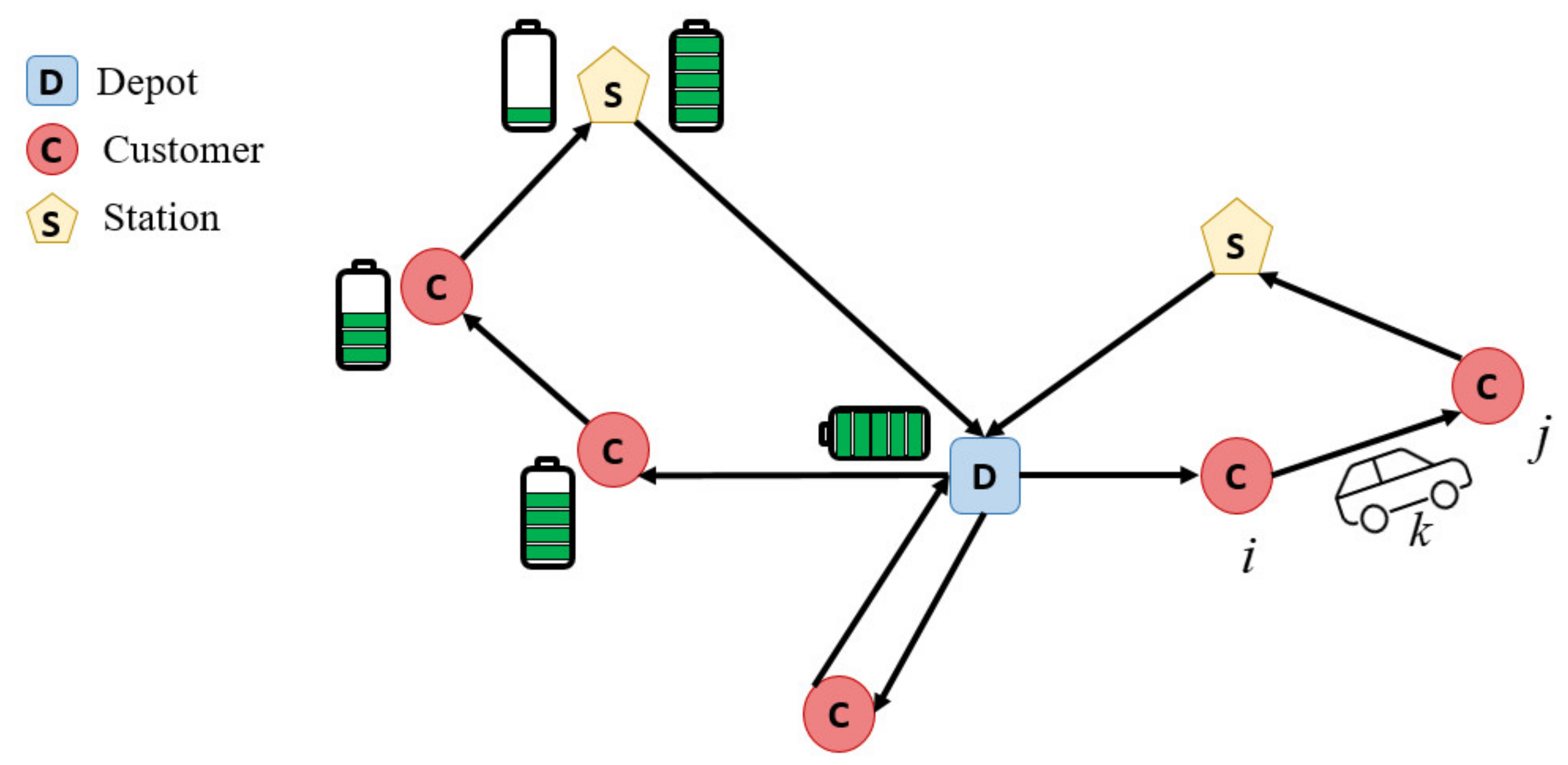
4. Routing and Charging
5. EVs in the Energy Market: Demand Response and Multi Decision-Maker Optimization
5.1. Electric Vehicles in Energy Communities
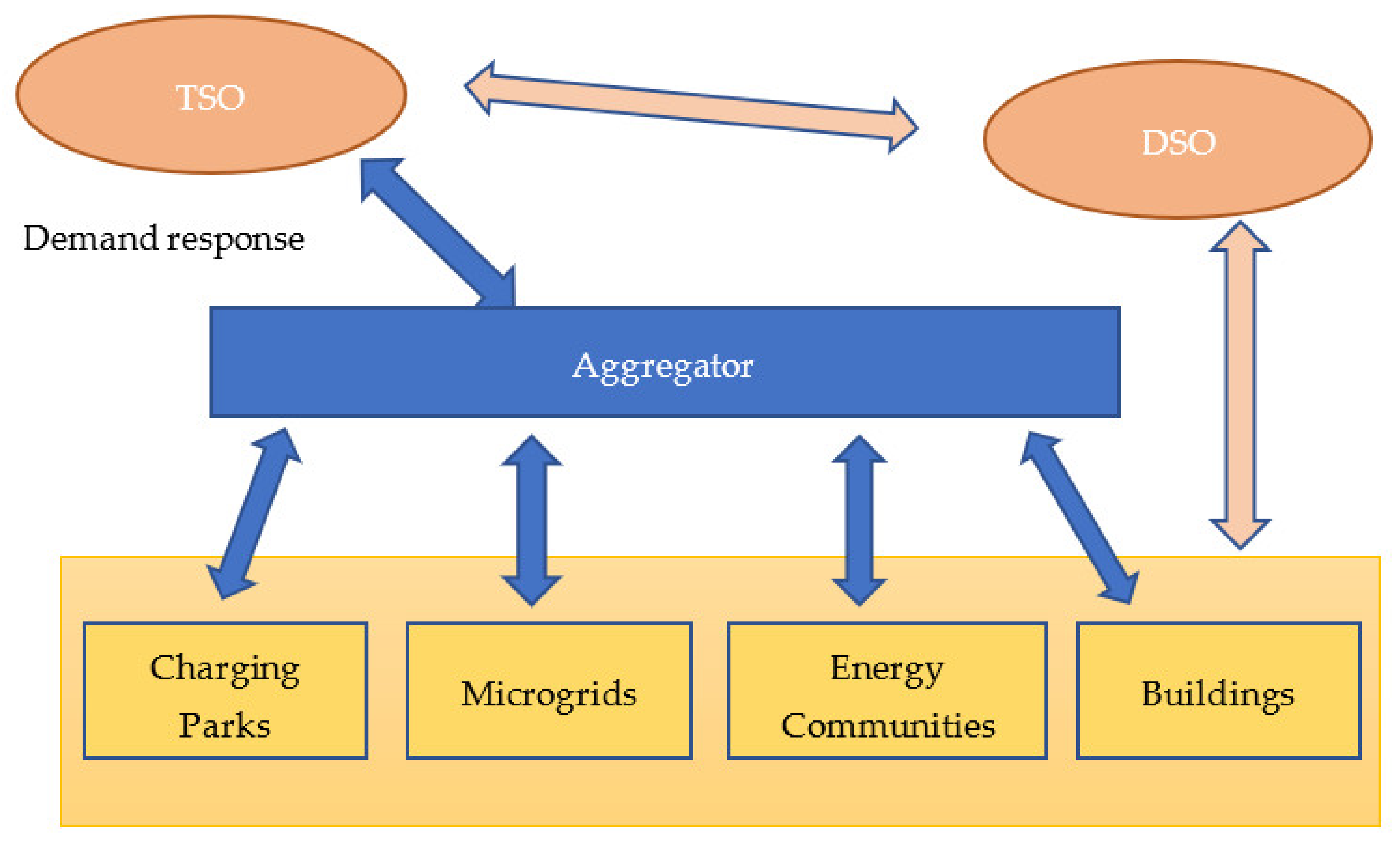
5.2. Electric Vehicles in Balancing Market through an Aggregator
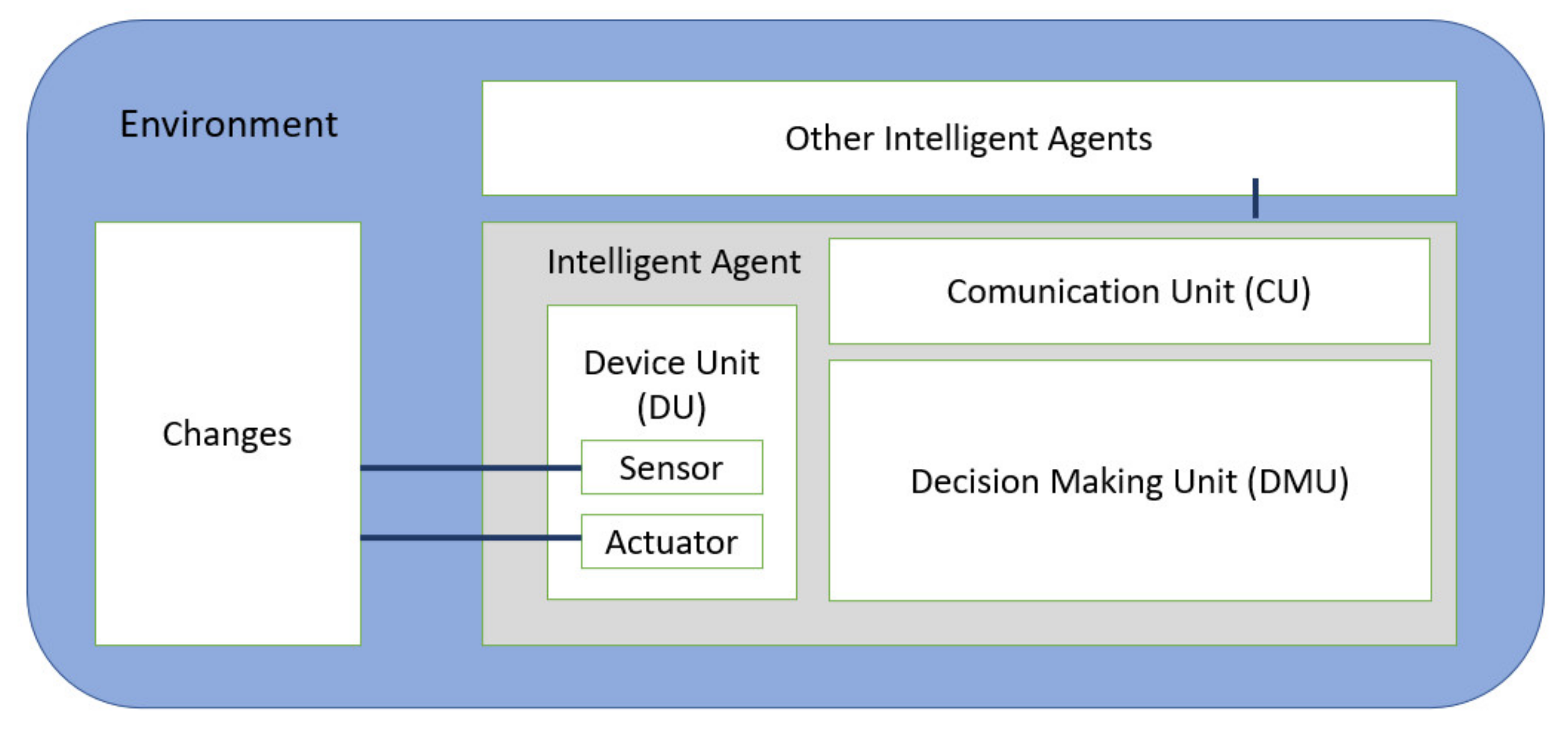
5.3. The Role of Distributed ICT Architectures and Multi-Agent Systems
6. Conclusions and Future Challenges
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Acronym | Description |
| ACO | Ant Colony Optimization |
| ADMM | Alternating Direction Method of Multipliers |
| ALNS | Adaptive Large Neighborhood Search |
| BEMS | Building Energy Management System |
| BIES | Building Integrated Energy System |
| CHP | Combined Heat and Power |
| CS | Charging Station |
| DADRP | Day-Ahead Demand Response Program |
| DER | Distributed Energy Resources |
| DG | Distributed Generation |
| DR | Demand Response |
| EB | Electric Bus |
| EC | Energy Communitiy |
| ECR | Energy Consumption Rate |
| EMS | Energy Management System |
| ESS | Energy Storage Systems |
| EV | Electric Vehicle |
| EVA | Evs Aggregator |
| EVRP | Electric Vehicle Routing Problem |
| GA | Genetic Algorithms |
| GHG | Greenhouse Gas |
| GIS | Geographic Information System |
| HVAC | Heating, Ventilation, Air Conditioning |
| ICT | Information Communication Technology |
| IoT | Internet of Things |
| LEM | Local Electricity Markets |
| MAS | Multiagent System |
| MCDA | Multi-Criteria Decision Analysis |
| MCLP | Maximum Coverage Location Problem |
| MILP | Mixed-Integer Linear Programming |
| MIP | Mixed-Integer Programming |
| P2P | Peer-to-Peer |
| PAC | Proximal Atomic Coordination |
| PDN | Power Distribution Network |
| PV | Photovoltaic |
| RES | Renewable Energy Sources |
| SDISCO | Smart Distribution Company |
| SOC | State of Charge |
| SRC | Special Case Resource |
| SUE | Stochastic User Equilibrium |
| TN | Transportation Network |
| TSO | Transmission System Operator |
| TW | Time Window |
| UE | User Equilibrium |
| V2B | Vehicle-to-Building |
| V2G | Vehicle-to-Grid |
| V2H | Vehicle-to-Home |
| V2X | Vehicle-to-Anything |
| VNS | Variable Neighborhood Search |
| VRP | Vehicle Routing Problem |
References
- European Environment Agency. Greenhouse Gas Emissions from Transport in Europe. 2021. Available online: https://www.eea.europa.eu/ims/greenhouse-gas-emissions-from-transport (accessed on 1 April 2022).
- Venegas, F.G.; Petit, M.; Perez, Y. Impact of Non-Systematic Electric Vehicle Charging Behaviour on a Distribution Substation. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Bucharest, Romania, 29 September–2 October 2019; pp. 1–5. [Google Scholar] [CrossRef] [Green Version]
- Mor, A.; Speranza, M.G. Vehicle routing problems over time: A survey. 4OR 2020, 18, 129–149. [Google Scholar] [CrossRef]
- Lin, J.; Zhou, W.; Wolfson, O. Electric vehicle routing problem. Transp. Res. Procedia 2016, 12, 508–521. [Google Scholar] [CrossRef] [Green Version]
- Fontenot, H.; Dong, B. Modeling and control of building-integrated microgrids for optimal energy management—A review. Appl. Energy 2019, 254, 113689. [Google Scholar] [CrossRef]
- Solanke, T.U.; Ramachandaramurthy, V.K.; Yong, J.Y.; Pasupuleti, J.; Kasinathan, P.; Rajagopalan, A. A review of strategic charging–discharging control of grid-connected electric vehicles. J. Energy Storage 2020, 28, 101193. [Google Scholar] [CrossRef]
- Machlev, R.; Zargari, N.; Chowdhury, N.R.; Belikov, J.; Levron, Y. A review of optimal control methods for energy storage systems—Energy trading, energy balancing and electric vehicles. J. Energy Storage 2020, 32, 101787. [Google Scholar] [CrossRef]
- Solanke, T.U.; Khatua, P.K.; Ramachandaramurthy, V.K.; Yong, J.Y.; Tan, K.M. Control and management of a multilevel electric vehicles infrastructure integrated with distributed resources: A comprehensive review. Renew. Sustain. Energy Rev. 2021, 144, 111020. [Google Scholar] [CrossRef]
- Nimalsiri, N.I.; Mediwaththe, C.P.; Ratnam, E.L.; Shaw, M.; Smith, D.B.; Halgamuge, S.K. A Survey of Algorithms for Distributed Charging Control of Electric Vehicles in Smart Grid. IEEE Trans. Intell. Transp. Syst. 2020, 21, 4497–4515. [Google Scholar] [CrossRef] [Green Version]
- Lü, X.; Wu, Y.; Lian, J.; Zhang, Y.; Chen, C.; Wang, P.; Meng, L. Energy management of hybrid electric vehicles: A review of energy optimization of fuel cell hybrid power system based on genetic algorithm. Energy Convers. Manag. 2020, 205, 112474. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y. A comprehensive review on electric vehicles integrated in virtual power plants. Sustain. Energy Technol. Assess. 2021, 48, 101678. [Google Scholar] [CrossRef]
- Hussain, M.T.; Sulaiman, D.N.B.; Hussain, M.S.; Jabir, M. Optimal Management strategies to solve issues of grid having Electric Vehicles (EV): A review. J. Energy Storage 2021, 33, 102114. [Google Scholar] [CrossRef]
- Tan, K.M.; Ramachandaramurthy, V.K.; Yong, J.Y. Integration of electric vehicles in smart grid: A review on vehicle to grid technologies and optimization techniques. Renew. Sustain. Energy Rev. 2016, 53, 720–732. [Google Scholar] [CrossRef]
- Hu, J.; Morais, H.; Sousa, T.; Lind, M. Electric vehicle fleet management in smart grids: A review of services, optimization and control aspects. Renew. Sustain. Energy Rev. 2016, 56, 1207–1226. [Google Scholar] [CrossRef] [Green Version]
- Ferro, G.; Laureri, F.; Minciardi, R.; Robba, M. An optimization model for electrical vehicles scheduling in a smart grid. Sustain. Energy Grids Netw. 2018, 14, 62–70. [Google Scholar] [CrossRef]
- Tao, Y.; Huang, M.; Chen, Y.; Yang, L. Orderly charging strategy of battery electric vehicle driven by real-world driving data. Energy 2020, 193, 116806. [Google Scholar] [CrossRef]
- Ding, Z.; Lu, Y.; Lai, K.; Yang, M.; Lee, W.J. Optimal coordinated operation scheduling for electric vehicle aggregator and charging stations in an integrated electricity-transportation system. Int. J. Electr. Power Energy Syst. 2020, 121, 106040. [Google Scholar] [CrossRef]
- Ferro, G.; Laureri, F.; Minciardi, R.; Robba, M. A predictive discrete event approach for the optimal charging of electric vehicles in microgrids. Control Eng. Pract. 2019, 86, 11–23. [Google Scholar] [CrossRef]
- Ferro, G.; Minciardi, R.; Parodi, L.; Robba, M. Discrete event optimization of a vehicle charging station with multiple sockets. Discrete Event Dyn. Syst. Theory Appl. 2020, 31, 219–249. [Google Scholar] [CrossRef]
- Heinisch, V.; Göransson, L.; Erlandsson, R.; Hodel, H.; Johnsson, F.; Odenberger, M. Smart electric vehicle charging strategies for sectoral coupling in a city energy system. Appl. Energy 2021, 288, 116640. [Google Scholar] [CrossRef]
- Fachrizal, R.; Shepero, M.; van der Meer, D.; Munkhammar, J.; Widén, J. Smart charging of electric vehicles considering photovoltaic power production and electricity consumption: A review. eTransportation 2020, 4, 100056. [Google Scholar] [CrossRef]
- Hoarau, Q.; Perez, Y. Interactions between electric mobility and photovoltaic generation: A review. Renew. Sustain. Energy Rev. 2018, 94, 510–522. [Google Scholar] [CrossRef] [Green Version]
- Fachrizal, R.; Munkhammar, J. Improved photovoltaic self-consumption in residential buildings with distributed and centralized smart charging of electric vehicles. Energies 2020, 13, 1153. [Google Scholar] [CrossRef] [Green Version]
- Pearre, N.S.; Ribberink, H. Review of research on V2X technologies, strategies, and operations. Renew. Sustain. Energy Rev. 2019, 105, 61–70. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.; Liu, J. Vehicle to Grid Frequency Regulation Capacity Optimal Scheduling for Battery Swapping Station Using Deep Q-Network. IEEE Trans. Ind. Inform. 2021, 17, 1342–1351. [Google Scholar] [CrossRef]
- Amamra, S.A.; Marco, J. Vehicle-to-Grid Aggregator to Support Power Grid and Reduce Electric Vehicle Charging Cost. IEEE Access 2019, 7, 178528–178538. [Google Scholar] [CrossRef]
- Rahman, M.S.; Hossain, M.J.; Lu, J.; Rafi, F.H.M.; Mishra, S. A Vehicle-to-Microgrid Framework with Optimization-Incorporated Distributed EV Coordination for a Commercial Neighborhood. IEEE Trans. Ind. Inform. 2020, 16, 1788–1798. [Google Scholar] [CrossRef]
- Ur Rehman, U.; Yaqoob, K.; Khan, M.A. Optimal power management framework for smart homes using electric vehicles and energy storage. Int. J. Electr. Power Energy Syst. 2022, 134, 107358. [Google Scholar] [CrossRef]
- Aguilar-Dominguez, D.; Dunbar, A.; Brown, S. The electricity demand of an EV providing power via vehicle-to-home and its potential impact on the grid with different electricity price tariffs. Energy Rep. 2020, 6, 132–141. [Google Scholar] [CrossRef]
- Al-Ogaili, A.S.; Hashim, T.J.T.; Rahmat, N.A.; Ramasamy, A.K.; Marsadek, M.B.; Faisal, M.; Hannan, M.A. Review on scheduling, clustering, and forecasting strategies for controlling electric vehicle charging: Challenges and recommendations. IEEE Access 2019, 7, 128353–128371. [Google Scholar] [CrossRef]
- Alsabbagh, A.; Member, S.; Ma, C.; Member, S. Distributed Charging Management of Electric Vehicles Considering Different Customer Behaviors. IEEE Trans. Ind. Inform. 2020, 16, 5119–5127. [Google Scholar] [CrossRef]
- Luo, Y.; Feng, G.; Wan, S.; Zhang, S.; Li, V.; Kong, W. Charging scheduling strategy for different electric vehicles with optimization for convenience of drivers, performance of transport system and distribution network. Energy 2020, 194, 116807. [Google Scholar] [CrossRef]
- Chung, H.M.; Li, W.T.; Yuen, C.; Wen, C.K.; Crespi, N. Electric Vehicle Charge Scheduling Mechanism to Maximize Cost Efficiency and User Convenience. IEEE Trans. Smart Grid 2019, 10, 3020–3030. [Google Scholar] [CrossRef] [Green Version]
- Rezaeimozafar, M.; Eskandari, M.; Savkin, A.V. A Self-Optimizing Scheduling Model for Large-Scale EV Fleets in Microgrids. IEEE Trans. Ind. Inform. 2021, 17, 8177–8188. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; León-Japa, R.S.; Jurado, F. Optimal electrification of off-grid smart homes considering flexible demand and vehicle-to-home capabilities. Appl. Energy 2021, 298, 117184. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmed, M.A.; Kim, Y.C. Efficient Power Management Algorithm Based on Fuzzy Logic Inference for Electric Vehicles Parking Lot. IEEE Access 2019, 7, 65467–65485. [Google Scholar] [CrossRef]
- Ioakimidis, C.S.; Thomas, D.; Rycerski, P.; Genikomsakis, K.N. Peak shaving and valley filling of power consumption profile in non-residential buildings using an electric vehicle parking lot. Energy 2018, 148, 148–158. [Google Scholar] [CrossRef]
- Jiang, W.; Zhen, Y. A Real-Time EV Charging Scheduling for Parking Lots with PV System and Energy Store System. IEEE Access 2019, 7, 86184–86193. [Google Scholar] [CrossRef]
- Sadati, S.M.B.; Moshtagh, J.; Shafie-khah, M.; Rastgou, A.; Catalão, J.P.S. Operational scheduling of a smart distribution system considering electric vehicles parking lot: A bi-level approach. Int. J. Electr. Power Energy Syst. 2019, 105, 159–178. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, Z.; Xu, Z.; Song, Y. Evaluation of Achievable Vehicle-to-Grid Capacity Using Aggregate PEV Model. IEEE Trans. Power Syst. 2017, 32, 784–794. [Google Scholar] [CrossRef]
- Deng, R.; Liu, Y.; Chen, W.; Liang, H. A Survey on Electric Buses—Energy Storage, Power Management, and Charging Scheduling. IEEE Trans. Intell. Transp. Syst. 2021, 22, 9–22. [Google Scholar] [CrossRef]
- Xie, S.; Qi, S.; Lang, K.; Tang, X.; Lin, X. Coordinated management of connected plug-in hybrid electric buses for energy saving, inter-vehicle safety, and battery health. Appl. Energy 2020, 268, 115028. [Google Scholar] [CrossRef]
- Brendel, A.B.; Lichtenberg, S.; Brauer, B.; Nastjuk, I.; Kolbe, L.M. Improving electric vehicle utilization in car-sharing: A framework and simulation of an e-carsharing vehicle utilization management system. Transp. Res. Part D Transp. Environ. 2018, 64, 230–245. [Google Scholar] [CrossRef]
- Hua, Y.; Zhao, D.; Wang, X.; Li, X. Joint infrastructure planning and fleet management for one-way electric car sharing under time-varying uncertain demand. Transp. Res. Part B Methodol. 2019, 128, 185–206. [Google Scholar] [CrossRef]
- Van der Meer, D.; Mouli, G.R.C.; Mouli, G.M.E.; Elizondo, L.R.; Bauer, P. Energy Management System with PV Power Forecast to Optimally Charge EVs at the Workplace. IEEE Trans. Ind. Inform. 2018, 14, 311–320. [Google Scholar] [CrossRef] [Green Version]
- Thomas, D.; Deblecker, O.; Ioakimidis, C.S. Optimal operation of an energy management system for a grid-connected smart building considering photovoltaics’ uncertainty and stochastic electric vehicles’ driving schedule. Appl. Energy 2018, 210, 1188–1206. [Google Scholar] [CrossRef]
- Kimura, S.; Susuki, Y.; Ishigame, A. A reactive management system for reliable power supply in a building microgrid with vehicle-to-grid interaction. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2018, E101A, 1172–1184. [Google Scholar] [CrossRef]
- Negarestani, S.; Fotuhi-Firuzabad, M.; Rastegar, M.; Rajabi-Ghahnavieh, A. Optimal Sizing of Storage System in a Fast Charging Station for Plug-in Hybrid Electric Vehicles. IEEE Trans. Transp. Electrif. 2016, 2, 443–453. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Abunasri, A.; Zare, A.; Hoseinzadeh, R. Impact of plug-in hybrid electric vehicles charging demand on the optimal energy management of renewable micro-grids. Energy 2014, 78, 904–915. [Google Scholar] [CrossRef]
- Kizhakkan, A.R.; Rathore, A.K.; Awasthi, A. Review of Electric Vehicle Charging Station Location Planning. In Proceedings of the 2019 IEEE Transportation Electrification Conference (ITEC-India), Bengaluru, India, 17–19 December 2019; pp. 6–10. [Google Scholar] [CrossRef]
- Bilal, M.; Rizwan, M.; Rizwan, M. Electric vehicles in a smart grid: A comprehensive survey on optimal location of charging station. IET Smart Grid 2020, 3, 267–279. [Google Scholar] [CrossRef]
- Battapothula, G.; Yammani, C.; Maheswarapu, S. Multi-objective optimal planning of fast charging stations by considering various load models in distribution system. Int. J. Emerg. Electr. Power Syst. 2021, 22, 439–450. [Google Scholar] [CrossRef]
- Erdinc, O.; Tascikaraoglu, A.; Paterakis, N.G.; Dursun, I.; Sinim, M.C.; Catalao, J.P.S. Comprehensive Optimization Model for Sizing and Siting of DG Units, EV Charging Stations, and Energy Storage Systems. IEEE Trans. Smart Grid 2018, 9, 3871–3882. [Google Scholar] [CrossRef]
- Sheffi, Y. Urban Transportation Networks; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985; Volume 6. [Google Scholar]
- Ferro, G.; Minciardi, R.; Robba, M. A user equilibrium model for electric vehicles: Joint traffic and energy demand assignment. Energy 2020, 198, 117299. [Google Scholar] [CrossRef]
- Ferro Giulio Minciardi, R.; Parodi, L.; Robba, M. Optimal Planning of Charging Stations in Coupled Transportation and Power Networks Based on User Equilibrium Conditions. IEEE Trans. Autom. Sci. Eng. 2021, 19, 48–59. [Google Scholar] [CrossRef]
- Zhou, Z.; Sun, H.; Guo, Q. Stochastic User Equilibrium in Charging Station Selection Based on Discrete Choice Model. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018. [Google Scholar] [CrossRef]
- Heting, Q.; Shuihai, D.; Huayan, S.; Jun, Z. Charging station planning based on the accumulation prospect theory and dynamic user equilibrium. Complex Intell. Syst. 2021. [Google Scholar] [CrossRef]
- Qian, Z.; Yi, Z.; Zhong, W.; Yue, H.; Yaojia, S. Siting and sizing of electric vehicle fast-charging station based on quasi-dynamic traffic flow. IET Renew. Power Gener. 2021, 14, 4204–4214. [Google Scholar] [CrossRef]
- Wang, X.; Shahidehpour, M.; Jiang, C.; Li, Z. Coordinated Planning Strategy for Electric Vehicle Charging Stations and Coupled Traffic-Electric Networks. IEEE Trans. Power Syst. 2019, 34, 268–279. [Google Scholar] [CrossRef]
- Deb, S.; Tammi, K.; Gao, X.Z.; Kalita, K.; Mahanta, P.; Cross, S. A Robust Two-Stage Planning Model for the Charging Station Placement Problem Considering Road Traffic Uncertainty. IEEE Trans. Intell. Transp. Syst. 2021, 1–15. [Google Scholar] [CrossRef]
- Sisman, S.; Ergul, I.; Aydinoglu, A.C. Designing GIS-based site selection model for urban investment planning in smart cities with the case of electric vehicle charging stations. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2021, 46, 515–522. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, Y.; Wu, C.; He, F.; Zhang, B.; Liu, F. A geographical information system based multi-criteria decision-making approach for location analysis and evaluation of urban photovoltaic charging station: A case study in Beijing. Energy Convers. Manag. 2020, 205, 112340. [Google Scholar] [CrossRef]
- Zafar, U.; Bayram, I.S.; Bayhan, S. A GIS-based Optimal Facility Location Framework for Fast Electric Vehicle Charging Stations. In Proceedings of the 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 20–23 June 2021. [Google Scholar] [CrossRef]
- Lin, H.; Bian, C.; Wang, Y.; Li, H.; Sun, Q.; Wallin, F. Optimal planning of intra-city public charging stations. Energy 2022, 238, 121948. [Google Scholar] [CrossRef]
- Kalakanti, A.K.; Rao, S. Charging Station Planning for Electric Vehicles. Systems 2022, 10, 6. [Google Scholar] [CrossRef]
- Straka, M.; Buzna, L. Preprocessing of GIS data for electric vehicle charging stations analysis and evaluation of the predictors significance. Transp. Res. Procedia 2019, 40, 1583–1590. [Google Scholar] [CrossRef]
- Erdoğan, S.; Miller-Hooks, E. A green vehicle routing problem. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 100–114. [Google Scholar] [CrossRef]
- Conrad, R.G.; Figliozzi, M.A. The recharging vehicle routing problem. In Proceedings of the 2011 Industrial Engineering Research Conference, Reno, NV, USA, 21–25 May 2011; IISE: Norcross, GA, USA, 2011; p. 8. [Google Scholar]
- Schneider, M.; Stenger, A.; Goeke, D. The electric vehicle-routing problem with time windows and recharging stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef] [Green Version]
- Pelletier, S.; Jabali, O.; Laporte, G. Charge scheduling for electric freight vehicles. Transp. Res. Part B Methodol. 2018, 115, 246–269. [Google Scholar] [CrossRef]
- Jie, W.; Yang, J.; Zhang, M.; Huang, Y. The two-echelon capacitated electric vehicle routing problem with battery swapping stations: Formulation and efficient methodology. Eur. J. Oper. Res. 2019, 272, 879–904. [Google Scholar] [CrossRef]
- Felipe, Á.; Ortuño, M.T.; Righini, G.; Tirado, G. A heuristic approach for the green vehicle routing problem with multiple technologies and partial recharges. Transp. Res. Part E Logist. Transp. Rev. 2014, 71, 111–128. [Google Scholar] [CrossRef]
- Bruglieri, M.; Pezzella, F.; Pisacane, O.; Suraci, S. A variable neighborhood search branching for the electric vehicle routing problem with time windows. Electron. Notes Discrete Math. 2015, 47, 221–228. [Google Scholar] [CrossRef]
- Bruglieri, M.; Mancini, S.; Pezzella, F.; Pisacane, O.; Suraci, S. A three-phase matheuristic for the time-effective electric vehicle routing problem with partial recharges. Electron. Notes Discrete Math. 2017, 58, 95–102. [Google Scholar] [CrossRef]
- Desaulniers, G.; Errico, F.; Irnich, S.; Schneider, M. Exact algorithms for electric vehicle-routing problems with time windows. Oper. Res. 2016, 64, 1388–1405. [Google Scholar] [CrossRef] [Green Version]
- Keskin, M.; Çatay, B. Partial recharge strategies for the electric vehicle routing problem with time windows. Transp. Res. Part C Emerg. Technol. 2016, 65, 111–127. [Google Scholar] [CrossRef]
- Goeke, D. Granular tabu search for the pickup and delivery problem with time windows and electric vehicles. Eur. J. Oper. Res. 2019, 278, 821–836. [Google Scholar] [CrossRef]
- Hiermann, G.; Puchinger, J.; Ropke, S.; Hartl, R.F. The electric fleet size and mix vehicle routing problem with time windows and recharging stations. Eur. J. Oper. Res. 2016, 252, 995–1018. [Google Scholar] [CrossRef] [Green Version]
- Macrina, G.; Pugliese, L.D.P.; Guerriero, F.; Laporte, G. The green mixed fleet vehicle routing problem with partial battery recharging and time windows. Comput. Oper. Res. 2019, 101, 183–199. [Google Scholar] [CrossRef]
- Montoya, A.; Guéret, C.; Mendoza, J.E.; Villegas, J.G. The electric vehicle routing problem with nonlinear charging function. Transp. Res. Part B Methodol. 2017, 103, 87–110. [Google Scholar] [CrossRef] [Green Version]
- Froger, A.; Mendoza, J.E.; Jabali, O.; Laporte, G. Improved formulations and algorithmic components for the electric vehicle routing problem with nonlinear charging functions. Comput. Oper. Res. 2019, 104, 256–294. [Google Scholar] [CrossRef] [Green Version]
- Koç, Ç.; Jabali, O.; Mendoza, J.E.; Laporte, G. The electric vehicle routing problem with shared charging stations. Int. Trans. Oper. Res. 2019, 26, 1211–1243. [Google Scholar] [CrossRef]
- Zuo, X.; Xiao, Y.; You, M.; Kaku, I.; Xu, Y. A new formulation of the electric vehicle routing problem with time windows considering concave nonlinear charging function. J. Clean. Prod. 2019, 236, 117687. [Google Scholar] [CrossRef]
- Lee, C. An exact algorithm for the electric-vehicle routing problem with nonlinear charging time. J. Oper. Res. Soc. 2021, 72, 1461–1485. [Google Scholar] [CrossRef]
- Karakatič, S. Optimizing nonlinear charging times of electric vehicle routing with genetic algorithm. Expert Syst. Appl. 2021, 164, 114039. [Google Scholar] [CrossRef]
- Zhang, S.; Gajpal, Y.; Appadoo, S.; Abdulkader, M. Electric vehicle routing problem with recharging stations for minimizing energy consumption. Int. J. Prod. Econ. 2018, 203, 404–413. [Google Scholar] [CrossRef]
- Joo, H.; Lim, Y. Ant colony optimized routing strategy for electric vehicles. J. Adv. Transp. 2018, 2018, 5741982. [Google Scholar] [CrossRef]
- Pelletier, S.; Jabali, O.; Laporte, G. The electric vehicle routing problem with energy consumption uncertainty. Transp. Res. Part B Methodol. 2019, 126, 225–255. [Google Scholar] [CrossRef]
- Ferro, G.; Paolucci, M.; Robba, M. Optimal charging and routing of electric vehicles with power constraints and time-of-use energy prices. IEEE Trans. Veh. Technol. 2020, 69, 14436–14447. [Google Scholar] [CrossRef]
- Moret, F.; Pinson, P. Energy Collectives: A Community and Fairness Based Approach to Future Electricity Markets. IEEE Trans. Power Syst. 2019, 34, 3994–4004. [Google Scholar] [CrossRef] [Green Version]
- Caramizaru, E.; Uihlein, A. Energy Communities: An Overview of Energy and Social Innovation; Publications Office of the European Union: Luxembourg, 2020. [Google Scholar]
- Nudell, T.R.; Brignone, M.; Robba, M.; Bonfiglio, A.; Ferro, G.; Delfino, F.; Annaswamy, A.M. Distributed control for polygeneration microgrids: A Dynamic Market Mechanism approach. Control Eng. Pract. 2022, 121, 105052. [Google Scholar] [CrossRef]
- Sousa, T.; Soares, T.; Pinson, P.; Moret, F.; Baroche, T.; Sorin, E. Peer-to-peer and community-based markets: A comprehensive review. Renew. Sustain. Energy Rev. 2019, 104, 367–378. [Google Scholar] [CrossRef] [Green Version]
- Paiho, S.; Kiljander, J.; Sarala, R.; Siikavirta, H.; Kilkki, O.; Bajpai, A.; Duchon, M.; Pahl, M.-O.; Wüstrich, L.; Lübben, C.; et al. Towards cross-commodity energy-sharing communities—A review of the market, regulatory, and technical situation. Renew. Sustain. Energy Rev. 2021, 151, 111568. [Google Scholar] [CrossRef]
- Ceglia, F.; Esposito, P.; Marrasso, E.; Sasso, M. From smart energy community to smart energy municipalities: Literature review, agendas and pathways. J. Clean. Prod. 2020, 254, 120118. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Squartini, S.; Zaman, F.; Muttaqi, K.M. Energy management of community microgrids considering degradation cost of battery. J. Energy Storage 2019, 22, 257–269. [Google Scholar] [CrossRef]
- Lyu, C.; Jia, Y.; Xu, Z. Fully decentralized peer-to-peer energy sharing framework for smart buildings with local battery system and aggregated electric vehicles. Appl. Energy 2021, 299, 117243. [Google Scholar] [CrossRef]
- Hashemipour, N.; del Granado, P.C.; Aghaei, J. Dynamic allocation of peer-to-peer clusters in virtual local electricity markets: A marketplace for EV flexibility. Energy 2021, 236, 121428. [Google Scholar] [CrossRef]
- Hutty, T.D.; Pena-Bello, A.; Dong, S.; Parra, D.; Rothman, R.; Brown, S. Peer-to-peer electricity trading as an enabler of increased PV and EV ownership. Energy Convers. Manag. 2021, 245, 114634. [Google Scholar] [CrossRef]
- O’Donovan, A.N.A.; McKerracher, C.; Soulopoulos, N. EVO Report 2021|BloombergNEF|Bloomberg Finance LP. July 2021. Available online: https://about.bnef.com/electric-vehicle-outlook/ (accessed on 1 April 2022).
- Cappers, P.; Goldman, C.; Kathan, D. Demand response in U.S. electricity markets: Empirical evidence. Energy 2010, 35, 1526–1535. [Google Scholar] [CrossRef] [Green Version]
- Albadi, M.H.; El-Saadany, E.F. Demand Response in Electricity Markets: An Overview. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007. [Google Scholar]
- Saber, A.Y.; Venayagamoorthy, G.K. Optimization of vehicle-to-grid scheduling in constrained parking lots. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Ovalle, P.N.; Vuelvas, J.; Fajardo, A.; Correa-Flórez, C.A.; Ruiz, F. Optimal Portfolio Selection Methodology for a Demand Response Aggregator. Energies 2021, 14, 7923. [Google Scholar] [CrossRef]
- Hou, H.; Wang, Y.; Xie, C.; Xiong, B.; Zhang, Q.; Huang, L. A dispatching strategy for electric vehicle aggregator combined price and incentive demand response. IET Energy Syst. Integr. 2021, 3, 508–519. [Google Scholar] [CrossRef]
- Sharma, S.; Jain, P. Risk-averse integrated demand response and dynamic G2V charge scheduling of an electric vehicle aggregator to support grid stability. Int. Trans. Electr. Energy Syst. 2021, 31, e12867. [Google Scholar] [CrossRef]
- Contreras-Ocana, J.E.; Sarker, M.R.; Ortega-Vazquez, M.A. Decentralized Coordination of a Building Manager and an Electric Vehicle Aggregator. IEEE Trans. Smart Grid 2018, 9, 2625–2637. [Google Scholar] [CrossRef]
- Huang, J.; Yang, Z.; Zeng, X.; Zou, H.; Tang, Y.; Zhang, L. Demand Response of Electric Vehicles for Building Integrated Energy System. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018. [Google Scholar]
- Wu, H.; Li, H.; Zhang, J.; Wang, Z.; Zhang, J. Generating individual intrinsic reward for cooperative multi-agent reinforcement learning. Int. J. Adv. Robot. Syst. 2021, 18, 172988142110449. [Google Scholar] [CrossRef]
- Zhu, B.; Zhu, W.; Li, W. An Improved Method of Q-Learning Algorithm. J. Phys. Conf. Ser. 2021, 2035, 012014. [Google Scholar] [CrossRef]
- Ahrarinouri, M.; Rastegar, M.; Seifi, A.R. Multi-agent Reinforcement Learning for Energy Management in Residential Buildings. IEEE Trans. Ind. Inform. 2021, 17, 659–666. [Google Scholar] [CrossRef]
- Han, G.; Lee, S.; Lee, J.; Lee, K.; Bae, J. Deep-learning- and reinforcement-learning-based profitable strategy of a grid-level energy storage system for the smart grid. J. Energy Storage 2021, 41, 102868. [Google Scholar] [CrossRef]
- Shin, M.; Choi, D.-H.; Kim, J. Cooperative Management for PV/ESS-Enabled Electric Vehicle Charging Stations: A Multi-agent Deep Reinforcement Learning Approach. IEEE Trans. Ind. Inform. 2020, 16, 3493–3503. [Google Scholar] [CrossRef]
- Silva, F.L.D.; Nishida, C.E.H.; Roijers, D.M.; Costa, A.H.R. Coordination of Electric Vehicle Charging Through Multiagent Reinforcement Learning. IEEE Trans. Smart Grid 2020, 11, 2347–2356. [Google Scholar] [CrossRef]
- Shobole, A.A.; Wadi, M. Multi-agent systems application for the smart grid protection. Renew. Sustain. Energy Rev. 2021, 149, 111352. [Google Scholar] [CrossRef]
- Nizami, M.S.H.; Hossain, M.J.; Mahmud, K. A Coordinated Electric Vehicle Management System for Grid-Support Services in Residential Networks. IEEE Syst. J. 2021, 15, 2066–2077. [Google Scholar] [CrossRef]
- Molzahn, D.K.; Dorfler, F.; Sandberg, H.; Low, S.H.; Chakrabarti, S.; Baldick, R.; Lavaei, J. A Survey of Distributed Optimization and Control Algorithms for Electric Power Systems. IEEE Trans. Smart Grid 2017, 8, 2941–2962. [Google Scholar] [CrossRef]
- Boyd, S. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends® Mach. Learning 2011, 3, 1–122. [Google Scholar]
- Bertsekas, D.P.; Tsitsiklis, J.N. Parallel and Distributed Computation: Numerical Methods; Athena Scientific: Belmont, MA, USA, 2003. [Google Scholar]
- Iutzeler, F.; Bianchi, P.; Ciblat, P.; Hachem, W. Explicit Convergence Rate of a Distributed Alternating Direction Method of Multipliers. IEEE Trans. Autom. Control 2016, 61, 892–904. [Google Scholar] [CrossRef] [Green Version]
- Mokhtari, A.; Shi, W.; Ling, Q.; Ribeiro, A. DQM: Decentralized Quadratically Approximated Alternating Direction Method of Multipliers. IEEE Trans. Signal Processing 2016, 64, 5158–5173. [Google Scholar] [CrossRef]
- Shi, W.; Ling, Q.; Yuan, K.; Wu, G.; Yin, W. On the Linear Convergence of the ADMM in Decentralized Consensus Optimization. IEEE Trans. Signal Processing 2014, 62, 1750–1761. [Google Scholar] [CrossRef] [Green Version]
- Eisen, M.; Mokhtari, A.; Ribeiro, A. Decentralized Quasi-Newton Methods. IEEE Trans. Signal Processing 2017, 65, 2613–2628. [Google Scholar] [CrossRef]
- França, G.; Robinson, D.P.; Vidal, R. A nonsmooth dynamical systems perspective on accelerated extensions of ADMM. arXiv 2018, arXiv:1808.04048. [Google Scholar]
- Jakovetic, D.; Xavier, J.; Moura, J.M.F. Fast Distributed Gradient Methods. IEEE Trans. Autom. Control 2014, 59, 1131–1146. [Google Scholar] [CrossRef] [Green Version]
- Nesterov, Y.E. A method for solving the convex programming problem with convergence rate O (1/k^2). Dokl. Akad. Nauk Sssr 1983, 269, 543–547. [Google Scholar]
- Matveev, V.A. Method for the approximate solution of a system of nonlinear equations. USSR Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Ghadimi, E.; Teixeira, A.; Shames, I.; Johansson, M. Optimal Parameter Selection for the Alternating Direction Method of Multipliers (ADMM): Quadratic Problems. IEEE Trans. Autom. Control 2015, 60, 644–658. [Google Scholar] [CrossRef] [Green Version]
- Romvary, J.J.; Ferro, G.; Haider, R.; Annaswamy, A.M. A Proximal Atomic Coordination Algorithm for Distributed Optimization. IEEE Trans. Autom. Control 2022, 67, 646–661. [Google Scholar] [CrossRef]
- Ferro, G.; Robba, M.; Haider, R.; Annaswamy, A.M. A distributed optimization based architecture for management of interconnected energy hubs. IEEE Trans. Control Netw. Syst. 2022. [Google Scholar] [CrossRef]
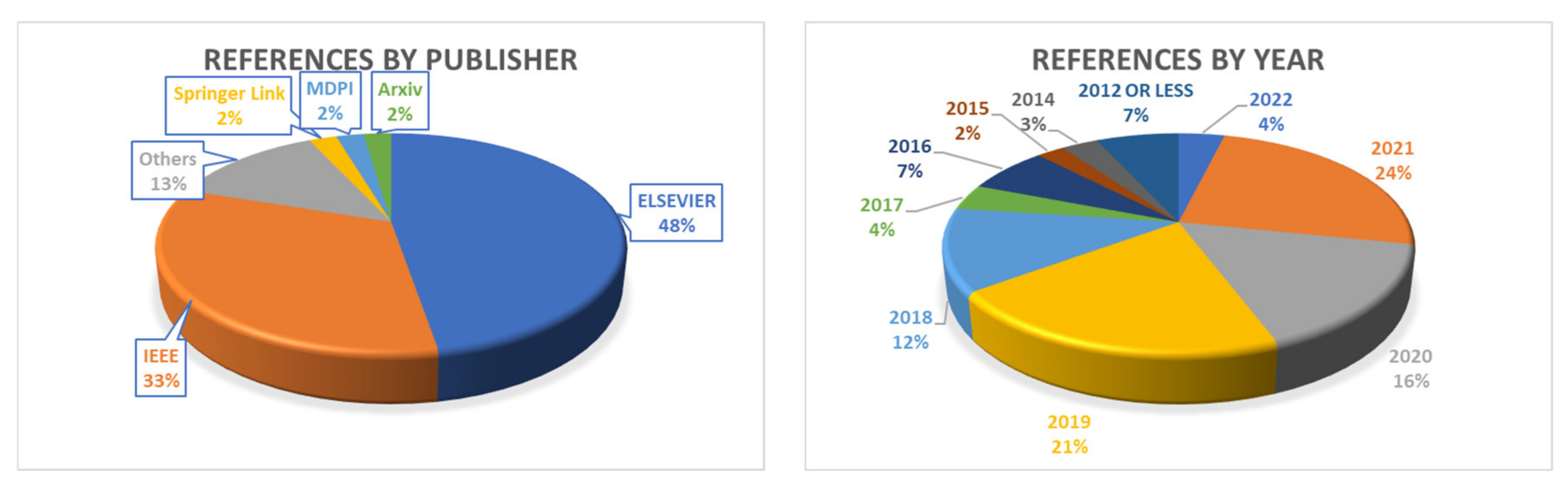
| Topics | Refs. |
|---|---|
| EVs’ optimal scheduling in a smart grid | [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46] |
| Charging stations planning | [47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63] |
| Routing and Charging | [64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86] |
| EVs in the energy market: Energy Communities | [87,88,89,90,91,92,93,94,95,96] |
| EVs in the energy market: Balancing Market | [97,98,99,100,101,102,103,104,105] |
| Distributed ICT architectures and multi-agent systems | [105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casella, V.; Fernandez Valderrama, D.; Ferro, G.; Minciardi, R.; Paolucci, M.; Parodi, L.; Robba, M. Towards the Integration of Sustainable Transportation and Smart Grids: A Review on Electric Vehicles’ Management. Energies 2022, 15, 4020. https://doi.org/10.3390/en15114020
Casella V, Fernandez Valderrama D, Ferro G, Minciardi R, Paolucci M, Parodi L, Robba M. Towards the Integration of Sustainable Transportation and Smart Grids: A Review on Electric Vehicles’ Management. Energies. 2022; 15(11):4020. https://doi.org/10.3390/en15114020
Chicago/Turabian StyleCasella, Virginia, Daniel Fernandez Valderrama, Giulio Ferro, Riccardo Minciardi, Massimo Paolucci, Luca Parodi, and Michela Robba. 2022. "Towards the Integration of Sustainable Transportation and Smart Grids: A Review on Electric Vehicles’ Management" Energies 15, no. 11: 4020. https://doi.org/10.3390/en15114020
APA StyleCasella, V., Fernandez Valderrama, D., Ferro, G., Minciardi, R., Paolucci, M., Parodi, L., & Robba, M. (2022). Towards the Integration of Sustainable Transportation and Smart Grids: A Review on Electric Vehicles’ Management. Energies, 15(11), 4020. https://doi.org/10.3390/en15114020







