Overview of Battery Impedance Modeling Including Detailed State-of-the-Art Cylindrical 18650 Lithium-Ion Battery Cell Comparisons ^†

Abstract

Electrical models of battery cells are used in simulations to represent batteries’ behavior in various fields of research and development involving battery cells and systems. Electrical equivalent circuit models, either linear or nonlinear, are commonly used for this purpose and are presented in this article. Various commercially available cylindrical, state-of-the-art lithium-ion battery cells, both protected and unprotected, are considered. Their impedance properties, according to four different equivalent circuit models, are measured using electrochemical impedance spectroscopies. Furthermore, the pricing, impedance, specific energy, and C-rate of the chosen battery cells are compared. For example, it is shown that the energy density of modern 18650 cells can vary from a typical value of 200 to about 260 Wh kg⁻¹, whereas the cell price can deviate by a factor of about 3 to 5. Therefore, as a result, this study presents a concise but comprehensive battery parameter library that should aid battery system designers or power electronic engineers in conducting battery simulations and in selecting appropriate battery cells based on application-specific requirements. In addition, the accuracies and computational efforts of the four equivalent circuit models are compared.

1. Introduction

Lithium-ion batteries have been widely employed in electronic devices such as cell phones and laptop computers since the 1990s [1]. Such batteries have significant advantages over other battery cell chemistries such as sodium, nickel, zinc, or lead-acid-based cells in terms of self-discharge, specific energy and power, calendar and cycle life, round-trip efficiency, charge and discharge times, safety, and initial costs. Potential disadvantages are the damage to cells in case of deep discharge as well as safety risks in case of overcharging [2]. Lithium-ion batteries are increasingly being used in electric bicycles, power tools, energy storage for buffering renewable energy [3], and, most notably, electric vehicles (EVs) [1]. The number of electric vehicles on the road has expanded dramatically in recent years [4,5], and vehicle battery capacities have improved enormously [6]. This pattern is expected to persist in the future [6,7]. As described in [8], battery pricing (pack) has decreased from USD 540 per kWh in 2010 to around USD 200 per kWh in 2018. Moreover, as predicted in 2018, the prices of batteries should drop to around USD 125 per kWh by 2022. This aspect is largely responsible for the rising use and application of lithium battery cells.

However, the rapid advancements in the development of lithium battery technologies make it difficult for other fields of research and development with links to battery applications to keep up. Existing literature quickly becomes outdated and, therefore, may not accurately reflect current state-of-the-art battery cells. As a result, to conduct predevelopment studies such as the estimation of ohmic battery losses for different driving cycles [9,10], the estimation of the dynamic equalization current for reconfigurable battery systems [11,12], or the development of battery diagnostics [13,14], reliable simulation models and parameters of state-of-the-art lithium-ion battery cells are required. Datasheets for commercially available battery cells rarely include all of the necessary information. Battery impedance is of special relevance since it relates to battery dynamics and describes critical properties of a battery, such as power capability and energy efficiency, as discussed in [15]. Within the literature, there are several battery equivalent circuit models (ECMs), e.g., [16,17,18,19,20]. The overall conclusion according to [21] is that a dynamic model with up to three $RC$-elements can accurately represent the dynamics of batteries. A Warburg impedance element can also increase the diffusion impedance characteristic of the battery model, which is significant when dealing with low-frequency components (≤$1\mathrm{Hz}$). Individual battery pack impedance is reported in the accessible literature [9,22,23,24]. Nevertheless, quick but thorough comparisons of several state-of-the-art battery cells in terms of price, impedance, specific energy, and C-rate are lacking in the generally available literature.

As a result, the purpose of this post conference article based on [25] is to provide concise but detailed comparisons of a selection of state-of-the-art cylindrical 18650 battery cells. This type of cell is used primarily by Tesla and several Asian car manufacturers. The favorable manufacturing processes, the high degree of modularity, and a lower degree of severity in the event of a fault speak in favor of this cell type. Disadvantages are the high number of cells required and the associated probability of failure, as well as the less favorable surface-to-volume ratio of the cylindrical round cells, which increases the cooling requirements [26].

All cells analyzed within the scope of this paper were acquired in 2021, and therefore represent the current state of development as best as possible. The battery impedances of the cells are calculated in particular, resulting in a data collection that may be used as a starting point for future predevelopment simulations or hardware design considerations. Dynamic models with one to three $RC$-elements and a Warburg impedance model are used to assess the batteries’ impedances. Electrochemical impedance spectroscopies (EISs) are used to parameterize the impedance models for each of the individual battery cells. The models’ goodness of fit and computational effort are compared. In Appendix A, the EIS data from the studied battery cells can be found. The comparisons are concluded by comparing the cells’ specific energy, price, and C-rate.

2. Recent Research on 18650 Lithium-Ion Battery Cells

In this section, recent research on 18650 cells will be presented and an outlook on future developments in this field will be given.

One key aspect of the research relates to the materials used in the cells. For example, Zeng et al. demonstrated, in [27], an approach to optimize the properties of the electrolyte in an 18650 cell by changing its composition. Thus, the molar ratio of conducting salts to solvent was increased, which improved the chemical stability of the electrolyte. In this way, the flammability of the electrolyte was reduced and the reactivity of the electrolyte with the active materials was lowered. Sturm et al. investigated novel components of active materials in high-energy 18650 round cells (nickel-rich, silicon–graphite lithium-ion) with respect to the influence of inhomogeneities during fast charging in [28].

The second major research focus is on better understanding and modeling of the battery cells in order to be able to make optimizations here. For example, in [29], the authors developed a deep-learning-based capacity estimator with the goal of speeding up the otherwise costly and time-consuming process of collecting long-term cycling data. The training data were collected over a ten-year period of daily cycling, and were verified with 20 18650 Li-ion cells.

In the future, round cells are expected to continue to play an important role in the automotive powertrain. However, the diameter of the round cell format will grow, as Tesla is already demonstrating with its 4680 cells [30]. The dimensions of the new round cells will be the result of an optimization process that takes into account aspects such as costs, cooling requirements, and the complexity of the battery system. With regard to the cell chemistry used, a trend toward LFP cells is expected, which will make the cells safer and more cost-effective but will entail compromises in terms of the specific energy density [31].

3. Battery Modeling and Parameter Extraction Using Electrochemical Impedance Spectroscopy

This section provides a theoretical overview of the commonly used battery models as well as the EIS concept for extracting battery model characteristics. The actual meaning of the ECMs’ components is often not evident, as stated in [32]. However, ECMs may be used to characterize battery behavior in terms of the current-voltage relationship and, as a result, to predict battery performance characteristics such as energy efficiency, maximum power capability, or relaxation time.

3.1. Battery Modeling

Different ways to model batteries exist, each differing in complexity, accuracy, and the goal pursued with the model. The methods may be divided into three categories: electrochemical models, analytical models, and equivalent circuit models [33].

Electrochemical battery models are defined by the fact that they describe the processes that occur within a battery in terms of chemical reactions within the cell. This makes them the most accurate battery models, but it also means they take the most time to parameterize. This is made more difficult by the fact that many of the characteristics are unknown or are kept secret by the cell manufacturers. The thickness of the electrode layers or the concentration of conducting salts in the electrolyte are examples of such hard-to-determine parameters. When such parameters are available, however, electrochemical models are so well trusted that other battery models are compared to electrochemical models as a benchmark rather than performing experimental comparisons. Key publications regarding electrochemical battery models were published by Doyle, Fuller, and Newman [34,35,36].

When opposed to electrochemical models, analytical battery models are more abstracted from the cell system and need less parameterization and computation effort. The objective is to be able to efficiently simulate cell behavior using a mathematical description without having to account for the chemical and physical processes that occur inside the cell. Peukert (Peukert’s law) [37,38], Rakhmatov and Vrudhula [37,39,40], and Manwell and McGowan (Kinetic Battery Model) [41,42,43] developed widely used analytical battery models.

Electrical equivalent circuit models are a good way to model batteries because they approximate their behavior using a set of electrical components that are considered to be ideal. Voltage sources, resistors, and capacitors, as well as inductors, are commonly used for this purpose. The parameterization and computing effort of such circuits grow as their complexity increases, as does their accuracy, to some extent. Here, a compromise appropriate for the application must be found. Hageman [44] was the first to introduce ECMs for battery modeling. Fractional-order modeling can be seen as an extension of ECM, where non-integer differentiation orders are used. Such a generalization allows an optimization of the equivalent circuits, and is described in more detail, for example, in [45].

3.1.1. RC-Link Models

A dynamic battery model with three $RC$-elements, as depicted in Figure 1, can be used to represent a battery’s dynamic behavior, as described in [21,46]. A series inductor $L_{\mathrm{R}}$, a series resistor $R_0$, and three $RC$-elements, $R_1{C}_1$ to $R_3{C}_3$, make up the ECM. The voltage source $V_{\mathrm{OCV}}$ indicates the open-circuit voltage after a sufficient battery relaxation time. All metrics are dependent on the battery’s state of charge (SOC) and temperature [47].

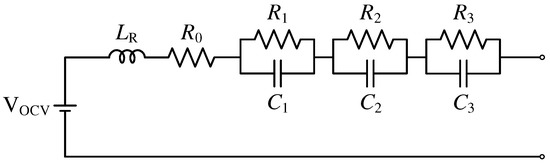
Figure 1. Dynamic battery model with three $RC$-pairs.

The overall battery cell impedance of an $RC$-element model including n $RC$-elements can be described as

$${\overline{Z}}_{\mathrm{Cell},\mathrm{RC}}=j\omega L_{\mathrm{R}}+R_0+\sum _{i=1}^n\frac{R_i}{1+j\omega R_i{C}_i}.$$

(1)

With two or more $RC$-elements, such a model properly represents the dynamic behavior of the battery cell throughout a frequency range of a few Hz to several $\mathrm{k}$$\mathrm{Hz}$ [21]. However, the model’s accuracy is determined by the battery cell and the battery behavior to be described, both of which are largely determined by the application. With such a simple model, an accuracy of 92.1% to 98.5% can be reached, as illustrated in [9].

An $RC$-element model is typically insufficient to represent diffusion impedance (≤$1\mathrm{Hz}$) [48] or inductive behavior at higher frequencies ($\gg 5\mathrm{kHz}$), which is often solely related to cable connections or solder joints.

3.1.2. Warburg Model

A special constant phase element called Warburg impedance, as described in [49], can be used to replace one of the previously specified $RC$-elements to better represent the battery cell’s low-frequency behavior. In addition, the series inductance $L_{\mathrm{R}}$ can be supplemented with an extra parallel resistance $R_{\mathrm{L}}$ to represent the inductive high-frequency behavior. As a result, the battery cell model shown in Figure 2 is generated, which is referred to in this study as the Warburg impedance model or Warburg model.

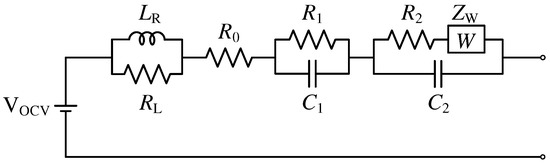
Figure 2. Dynamic battery model with a Warburg impedance element.

The mathematical representation of the Warburg impedance element can be written as

$${\overline{Z}}_W=(1-j)\sigma {\omega }^{-\frac{1}{2}}$$

(2)

with $\sigma [\mathsf{\Omega }/\sqrt{\mathrm{s}}]$ being the Warburg coefficient. Thus, the impedance of the entire Warburg impedance model can be described as

$$\begin{array}{c}\hfill {\overline{Z}}_{\mathrm{Cell},\mathrm{Warburg}}=\frac{R_{\mathrm{L}}+j\omega L_{\mathrm{R}}}{j\omega L_{\mathrm{R}}{R}_{\mathrm{L}}}+R_0+\frac{R_1}{1+j\omega R_1{C}_1}+\frac{R_2+(1-j)\sigma {\omega }^{-\frac{1}{2}}}{1+j\omega C_2(R_2+(1-j)\sigma {\omega }^{-\frac{1}{2}})}.\end{array}$$

(3)

3.2. Electrochemical Impedance Spectroscopy

EIS is a method for assessing the impedance behavior of an electrochemical system, i.e., the ability of a system to restrict its current flow. This measuring method is often used to estimate the impedance of a battery across a wide frequency range [50]. Individual battery cells, modules, or even packs are exposed to an alternating current or voltage with a constant RMS value in order to perform an EIS. Typically, a wide frequency range is explored and the cell’s response to each frequency is assessed. The complex-valued, frequency-specific impedances may be estimated later from the set of observed alternating values using the magnitudes of current and voltage, including their phase shift. It is necessary to distinguish between galvanostatic and a potentiostatic EIS: one speaks of galvanostatic EIS when a current perturbation is applied to a cell and the voltage response is measured; on the other hand, the term potentiostatic EIS is used when a voltage perturbation is supplied to a cell and the current response is measured. The findings of an EIS are often displayed using Bode and Nyquist graphs. The phase offset between voltage and current can be represented in the Bode plot over a logarithmically spaced frequency. A visualization of the absolute value of the impedance vs. the logarithmic frequency is also part of a Bode plot.

A cylindrical 18650 battery cell installed into a battery holder to perform an EIS using a battery cell tester is shown in Figure 3. The current injection and voltage measurement cables are designated with their matching cable connectors. Furthermore, Figure 4 (Nyquist plot) depicts the obtained battery impedance for a cylindrical 18650 cell from LG Chem, model type HG2, with a nominal capacity of 3000 mAh. Different SOCs and a frequency range of 10 mHz to 100 kHz are taken into account.

Figure 3. Battery cell testing of a cylindrical 18650 battery cell [25].

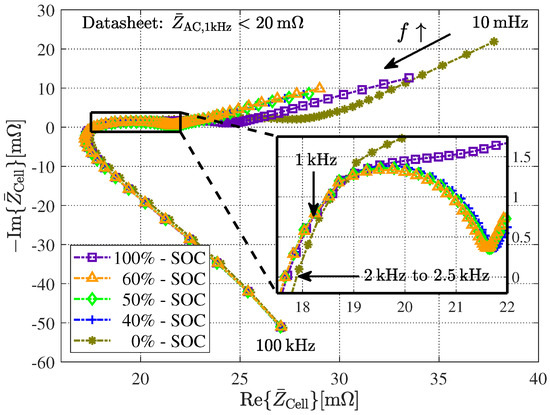
Figure 4. Obtained Nyquist plot from EIS measurements for a cylindrical 18650 battery cell from LG Chem of model type HG2 with a nominal capacity of 3000 mAh.

It can be seen from Figure 4 that the impedance curves for medium SOCs (40–60%) hardly differ, whereas the curves for 0% and 100% SOC show significantly different behavior. This effect will be referred to in Section 3.3. A typical three-way split can be seen in all the curves: At low impedances, there is a quasilinear impedance curve, which is generally attributed to diffusion processes in the solid material of the cell. At increasing frequencies, a capacitive semicircle appears, followed by an inductively dominated impedance behavior at high frequencies (Im$\left\{{\overline{Z}}_{\mathrm{Cell}}\right\}>0$). The latter is usually associated with the tabs of the cell as well as with the test leads [20].

3.3. Parameter Extraction

The battery models in Section 3.1 can be parameterized based on the data collected from EISs to reflect the batteries’ behavior for specified frequency ranges in order to represent battery cells in simulation models with acceptable computing effort and accuracy. The relevant frequency range and desired precision, which typically depend on the associated application, should be considered when choosing a battery model.

Using a Nyquist plot, Figure 5 emphasizes the influence and significance of the circuit’s parts of an $RC$-element model and the Warburg model in comparison. The more $RC$-elements added to the ECM, the easier it is for the model to adapt to the observed data, resulting in increased accuracy. However, as a result of this, the simulation model’s computing effort increases, which can become troublesome, especially for simulation models with a large number of cells. As a result, the inclusion of $RC$-elements must be justified by a relevant increase in accuracy.

Figure 5. Model of a battery cell with respect to the effect of the model’s individual components on the Nyquist plot. (a) Three-$RC$-pair model. (b) Warburg impedance model. In addition to the color highlighting, the labeled arrows represent the resistive and inductive parameters of the equivalent circuits.

The Warburg impedance element, colored in green in Figure 5b, has an influence on the battery impedance’s low-frequency (≤$1\mathrm{Hz}$) behavior. The Warburg impedance would display a straight line of 45° with respect to the real axis of the Nyquist plot, referred to as diffusion resistance, if the real and imaginary axes were equally sized. The inductance $L_{\mathrm{R}}$ and its parallel resistance $R_{\mathrm{L}}$, colored in blue, are related to the battery impedance’s high-frequency (≥3 kHz) behavior. The medium-frequency component, colored in red, is also reliant on the series resistance $R_0$ and the two $RC$-elements.

The three-$RC$-pair model in Figure 5a represents the battery impedance’s medium-frequency behavior similarly to the Warburg impedance model, however the low- and high-frequency behavior is significantly compromised due to the model’s simplicity.

The battery models, represented in Figure 1 and Figure 2, were parameterized using the impedance data ${\overline{Z}}_{\mathrm{Cell},\mathrm{EIS}}$ acquired from EIS measurements. An optimization problem is typically formulated for this purpose and solved using a computer tool such as Matlab’s optimization toolbox. The following optimization problem may be stated using the sum of the squared differences between the estimated ${\overline{Z}}_{\mathrm{Cell},\mathrm{Est}}$ and measured impedance values ${\overline{Z}}_{\mathrm{Cell},\mathrm{EIS}}$:

$$\underset{x}{\mathrm{minimize}}\sum _{f=f_{\mathrm{start}}}^{f_{\mathrm{end}}}\sqrt{{\left({\overline{Z}}_{\mathrm{Cell},\mathrm{Est}}\left(x\right)-{\overline{Z}}_{\mathrm{Cell},\mathrm{EIS}}\right)}^2}$$

(4)

with x being the parameter vector to be estimated. For example, for the Warburg impedance model, x becomes

$$x=\left[L_{\mathrm{R}}{R}_{\mathrm{L}}{R}_0{R}_1{C}_1{R}_2{C}_2\sigma \right]$$

(5)

The elements of x should be given suitable initial values. The selected optimization-solver typically changes the estimated parameters x over several iterations to minimize the sum of the root of the squared differences between the estimated ${\overline{Z}}_{\mathrm{Cell},\mathrm{Est}}$ and the measured impedance values ${\overline{Z}}_{\mathrm{Cell},\mathrm{EIS}}$ for the frequency range $f_{\mathrm{start}}$ to $f_{\mathrm{end}}$. The battery impedance variation related to the SOC becomes nearly neglectable around medium SOCs, as can be seen in Figure 4. As a result, the impedance of battery cells is measured at a characteristic SOC of 50%.

In comparison to the EIS measurements (green), Figure 6 and Figure 7 show an exemplary Bode and a Nyquist plot with the parameterized Warburg impedance model (red) and the $RC$-element models (3$RC$—blue, 2$RC$—purple, 1$RC$—yellow).

Figure 6. Obtained Bode plot from EIS measurements (green) in comparison to the parameterized Warburg impedance (red) and three-$RC$-pair (blue) model for a cylindrical 18650 battery cell from LG Chem of model type HG2 with a nominal capacity of 3000 mAh.

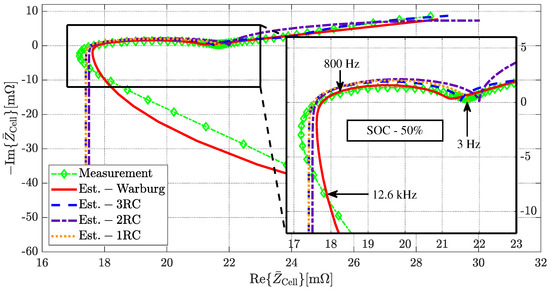
Figure 7. Obtained Nyquist plot from EIS measurements (green) in comparison to the parameterized Warburg impedance (red) and three-$RC$-pair (blue) model for a cylindrical 18650 battery cell from LG Chem of model type HG2 with a nominal capacity of 3000 mAh.

The EIS was performed using a cylindrical LG Chem 18650 battery cell, model type HG2, with a nominal capacity of 3000 mAh and a characteristic impedance of 50%. For the HG2 cell from LG Chem and all other cells listed in Table 1, the predicted parameters of the $RC$-element and Warburg impedance models can be found in Table 2, Table 3, Table 4 and Table 5, respectively. The parameterized Warburg impedance model correctly describes the magnitude of the impedance as well as its phase quantity for the displayed frequency range of 10 mHz to 100 kHz, as shown in Figure 6. The parameterized two- and three-$RC$-element models, on the other hand, accurately characterize the magnitude and phase quantity of the impedance from 10 mHz to just 10 kHz. The one-$RC$-element model, on the other hand, only produces acceptable results in the 1 Hz to 10 kHz frequency range. A satisfactory agreement between the measured impedance and the parameterized models can be concluded based on the Nyquist plot given in Figure 7 example.

3.4. Simulation in Time-Domain

To test the models parameterized using EIS data, a current pulse can be applied to a battery cell while the voltage response is measured [51]. The same current pulse can be applied to a virtual cell in a simulation model, which includes the respective equivalent circuit models. Subsequently, the measured and the simulated voltage responses can be compared to evaluate the quality of the parameterized equivalent circuit models. This experiment was carried out using the HG2 cell by LG Chem, applying a discharge current of 3 A for 10 s at an SOC of the cell of 50%. Verification of the Warburg model in the time domain is omitted within the scope of this paper, since the use of this model in the time domain is unusual. When using a time domain simulation tool, the Warburg impedance itself can be tuned only for one frequency and, therefore, the Warburg impedance model cannot be used to reflect the voltage-current relation for a specific current pulse. For this problem, there are computationally intensive workarounds, the use of which is usually not profitable with respect to the alternative of using additional RC elements instead. If the modeling of a Warburg impedance should be relevant for the reader, corresponding literature can be found in [52]. The results are depicted in Figure 8.

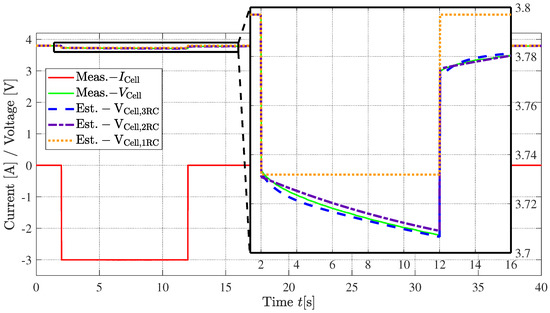
Figure 8. Measured cell voltage behavior for a current step in comparison to simulations for a cylindrical 18650 battery cell from LG Chem of model type HG2 with a nominal capacity of 3000 mAh.

As can be seen from Figure 8, both the two- and three-$RC$-pair models are able to represent the voltage drop well, with the three-$RC$ model still being able to represent the cells’ dynamics with a slightly better curvature. The one-$RC$ model shows a comparable initial voltage drop. However, as the current pulse is maintained longer, the simpler one-$RC$ model deviates more from the measured data since it lacks the longer-term time constants. In addition, the discharge pulse with a duration of 10 s is in a low-frequency range, which no longer exhibits any capacitive behavior (see Figure 7). Thus, the low-frequency pulse response of the one-$RC$ model is similar to that of a purely resistive battery model. In [53], however, an example of a one-$RC$ model can be found that was fitted for a low-frequency range, and can therefore represent the dynamics accordingly.

4. Battery Cell Comparisons

This section compares several state-of-the-art battery cells in terms of various key battery parameters in a brief yet thorough manner. The estimated impedance parameters of the battery cells for the Warburg impedance and $RC$-element models are provided. The accuracy and computing effort of the models themselves are compared.

The battery cells listed in Table 1 are considered within the scope of this paper’s battery cell comparisons. Individual battery cells will now be referred to by their manufacturer name and model type description to identify them. Except for the Lithium Werks ANR26650M1B, which is a high-power cell with a 26650 geometry and a lithium–iron–phosphate chemistry (${\mathrm{LiFePO}}_4$), all of the listed cells have a cylindrical 18650 geometry and NMC-based chemistry. The primary characteristic parameters included in Table 1 are mostly taken from the datasheets of the cells or may be found in [54]. Aside from [54], ref. [55] provides a full overview of battery cell characteristics and additional test results.

Table 1. Nominal parameters of the examined battery cells.

Manufacturer	Model	Capacity Q [mAh]	Voltage ${}^1$ ${\mathit{V}}_{\mathbf{Nom}}$ [V]	C-Rate ${}^2$	Spec. Energy ${\mathit{e}}_{\mathbf{Cell}}\left[{\displaystyle \frac{\mathbf{Wh}}{\mathbf{kg}}}\right]$	Price ${}^3$ [USD]
Keeppower	P1834J	3400	3.7	2	262.08	11.53
LG Chem	HG2	3000	3.6	6.7	226.53	14.43
LG Chem	M26	2600	3.65	4	200.42	5.45
LG Chem	MJ1	3500	3.635	3	264.29	8.43
Lithium Werks	M1B	2500	3.3	28	112.89	6.55
Murata	V3	2250	3.7	4.4	189.20	2.73
Murata	VTC5A	2250	3.7	13.5	213.78	10.85
Murata	VTC6	3120	3.7	10	247.73	9.64
Nitecore	NL1835HP	3500	3.6	2.3	239.81	29.04
Samsung	30Q	3000	3.6	5	231.25	12.01
Sanyo	ZT	2700	3.7	2	207.26	2.61

¹ Nominal battery cell voltage at an SOC of 50%. ² Maximum permissible C-rate at discharge. ³ Price per piece taken from [54].

Table 1. Nominal parameters of the examined battery cells.

Manufacturer	Model	Capacity Q [mAh]	Voltage ${}^1$ ${\mathit{V}}_{\mathbf{Nom}}$ [V]	C-Rate ${}^2$	Spec. Energy ${\mathit{e}}_{\mathbf{Cell}}\left[{\displaystyle \frac{\mathbf{Wh}}{\mathbf{kg}}}\right]$	Price ${}^3$ [USD]
Keeppower	P1834J	3400	3.7	2	262.08	11.53
LG Chem	HG2	3000	3.6	6.7	226.53	14.43
LG Chem	M26	2600	3.65	4	200.42	5.45
LG Chem	MJ1	3500	3.635	3	264.29	8.43
Lithium Werks	M1B	2500	3.3	28	112.89	6.55
Murata	V3	2250	3.7	4.4	189.20	2.73
Murata	VTC5A	2250	3.7	13.5	213.78	10.85
Murata	VTC6	3120	3.7	10	247.73	9.64
Nitecore	NL1835HP	3500	3.6	2.3	239.81	29.04
Samsung	30Q	3000	3.6	5	231.25	12.01
Sanyo	ZT	2700	3.7	2	207.26	2.61

¹ Nominal battery cell voltage at an SOC of 50%. ² Maximum permissible C-rate at discharge. ³ Price per piece taken from [54].

Except for the ANR26650M1B from Lithium Werks, which has a nominal voltage of around 3.3 V, all cells in Table 1 have a nominal battery voltage $V_{\mathrm{Nom}}$ of about 3.6 V to 3.7 V. This potential difference is derived from the galvanic series, and is specific to an NMC cell chemistry. Unlike cell voltage, cell capacitance is a design parameter that manufacturers can define on an application-specific basis. It essentially depends on the amount of active material used in the cell. The battery cell capacity and the maximum allowable C-rate during discharge are the main characteristics extracted from datasheets. Another key benchmark characteristic is the specific energy $e_{\mathrm{Cell}}$ of a battery cell, which can be calculated using

$$e_{\mathrm{Cell}}=\frac{E_{\mathrm{Cell}}}{m_{\mathrm{Cell}}}$$

(6)

where $E_{\mathrm{Cell}}$ and $m_{\mathrm{Cell}}$ are the nominal energy capacity and weight of the cell, respectively. Furthermore, using the nominal battery voltage $V_{\mathrm{Nom}}$ and capacity $Q_{\mathrm{Cell}}$, the nominal energy content $E_{\mathrm{Cell}}$ of battery cells may be calculated using

$$E_{\mathrm{Cell}}\approx V_{\mathrm{Nom}}·Q_{\mathrm{Cell}}$$

(7)

Furthermore, in addition to the electrical battery specifications, the price of the battery cell is taken into account in Table 1, since it is an essential design consideration for battery systems [56]. Table 2, Table 3, Table 4 and Table 5, respectively, list the calculated parameters of the Warburg impedance model and the RC-element models.

Table 2. Estimated battery parameters for the Warburg impedance model.

Manufacturer	Model	${\mathit{L}}_{\mathit{R}}\left[\mathbf{nH}\right]$	${\mathit{R}}_{\mathit{L}}\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{R}}_0\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{R}}_1\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_1\left[\mathbf{F}\right]$	${\mathit{R}}_2\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_2\left[\mathbf{F}\right]$	$\mathit{\sigma }\left[{\displaystyle \frac{\mathbf{m}\mathsf{\Omega }}{\sqrt{\mathbf{s}}}}\right]$
Keeppower	P1834J	147.40	250.73	100.07	6.90	1.06	8.16	0.08	1.96
LG Chem	HG2	88.88	251.07	17.76	1.00	1.84	2.49	0.18	1.80
LG Chem	M26	409.17	882.39	40.66	5.91	0.24	1.64	3.77	2.00
LG Chem	MJ1	410.74	755.26	43.93	4.47	0.35	0.09	28.79	1.91
Lithium Werks	V3	25.78	145.36	6.63	0.72	11.22	1.59	0.27	1.86
Murata	V3	414.44	816.17	33.86	1.81	5.64	7.05	0.19	2.46
Murata	VTC5A	79.91	208.19	73.56	3.05	0.16	1.61	1.26	1.70
Murata	VTC6	74.23	209.11	12.74	1.38	1.51	3.30	0.13	1.76
Nitecore	NL1835HP	187.59	226.58	53.67	5.38	1.59	8.23	0.13	2.17
Samsung	30Q	73.97	178.70	13.24	2.57	0.16	0.78	1.81	1.98
Sanyo	ZT	274.49	476.19	41.10	30.18	0.10	48.17	0.44	4.47

Table 2. Estimated battery parameters for the Warburg impedance model.

Manufacturer	Model	${\mathit{L}}_{\mathit{R}}\left[\mathbf{nH}\right]$	${\mathit{R}}_{\mathit{L}}\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{R}}_0\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{R}}_1\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_1\left[\mathbf{F}\right]$	${\mathit{R}}_2\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_2\left[\mathbf{F}\right]$	$\mathit{\sigma }\left[{\displaystyle \frac{\mathbf{m}\mathsf{\Omega }}{\sqrt{\mathbf{s}}}}\right]$
Keeppower	P1834J	147.40	250.73	100.07	6.90	1.06	8.16	0.08	1.96
LG Chem	HG2	88.88	251.07	17.76	1.00	1.84	2.49	0.18	1.80
LG Chem	M26	409.17	882.39	40.66	5.91	0.24	1.64	3.77	2.00
LG Chem	MJ1	410.74	755.26	43.93	4.47	0.35	0.09	28.79	1.91
Lithium Werks	V3	25.78	145.36	6.63	0.72	11.22	1.59	0.27	1.86
Murata	V3	414.44	816.17	33.86	1.81	5.64	7.05	0.19	2.46
Murata	VTC5A	79.91	208.19	73.56	3.05	0.16	1.61	1.26	1.70
Murata	VTC6	74.23	209.11	12.74	1.38	1.51	3.30	0.13	1.76
Nitecore	NL1835HP	187.59	226.58	53.67	5.38	1.59	8.23	0.13	2.17
Samsung	30Q	73.97	178.70	13.24	2.57	0.16	0.78	1.81	1.98
Sanyo	ZT	274.49	476.19	41.10	30.18	0.10	48.17	0.44	4.47

Table 3. Estimated battery parameters for the three-$RC$-pair model.

Manufacturer	Model	${\mathit{L}}_{\mathit{R}}\left[\mathbf{nH}\right]$	${\mathit{R}}_0\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{R}}_1\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_1\left[\mathbf{mF}\right]$	${\mathit{R}}_2\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_2\left[\mathbf{F}\right]$	${\mathit{R}}_3\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_3\left[\mathbf{F}\right]$
Keeppower	P1834J	136.71	99.10	9.53	67.71	7.85	1.29	16.93	1033.82
LG Chem	HG2	86.38	17.41	4.11	157.65	2.60	347.27	19.80	1391.13
LG Chem	M26	389.73	38.15	9.68	128.17	2.43	77.34	23.67	1057.06
LG Chem	MJ1	357.66	40.95	7.23	808.75	0.60	2.11	9.85	2428.49
Lithium Werks	M1B	24.58	6.41	1.91	902.01	1.49	19.27	4.73	4432.25
Murata	V3	399.52	29.91	4.82	42.58	8.97	0.20	11.13	406.26
Murata	VTC5A	72.75	73.36	5.14	150.13	1.96	390.15	19.26	1291.63
Murata	VTC6	67.50	12.51	5.26	129.85	2.28	4047.82	20.65	1344.85
Nitecore	NL1835HP	143.74	52.41	9.36	97.67	6.79	1.60	17.61	850.42
Samsung	30Q	72.70	12.98	1.83	123.45	2.24	0.14	15.08	861.11
Sanyo	ZT	261.80	39.80	40.58	828.57	18.32	499.70	43.43	0.10

Table 3. Estimated battery parameters for the three-$RC$-pair model.

Manufacturer	Model	${\mathit{L}}_{\mathit{R}}\left[\mathbf{nH}\right]$	${\mathit{R}}_0\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{R}}_1\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_1\left[\mathbf{mF}\right]$	${\mathit{R}}_2\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_2\left[\mathbf{F}\right]$	${\mathit{R}}_3\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_3\left[\mathbf{F}\right]$
Keeppower	P1834J	136.71	99.10	9.53	67.71	7.85	1.29	16.93	1033.82
LG Chem	HG2	86.38	17.41	4.11	157.65	2.60	347.27	19.80	1391.13
LG Chem	M26	389.73	38.15	9.68	128.17	2.43	77.34	23.67	1057.06
LG Chem	MJ1	357.66	40.95	7.23	808.75	0.60	2.11	9.85	2428.49
Lithium Werks	M1B	24.58	6.41	1.91	902.01	1.49	19.27	4.73	4432.25
Murata	V3	399.52	29.91	4.82	42.58	8.97	0.20	11.13	406.26
Murata	VTC5A	72.75	73.36	5.14	150.13	1.96	390.15	19.26	1291.63
Murata	VTC6	67.50	12.51	5.26	129.85	2.28	4047.82	20.65	1344.85
Nitecore	NL1835HP	143.74	52.41	9.36	97.67	6.79	1.60	17.61	850.42
Samsung	30Q	72.70	12.98	1.83	123.45	2.24	0.14	15.08	861.11
Sanyo	ZT	261.80	39.80	40.58	828.57	18.32	499.70	43.43	0.10

Table 4. Estimated battery parameters for the two-$RC$-pair model.

Manufacturer	Model	${\mathit{L}}_{\mathit{R}}\left[\mathbf{nH}\right]$	${\mathit{R}}_0\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{R}}_1\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_1\left[\mathbf{mF}\right]$	${\mathit{R}}_2\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_2\left[\mathbf{F}\right]$
Keeppower	P1834J	136.55	99.90	15.55	128.77	15.13	884.67
LG Chem	HG2	86.37	17.48	4.53	175.10	14.74	985.19
LG Chem	M26	389.91	38.32	10.47	142.26	19.31	895.38
LG Chem	MJ1	357.66	40.95	7.83	434.08	4.94	1361.57
Lithium Werks	M1B	25.75	6.36	2.85	363.34	11.85	859.94
Murata	V3	399.65	30.65	12.75	123.38	16.67	681.21
Murata	VTC5A	78.66	73.11	5.35	151.62	15.12	1015.36
Murata	VTC6	73.61	12.14	5.41	130.77	15.04	995.59
Nitecore	NL1835HP	169.14	52.30	15.86	154.31	17.04	813.53
Samsung	30Q	72.80	12.62	4.43	137.29	15.36	872.87
Sanyo	ZT	235.60	38.02	87.16	509.41	22.89	1138.59

Table 4. Estimated battery parameters for the two-$RC$-pair model.

Manufacturer	Model	${\mathit{L}}_{\mathit{R}}\left[\mathbf{nH}\right]$	${\mathit{R}}_0\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{R}}_1\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_1\left[\mathbf{mF}\right]$	${\mathit{R}}_2\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_2\left[\mathbf{F}\right]$
Keeppower	P1834J	136.55	99.90	15.55	128.77	15.13	884.67
LG Chem	HG2	86.37	17.48	4.53	175.10	14.74	985.19
LG Chem	M26	389.91	38.32	10.47	142.26	19.31	895.38
LG Chem	MJ1	357.66	40.95	7.83	434.08	4.94	1361.57
Lithium Werks	M1B	25.75	6.36	2.85	363.34	11.85	859.94
Murata	V3	399.65	30.65	12.75	123.38	16.67	681.21
Murata	VTC5A	78.66	73.11	5.35	151.62	15.12	1015.36
Murata	VTC6	73.61	12.14	5.41	130.77	15.04	995.59
Nitecore	NL1835HP	169.14	52.30	15.86	154.31	17.04	813.53
Samsung	30Q	72.80	12.62	4.43	137.29	15.36	872.87
Sanyo	ZT	235.60	38.02	87.16	509.41	22.89	1138.59

Table 5. Estimated battery parameters for the one-$RC$-pair model.

Manufacturer	Model	${\mathit{L}}_{\mathit{R}}\left[\mathbf{nH}\right]$	${\mathit{R}}_0\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{R}}_1\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_1\left[\mathbf{mF}\right]$
Keeppower	P1834J	136.63	99.49	3.43	131.24
LG Chem	HG2	86.37	17.44	4.29	165.40
LG Chem	M26	389.91	38.28	10.11	138.14
LG Chem	MJ1	384.75	41.46	7.27	151.23
Lithium Werks	M1B	25.56	6.66	2.77	498.62
Murata	V3	391.38	31.52	11.49	121.36
Murata	VTC5A	77.25	73.37	5.24	159.57
Murata	VTC6	72.11	12.53	5.33	135.56
Nitecore	NL1835HP	163.25	52.67	14.68	147.01
Samsung	30Q	71.17	12.97	4.11	147.28
Sanyo	ZT	255.02	41.93	76.10	144.48

Table 5. Estimated battery parameters for the one-$RC$-pair model.

Manufacturer	Model	${\mathit{L}}_{\mathit{R}}\left[\mathbf{nH}\right]$	${\mathit{R}}_0\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{R}}_1\left[\mathbf{m}\mathsf{\Omega }\right]$	${\mathit{C}}_1\left[\mathbf{mF}\right]$
Keeppower	P1834J	136.63	99.49	3.43	131.24
LG Chem	HG2	86.37	17.44	4.29	165.40
LG Chem	M26	389.91	38.28	10.11	138.14
LG Chem	MJ1	384.75	41.46	7.27	151.23
Lithium Werks	M1B	25.56	6.66	2.77	498.62
Murata	V3	391.38	31.52	11.49	121.36
Murata	VTC5A	77.25	73.37	5.24	159.57
Murata	VTC6	72.11	12.53	5.33	135.56
Nitecore	NL1835HP	163.25	52.67	14.68	147.01
Samsung	30Q	71.17	12.97	4.11	147.28
Sanyo	ZT	255.02	41.93	76.10	144.48

As mentioned before, the addition of more $RC$-links helps to better approximate a battery’s behavior in accordance to the measurement data (Nyquist plot). For example, for the Sanyo cell, according to (4), the mean error between the estimated data and the measured data is reduced by a factor of $2.26$ if two $RC$-links are used instead of one. Between two and three $RC$-links, a factor of $3.82$ and, between one and three $RC$-links, a factor of $8.65$ is obtained.

In order to compare the computational effort of the ECMs, a simple simulation environment was set up in Simulink, in which 100 cells of the corresponding cell model were loaded with current pulses. The relative comparison of the resulting simulation time serves as a comparison parameter of the required computational effort. In this way, it is shown that the one-$RC$ model has a lower computational effort than the two-$RC$ and three-$RC$ models, reduced by a factor of $2.00$ and $3.51$, respectively. The two-$RC$ model required $1.75$ times less computation time than the three-$RC$ model. Figure 9 illustrates the obtained results.

Figure 9. Comparisons of the different $RC$-pair models relative to the computational effort (red) and accuracy (green).

A comparative overview of the impedance data for all eleven cells for SOCs of 20%, 50%, and 80% respectively, is shown in Figure 10. According to Table 1, LG Chem’s MJ1, the Nitecore, and the Keeppower cells have the greatest nominal capacity, ranging from 3400 mAh to 3500 mAh, which equates to a specific energy of 240 Wh kg⁻¹ and 280 Wh kg⁻¹, respectively. Their discharge C-rates are in the two to three range. As a result, both cells are considered typical high-energy cells. The Nitecore cell also has the highest price, about USD 29, partially because of the inbuilt protective circuitry. The chosen Keeppower cell also has an incorporated protective system, and it costs only USD $11.53$. Because it is not fitted with any protective circuitry, the LG Chem MJI cell has a reduced price of USD $8.43$. When comparing the impedances of the cells based on the internal resistance $R_0$, it can be seen that the Keeppower cell’s impedance ($R_0\approx 100\mathrm{m}\mathsf{\Omega }$) is almost double that of the Nitecore cell ($R_0\approx 54\mathrm{m}\mathsf{\Omega }$) and the LG Chem ($R_0\approx 43\mathrm{m}\mathsf{\Omega }$).

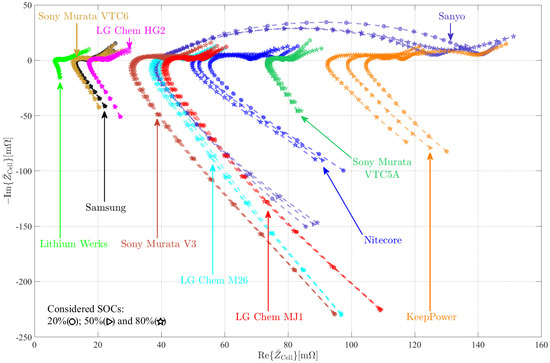
Figure 10. Electrochemical impedance spectroscopy sweep of all selected cells.

The Sanyo call and the V3 cell from Sony Murata Konion, in contrast to the mentioned high-energy and high-power cells, may be obtained for the lowest costs of USD 2.61 and USD 2.73, respectively. As a result, these cells might be classified as “low-price” cells. On the one hand, the specific energy of the Sanyo cell is around 207 Wh kg⁻¹, which is roughly 10% more than the V3 cell from Sony Murata Konion (189 Wh kg⁻¹). The highest allowed C-rate of the V3 cell, on the other hand, is four, which is almost double that of the Sanyo cell.

The other cells (LG Chem HG2, LG Chem M26, Samsung 30Q, and Sony Murata Konion VTC6) cannot be classified as high-energy or high-power cells directly. These are tuned for a variety of factors including battery cell power capacity, energy content, pricing, and cycle life [57,58].

Figure 11 presents a four-axis radar chart that considers the cells’ C-rate, price, impedance, and specific energy to explain the supplied battery cell comparisons. The price and impedance have been adjusted: the battery cell with the lowest impedance and price but the highest C-rate and specific energy would potentially cover the most area on the radar chart.

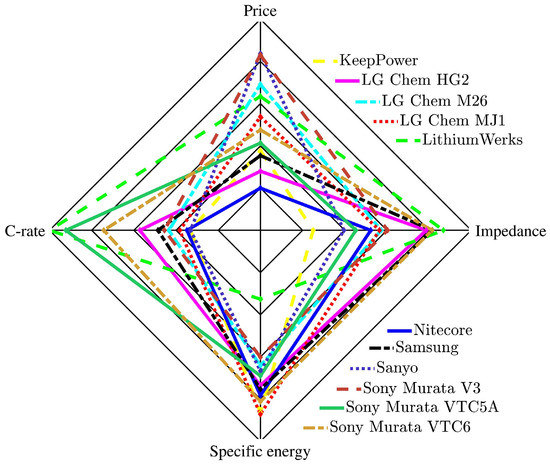
Figure 11. Radar chart: multiple-criteria evaluation of the selected state-of-the-art battery cells.

5. Conclusions

First, this article looked at how to represent the impedance of battery cells using four alternative battery models: one with a Warburg impedance and three $RC$-pair models with varying amounts of $RC$-elements. For a wide frequency range, including lower and higher frequencies, the Warburg impedance model accurately characterizes battery behavior. In contrast, the simple one-$RC$-pair model describes batteries’ behavior for medium frequencies from a couple of Hz to a couple of $\mathrm{k}$$\mathrm{Hz}$. The two- and three-$RC$ models cannot represent very high frequencies, similar to the one-$RC$ model, but low frequencies can be represented as well as in the Warburg model. The accuracy of the model and its computational effort depend on the number of $RC$-links used.

Furthermore, several state-of-the-art cylindrical battery cells were investigated within the scope of this work, and their impedance characteristics were evaluated using EISs according to different ECMs. The reader may utilize the generated EIS data and battery cell parameters in simulations to reflect battery behavior, such as estimating battery energy efficiency or power capabilities for various applications. The EIS data given can be utilized to develop and parameterize further ECMs.

In addition, the impedance, price, C-rate, and specific energy of the selected battery cells were compared. The offered comparisons can assist battery pack or battery system designers in selecting an appropriate cell based on the application and design criteria, such as power capability and energy content.