Influence of Thermoelectric Properties and Parasitic Effects on the Electrical Power of Thermoelectric Micro-Generators
Abstract
:1. Introduction
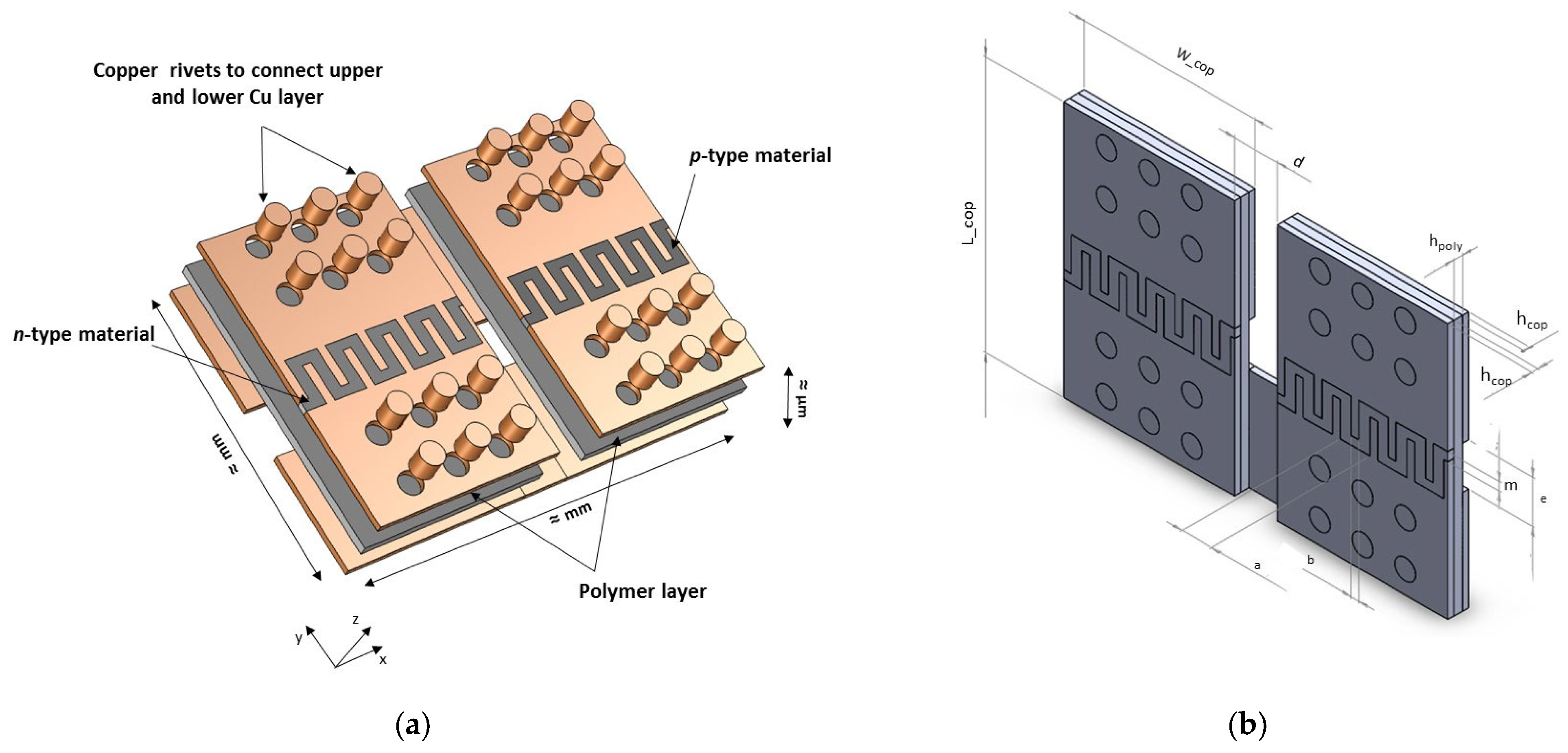
2. Numerical Modelling
3. Results and Discussion
3.1. Fixed Temperature Boundary Conditions
3.2. Mixed Temperature Boundary Conditions
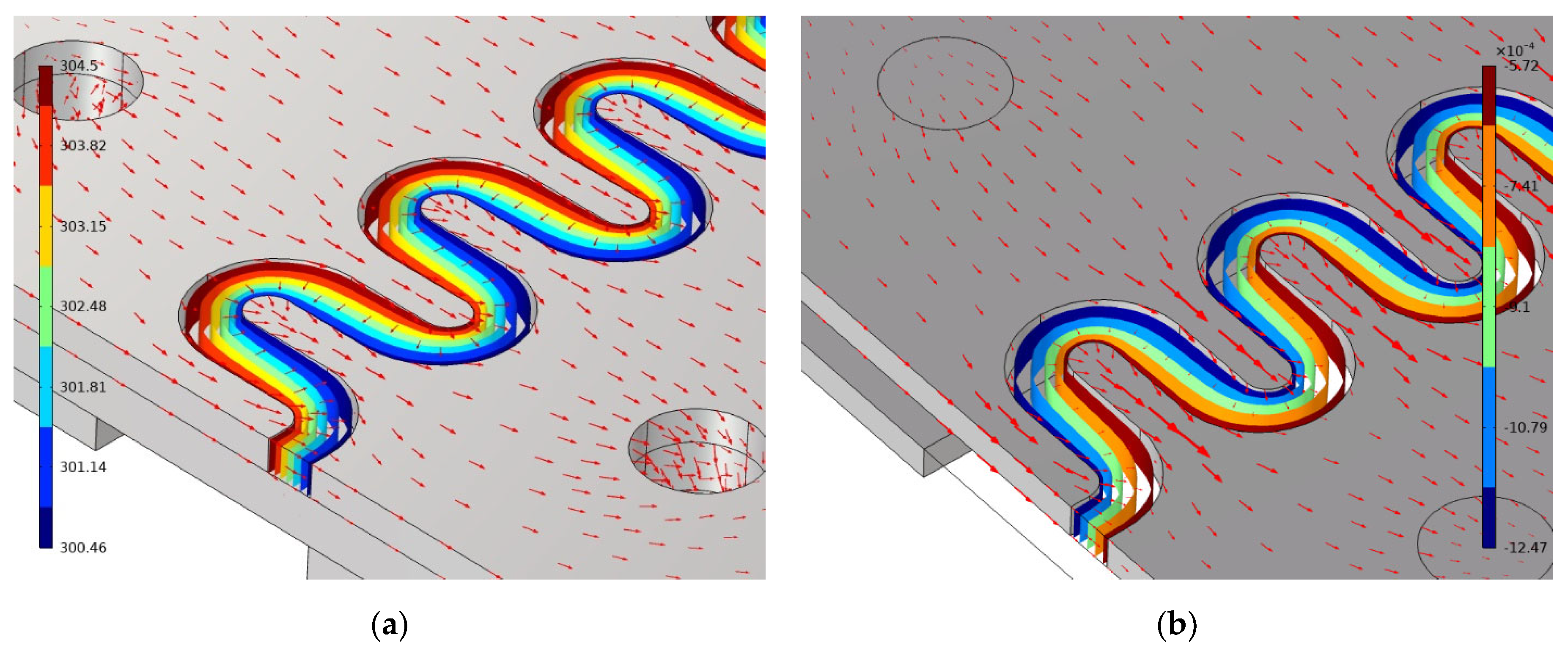
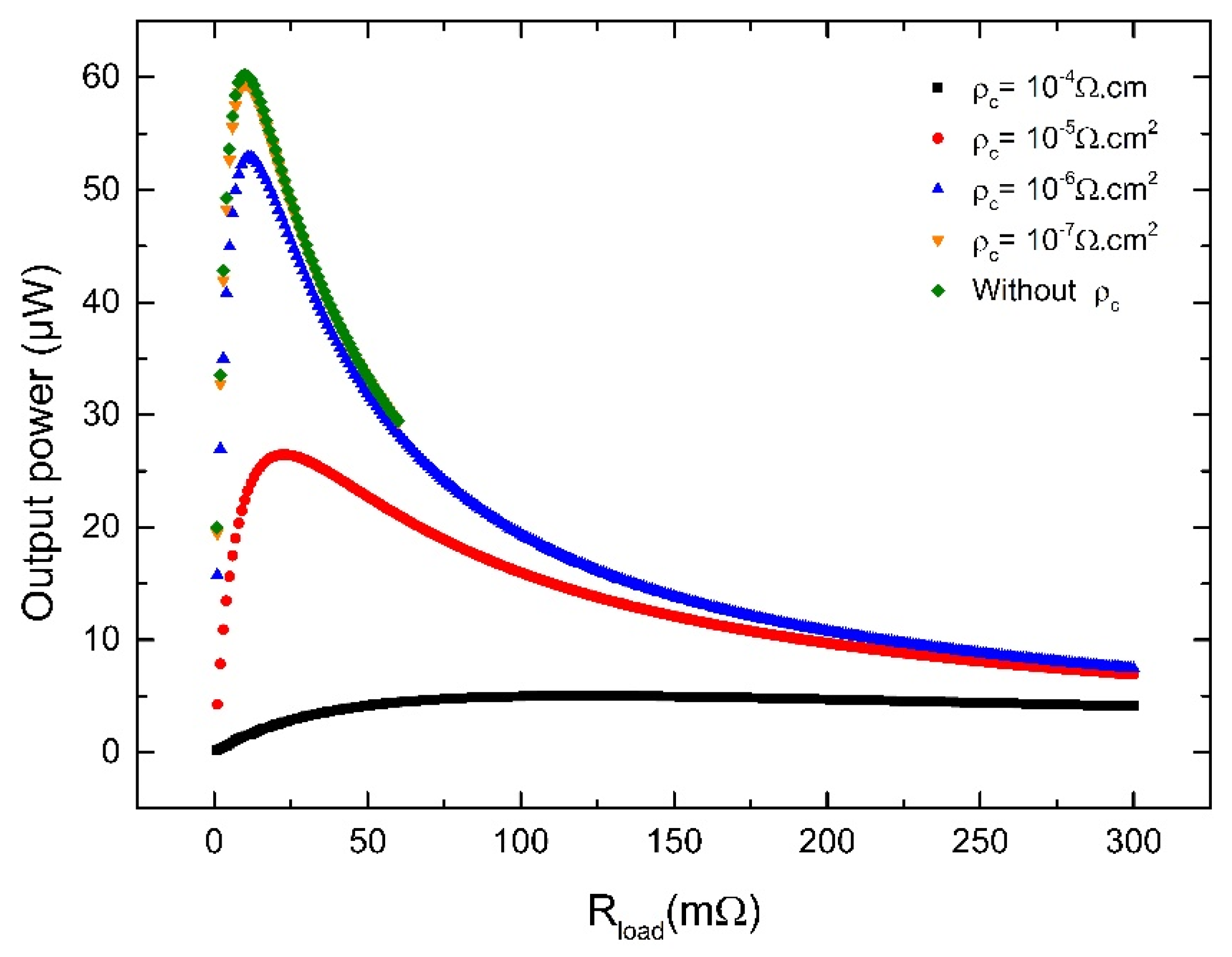
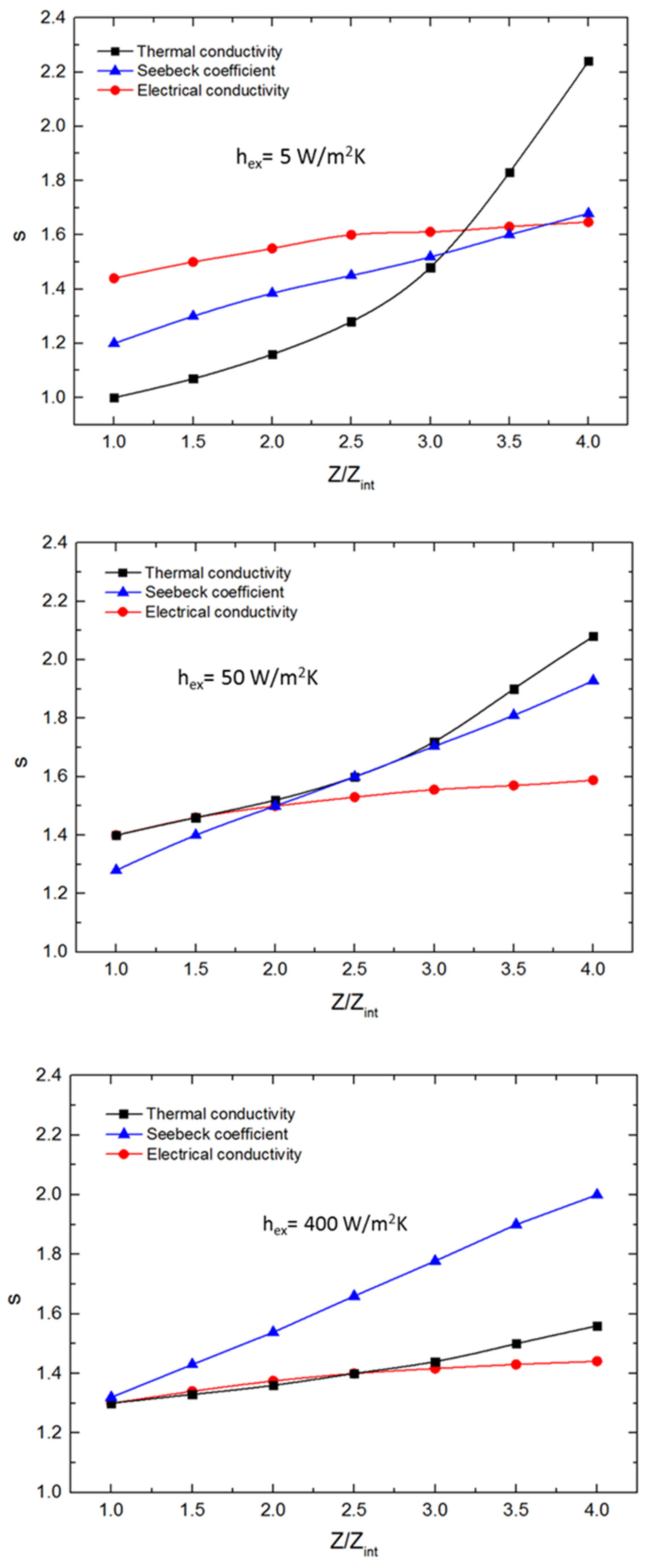
3.2.1. Influence of Parasitic Effects
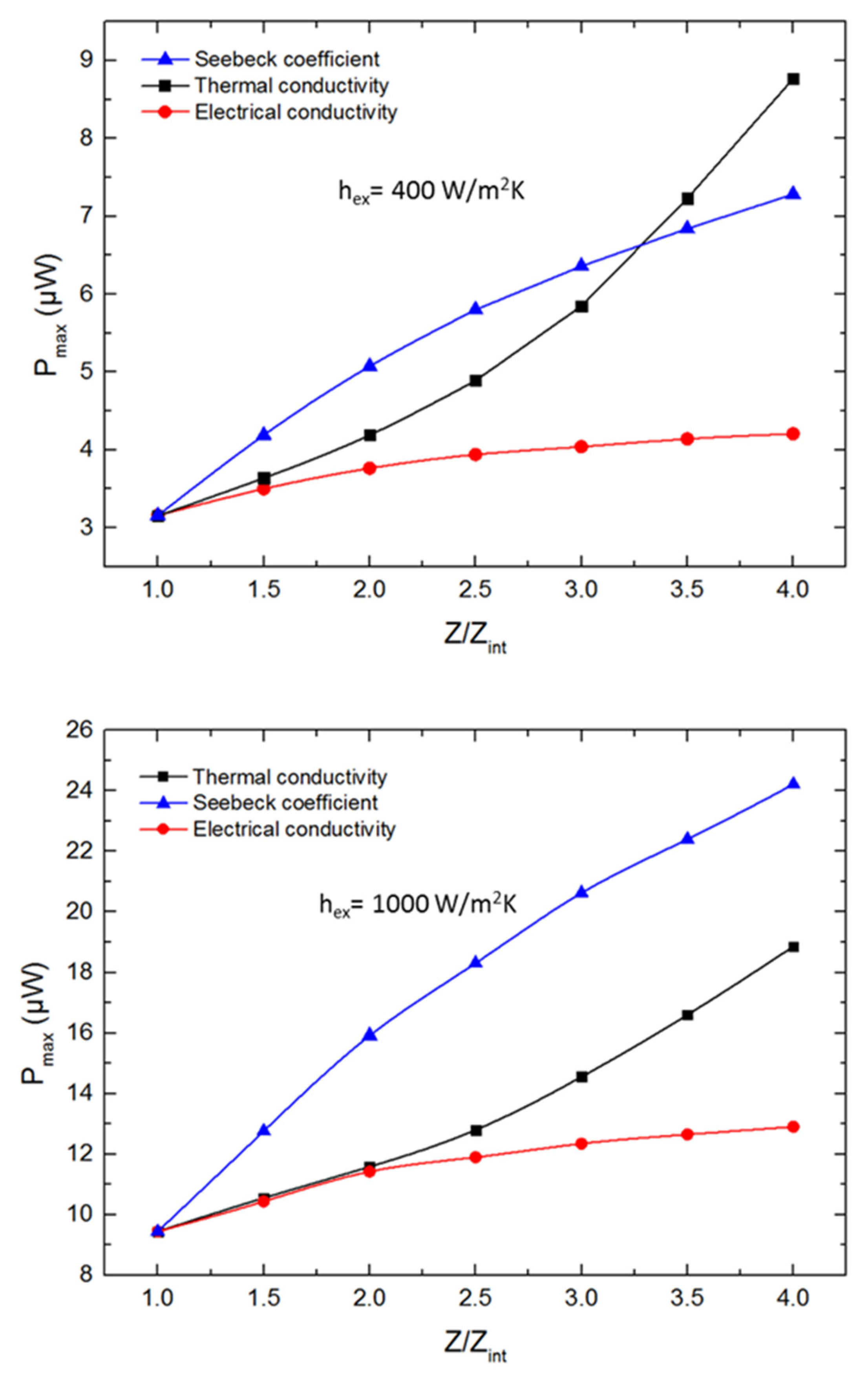
3.2.2. Influence of Thermoelectric Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thongkham, W.; Lertsatitthanakorn, C.; Jiramitmongkon, K.; Tantisantisom, K.; Boonkoom, T.; Jitpukdee, M.; Sinthiptharakoon, K.; Klamchuen, A.; Liangruksa, M.; Khanchaitit, P. Self-Assembled Three-Dimensional Bi2Te3 Nanowire–PEDOT:PSS Hybrid Nanofilm Network for Ubiquitous Thermoelectrics. ACS Appl. Mater. Interfaces 2019, 11, 6624–6633. [Google Scholar] [CrossRef]
- We, J.H.; Kim, S.J.; Cho, B.J. Hybrid composite of screen-printed inorganic thermoelectric film and organic conducting polymer for flexible thermoelectric power generator. Energy 2014, 73, 506–512. [Google Scholar] [CrossRef]
- Rösch, A.G.; Gall, A.; Aslan, S.; Hecht, M.; Franke, L.; Mallick, M.M.; Penth, L.; Bahro, D.; Friderich, D.; Lemmer, U. Fully printed origami thermoelectric generators for energy-harvesting. Npj Flex. Electron. 2021, 5, 1. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Liu, Y.; Wang, B.; Fang, L.; Qiu, J.; Zhang, K.; Wang, S. Exceptional thermoelectric properties of flexible organic−inorganic hybrids with monodispersed and periodic nanophase. Nat. Commun. 2018, 9, 3817. [Google Scholar] [CrossRef]
- Kim, M.-K.; Kim, M.S.; Lee, S.; Kim, C.; Kim, Y.-J. Wearable thermoelectric generator for harvesting human body heat energy. Smart Mater. Struct. 2014, 23, 105002. [Google Scholar] [CrossRef]
- Inayat, S.B.; Rader, K.R.; Hussain, M.M. Manufacturing of Thermoelectric Nanomaterials (Bi0.4Sb1.6Te3/Bi1.75Te3.25) and Integration into Window Glasses for Thermoelectricity Generation. Energy Technol. 2014, 2, 292–299. [Google Scholar] [CrossRef]
- Liang, J.; Wang, T.; Qiu, P.; Yang, S.; Ming, C.; Chen, H.; Song, Q.; Zhao, K.; Wei, T.-R.; Ren, D.; et al. Flexible thermoelectrics: From silver chalcogenides to full-inorganic devices. Energy Environ. Sci. 2019, 12, 2983–2990. [Google Scholar] [CrossRef]
- Shang, H.; Li, T.; Luo, D.; Yu, L.; Zou, Q.; Huang, D.; Xiao, L.; Gu, H.; Ren, Z.; Ding, F. High-Performance Ag-Modified Bi0.5Sb1.5Te3 Films for the Flexible Thermoelectric Generator. ACS Appl. Mater. Interfaces 2020, 12, 7358–7365. [Google Scholar] [CrossRef]
- Chen, B.; Kruse, M.; Xu, B.; Tutika, R.; Zheng, W.; Bartlett, M.D.; Wu, Y.; Claussen, J.C. Flexible thermoelectric generators with inkjet-printed bismuth telluride nanowires and liquid metal contacts. Nanoscale 2019, 11, 5222–5230. [Google Scholar] [CrossRef] [Green Version]
- Suarez, F.; Parekh, D.P.; Ladd, C.; Vashaee, D.; Dickey, M.D.; Öztürk, M.C. Flexible thermoelectric generator using bulk legs and liquid metal interconnects for wearable electronics. Appl. Energy 2017, 202, 736–745. [Google Scholar] [CrossRef]
- Mu, E.; Yang, G.; Fu, X.; Wang, F.; Hu, Z. Fabrication and characterization of ultrathin thermoelectric device for energy conversion. J. Power Sources 2018, 394, 17–25. [Google Scholar] [CrossRef]
- Takashiri, M.; Shirakawa, T.; Miyazaki, K.; Tsukamoto, H. Fabrication and characterization of bismuth–telluride-based alloy thin film thermoelectric generators by flash evaporation method. Sens. Actuators Phys. 2007, 138, 329–334. [Google Scholar] [CrossRef] [Green Version]
- Roth, R.; Rostek, R.; Cobry, K.; Kohler, C.; Groh, M.; Woias, P. Design and Characterization of Micro Thermoelectric Cross-Plane Generators with Electroplated Bi2Te3, SbxTey, and Reflow Soldering. J. Microelectromechanical Syst. 2014, 23, 961–971. [Google Scholar] [CrossRef]
- Glatz, W.; Schwyter, E.; Durrer, L.; Hierold, C. Bi2Te3-Based Flexible Micro Thermoelectric Generator with Optimized Design. J. Microelectromechanical Syst. 2009, 18, 763–772. [Google Scholar] [CrossRef]
- Kim, S.J.; We, J.H.; Cho, B.J. A wearable thermoelectric generator fabricated on a glass fabric. Energy Environ. Sci. 2014, 7, 1959–1965. [Google Scholar] [CrossRef]
- Kim, I.H. (Bi,Sb)2(Te,Se)3-based thin film thermoelectric generators. Mater. Lett. 2000, 43, 221–224. [Google Scholar] [CrossRef]
- Sun, T.; Zhou, B.; Zheng, Q.; Wang, L.; Jiang, W.; Snyder, G.J. Stretchable fabric generates electric power from woven thermoelectric fibers. Nat. Commun. 2020, 11, 572. [Google Scholar] [CrossRef]
- Nan, K.; Kang, S.D.; Li, K.; Yu, K.J.; Zhu, F.; Wang, J.; Dunn, A.C.; Zhou, C.; Xie, Z.; Agne, M.T.; et al. Compliant and stretchable thermoelectric coils for energy harvesting in miniature flexible devices. Sci. Adv. 2018, 4, eaau5849. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Zhang, Q.; Jin, W.; Jing, Y.; Chen, X.; Han, X.; Bao, Q.; Liu, Y.; Wang, X.; Wang, S.; et al. Carbon nanotube yarn based thermoelectric textiles for harvesting thermal energy and powering electronics. J. Mater. Chem. A 2020, 8, 2984–2994. [Google Scholar] [CrossRef]
- Zhang, Z.; Qiu, J.; Wang, S. Roll-to-roll printing of flexible thin-film organic thermoelectric devices. Manuf. Lett. 2016, 8, 6–10. [Google Scholar] [CrossRef]
- Leonov, V.; Torfs, T.; Fiorini, P.; Hoof, C.V. Thermoelectric Converters of Human Warmth for Self-Powered Wireless Sensor Nodes. IEEE Sens. J. 2007, 7, 650–657. [Google Scholar] [CrossRef]
- Lin, J.R.; Snyder, G.J.; Huang, C.-K.; Herman, J.A.; Ryan, M.A.; Fleurial, J.-P. Thermoelectric microdevice fabrication process and evaluation at the Jet Propulsion Laboratory (JPL). In Proceedings of the Twenty-First International Conference on Thermoelectrics, Long Beach, CA, USA, 25–29 August 2002; pp. 535–539. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, J.; Xu, D. A High Power Density Micro-Thermoelectric Generator Fabricated by an Integrated Bottom-Up Approach. J. Microelectromechanical Syst. 2016, 25, 744–749. [Google Scholar] [CrossRef]
- Jacquot, A.; Chen, G.; Scherrer, H.; Dauscher, A.; Lenoir, B. Modeling of on-membrane thermoelectric power supplies. Sens. Actuators Phys. 2004, 116, 501–508. [Google Scholar] [CrossRef]
- Strasser, M.; Aigner, R.; Franosch, M.; Wachutka, G. Miniaturized thermoelectric generators based on poly-Si and poly-SiGe surface micromachining. Sens. Actuators Phys. 2002, 97–98, 535–542. [Google Scholar] [CrossRef]
- Tainoff, D.; Proudhom, A.; Tur, C.; Crozes, T.; Dufresnes, S.; Dumont, S.; Bourgault, D.; Bourgeois, O. Network of thermoelectric nanogenerators for low power energy harvesting. Nano Energy 2019, 57, 804–810. [Google Scholar] [CrossRef] [Green Version]
- Ziouche, K.; Yuan, Z.; Lejeune, P.; Lasri, T.; Leclercq, D.; Bougrioua, Z. Silicon-Based Monolithic Planar Micro Thermoelectric Generator Using Bonding Technology. J. Microelectromechanical Syst. 2017, 26, 45–47. [Google Scholar] [CrossRef]
- Yu, Y.; Guo, Z.; Zhu, W.; Zhou, J.; Guo, S.; Wang, Y.; Deng, Y. High-integration and high-performance micro thermoelectric generator by femtosecond laser direct writing for self-powered IoT devices. Nano Energy 2022, 93, 106818. [Google Scholar] [CrossRef]
- Wu, B.; Guo, Y.; Hou, C.; Zhang, Q.; Li, Y.; Wang, H. From carbon nanotubes to highly adaptive and flexible high-performance thermoelectric generators. Nano Energy 2021, 89, 106487. [Google Scholar] [CrossRef]
- Zhou, J.; Zhu, W.; Xie, Y.; Yu, Y.; Guo, Z.; Zhang, Q.; Liu, Y.; Deng, Y. Rapid Selective Ablation and High-Precision Patterning for Micro-Thermoelectric Devices Using Femtosecond Laser Directing Writing. ACS Appl. Mater. Interfaces 2022, 14, 3066–3075. [Google Scholar] [CrossRef]
- Stordeur, M.; Willers, G. Thermoelectric films–potential for new miniaturized devices. In Proceedings of the 2nd European Conference on Thermoelectrics, Kraków, Poland, 15–17 September 2004. [Google Scholar]
- Yan, J.; Liao, X.; Yan, D.; Chen, Y. Review of Micro Thermoelectric Generator. J. Microelectromechanical Syst. 2018, 27, 1–18. [Google Scholar] [CrossRef]
- Ihou Mouko, H.; Romanjek, K.; Mejri, M.; Oulfarsi, M.; El Oualid, S.; Malinconi, P.; Thimont, Y.; Malard, B.; Estournès, C.; David, N.; et al. Manufacturing and performances of silicide-based thermoelectric modules. Energy Convers. Manag. 2021, 242, 114304. [Google Scholar] [CrossRef]
- El Oualid, S.; Kogut, I.; Benyahia, M.; Geczi, E.; Kruck, U.; Kosior, F.; Masschelein, P.; Candolfi, C.; Dauscher, A.; Koenig, J.D.; et al. High-Power Density Thermoelectric Generators with Skutterudites. Adv. Energy Mater. 2021, 11, 2100580. [Google Scholar] [CrossRef]
- El Oualid, S.; Kosior, F.; Dauscher, A.; Candolfi, C.; Span, G.; Mehmedovic, E.; Paris, J.; Lenoir, B. Innovative design of bismuth-telluride-based thermoelectric micro-generators with high output power. Energy Environ. Sci. 2020, 13, 3579–3591. [Google Scholar] [CrossRef]
- Nozariasbmarz, A.; Suarez, F.; Dycus, J.H.; Cabral, M.J.; LeBeau, J.M.; Öztürk, M.C.; Vashaee, D. Thermoelectric generators for wearable body heat harvesting: Material and device concurrent optimization. Nano Energy 2020, 67, 104265. [Google Scholar] [CrossRef]
- Mayer, P.M.; Ram, R.J. Optimization of Heat Sink–Limited Thermoelectric Generators. Nanoscale Microscale Thermophys. Eng. 2006, 10, 143–155. [Google Scholar] [CrossRef]
- Apertet, Y.; Ouerdane, H.; Glavatskaya, O.; Goupil, C.; Lecoeur, P. Optimal working conditions for thermoelectric generators with realistic thermal coupling. EPL Europhys. Lett. 2012, 97, 28001. [Google Scholar] [CrossRef]





| n Type | p Type | Copper | Polyimide | |
|---|---|---|---|---|
| Electrical conductivity (S m−1) | 105,000 | 76,000 | 5.99 × 108 | - |
| Thermal conductivity (W m−1 K−1) | 0.75 | 0.75 | 400 | 0.15 |
| Specific heat (J kg−1 K−1) | 190 | 190 | 385 | 0.904 |
| Density (g cm−3) | 7.70 | 7.74 | 8.96 | 1.4 |
| Seebeck coefficient (µV K−1) | −130 | 210 | 6.5 | - |
| Geometrical Parameter | Lcop | Wcop | hcop | hpoly | b | lgap | m | e | d |
|---|---|---|---|---|---|---|---|---|---|
| Value (mm) | 2 | 3 | 0.07 | 0.10 | 0.09 | 0.50 | 0.10 | 0.50 | 0.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Oualid, S.; Kosior, F.; Span, G.; Mehmedovic, E.; Paris, J.; Candolfi, C.; Lenoir, B. Influence of Thermoelectric Properties and Parasitic Effects on the Electrical Power of Thermoelectric Micro-Generators. Energies 2022, 15, 3746. https://doi.org/10.3390/en15103746
El Oualid S, Kosior F, Span G, Mehmedovic E, Paris J, Candolfi C, Lenoir B. Influence of Thermoelectric Properties and Parasitic Effects on the Electrical Power of Thermoelectric Micro-Generators. Energies. 2022; 15(10):3746. https://doi.org/10.3390/en15103746
Chicago/Turabian StyleEl Oualid, Soufiane, Francis Kosior, Gerhard Span, Ervin Mehmedovic, Janina Paris, Christophe Candolfi, and Bertrand Lenoir. 2022. "Influence of Thermoelectric Properties and Parasitic Effects on the Electrical Power of Thermoelectric Micro-Generators" Energies 15, no. 10: 3746. https://doi.org/10.3390/en15103746
APA StyleEl Oualid, S., Kosior, F., Span, G., Mehmedovic, E., Paris, J., Candolfi, C., & Lenoir, B. (2022). Influence of Thermoelectric Properties and Parasitic Effects on the Electrical Power of Thermoelectric Micro-Generators. Energies, 15(10), 3746. https://doi.org/10.3390/en15103746







