A Novel Layered Slice Algorithm for Soil Heat Storage and Its Solving Performance Analysis
Abstract
:1. Introduction
2. Physical and Mathematical Models
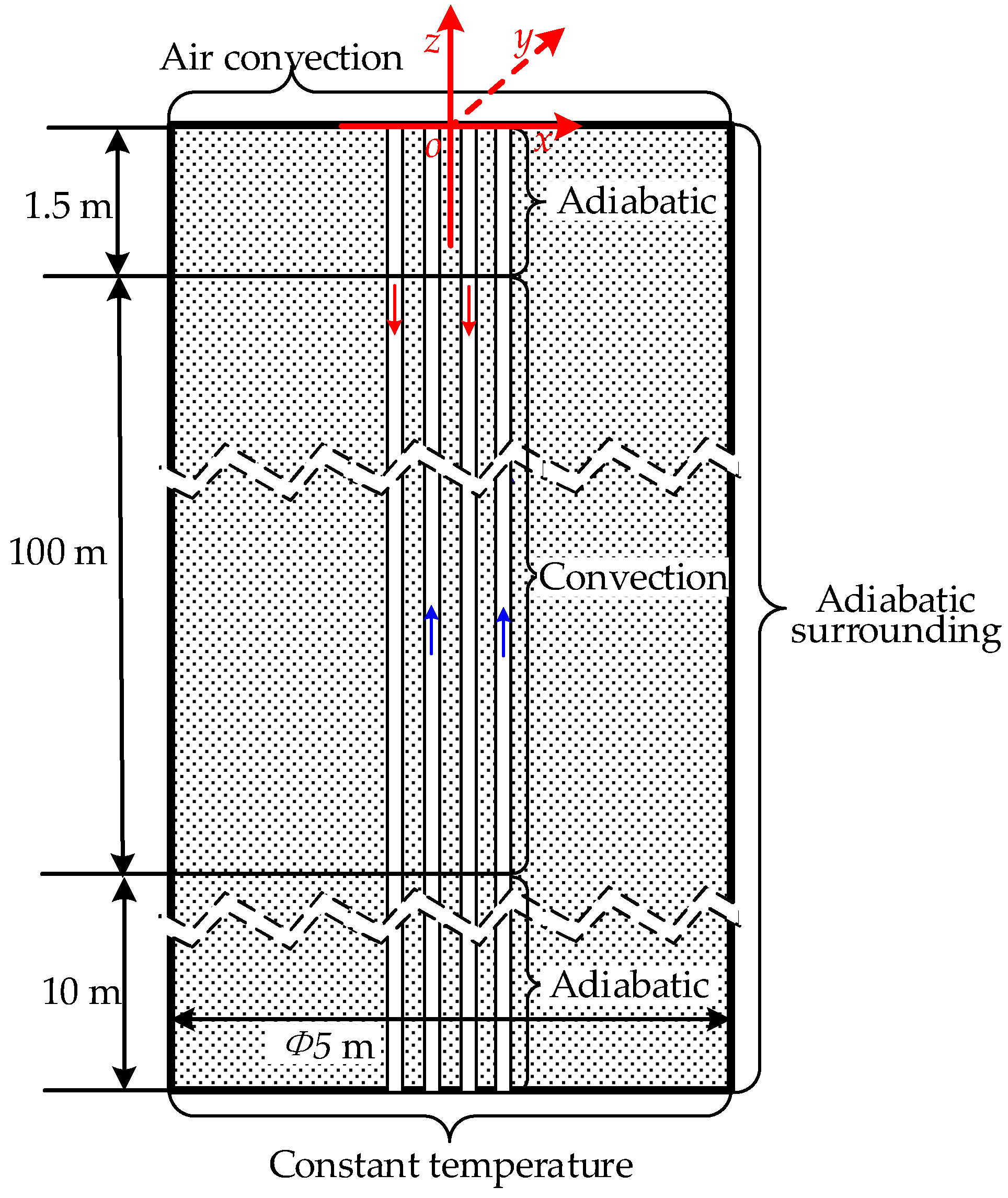
2.1. Physical Model
- (1)
- The backfill still uses the original soil;
- (2)
- The effective thermophysical properties are adopted instead of the actual soil parameter and are set as constants. Then, the complex coupling process in the soil can be regarded as a single heat conduction problem;
- (3)
- Water is selected as the working medium in the U-type tube and is assumed to be an incompressible fluid;
- (4)
- A U-type tube is simplified as two straight tubes with opposite flow directions and equal bottom temperature.
2.2. Mathematical Model
2.2.1. Governing Equation for Convection Heat Transfer Inside the Tube
2.2.2. Governing Equation for Generalized Heat-Storage Body
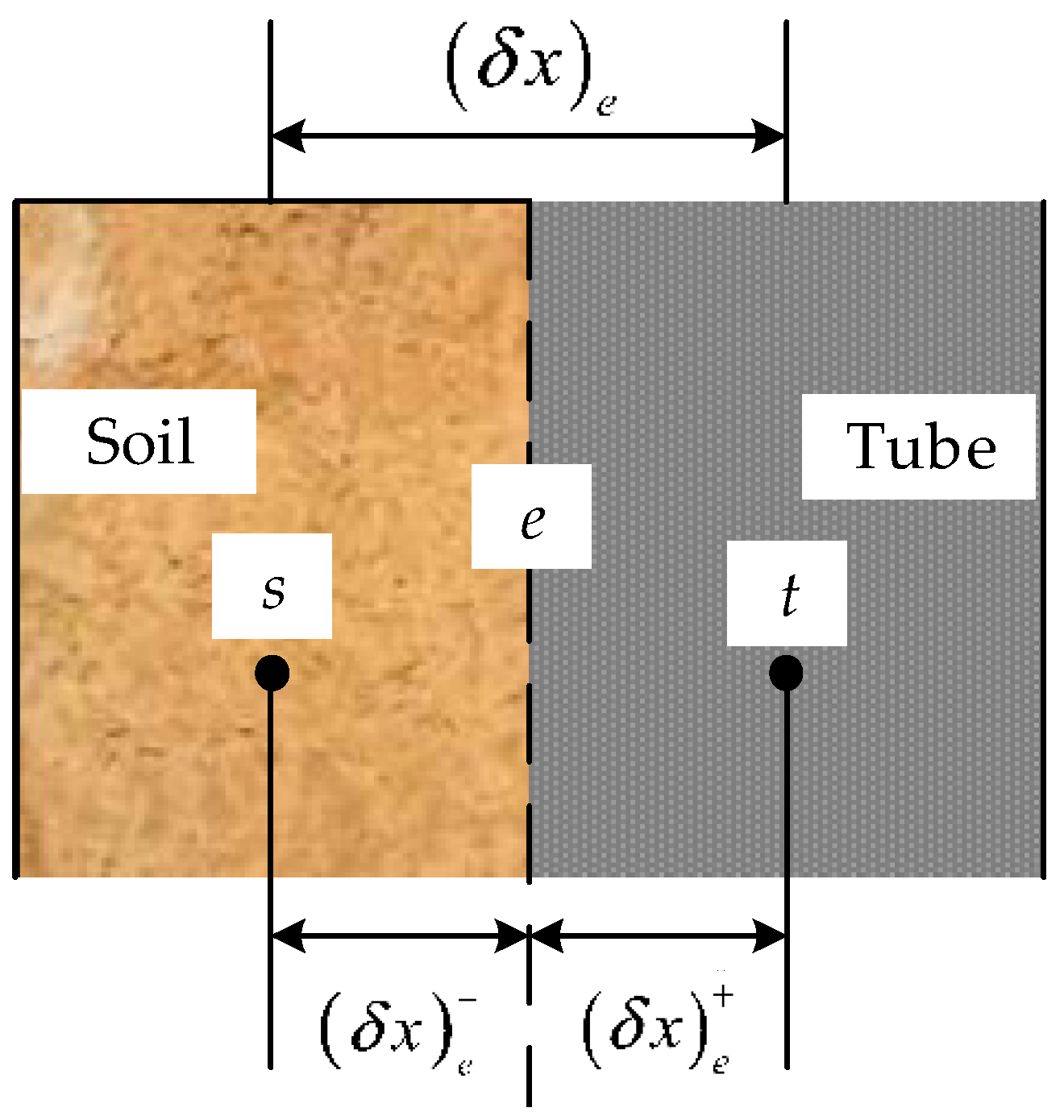
2.2.3. Treatment of Interface between Tube and Soil
2.2.4. Boundary Conditions
3. Numerical Simulation Method
3.1. Traditional 3D Simulation Algorithm
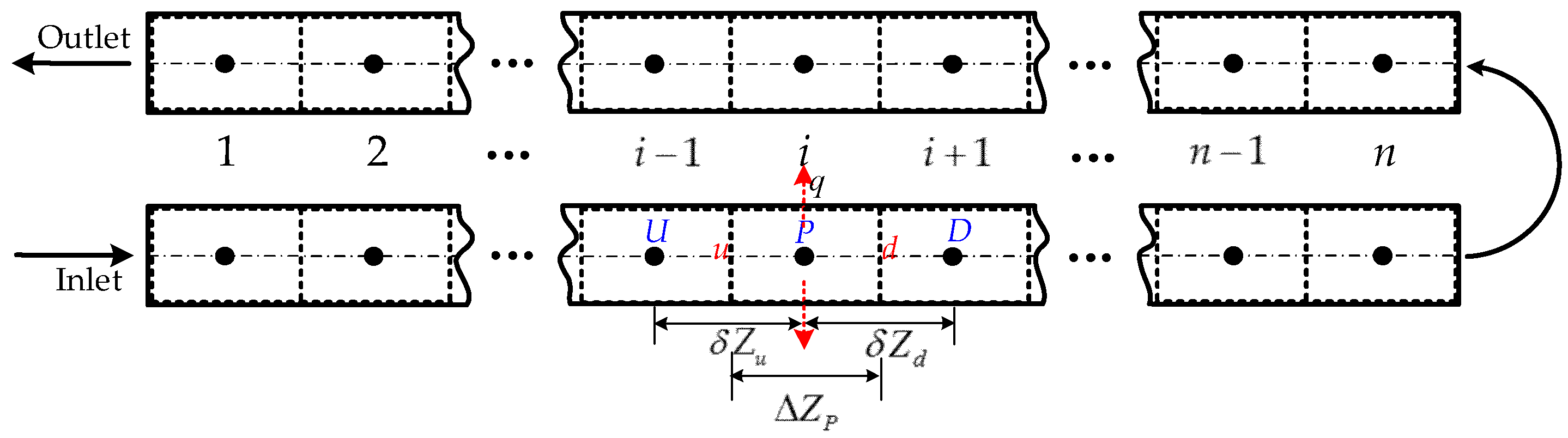
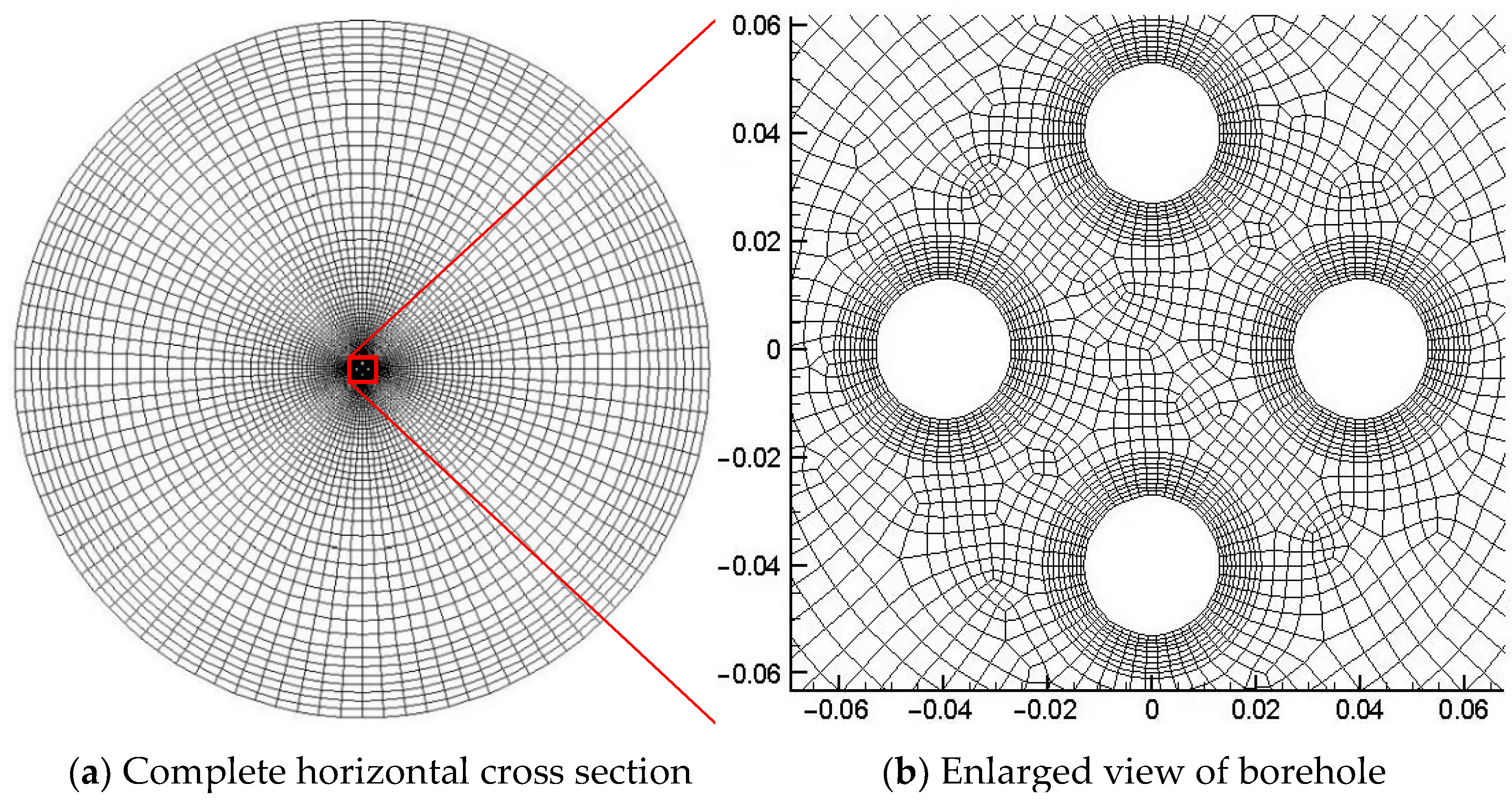
3.1.1. Discretization of the Computation Domain
3.1.2. Discretization and Solution of Energy Equation for In-Tube Fluid
3.1.3. Discretization and Solution of Energy Equation for Generalized Heat-Storage Body
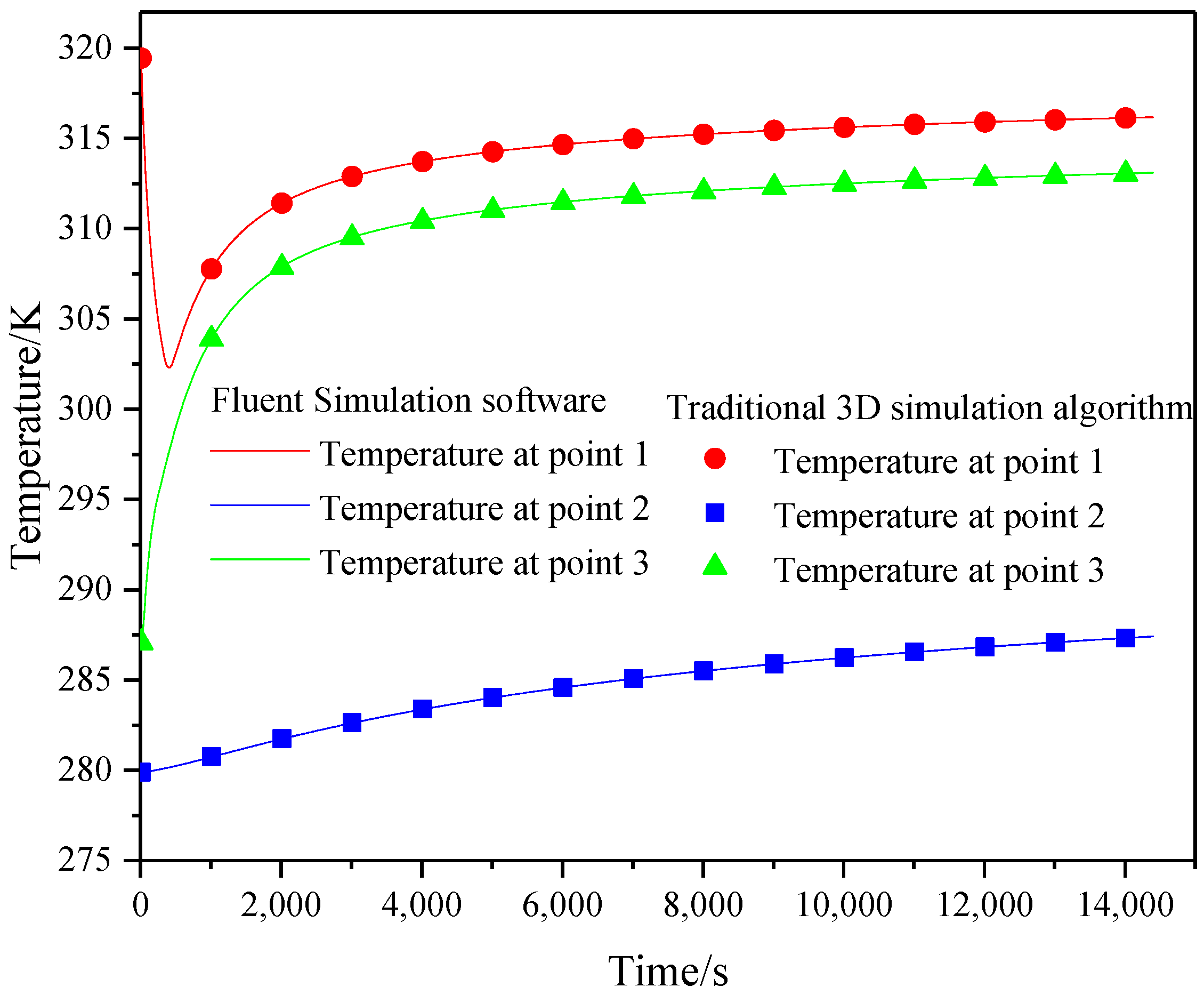
3.1.4. Traditional 3D Simulation Algorithm Self-Programming Accuracy Verification
3.2. Layered Slice Algorithm
3.2.1. Discretization of the Computation Domain
3.2.2. Solution Procedure of Layered Slice Algorithm
4. Numerical Comparisons and Analyses
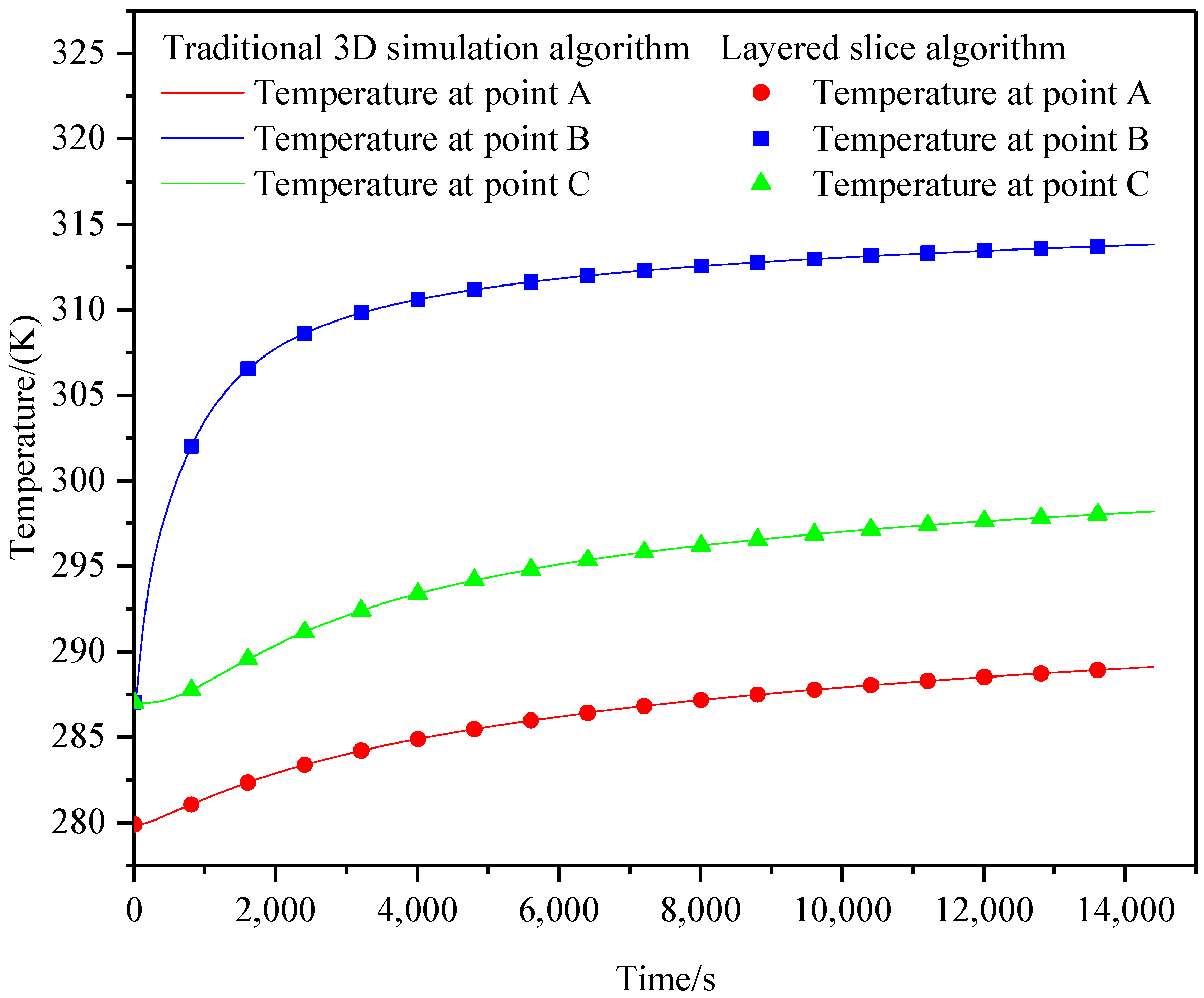
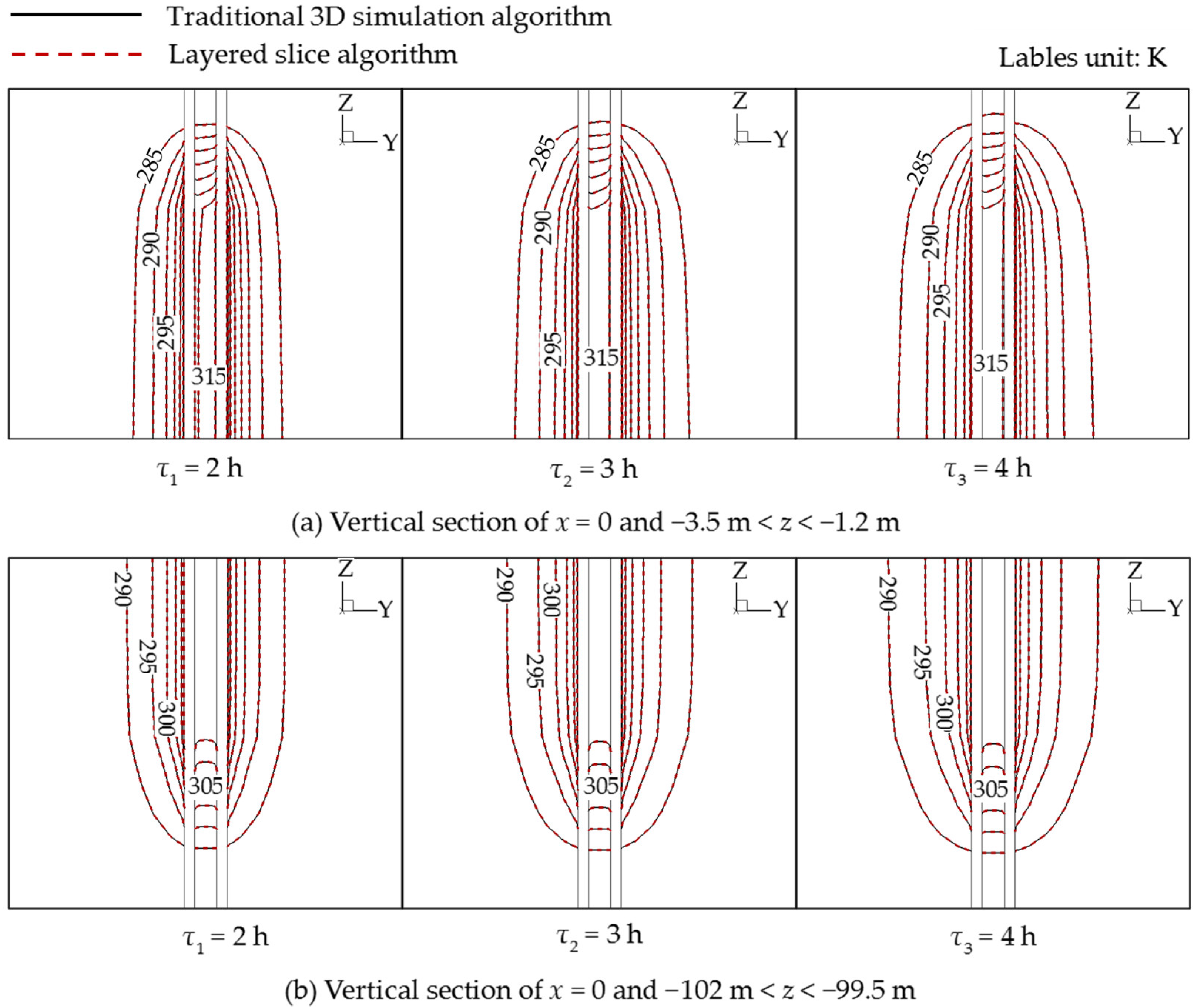
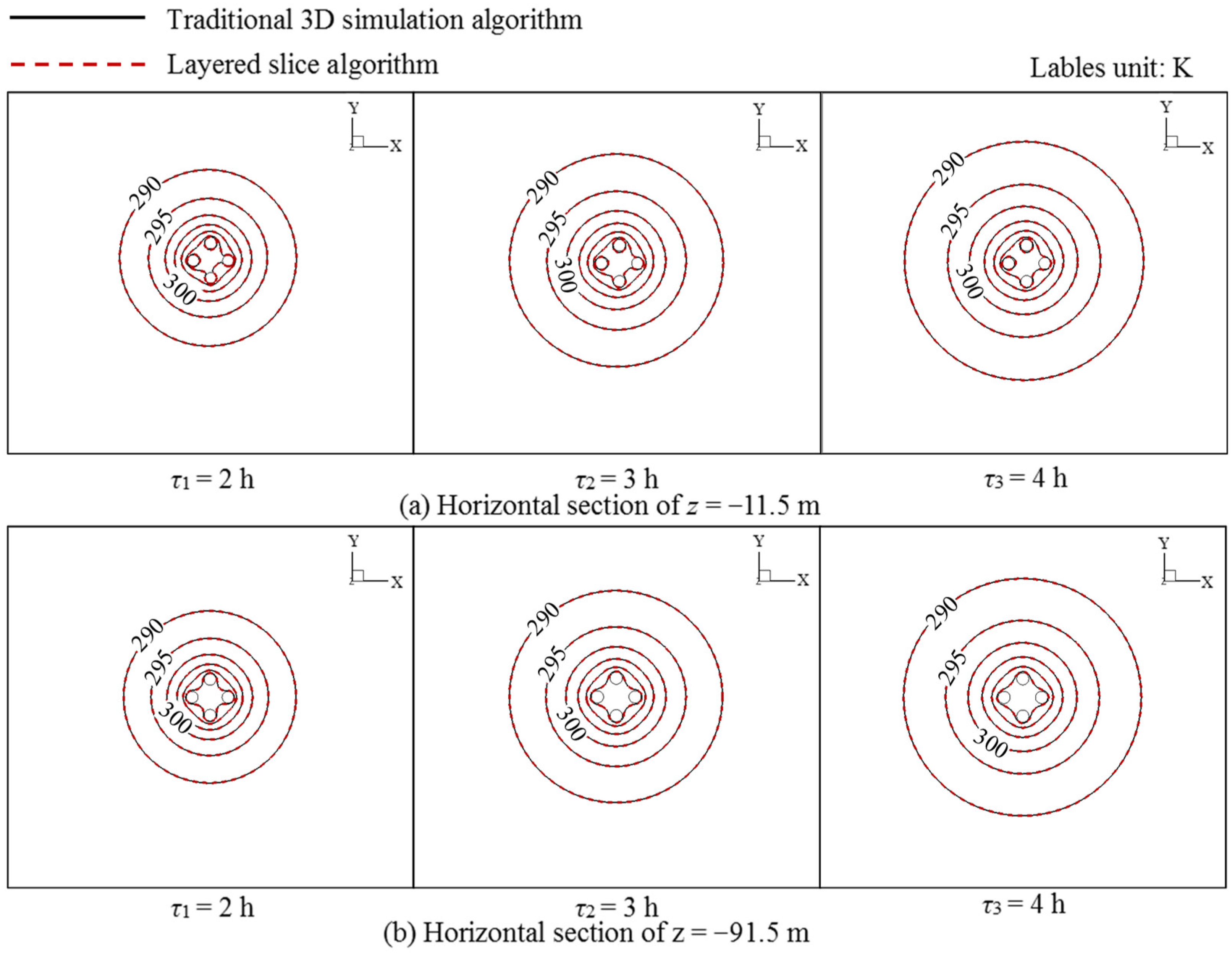
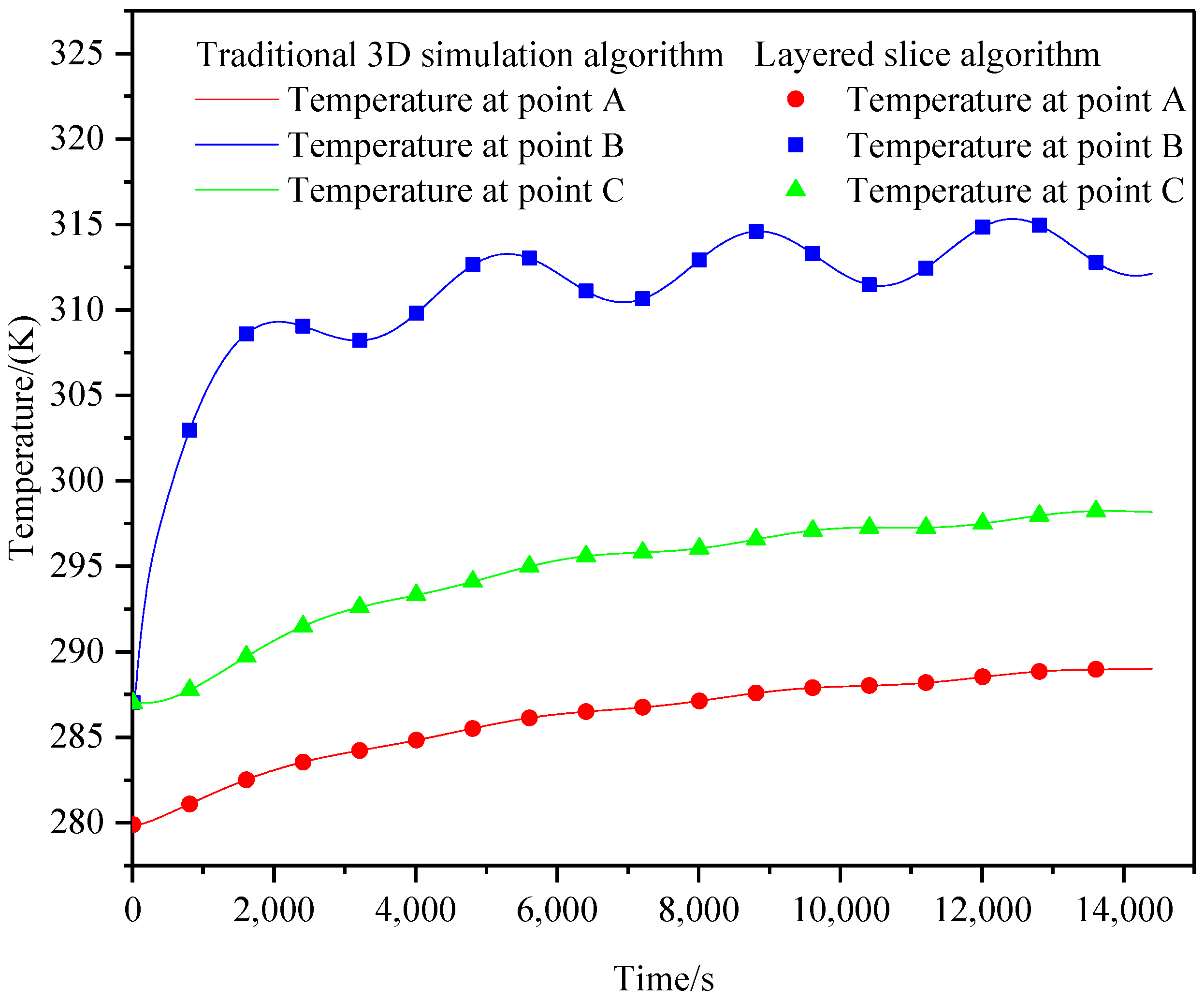
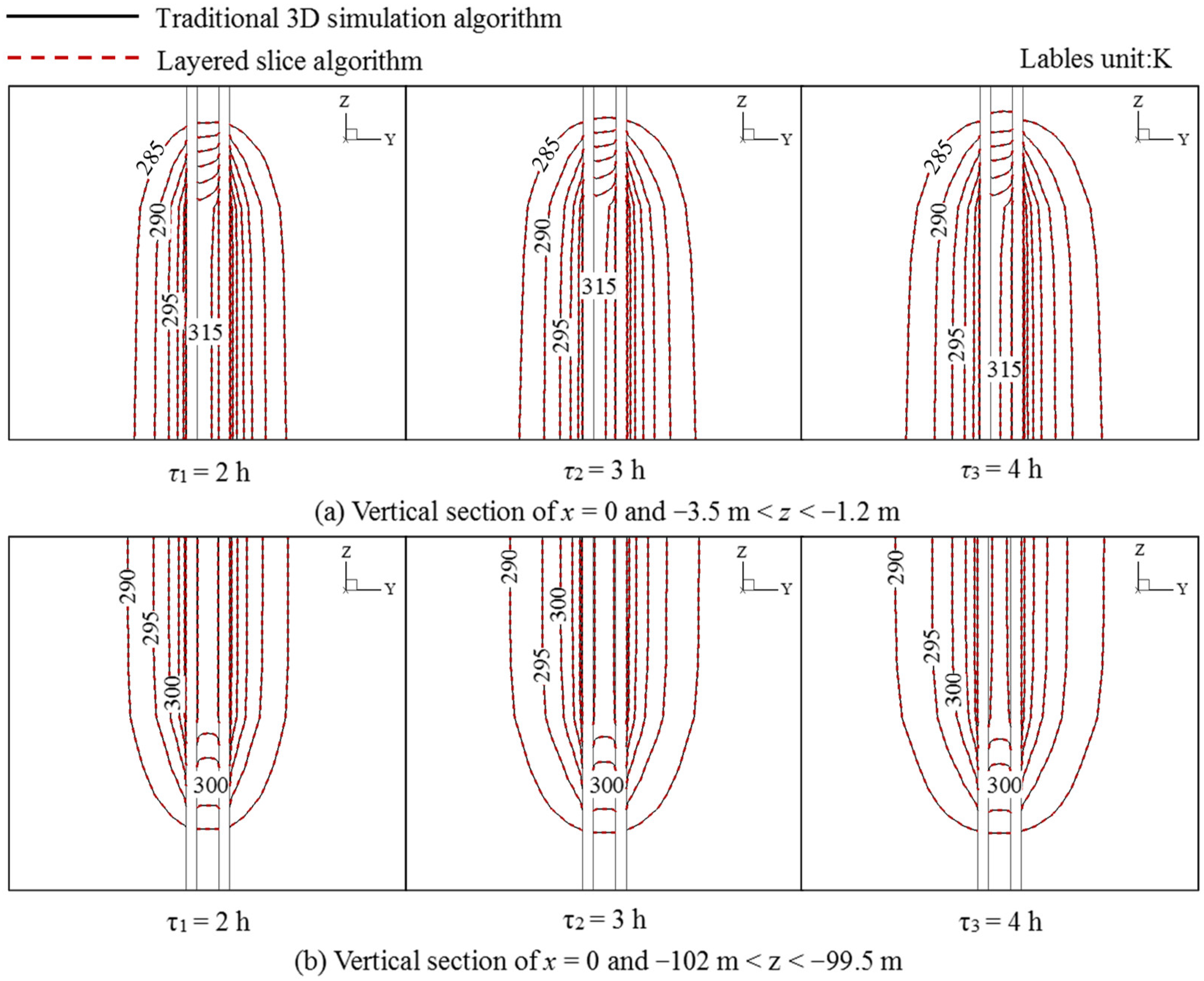
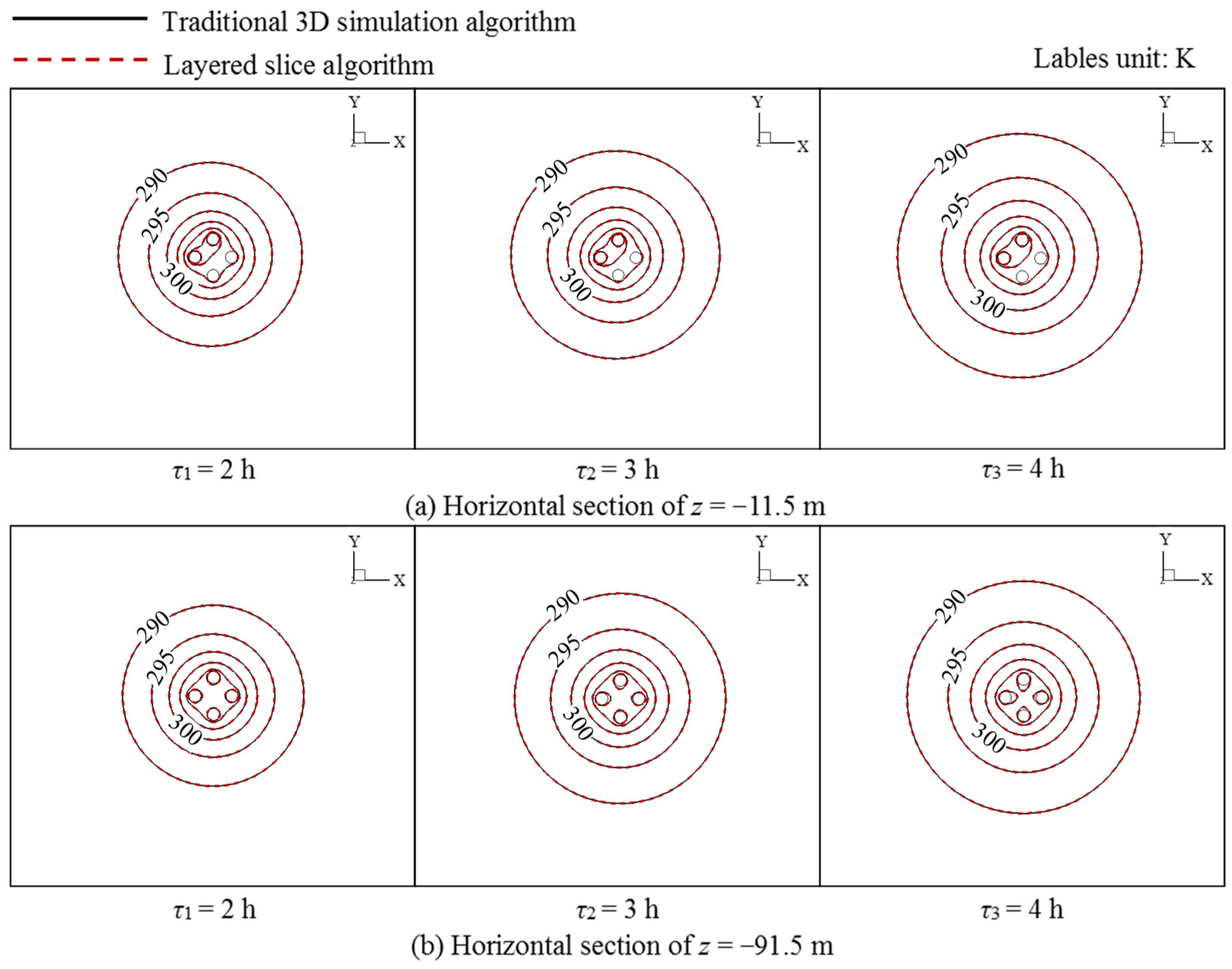
4.1. Accuracy Verification of Layered Slice Algorithm
4.1.1. Fixed Inlet Temperature
4.1.2. Periodic Inlet Temperature
4.2. Solution Speed Analysis of Layered Slice Algorithm
4.2.1. The Influence of Grid Number
4.2.2. The Influence of Time Step
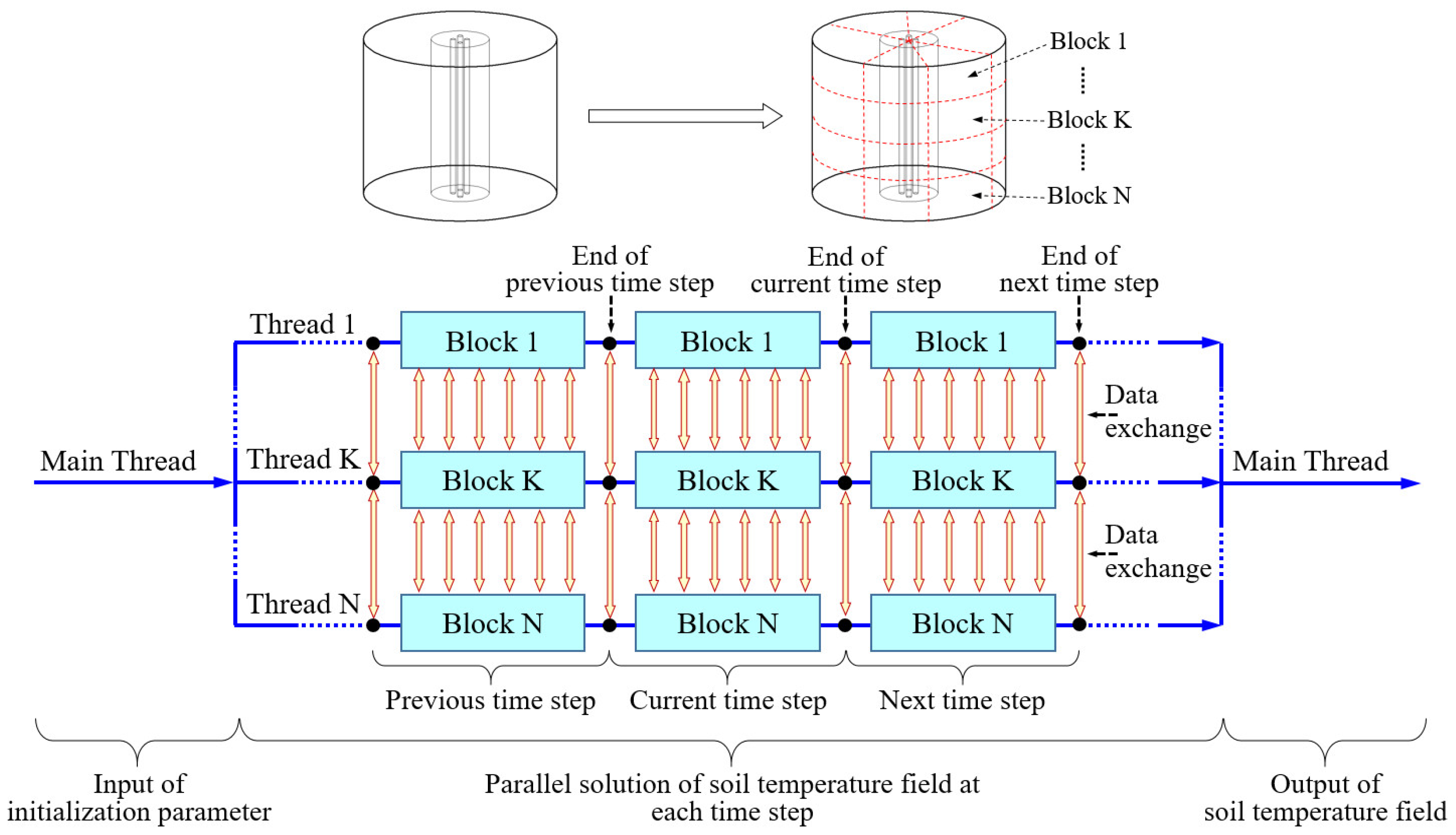
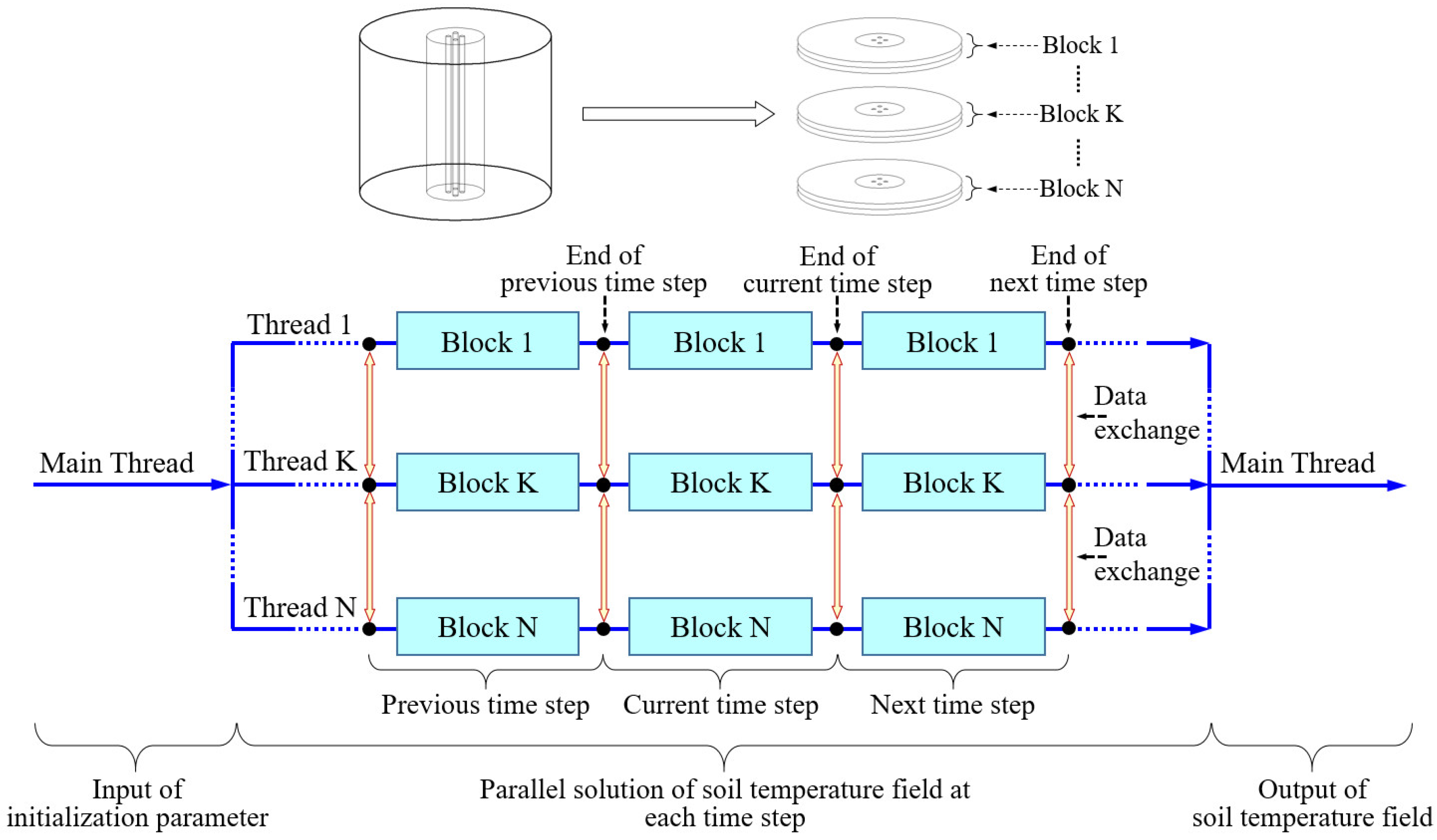
4.3. Parallel Characteristic Analysis of Layered Slice Algorithm
4.3.1. Parallel Computing Principle
4.3.2. Parallel Performance Analysis
- (1)
- Qualitative analysis
- (2)
- Quantitative comparison
5. Conclusions
- (1)
- The layered slice algorithm has a high simulation precision. For both cases of the fixed and periodic inlet temperatures, the maximum relative errors are only 0.18% and 0.19%, respectively;
- (2)
- The layered slice algorithm can simplify and speed up the solution process. The layered slice algorithm transforms the 3D solution process into 2D heat transfer solutions on different horizontal slices. Due to the reduction of dimensionality, the proposed algorithm has an evident accelerating effect. Compared with the traditional 3D algorithm, its calculation speed improves by 2.2~2.56 times under different grid numbers and time steps;
- (3)
- The layered slice algorithm has an excellent parallel characteristic. The parallel acceleration effect of the layered slice algorithm is better than that of the traditional 3D algorithm. The maximum parallel speedup ratio of the layered slice algorithm is 4.17, while the traditional 3D algorithm is only 1.75.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| area vector of control-volume face j, m2 | |
| c | specific heat, J/(kg·K) |
| normal diffusion fluxes, W | |
| cross diffusion fluxes, W | |
| h | convective heat transfer coefficient, W/(m2·K) |
| n | thread number |
| r | tube radius, m |
| Sp | parallel speedup ratio |
| T | temperature, K |
| , | volume of the control volume, m3 |
| , | interpolation factors |
| z | soil depth, m |
| λ | thermal conductivity coefficient, W/(m·K) |
| ρ | density, kg/m3 |
| τ1 | time consumption of necessary serial computing part, s |
| τ2 | time consumption of parallel computing part, s |
| τ3 | time consumption of data exchange among different threads, s |
| Subscript | |
| D | downstream grid point of control volume |
| d | downstream face of control volume |
| e | interface between soil and tube |
| f | fluid in the tube |
| L | layered slice algorithm |
| opt | optimal thread number |
| P | grid point of control volume |
| s | soil |
| T | traditional 3D simulation algorithm |
| t | tube |
| ts | inner surface of the tube |
| U | upstream grid point of control volume |
| u | upstream face of control volume |
| Superscript | |
| 0 | current time step |
References
- Riahi, S.; Jovet, Y.; Saman, W.Y.; Belusko, M.; Bruno, F. Sensible and latent heat energy storage systems for concentrated solar power plants, exergy efficiency comparison. Sol. Energy 2019, 180, 104–115. [Google Scholar] [CrossRef]
- Tehrani, S.S.M.; Shoraka, Y.; Nithyanandam, K.; Taylor, R.A. Shell-and-tube or packed bed thermal energy storage systems integrated with a concentrated solar power: A techno-economic comparison of sensible and latent heat systems. Appl. Energy 2019, 238, 887–910. [Google Scholar] [CrossRef]
- Henríquez-Vargas, L.; Angel, F.; Reyes, A.; Pailahueque, N.; Donoso-García, P. Simulation of a solar energy accumulator based on phase change materials. Numer. Heat Transf. Part A Appl. 2020, 77, 443–459. [Google Scholar] [CrossRef]
- Kursun, B. Thermal stratification enhancement in cylindrical and rectangular hot water tanks with truncated cone and pyramid shaped insulation geometry. Sol. Energy 2018, 169, 512–525. [Google Scholar] [CrossRef]
- Dahash, A.; Ochs, F.; Janetti, M.B.; Streicher, W. Advances in seasonal thermal energy storage for solar district heating applications: A critical review on large-scale hot-water tank and pit thermal energy storage systems. Appl. Energy 2019, 239, 296–315. [Google Scholar] [CrossRef]
- Erdemir, D.; Atesoglu, H.; Altuntop, N. Experimental investigation on enhancement of thermal performance with obstacle placing in the horizontal hot water tank used in solar domestic hot water system. Renew. Energy 2019, 138, 187–197. [Google Scholar] [CrossRef]
- Lee, K.S. Numerical Simulation on the Continuous Operation of an Aquifer Thermal Energy Storage System Under Regional Groundwater Flow. Energy Sources Part A-Recovery Util. Environ. Eff. 2011, 33, 1018–1027. [Google Scholar] [CrossRef]
- Fleuchaus, P.; Godschalk, B.; Stober, I.; Blum, P. Worldwide application of aquifer thermal energy storage—A review. Renew. Sustain. Energy Rev. 2018, 94, 861–876. [Google Scholar] [CrossRef]
- Lu, H.; Tian, P.; Guan, Y.; Yu, S. Integrated suitability, vulnerability and sustainability indicators for assessing the global potential of aquifer thermal energy storage. Appl. Energy 2019, 239, 747–756. [Google Scholar] [CrossRef]
- Li, Y.; Liu, S.; Wang, S.; Miao, Y.; Chen, B. Comparative study on methods for computing soil heat storage and energy balance in arid and semi-arid areas. J. Meteorol. Res. 2014, 28, 308–322. [Google Scholar] [CrossRef]
- Tong, C.; Li, X.; Duanmu, L.; Wang, Z. Research on heat transfer characteristics of soil thermal storage in the non-heating season. Procedia Eng. 2017, 205, 3293–3300. [Google Scholar] [CrossRef]
- Jahangir, M.H.; Ghazvini, M.; Pourfayaz, F.; Ahmadi, M.H.; Sharifpur, M.; Meyer, J.P. Numerical investigation into mutual effects of soil thermal and isothermal properties on heat and moisture transfer in unsaturated soil applied as thermal storage system. Numer. Heat Transf. Part A Appl. 2018, 73, 466–481. [Google Scholar] [CrossRef]
- Pfeil, M.; Koch, H. High performance–low cost seasonal gravel/water storage pit. Sol. Energy 2000, 69, 461–467. [Google Scholar] [CrossRef]
- Novo, A.V.; Bayon, J.R.; Castro-Fresno, D.; Rodriguez-Hernandez, J. Review of seasonal heat storage in large basins: Water tanks and gravel–water pits. Appl. Energy 2010, 87, 390–397. [Google Scholar] [CrossRef]
- Bott, C.; Dressel, I.; Bayer, P. State-of-technology review of water-based closed seasonal thermal energy storage systems. Renew. Sustain. Energy Rev. 2019, 113, 109241. [Google Scholar] [CrossRef]
- Umair, M.M.; Zhang, Y.; Iqbal, K.; Zhang, S.; Tang, B. Novel strategies and supporting materials applied to shape-stabilize organic phase change materials for thermal energy storage-A review. Appl. Energy 2019, 235, 846–873. [Google Scholar] [CrossRef]
- Wang, N.; Liu, K.; Hu, J.; Wang, X. Simulation of operation performance of a solar assisted ground heat pump system with phase change thermal storage for heating in a rural building in Xi’an. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Hong Kong, China, 3–5 December 2018; p. 012062. [Google Scholar]
- Liu, C.; Xu, Z.; Song, Y.; Lv, P.; Zhao, J.; Liu, C.; Huo, Y.; Xu, B.; Zhu, C.; Rao, Z. A novel shape-stabilization strategy for phase change thermal energy storage. J. Mater. Chem. A 2019, 7, 8194–8203. [Google Scholar] [CrossRef]
- Guo, P.; Wang, Y.; Li, J.; Wang, Y. Thermodynamic analysis of a solar chimney power plant system with soil heat storage. Appl. Therm. Eng. 2016, 100, 1076–1084. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, P.; Mao, J.; Tang, X.; Li, Z.; Shi, J. A low cost seasonal solar soil heat storage system for greenhouse heating: Design and pilot study. Appl. Energy 2015, 156, 213–222. [Google Scholar] [CrossRef]
- Zhu, N.; Hu, P.; Xu, L.; Jiang, Z.; Lei, F. Recent research and applications of ground source heat pump integrated with thermal energy storage systems: A review. Appl. Therm. Eng. 2014, 71, 142–151. [Google Scholar] [CrossRef]
- You, T.; Wu, W.; Shi, W.; Wang, B.; Li, X. An overview of the problems and solutions of soil thermal imbalance of ground-coupled heat pumps in cold regions. Appl. Energy 2016, 177, 515–536. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, W.; Zhai, X.; Qian, C.; Chen, X. Feasibility and performance study of the hybrid ground-source heat pump system for one office building in Chinese heating dominated areas. Renew. Energy 2017, 101, 1131–1140. [Google Scholar] [CrossRef]
- Nouri, G.; Noorollahi, Y.; Yousefi, H. Solar assisted ground source heat pump systems—A review. Appl. Therm. Eng. 2019, 163, 114351. [Google Scholar] [CrossRef]
- Nouri, G.; Noorollahi, Y.; Yousefi, H. Designing and optimization of solar assisted ground source heat pump system to supply heating, cooling and hot water demands. Geothermics 2019, 82, 212–231. [Google Scholar] [CrossRef]
- Guo, D.; Zhu, J. Application of industrial waste heat to water-source heat pump. Refrig. Air-Cond. 2008, 8, 140–145. [Google Scholar]
- Guo, M.; Diao, N.; Man, Y.; Fang, Z. Research and development of the hybrid ground-coupled heat pump technology in China. Renew. Energy 2016, 87, 1033–1044. [Google Scholar] [CrossRef]
- Naranjo-Mendoza, C.; Oyinlola, M.A.; Wright, A.J.; Greenough, R.M. Experimental study of a domestic solar-assisted ground source heat pump with seasonal underground thermal energy storage through shallow boreholes. Appl. Therm. Eng. 2019, 162, 114218. [Google Scholar] [CrossRef]
- Cui, P.; Diao, N.; Gao, C.; Fang, Z. Thermal investigation of in-series vertical ground heat exchangers for industrial waste heat storage. Geothermics 2015, 57, 205–212. [Google Scholar] [CrossRef]
- Guo, F.; Yang, X.; Xu, L.; Torrens, I.; Hensen, J. A central solar-industrial waste heat heating system with large scale borehole thermal storage. Procedia Eng. 2017, 205, 1584–1591. [Google Scholar] [CrossRef]
- Li, M.; Yu, Y. Research progress of thermal response test for GSHP system. Refrig. Air-Cond. 2010, 10, 31–34. [Google Scholar]
- Spitler, J.D.; Gehlin, S.E.A. Thermal response testing for ground source heat pump systems—An historical review. Renew. Sustain. Energy Rev. 2015, 50, 1125–1137. [Google Scholar] [CrossRef]
- Zeng, H.Y.; Diao, N.R.; Fang, Z.H. A finite line-source model for boreholes in geothermal heat exchangers. Heat Transf.—Asian Res. 2002, 31, 558–567. [Google Scholar] [CrossRef]
- Lamarche, L.; Beauchamp, B. A new contribution to the finite line-source model for geothermal boreholes. Energy Build. 2007, 39, 188–198. [Google Scholar] [CrossRef]
- Deerman, J.D.; Kavanaugh, S.P. Simulation of vertical U-tube ground-coupled heat pump systems using the cylindrical heat source solution. ASHRAE Trans. Res. 1990, 3472, 287–295. [Google Scholar]
- Yang, W.; Shi, M. Study on cylindrical source theory based on vertical u-tube ground heat exchangers and it’s application. J. Refrig. 2006, 27, 51–57. [Google Scholar]
- Lee, C.K.; Lam, H.N. Computer simulation of borehole ground heat exchangers for geothermal heat pump systems. Renew. Energy 2008, 33, 1286–1296. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, M. Development of a numerical model for the simulation of vertical U-tube ground heat exchangers. Appl. Therm. Eng. 2009, 29, 920–924. [Google Scholar] [CrossRef]
- Yv, C.Y. Research on Heating System of Solar Energy Inter Seasonal Heat Storage Composite Ground Source Heat Pump for Agricultural Greenhouse. Master’s Thesis, Beijing Institute of Petrochemical Technology, Beijing, China, 2020. [Google Scholar]
- Sun, D.; Wang, L.; Xu, J.; Lu, X. Research and Application of Temperature Stratification Model for Seasonal Water Tank Heat Storage. Acta Energ. Sol. Sin. 2014, 35, 291–298. [Google Scholar]
- Tao, W. Modern Development of Computational Heat Transfer; Science Press: Beijing, China, 2000. [Google Scholar]
- Peng, X.; Chen, G.; Yu, P.; Zhang, Y.; Guo, L.; Wang, C.; Cheng, X.; Niu, H. Parallel computing of three-dimensional discontinuous deformation analysis based on OpenMP. Comput. Geotech. 2019, 106, 304–313. [Google Scholar] [CrossRef]

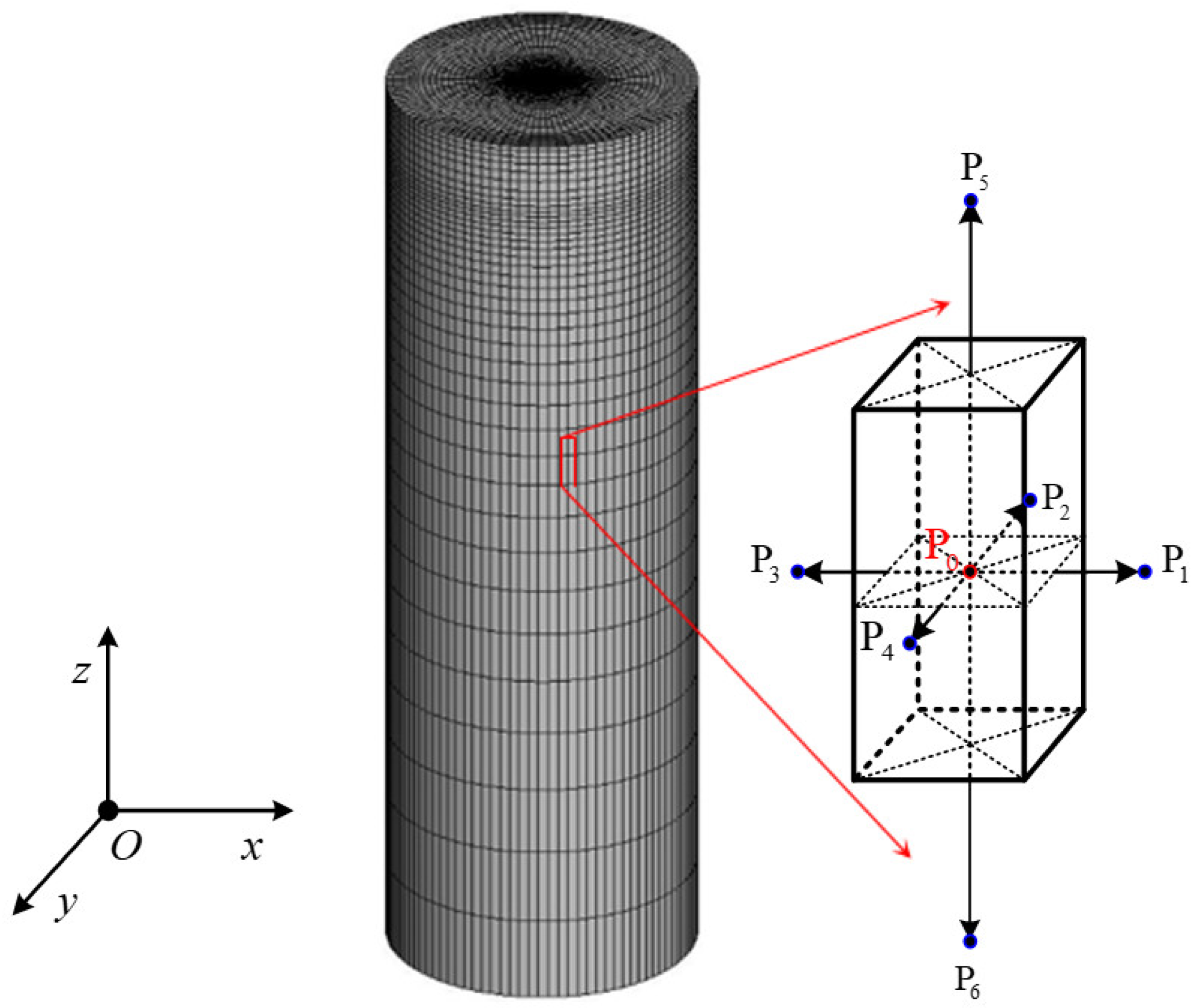

| Medium | Thermal Conductivity Coefficient λ [W/(m·K)] | Density ρ [kg/m3] | Specific Heat cp [J/(kg·K)] |
|---|---|---|---|
| Soil | 1.40 | 1500.0 | 848.0 |
| Tube wall | 0.35 | 1230.0 | 1510.0 |
| In-tube fluid | 0.64 | 988.1 | 4181.5 |
| Error | Point 1 | Point 2 | Point 3 |
|---|---|---|---|
| Absolute error [K] | 0.0095 | 0.019 | 0.039 |
| Relative error [%] | 0.056 | 0.25 | 0.15 |
| Parameter | Value |
|---|---|
| Initial temperature of the soil | |
| Initial temperature of the in-tube fluid | 323 K |
| Fixed inlet temperature | 323 K |
| Periodic inlet temperature | |
| Inlet velocity | 0.5 m/s |
| Air temperature | 303 K |
| Error | Point A | Point B | Point C |
|---|---|---|---|
| Absolute error [K] | 0.017 | 3.0 × 10−6 | 0.0019 |
| Relative error [%] | 0.18 | 0.000011 | 0.017 |
| Error | Point A | Point B | Point C |
|---|---|---|---|
| Absolute error [K] | 0.017 | 8.8 × 10−4 | 0.0021 |
| Relative error [%] | 0.19 | 0.0031 | 0.019 |
| Algorithm | Grid Number | Computation Time/s | Speedup Ratio |
|---|---|---|---|
| Traditional 3D simulation algorithm | 600,000 | 1180 | — |
| 900,000 | 1813 | — | |
| 1,200,000 | 2494 | — | |
| Layered slice algorithm | 600,000 | 505 | 2.34 |
| 900,000 | 768 | 2.36 | |
| 1,200,000 | 1048 | 2.38 |
| Algorithm | Time Step/s | Computation Time/s | Speedup Ratio |
|---|---|---|---|
| Traditional 3D simulation algorithm | 1 | 6128 | — |
| 10 | 1180 | — | |
| 100 | 261 | — | |
| Layered slice algorithm | 1 | 2788 | 2.20 |
| 10 | 505 | 2.34 | |
| 100 | 102 | 2.56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Sun, D.; Han, D.; Yu, B. A Novel Layered Slice Algorithm for Soil Heat Storage and Its Solving Performance Analysis. Energies 2022, 15, 3743. https://doi.org/10.3390/en15103743
Li G, Sun D, Han D, Yu B. A Novel Layered Slice Algorithm for Soil Heat Storage and Its Solving Performance Analysis. Energies. 2022; 15(10):3743. https://doi.org/10.3390/en15103743
Chicago/Turabian StyleLi, Guolong, Dongliang Sun, Dongxu Han, and Bo Yu. 2022. "A Novel Layered Slice Algorithm for Soil Heat Storage and Its Solving Performance Analysis" Energies 15, no. 10: 3743. https://doi.org/10.3390/en15103743
APA StyleLi, G., Sun, D., Han, D., & Yu, B. (2022). A Novel Layered Slice Algorithm for Soil Heat Storage and Its Solving Performance Analysis. Energies, 15(10), 3743. https://doi.org/10.3390/en15103743






