The framework proposed here was applied in a hydroelectric power plant located near the city of São Paulo, Brazil. The hydroelectric plant is called Usina Henry Borden (UHB), and is an old company, founded in 1926, but which over time has expanded and modernized its facilities, in terms of processes and equipment. One of the aspects that has been updated is the systematic data collection process for monitoring the plant’s equipment. A significant set of sensors was installed in most equipment, generating a considerable amount of data.
The plant is installed in a coastal city in the state of São Paulo, Brazil, about 60 km from the state capital. The location at sea level favors the generation of energy, since from the plateau, where the capital of São Paulo is located, there is a water reservoir that supplies the plant, with a drop in the level of the plateau to the plant of 720 m, which is fundamental in the energy generation process in hydroelectric plants, as will be seen later in the description of this energy generation process.
The installation under study has two plants, one external, with a generation capacity of 469 MW, and another underground, whose installed capacity is 420 MW, thus having a total energy generation capacity of 889 MW. The underground part is installed in the rock in a cave 120 m long by 21 m wide and 39 m high.
The external plant is made up of eight power generation units (GU), and the underground plant has six of these generator groups. Each UG is composed of a generator, powered by two turbines, which rotate by virtue of the water flow they receive from the reservoir. The flows initially pass, still at the level of the plateau, through two butterfly valves in penstocks, where they can be controlled. Then they descend the slope, reaching the turbines. Each turbine is driven by four jets of water. In total, the water flow covers a distance of approximately 1500 m.
The operation of the UHB is part of an integrated electricity generation system that is composed of four large interdependent and interrelated subsystems. The electric energy generated at the plant is passed on to the Brazilian Interconnected System, a system that distributes energy throughout the country.
Besides the sensors, UHB has already incorporated other modern instruments into its practices, such as monitoring systems and dashboards that enable managers to visualize a set of indicators of the plant’s operation. There is also an operations control center, which monitors the entire system, providing, when necessary, indications that interventions in the system should be made. It happens, however, that a good part of the parameters and metrics on which the systems are based were defined from the practice of the operation, that is, they are empirical parameters. This situation has an impact on several aspects of the plant, which, if treated scientifically, would lead to cost reductions. Note that the operation of a hydroelectric plant involves very high costs, and even a small percentage reduction can imply relevant values. The stoppage of equipment for maintenance, for example, could be minimized with the use of predictive maintenance and not preventive, as it is done today, in which the intervals between stops are fixed and empirically defined. Additionally to cost reduction, a hydroelectric plant seeks to maximize the supply of energy and this can only be achieved if, maintenance stoppages are minimized, which can be achieved with the use of more advanced data science techniques. This is the aim of this case study, which is to deal with the development of a model able to predict failures in the operation of the turbines, which would enable the implementation of a predictive maintenance program for this equipment.
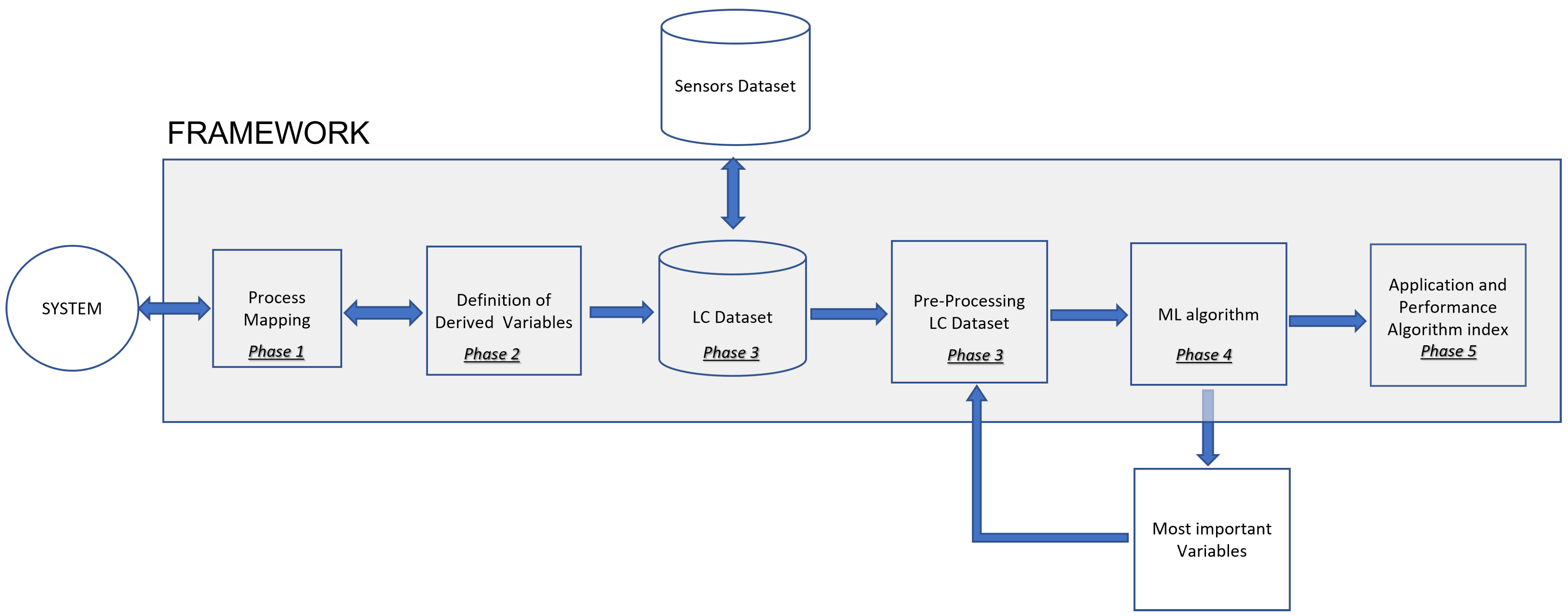
4.3. Application of the Proposed Framework
The proposed framework was applied to the case study, in order to develop a predictive model aimed at optimizing the predictive maintenance scheduling of one GU of the UHB.
The framework was followed, according to the phases defined in
Section 3, which are described next.
A mapping process was developed to represent the operation of the UHB power plant. A methodology based on BPM was applied.
Figure 2 shows a mapping of the macro representation of the full process of generating energy.
The UHB has a wide system of sensors installed in its equipment allowing the monitoring of an expressive set of variables all over the processes showed in
Figure 2. Thus, among this set of variables, those related to the research problem should be chosen. In this case, the objective was to focus exclusively on the issue of the TLC, which occurs in the turbine system, but which is affected by some sub-processes of other systems. Following the directions defined in the framework, technical documents and interviews with the operation team showed that most of the critical points to be monitored were not just in the turbine system, as was expected, but an expressive number of critical points were also in the adduction system. General views of these systems are presented in
Appendix A. As these systems are somewhat complex in terms of components, interrelations and numbers of variables, the purpose of the figures is really to provide just an overview of the breadth of the systems.
In the adduction system 9 variables were identified, and in the turbine system 12 variables associated with the TLC were found. Two more variables were discovered in the generator and transmission systems. In this way, a set of 23 variables monitored directly by the sensors was defined. To this original set, 3 more variables were added that reveal anomalies in the system. Once detected, they trigger system alarms, which are registered.
In phase 1, 26 variables were defined. To this set, another 9 variables were added, derived from data collected. These computed variables were determined through some metrics defining specific characteristics of the TLC behavior. The final set of variables was composed of 35 indicators, plus the date and time stamp of the collection of each piece of information, resulting in a dataset with 36 attributes. In this dataset, a group of seven variables associated with pressure in valves was established. There was also a pair of two variables related to water flow measurements, and another group of six variables measuring the position of the water injection needles and jet deflectors. A variable was selected to record the condition of the circuit breaker (on or off), and another one to register the active power generated. A group of seven variables measure frequencies of rotation of the equipment, and a last pair of variables that detect anomalies was defined. These are the original variables collected directly by sensors. Regarding the derived variables, a set of nine indicators was established to define metrics related to the characteristics of the TLC, and one more variable was defined to calculate a metric about the alarms. The whole set of variables is presented in
Table 1.
The data in UHB are collected continuously by the sensors installed in the equipment of the plant. For the purpose of this research, a sample of a period of 16 months was selected, from June, 2018 to October, 2019. The data collection focused on one UHB generating unit (GU), known as GU6. The data were extracted from a supervisory system database fed by the sensors coupled to the plant equipment, which were connected to this system. This extraction generated the dataset employed in the analyses.
Preceding the construction of the model, the raw data were submitted to a preprocessing treatment to identify any kind of noising, including missing data, inconsistency and outliers. This preprocessing phase must always be performed when dealing with databases, and in this specific case, the following aspects were considered:
- -
missing values, which in some cases were identified and recovered, but in others the examples could not be recovered and were then eliminated;
- -
inconsistencies, such as finding a character in some attribute, where there should be a numerical value, which in some cases it was possible to retrieve the correct information, and in others it was not possible to do this recovery and the copy was thus eliminated;
- -
analysis of outliers, which in some cases were errors due to malfunctioning sensors and in other cases were maintained, as they corresponded to situations of effective anomalies that were occurring in the operation;
- -
data normalization, as some of the techniques used require this type of data processing;
A task usually developed in the pre-processing is an analysis of the attributes, checking if there is a need for a data dimensionality reduction (DDR). However, in this case, as the mapping developed had selected just a limited number of relevant variables, there was no need for DDR at this phase. Once the data were cleaned they were stored in a database and the derived variables presented in phase 2 were computed. The result was a final dataset composed of 1,406,734 examples and 36 attributes.
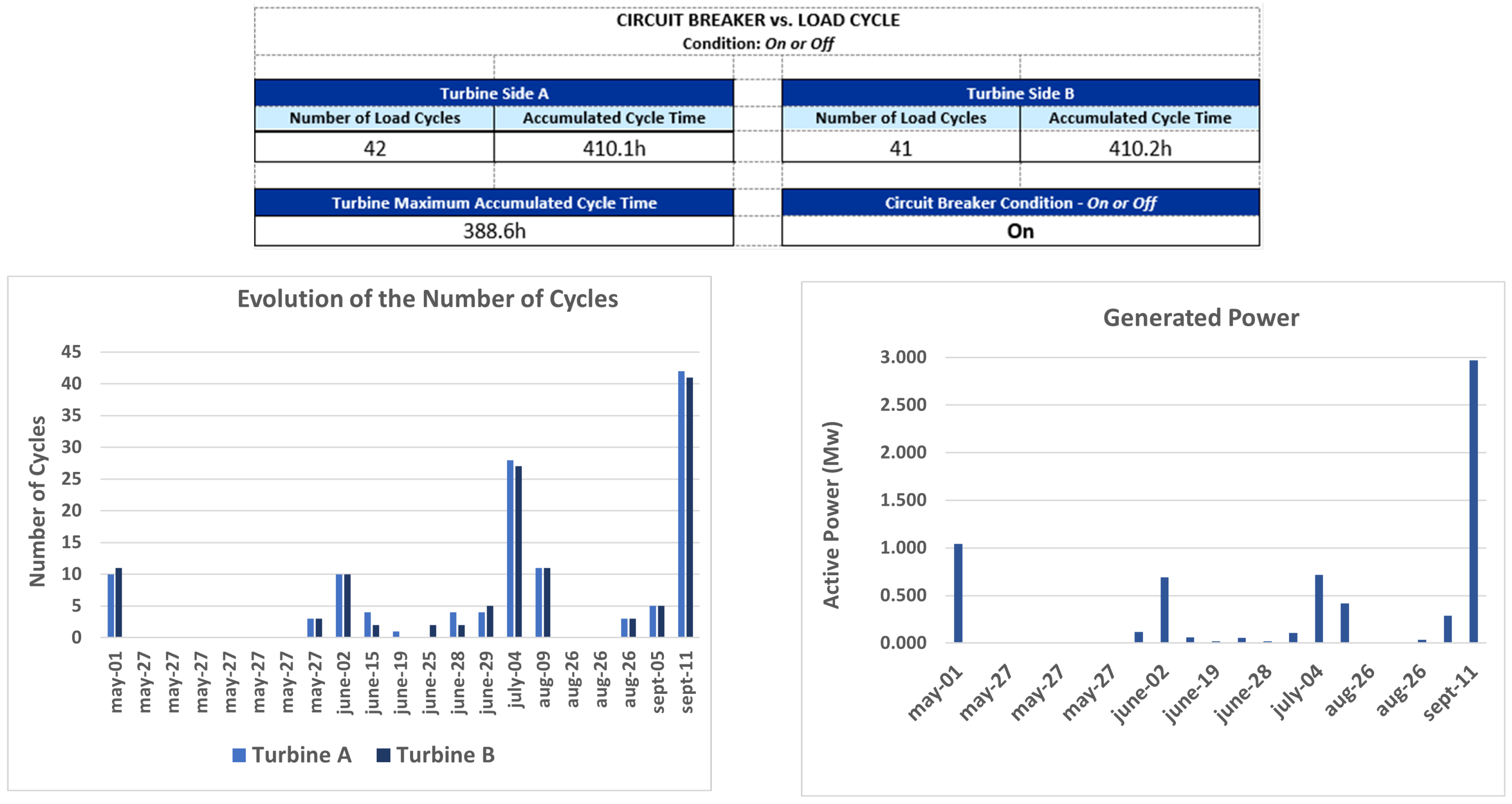
Once the data preparation and transformation was done, exploratory data analysis was developed to understand the data behavior. Moreover, a dashboard was developed that may have different information and statistics, and can be used to monitor the processes by the operations team.
Figure 3 presents an example of some statistics for a specific period, as an illustration of this process.
Once the data quality was assured in phase 3, the modelling phase took place, and the six steps defined in
Section 3 were followed, namely: the definition of techniques to be employed and data modeling; algorithm construction; model training, validation and testing; results analysis, variable importance analysis and dimensionality reduction; final results visualization and analysis.
Before defining the methods to be used, it should be considered that regardless of the technique, there is an essential issue that is the approach to building the predictive model, since the same dataset and the input variables of a model can be used and modeled in different ways, depending on the strategy of construction and, eventually, even the set of variables can be changed depending on the approach.
In a first approach that could be considered, a predictive model can be defined in such a way that the prediction of the optimal time of shutdown for maintenance can be predicted from a single variable, an alarm, for example, that indicates a degradation effect of a piece of equipment. Projecting this variable into the future would lead to a prediction of when an interruption of the operation should occur and, therefore, maintenance is scheduled for some time before this predicted occurrence.This could be a classic time series analysis and forecasting approach.
Another approach to consider would be to work with two predictive models. A first mathematical model must represent a relationship between variables (explanatory attributes), which would be causes of wear, and the occurrence of failures in future periods (dependent variable). There must also still be a second model to project these explanatory variables for future periods, being able to identify, when applying the first model, a time horizon in which a failure should occur. Note that this is an approach that requires the projection of a set of variables, not just one. These projections must be able to predict non-standard values of these variables, and not just average values or trends, as it is the outliers which, in general, indicate equipment failure trends. Thus, there is a predictive modeling task that is not trivial.
A third approach would be to consider a set of variables that may indicate future failures, as in the second strategy, but without the need to create mathematical relationships between the dependent variable and explanatory variables. In this case, you must have a historical database that stores values collected from these variables with the respective timestamps of data collection. From these data, it is possible to identify for each instance (each example) the occurrence or not of a failure in fixed time horizons, defined as time intervals from the instant associated with that instance. With this, it is possible to build a data modeling and a predictive model which, considering only the current conditions of these variables, would be able to project the occurrence of a failure in the considered time horizons. In this case, a time series forecasting problem, mainly based in regression models, is transformed in a data classification problem. The research presented here adopted the latter approach, as detailed below.
The data modeling needed to be constructed in a way that allowed the transformation of a time series forecasting problem into a data classification problem. It was assumed, therefore, that the approach to be adopted in modeling would be the use of supervised ML techniques. Data modeling, therefore, should be appropriate for this paradigm.
For this, we started from the premise that it would be important to have at least 12 h in advance, a prediction that an equipment failure could occur. Thus, the final modeling considered predictions for 12 h and also 24 h and 48 h in advance.
The data should be modeled for this strategy. Therefore, new labels were created to identify occurrences that could generate a failure alarm in the future periods of 12, 24 and 48 h.
For this, an algorithm was built to identify all failure alarms registered in the data set, which is represented by the variable number 36, and their date and time, correspondent to the variable number 01, timestamp.
Initially, three new fields were created in the database, as shown in the
Table 2.
Subsequently, the dataset is sorted in descending order by date/time, and a search is started from the first record, looking for records that indicate the occurrence of an alarm. Once the record of the first alarm is found, a new search is made, based on the date/time information, to find the first record with a date/time before that alarm whose time interval is greater than or equal to 12 h. This first record found is labeled with a 12-h flag (variable t12 = True). This routine is applied to all records in the database and, once completed, it is repeated considering the intervals of 24 and 48 h (variables t24 and t48).
With this data modeling, the dataset was prepared to deal with a data classification problem, and a suite of machine learning techniques was applied to the transformed dataset, as showed in the following.
Regarding the methods selected for the prediction models, it should be considered that one of the objectives of the paper was to verify whether it would be feasible to apply ML to the data of the specific problem at hand. There are references in the literature about the use of ML in PdM, but there is a gap in relation to the specific problem of a hydroelectric power plant. There are many references dealing with wind power plants, but not with hydroelectric power plants. Thus, it was necessary to verify if ML could adapt well to the data to predict equipment failures of this other type of power plant, and for that it would be necessary to test some ML methods.
The objective, therefore, was to apply ML techniques, and demonstrate that PdM related to a key subsystem of a hydroelectric power plant could benefit from the algorithms of this area of knowledge.
In this sense, it was necessary to select classic ML methods that were representative of ML algorithms and that had different complexity and characteristics. Thus, three methods were initially chosen that met these criteria: decision tree (DT), artificial neural network (ANN) and logistic regression (LR).
DT has a structure based on logical rules distributed in a hierarchical flowchart-like tree structure, and is a “white box” algorithm, which generates a model that is a set of logical rules [
55].
ANN works with a somewhat complex mathematical model involving different learning strategies, a network of neurons (nodes) connected by links (synapses) in multiple layers, link weights, various types of hyper-parameters, and functions of different types, and is a “black box” model with high complexity [
56].
The third technique chosen, LR, is a particular case of the generalized linear models (GLM). Proposed by [
57] and reintroduced by [
58], it is an extension of the linear model based on the normal distribution. LR classifies data by determining probabilities [
59], which in turn are determined through regression equations, whose parameters are estimated by well-known classical statistical methods. These three methods, with very different characteristics and different levels of complexity, could lead to different levels of accuracy and performance of the models. To complete this picture, a fourth approach based on a composition of models was included (an ensemble), for which the RF [
60] was selected, a traditional technique that is widely used in many types of applications.
Therefore, a set of four methods was consolidated to be applied to the dataset.
This set of varied techniques, representative of different ML algorithms, made it possible to evaluate the feasibility of applying ML to the data. If some or all of them were reasonably accurate, this could be interpreted as an indication that ML could be applied to this type of data/problem.
To shed a little more light on the selected methods, it is worth saying that decision tree is a classical data classification technique and it is possibly the most used algorithm for classification. Eventually, it could be said that this would be a technique that at least deserves to be explored whenever you have a data classification problem.
Artificial neural network (ANN) is another classical machine learning technique often used for data classification. It is versatile, being able to be used in different types of problems, and many times presents a performance at the highest level.
Logistic regression is a method that seems to be perfectly suited to the type of problem being studied. Regression defines a relationship between a dependent variable and one or more independent variables, which would explain the behavior of the first variable. When the dependent variable is binomial, there is the case of a logistic regression, which is specifically the situation of the present study.
Finally, random forest is the case of an ensemble method, which is a composite of multiple models. This is a different strategy from the previous techniques and, therefore, it is an alternative that deserves to be considered among the tested approaches. Specifically, the random forest is a set of decision trees and is, therefore, well suited to the problem under study.
At this stage, the data classification techniques were implemented to classify the examples into two categories: normal situations and imminent failure situations.
The classification models were built based on the algorithms presented in the prior step. The implementation was carried out in the environment of the R programming language and the R Studio tool, and making use of R libraries, which are available in more than one version, for all tested algorithms and for the development of predictions and indicator generation, which were used to evaluate the models. For the training of the models and for the validation and testing phases, resources from the R programming language environment were also used, as explained in the following.
For the implementation of the DT model, the library “rpart—Recursive Partitioning and Regression Trees”, for the R language environment was used [
61], which is an implementation of the main functionalities of the 1984 proposal by [
60]. The implementation of the model, was done with the “rpart” function. The main parameters, which provided the best results, are presented below:
. method = “class”: specifies a classification problem
. minsplit = 1: minimum number for split in a node
. split = “Information”: specifies the criterion on which attributes will be selected for splitting.
The entropies of all attributes are computed and the one with the least entropy is selected for split.
. Default parameters having been used in all other arguments.
As a criterion for evaluating the model for the purpose of its construction, the metric of “information gain” was used.
Regarding the MLP network, the implementation was possible through the package RSNNS, which is implemented in R, the library SNNS (Stuttgart neural network simulator) [
62], which is a library containing standard implementations of neural networks. By this package, the most common neural network topologies and learning algorithms are directly accessible by R, including MLP. For the implementation of the model, the “mlp” function was used. The list of the main arguments, which enabled the best results, is presented below:
. MLP, which is a fully connected feedforward network
. Two hidden layers
. First layer with five neurons and the other with seven neurons
. Standard backpropagation
. Random weights for network initialization
. A logistic activation function
. Learning rate = 0.1
. Maximum number of iterations = 50
. Default values for the rest of the parameters.
In the case of LR implementation, the function “glm” was used, which is a native function of R, aiming to fit generalized linear models to the data, providing a symbolic description of the linear predictor and a description of the error distribution. The main arguments, which generated the best performance indicators, are presented below:
. Error distribution (family) = binomial, which provides a logistic regression model
. method = iteratively reweighted least squares (used in fitting the model)
. intercept = True (include an intercept)
. Default values for all other parameters
For the implementation of the RF algorithm, the package “randomForest—Breiman and Cutler’s Random Forests for Classification and Regression” was used [
63,
64], which is offered for use in the R environment, and which uses random inputs, as proposed by [
60]. The model itself was built with a function from this library, with the same name as randomForest. As for the main arguments, which provided the best results, their list is presented below:
. Number of trees to grow (ntree) = 200
. Number of variables randomly sampled as candidates at each split (mtry) = square root of the number of variables (default)
. cutoff = 1/(number of classes) The ‘winning’ class for an observation is the one with the maximum ratio of the proportion of votes to cutoff (in this case, majority vote wins)
. Minimum size of terminal nodes (nodesize) = 1 (Default)
. Maximum number of terminal nodes trees (maxnodes) = Subject to limits by nodesize
. Default values for the other arguments.
Regarding the training of the models used in this study, a resampling process was adopted.
There are several resampling techniques, which basically subdivide the data into learning and testing sets, and can vary in terms of complexity [
65]. One of the best techniques to verify the effectiveness of a machine learning model is the K-fold crossvalidation, which was used here. The parameter k represents the number of folders (samples) to be created for training, validation and testing. In this study, the value of K = 5 was used. Thus, four folders (80% of the data) were used to train and validate the model, and one of them (20% of the data) to perform the final test of the model. This parameterization proved to be adequate for conducting the experiments, having generated results with high accuracy.
The four folders (samples) were selected by random sampling, and as the model is applied to the examples of each folder, its hyper parameters are adjusted. Once these parameters are properly calibrated, the model is then applied in the folder dedicated to the final test.
For the training and testing of the models with the cross-validation technique, the library “cvTools—Cross-validation Tools for Regression Models” [
66] was used, which offers tools in the R environment for the application of this technique. For all models, the proportion of 80% of the data for training and 20% for tests was maintained.
The four models described in step 4.1 were applied to the dataset in order to predict a failure in the equipment in a period of 12 h, 24 h and 48 h.
In a first approach, the models were applied to the data considering all attributes of the database as explanatory variables.
The performance was evaluated initially through a confusion matrix [
67], which is particularly indicated to classification procedures where there are two possible states: TRUE or FALSE.
The structure of a confusion matrix is presented in
Table 3.
For this matrix we have:
TP = Number of True Positive Cases
FP = Number of False Positive Cases
FN = Number of False Negative Cases
TN = Number of True Negative Cases.
TP are the cases for which the actual class of the data was TRUE and the model predicted TRUE (correct). FP, on the other hand, are the cases when the actual class of the data was FALSE but the predicted was TRUE (incorrect).
FN measures incorrect FALSE predictions. These are the cases when the actual class of the data was TRUE and the predicted was FALSE (incorrect). Finally, TN are the correct predictions for FALSE cases. The cases where the actual class of the data was FALSE and the classifier predicted FALSE (correct).
In the experiments carried out in this research, it was considered that an Actual Positive condition of the system was TRUE when an Alarm occurred in an period of 12 h or less, or 24/48 h if these were the time intervals considered. On the other hand, the TN counter was increased by one each time a normal prediction was correct.
The confusion matrix is not a complete performance metric in itself, but most KPI‘s (key performance indicators) used to evaluate models are based on this matrix, see [
68,
69,
70].
In this experiment, a set of KPI‘s were utilized, which are generated by a package available in the R language, called caret (classification and regression training) [
71], which computes a set of indicators from a confusion matrix, as described below:
. Accuracy (Acc), which shows the proportion of classification performed correctly, that is, TP + TN as a proportion of the total classified items.
. Precision or positive predictive value (Pos Pred Value), that is a proportion of cases predicted as TRUE that were really TRUE.
. Negative predictive value (Neg Pred Value), presents the number of negative class correctly predicted as a proportion of the total negative class predictions made.
. Sensitivity or recall, a proportion of cases classified as TRUE over the total TRUE cases.
. Specificity, which represents the proportion of cases classified as FALSE over the total FALSE cases.
. Prevalence, which presents the total actual positive classes as a proportion of the total number of examples.
. Detection rate, corresponds to the true positive class predictions as a proportion of all of the predictions made:
. Detection prevalence, corresponds to the number of positive class predictions made as a proportion of all predictions:
. Balanced accuracy, corresponds to the average between sensitivity and specificity.
This is the accuracy that would be achieved simply by always predicting the majority class [
72]. It is a good KPI to compare against calculated accuracy.
This is an one-sided hypothesis test to see if the accuracy (Acc) is better than the “No Information Rate (NIR)”.
The null hypothesis (Ho) of the test is presented below:
For a p-value ≤ 0.05, Ho can be rejected.
The Kappa coefficient, discussed in [
72,
73], is considered a standard for assessing agreement between rates. The calculation is made considering the rates observed in an experiment versus the rates that would be expected due to chance alone.
In terms of confusion matrix, it is a measure of the percentage of values on the main diagonal of the matrix adjusted to the volume of agreements that one could expect as a function of chance alone.
Kappa ranges between 0 and 1.0, and when K is within the range 0.6 < K < 0.8, indicates substantial agreement.
The Kappa coefficient is computed through the formula below;
where:
= Observed probability (percentage);
= Chance probability (percentage).
This test [
74] is applied to a contingency table, similar to a confusion matrix. This tests a null hypothesis of marginal homogeneity that states that the two marginal probabilities for each outcome are the same, i.e.,
where:
Thus, this can be synthesised to the following null hypothesis:
The McNemar test statistic is given by:
We can reject Ho, if the p-value for the test is less than 0.05.
With this last statistical test, the set of metrics used in the analysis of the results generated by the models was consolidated.
In addition to analyzing the performance of the models, it should be considered that in data mining, the input variables of the model hardly have the same relevance [
75]. In most cases, only a part of these variables really contributes to explaining the dependent variable. Thus, it is important to identify the most important variables because, in this way, it is possible to reduce the dimensions of the problem, reducing the complexity of the model and, consequently, requiring less computational resources.
In this research, a first round of executions of the models was carried out, which allowed the identification of the most important variables (MIV) in each model. Then, in a second round of experiments, only the MIV of each technique were considered, applying, therefore, a data dimensionality reduction.
After this second stage of applying the models, a panel of metrics (tables and graphs) was developed to assess the accuracy and significance of the results, in order to allow a clearer visualization of those results generated by each model developed.
The importance of a variable could be described, more generally, as the level of impact that this variable has on the outcome of the response variable. This can be represented as a value. So, variables with a greater importance value (IV) would have more impact in an expected outcome.
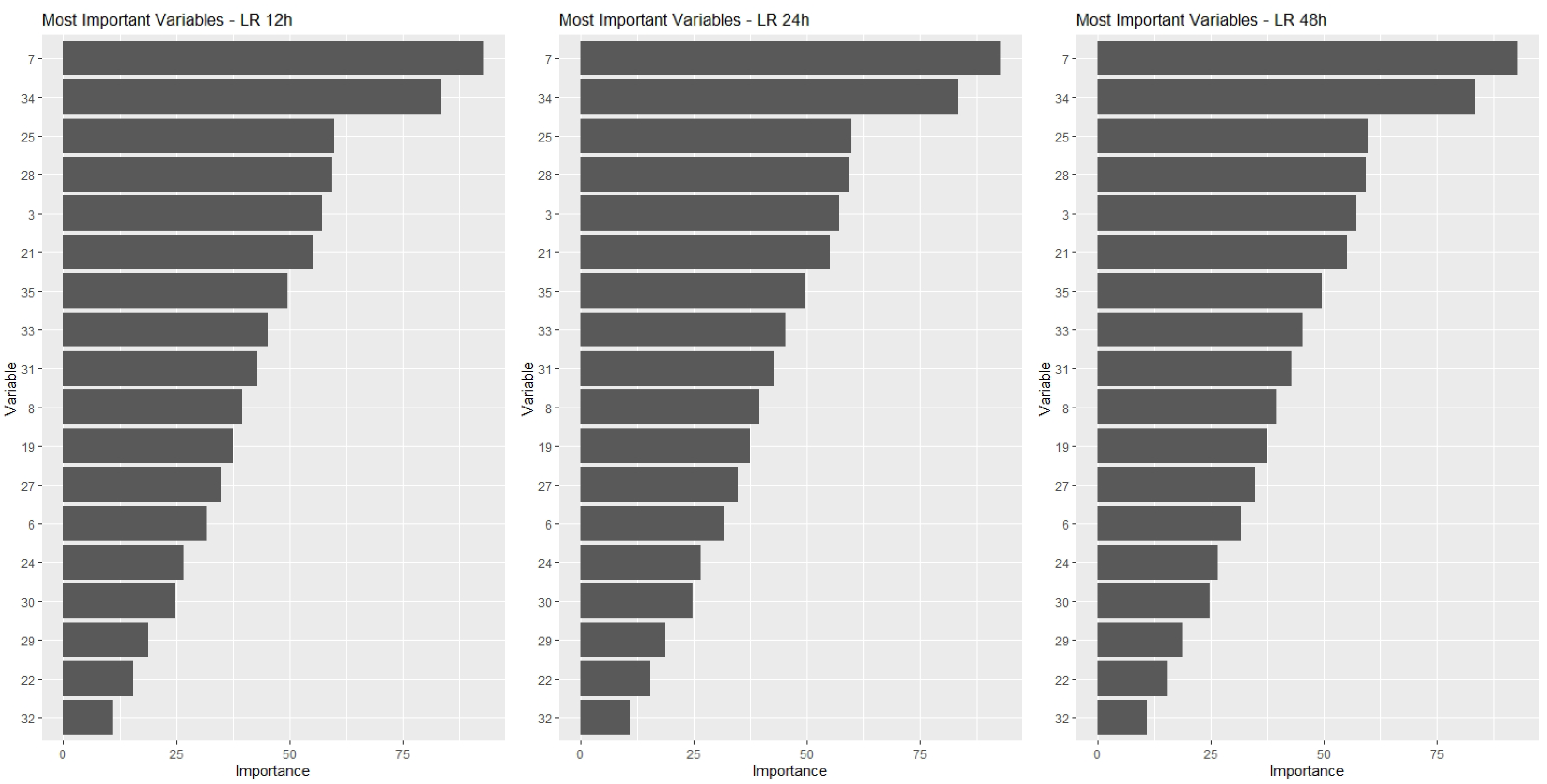
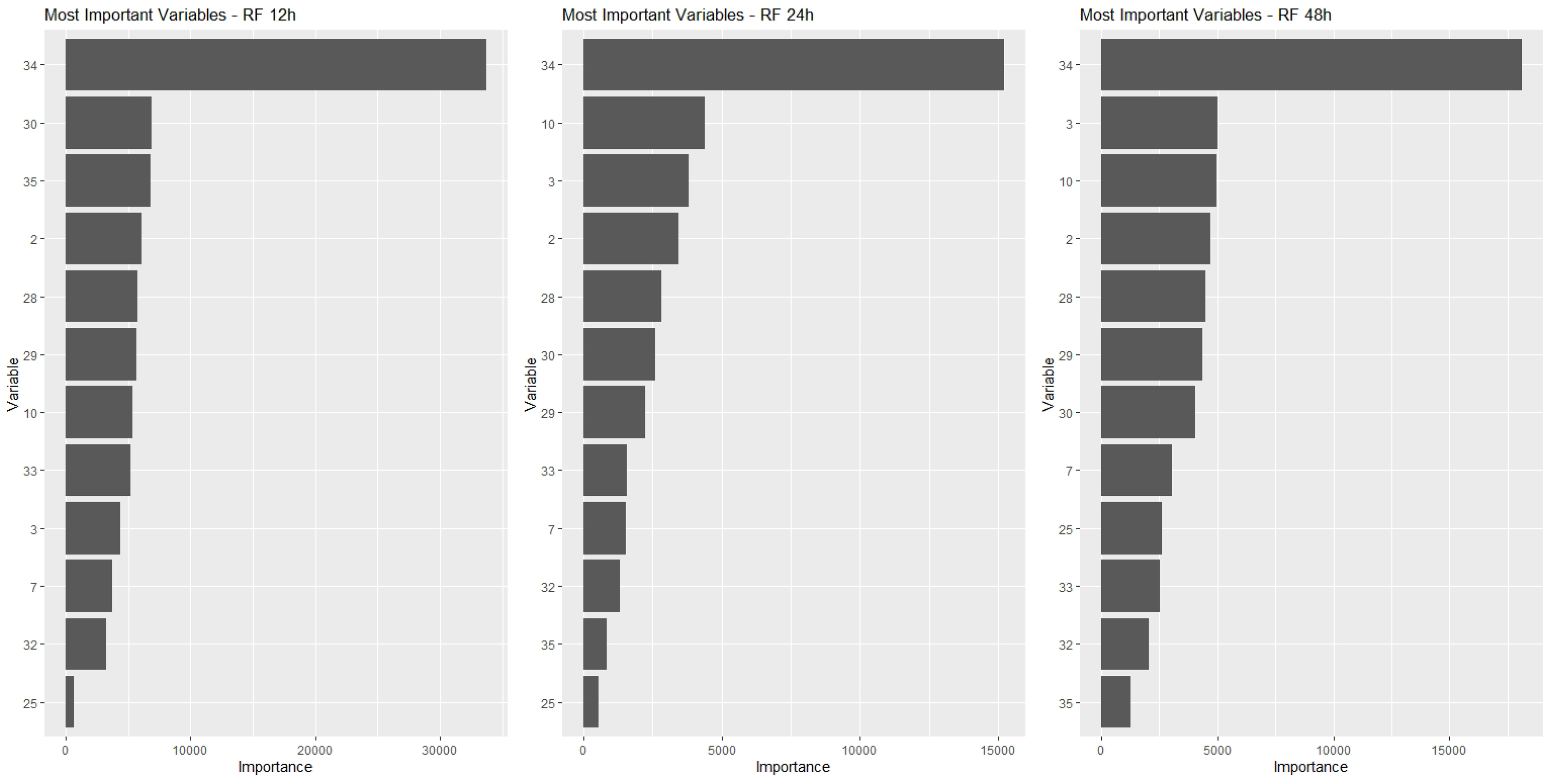
In this paper, the IVs were computed for all variables in the models, and sets of 10 MIVs were identified for each one of the prediction models and for each of the time horizons considered: 12 h, 24 h and 48 h prediction.
Next, the common top 10 variables to the three time horizons for each technique were identified. Each set of common MIV then became a number greater than or equal to 10 variables.
Thus, for each type of model, the following results were obtained:
. DT Model: 14 MIV;
. MLP model: 17 MIV;
. LR model: 18 MIV;
. RF model: 12 MIV.
These MIVs are presented in
Table 4.
One aspect that is important to explain about the IV calculations is that each model/ technique has its own procedure for determining IV.
These procedures, which are used in the techniques applied in this paper, are presented below.
In decision trees, the attribute chosen for each node of the tree is defined so that it maximizes the chosen metric to provide a gain in the accuracy of the results. Thus, the relative importance of a given variable (or attribute) is defined as the sum of the quadratic gains of all nodes in the tree where that variable was chosen to define the partitioning of the instances that pass through the node. This same concept can be extended to one or more sets of decision trees, as is the case with random forests [
76].
In this work, a proposal developed by [
77] was used. In this method, the weights of the connections between the layers of a neural network constitute the basis for establishing the values of the VI. The method calculates the importance of a variable as the product of the weights of each input and output connection of all neurons, of all hidden layers of the network, and sums all these products. An advantage of this approach is that the relative contributions of each weight of a link are considered in terms of magnitude and sign. Thus, in a case where the weights change sign (positive to negative or vice versa) between the input and output layers, these would have a cancellation effect. Other algorithms can give misleading results by considering only the absolute magnitude. Another additional advantage is that the [
77] is able to assess neural networks with many hidden layers. It should be noted, however, that the values of the importance attributed to the variables are measured in units based directly on the summed product of the connection weights of the specific neural network model under analysis. Thus, these values should only be used in terms of sign and magnitude as a standard for comparing the explanatory variables of the model being analyzed. Comparisons with other models can lead to misunderstandings [
78].
In linear models, the absolute value of the t-statistic or equivalent is usually used as a measure of variable importance [
76]. The t-statistic or equivalent is related to the null hypothesis (
Ho) tested in a linear model. This hypothesis,
Ho, states that the coefficient
of an explanatory variable
would be zero (
Ho:
= 0). The larger the value of t or equivalent, the smaller the
p-value, which is the P(
Ho = True), and which means that we should reject
Ho, for very small
p-values. Therefore, using the t-statistic as a measure of VI is a criterion that makes sense, because the larger the t-value or equivalent, the smaller is the
p-value, and, consequently, the more significant is the correspondent variable. The same concept extends to the case of generalized linear models (GLMs), used in this work for the construction of the logistic regression models. In the LR models developed in this work, the R language library used for the VI calculations generated values that exactly coincide with the Z value generated in the statistical analysis of the model.
In this article, the determination of MIV and its respective IV’s were developed through an R language library, called “vip” (variable importance plot) [
76], which applies all these concepts that we have just seen, computing the IV of each variable.
The
Table 4 presents the MIV for each model.
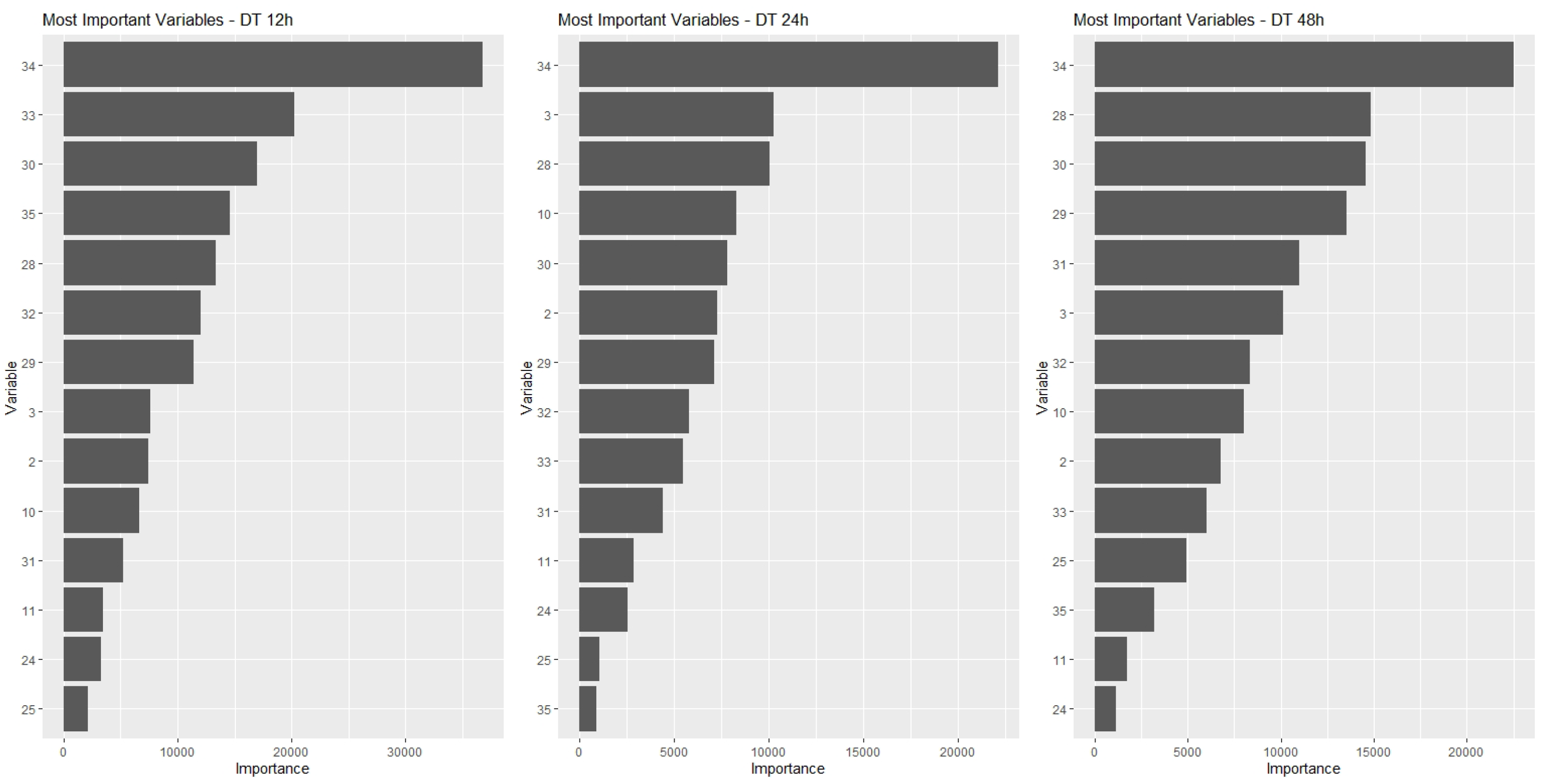
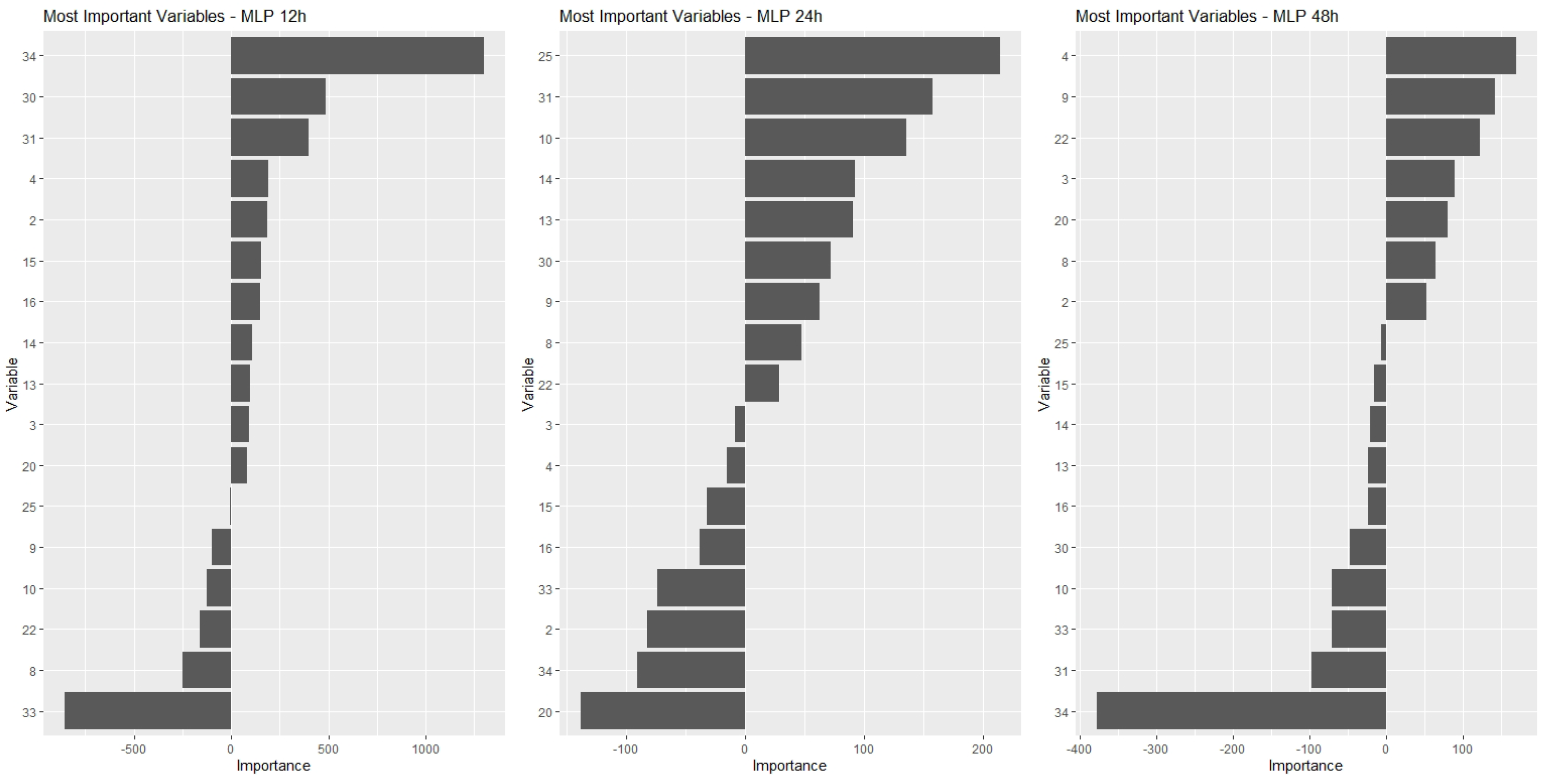
Figure 4,
Figure 5,
Figure 6 and
Figure 7, show for each type of model the MIV’s and their respective IV’s. Each figure presents three graphics showing the IV’s for the three time period predictions considered in the study: 12-h, 24-h and 48-h.
By observing these graphs, it can be seen that the best ranked variables have IV’s much higher than those at the bottom of the list. However, given the shape of the curves, it could not be said that this decrease is linear. Note that there is a certain stabilization or small reductions in the IV for variables positioned towards the end of the ranking, which means that there is not much difference in the importance of these variables. It is possible, eventually, to use one or another variable without much difference in the results obtained. On the other hand, if any of the variables from the beginning of the ranking are not included in the model, the impacts on the results can be significant, given the relative magnitude of their IV’s. This behavior could lead us to think of a decrease in IV associated with the inverse of a power curve.
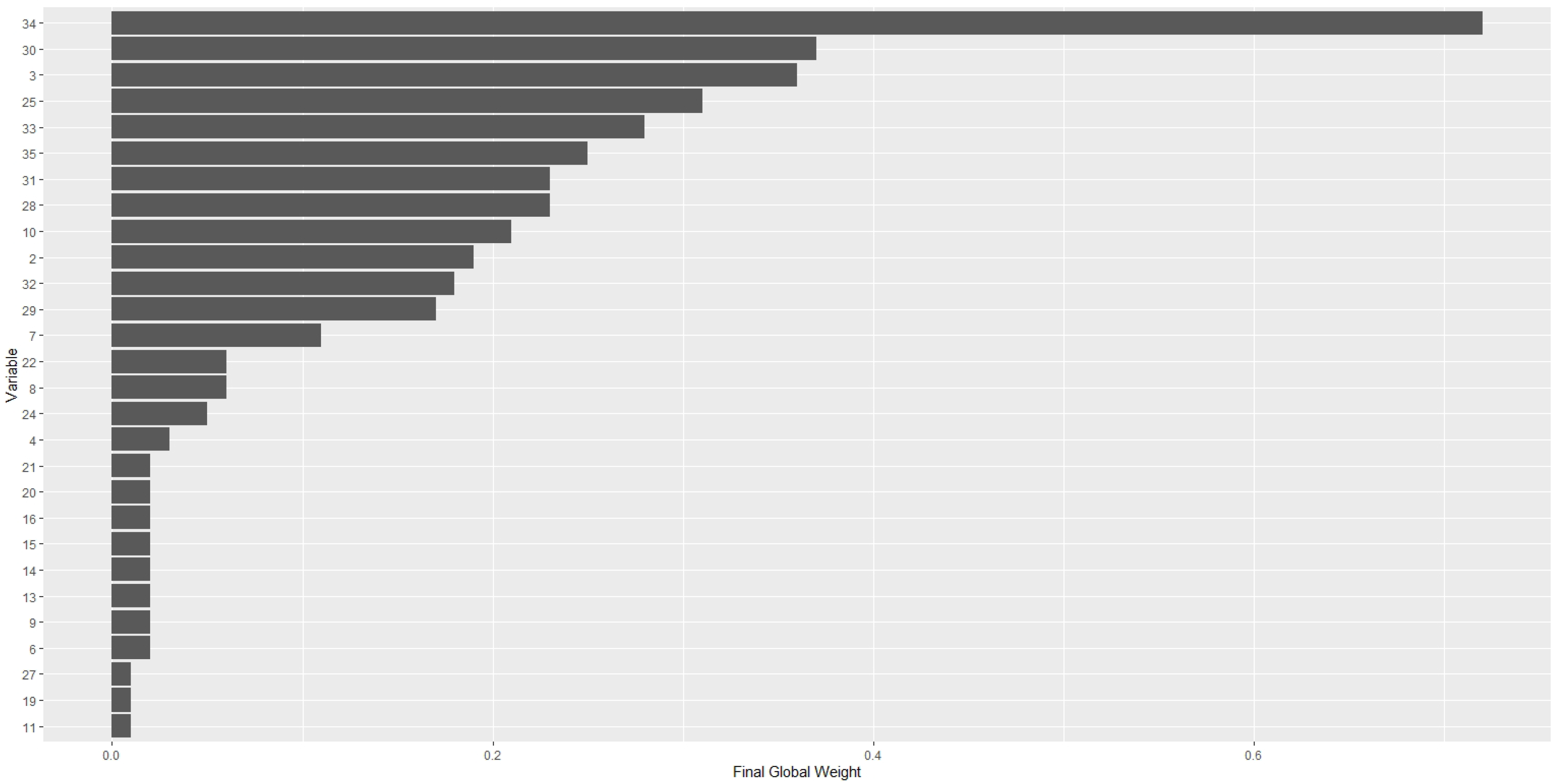
In addition to determining the MIV’s for each type of model, it would also be important to establish the most important variables globally, considering the entire set of models developed, thus defining a global ranking of variables.
In order to develop this ranking, two types of weights associated with the importance of the variables were defined, and a final weight was determined through a combination of these two weights.
The first of these weights () set a numerical value for each time a variable appeared in the list of MIV. As four modeling techniques were used, the number of times a variable could appear would vary between 1 and 4 and, therefore, the relative weights that were adopted () range from 0.25 to 1.0.
A second weight () was defined based on the position of the variable in the MIV ranking. These weights, therefore, should be inversely proportional to the variable’s rank.
To establish the inverse relationship, a regression model was estimated to represent the normalized mean IVs of the variables in the model set, as a function of the positions of the variables in the ranking of importance.
The process of determining these weights, therefore, started with the normalization of the IVs of the variables in each model, and then a general average of these normalized values was computed for each position of the ranking, considering all the developed models.
The IVs were normalized using Equation (
4):
where
= normalized of variable i, of model j
= of variable i, in model j
= maximum observed of the variables in the model j
= minimum observed of the variables in the model j
i = 1, 2, ..., ; j = 1, 2, 3, 4
= number of MIV in model type j.
This normalization was carried out for the 12 models developed: four types of models, with three forecast time horizons, 12 h, 24 h and 48 h. Then, the averages of the 12 models of the normalized IVs of each position in the ranking were computed.
As the number of MIVs in each type of model was not the same, the averages were computed so that there were always 12 observations in the calculation of each average.
For this criterion to be met, the means were computed up to a number
m of MIVs, where
With this procedure, a vector of average normalized IVs was generated. This vector allowed the representation of the average normalized IVs as a function of the positions of the variables in the ranking of importance.
A regression model to represent this relationship was then developed, presented in Equation (
6), which obtained a coefficient of determination (
) of 0.9843. The normalized values estimated through this model were adopted as the second weight (
) associated with the MIVs ranking.
where:
= weight 2, associated with the MIV rank
r = position of the variable in the MIV ranking.
Regarding this Equation (
6), it should be remembered that it must be fitted to the data of each application.
Graphically, a normalized mean curve of the observed IVs and the respective curve adjusted to the data is presented in
Figure 8.
Through Equation (
6) the weights of each variable were estimated. As in the case of the first weight (
), here too, a relative weight was computed. By the model (
6), the
of a variable positioned in the first place of the ranking (
r = 1) would be 0.9858. Now, considering the four models developed, the maximum sum of
would be 4 times 0.9858, or 11.8, which we rounded to 12. Having this total maximum absolute value as a reference, the normalized IVs of each variable in the models were added and divided by 12, generating a relative weight (
) for each variable.
The final global weight of each variable corresponds to the multiplication of the two weights, as shown in Equation (
7):
The
Table 5 shows the weight compositions for all variables.
The relevance of these global MIVs is that this finding can be a reference for the selection of variables for predictive models in new applications.
Table 6 shows the final global weights and the final global ranking of the variables.
It should be noted, from
Table 6, that of the first five most important variables, four are related to times and amounts of charge cycles, and one is related to valve pressure.
Thus, in view of these results, and in order to seek a reduction in the dimensionality of the data, it was decided to work only with the MIVs, thus reducing the computational and analysis effort, without compromising quality, and new experiments were performed only with the MIVs. The complete set of results obtained in the experiments are presented in the next step 4.6.
Table 7,
Table 8 and
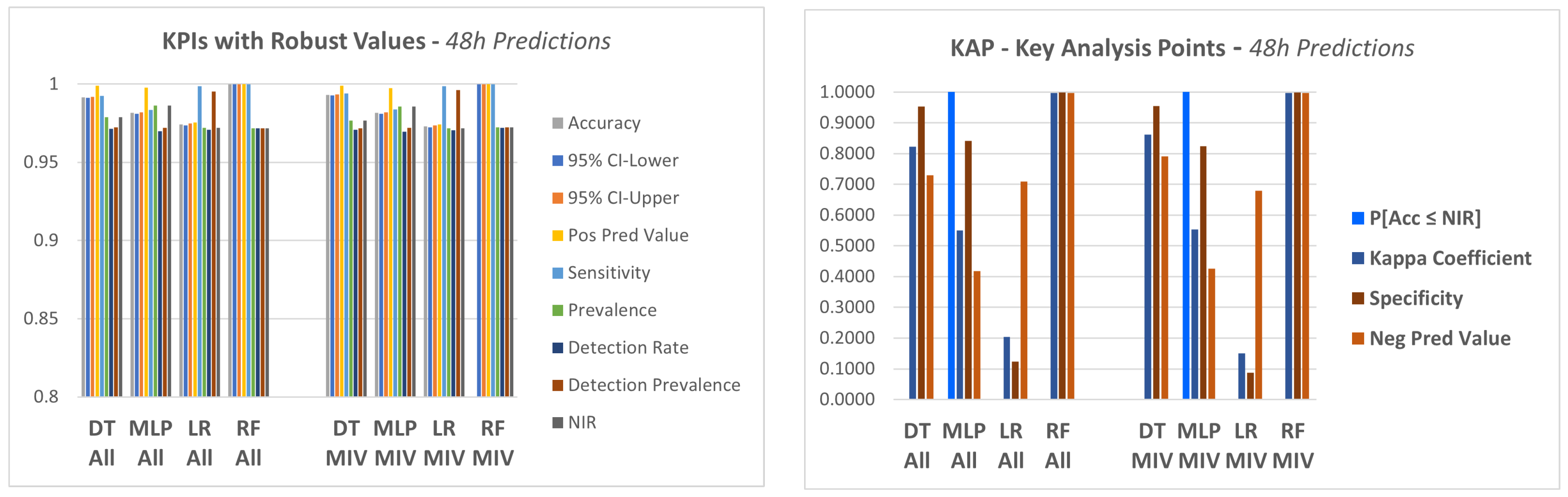
Table 9 show the results of experiments considering the entire set of variables (All Variables) and only the most important variables (Top Variables). The results obtained in these experiments with the Top Variables remained at the same level as those generated with the full set of variables, and in some cases, were even better.
In relation to these results, most of the KPIs showed reasonably robust results, not significantly differentiating the four models explored in the experiments. In this set of KPIs with robust values, the accuracy in particular, which, as a rule, is one of the most used metrics, was very high in all tests of all models. If the analysis was based on this set of KPIs with robust values, there would be some difficulty in differentiating the models. Looking only at this set of KPIs, it could be considered that all models are reasonably robust. There is practically no difference between the results. There are, however, five KPIs that stand out from the others, showing important differences between the models. Although, of these five, there are four that effectively differ, because two of them, Balanced Accuracy and Specifity, are related to each other.
A visualization of this Final Global Rank is shown in
Figure 9.
Therefore, the final group was left with four KPIs, and we named it Key Analysis Points (KAP), which are presented below:
. P[]
. Kappa coefficient
. Negative predicted value
. Specificity
When considering this specific KAP, the picture changes considerably and it is possible to identify performance differences between the models, which draws our attention to the importance of analyzing the results from different angles.
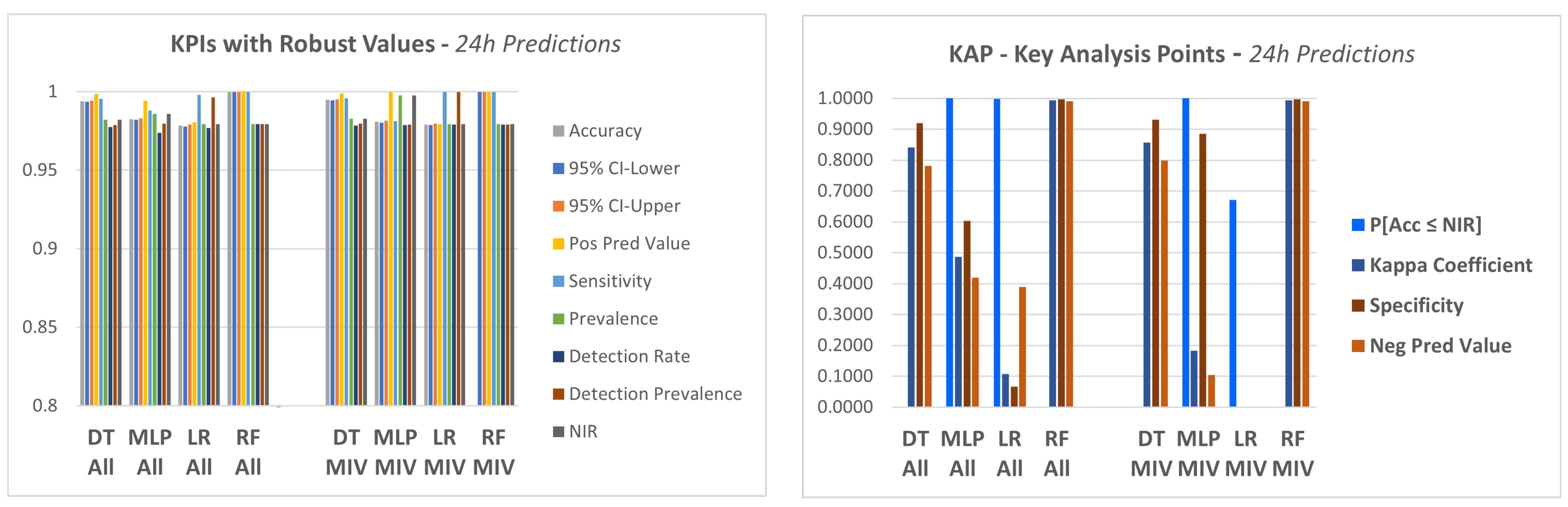
A visualization of the KPIs for the three time horizon of predictions can be seen in
Figure 10,
Figure 11 and
Figure 12. The figures present the KPIs computed for the models with “all variables” (All) and for the models with only the MIV. Moreover, for each time horizon, there are two graphics: the first one considering the set of KPIS with robust values for all four models, and a second graphic with the set of KAP, the key analysis points, which are the KPIs with a significant variation between the models. These figures provide a clear comparison between the methods.
From this group of
Figure 10,
Figure 11 and
Figure 12, it appears that there are important differences between the methods, but that these differences are only shown by a restricted group of indicators.
The DT and RF models both had satisfactory KPIs in all experiments, but this was not true for the other models. In some cases, the KPIs indicate that the model should in fact be discarded, as the KPI result showed that the results obtained with that model lacked significance.
The models that did not show satisfactory results for this KAP group of KPIs were the logistic regression (LR) model and MLP (multilayer perceptron). In these two cases, the behavior of the KPIs was different depending on the time horizon of predictions: equipment failure in 12 h, 24 h or 48 h.
By analyzing the indicators and graphs, it can be seen that the regression modeling was not able to capture the behavior of the data as well as other models. This can be seen specifically by the indicators:
. P [];
. Kappa coefficient;
. Negative predicted value and
. Specificity.
The same can be said about MLP. It was not possible to get to a model based on MLP that would lead to results of the same level obtained with DT and RF, and the model runtime is also an issue. While some models reach the solution in seconds, the MLP took more than 1 h. On the other hand, the DT and the ensemble, RF, found logical rules in the database, which led to results with high values for all indicators and with the advantage of having low execution times.
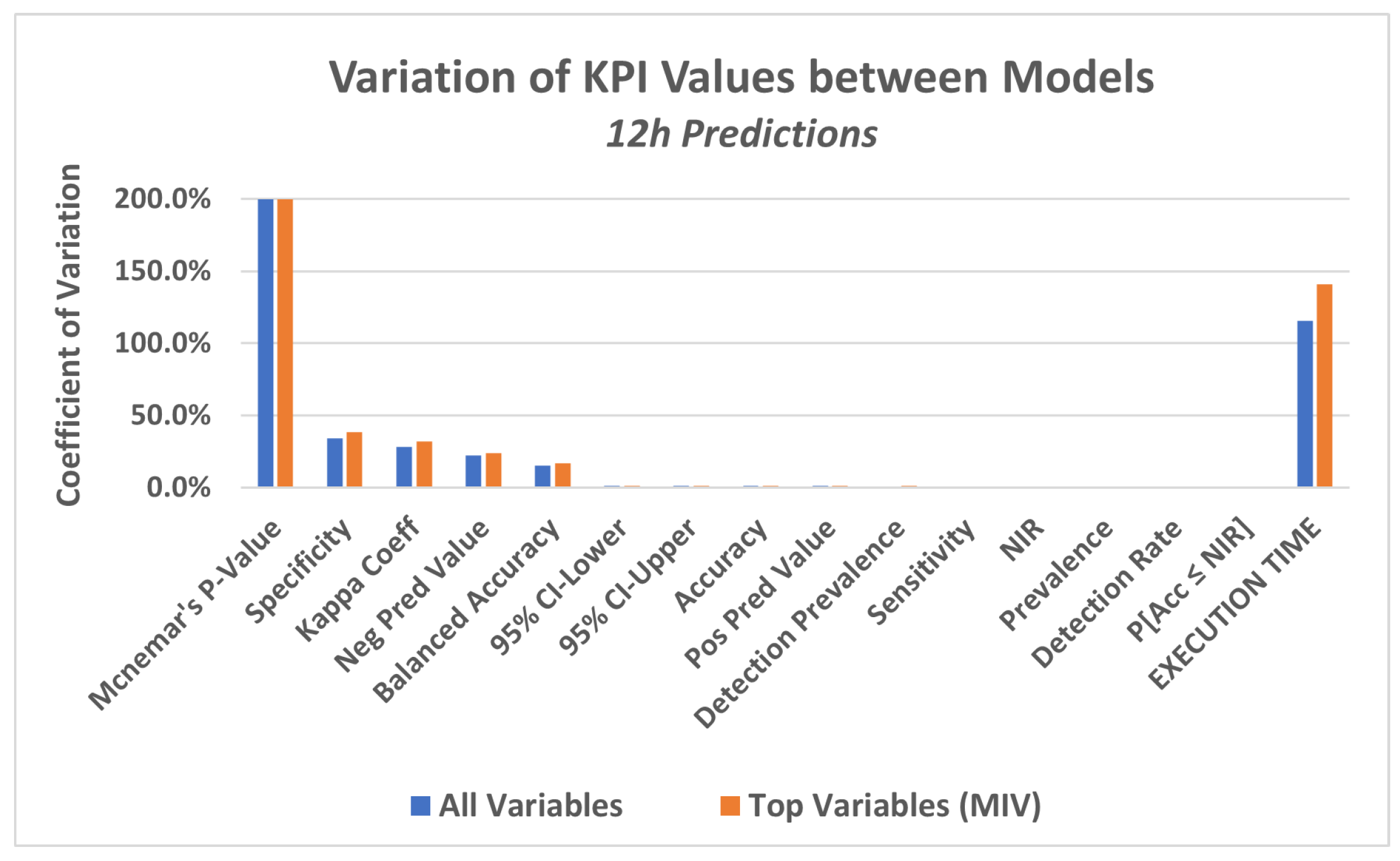
For the 12 h predictions, the kappa coefficient had a value below 0.5 for the LR, which is not a satisfactory result, and this happened both for the “All Variables” experiments, as in the case of “Top Variables”. The kappa coefficient, as mentioned before, is considered a standard to assess agreement between rates. In our case, it measures the hits that could be expected in the confusion matrix as a function of chance alone. A value above 0.6 would indicate a good quality of the model’s response. The closer to 1, the better the prediction.
Another situation in the 12 h prediction happened with MLP which gave a value for the negative predicted value below 0.6 in both cases: all variables and top variables.
When checking the results of the 24 h predictions, MLP and LR again did not show satisfactory responses for some KPIs. In the case of MLP, we had NIR > Acc in both types of experiments, which resulted in a P[] = 1.0. The kappa coefficient was 0.4865 for all variables and 0.1833 for top variables. The negative predicted value was 0.4194 for the all variables experiment and 0.1045 for the top variables experiment. In the case of LR, the results were very similar, and still had very low values for the specificity coefficient and negative predicted value.
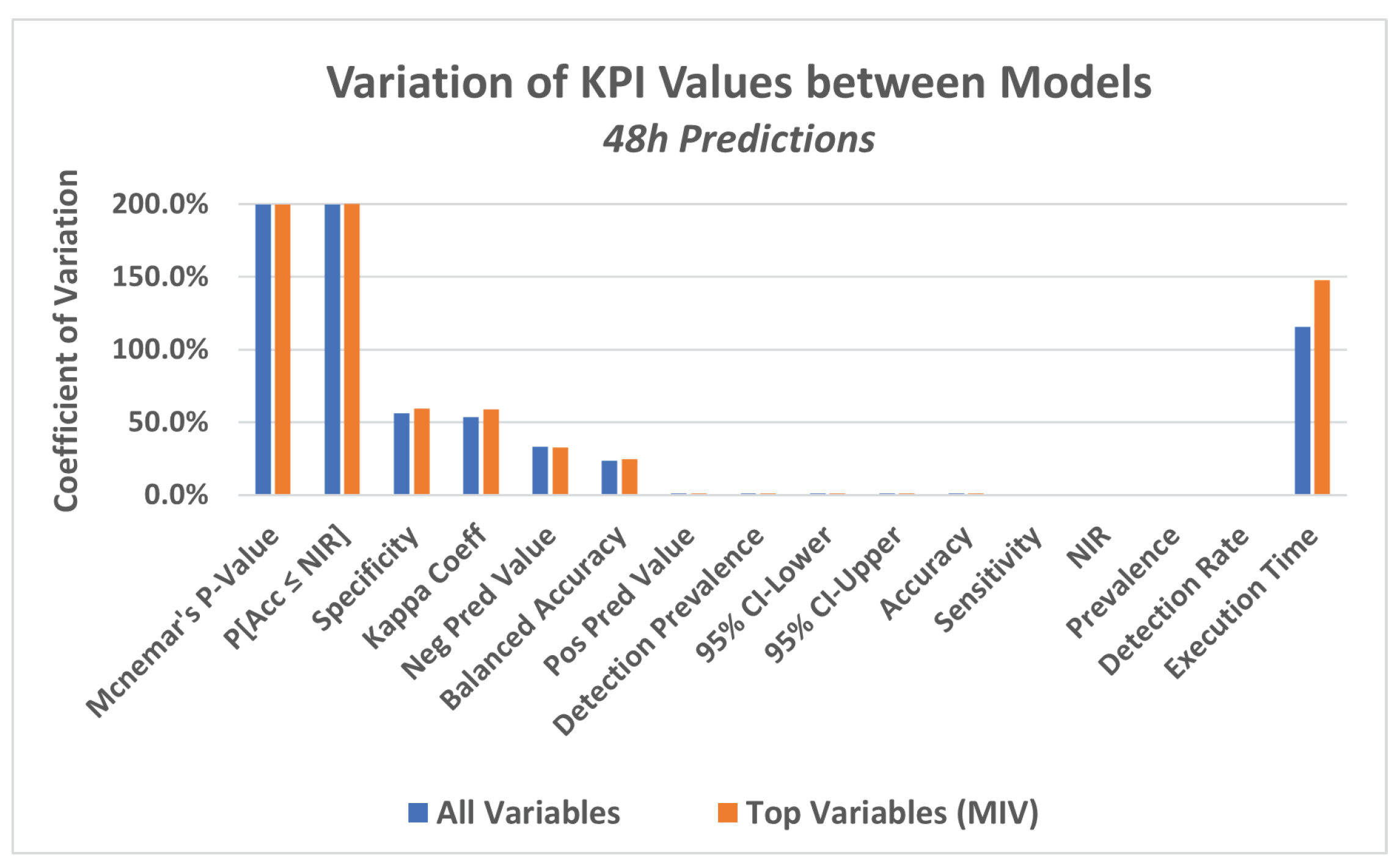
The 48-h predictions presented results very similar to the 12-h ones, for all KPIS mentioned: NIR, the p-Value [], specificity and negative predicted value, for both MLP and LR, and in both experiments: all variables and top variables.
Another way to see this difference in KPI values between the models is to analyze the coefficient of variation (CV) for each KPI. CV is the standard deviation divided by the mean value of the KPI in the four models. It represents the standard deviation as a proportion of the mean. A visualization of the CVs, for the three time horizons of predictions, can be seen in
Figure 13,
Figure 14 and
Figure 15.
From these last
Figure 13,
Figure 14 and
Figure 15, which present KAP, it appears again that there are important differences between the models, but that these differences are only shown by a restricted group of indicators.
In particular, these last figures show that while for some KPIs, there is a high level of variation between the models, for others, the variation, expressed by the coefficient of variation (CV), is very close to zero, meaning that in all models, those KPIs got to almost the same value (almost no variation, at all).
The variation implies that, for some models, the value of the KPI is high, while for others it is low, meaning that the models with low KPI values did not achieve a consistent prediction, which confirms the conclusions obtained from the previous
Figure 10,
Figure 11 and
Figure 12.
As a summary of these analyses, there are, therefore, results that could be considered satisfactory, particularly for the DT and RF models, given the KPIs’ presented high values in all tested conditions.
On the other hand, in the case of MLP and LR, a set of KPIs showed good results, but other KPIs did not. This happened precisely with the important KPIs such as p-Value [Accuracy ≤ NIR], and also with the kappa coefficient.
Regardless, the objective of showing that ML algorithms could be employed for PdM in a hydroelectric power plant environment was achieved for at least two of the algorithms tested.
Finally, these analyses of results confirm, as mentioned earlier, the importance of not considering only a few KPIs to analyze a model, as, for example, only those coefficients that revolve around accuracy, such as specificity, sensitivity and others. The indicators that provide greater statistical significance to the results are also fundamental in these analyses of the prediction model responses.