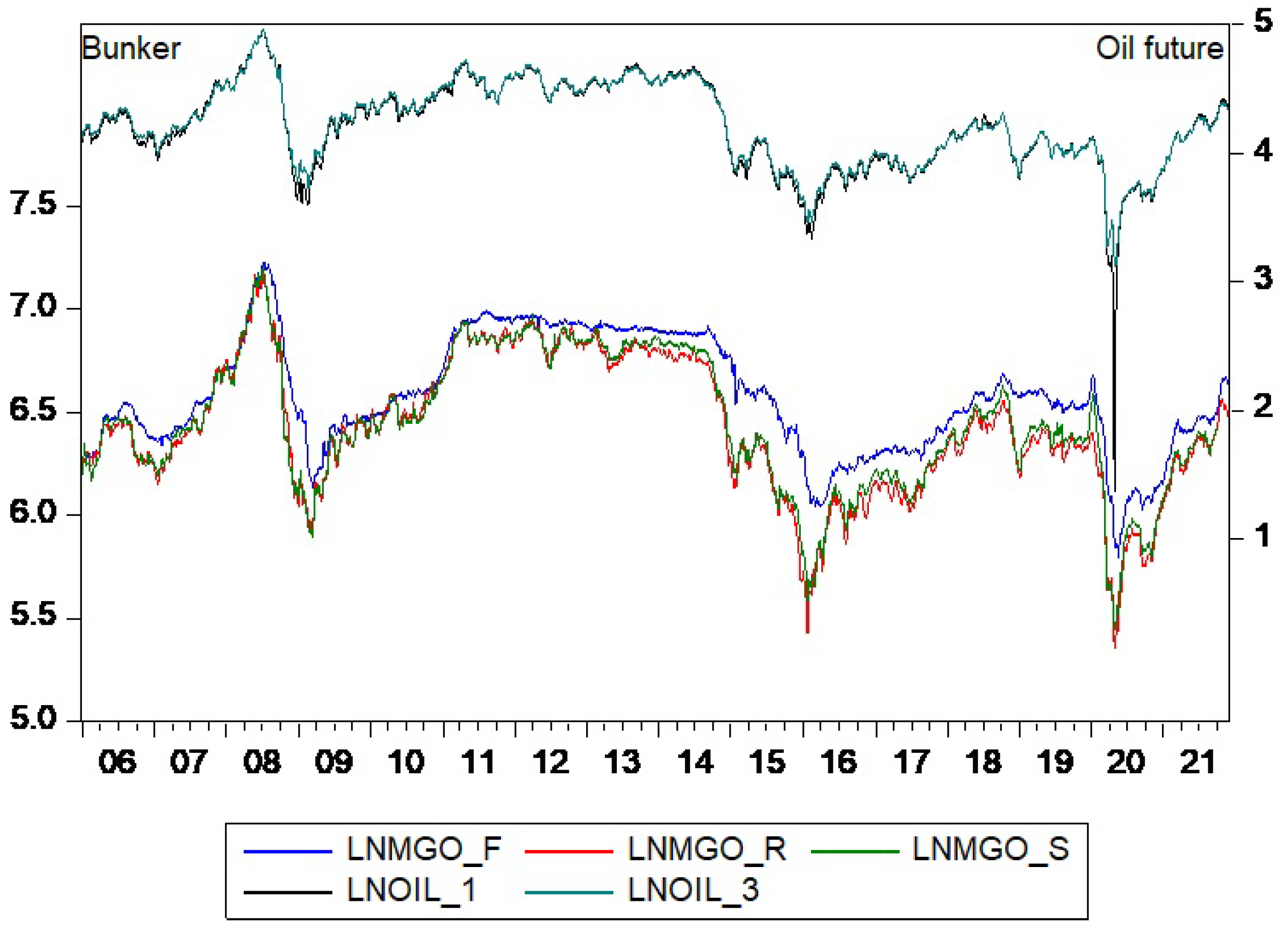
1. Introduction
Marine transportation is an integral part of transportation networks, and one of the most important ways for international trade. With the acceleration of the economic globalization process, international trade is more and more frequent. With its natural navigation channel, large carrying capacities, and relatively low freight charges, marine transportation is active and accounts for more than 80% of the total volume of international freight [
1]. Other than the large investment in infrastructure construction, a bunker is a significant operating cost for shipping companies, accounting for about 30–70% of the operating cost based on different bunker prices [
2,
3]. Bunker is mainly the heavy residual product left after gasoline, kerosene, and diesel oil from crude oil refining, as a result, its price is closely linked to the crude oil price. However, it is also affected by the relationship between supply and demand, showing volatility related to but inconsistent with the crude oil price. In the first quarter of 2021, WTI and Brent crude oil spot prices increased by 24.95% and 23.00%, respectively, because of world economic recovery and US inflation. During this period, the MGO (Marine Gas Oil) prices of Fujairah, Rotterdam, and Singapore increased by 26.31%, 20.72%, and 20.03%, respectively, and the VLSFO (Very Low Sulphur Fuel Oil) of these three ports increased by 19.38%, 17.41%, and 16.28%, respectively. Due to the uncertainty of bunker prices, shipping companies are exposed to the risk of bunker price changes. The analysis and forecasting of bunker prices are of great importance so that shipping companies can control the risk of bunker price fluctuations and control their operating costs.
Although previous studies have realized the importance of bunker, they mainly focus on controlling bunker fuel cost and reducing the purchase cost by optimizing refueling strategy. As for crude oil futures prices, most of the existing literature has studied the cointegration relationship between crude oil future prices and spot prices, or the relationship between crude oil future market and other commodity markets. At present, there is no literature on the relationship between the bunker price and the crude oil future price, which is also the novelty and originality of this paper.
This paper aims to analyze the relationship between bunker and crude oil future prices quantitatively. Firstly, this paper confirms the cointegration relationship between bunker and oil future prices. As a result, the VECM becomes reasonable to capture the long-term equilibrium relationship of bunker and oil future prices. ARMA, ARMAX, and VAR are also considered in predicting bunker prices which can test whether the cointegration relationship is effective in prediction. One-step-ahead and four-step-ahead forecasts are considered because these two prices are the most concerning issue in the industry. Moreover, two crude oil futures contracts are involved in the analysis because we want to check which contract implies future bunker prices more reliably and suitably. The results show that the VECM model performs better than the other three models, which means oil futures prices imply bunker prices through the long-term equilibrium cointegration relationship. The results also show crude oil future contract 1 is more reliable in the one-step-ahead prediction. Oil future contract 3 is just a little better in four-step-ahead prediction. As a result, in four-step-ahead prediction, the prediction results based on two future contracts should be considered. The results of this paper are conducive to the liner companies to have sufficient time to adjust the transportation refueling plan and use crude oil futures for hedging to avoid economic losses in time. Moreover, forward trading regarding bunker oil has gained the attention of some large financial firms, such as Goldman Sachs, in recent years. Though accurate forecasting of bunker oil prices is of great importance and helps shipping companies make timely adjustments to their operating strategies.
The structure of this paper is as follows.
Section 2 reviews the literature.
Section 3 presents the data and the cointegration analysis.
Section 4 focuses on the prediction analysis.
Section 5 conducts the impulse response analysis and makes a supplementary. Finally,
Section 6 concludes this study.
2. Literature Review
Bunker price is crucial for ship operators, Abouarghoub and Haider [
1] mention that the cost of the bunker is the key cost for ship operators, and the change in bunker price will have a great impact on the operation capacity. Notteboom and Vernimmen [
2] study the impact of bunker oil price changes on the cost of liner service operations. The rise in bunker oil prices correspondingly increases the transportation costs of shipping companies. The purpose of profit-making companies is to maximize corporate profits. As a result, price analysis of bunkers used in ship transportation cargo is of great importance. However, most of the existing studies focus on controlling fuel oil costs through bunker management strategy. For example, Yao et al. [
4] investigated a bunker fuel management strategy for a single shipping liner service and studied the relationship between sailing speed and fuel consumption rate. They use an empirical model to explain the relationship between bunker oil consumption rate and sailing speed for container ships of different sizes, which is conducive to reducing shipping costs and improving service quality and efficiency for shipping companies. Wang, Gao et al. [
5] use a mixed-integer nonlinear programming model which simultaneously considers sailing speeds, bunkering ports, bunkering volume, and loading amounts to maximize cargo revenue and minus bunker cost. Ghosh, Lee et al. [
6] focus on the cost optimization strategy with bunkering contracts, and formulate a dynamic programming model to minimize the total bunkering cost. There are also many studies in the extant literature on the optimal bunker refueling strategies for liner shipping, in which ways the operators can control the cost of bunker oil. Plum, Pisinger et al. [
7] mention that fluctuations in bunker prices are usually related to crude oil prices, but prices vary significantly between ports, so the bunker purchasing cost optimization problem needs to be reformulated daily, but bunker purchasing is generally made by contract a few weeks prior to arrival the port, which complicates the adjustment of the optimal plan. De, Choudhary et al. [
8] consider stochastic fuel consumption for different segments, stochastic bunker prices for each port, and different fuel refueling strategies to determine the optimal fuel management strategy. These researches show that bunker oil price is closely related to the operation of shipping companies and occupies an important position. Because the general trend of bunker prices is fluctuating and uncertain, even on the same day, bunker oil prices may vary significantly from port to port [
6].
Although the bunker price is important, the direct analysis of the bunker price is few. Stefanakos and Schinas [
9] argue that the efficient forecasting of bunker prices is of ship operators’ interest, and there is also a direct relationship between bunker prices and financial results, and that incorrect forecasting of bunker prices leads to incorrect estimates of bunker price fluctuations, resulting in incorrect hedging ratios and risk management strategies, which means catastrophe for the normal operation of liner service operations. They used Vector Auto-Regressive Moving Average (VAR-MA) model to forecast a tetra-variate and an octa-variate time series of bunker prices, the predicted results are in good agreement with the actual values. Due to the importance of bunker price prediction, they also use fuzzy time series forecasting techniques to predict bunker prices [
10].
In a short summary, most of the existing literature focuses on the optimal bunker refueling strategy and bunker management. Bunker price prediction is an interest of the researchers; however, these researchers just considered the bunker market. There is limited literature to study the bunker price considering another energy market.
For crude oil futures, it has two indispensable functions; one is to hedge and reduce the potential risk for investors, the other is the function of price discovery. The oil futures prices reflect the price that both the buyer and the seller agree on. Thus, crude oil futures prices contain direct information about investors’ expectations of future prices for the crude oil commodity [
11]. Most of the existing literature investigates the relationship between crude oil future prices and spot oil prices or other commodity markets. Silvério and Szklo [
12] through the empirical analysis of WTI spot and WTI futures, find that for WTI, the contribution of the future market in price discovery is increasing. Zhang and Wang [
13] find that there is a long-term equilibrium relationship between futures and spot prices of crude oil, but the futures market is more mature and has better market efficiency and price discovery functions. Jiang, Marsh [
14] use a vector error correction model to study the price transmission between the U.S. crude oil, corn, and plastic markets and find that the crude oil price is a factor that causes the changes in the plastic and corn futures markets. In addition, there is also a correlation between the crude oil and corn futures markets. Alizadeh and Nomikos [
15] investigate the dynamic relationship between oil future prices and tanker freight rates. Chu, Hoff et al. [
16] indicate that in the prediction of oil spot price, futures-based forecasts perform better than the no-change forecast across long-term horizons (one to five years). Bai and Kavussanos [
17] examine how to use the petroleum future contracts to manage the risk results from the bunker spot price fluctuations. Other related literature includes Chang and Lee [
18], Lee and Zeng [
19], Chen, Lee et al. [
20], Gulley and Tilton [
21], and Liu Wang et al. [
22]. The existing literature on the relationship between crude oil future prices and spot prices has been very sufficient. However, at present, there is limited literature on the relationship between crude oil futures and bunker oil. Bunker is a product of crude oil split distillation, so its price should be closely related to the oil price. As oil future price contains the information of future spot oil price; it is reasonable to investigate how oil future prices imply bunker prices. In this way, shipping enterprises can make timely adjustments and decisions. As crude oil future is the most active futures contract in the world shipping enterprises and can consider using the crude oil future to manage risk when the bunker prices change, thus controlling their operation costs and maximizing profits. For this reason, this research fills this gap by investigating the relationship between bunker prices and oil future prices.
Cointegration analysis is very popular in analyzing the co-movement of two non-stationary time series. For example, Aftab, Ahmed et al. [
23] investigate the nexus between carbon emissions, energy consumption and economic progress for Pakistan by cointegration and autoregressive distribution lag methods. Zakaria, Khiam et al. [
24] analyze the impact of world oil prices on inflation in South Asian countries, using Cointegration, VAR, and nonlinear analysis. After the cointegration relationship is confirmed, the vector error correction model (VECM) is usually applied to the model time series. For example, Alizadeh and Nomikos [
15] check the causal relationship between WTI futures and shipping freight costs using the Vector Error Correction model. Besides ARDL, Aftab, Ahmed et al. [
23] also apply the VECM to determine feedback effect in a bivariate model. Impulse response analysis is often used with VECM too because it can provide the support of causality status between the variables in the VECM system [
25]. For example, Danish Wang et al. [
26] use the impulse response function to reveal that CO
emission rises due to forecast error stemming from energy crises. Mensah, Triacca et al. [
27] also conduct impulse response analysis with VECM. So this paper adopts their research methods to explore how crude oil future prices imply bunker prices.
4. Prediction Analysis
4.1. Model Specification
It is found that the crude oil future prices and the MGO prices are cointegrated in the last section. By utilizing the cointegration relationship, the VECM model can be built to predict the price of MGO. In addition, we also considered the ARMA, ARMAX, and VAR models to explore the performance of these models in predicting the MGO prices.
4.1.1. ARMA and ARMAX
Autoregressive Moving Average (ARMA) is the most basic model in time series analysis and it is usually taken as the benchmark model in prediction performance evaluation. ARMAX is an extension of ARMA by including exogenous variables.
The ARMA model considers the effect of the series’ own lagged term and random disturbance term on the current series value (Shown in Equation (
4)). The ARMAX model adds exogenous variables to investigate the impacts of these exogenous variables. In this paper, the return series of crude oil future prices lagging by one period is taken as the exogenous variable in ARMAX, and the influence on the prediction effect of MGO price after adding the exogenous variable of the return of crude oil futures is considered (Shown in Equation (
5)).
4.1.2. VAR
VAR is constructed as a function of the lagged terms of each endogenous variable in the system. In this paper, the VAR model is constructed by taking the MGO returns and crude oil future returns as the endogenous variables in the system and using their lagged terms to construct a model to analyze and forecast MGO prices (Shown in Equation (
6)).
The best lag order of VAR is determined by Schwarz Criterion (SC), which is also known as Bayesian Information Criterion (BIC), because it also considers the number of the parameters in the models. The value of SC is calculated by the following equation:
where
n is the number of the estimated parameters and
l is the log-likelihood value which is calculated by assuming that it obeys multivariate normal distribution.
Table 4 shows the BIC values for lags 1–5. The values in bold indicate the optimal lags selected by the criteria.
4.1.3. VECM
The VECM is a model of VAR with cointegration constraints. Using the information presented in the previous section, one can construct a VECM model to analyze the dynamic relationship between MGO and crude oil futures yields.
in Equation (
8) is the error correction term, which is established on the basis that bunker and crude oil future prices have a cointegration relationship. The error correction term indicates the long-run dynamics that although bunker and crude oil future prices are disequilibrium at any given time, but they have the tendency to adjust themselves towards equilibrium. The short-run dynamics is presented by
in Equation (
8). In the following equation,
p is the optimal lag in the VAR model. So the lag order of VECM is
.
4.2. Model Estimation Results
According to statistics, considering Singapore ranks first among the ten largest refueling ports in the world in 2020, it is more representative than the other two ports. This section discusses the estimation results based on the MGO prices in Singapore. The model parameter estimation results of the models used in this research are shown in
Table 5.
In
Table 5, the optimal lags of ARMA and ARMA are also determined by the BIC value. For crude oil future 1, almost all of the parameters estimation results of AR terms and MA terms in ARMA and ARMAX are significant at the 1% level. The parameter before the exogenous variable, crude oil future price return, is significant at 1%. The positive value indicates the bunker price increases with the oil crude future price. Additionally, the random disturbances term is negatively related to the current return rate. The VAR model considers the lagging terms of both the MGO return and the crude oil future return. The results indicate that the lagging terms of both returns have certain impacts on the MGO price return. For both datasets, the parameters’ signs of the AR terms in the VECM are consistent with those of the VAR. For the MGO returns and oil future contract 1 returns, the parameter’s sign of the MA(2) term in the VECM is not consistent with that of the VAR. But both of them are not significant. For both datasets, the parameters of the error correction terms are significant, which indicates the long-run equilibrium conditions significantly affect the short-run dynamics of bunker prices through an error correction mechanism. The parameters are negative, indicating that the increase in the error correction term’s value has the effect of lowering the MGO returns, and the decrease in the error correction term’s value has the effect of increasing the MGO price returns; in other words, the long-run equilibrium between MGO and oil future prices stabilizes the MGO price returns. Referring to the short-run dynamics between the MGO and oil future prices, the first lag of the oil future returns has a positive impact on the MGO price returns. The oil future contract 1 returns increase by 1% and, consequently, the MGO returns increase by 0.0489%. The oil future contract 3 returns increase by 1% and the MGO returns increase by 0.3969%. The second lag of the oil future contract 1 returns also impacts the MGO returns. However, this impact is weaker than the impact from the first lag.
4.3. Prediction Performance
Two prediction performance evaluation methods are used in this paper. Root mean square error (RMSE) is the most widely used method of evaluation. The better the forecast is, the smaller the mean square forecast error is. The closer to zero the value is, the better the forecasting performs. Another method is the Theil’s inequality coefficient, also known as Theil’s U. It provides a measure of how well the predicted value compares to the observed value, which helps to assess whether a good forecasting model is better than a naive prediction that repeats the previous observation, with the same evaluation criteria as RMSE. The calculation of RMSE and Theil’s U is shown in Equations (
9) and (
10).
While the in-sample performance of the prediction model is not necessary to indicate the out-of-sample performance. Out-of-sample prediction can be used to measure the model’s performance more subjectively. In this paper, the out-of-sample forecast period is from 1 March 2019 to 26 November 2021, which includes 144 observations. There are two types of forecast intervals, the one-step-ahead forecast and four-step-ahead forecast.
The results of RMSE and Theil’s indicators in the one-step-ahead are shown in
Table 6. When the ARMA, ARMAX, VAR, and VECM models are used to forecast the price of MGO, the effect of the MGO price predicted by the ARMA model is better than that of the ARMAX model, indicating that the prediction performance of the ARMA model will be reduced when considering the crude oil future returns. So only simply involving crude oil future returns is not effective in predicting MGO prices. In the out-of-sample forecast results of crude oil futures contract 1 and MGO price, the VECM model has the smallest root mean square error-index and Theil’s U index. It appears that the VECM model demonstrates better forecasting performance than ARMA, ARMAX, and VAR models.
Referring to crude oil future contract 3 and MGO prices, when it comes to predicting MGO prices of Rotterdam and Fujairah, the VECM performs better than the other two models. In the prediction of MGO price of Singapore, the ARMAX model is the best and it performs slightly better than the VAR and VECM models. Compared with crude oil futures contract 1 and crude oil futures contract 3, crude oil futures contract 1 has better prediction performance using the VECM model, which indicates that the prediction ability of the model is improved after considering the cointegration relationship between the returns of MGO and crude oil future contract 1. As compared to Rotterdam, Singapore, and Fujairah, the RMSE and Theil’s of the one-step-ahead forecast for Fujairah have the smallest weekly price relationship with crude oil futures, which indicates that the forecast effect on the MGO price of Fujairah port is good.
The results of the four-step-ahead prediction are shown in
Table 7. When the crude oil future contract 3 is used to make an out-of-sample prediction on MGO, the values of RMSE and Theil’s U of the VECM model are lower than those of other models. This implies that the VECM model based on the cointegration between the MGO returns and the crude oil future returns can improve prediction accuracy. However, it doesn’t mean crude oil future 3 with VECM is most suitable to conduct a four-step-ahead prediction, because crude oil future 1 with VECM achieves better RMSE and Theil’s U values in predicting the MGO prices in Rotterdam.
Comparing the one-step-ahead forecast with the four-step-ahead forecast, using the VECM model, crude oil future contract 1 has a better performance on MGO price in the one-step forward forecast, while in the four-step forward forecast, crude oil future contract 3 has a slightly better performance than crude oil future contract 1.
4.4. Robustness Checks
To test whether the above conclusions are reliable, this section adjusts the forecast period to a total of 72 weeks from 17 July 2020 to 26 November 2021 to test whether the above conclusions are robust under the condition of shortening the time window. In the robustness test, the out-of-sample forecast is still divided into one-step-ahead and four-step-ahead; the forecast performance is shown in
Table 8 and
Table 9.
In the one-step-ahead forecast, when using ARMA, ARMAX, VAR, and VECM models to forecast the price of MGO, the effect of using the ARMA model to forecast the price of MGO is better than that of the ARMAX model, which indicates that considering the yield of crude oil futures can reduce the forecast performance of the model. In the relationship between crude oil future contract 1 and MGO price, the VECM model with cointegration constraint is still better than other models. In crude oil future contract 3, With respect to the forecast of MGO price of Rotterdam and Fujairah, VECM performs slightly better than the other two models. The ARMAX model performs slightly better than the VAR and VECM in the forecast of the MGO price of Singapore. The prediction performances of MGO prices using ARMA, ARMAX, and VECM models are consistent with the results obtained in
Table 5, which indicates that the VECM model has good prediction performance. Moreover, oil future contract 1 is effective in one-step-ahead prediction. The RMSE and Theil’s U values of crude oil futures contract 1 are smaller than those of crude oil futures contract 3, indicating that the cointegration relationship between crude oil future contract 1 and MGO has a good prediction effect on MGO.
In the four-step-ahead prediction, the prediction effect of the ARMA model is slightly lower than the other three models. The VECM model considering the cointegration relationship between MGO return rate and crude oil future contract 3 is better in predicting MGO prices. Comparing
Table 6 with
Table 8, the results of futures contracts with better performance are inconsistent for the MGO price forecast of Rotterdam, the results of crude oil future contract 3 used in the MGO price forecast of other ports are consistent. In addition, it is consistent in its superior performance in the MGO price forecast that the VECM model is based on the cointegration relationship between crude oil futures contracts and MGO. Although contract 3 performs better in four-step-ahead prediction in most cases, but this paper still recommends using both contract 1 and 3 to predict four-step-ahead values since contract 3 is not better than contract 1 in Rotterdam.
In light of the above analysis, it can be shown that the result that VECM performs better than other models is robust and consistent irrespective of how the prediction window is chosen. In other words, the MGO price can be more accurately predicted when a one-step-ahead prediction is made using the crude oil future contract 1. With the four-step-ahead prediction, crude oil future contract 3 outperforms crude oil futures contract 1, but only by a small margin. In the one-step-ahead forecast and the four-step-ahead forecast, the cointegration relationship is helpful in the forecast of MGO price.