Forecasting Regional Carbon Prices in China Based on Secondary Decomposition and a Hybrid Kernel-Based Extreme Learning Machine
Abstract
:1. Introduction
2. Literature Review
3. Methods
3.1. Variational Mode Decomposition
3.2. Improved Complementary Ensemble-Based Empirical Mode Decomposition with Adaptive Noise
3.3. Range Entropy
3.4. Hybrid Kernel-Based Extreme Learning Machine Optimized by the Sparrow Search Algorithm
3.4.1. Hybrid Kernel-Based Extreme Learning Machine
- ➀
- RBF kernel function:
- ➁
- Poly-kernel function:
3.4.2. Sparrow Search Algorithm
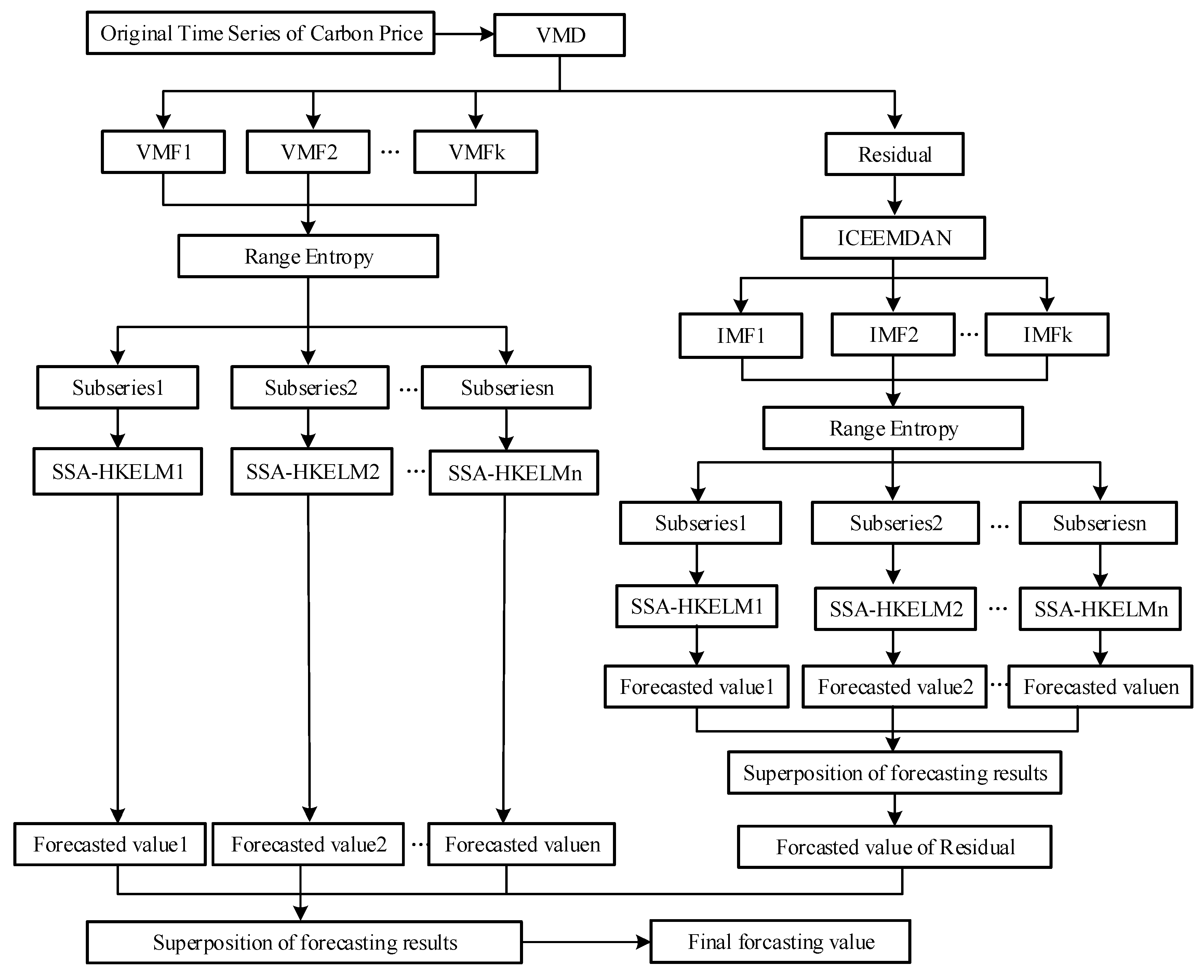
3.5. Framework of the Proposed Carbon Price Forecasting Model
- (1)
- VMD technology is used to decompose the original sequence of carbon prices to obtain each VMF, and the sum of the data is subtracted from the original time sequence of carbon prices to obtain the residual term of VMD.
- (2)
- Reconstruction and forecasting are carried out after VMD decomposition. We calculate RE of each VMF, and merge VMF components with lower entropies into a subseries. Each subseries is then forecasted using the SSA-HKELM model, and the results of each VMD-RE are obtained.
- (3)
- ICEEMDAN technology is used to decompose the residual term after VMD has been applied to the original sequence of carbon prices. Range entropy is introduced to measure the complexity of the signals of each IMF of the residual term, and IMF components with lower entropy values are merged into a new subseries. The SSA-HKELM model is then used to separately forecast each subseries of the residual term after applying ICEEMDAN-RE, and the results of the forecasts of each are further superimposed to obtain the final results of the residual term of the carbon price.
- (4)
- The results of the forecasting of each VMF and the residual term after the decomposition of the original sequence of carbon prices are superimposed to obtain the final forecasts of the carbon price.
4. Empirical Analysis of Price Forecasting of China’s Regional Carbon Markets
4.1. Sample Selection and Criteria for Evaluating Forecasts
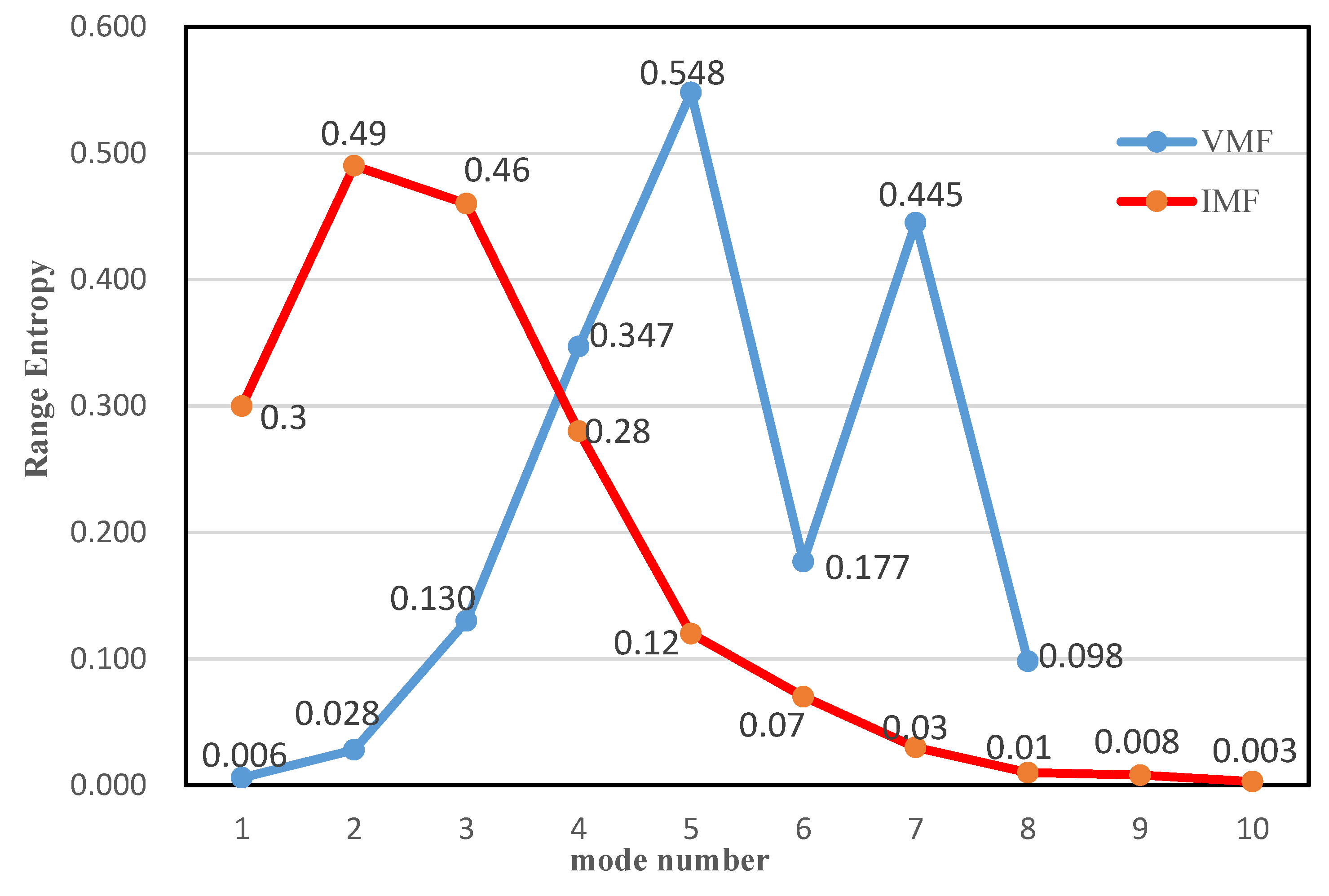
4.2. Analysis of the Decomposition and Reconstruction of the Market Price of Carbon
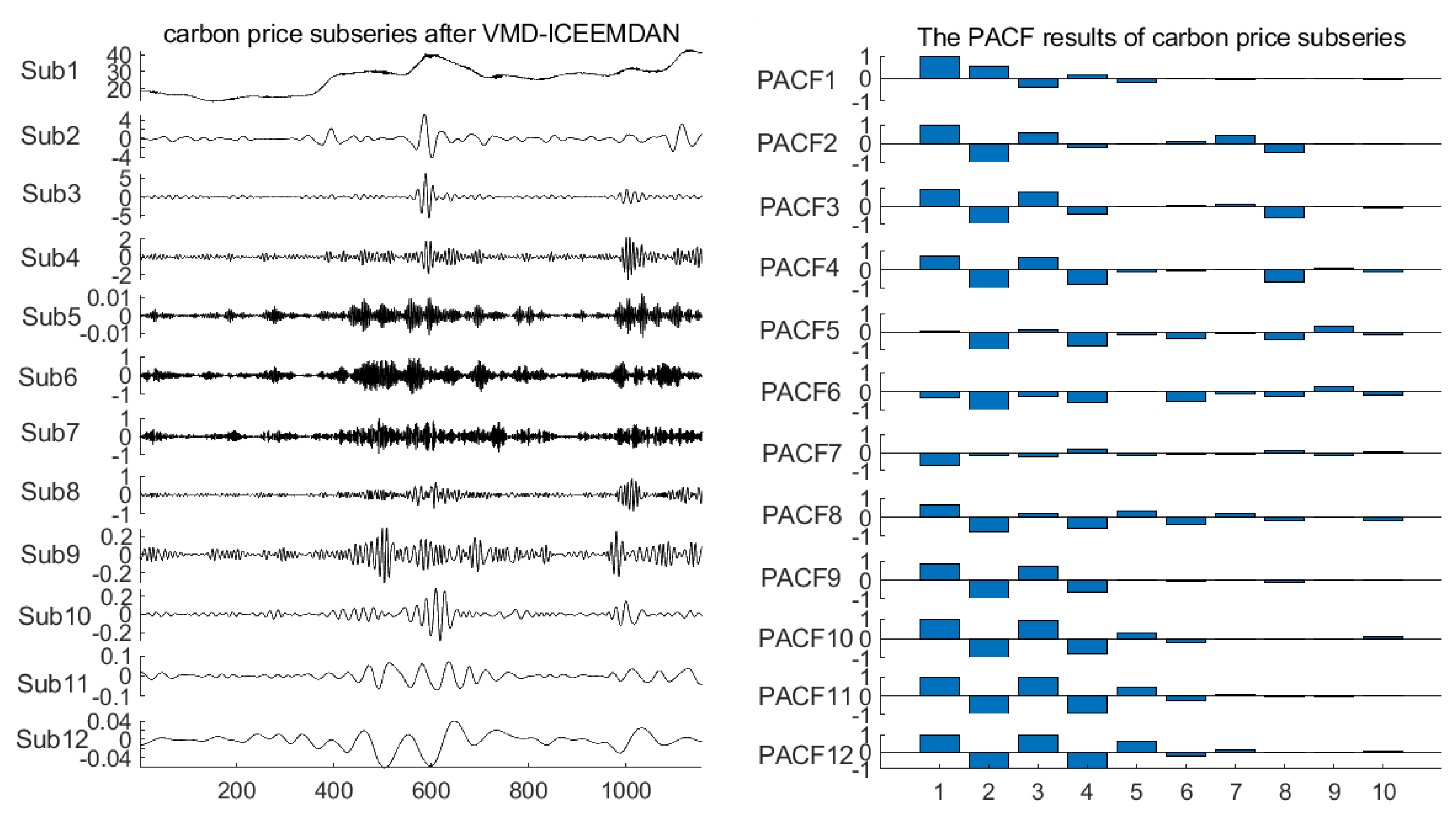
4.3. Partial Autocorrelation Test of Subseries of the Carbon Price
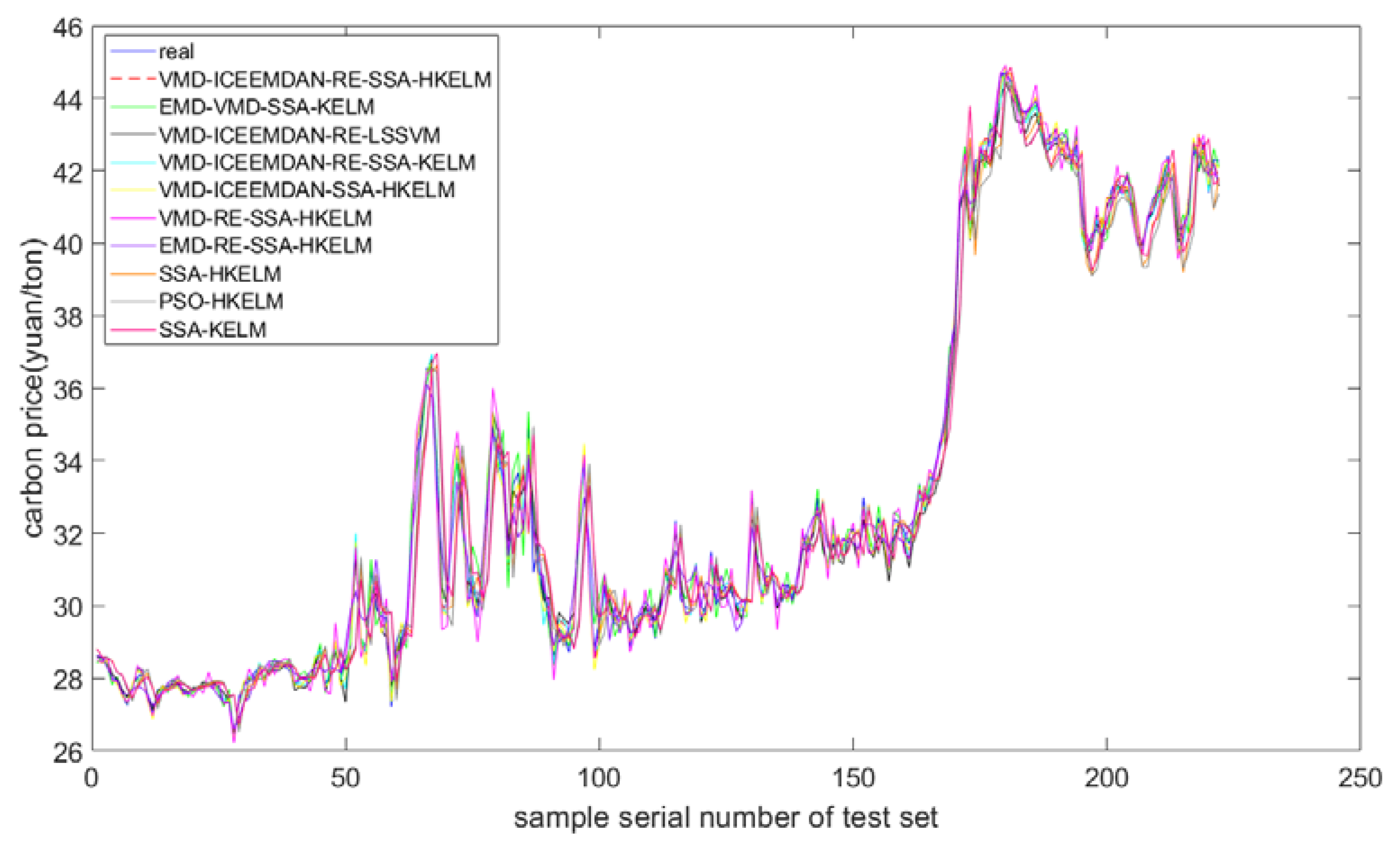
4.4. Analysis of the Forecasted Carbon Price
4.5. Robustness
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, H.; Samuel, C.A.; Amissah, J.C.K.; Taghizadeh-Hesary, F.; Mensah, I.A. Non-linear nexus between CO2 emissions and economic growth: A comparison of OECD and B&R countries. Energy 2020, 212, 118637. [Google Scholar] [CrossRef]
- Sun, H.; Edziah, B.K.; Sun, C.; Kporsu, A.K. Institutional quality and its spatial spillover effects on energy efficiency. Socio-Econ. Plan. Sci. 2021, 101023. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Su, C.; Umar, M.; Shao, X. Exploring the asymmetric impact of economic policy uncertainty on China’s carbon emissions trading market price: Do different types of uncertainty matter? Technol. Forecast. Soc. Chang. 2022, 178, 121601. [Google Scholar] [CrossRef]
- Zheng, J.; Mi, Z.; Coffman, D.; Milcheva, S.; Shan, Y.; Guan, D.; Wang, S. Regional development and carbon emissions in China. Energy Econ. 2019, 81, 25–36. [Google Scholar] [CrossRef]
- Huang, W.; Wang, Q.; Li, H.; Fan, H.; Qian, Y.; Klemeš, J. Review of recent progress of emission trading policy in China. J. Clean. Prod. 2022, 349, 131480. [Google Scholar] [CrossRef]
- Liu, B.; Sun, Z.; Li, H. Can Carbon Trading Policies Promote Regional Green Innovation Efficiency? Empirical Data from Pilot Regions in China. Sustainability 2021, 13, 52891. [Google Scholar] [CrossRef]
- Ren, C.; Lo, A.Y. Emission trading and carbon market performance in Shenzhen, China. Appl. Energy 2017, 193, 414–425. [Google Scholar] [CrossRef] [Green Version]
- Zeng, S.; Nan, X.; Liu, C.; Chen, J. The response of the Beijing carbon emissions allowance price (BJC) to macroeconomic and energy price indices. Energy Policy 2017, 106, 111–121. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.; Xu, Y. Carbon price volatility: The case of China. PLoS ONE 2018, 13, e0205317. [Google Scholar] [CrossRef] [Green Version]
- Han, M.; Ding, L.; Zhao, X.; Kang, W. Forecasting carbon prices in the Shenzhen market, China: The role of mixed-frequency factors. Energy 2019, 171, 69–76. [Google Scholar] [CrossRef]
- Huang, Y.; Hu, J.; Liu, H.; Liu, S. Research on price forecasting method of China’s carbon trading market based on PSO-RBF algorithm. Syst. Sci. Control. Eng. 2019, 7, 40–47. [Google Scholar] [CrossRef]
- Xie, Q.; Hao, J.; Li, J.; Zheng, X. Carbon price prediction considering climate change: A text-based framework. Econ. Anal. Policy 2022, 74, 382–401. [Google Scholar] [CrossRef]
- Liu, J.; Wang, P.; Chen, H.; Zhu, J. A combination forecasting model based on hybrid interval multi-scale decomposition: Application to interval-valued carbon price forecasting. Expert Syst. Appl. 2022, 191, 116267. [Google Scholar] [CrossRef]
- Fan, J.; Todorova, N. Dynamics of China’s carbon prices in the pilot trading phase. Appl. Energy 2017, 208, 1452–1467. [Google Scholar] [CrossRef] [Green Version]
- Zhu, B. A novel multiscale ensemble carbon price prediction model integrating empirical mode decomposition, genetic algorithm and artificial neural network. Energies 2012, 5, 355–370. [Google Scholar] [CrossRef]
- Li, W.; Lu, C. The research on setting a unified interval of carbon price benchmark in the national carbon trading market of China. Appl. Energy 2015, 155, 728–739. [Google Scholar] [CrossRef]
- Yao, Y.; Lv, J.; Zhang, C. Price formation mechanism and price forecast of Hubei carbon market. Stat. Decis. 2017, 19, 166–169. [Google Scholar]
- Zhou, J.; Yu, X.; Yuan, X. Predicting the carbon price sequence in the Shenzhen Emissions Exchange using a multiscale ensemble forecasting model based on ensemble empirical mode decomposition. Energies 2018, 11, 1907. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Liu, Z. Forecasting the carbon price sequence in the Hubei emissions exchange using a hybrid model based on ensemble empirical mode decomposition. Energy Sci. Eng. 2020, 8, 2708–2721. [Google Scholar] [CrossRef] [Green Version]
- Lu, H.; Ma, X.; Huang, K.; Azimi, M. Carbon trading volume and price forecasting in China using multiple machine learning models. J. Clean. Prod. 2020, 249, 119386. [Google Scholar] [CrossRef]
- Jiang, P.; Liu, Z. Variable weights combined model based on multi-objective optimization for short-term wind speed forecasting. Appl. Soft. Comput. 2019, 82, 105587. [Google Scholar] [CrossRef]
- Hao, Y.; Tian, C.; Wu, C. Modelling of carbon price in two real carbon trading markets. J. Clean. Prod. 2020, 244, 118556. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, D. Carbon Price forecasting based on improved CEEMDAN and extreme learning machine optimized by sparrow search algorithm. Sustainability 2021, 13, 94896. [Google Scholar] [CrossRef]
- Sun, G.; Chen, T.; Wei, Z.; Sun, Y.; Zang, H.; Chen, S. A carbon price forecasting model based on variational mode decomposition and spiking neural networks. Energies 2016, 9, 54. [Google Scholar] [CrossRef] [Green Version]
- Chai, S.; Zhang, Z.; Zhang, Z. Carbon price prediction for China’s ETS pilots using variational mode decomposition and optimized extreme learning machine. Ann. Oper. Res. 2021. [Google Scholar] [CrossRef]
- Sun, S.; Jin, F.; Li, H.; Li, Y. A new hybrid optimization ensemble learning approach for carbon price forecasting. Appl. Math. Model. 2021, 97, 182–205. [Google Scholar] [CrossRef]
- Sun, W.; Huang, C. A carbon price prediction model based on secondary decomposition algorithm and optimized back propagation neural network. J. Clean. Prod. 2020, 243, 118671. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, S. A carbon price prediction model based on the secondary decomposition algorithm and influencing factors. Energies 2021, 14, 1328. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Q. Forecasting carbon price with secondary decomposition algorithm and optimized extreme learning machine. Sustainability 2021, 13, 58413. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Li, H.; Jin, F.; Sun, S.; Li, Y. A new secondary decomposition ensemble learning approach for carbon price forecasting. Knowl.-Based Syst. 2021, 214, 106686. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control. 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Jia, S.; Ma, B.; Guo, W.; Li, Z.S. A sample entropy based prognostics method for lithium-ion batteries using relevance vector machine. J. Manuf. Syst. 2021, 61, 773–781. [Google Scholar] [CrossRef]
- Ru, Y.; Li, J.; Chen, H.; Li, J. Epilepsy Detection Based on Variational Mode Decomposition and Improved Sample Entropy. Comput. Intell. Neurosci. 2022, 2022, 6180441. [Google Scholar] [CrossRef]
- Omidvarnia, A.; Mesbah, M.; Pedersen, M.; Jackson, G. Range entropy: A bridge between signal complexity and self-similarity. Entropy 2018, 20, 962. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B-Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Tang, Z.; Wu, J.; Du, X.; Chen, K. Multi-step-ahead crude oil price forecasting based on two-layer decomposition technique and extreme learning machine optimized by the particle swarm optimization algorithm. Energy 2021, 229, 120797. [Google Scholar] [CrossRef]
- Qi, X.; Li, K.; Yu, X.; Zhang, Z.; Lou, J. Transformer top oil temperature interval prediction based on kernel extreme learning machine and bootstrap method. Proc. CSEE 2017, 37, 5821–5828. [Google Scholar]
- Zhou, C.; Yin, K.; Cao, Y.; Intrieri, E.; Ahmed, B.; Catani, F. Displacement prediction of step-like landslide by applying a novel kernel extreme learning machine method. Landslides 2018, 15, 2211–2225. [Google Scholar] [CrossRef] [Green Version]
- Hou, Z.; Lao, W.; Wang, Y.; Lu, W. Hybrid homotopy-PSO global searching approach with multi-kernel extreme learning machine for efficient source identification of DNAPL-polluted aquifer. Comput. Geosci. 2021, 155, 104837. [Google Scholar] [CrossRef]
- Li, T.; Qian, Z.; He, T. Short-Term Load Forecasting with Improved CEEMDAN and GWO-Based Multiple Kernel ELM. Complexity 2020, 2020, 1209547. [Google Scholar] [CrossRef]
- Lv, L.; Wang, W.; Zhang, Z.; Liu, X. A novel intrusion detection system based on an optimal hybrid kernel extreme learning machine. Knowl.-Based Syst. 2020, 195, 105648. [Google Scholar] [CrossRef]
- Xue, J.K.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Xin, J.; Chen, J.; Li, C.; Lu, R.; Li, X.; Wang, C.; Zhu, H.; He, R. Deformation characterization of oil and gas pipeline by ACM technique based on SSA-BP neural network model. Measurement 2022, 189, 110654. [Google Scholar] [CrossRef]
- Niu, M.; Hu, Y.; Sun, S.; Liu, Y. A novel hybrid decomposition-ensemble model based on VMD and HGWO for container throughput forecasting. Appl. Math. Model. 2018, 57, 163–178. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, G.; Chen, B.; Han, J.; Zhao, Y.; Zhang, C. Short-term wind speed prediction model based on GA-ANN improved by VMD. Renew. Energy 2020, 156, 1373–1388. [Google Scholar] [CrossRef]

| Market | Max | Min | Mean | Std | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| Hubei | 53.85 | 11.26 | 25.74 | 8.21 | 0.10 | 2.46 |
| Index | Formula | |
|---|---|---|
| Forecasting accuracy | RMSE | |
| MAE | ||
| MAPE | ||
| Forecasting direction | DS |
| Original Carbon Price | Carbon Price Residual Sequence | ||
|---|---|---|---|
| Subseries | VMD Modes | Subseries | ICEEMDAN Modes |
| Sub1 | VMF1, VMF2, VMF8 | Sub7 | IMF1 |
| Sub2 | VMF3 | Sub8 | IMF2 |
| Sub3 | VMF4 | Sub9 | IMF3 |
| Sub4 | VMF5 | Sub10 | IMF4 |
| Sub5 | VMF6 | Sub11 | IMF5 |
| Sub6 | VMF7 | Sub12 | IMF6, IMF7, IMF8, IMF9, IMF10 |
| Carbon Price Subseries | Input to Each HKELM Forecasting Model |
|---|---|
| Sub1 | y(t − 1), y(t − 2), y(t − 3), y(t − 4), y(t − 5) |
| Sub2 | y(t − 1), y(t − 2), y(t − 3), y(t − 4), y(t − 6) |
| Sub3 | y(t − 1), y(t − 2), y(t − 3), y(t − 4) |
| Sub4 | y(t − 1), y(t − 2), y(t − 3), y(t − 4), y(t − 5) |
| Sub5 | y(t − 1), y(t − 2), y(t − 3), y(t − 4), y(t − 5), y(t − 6) |
| Sub6 | y(t − 1), y(t − 2), y(t − 3), y(t − 4), y(t − 6) |
| Sub7, Sub8 | y(t − 1), y(t − 2), y(t − 3), y(t − 4), y(t − 5) |
| Sub9 | y(t − 1), y(t − 2), y(t − 3), y(t − 4) |
| Sub10, Sub11, Sub12 | y(t − 1), y(t − 2), y(t − 3), y(t − 4), y(t − 5), y(t − 6) |
| Carbon Price Subseries | C | a | c | d | w |
|---|---|---|---|---|---|
| Sub1 | 804.2335 | 42.4727 | 406.3407 | 3 | 0.4152 |
| Sub2 | 218.1153 | 20.4560 | 368.6420 | 2 | 0.7566 |
| Sub3 | 285.8397 | 757.2005 | 753.7293 | 4 | 0.9172 |
| Sub4 | 781.7228 | 490.4006 | 148.4659 | 1 | 0.1264 |
| Sub5 | 281.9055 | 6.3548 | 273.3429 | 1 | 0.1022 |
| Sub6 | 266.7218 | 100.3802 | 846.0002 | 1 | 0.7839 |
| Sub7 | 641.6777 | 128.6927 | 0.0015 | 3 | 0.4092 |
| Sub8 | 745.3274 | 424.0307 | 811.8651 | 1 | 0.4083 |
| Sub9 | 0.0184 | 646.2312 | 332.7460 | 3 | 0.4833 |
| Sub10 | 751.5801 | 363.3060 | 35.1337 | 3 | 0.0656 |
| Sub11 | 260.3775 | 184.9134 | 115.1786 | 5 | 0.3729 |
| Sub12 | 341.7896 | 590.9369 | 468.3994 | 4 | 0.7054 |
| Models | RMSE | MAE | MAPE | DS |
|---|---|---|---|---|
| SSA-KELM | 1.1760 | 0.8021 | 0.0243 | 0.5270 |
| PSO-HKELM | 1.2025 | 0.8598 | 0.0258 | 0.5450 |
| SSA-HKELM | 1.1697 | 0.8259 | 0.0250 | 0.5135 |
| EMD-RE-SSA-HKELM | 0.5257 | 0.3880 | 0.0120 | 0.8288 |
| VMD-RE-SSA-HKELM | 0.4181 | 0.3137 | 0.0096 | 0.8378 |
| VMD-ICEEMDAN-SSA-HKELM | 0.2578 | 0.1865 | 0.0058 | 0.8964 |
| VMD-ICEEMDAN-RE-SSA-KELM | 0.3092 | 0.2245 | 0.0069 | 0.8604 |
| VMD-ICEEMDAN-RE-LSSVM | 0.4086 | 0.2944 | 0.0089 | 0.8243 |
| EMD-VMD-SSA-KELM | 0.2869 | 0.2105 | 0.0064 | 0.8604 |
| VMD-ICEEMDAN-RE-SSA-HKELM | 0.2493 * | 0.1796 * | 0.0056 * | 0.9054 * |
| Models | RMSE | MAE | MAPE | DS |
|---|---|---|---|---|
| SSA-KELM | 0.7380 | 0.5455 | 0.0146 | 0.4955 |
| PSO-HKELM | 0.7663 | 0.5453 | 0.0144 | 0.5631 |
| SSA-HKELM | 0.6191 | 0.4423 | 0.0118 | 0.5676 |
| EMD-RE-SSA-HKELM | 0.2927 | 0.2217 | 0.0059 | 0.8514 |
| VMD-RE-SSA-HKELM | 0.1352 | 0.1026 | 0.0027 | 0.9054 |
| VMD-ICEEMDAN-SSA-HKELM | 0.1057 | 0.0861 | 0.0023 | 0.8964 |
| VMD-ICEEMDAN-RE-SSA-KELM | 0.5669 | 0.4623 | 0.0118 | 0.6486 |
| VMD-ICEEMDAN-RE-LSSVM | 0.5218 | 0.4202 | 0.0108 | 0.6577 |
| EMD-VMD-SSA-KELM | 0.2884 | 0.2445 | 0.0065 | 0.7748 |
| VMD-ICEEMDAN-RE-SSA-HKELM | 0.0934 * | 0.0706 * | 0.0019 * | 0.9189 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Hu, B. Forecasting Regional Carbon Prices in China Based on Secondary Decomposition and a Hybrid Kernel-Based Extreme Learning Machine. Energies 2022, 15, 3562. https://doi.org/10.3390/en15103562
Cheng Y, Hu B. Forecasting Regional Carbon Prices in China Based on Secondary Decomposition and a Hybrid Kernel-Based Extreme Learning Machine. Energies. 2022; 15(10):3562. https://doi.org/10.3390/en15103562
Chicago/Turabian StyleCheng, Yunhe, and Beibei Hu. 2022. "Forecasting Regional Carbon Prices in China Based on Secondary Decomposition and a Hybrid Kernel-Based Extreme Learning Machine" Energies 15, no. 10: 3562. https://doi.org/10.3390/en15103562
APA StyleCheng, Y., & Hu, B. (2022). Forecasting Regional Carbon Prices in China Based on Secondary Decomposition and a Hybrid Kernel-Based Extreme Learning Machine. Energies, 15(10), 3562. https://doi.org/10.3390/en15103562





