Effective Condensing Dehumidification in a Rotary-Spray Honey Dehydrator
Abstract
:1. Introduction
2. Materials and Methods
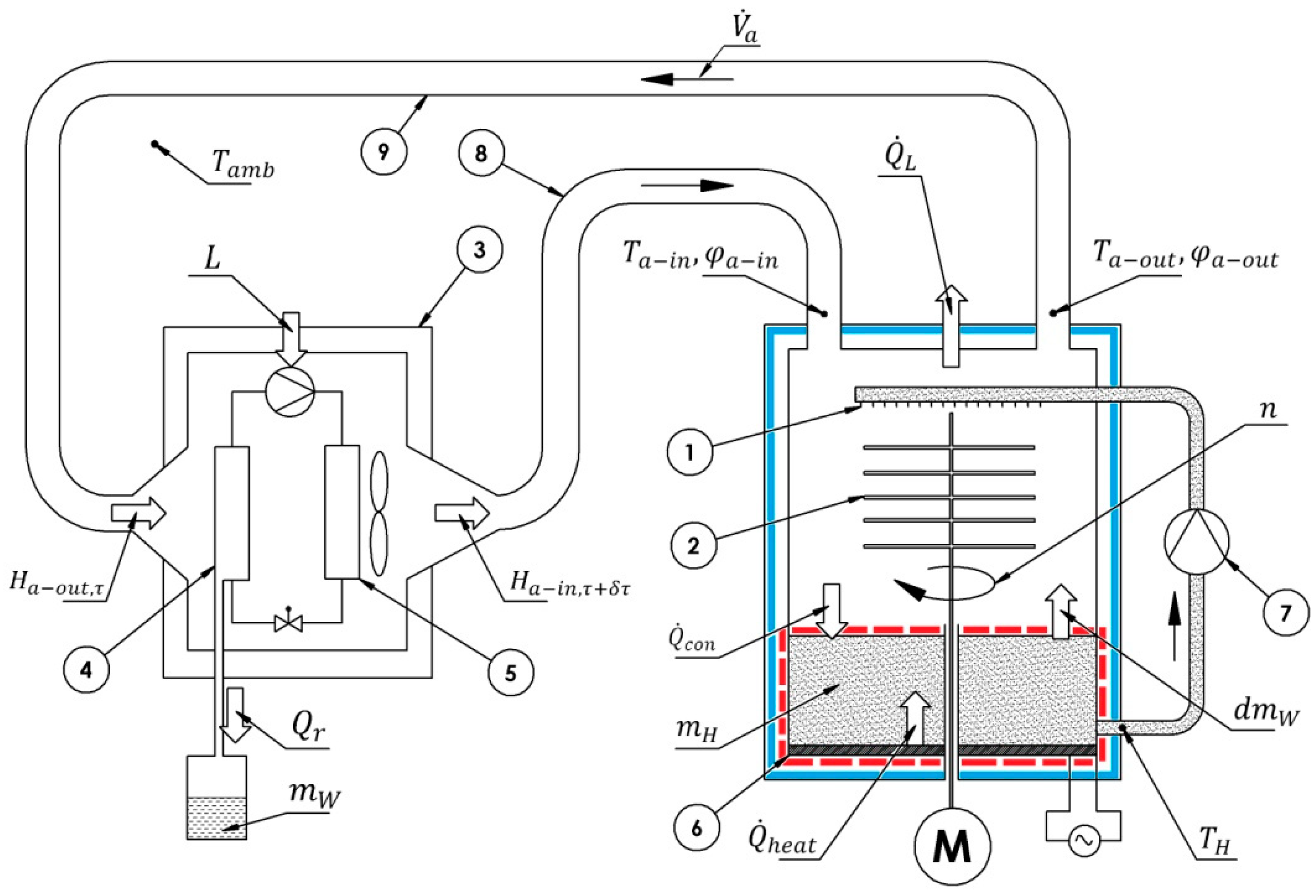
2.1. Heat and Mass Exchange in a Honey Dehydrator
- -
- The heat and mass transfer processes under consideration are transient;
- -
- In the initial phase, the heaters and air transfer heat to the honey changing its temperature—the heating phase;
- -
- Once the temperature difference between the inlet air and the honey has stabilised, the dominant process occurring between the honey and air is the mass exchange process—the drying phase.
- -
- The stabilisation of the mass flux of evaporating water is accompanied by the maximisation of the heat flux transferred by air to honey by convection and maximisation of the values of heat transfer coefficients;
- -
- Low mixer speeds corresponded to the maximum values of heat transfer and mass transfer coefficients;
- -
- Higher air flow velocities and higher heat flux densities are conducive to higher values of heat transfer coefficients;
- -
- In the case of mass transfer coefficients, a clear effect of the actual honey–air contact area (mixer speed) on the intensity of the mass exchange process was observed. The effect of air velocity on the mass transfer rate was significant until a certain limit of air velocity was reached due to the limited drying capability of the external cooling unit.
- -
- With the increase in the driving force of the mass transfer process (ΔX = X″(TH, Aw) − X(Ta-in, φa-in)), a slight decrease in mass transfer coefficients was observed.
2.2. Mathematical Model of the Heat and Mass Transfer Process for the Dehydrator
- The process is transient;
- The dry air mass flux is constant;
- The ambient temperature is constant;
- At the time τ, the output parameters of the air from the dehydrator tank are the input parameters for the cooling unit;
- At the time τ, the output parameters of the air from the cooling device are the input parameters for the dehydrator tank at the time τ + δτ;
- The effect of honey pump operation on the heat balance of the dehydrator tank is ignored;
- The heat exchange process of the heat pump with the environment is omitted.
- Initial mass of honey in the tank, mH;
- Initial temperature of honey and its moisture content, T, X;
- Initial temperature and relative humidity (of air), Ta, φa, (Xa);
- Ambient temperature, Tamb.
- Values , Aw, β, δmh, α respectively from Equations (1), (2), (6), (7) and (11);
- Honey temperature (Tτ + δτ) from Equations (3)–(5);
- Air enthalpy (Ha-out,τ) at the dehydrator outlet at time τ from Equation (13);
- RCJ values, , from Equations (14), (16) and (17), respectively;
- Actual mass of water δm removed from honey from relationship (12) and relationship );
- The degree of humidity of the air () returning to the dehydrator tank in time τ + δτ from Equation (10);
- Specific air enthalpy from Equation (9);
- Temperature of the air () returning to the dehydrator tank in time τ + δτ from Equation (11).
3. Results and Discussion
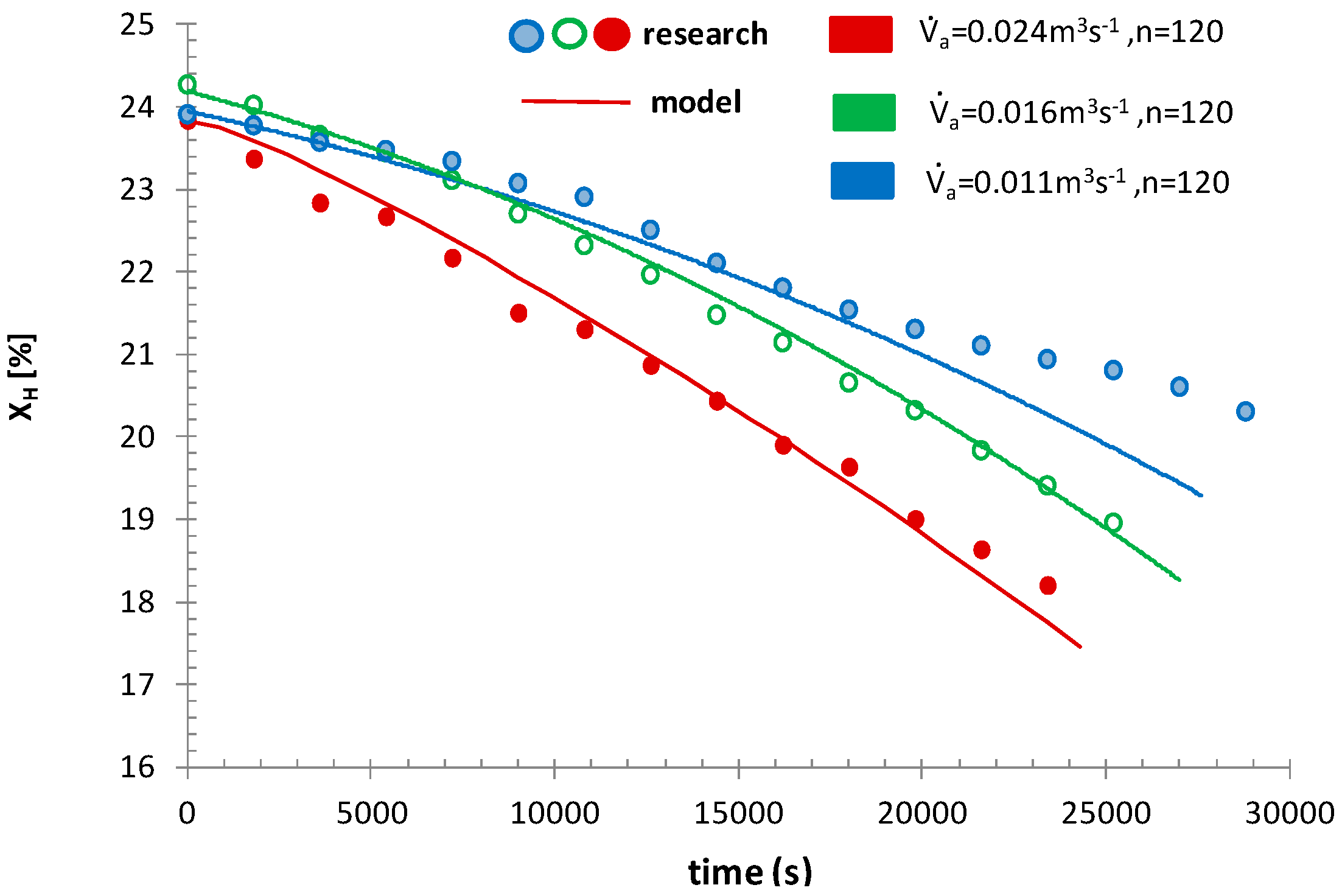
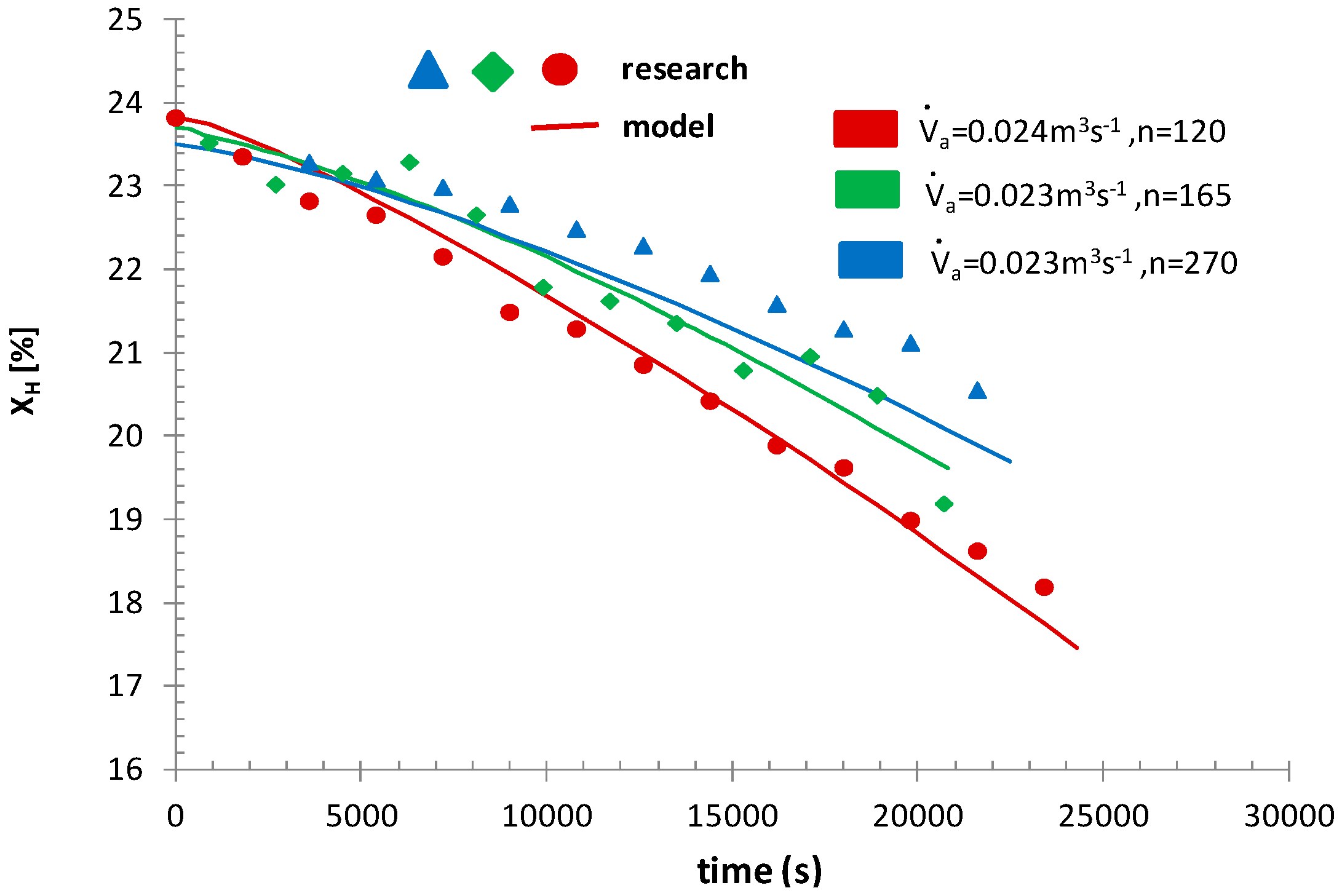
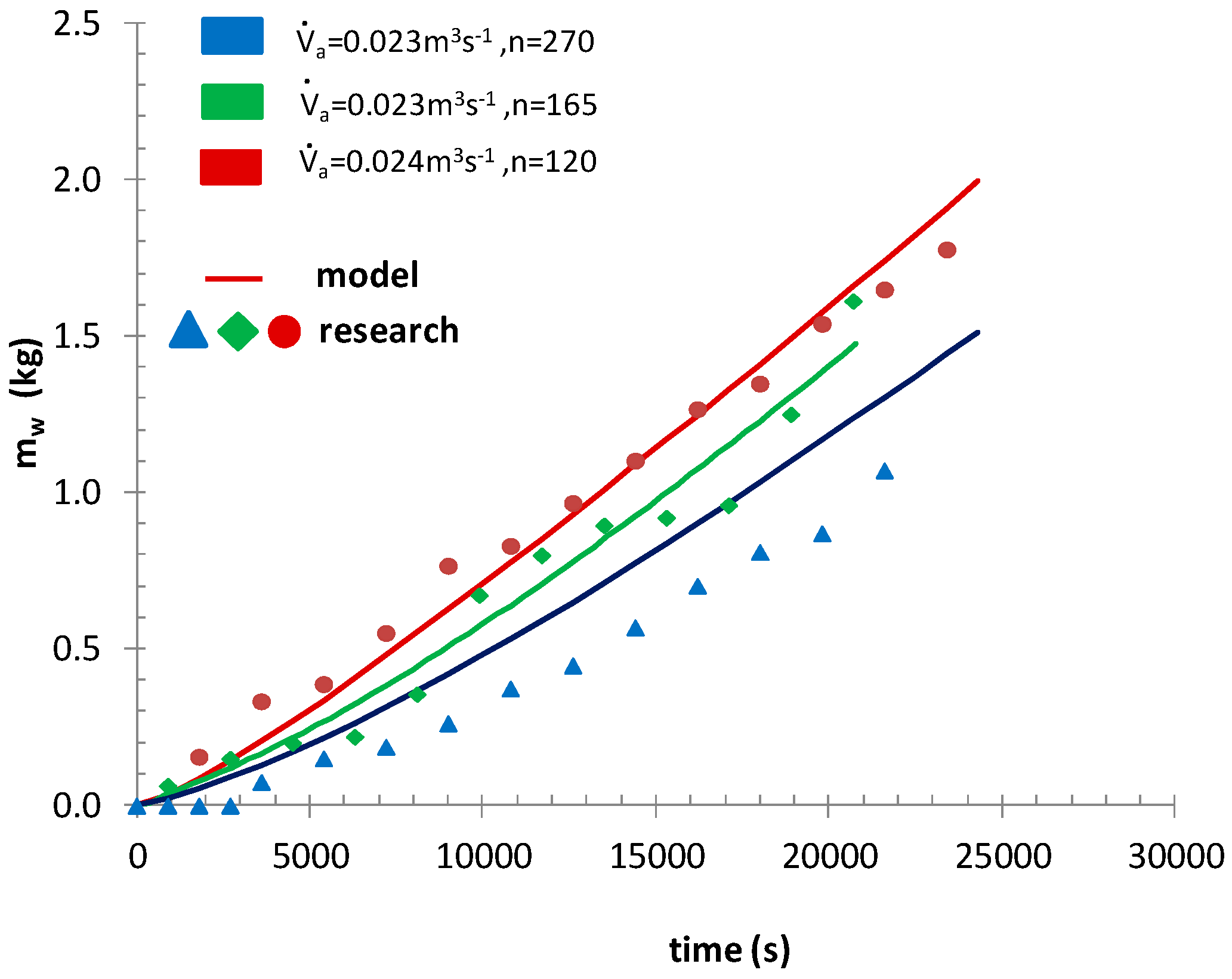
3.1. Experimental Verification of the Numerical Model of the Honey Dehydrator
- Mixer speeds: n = 120, 165, 270 rpm.
- Average air volume flow, its initial moisture content and initial temperature: = 0.01; 0.016, 0.024 m3s−1, , .
- Mass of honey, its initial moisture content and initial temperature: mH = 28 kg, Xτ=0 ≈ 0.24, .
- Ambient temperature .
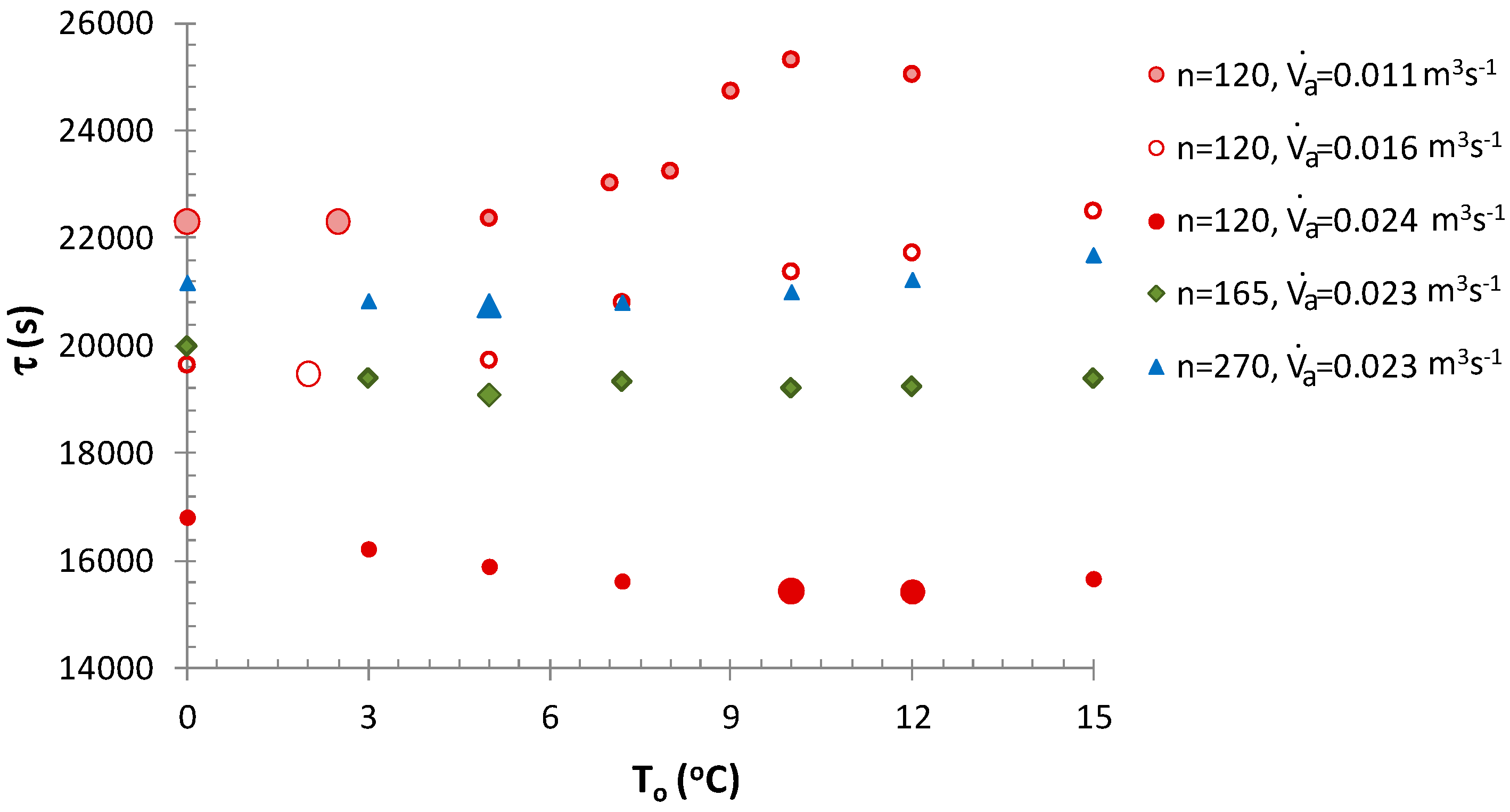
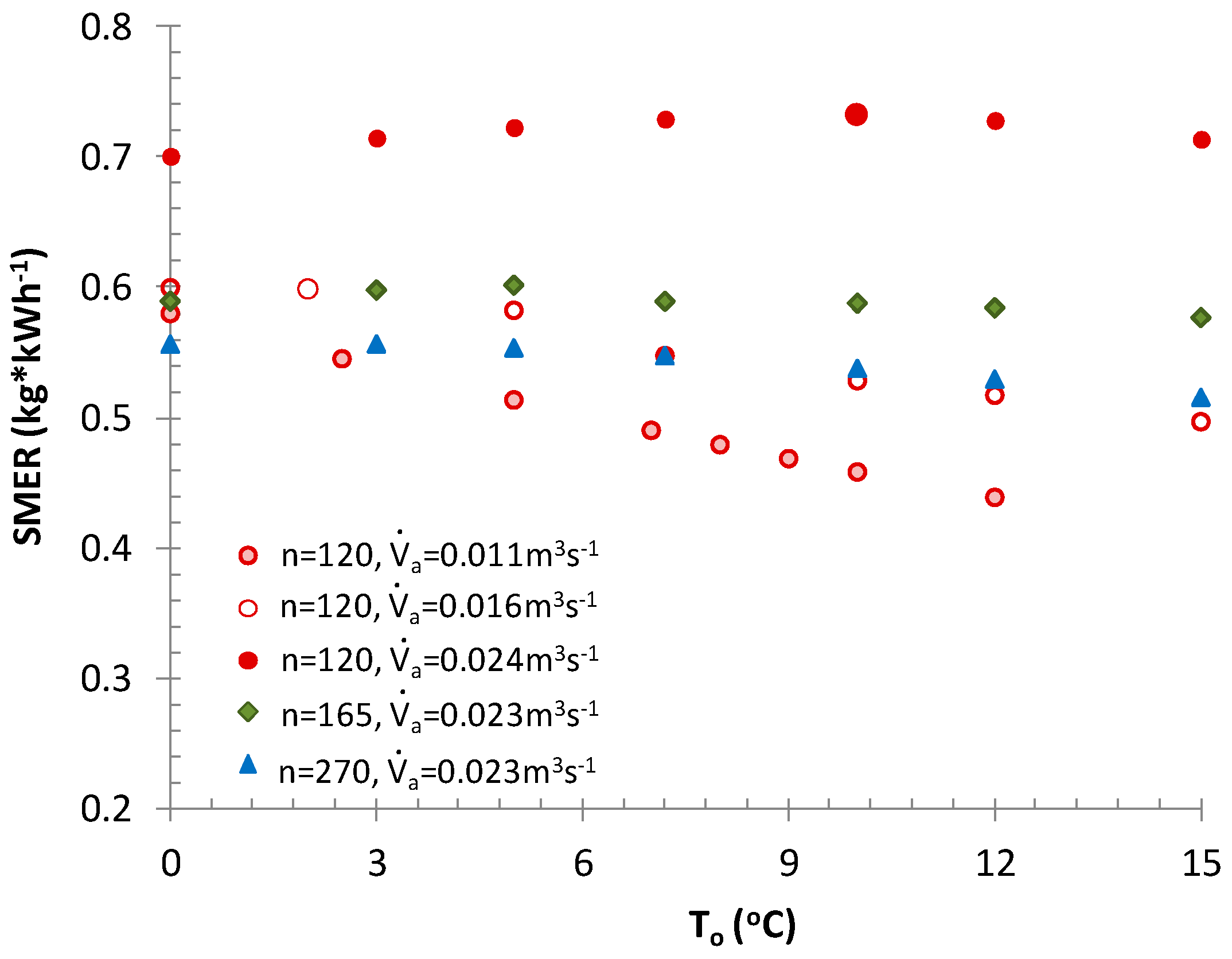
3.2. Selection of Optimal Operating Parameters for the Cooling Unit
4. Conclusions
5. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A | surface area (m2) |
| Aw | water activity of honey, (-) |
| Bi | coefficient in Equation (1), (-) |
| Ci | coefficient in Equation (2), (-) |
| cp | specific heat, (Jkg−1K−1) |
| dH | hydraulic diameter, dh = 4V/AV, (m), |
| dm | diameter of mixer, (m) |
| D | water vapor diffusion coefficient in air, (m2s−1) |
| h | specific enthalpy, (Jkg−1) |
| h″ | specific enthalpy of water vapour at the temperature T, (Jkg−1) |
| H | entalpy, (J) |
| HBP | hight pressure compressors |
| K | , (-) |
| compressor power input, (W) | |
| m | mass, (kg) |
| dry air mass flow rate, (kg) | |
| n | rotational speed of the mixer (rpm) |
| Nu | |
| pa | atmospheric pressure, (Pa) |
| pw | partial pressure of water vapour, (Pa) |
| p″ | water vapour pressure in air at the state of saturation, (Pa) |
| Pr | r– heat of water evaporation at 0 °C, (Jkg−1) |
| Prandtl number | |
| Rea | |
| ReH | |
| RCJ | degree of process openness, (-) |
| Q | amount of heat, (J) |
| heat flow, (W) | |
| latent heat flux exchanged in the evaporator of the cooling unit, (W) | |
| ua | |
| S | |
| Sc | |
| Sh | |
| SMER | specific moisture extraction, (kg kWh−1) |
| U | overall heat transfer coefficient, (Wm−2K−1) |
| V | volume occupied by air in the dehydrator tank, m3 |
| flow rate, (m3s−1) | |
| T | temperature, (°C) |
| Tτ | temperature of honey in time τ, (°C) |
| TXV | type of thermostatic expansion valve |
| X | absolute humidity in air, (kgkg−1) |
| X″ | absolute humidity in air at the state of saturation, (kgkg−1) |
| XH | mass fraction of water in honey*100%, (%) |
| Xτ | mass fraction of water in honey in time, (kgkg−1) |
| ΔX | difference in the absolute humidity, ΔX = X″(Tτ, Aw) − X(Ta-in, φa-in), (kgkg−1) |
| Symbols | |
| α | heat transfer coefficient, (Wm−2K−1) |
| β | mass transfer coefficient, (kgm−2s−1)δ, |
| Δ | increase |
| δmH | the mass of water downloaded by the air from the honey over time τ, (kg) |
| δmw | mass of water condensed from the air in the evaporator of the refrigerating device |
| over time τ, (kg) | |
| δτ | time interval, (s) |
| ε | directional coefficient of conversion, (kJ kg−1) |
| φ | relative humidity, (%) |
| λ | thermal conductivity, Wm−1K−1 |
| μ | dynamic viscosity coefficient, Pas |
| ρ | density, (kgm−3) |
| σ | standard deviation for differences between calculated and measured values |
| τ | time, (s) |
| Indices | |
| * | filled with honey |
| ″ | state of saturation |
| - | mean value |
| τ = 0 | for initial conditions |
| τ + δτ | in time τ + δτ, (s) |
| a | air |
| amb | ambient temperature |
| cal | calculated value |
| con | convection |
| CS | horizontal cross-section of the dehydrator tank |
| exp | measured value |
| H | honey |
| h | hydraulic |
| heat | heaters |
| in | inlet |
| k | condensation |
| L | heat loss due to penetration and accumulation of heat in the tank |
| o | evaporation |
| opt | optimal value |
| out | outlet |
| r | latent heat |
| s | system |
| tank | tank |
| To | at evaporation temperature To |
| w | water |
| w-out | external heat exchange surface of the evaporator |
References
- Umesh Hebbar, H.; Rastogi, N.K.; Subramanian, R. Properties of Dried and Intermediate Moisture Honey Products: A Review. Int. J. Food Prop. 2008, 11, 804–819. [Google Scholar] [CrossRef]
- Singh, I.; Singh, S. Honey moisture reduction and its quality. J. Food Sci. Tecnol. 2018, 55, 3861–3971. [Google Scholar] [CrossRef] [PubMed]
- Zlatanović, I. Types, Classification and Selection of Dryers in Agro Industry. Sci. J. Agric. Eng. 2012, 37, 1–13. [Google Scholar]
- Platt, J.L., Jr.; Ellis, J.R.B. Removing Water from Honey at Ambient Pressure. U.S. Patent No. 4472450, 18 September 1984. [Google Scholar]
- Wakhle, D.M.; Nair, S.K.; Phadke, R. Reduction of excess moisture in honey-I, a small scale unit. Indian Bee J. 1988, 50, 98–100. [Google Scholar]
- Kuehl, L.J. Apparatus for Removing Moisture from Honey. U.S. Patent No. 4763572, 16 August 1988. [Google Scholar]
- Ellis, M. Lowering the moisture content of small lots of extracted honey. Am. Bee J. 1987, 127, 182–183. [Google Scholar]
- Maxwell, H. A small-scale honey drying system. Am. Bee J. 1987, 127, 284–286. [Google Scholar]
- Singh, S.; Gill, R.S.; Singh, P.P. Desiccant honey dehydrator. Int. J. Ambient Energy 2011, 32, 62–69. [Google Scholar] [CrossRef]
- Gill, R.S.; Hans, V.S.; Singh, S.; Singh, P.P.; Dhaliwal, S.S. A small scale honey dehydrator. J. Food. Sci. Technol. 2015, 52, 6695–6702. [Google Scholar] [CrossRef] [Green Version]
- Chaudhary, O.P.; Wakhle, D.M. Honey processing plant with moisture reduction unit. J. Insect Sci. 1999, 12, 46–50. [Google Scholar]
- Wang, W.; Wu, L.; Li, Z.; Fang, Y.; Ding, J.; Xiao, J. An Overview of Adsorbents in the Rotary Desiccant Dehumidifier for Air Dehumidification. Dry. Technol. 2013, 31, 1334–1345. [Google Scholar] [CrossRef]
- Ramli, A.S.; Basrawi, F.; Ibrahim, T.K.; Bin Yusof, M.H.; Oumer, A.N.; Johari, N.A.; Muhamad, A.; Mamat, M.R.; Habib, K. Experimental analysis on a novel low-temperature vacuum drying with induced nucleation technique for dewatering stingless bees honey. Dry. Technol. 2018, 37, 149–155. [Google Scholar] [CrossRef]
- Nedić, N.M.; Gojak, M.D.; Zlatanović, I.J.; Rudonja, N.R.; Lazarević, K.B.; Dražić, M.S.; Gligorević, K.B.; Pajić, M.B. Study of Vacuum and Freeze Drying of Bee Honey. Therm. Sci. 2020, 24, 4241–4251. [Google Scholar] [CrossRef]
- Patel, K.K.; Kar, A. Heat pump assisted drying of agricultural produce—An overview. J. Food Sci. Technol. 2012, 49, 142–160. [Google Scholar] [CrossRef] [Green Version]
- Subramanian, R.; Umesh Hebbar, H.; Rastogi, N.K. Processing of Honey: A Review. Int. J. Food Prop. 2007, 10, 127–143. [Google Scholar] [CrossRef]
- Malec, M.; Morawski, M.; Niezgoda-Żelasko, B. Heat and mass transfer in a honey dehydrator with closed air circulation. Food Bioprod. Process. 2021, 125, 113–125. [Google Scholar] [CrossRef]
- Halasz, B.A. General mathematical model of evaporative cooling devices. Rev. Gen. Therm. 1998, 37, 245–255. [Google Scholar] [CrossRef]
- Camargo, J.R.; Ebinuma, C.D.; Cardoso, S. A mathematical model for direct evaporative cooling air conditioning system. Rev. Eng. Térmica 2003, 4, 30–34. [Google Scholar] [CrossRef]
- Dhamneya, A.K.; Rajput, S.P.S.; Singh, A. Thermodynamic performance analysis of direct evaporative cooling system for increased heat and mass transfer area. Ain Shams Eng. J. 2018, 9, 2951–2960. [Google Scholar] [CrossRef]
- Zalewski, W.; Niezgoda-Żelasko, B.; Litwin, M. Optimization of evaporative fluid coolers. Int. J. Refrig. 2000, 23, 553–565. [Google Scholar] [CrossRef]
- Camargo, J.R.; Ebinuma, C.D. A mathematical model for direct and indirect evaporative cooling air conditioning systems. In Proceedings of the 9th Brazilian Congress of Thermal Engineering and Sciences, Caxambu, Brazil, 15–18 October 2002. [Google Scholar] [CrossRef] [Green Version]
- Haghi, A.K. A Mathematical Model of the Drying Process. Acta Polytech. 2001, 41, 20–23. [Google Scholar] [CrossRef]
- Adapa, P.K.; Schoenau, G.J.; Sokhansanj, S. Performance study of a heat pump dryer system for specialty crops, Part 1: Development of a simulation model. Int. J. Energy Res. 2002, 26, 1001–1019. [Google Scholar] [CrossRef]
- Adapa, P.K.; Schoenau, G.J.; Sokhansanj, S. Performance study of a heat pump dryer system for specialty crops, Part 2: Model verification. Int. J. Energy Res. 2002, 26, 1021–1033. [Google Scholar] [CrossRef]
- Teeboonma, U.; Tiansuwan, J.; Soponronnarit, S. Optimization of heat pump fruit dryers. J. Food Eng. 2003, 59, 369–377. [Google Scholar] [CrossRef]
- Louarn, S.; Ploteau, J.P.; Glouannec, P.; Noel, H. Experimental and Numerical Study of Flat Plate Sludge Drying at Low Temperature by Convection and Direct Conduction. Dry. Technol. 2014, 32, 1664–1674. [Google Scholar] [CrossRef]
- Hossain, M.A.; Gottschalk, K.; Hassan, M.S. Mathematical model for a heat pump dryer for aromatic plant. Procedia Eng. 2013, 56, 510–520. [Google Scholar] [CrossRef] [Green Version]
- Hamid, M.; Usman, M.; Zubair, T.; Haq, R.U.; Wang, W. Shape effects of MoS2 nanoparticles on rotating flow of nanofluid along a stretching surface with variable thermal conductivity: A Galerkin approach. Int. J. Heat Mass Transf. 2018, 124, 706–714. [Google Scholar] [CrossRef]
- Hamid, M.; Khan, Z.H.; Khan, W.A.; Haq, R.U. Natural convection of water-based carbon nanotubes in a partially heated rectangular fin-shaped cavity with an inner cylindrical obstacle. Phys. Fluids 2019, 31, 103607. [Google Scholar] [CrossRef]
- Khan, Z.H.; Khan, W.A.; Hamid, M.; Liu, H. Finite element analysis of hybrid nanofluid flow and heat transfer in a split lid-driven square cavity with Y-shaped obstacle. Phys. Fluids 2020, 32, 093609. [Google Scholar] [CrossRef]
- Malec, M.; Morawski, M. Vertical, Centrifugal, Honey Dehydrator. PL. Patent No. Pat. 239466, 8 September 2021. [Google Scholar]
- Chen, C.H. Relationship between Water Activity and Moisture Content in Floral Honey. Foods 2019, 8, 30. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Recknagel, H.; Sprenger, E.; Hönmann, W.; Schramek, E.R. Ogrzewanie, Klimatyzacja-Poradnik (Heating, Air Conditioning—Guide); EWFE: Gdańsk, Poland, 1994. [Google Scholar]
- Niezgoda-Żelasko, B.; Żelasko, J. Free and forced convection on the outer surface of vertical longitudinally finned tubes. Exp. Therm. Fluid Sci. 2014, 57, 145–156. [Google Scholar] [CrossRef]
- Niesteruk, R. Rozprawy Naukowe (62). In Właściwości Termofizyczne Żywności, Część II (Thermo-Physical Properties of Food, Part II); Politechnika Białostocka: Białytsok, Poland, 1999. [Google Scholar]
- Mehryar, L.; Esmaiili, M.; Hassanzadeh, A. Evaluation of Some Physicochemical and Rheological Properties of Iranian Honeys and the Effect of Temperature on its Viscosity. Am. Eurasian J. Agric. Environ. Sci. 2013, 13, 807–819. [Google Scholar] [CrossRef]
- Yanniotis, S.; Skaltsi, S.; Karaburnioti, S. Effect of moisture content on the viscosity of honey at different temperatures. J. Food Eng. 2006, 72, 372–377. [Google Scholar] [CrossRef]
- Properties of Dry Air. VDI Heat Atlas; VDI Verlag: Düsseldorf, Germany, 2010. [Google Scholar] [CrossRef]

| Nu (1) | B1 | B2 | B3 | B4 | ||
| transient | steady state | transient | steady state | |||
| 140.8 | 601.9 | 0.4203 | −0.4718 | −0.6313 | 0 | |
| Sh (2) | C1 | C2 | C3 | C4 | ||
| transient | steady state | transient | steady state | |||
| 0.8479 | 1.299 | 0.9728 | −0.4072 | 0.3713 | 0 | |
| Calc. Variant | n = 120 rpm | n = 165 rpm | n = 270 rpm | ||
|---|---|---|---|---|---|
| max. err (%) | 7.7 | 0.6 | 2.4 | 2.1 | 1.9 |
| avg. err (%) | 2 | 0.02 | 0.2 | 0.03 | 1.1 |
| 0.36 | 0.10 | 0.25 | 0.30 | 0.26 | |
| 0.46 | 0.013 | 0.062 | 0.084 | 0.24 | |
| Time Step δτ (s) | 100 | 300 | 900 | 1200 |
|---|---|---|---|---|
| Calculation Variant | XH (%) | |||
| n = 0.024 m3s−1 | 17.44 | 17.44 | 17.46 | 17.47 |
| n = 0.023 m3s−1 | 19.22 | 19.24 | 19.29 | 19.39 |
| n = 0.016 m3s−1 | 19.46 | 19.42 | 19.17 | 18.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morawski, M.; Malec, M.; Niezgoda-Żelasko, B. Effective Condensing Dehumidification in a Rotary-Spray Honey Dehydrator. Energies 2022, 15, 100. https://doi.org/10.3390/en15010100
Morawski M, Malec M, Niezgoda-Żelasko B. Effective Condensing Dehumidification in a Rotary-Spray Honey Dehydrator. Energies. 2022; 15(1):100. https://doi.org/10.3390/en15010100
Chicago/Turabian StyleMorawski, Marcin, Marcin Malec, and Beata Niezgoda-Żelasko. 2022. "Effective Condensing Dehumidification in a Rotary-Spray Honey Dehydrator" Energies 15, no. 1: 100. https://doi.org/10.3390/en15010100
APA StyleMorawski, M., Malec, M., & Niezgoda-Żelasko, B. (2022). Effective Condensing Dehumidification in a Rotary-Spray Honey Dehydrator. Energies, 15(1), 100. https://doi.org/10.3390/en15010100






