Experimental Evaluation and Modeling of Air Heating in a Ceramic Foam Volumetric Absorber by Effective Parameters
Abstract
1. Introduction
2. Materials and Methods
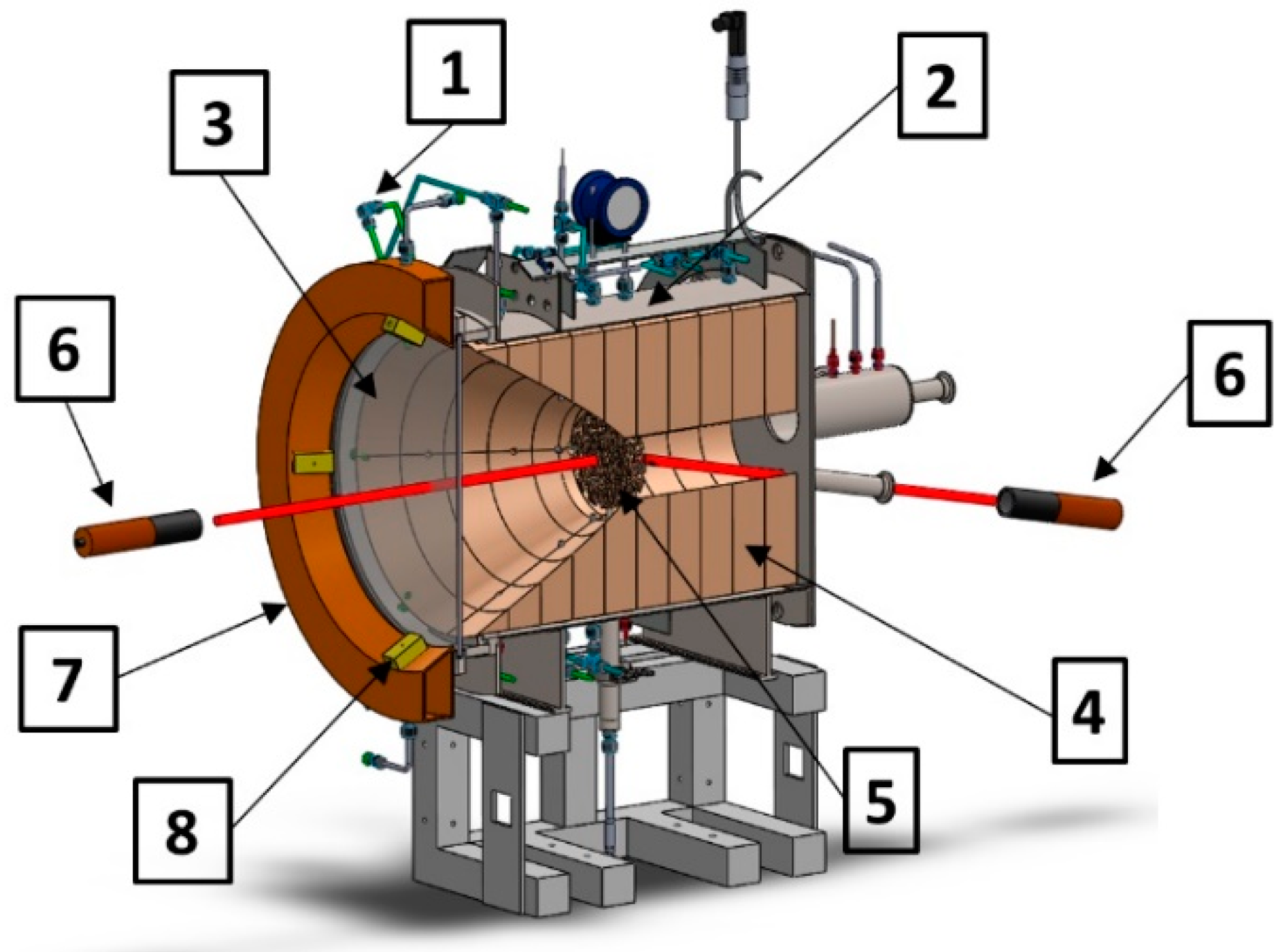
2.1. Volumetric Absorber and Solar Reactor
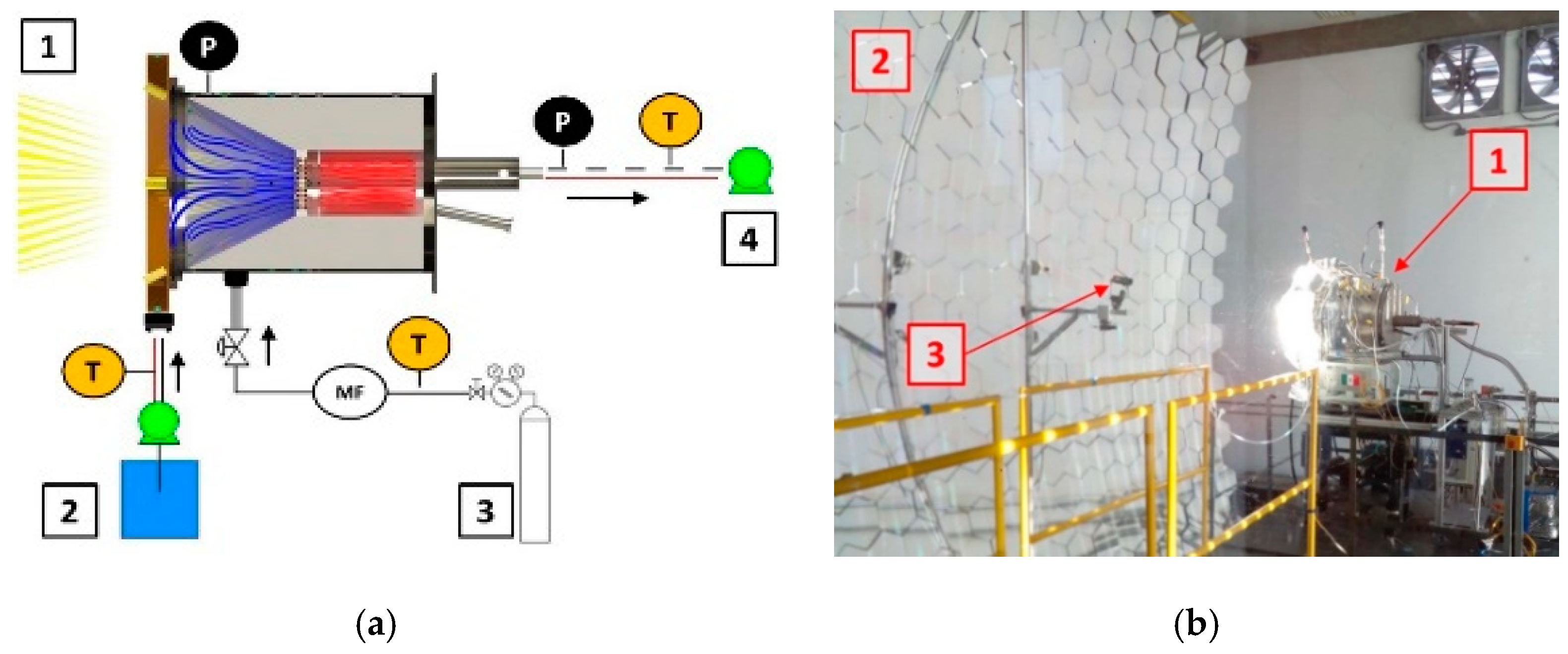
2.2. Instrumentation and Operation
2.3. Numerical Methods
2.4. Analytical Approximation
3. Results
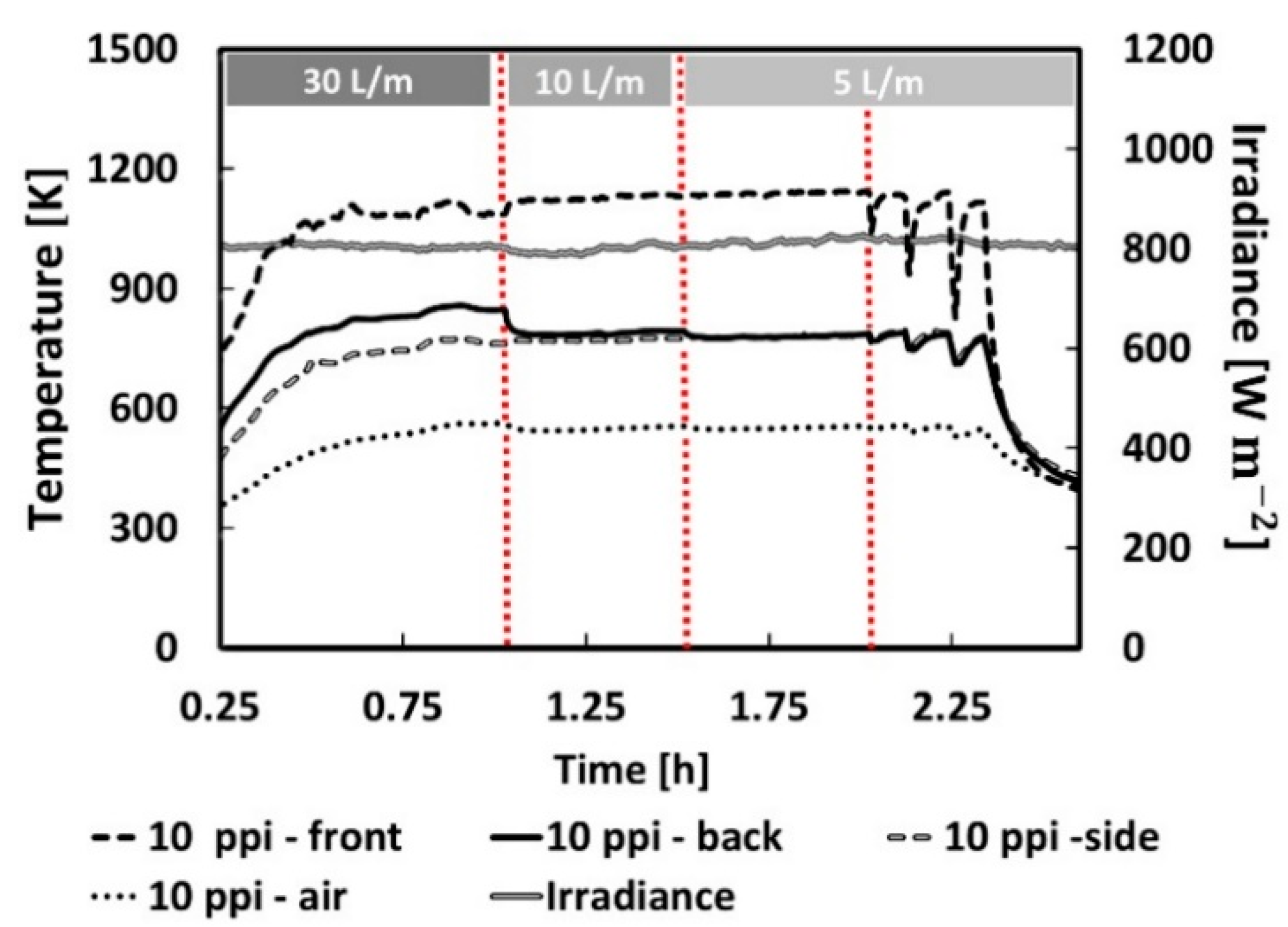
3.1. Experimental
3.2. Theoretical
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Funk, J.E. Thermochemical hydrogen production: Past and present. Int. J. Hydrogen Energy 2001, 26, 185–190. [Google Scholar] [CrossRef]
- Kodama, T. High-temperature solar chemistry for converting solar heat to chemical fuels. Prog. Energy Combust. Sci. 2003, 29, 567–597. [Google Scholar] [CrossRef]
- Nakamura, T. Hydrogen production from water utilizing solar heat at high temperatures. Sol. Energy 1977, 19, 467–475. [Google Scholar] [CrossRef]
- Charvin, P.; Abanades, S.; Flamant, G.; Lemort, F. Two-step water splitting thermochemical cycle based on iron oxide redox pair for solar hydrogen production. Energy 2007, 32, 1124–1133. [Google Scholar] [CrossRef]
- Muhich, C.L.; Ehrhart, B.D.; Al-Shankiti, I.; Ward, B.J.; Musgrave, C.B.; Weimer, A.W. A review and perspective of efficient hydrogen generation via solar thermal water splitting. Wiley Interdiscip. Rev. Energy Environ. 2015, 5, 261–287. [Google Scholar] [CrossRef]
- Kruesi, M.; Jovanovic, Z.R.; Steinfeld, A. A two-zone solar-driven gasifier concept: Reactor design and experimental evaluation with bagasse particles. Fuel 2014, 117, 680–687. [Google Scholar] [CrossRef]
- Wieckert, C.; Palumbo, R.; Frommherz, U. A two-cavity reactor for solar chemical processes: Heat transfer model and application to carbothermic reduction of ZnO. Energy 2004, 29, 771–787. [Google Scholar] [CrossRef]
- Steinfeld, A.; Weimer, A.W. Thermochemical production of fuels with concentrated solar energy. Opt. Express 2010, 18, A100–A111. [Google Scholar] [CrossRef] [PubMed]
- Villafán-Vidales, H.; Arancibia-Bulnes, C.; Riveros-Rosas, D.; Romero-Paredes, H.; Estrada, C. An overview of the solar thermochemical processes for hydrogen and syngas production: Reactors, and facilities. Renew. Sustain. Energy Rev. 2017, 75, 894–908. [Google Scholar] [CrossRef]
- Villafán-Vidales, H.; Abanades, S.; Caliot, C.; Romero-Paredes, H. Heat transfer simulation in a thermochemical solar reactor based on a volumetric porous receiver. Appl. Therm. Eng. 2011, 31, 3377–3386. [Google Scholar] [CrossRef]
- Mohamedali, M.; Henni, A.; Ibrahim, H. Recent Advances in Supported Metal Catalysts for Syngas Production from Methane. ChemEngineering 2018, 2, 9. [Google Scholar] [CrossRef]
- Furler, P.; Scheffe, J.; Gorbar, M.; Moes, L.; Vogt, U.; Steinfeld, A. Solar Thermochemical CO2 Splitting Utilizing a Reticulated Porous Ceria Redox System. Energy Fuels 2012, 26, 7051–7059. [Google Scholar] [CrossRef]
- Furler, P.; Scheffe, J.R.; Steinfeld, A. Syngas production by simultaneous splitting of H2O and CO2via ceria redox reactions in a high-temperature solar reactor. Energy Environ. Sci. 2011, 5, 6098–6103. [Google Scholar] [CrossRef]
- Agrafiotis, C.; Roeb, M.; Konstandopoulos, A.; Nalbandian, L.; Zaspalis, V.; Sattler, C.; Stobbe, P.; Steele, A. Solar water splitting for hydrogen production with monolithic reactors. Sol. Energy 2005, 79, 409–421. [Google Scholar] [CrossRef]
- Roeb, M.; Sattler, C.; Klüser, R.; Monnerie, N.; De Oliveira, L.; Konstandopoulos, A.G.; Agrafiotis, C.; Zaspalis, V.T.; Nalbandian, L.; Steele, A.; et al. Solar Hydrogen Production by a Two-Step Cycle Based on Mixed Iron Oxides. J. Sol. Energy Eng. 2005, 128, 125–133. [Google Scholar] [CrossRef]
- Roeb, M.; Neises, M.; Säck, J.-P.; Rietbrock, P.; Monnerie, N.; Dersch, J.; Schmitz, M.; Sattler, C. Operational strategy of a two-step thermochemical process for solar hydrogen production. Int. J. Hydrogen Energy 2009, 34, 4537–4545. [Google Scholar] [CrossRef]
- Cho, H.; Myojin, T.; Kawakami, S.; Gokon, N.; Kodama, T.; Kang, Y.; Lee, S.; Chai, K.; Yoon, H.; Lee, H. Solar Demonstration of Thermochemical Two-step Water Splitting Cycle Using CeO2/MPSZ Ceramic foam Device by 45kWth KIER Solar Furnace. Energy Procedia 2014, 49, 1922–1931. [Google Scholar] [CrossRef]
- Avila-Marin, A.; Fernandez-Reche, J.; Martinez-Tarifa, A. Modelling strategies for porous structures as solar receivers in central receiver systems: A review. Renew. Sustain. Energy Rev. 2019, 111, 15–33. [Google Scholar] [CrossRef]
- Ho, C.K.; Iverson, B.D. Review of high-temperature central receiver designs for concentrating solar power. Renew. Sustain. Energy Rev. 2014, 29, 835–846. [Google Scholar] [CrossRef]
- Ávila-Marín, A.; Alvarez-Lara, M.; Fernandez-Reche, J. Experimental Results of Gradual Porosity Wire Mesh Absorber for Volumetric Receivers. Energy Procedia 2014, 49, 275–283. [Google Scholar] [CrossRef]
- Wu, Z.; Caliot, C.; Flamant, G.; Wang, Z. Numerical simulation of convective heat transfer between air flow and ceramic foams to optimise volumetric solar air receiver performances. Int. J. Heat Mass Transf. 2011, 54, 1527–1537. [Google Scholar] [CrossRef]
- Kribus, A.; Grijnevich, M.; Gray, Y.; Caliot, C. Parametric Study of Volumetric Absorber Performance. Energy Procedia 2014, 49, 408–417. [Google Scholar] [CrossRef]
- Mey, S.; Caliot, C.; Flamant, G.; Kribus, A.; Gray, Y. Optimization of High Temperature SiC Volumetric Solar Absorber. Energy Procedia 2014, 49, 478–487. [Google Scholar] [CrossRef]
- Fend, T.; Schwarzbozl, P.; Smirnova, O.; Schollgen, D.; Jakob, C. Numerical investigation of flow and heat transfer in a volumetric solar receiver. Renew. Energy 2013, 60, 655–661. [Google Scholar] [CrossRef]
- Petrasch, J.; Wyss, P.; Steinfeld, A. Tomography-based Monte Carlo determination of radiative properties of reticulate porous ceramics. J. Quant. Spectrosc. Radiat. Transf. 2007, 105, 180–197. [Google Scholar] [CrossRef]
- Lee, H.-J.; Kim, J.-K.; Lee, S.-N.; Kang, Y.-H. Consistent heat transfer analysis for performance evaluation of multichannel solar absorbers. Sol. Energy 2012, 86, 1576–1585. [Google Scholar] [CrossRef]
- Wang, F.; Shuai, Y.; Tan, H.; Yu, C. Thermal performance analysis of porous media receiver with concentrated solar irradiation. Int. J. Heat Mass Transf. 2013, 62, 247–254. [Google Scholar] [CrossRef]
- Gomez-Garcia, F.; González-Aguilar, J.; Tamayo-Pacheco, S.; Olalde, G.; Romero, M. Numerical analysis of radiation propagation in a multi-layer volumetric solar absorber composed of a stack of square grids. Sol. Energy 2015, 121, 94–102. [Google Scholar] [CrossRef]
- Konstandopoulos, A.G.; Lorentzou, S. Novel Monolithic Reactors for Solar Thermochemical Water Splitting. In On Solar Hydrogen & Nanotechnology; Wiley: Hoboken, NJ, USA, 2010; pp. 621–639. [Google Scholar]
- Kawakami, S.; Myojin, T.; Cho, H.-S.; Hatamachi, T.; Gokon, N.; Kodama, T. Thermochemical Two-step Water Splitting Cycle using Ni-ferrite and CeO2 Coated Ceramic foam Devices by Concentrated Xe-light Radiation. Energy Procedia 2014, 49, 1980–1989. [Google Scholar] [CrossRef]
- Patil, V.R.; Kiener, F.; Grylka, A.; Steinfeld, A. Experimental testing of a solar air cavity-receiver with reticulated porous ceramic absorbers for thermal processing at above 1000 °C. Sol. Energy 2021, 214, 72–85. [Google Scholar] [CrossRef]
- Helte, A. Radiative and conductive heat transfer in porous media: Estimation of the effective thermal conductivity. J. Appl. Phys. 1993, 73, 7167–7173. [Google Scholar] [CrossRef]
- Haussener, S.; Jerjen, I.; Wyss, P.; Steinfeld, A. Tomography-Based Determination of Effective Transport Properties for Reacting Porous Media. J. Heat Transf. 2011, 134, 012601. [Google Scholar] [CrossRef]
- Wu, Z.; Caliot, C.; Bai, F.; Flamant, G.; Wang, Z.; Zhang, J.; Tian, C. Experimental and numerical studies of the pressure drop in ceramic foams for volumetric solar receiver applications. Appl. Energy 2010, 87, 504–513. [Google Scholar] [CrossRef]
- Bicer, A.; Kar, F. A Model for Determining the Effective Thermal Conductivity of Porous Heterogeneous Materials. Int. J. Thermophys. 2018, 40, 1–23. [Google Scholar] [CrossRef]
- Rousseau, B.; De Sousa, D.M.; Echegut, P.; Thovert, J.F. Characterization of the thermal radiative properties of heterogeneous porous materials up to T = 2500 K by a spectroscopic device. In Proceedings of the Eurotherm Seminar N°81 Reactive Heat Transfer in Porous Media, Albi, France, 4–6 June 2007. [Google Scholar]
- Wolfbeisser, A.; Sophiphun, O.; Bernardi, J.; Wittayakun, J.; Föttinger, K.; Rupprechter, G. Methane dry reforming over ceria-zirconia supported Ni catalysts. Catal. Today 2016, 277, 234–245. [Google Scholar] [CrossRef]
- Ueda, K.; Hirata, Y.; Sameshima, S.; Shimonosono, T.; Yamaji, K. Formation of hydrogen from the CO–H2O system using porous Gd-doped ceria electrochemical cell with MnO cathode and Fe3O4 anode. J. Asian Ceram. Soc. 2015, 3, 82–87. [Google Scholar] [CrossRef][Green Version]
- Riveros-Rosas, D.; Herrera-Vázquez, J.; Pérez-Rábago, C.; Bulnes, C.A.A.; Vázquez-Montiel, S.; Sanchez-Gonzalez, M.; Granados-Agustín, F.; Jaramillo, O.; Estrada, C. Optical design of a high radiative flux solar furnace for Mexico. Sol. Energy 2010, 84, 792–800. [Google Scholar] [CrossRef]
- Pérez-Enciso, R.; Brito-Bazan, E.; Pérez-Rábago, C.A.; Arancibia-Bulnes, C.A.; Riveros-Rosas, D.; Estrada, C.A. Correction of the concentrated sunlight spot’s drift of the IER-UNAM’s solar furnace. Appl. Therm. Eng. 2015, 75, 1187–1191. [Google Scholar] [CrossRef]
- Wang, P.; Vafai, K.; Liu, D.Y. Analysis of the volumetric phenomenon in porous beds subject to irradiation. Numer. Heat Transfer. Part A Appl. 2016, 70, 567–580. [Google Scholar] [CrossRef]
- Wu, Z.; Caliot, C.; Flamant, G.; Wang, Z. Coupled radiation and flow modeling in ceramic foam volumetric solar air receivers. Sol. Energy 2011, 85, 2374–2385. [Google Scholar] [CrossRef]
- Macias, J.D.; Bacelis-Martinez, R.D.; Ruiz-Gomez, M.A.; Bante-Guerra, J.; Villafan-Vidales, H.I.; Rodriguez-Gattorno, G.; Romero-Paredes, H.; Alvarado-Gil, J.J. Thermophysical and optical properties of NiCo2O4@ZrO2: A potential composite for thermochemical processes. Int. J. Hydrogen Energy 2021, 46, 10632–10641. [Google Scholar] [CrossRef]
- Glover, P.W.J. A generalized Archie’s law for n phases. Geophysics 2010, 75, E247–E265. [Google Scholar] [CrossRef]
- Sun, L.; Guo, H.; Peng, H.; Gong, S.; Xu, H. Phase stability and thermal conductivity of ytterbia and yttria co-doped zirconia. Prog. Nat. Sci. 2013, 23, 440–445. [Google Scholar] [CrossRef]
- Gong, P.; Buahom, P.; Tran, M.-P.; Saniei, M.; Park, C.B.; Pötschke, P. Heat transfer in microcellular polystyrene/multi-walled carbon nanotube nanocomposite foams. Carbon 2015, 93, 819–829. [Google Scholar] [CrossRef]
- Zhao, J.-J.; Duan, Y.-Y.; Wang, X.-D.; Wang, B.-X. Radiative properties and heat transfer characteristics of fiber-loaded silica aerogel composites for thermal insulation. Int. J. Heat Mass Transf. 2012, 55, 5196–5204. [Google Scholar] [CrossRef]
- Bi, C.; Tang, G.; Tao, W. Prediction of the gaseous thermal conductivity in aerogels with non-uniform pore-size distribution. J. Non-Crystalline Solids 2012, 358, 3124–3128. [Google Scholar] [CrossRef]
- Du, S.; Xia, T.; He, Y.-L.; Li, Z.-Y.; Li, D.; Xie, X.-Q. Experiment and optimization study on the radial graded porous volumetric solar receiver matching non-uniform solar flux distribution. Appl. Energy 2020, 275, 115343. [Google Scholar] [CrossRef]
- Du, S.; Tong, Z.-X.; Zhang, H.-H.; He, Y.-L. Tomography-based determination of Nusselt number correlation for the porous volumetric solar receiver with different geometrical parameters. Renew. Energy 2019, 135, 711–718. [Google Scholar] [CrossRef]
- Song, X.; Xie, M.; Zhou, F.; Jia, G.; Hao, X.; An, S. High-temperature thermal properties of yttria fully stabilized zirconia ceramics. J. Rare Earths 2011, 29, 155–159. [Google Scholar] [CrossRef]
- Yuan, B.; Ding, S.; Wang, D.; Wang, G.; Li, H. Heat insulation properties of silica aerogel/glass fiber composites fabricated by press forming. Mater. Lett. 2012, 75, 204–206. [Google Scholar] [CrossRef]
- Ackermann, S.; Takacs, M.; Scheffe, J.; Steinfeld, A. Reticulated porous ceria undergoing thermochemical reduction with high-flux irradiation. Int. J. Heat Mass Transf. 2017, 107, 439–449. [Google Scholar] [CrossRef]
- Barreto, G.; Canhoto, P.; Collares-Pereira, M. Three-dimensional modelling and analysis of solar radiation absorption in porous volumetric receivers. Appl. Energy 2018, 215, 602–614. [Google Scholar] [CrossRef]
- Zhao, C.; Lu, T.; Hodson, H. Thermal radiation in ultralight metal foams with open cells. Int. J. Heat Mass Transf. 2004, 47, 2927–2939. [Google Scholar] [CrossRef]
- Nait-Ali, B.; Haberko, K.; Vesteghem, H.; Absi, J.; Smith, D. Thermal conductivity of highly porous zirconia. J. Eur. Ceram. Soc. 2006, 26, 3567–3574. [Google Scholar] [CrossRef]
- Ramirez-Cabrera, M.A.; Valades-Pelayo, P.J. Simplified estimation of anisotropic non-homogeneous extinction coefficients in porous solids considering spherical and cylindrical pore networks. Int. J. Chem. React. Eng. 2021. [Google Scholar] [CrossRef]
- Liu, Z.-W.; Li, W.-Q.; Wang, J.-K.; Ma, X.-C.; Liang, C.; Liu, P.; Chu, Z.; Dang, Y.-H. Zirconium oxide ceramic foam: A promising supporting biomaterial for massive production of glial cell line-derived neurotrophic factor. J. Zhejiang Univ. Sci. B 2014, 15, 1013–1022. [Google Scholar] [CrossRef] [PubMed]

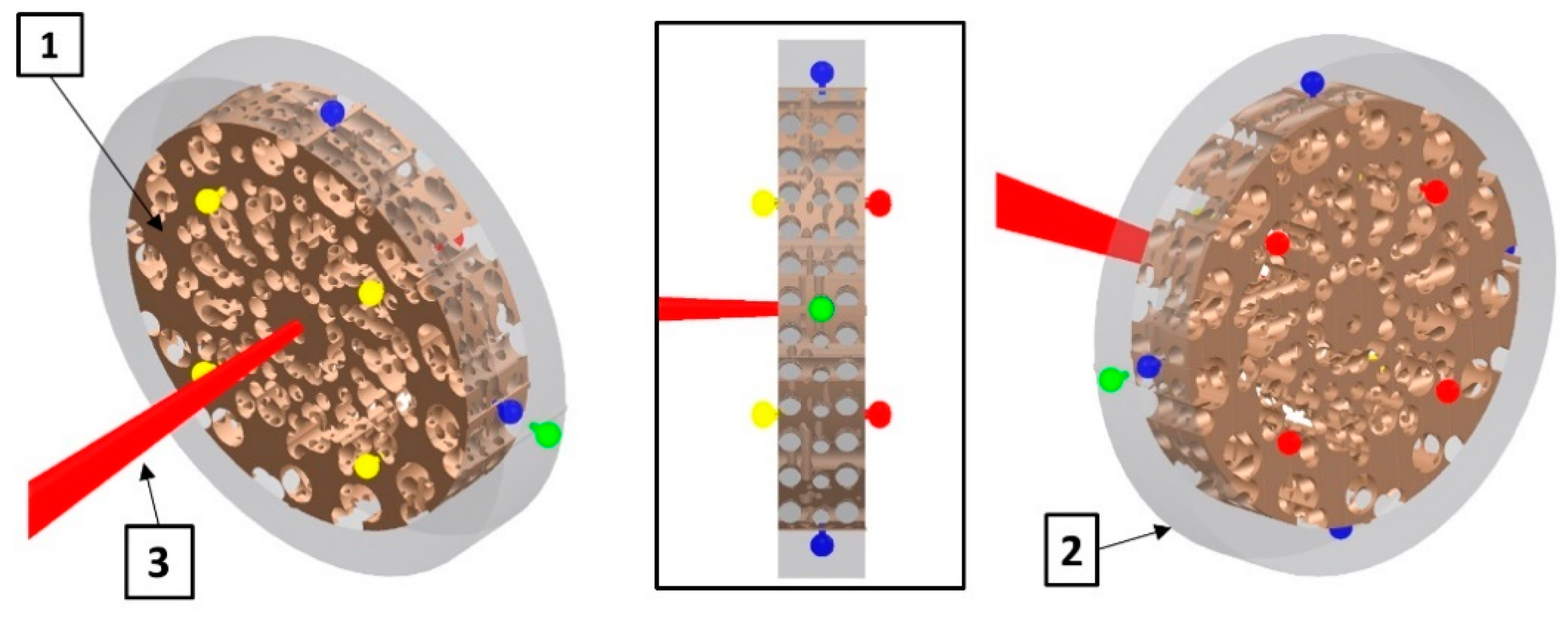
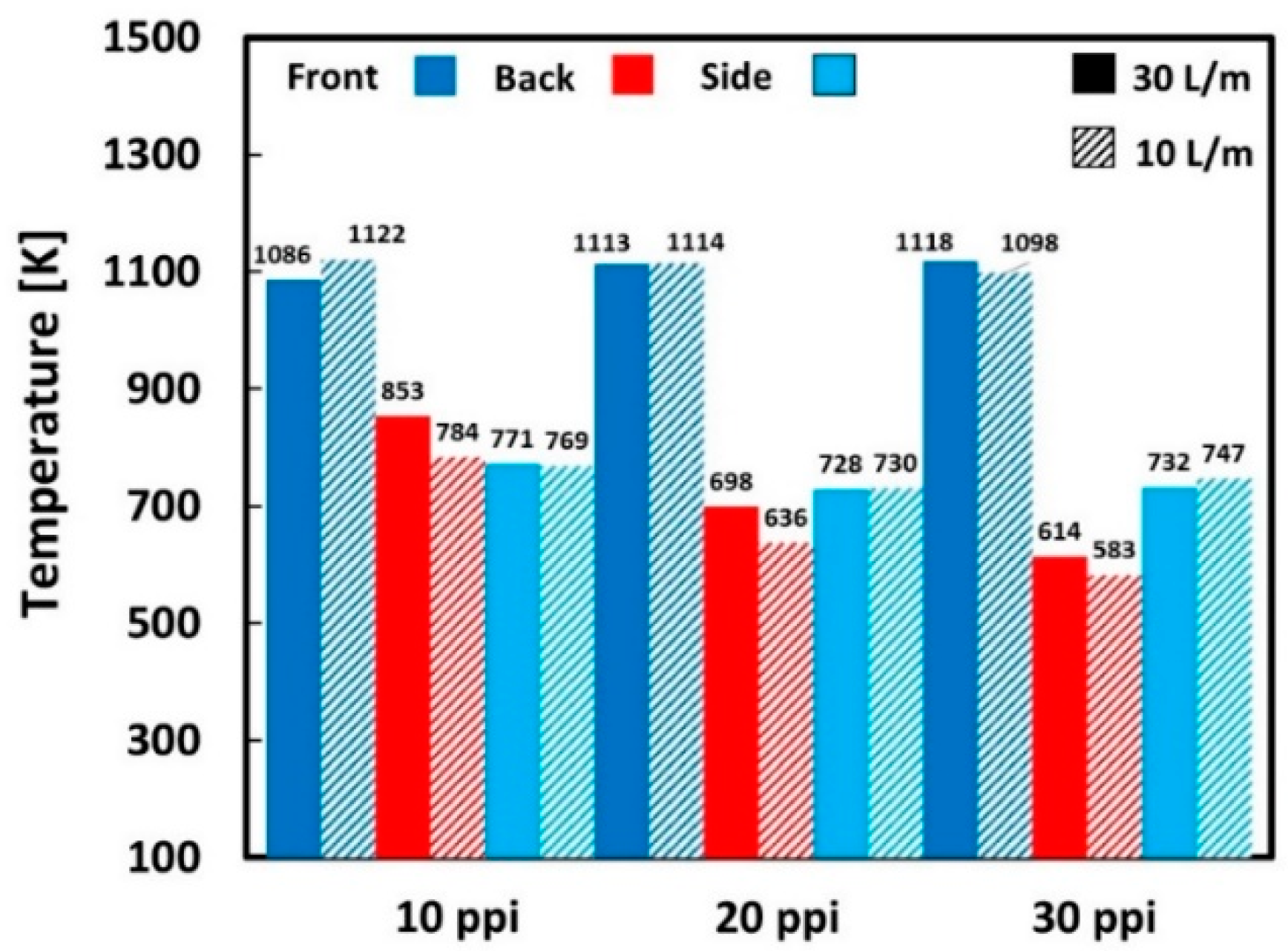
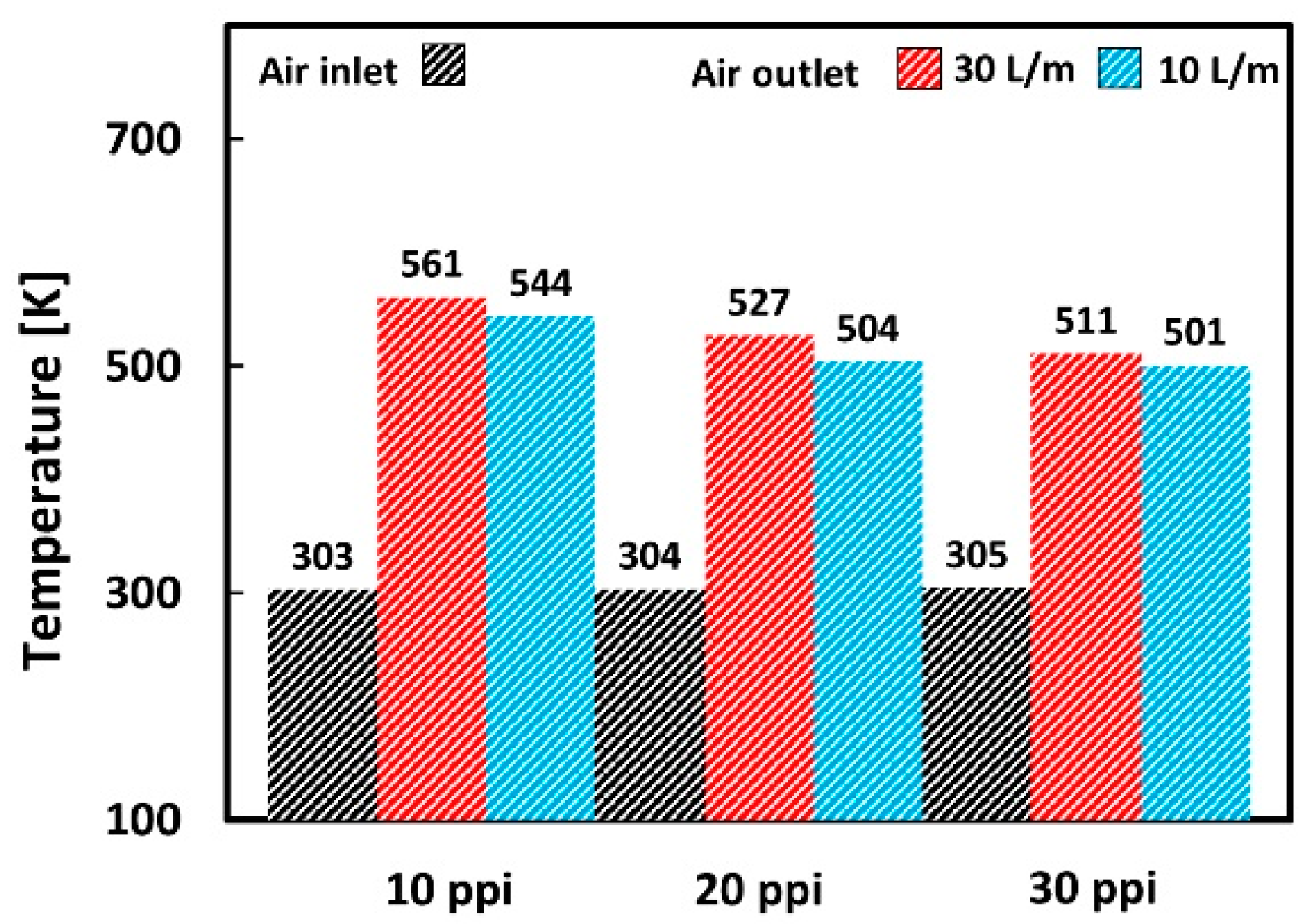
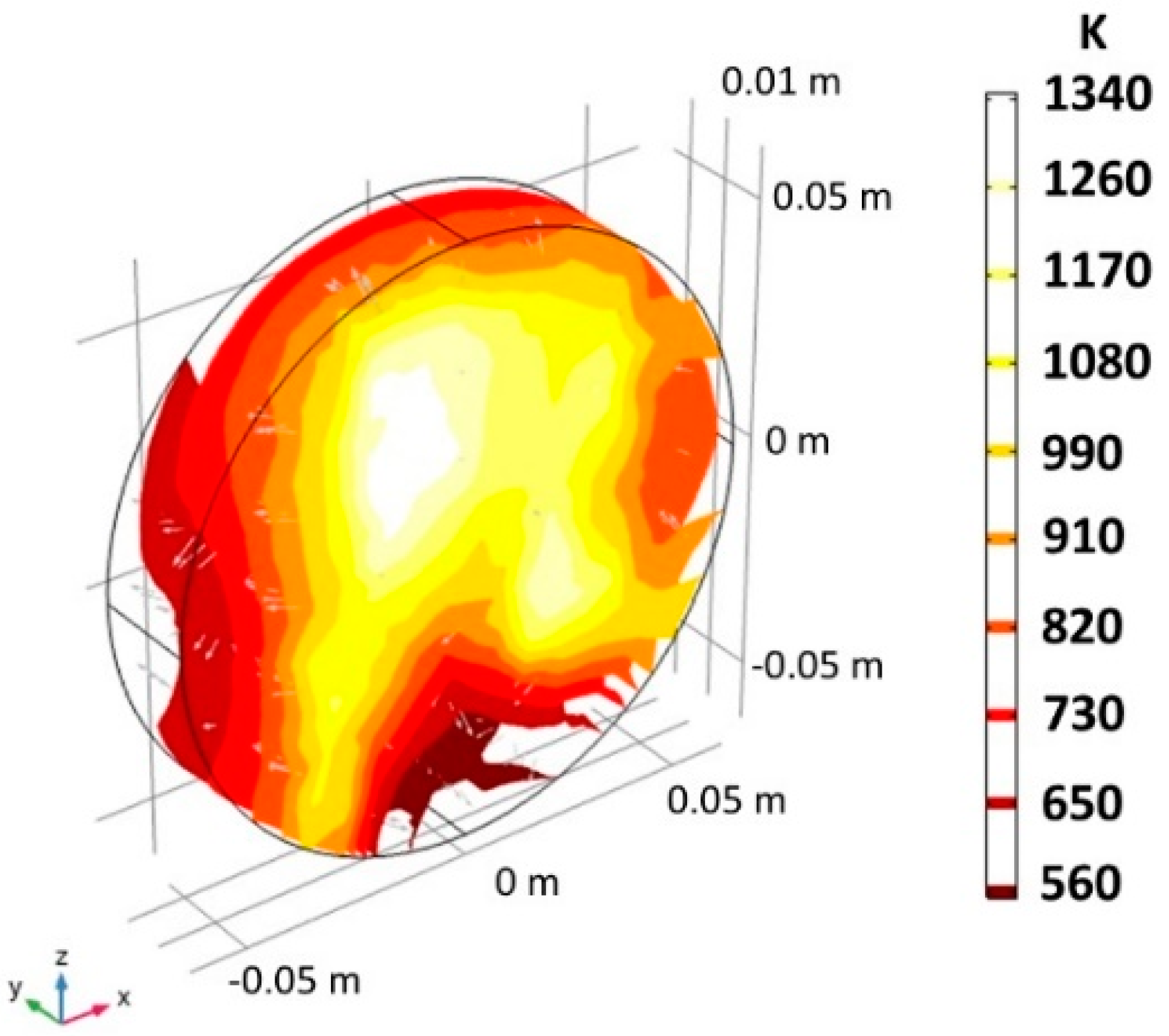
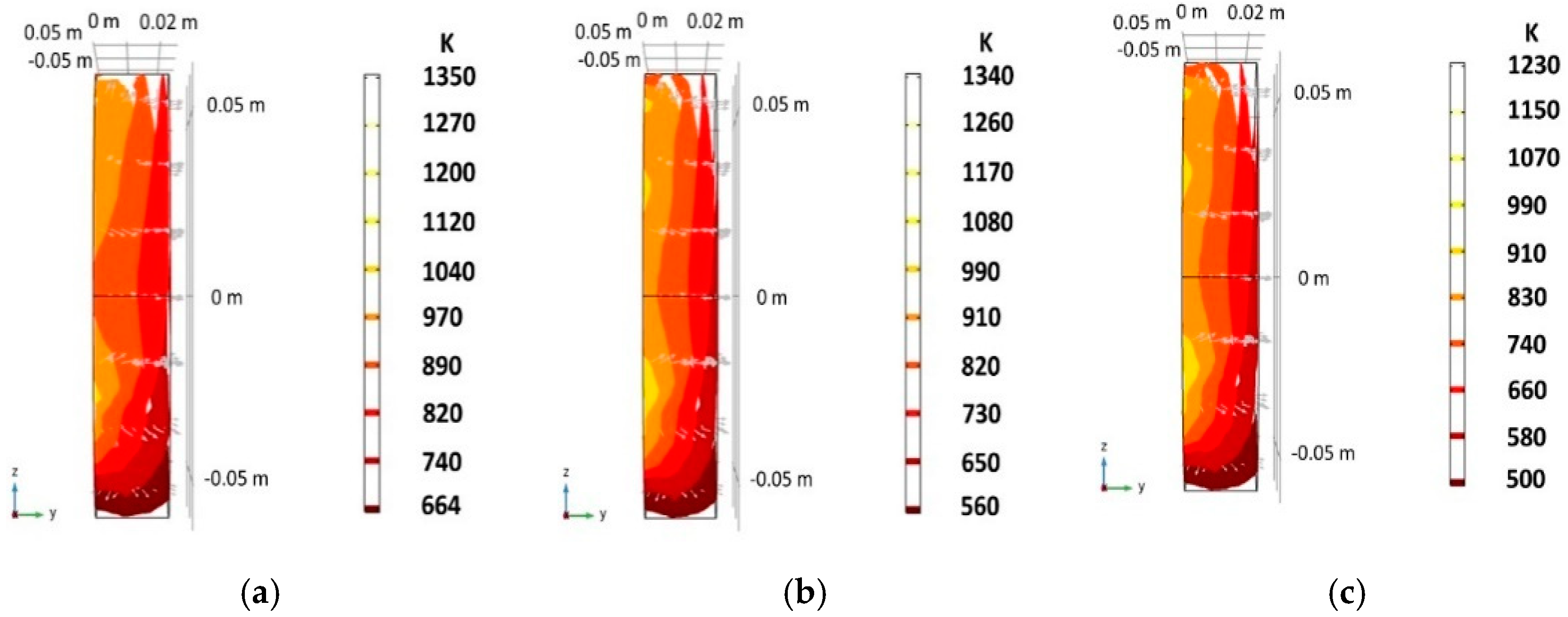
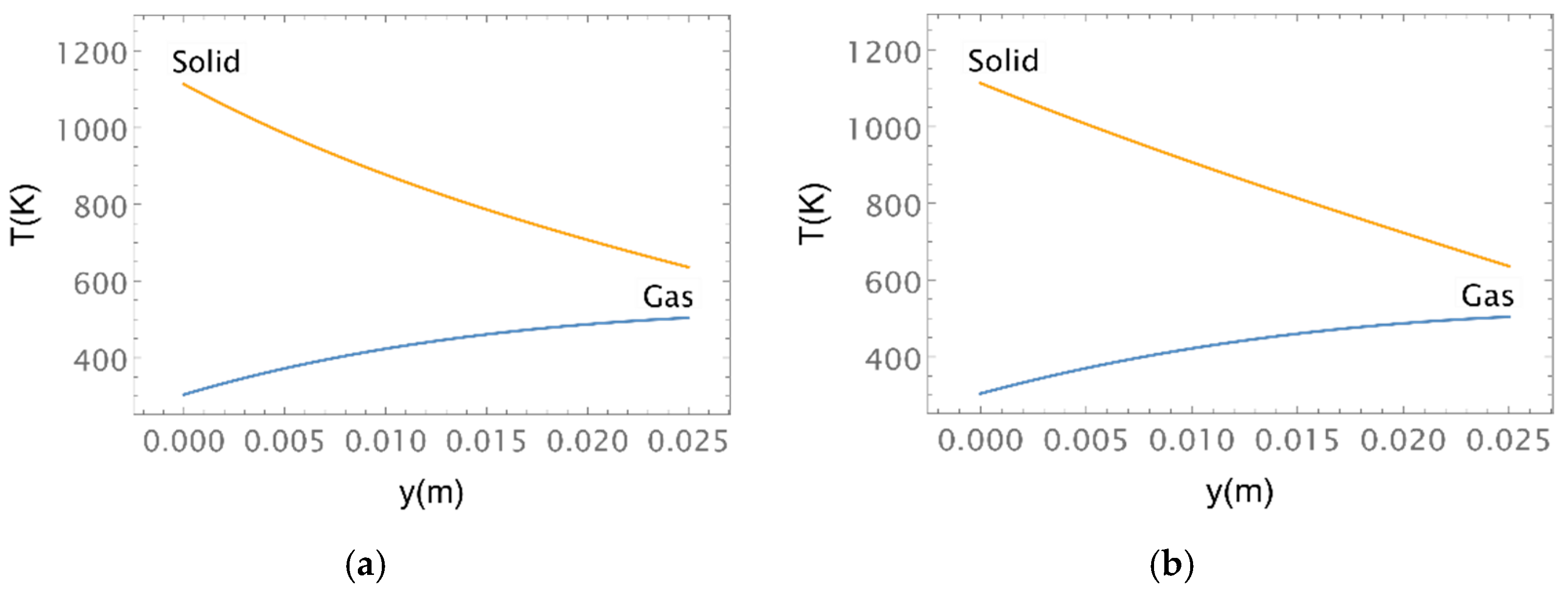
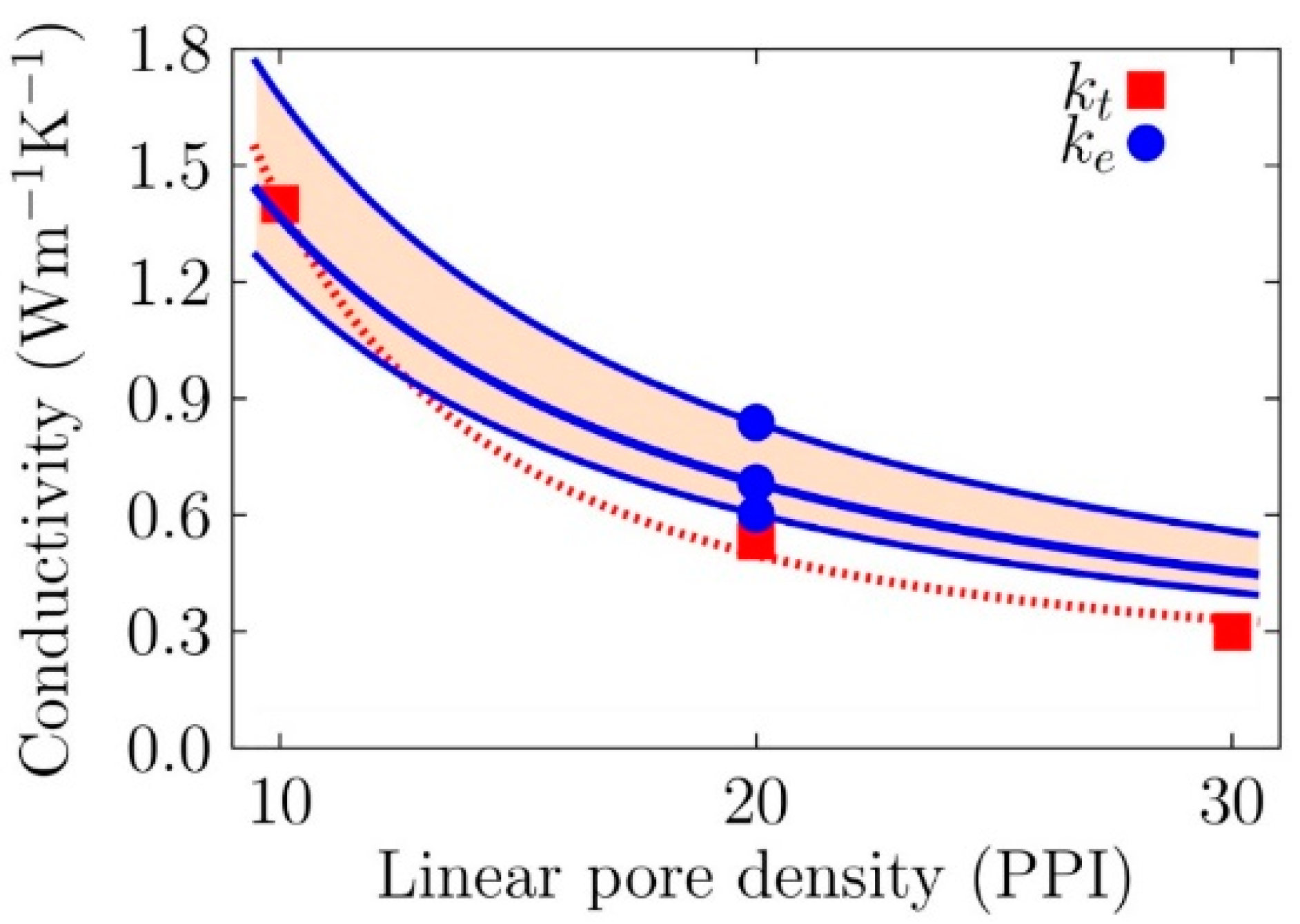
| Location | 10 PPI | 20 PPI | 30 PPI | |||||
|---|---|---|---|---|---|---|---|---|
| x (mm) | y (mm) | z (mm) | Exp (K) | Sim (K) | Exp (K) | Sim (K) | Exp (K) | Sim (K) |
| 27 | 0 | 27 | 1172 | 1196 | 1203 | 1204 | 1203 | 1108 |
| 27 | 23 | 27 | 786 | 795 | 685 | 681 | 685 | 603 |
| −30 | 0 | 27 | 1108 | 1210 | 1103 | 1201 | 1103 | 1102 |
| −30 | 23 | 27 | 795 | 804 | 642 | 688 | 642 | 609 |
| −30 | 0 | −30 | 1107 | 1056 | 1086 | 1077 | 1086 | 994 |
| −30 | 23 | −30 | 820 | 727 | 645 | 630 | 645 | 560 |
| 27 | 0 | −30 | 1101 | 1101 | 1063 | 1112 | 1063 | 1024 |
| 27 | 23 | −30 | 735 | 745 | 574 | 644 | 574 | 572 |
| RMS | 5% | 6% | 7% | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arreola-Ramos, C.E.; Álvarez-Brito, O.; Macías, J.D.; Guadarrama-Mendoza, A.J.; Ramírez-Cabrera, M.A.; Rojas-Morin, A.; Valadés-Pelayo, P.J.; Villafán-Vidales, H.I.; Arancibia-Bulnes, C.A. Experimental Evaluation and Modeling of Air Heating in a Ceramic Foam Volumetric Absorber by Effective Parameters. Energies 2021, 14, 2506. https://doi.org/10.3390/en14092506
Arreola-Ramos CE, Álvarez-Brito O, Macías JD, Guadarrama-Mendoza AJ, Ramírez-Cabrera MA, Rojas-Morin A, Valadés-Pelayo PJ, Villafán-Vidales HI, Arancibia-Bulnes CA. Experimental Evaluation and Modeling of Air Heating in a Ceramic Foam Volumetric Absorber by Effective Parameters. Energies. 2021; 14(9):2506. https://doi.org/10.3390/en14092506
Chicago/Turabian StyleArreola-Ramos, Carlos E., Omar Álvarez-Brito, Juan Daniel Macías, Aldo Javier Guadarrama-Mendoza, Manuel A. Ramírez-Cabrera, Armando Rojas-Morin, Patricio J. Valadés-Pelayo, Heidi Isabel Villafán-Vidales, and Camilo A. Arancibia-Bulnes. 2021. "Experimental Evaluation and Modeling of Air Heating in a Ceramic Foam Volumetric Absorber by Effective Parameters" Energies 14, no. 9: 2506. https://doi.org/10.3390/en14092506
APA StyleArreola-Ramos, C. E., Álvarez-Brito, O., Macías, J. D., Guadarrama-Mendoza, A. J., Ramírez-Cabrera, M. A., Rojas-Morin, A., Valadés-Pelayo, P. J., Villafán-Vidales, H. I., & Arancibia-Bulnes, C. A. (2021). Experimental Evaluation and Modeling of Air Heating in a Ceramic Foam Volumetric Absorber by Effective Parameters. Energies, 14(9), 2506. https://doi.org/10.3390/en14092506






