Comparison of Tank and Battery Storages for Photovoltaic Water Pumping
Abstract
1. Introduction
2. Methodology
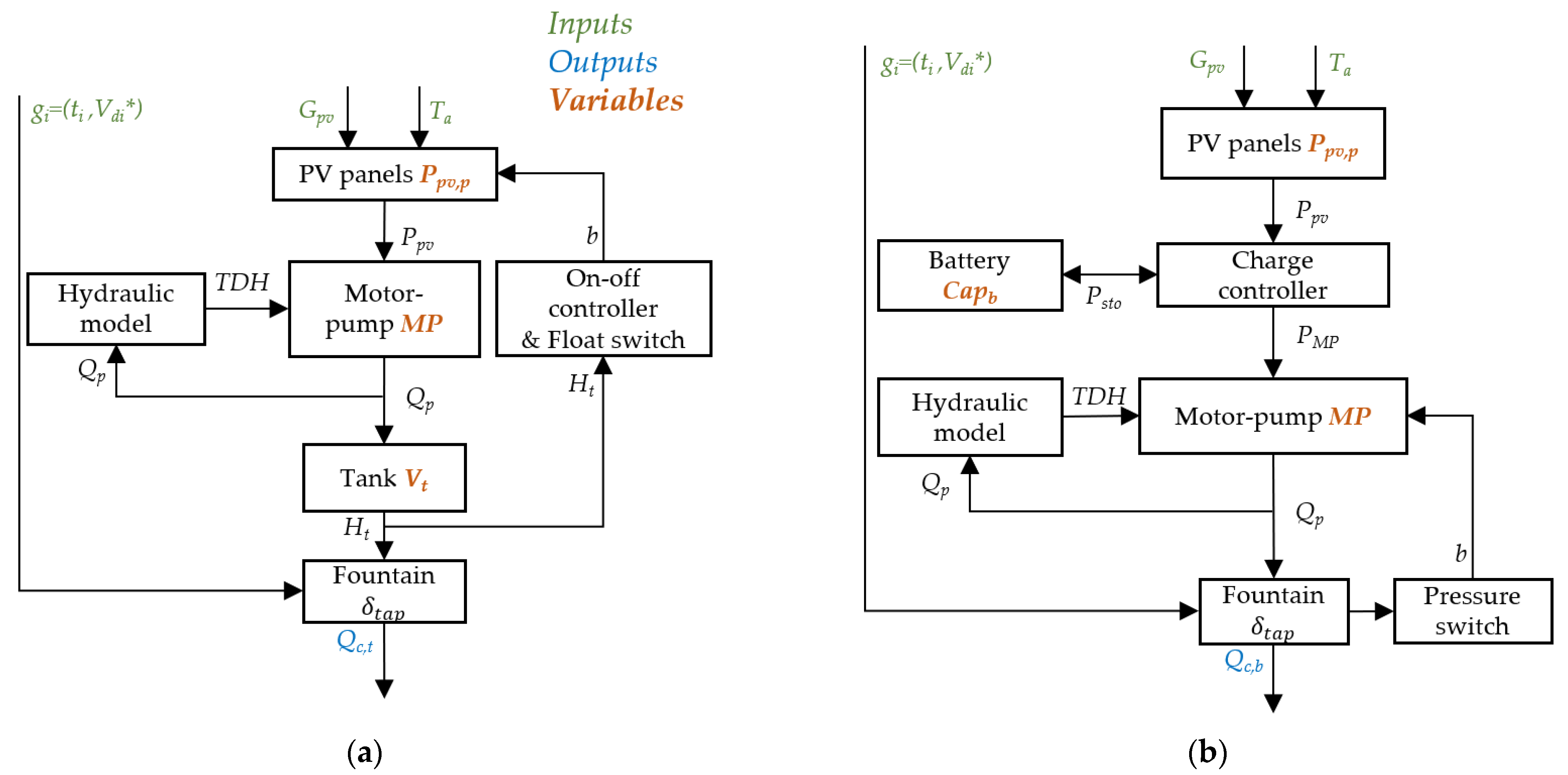
2.1. Architectures
2.2. Technical Models
2.2.1. Tank Architecture
2.2.2. Battery Architecture
2.3. Economic Model
3. Case Study
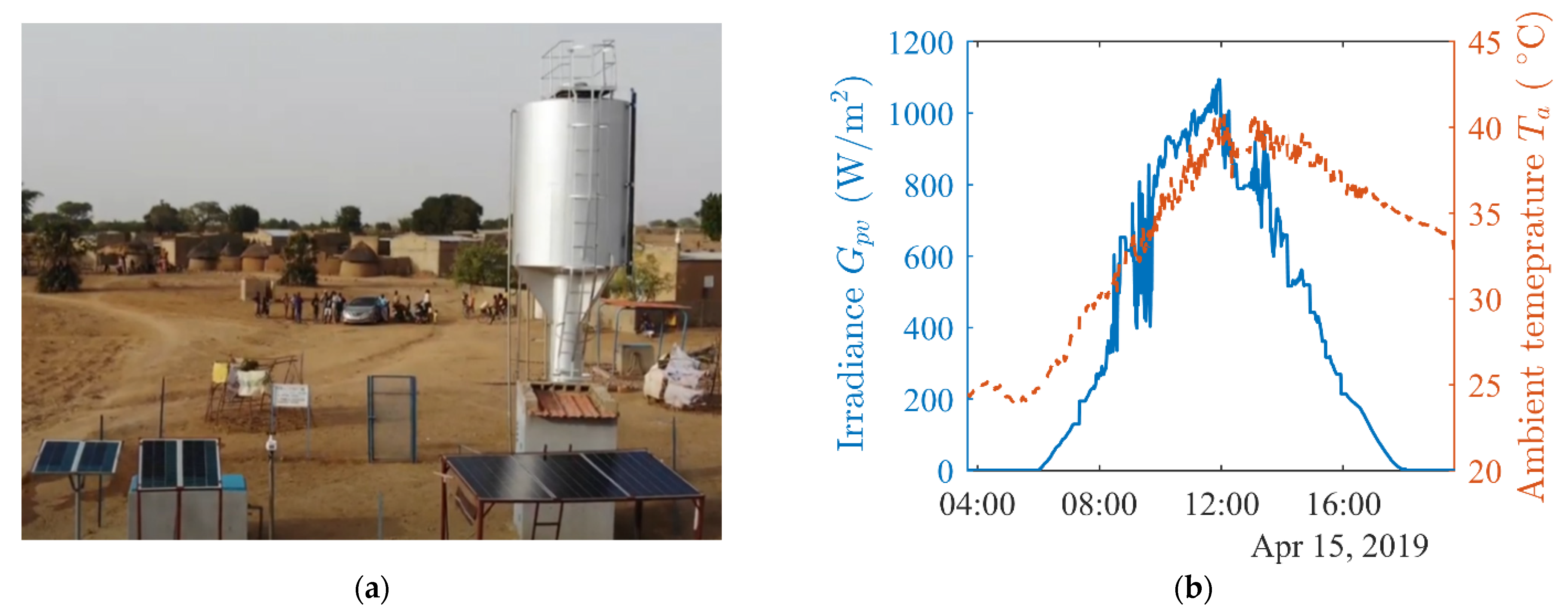
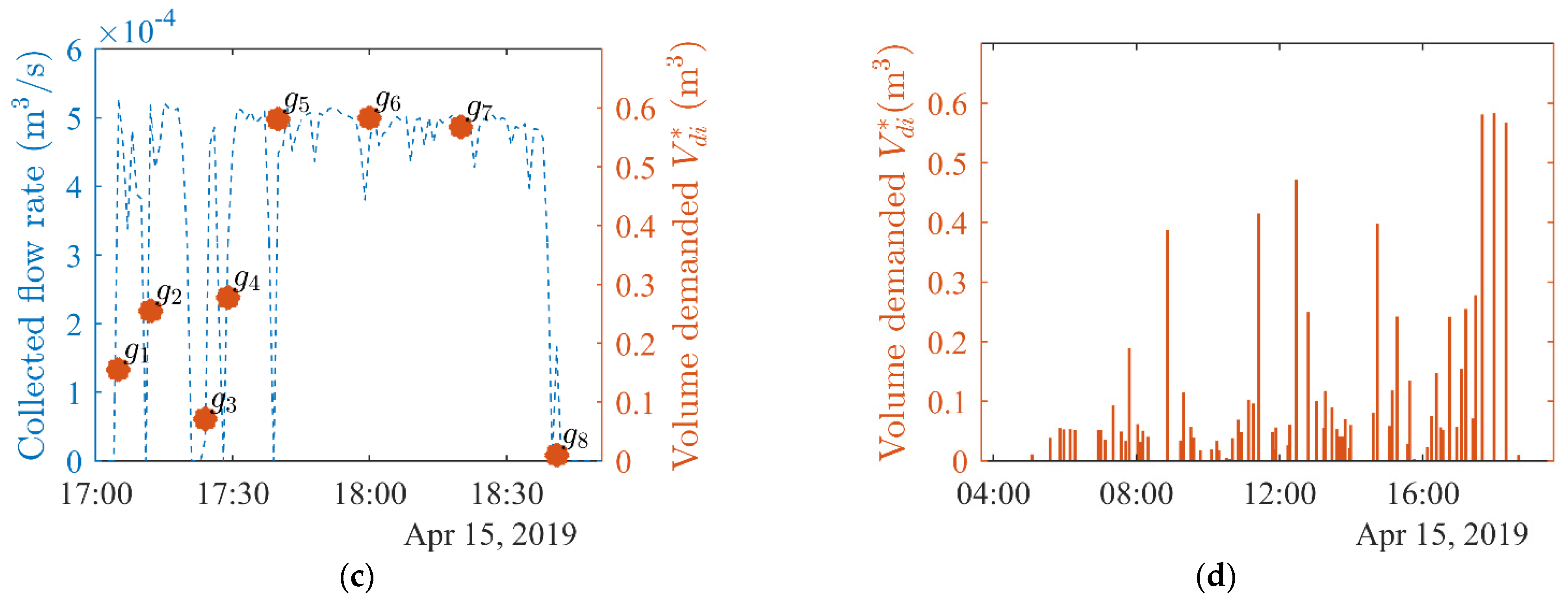
3.1. PVWPS in Gogma, Burkina Faso
3.2. Technical and Economic Models Parameters
4. Quantitative Comparison through Techno-Economic Optimization
4.1. Method
4.2. Formulation
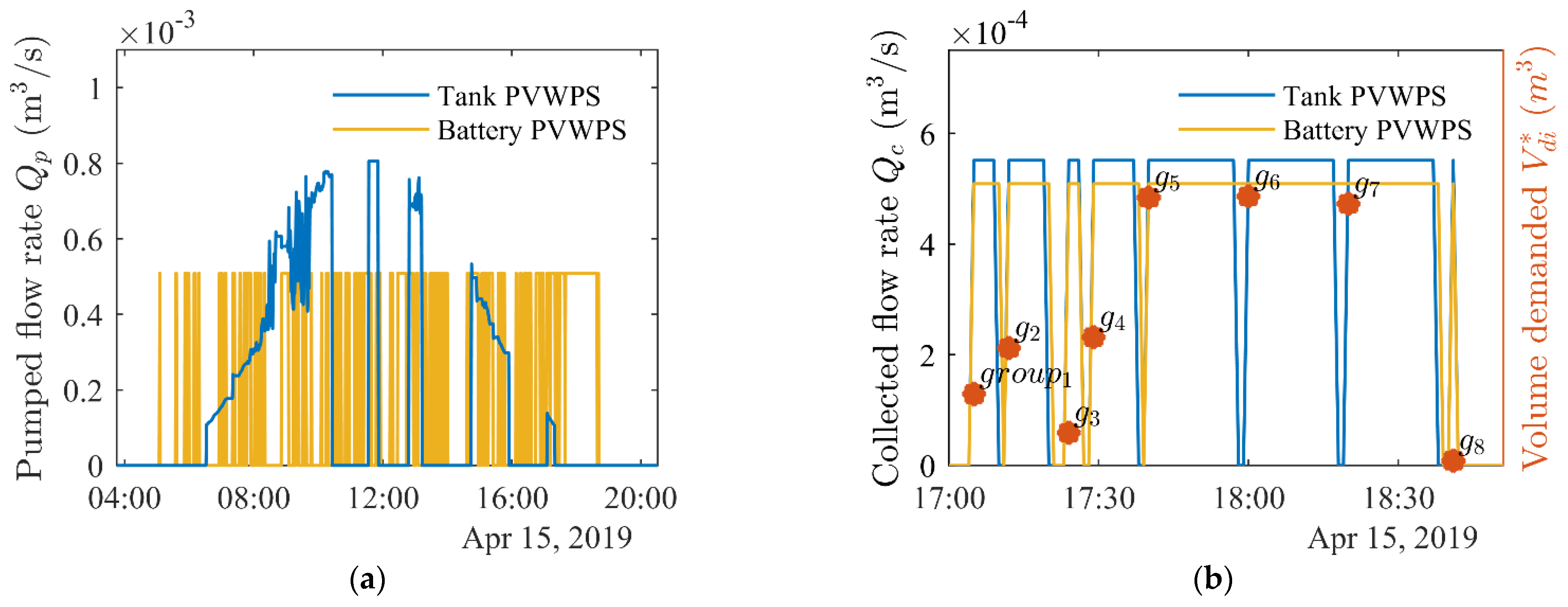
5. Results of the Optimizations and Comparison of Architectures
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| triggering signal from the switch | |
| battery capacity (Wh) | |
| CAPEX (battery, charge controller, motor-pump, PV array, tank) ($) | |
| final state of charge of cycle k | |
| initial variable cost ($) | |
| maintenance variable cost ($) | |
| replacement variable cost ($) | |
| temperature coefficient of the maximum power point (°C−1) | |
| depth of discharge of cycle k | |
| amplitude of reference | |
| discount rate | |
| state of the tap (open/close) | |
| type of architecture (battery/tank) | |
| activation energy (J/mol) | |
| energy stored in battery (Wh) | |
| irradiance on the plane of PV (W/m2) | |
| group of users (time of arrival, volume of water demanded (m3)) | |
| height between bottom of the tank and water level in the tank (m) | |
| height of tank (m) | |
| height between top of the tank and its entry level (m) | |
| height between entry level and stop level in the tank (m) | |
| height between stop level and restart level in the tank (m) | |
| level of water in the tank (m) | |
| height between ground level and static water level in the borehole (m) | |
| height between static water level and water level during pumping (m) | |
| height between ground level and fountain (m) | |
| maximum TDH for motor-pumps (m) | |
| efficiency of battery charging | |
| efficiency of charge controller | |
| current from battery to motor-pump (A) | |
| maximum current from battery (A) | |
| nominal current of motor-pump (A) | |
| aquifer losses coefficient (s/m2) | |
| lifetime (battery, charge controller, motor-pump, PV array, tank) (year) | |
| life cycle cost ($) | |
| fixed part of life cycle cost ($) | |
| reference of motor pump | |
| borehole losses coefficients (s2/m5) | |
| variable replacement costs of year i ($) | |
| NOCT | Normal Operating Cell Temperature |
| power consumed by the motor-pump (W) | |
| maximum power to motor-pump (W) | |
| power generated by PV array (W) | |
| peak power of PV array (Wp) | |
| power to battery (W) | |
| reference flow rate (m3/s) | |
| nominal flow rate of the fountain tank (m3/s) | |
| , | collected flow rate of tank/battery architecture (m3/s) |
| pumped flow rate (m3/s) | |
| battery resistance (Ω) | |
| Arrhenius constant (J.mol−1.K−1) | |
| surface of the base of the tank (m2) | |
| state of charge of the battery | |
| ambient temperature (°C) | |
| total dynamic head (m) | |
| voltage of battery during absorption/float phase (V) | |
| (t) | voltage of battery (V) |
| reconnection level of motor-pump for charge controller (V) | |
| disconnection level of motor-pump for charge controller (V) | |
| volume of tank (m3) | |
| pipe pressure losses coefficient (s2/m5) |
References
- Muhsen, D.H.; Khatib, T.; Nagi, F. A review of photovoltaic water pumping system designing methods, control strategies and field performance. Renew. Sustain. Energy Rev. 2017, 68, 70–86. [Google Scholar] [CrossRef]
- Barhdadi, A. Photovoltaic Water Pumping Systems in Rural Areas Photovoltaic Water Pumping Systems in Rural Areas. In Proceedings of the 4 International Conference on Water Resources and Arid Environments (ICWRAE 4), Riyadh, Saudi Arabia, 5–8 December 2010; pp. 836–843. [Google Scholar]
- Aliyu, M.; Hassan, G.; Elamin, I.M.; Said, S.A.; Siddiqui, M.U.; Alawami, A.T. A review of solar-powered water pumping systems. Renew. Sustain. Energy Rev. 2018, 87, 61–76. [Google Scholar] [CrossRef]
- Li, G.; Jin, Y.; Akram, M.W.; Chen, X. Research and current status of the solar photovoltaic water pumping system—A review. Renew. Sustain. Energy Rev. 2017, 79, 440–458. [Google Scholar] [CrossRef]
- Parajuli, R.; Pokharel, G.R.; Østergaard, P.A. A comparison of diesel, biodiesel and solar PV-based water pumping systems in the context of rural Nepal. Int. J. Sustain. Energy 2014, 33, 536–553. [Google Scholar] [CrossRef]
- Chilundo, R.J.; Mahanjane, U.S.; Neves, D. Design and Performance of Photovoltaic Water Pumping Systems: Comprehensive Review towards a Renewable Strategy for Mozambique. J. Power Energy Eng. 2018, 6, 32–63. [Google Scholar] [CrossRef]
- Skretas, S.B.; Papadopoulos, D.P. Systematic procedure for efficient design of electric water pumping systems fed by PV or/and WECS: Application using measured meteorological data for the city of Xanthi/Thrace, Greece. Energy Convers. Manag. 2008, 49, 596–607. [Google Scholar] [CrossRef]
- Chandel, S.S.; Nagaraju Naik, M.; Chandel, R. Review of solar photovoltaic water pumping system technology for irrigation and community drinking water supplies. Renew. Sustain. Energy Rev. 2015, 49, 1084–1099. [Google Scholar] [CrossRef]
- Chandel, S.S.; Naik, M.N.; Chandel, R. Review of performance studies of direct coupled photovoltaic water pumping systems and case study. Renew. Sustain. Energy Rev. 2017, 76, 163–175. [Google Scholar] [CrossRef]
- Dhiaa Muhsen, H.; Ghazali, A.B.; Khatib, T. Multiobjective differential evolution algorithm-based sizing of a standalone photovoltaic water pumping system. Energy Convers. Manag. 2016, 118, 32–43. [Google Scholar] [CrossRef]
- Bouzidi, B. New sizing method of PV water pumping systems. Sustain. Energy Technol. Assess. 2013, 4, 1–10. [Google Scholar] [CrossRef]
- Bakelli, Y.; Hadj Arab, A.; Azoui, B. Optimal sizing of photovoltaic pumping system with water tank storage using LPSP concept. Sol. Energy 2011, 85, 288–294. [Google Scholar] [CrossRef]
- Meunier, S. Optimal Design of Photovoltaic Water Pumping Systems for Rural Communities—A Technical, Economic and Social Approach. Ph.D. Thesis, Université Paris-Saclay, Gif-sur-Yvette, France, 2019. [Google Scholar]
- Anis, W.R.; Nour, M.A. Optimum design of a photovoltaic powered pumping system. Energy Convers. Manag. 1994, 35, 1123–1130. [Google Scholar] [CrossRef]
- Khan, M.T.A.; Ahmed, M.R.; Ahmed, S.I.; Khan, S.I. Design and performance analysis of water pumping using solar PV. In Proceedings of the 2nd International Conference on the Developments in Renewable Energy Technology, ICDRET 2012, Dhaka, Bangladesh, 26–28 March 2012; pp. 48–51. [Google Scholar]
- Meah, K.; Fletcher, S.; Ula, S. Solar photovoltaic water pumping for remote locations. Renew. Sustain. Energy Rev. 2008, 12, 472–487. [Google Scholar] [CrossRef]
- Gopal, C.; Mohanraj, M.; Chandramohan, P.; Chandrasekar, P. Renewable energy source water pumping systems—A literature review. Renew. Sustain. Energy Rev. 2013, 25, 351–370. [Google Scholar] [CrossRef]
- Chand, V.; Kalamkar, V.R. Solar photovoltaic water pumping system—A comprehensive review. Renew. Sustain. Energy Rev. 2016, 59, 1038–1067. [Google Scholar] [CrossRef]
- Khatib, T.; Mohamed, A.; Sopian, K. A review of photovoltaic systems size optimization techniques. Renew. Sustain. Energy Rev. 2013, 22, 454–465. [Google Scholar] [CrossRef]
- Muhsen, D.H.; Ghazali, A.B.; Khatib, T.; Abed, I.A.; Natsheh, E.M. Sizing of a standalone photovoltaic water pumping system using a multi-objective evolutionary algorithm. Energy 2016, 109, 961–973. [Google Scholar] [CrossRef]
- Basalike, P. Design, Optimization and Economic Analysis of Photovoltaic Water Pumping Technologies. Master’s Thesis, School of Business, Society and Engineering, Mälardalen University, Eskilstuna Västeras, Sweden, 2015. [Google Scholar]
- Sidrach-de-Cardona, M.; López, L.M. A simple model for sizing stand alone photovoltaic systems. Sol. Energy Mater. Sol. Cells 1998, 55, 199–214. [Google Scholar] [CrossRef]
- Vick, B.D.; Clark, R.N. Determining the optimum solar water pumping system for domestic use, livestock watering or irrigation. In Proceedings of the 38th ASES National Solar Conference, SOLAR, Buffalo, New York, NY, USA, 11–16 May 2009; Volume 4, pp. 2212–2239. [Google Scholar]
- Watson, S.; Bian, D.; Sahraei, N.; Winter, A.G.; Buonassisi, T.; Peters, I.M. Advantages of operation flexibility and load sizing for PV-powered system design. Sol. Energy 2018, 162, 132–139. [Google Scholar] [CrossRef]
- Pardo, M.Á.; Cobacho, R.; Bañón, L. Standalone photovoltaic direct pumping in urban water pressurized networks with energy storage in tanks or batteries. Sustainability 2020, 12, 738. [Google Scholar] [CrossRef]
- Meunier, S.; Queval, L.; Darga, A.; Dessante, P.; Marchand, C.; Heinrich, M.; Cherni, J.A.; De La Fresnaye, E.A.; Vido, L.; Multon, B.; et al. Modelling and optimal sizing of photovoltaic water pumping systems—Sensitivity analysis. In Proceedings of the 2019 14th International Conference on Ecological Vehicles and Renewable Energies, EVER 2019, Monte-Carlo, Monaco, 8–10 May 2019. [Google Scholar]
- Kazem, H.A.; Al-Waeli, A.H.A.; Chaichan, M.T.; Al-Mamari, A.S.; Al-Kabi, A.H. Design, measurement and evaluation of photovoltaic pumping system for rural areas in Oman. Environ. Dev. Sustain. 2017, 19, 1041–1053. [Google Scholar] [CrossRef]
- Meunier, S.; Heinrich, M.; Quéval, L.; Cherni, J.A.; Vido, L.; Darga, A.; Dessante, P.; Multon, B.; Kitanidis, P.K.; Marchand, C. A validated model of a photovoltaic water pumping system for off-grid rural communities. Appl. Energy 2019, 241, 580–591. [Google Scholar] [CrossRef]
- Grundfos SQFlex Data Booklet. Available online: https://www.solarpumpsafrica.com/wp-content/uploads/2014/07/SQ-Flex-Data-Booklet-May-2017.pdf (accessed on 3 April 2020).
- Soenen, C. An Analysis of Adapted Storage Approaches for Photovoltaic Water Pumping Systems in Developing Countries. Master’s Thesis, Imperial College London, London, UK, 2020. [Google Scholar]
- Dufo-Lopez, R.; Zubi, G.; Fracastoro, G.V. Tecno-economic assessment of an off-grid PV-powered community kitchen for developing regions. Appl. Energy 2012, 91, 255–262. [Google Scholar] [CrossRef]
- Stevens, J.W.; Corey, G.P. Study of lead-acid battery efficiency near top-of-charge and the impact on PV system design. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Washington, DC, USA, 13–17 May 1996; pp. 1485–1488. [Google Scholar]
- Dini, M. Modélisation et Identification des Paramètres Internes d’une Batterie au Plomb pour la Gestion d’un Microgrid. Master’s Thesis, Centrale Supélec, Gif-sur-Yvette, France, 2019. [Google Scholar]
- Victron Energy Gel et AGM Batteries Datasheet. Available online: https://www.victronenergy.com/upload/documents/Datasheet-GEL-and-AGM-Batteries-EN.pdf (accessed on 7 May 2020).
- Ultracell Ucg 100AH-12V Lead-Acid Battery. Available online: https://ultracell.co.uk/www.ultracell.co.uk/products/ucg-batteries/12v.html (accessed on 17 January 2020).
- Felicity Solar Solar Battery: User Instructions. Available online: https://www.energy-xprt.com/downloads/felicity-solar-model-fl-g-200ah12v-12v-200ah-gel-solar-battery-brochure-811472 (accessed on 17 January 2020).
- Gustavsson, M.; Mtonga, D. Lead-acid battery capacity in solar home systems—Field tests and experiences in Lundazi, Zambia. Sol. Energy 2005, 79, 551–558. [Google Scholar] [CrossRef]
- ACP-EU Energy Facility. Batteries—A Key Constraint for Off-Grid Solar. Experiences from EU-Supported Projects 2007–2019; FONDEM: Paris, France, 2019; pp. 1–27. [Google Scholar]
- Langella, R.; Testa, A.; Ventre, C. A new model of lead-acid batteries lifetime in smart grid scenario. In Proceedings of the Energycon 2014—IEEE International Energy Conference, Dubrovnik, Croatia, 13–16 May 2014; pp. 1343–1348. [Google Scholar]
- Nguyen, T.M.P. Lead Acid Batteries in Extreme Conditions: Accelerated Charge, Maintaining the Charge with Imposed Low Current, Polarity Inversions Introducing Non-Conventional Charge Methods. Ph.D. Thesis, Université Montpellier II, Montpellier, France, 2009. [Google Scholar]
- Vezin, T.; Meunier, S.; Quéval, L.; Cherni, J.A.; Vido, L.; Darga, A.; Dessante, P.; Kitanidis, P.K.; Marchand, C. Borehole water level model for photovoltaic water pumping systems. Appl. Energy 2020, 258, 114080. [Google Scholar] [CrossRef]
- Meunier, S.; Queval, L.; Heinrich, M.; De La Fresnaye, E.A.; Cherni, J.A.; Vido, L.; Darga, A.; Dessante, P.; Multon, B.; Kitanidis, P.K.; et al. Effect of irradiance data on the optimal sizing of photovoltaic water pumping systems. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Chicago, IL, USA, 16–21 June 2019; pp. 653–658. [Google Scholar]
- Meunier, S.; Queval, L.; Darga, A.; Dessante, P.; Marchand, C.; Heinrich, M.; Cherni, J.; Vido, L.; Multon, B. Influence of The Temporal Resolution of The Water Consumption Profile on Photovoltaic Water Pumping Systems Modelling and Sizing. In Proceedings of the 2018 7th International Conference on Renewable Energy Research and Applications, Paris, France, 14–17 October 2018; pp. 494–499. [Google Scholar]
- De La Fresnaye, E.A. A Financial and Technical Assessment of Solar Versus Hand Water Pumping for Off-Grid Area—The Case of Burkina Faso. Master’s Thesis, Imperial College London, London, UK, 2018. [Google Scholar]
- Meunier, S.; Queval, L.; Darga, A.; Dessante, P.; Marchand, C.; Heinrich, M.; Cherni, J.A.; De La Fresnaye, E.A.; Vido, L.; Multon, B.; et al. Sensitivity Analysis of Photovoltaic Pumping Systems for Domestic Water Supply. IEEE Trans. Ind. Appl. 2020, 56, 6734–6743. [Google Scholar] [CrossRef]
- Victron Energy Contrôleurs de Charge SmartSolar Avec Sortie de Charge. Available online: https://www.victronenergy.com/solar-charge-controllers/smartsolar-mppt-75-10-75-15-100-15-100-20 (accessed on 27 February 2021).
- Price, K.; Storn, R.; Lampinen, J. Differential Evolution: A Practical Approach to Global Optimization; Rozenberg, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 9783540209508. [Google Scholar]
- Lorentz the Solar Water Pumping Company PS2: The Complete, Efficient, Solar Water Pumping Solution Delivering You more Water! Available online: https://partnernet.lorentz.de/files/lorentz_ps2_product-brochure_en.pdf (accessed on 31 October 2019).
- Franklin Electric. Franklin Water Products. Available online: https://franklinwater.com/ (accessed on 12 July 2020).
- Hankins, M. Solar Electric Systems for Africa: A Guide for Plannning and Installing Solar Systems in Rural Africa; Simalenga, T., Ed.; Commonwealth Science Council: London, UK, 1995; ISBN 9781437735789.
- Short, T.D.; Oldach, R. Solar powered water pumps: The past, the present—And the future? J. Sol. Energy Eng. Trans. ASME 2003, 125, 76–82. [Google Scholar] [CrossRef]
- Dornan, M. Solar-based rural electrification policy design: The Renewable Energy Service Company (RESCO) model in Fiji. Renew. Energy 2011, 36, 797–803. [Google Scholar] [CrossRef]
- Martz, J.E.; Roberts, A.F. Operational Performance of the Photovoltaic-Powered Grain Mill and Water Pump at Tangaye, Burkina Faso (Formerly Upper Volta); Final Report; NASA: Washington, DC, USA, 1985.
- Foster, S.; Chilton, P. Groundwater: The processes and global significance of aquifer degradation. Philos. Trans. R. Soc. B Biol. Sci. 2003, 358, 1957–1972. [Google Scholar] [CrossRef]
- Narvarte, L.; Lorenzo, E.; Caamano, E. PV pumping analytical design and characteristics of boreholes. Sol. Energy 2000, 68, 49–56. [Google Scholar] [CrossRef]
- Doǧan, U.; Yilmaz, M. Natural and induced sinkholes of the Obruk Plateau and Karapidotlessnar-Hotam Plain, Turkey. J. Asian Earth Sci. 2011, 40, 496–508. [Google Scholar] [CrossRef]
- Teatini, P.; Ferronato, M.; Gambolati, G.; Gonella, M. Groundwater pumping and land subsidence in the Emilia-Romagna coastland, Italy: Modeling the past occurrence and the future trend. Water Resour. Res. 2006, 42, 1–19. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, C.; Zhang, X.; Liu, S. Study on the Environmental Risk Assessment of Lead-Acid Batteries. Procedia Environ. Sci. 2016, 31, 873–879. [Google Scholar] [CrossRef]
- United Nations Environment Programm. Workshop on Sound Management of Used Lead Acid Batteries in Africa; UNEP: Ouagadougou, Burkina Faso, 2017. [Google Scholar]
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Diouf, B.; Pode, R. Potential of lithium-ion batteries in renewable energy. Renew. Energy 2015, 76, 375–380. [Google Scholar] [CrossRef]
- Anuphappharadorn, S.; Sukchai, S.; Sirisamphanwong, C.; Ketjoy, N. Comparison the economic analysis of the battery between lithium-ion and lead-acid in PV stand-alone application. Energy Procedia 2014, 56, 352–358. [Google Scholar] [CrossRef]

| Common to the Tank and Battery PVWPS | Relative to the Tank PVWPS | Relative to the Battery PVWPS |
|---|---|---|
| System | Tank [45] | Lead-acid batteries [34,35,36] |
| L = 20 years | = 4.2 m | = 48 V |
| = 3.4 m | = 6 mΩ | |
| PV array [45] | = 0.4 m | = 43.2 V |
| = 0.1 m | = 7.5 V | |
| = 0.1 m | = 8 years | |
| Motor-pump [29,41] | Fountain | Charge controller [46] |
| = 8.4 A | 5.5 × 10−4 m3/s | = 44.4 V |
| Models: SQFlex 5A-3, SQFlex | = 55.2 V | |
| 0.6–2, SQFlex 8A-5, SQFlex8A- | = 57.6 V | |
| 3, SQFlex 11A-3, SQFlex 1.2-2 | = 55.2 V | |
| SQFlex 5A-7 and SQFlex2.5-2 | = 98% | |
| = 20 A | ||
| Hydraulic model [41] | ||
| = 2.4 × 103 s/m2 | Fountain | |
| = 8.4 × 105 s²/m5 | = 1 m | |
| = 4.9 × 106 s²/m5 | ||
| = 7.5 m |
| Common to Tank and Battery PVWPS | Relative to the Tank PVWPS | Relative to the Battery PVWPS |
|---|---|---|
| PV array [13] | Steel tank [13] | Lead-acid batteries [30] |
| [$] = 20 years | = = 20 years | is obtained from Equation (11) |
| Motor-pump [13] | Charge controller [30,46] | |
| $ = 10 years | 150 $ = 5 years | |
| Discount rate [44] | ||
| = 5.6% | ||
| Fixed costs [13] | ||
| Tank PVWPS | Battery PVWPS | ||
|---|---|---|---|
| Sizing | PV peak power | 410 Wp | 462 Wp |
| Motor-pump reference | SQFlex 2.5-2 | SQFlex 2.5-2 | |
| Tank volume | 5 m3 | ||
| Battery capacity | 1673 Wh | ||
| 30.4 L/min | |||
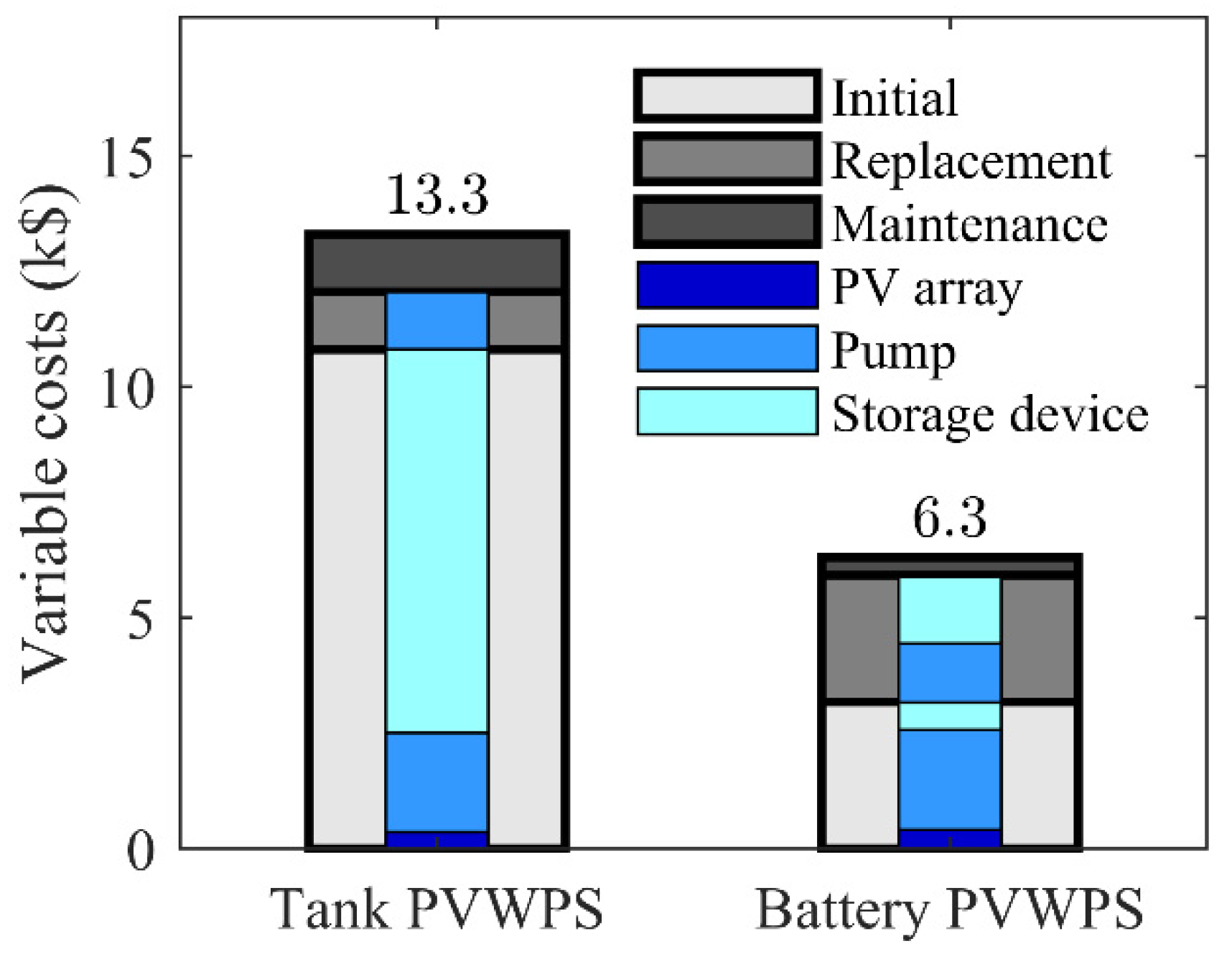
| Economic | Variable costs | $13.3 k | $6.3 k |
| Fixed costs | $17.8 k | $17.8 k | |
| $31.1 k | $24.1 k | ||
| Maintenance | Storage replacements | 0 | 5 |
| Starts and stops per day | max: 8–mean: 4 | max: 107–mean: 84 | |
| Availability of spare parts | Not applicable | Low | |
| Environment | Toxicity | Low | High (lead) |
| Maximum pumped flow rate | 48.3 L/min | 30.4 L/min | |
| Lowest water level in the borehole | −10.0 m | −8.9 m | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soenen, C.; Reinbold, V.; Meunier, S.; Cherni, J.A.; Darga, A.; Dessante, P.; Quéval, L. Comparison of Tank and Battery Storages for Photovoltaic Water Pumping. Energies 2021, 14, 2483. https://doi.org/10.3390/en14092483
Soenen C, Reinbold V, Meunier S, Cherni JA, Darga A, Dessante P, Quéval L. Comparison of Tank and Battery Storages for Photovoltaic Water Pumping. Energies. 2021; 14(9):2483. https://doi.org/10.3390/en14092483
Chicago/Turabian StyleSoenen, Camille, Vincent Reinbold, Simon Meunier, Judith A. Cherni, Arouna Darga, Philippe Dessante, and Loïc Quéval. 2021. "Comparison of Tank and Battery Storages for Photovoltaic Water Pumping" Energies 14, no. 9: 2483. https://doi.org/10.3390/en14092483
APA StyleSoenen, C., Reinbold, V., Meunier, S., Cherni, J. A., Darga, A., Dessante, P., & Quéval, L. (2021). Comparison of Tank and Battery Storages for Photovoltaic Water Pumping. Energies, 14(9), 2483. https://doi.org/10.3390/en14092483








