A Two-Dimensional Partitioning of Fracture–Matrix Flow in Fractured Reservoir Rock Using a Dual-Porosity Percolation Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Fracture Network Generation
2.2. Fracture Length Distribution
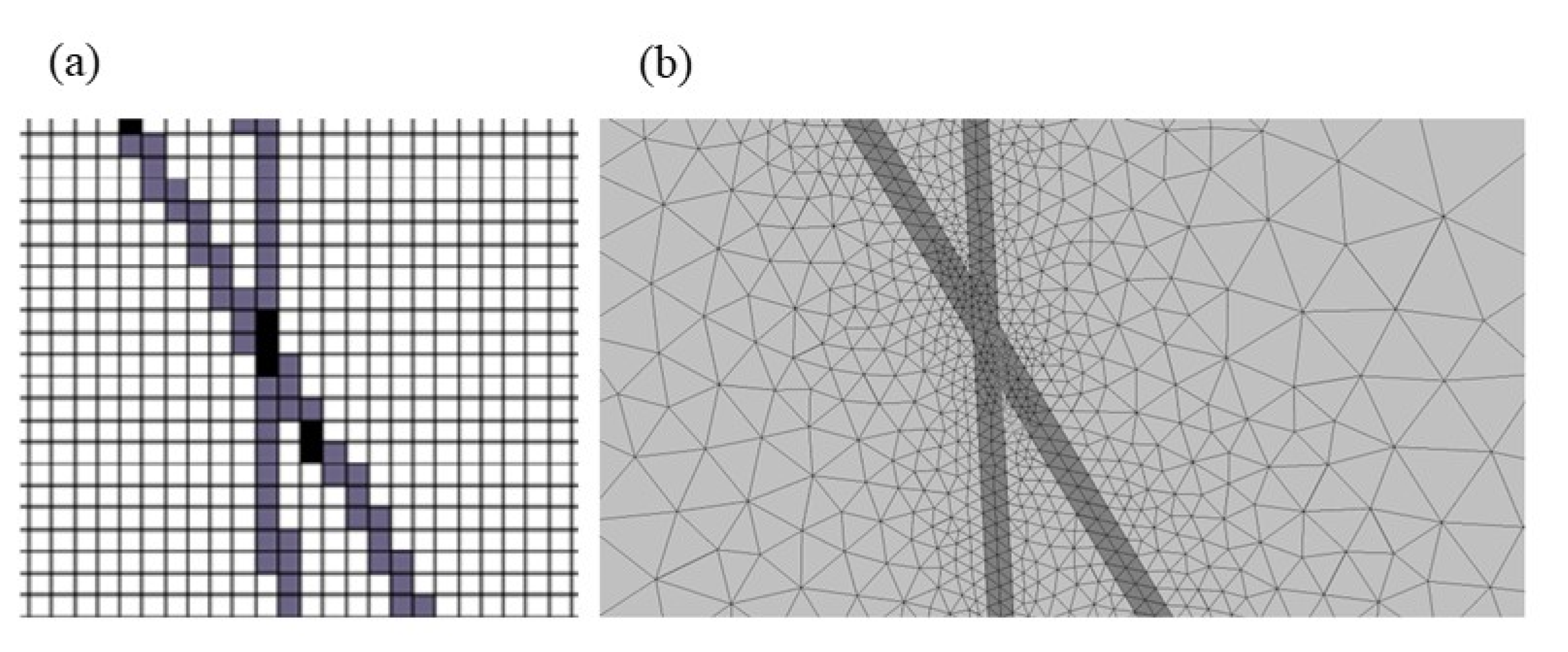
2.3. Determining Hydraulic Connections for a Given Fracture Network
2.4. Dual-Porosity Model for Gas Flow Simulation and Permeability () Calculations
2.5. Dual-Porosity Model Verification
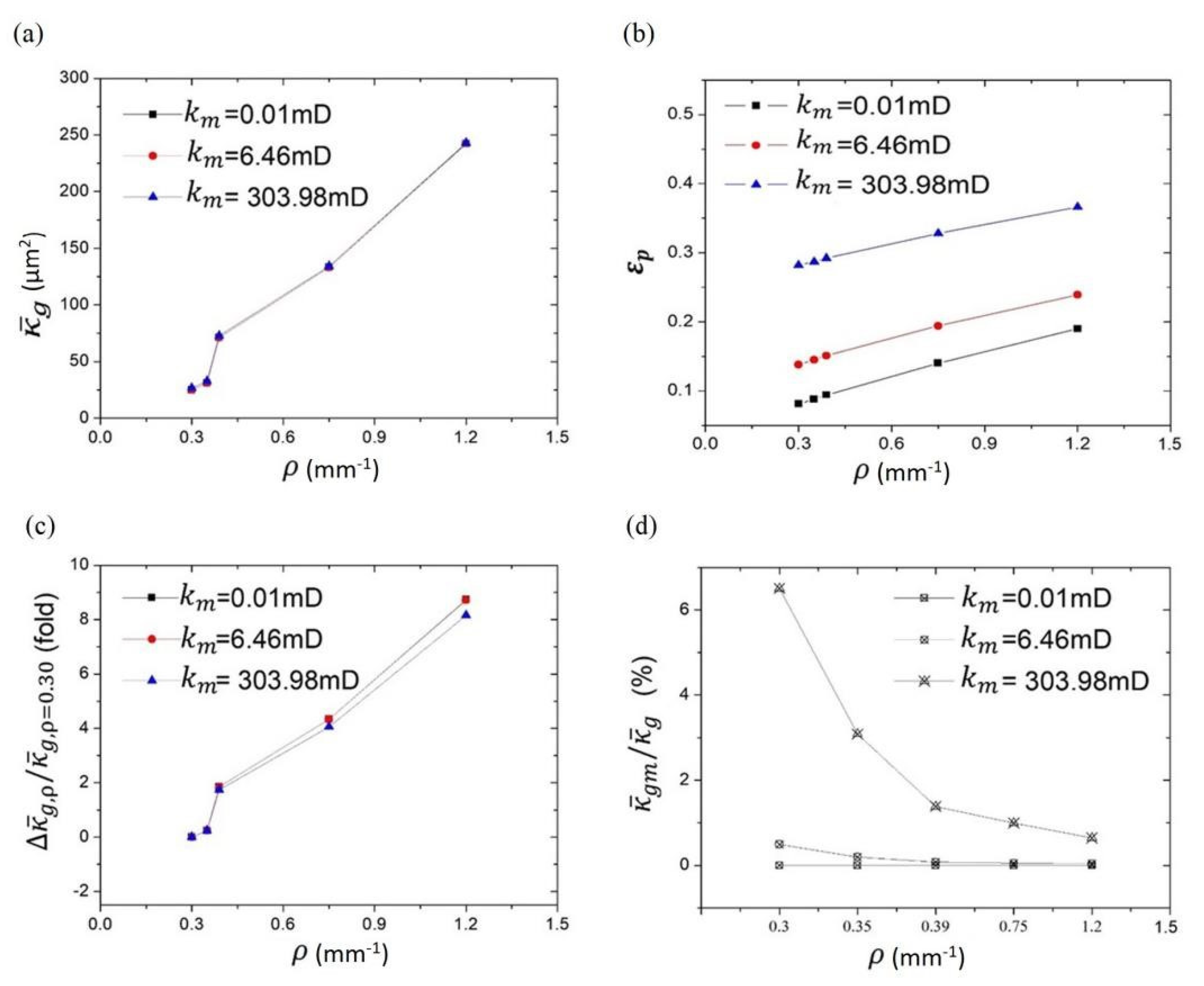
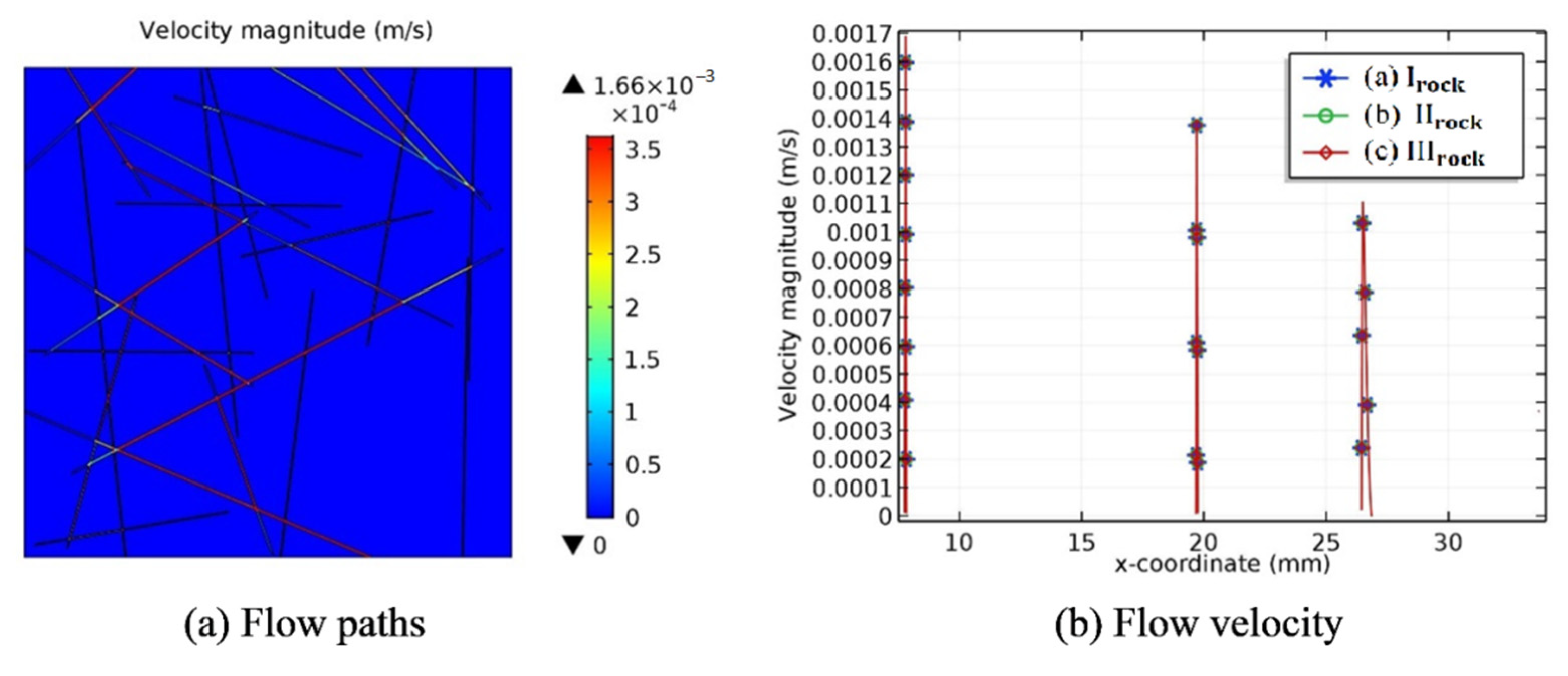
3. Results and Discussions
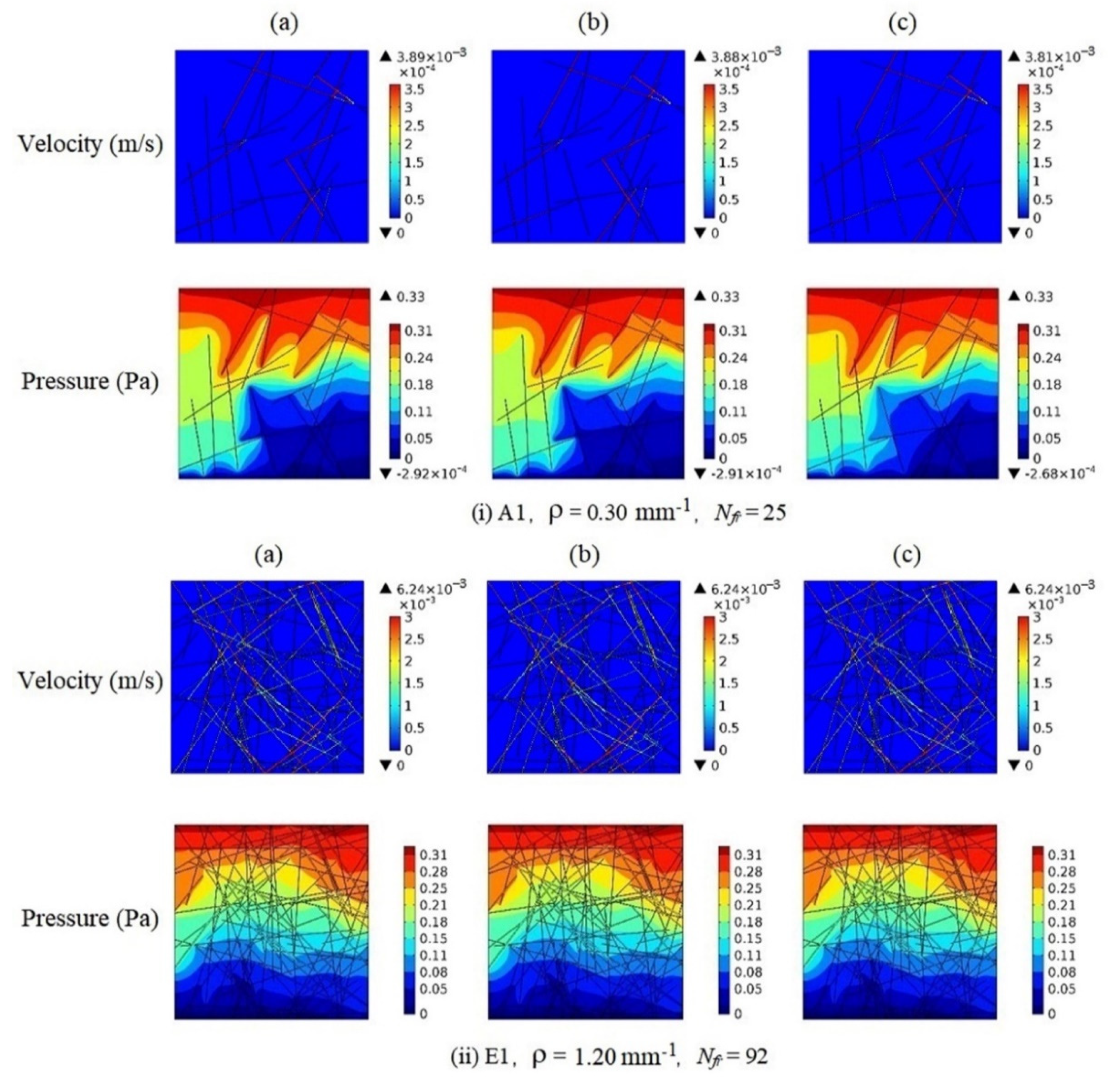
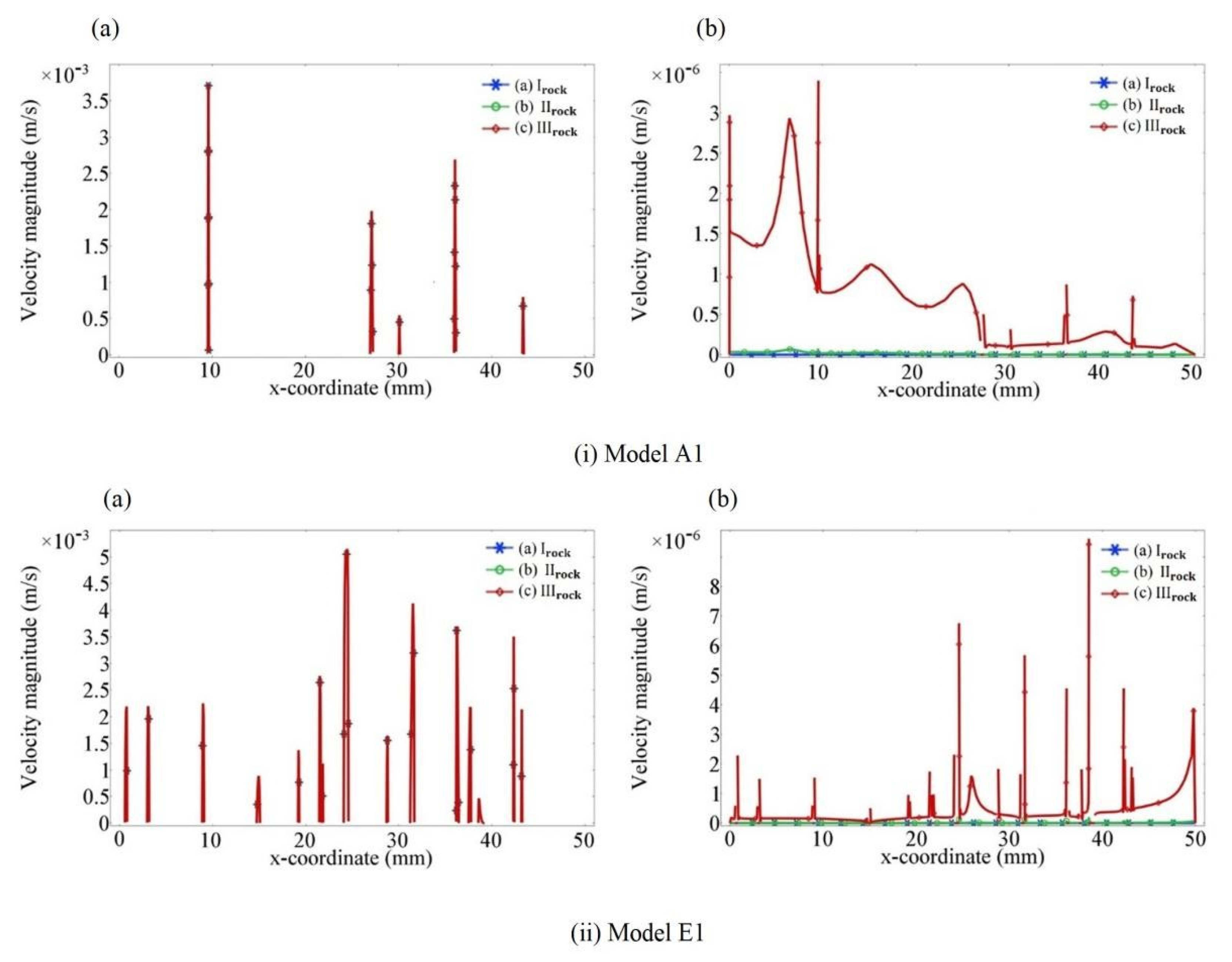
3.1. Flow Velocity and Pressure Profile
3.2. Estimation of Fractured Rock Permeability
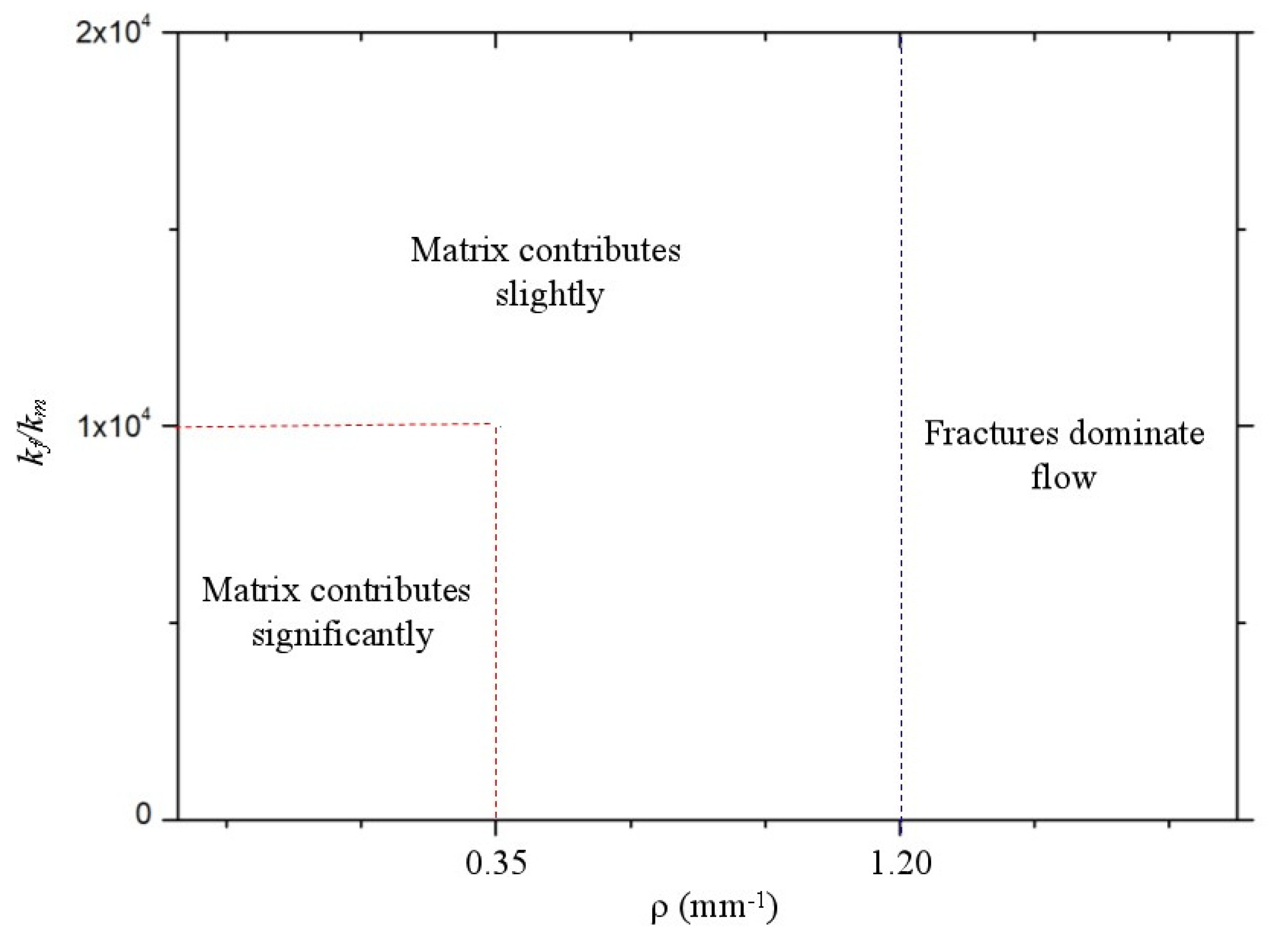
3.3. The Quantitative Relationship between Pore–Fracture Distribution and Permeability
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| n(l)dl | fracture number that has a length interval of [l, l+dl] |
| proportional coefficient that reflects the fracture density | |
| a | an exponent varying from one to three |
| l | fracture length (m) |
| total number of fractures with a length of l in a fracture system | |
| L | system size (m) |
| percolation parameter | |
| lmin | minimum fracture lengths in a fracture system (m) |
| lmax | maximum fracture lengths in a fracture system (m) |
| as | actual parameter |
| asc | critical parameter |
| r | ratio of as to asc |
| Wav | average facture aperture (m) |
| kf | fracture permeability (m2) |
| matrix permeability (m2) | |
| matrix porosity | |
| porosity | |
| fracture density | |
| fluid density (kg/m3) | |
| ρg | methane density (kg/m3) |
| dynamic viscosity (Pas) | |
| fluid velocity (m/s) | |
| pressure (Pa) | |
| gravity vector (m/s2) | |
| absolute permeability (m2) | |
| Q | total fluid flux (m3) |
| A | cross-sectional area of flow (m2) |
| pressure difference between inlets and outlets (Pa) | |
| section velocity (m/s) | |
| section area at outlets (m2) | |
| average gas pressure (Pa) | |
| b | coefficient of Klinkenberg effects |
| equivalent fracture permeability (m2) | |
| element length of a square (m) | |
| w | fracture aperture (m) |
| coefficient related to the roughness of the fracture surface | |
| downstream outlet flow rate (m2/s) | |
| water density (kg/m3) | |
| hydraulic head at the top (m) | |
| hydraulic head at the bottom (m) | |
| equivalent gas permeability (m2) |
References
- Chen, X.L.; Tang, X.M.; Qian, Y.P. Propagation characteristics of multipole acoustic logging in cracked porous tight formations. Chin. J. Geophys. 2014, 57, 2961–2970. [Google Scholar]
- Zhi, Z.W.; Cheng, W.Z.; Jun, W.H.; Jin, C.M. Research Advances and Exploration Significance of Large-area Accumulation of Low and Medium Abundance Lithologic Reservoirs. Acta Geol. Sin. 2008, 82, 463–476. [Google Scholar]
- Fu, P.; Johnson, S.M.; Carrigan, C.R. An explicitly coupled hydro-geomechanical model for simulating hydraulic fracturing in arbitrary discrete fracture networks. Int. J. Numer. Anal. Met. 2014, 37, 2278–2300. [Google Scholar] [CrossRef]
- Hu, X.; Xie, J.; Cai, W.; Wang, R.; Davarpanah, A. Thermodynamic effects of cycling carbon dioxide injectivity in shale reservoirs. J. Petrol. Sci. Eng. 2020, 195, 107717. [Google Scholar] [CrossRef]
- Teimoori, A.; Chen, Z.; Rahman, S.S.; Tran, T. Effective Permeability Calculation Using Boundary Element Method in Naturally Fractured Reservoirs. Liq. Fuels Technol. 2005, 23, 693–709. [Google Scholar] [CrossRef]
- Abdelazim, R.; Rahman, S.S. Estimation of Permeability of Naturally Fractured Reservoirs by Pressure Transient Analysis: An Innovative Reservoir Characterisation and Flow Simulation. J. Petrol. Sci. Eng. 2016, 145, 404–422. [Google Scholar] [CrossRef]
- Park, Y.C.; Sung, W.M.; Kim, S.J. Development of a FEM Reservoir Model Equipped with an Effective Permeability Tensor and its Application to Naturally Fractured Reservoirs. Energy Sources 2002, 24, 531–542. [Google Scholar] [CrossRef]
- Gang, T.; Kelkar, M.G. Efficient History Matching in Naturally Fractured Reservoirs. In Proceedings of the SPE/DOE Symposium on Improved Oil Recovery, Tulsa, OK, USA, 22–26 April 2006. [Google Scholar]
- Wang, C.; Zhai, P.; Wang, L.; Wang, C.; Zhang, X.; Wu, X.; Jiang, Y. Careful features of lithotype cracks based on Micro-CT technology. Coal Sci. Technol. 2017, 45, 137–142. [Google Scholar] [CrossRef]
- Peng, P.; Ju, Y.; Wang, Y.; Wang, S.; Gao, F. Numerical analysis of the effect of natural microcracks on the supercritical CO2 fracturing crack network of shale rock based on bonded particle models. Int. J. Numer. Anal. Met. 2017, 41, 1–23. [Google Scholar] [CrossRef]
- Cheng, H.; Ju, Y.; Xu, T.; Yue, S.; Jia, T.; Neupane, B.; Han, K.; Yu, Q.; Zhu, H.; Cai, J. Full-Scale and Multi-Method Combined Characterization of Micro/Nano Pores in Organic Shale. J. Nanosci. Nanotechnol. 2017, 17, 6634–6644. [Google Scholar]
- Hu, Q.; Zhang, Y.; Meng, X.; Li, Z.; Xie, Z.; Li, M. Characterization of micro-nano pore networks in shale oil reservoirs of Paleogene Shahejie Formation in Dongying Sag of Bohai Bay Basin, East China. Petrol. Explor. Dev. 2017, 44, 720–730. (In Chinese) [Google Scholar] [CrossRef]
- Chen, M.; Bai, M.; Roegiers, J.C. Permeability Tensors of Anisotropic Fracture Networks. Math. Geol. 1999, 31, 335–373. [Google Scholar] [CrossRef]
- Min, K.B.; Jing, L.; Stephansson, O. Determining the equivalent permeability tensor for fractured rock masses using a stochastic REV approach: Method and application to the field data from Sellafield, UK. Hydrogeol. J. 2004, 12, 497–510. [Google Scholar] [CrossRef]
- Snow, D.T. Anisotropie Permeability of Fractured Media. Water Resour. Res. 1969, 5, 1273–1289. [Google Scholar] [CrossRef]
- Wanniarachchi, W.A.M.; Ranjith, P.G.; Perera, M.S.A.; Rathnaweera, T.D.; Zhang, D.C.; Zhang, C. Investigation of effects of fracturing fluid on hydraulic fracturing and fracture permeability of reservoir rocks: An experimental study using water and foam fracturing. Eng. Fract. Mech. 2018, 194, S001379441731353X. [Google Scholar] [CrossRef]
- Uehara, S.; Takahashi, M.; Oikawa, Y.; Masuda, K. Depth dependency of fracture permeability in Neogene mudstone. Agu Fall Meet. Abstr. 2009, 2009, H13E-1023. [Google Scholar]
- Liang, Y.; Tsuji, S.; Jia, J.; Tsuji, T.; Matsuoka, T. Modeling CO2–Water–Mineral Wettability and Mineralization for Carbon Geosequestration. Acc. Chem. Res. 2017, 50, 1530–1540. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, H.; Shao, Z.; Li, K. Gas Transport Mechanisms in Micro- and Nano-Scale Matrix Pores in Shale Gas Reservoirs. Chem. Technol. Fuels Oil 2015, 51, 545–555. [Google Scholar] [CrossRef]
- Duan, Y.; Cao, T.; Yang, X.; Zhang, Y.; Wu, G. Simulation of gas flow in nano-scale pores of shale gas deposits. J. Southwest Petrol. Univ. 2015, 37, 63–68. [Google Scholar]
- Davarpanah, A.; Mirshekari, B. Experimental Investigation and Mathematical Modeling of Gas Diffusivity by Carbon Dioxide and Methane Kinetic Adsorption. Ind. Eng. Chem. Res. 2019, 58, 12392–12400. [Google Scholar] [CrossRef]
- Rasmussen, T.C.; Jim-Yeh, T.C.; Evans, D.D. Effect of variable Fracture Permeability/Matrix Permeability Ratios on Three-Dimensional Fractured Rock Hydraulic Conductivity. 1989. pp. 337–358. Available online: https://eurekamag.com/research/018/362/018362917.php (accessed on 23 March 2021).
- Lough, M.F.; Lee, S.H.; Kamath, J. An Efficient Boundary Integral Formulation for Flow Through Fractured Porous Media. J. Comput. Phys. 1998, 143, 462–483. [Google Scholar] [CrossRef]
- Lee, S.H.; Lough, M.F.; Jensen, C.L. Hierarchical modeling of flow in naturally fractured formations with multiple length scales. Water Resour. Res. 2001, 37, 443–455. [Google Scholar] [CrossRef]
- Neuman, S.P. Multiscale Relationships Between Fracture Length, Aperture, Density and Permeability. Geophys Res. Lett. 2015, 35, 1092–1104. [Google Scholar] [CrossRef]
- Bai, M.; Ma, Q.; Roegiers, J.C. Dual-porosity behaviour of naturally fractured reservoirs. Int. J. Numer. Anal. Met. 2010, 18, 359–376. [Google Scholar] [CrossRef]
- Cai, L.; Ding, D.Y.; Wang, C.; Wu, Y.S. Accurate and Efficient Simulation of Fracture–Matrix Interaction in Shale Gas Reservoirs. Transp. Porous Med. 2015, 107, 305–320. [Google Scholar] [CrossRef]
- Wang, W.; Wei, Y.; Hu, X.; Hua, L.; Wu, B. A Semi-analytical Model for Simulating Real Gas Transport in Nanopores and Complex Fractures of Shale Gas Reservoirs. AIChE J. 2017, 64, 326–337. [Google Scholar] [CrossRef]
- Abbasi, M.; Madani, M.; Sharifi, M.; Kazemi, A. Fluid flow in fractured reservoirs: Exact analytical solution for transient dual porosity model with variable rock matrix block size. J. Petrol. Sci. Eng. 2018, 164, 571–583. [Google Scholar] [CrossRef]
- Rahman, M.M.; Rahman, S.S. Studies of Hydraulic Fracture-Propagation Behavior in Presence of Natural Fractures: Fully Coupled Fractured-Reservoir Modeling in Poroelastic Environments. Int. J. Geomech. 2013, 13, 809–826. [Google Scholar] [CrossRef]
- Matthäi, S.K.; Belayneh, M. Fluid flow partitioning between fractures and a permeable rock matrix. Geophys Res. Lett. 2004, 31, 7. [Google Scholar] [CrossRef]
- Sanaee, R.; Oluyemi, G.F.; Hossain, M.; Oyeneyin, M.B. Fracture-Matrix Flow Partitioning and Cross Flow: Numerical Modeling of Laboratory Fractured Core Flood. In Proceedings of the 2012 COMSOL Conference, Milan, Italy, 10–12 October 2012. [Google Scholar]
- Lei, Q.; Wang, X.; Min, K.-B.; Rutqvist, J. Interactive roles of geometrical distribution and geomechanical deformation of fracture networks in fluid flow through fractured geological media. J. Rock Mech. Geotech. Eng. 2020, 12, 780–792. [Google Scholar] [CrossRef]
- Wong, D.L.Y.; Doster, F.; Geiger, S.; Kamp, A. Partitioning Thresholds in Hybrid Implicit-Explicit Representations of Naturally Fractured Reservoirs. Water Resour. Res. 2020, 56, e2019WR025774. [Google Scholar] [CrossRef]
- Jia, C. Characteristics of a Superimposed Basin and the Promise of a Buried Petroleum Play. In Characteristics of Chinese Petroleum Geology; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Karpyn, Z.T.; Alajmi, A.; Radaelli, F.; Halleck, P.M.; Grader, A.S. X-ray CT and hydraulic evidence for a relationship between fracture conductivity and adjacent matrix porosity. Eng. Geol. 2009, 103, 139–145. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, Y.; Zhao, Y. Progress in the Application of AE and CT in Research of Coal and Rock Fracture Propagation. Met. Mine 2008, 5, 63–66. [Google Scholar]
- Kock, T.D.; Boone, M.A.; Schryver, T.D.; Stappen, J.V.; Derluyn, H.; Masschaele, B.; Schutter, G.D.; Cnudde, V. A Pore-Scale Study of Fracture Dynamics in Rock Using X-ray Micro-CT Under Ambient Freeze–Thaw Cycling. Environ. Sci. Technol. 2015, 49, 2867–2874. [Google Scholar] [CrossRef] [PubMed]
- Ya, L.I.; Jie, Y.U.; Man, X.U.; Hui, W.U. SEM Study on Fracture Characteristic of Mineralized wall Rock Samples of Nannigou Gold Deposit in Guizhou under High Temperature and High Pressure. Bull. Miner. Petrol. Geochem. 2000, 39, 5271–5276. [Google Scholar]
- Neupane, B.; Ju, Y.; Huang, C. Micro/Nano-Pore Structure Characterization of Western and Central Nepal Coals Using Scanning Electron Microscopy and Gas Adsorption. J. Nanosci. Nanotechnol. 2017, 17, 1–7. [Google Scholar] [CrossRef]
- Yang, H.E.; Li, K.; Chai, J. Numerical Analysis of Unsteady Seepage Through Fracture Network in Rock Mass Simulated by the Monte-Carlo Method. J. Basic Sci. Eng. 2005, 13, 81–86. [Google Scholar]
- Canals, M.; Ayt Ougougdal, M. Percolation on anisotropic media, the Bethe lattice revisited. Application to fracture networks. Nonlinear Proc. Geoph. 1997, 4, 11–18. [Google Scholar] [CrossRef][Green Version]
- Sisavath, S.; Mourzenko, V.; Genthon, P.; Thovert, J.F.; Adler, P.M. Geometry, percolation and transport properties of fracture networks derived from line data. Geophys J. Int. 2004, 157, 917–934. [Google Scholar] [CrossRef]
- Reuschlé, T.; Darot, M.; Gueguen, Y. Mechanical and transport properties of crustal rocks: From single cracks to crack statistics. Phys. Earth Planet Inter. 1989, 55, 353–360. [Google Scholar] [CrossRef]
- Mo, H.; Bai, M.; Lin, D.; Roegiers, J.C. Study of flow and transport in fracture network using percolation theory. Appl. Math. Model 1998, 22, 277–291. [Google Scholar] [CrossRef]
- Rivard, C.; Delay, F. Simulations of solute transport in fractured porous media using 2D percolation networks with uncorrelated hydraulic conductivity fields. Hydrogeol. J. 2004, 12, 613–627. [Google Scholar] [CrossRef]
- Pardo, Y.A.; Donado, L.D. Optimization of flow modeling in fractured media with discrete fracture network via percolation theory. In Proceedings of the Agu Fall Meeting, San Francisco, CA, USA, 9–13 December 2013. [Google Scholar]
- Bagalkot, N.; Kumar, G.S. Effect of random fracture aperture on the transport of colloids in a coupled fracture-matrix system. Geosci. J. 2016, 21, 1–15. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Oldenburg, C.M.; Finsterle, S. Percolation-theory and fuzzy rule-based probability estimation of fault leakage at geologic carbon sequestration sites. Environ. Earth Sci. 2010, 59, 1447–1459. [Google Scholar] [CrossRef]
- Gudmundsson, A. Geometry, formation and development of tectonic fractures on the Reykjanes Peninsula, southwest Iceland. Tectonophysics 1987, 139, 295–308. [Google Scholar] [CrossRef]
- Scholz, C.H.; Cowie, P.A. Determination of total strain from faulting using slip measurements. Nature 1990, 346, 837–839. [Google Scholar] [CrossRef]
- Segall, P.; Pollard, D.D. Joint formation in granitic rock of the Sierra Nevada. Bull. Geol. Soc. Am. 1983, 94, 1005–1008. [Google Scholar] [CrossRef]
- Dreuzy, J.-R.d.; Davy, P.; Bour, O. Hydraulic properties of two-dimensional random fracture networks following a power law length distribution 1. Effective connectivity. Water Resour. Res. 2001, 37, 2079–2096. [Google Scholar] [CrossRef]
- Mourzenko, V.V.; Thovert, J.F.; Adler, P.M. Percolation of three-dimensional fracture networks with power-law size distribution. Phys. Rev. E 2005, 72, 066307. [Google Scholar] [CrossRef]
- Khamforoush, M.; Shams, K.; Thovert, J.F.; Adler, P.M. Permeability and percolation of anisotropic three-dimensional fracture networks. Phys. Rev. E 2008, 77, 056307. [Google Scholar] [CrossRef]
- Liu, D.M.; Yao, Y.B.; Cai, Y.D.; Zhang, B.R.; Zhang, K.M.; Li, J.Q. Characteristics of Porosity and Permeability and Their Geological Control of Permo-Carboniferous Coals in North China. Geoscience 2010, 24, 1198–1203. [Google Scholar]
- Boaca, T.; Malureanu, I. Determination of oil reservoir permeability and porosity from resistivity measurement using an analytical model. J. Petrol. Sci. Eng. 2017, 157, 884–893. [Google Scholar] [CrossRef]
- Youssef, A.A.; Awotunde, A.A. Modelling fluid flow in karst reservoirs using Darcy Model with estimated permeability distribution. Comput. Geosci. 2019, 133, 104311. [Google Scholar] [CrossRef]
- Tiab, D.; Donaldson, E.C. Experiment 11—Verification of the Klinkenberg Effect. Petrophys 2004, 822–825. [Google Scholar] [CrossRef]
- Tanikawa, W.; Shimamoto, T. Comparison of Klinkenberg-corrected gas permeability and water permeability in sedimentary rocks. Int. J. Rock Mech. Min. Sci. 2009, 46, 229–238. [Google Scholar] [CrossRef]
- Dong, J.; Hsu, J.; Wu, W.; Shimamoto, T.; Hung, J. Stress-dependence of the permeability and porosity of sandstone and shale from TCDP Hole-A. Int. J. Rock Mech. Min. Sci. 2010, 47, 1141–1157. [Google Scholar] [CrossRef]
- Konecny, P.; Kozusnikova, A. Influence of stress on the permeability of coal and sedimentary rocks of the Upper Silesian basin. Int. J. Rock Mech. Min. Sci. 2011, 48, 347–352. [Google Scholar] [CrossRef]
- Wang, Z.; Rutqvist, J.; Zuo, J.; Dai, Y. A modified equivalent permeability model of fracture element and its verification. Chin. J. Rock Mech. Eng. 2013, 32, 728–733. (In Chinese) [Google Scholar]
- Mckenna, S.A.; Reeves, P.C. Fractured Continuum Approach to Stochastic Permeability Modeling. AAPG Spec. Vol. 2006. [Google Scholar] [CrossRef]
- Svensson, U. A continuum representation of fracture networks. Part I: Method and basic test cases. J. Hydrol. 2001, 250, 170–186. [Google Scholar] [CrossRef]
- Maria, A.; Keller, A.A. Pore scale processes that control dispersion of colloids in saturated porous media. Water Resour. Res. 2004, 40, 114–125. [Google Scholar] [CrossRef]
- Chang, C.; Ju, Y.; Xie, H.; Zhou, Q.; Gao, F. Non-Darcy interfacial dynamics of air-water two-phase flow in rough fractures under drainage conditions. Sci. Rep. 2017, 7, 4570. [Google Scholar] [CrossRef] [PubMed]

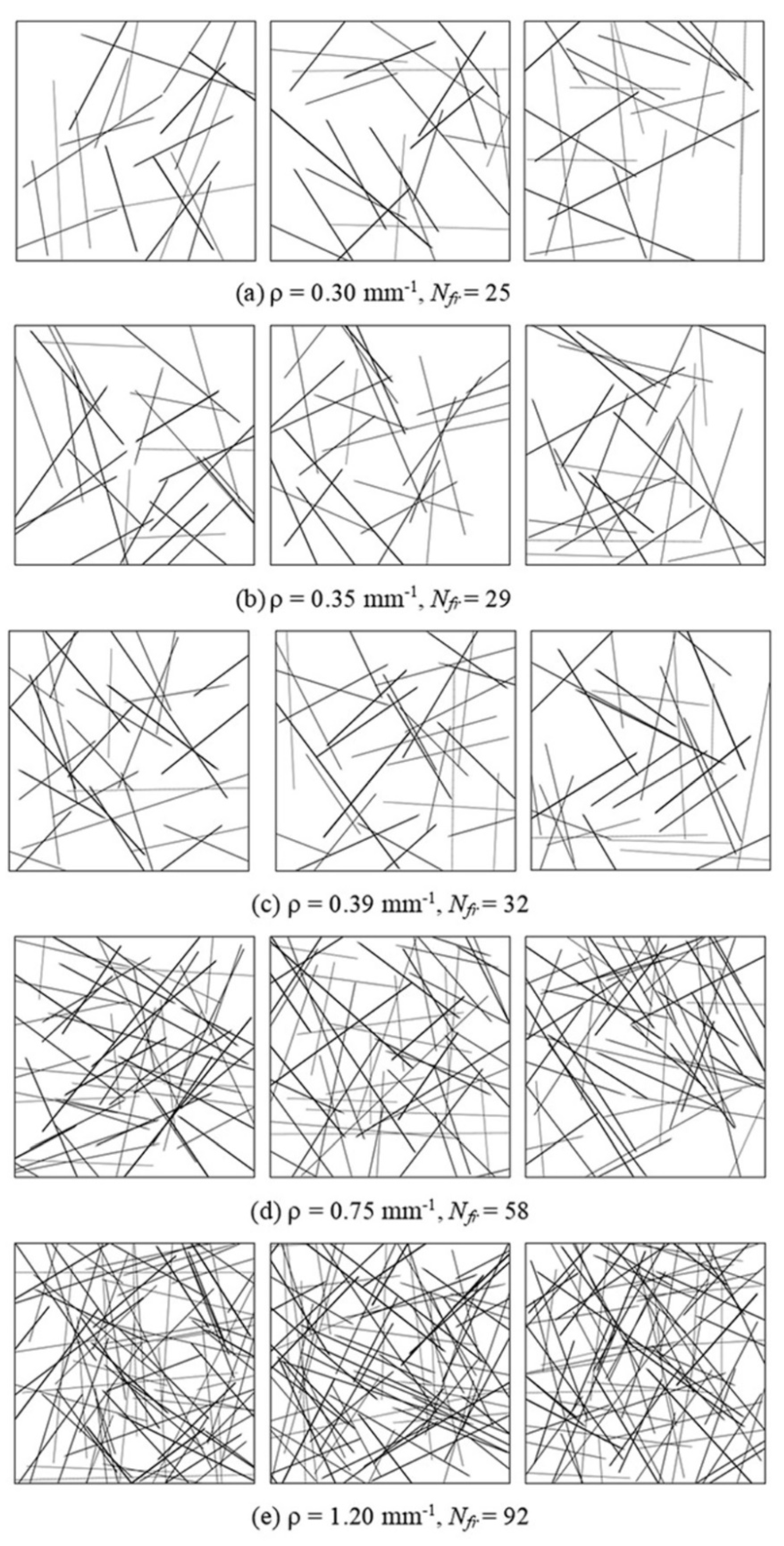




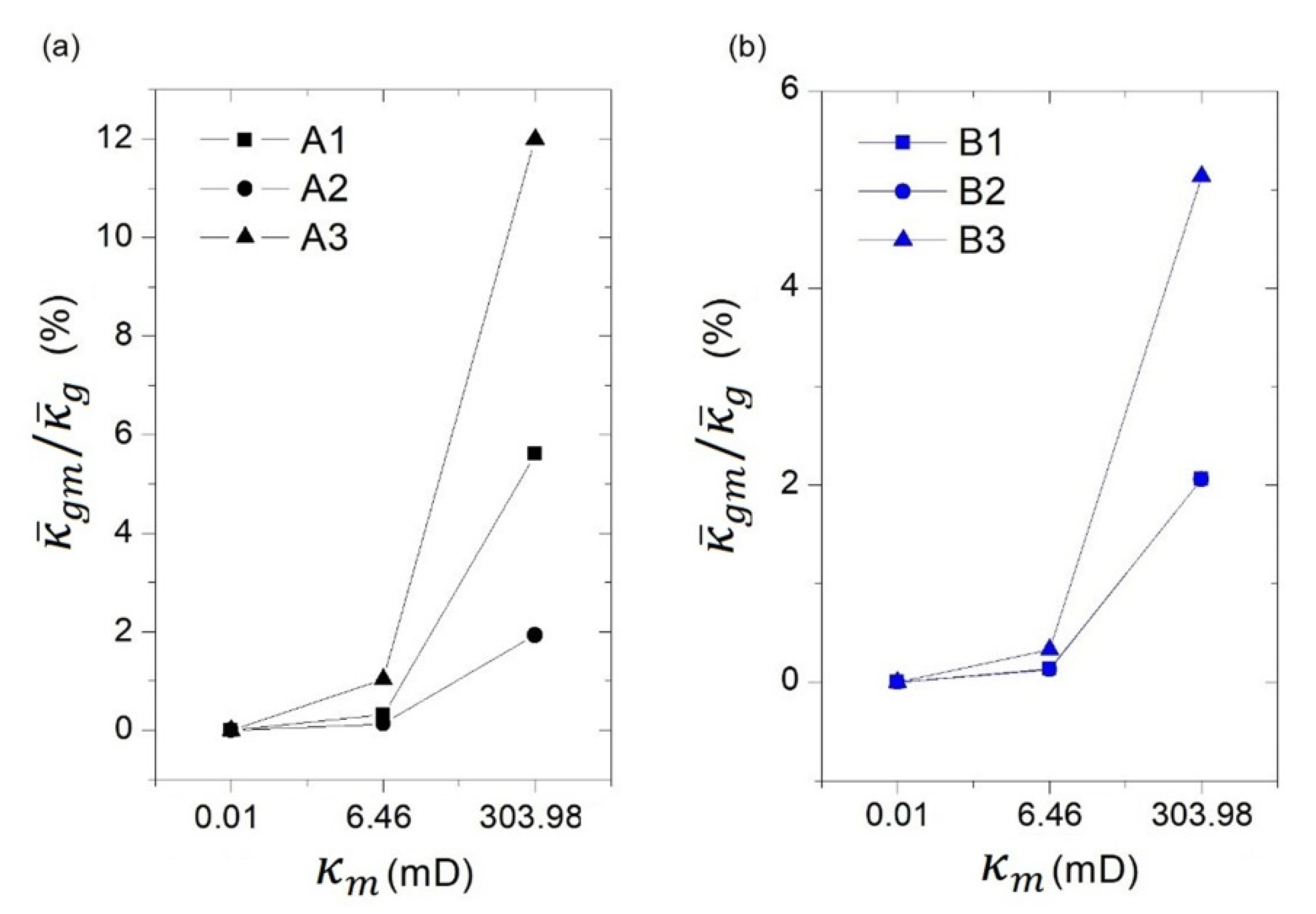

| Model No. | r | lmax | lmin | Nfr | (mm−1) | Fracture Aperture (mm) | |||
|---|---|---|---|---|---|---|---|---|---|
| wav | σ | wmin | wmax | ||||||
| A1 | 1.1 | 55.29 | 20 | 25 | 0.30 | 0.284 | 0.1 | 0.07 | 0.57 |
| A2 | 0.03 | 0.47 | |||||||
| A3 | 0.07 | 0.51 | |||||||
| B1 | 1.3 | 56.84 | 29 | 0.35 | 0.08 | 0.58 | |||
| B2 | 0.09 | 0.42 | |||||||
| B3 | 0.08 | 0.45 | |||||||
| C1 | 1.5 | 58.89 | 32 | 0.39 | 0.08 | 0.46 | |||
| C2 | 0.10 | 0.50 | |||||||
| C3 | 0.09 | 0.56 | |||||||
| D1 | 3.2 | 66.00 | 58 | 0.75 | 0.05 | 0.51 | |||
| D2 | 0.03 | 0.47 | |||||||
| D3 | 0.04 | 0.49 | |||||||
| E1 | 5.1 | 67.3 | 92 | 1.20 | 0.08 | 0.48 | |||
| E2 | 0.04 | 0.52 | |||||||
| E3 | 0.04 | 0.55 | |||||||
| Parameters | Value | Description |
|---|---|---|
| 0.67 kg/m3 | Methane density | |
| μ | 1.1 × 10−5 (Pa·s) | Methane dynamic viscosity |
| H | 50 mm | Hydraulic head |
| Fracture Azimuth (º) | |||
|---|---|---|---|
| Analytical Solutions | Numerical Simulation | Deviation (%) | |
| 50 | 0.0793 | 0.0826 | 4.16 |
| 55 | 0.0848 | 0.0848 | 0.00 |
| 60 | 0.0896 | 0.0882 | −1.56 |
| 65 | 0.0938 | 0.0928 | −1.07 |
| 70 | 0.0972 | 0.0937 | −3.60 |
| 75 | 0.0999 | 0.0997 | −0.20 |
| 80 | 0.1019 | 0.1002 | −1.67 |
| 85 | 0.1031 | 0.1008 | −2.23 |
| 90 | 0.1035 | 0.1010 | −2.42 |
| No. | Endpoint Coordinates (x, y) | Endpoint Coordinates (x, y) | Fracture Aperture (m) | ||
|---|---|---|---|---|---|
| Analytical Solutions | Numerical Simulation | ||||
| 1 | (0.7500, −10.0) | (−0.2500, 10.0) | 0.004 | 0.1426 | 0.1417 |
| 2 | (−2.8750, 5.0) | (−5.7500, 10.0) | 0.005 | ||
| 3 | (1.4375, −2.5) | (−2.8750, 5.0) | 0.005 | ||
| 4 | (5.7500, −10.0) | (1.4375, −2.5) | 0.005 | ||
| Fracture Azimuth (º) | |||
|---|---|---|---|
| MEPM Solutions | Numerical Simulation | Deviation (%) | |
| 50 | 0.0811 | 0.0826 | 1.85 |
| 55 | 0.0868 | 0.0848 | −2.30 |
| 60 | 0.0919 | 0.0882 | −4.03 |
| 65 | 0.0964 | 0.0928 | −3.73 |
| 70 | 0.1000 | 0.0937 | −6.30 |
| 75 | 0.0984 | 0.0997 | 1.32 |
| 80 | 0.1002 | 0.1002 | 0.00 |
| 85 | 0.1011 | 0.1008 | −0.30 |
| 90 | 0.1040 | 0.1010 | −2.88 |
| Fracture Density ρ (mm−1) | Equivalent Gas Permeability | Total Porosity εp | ||||
|---|---|---|---|---|---|---|
| Irock | II rock | IIIrock | Irock | II rock | IIIrock | |
| 0.30 | 24.91 | 24.96 | 26.53 | 0.081 | 0.138 | 0.282 |
| 0.35 | 30.96 | 31.00 | 32.65 | 0.088 | 0.145 | 0.287 |
| 0.39 | 71.13 | 71.17 | 72.75 | 0.094 | 0.151 | 0.292 |
| 0.75 | 133.01 | 133.03 | 134.08 | 0.140 | 0.194 | 0.328 |
| 1.20 | 242.35 | 242.6 | 242.97 | 0.190 | 0.239 | 0.366 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhou, Y.; Chen, J. A Two-Dimensional Partitioning of Fracture–Matrix Flow in Fractured Reservoir Rock Using a Dual-Porosity Percolation Model. Energies 2021, 14, 2209. https://doi.org/10.3390/en14082209
Liu J, Zhou Y, Chen J. A Two-Dimensional Partitioning of Fracture–Matrix Flow in Fractured Reservoir Rock Using a Dual-Porosity Percolation Model. Energies. 2021; 14(8):2209. https://doi.org/10.3390/en14082209
Chicago/Turabian StyleLiu, Jinhui, Yuli Zhou, and Jianguo Chen. 2021. "A Two-Dimensional Partitioning of Fracture–Matrix Flow in Fractured Reservoir Rock Using a Dual-Porosity Percolation Model" Energies 14, no. 8: 2209. https://doi.org/10.3390/en14082209
APA StyleLiu, J., Zhou, Y., & Chen, J. (2021). A Two-Dimensional Partitioning of Fracture–Matrix Flow in Fractured Reservoir Rock Using a Dual-Porosity Percolation Model. Energies, 14(8), 2209. https://doi.org/10.3390/en14082209





