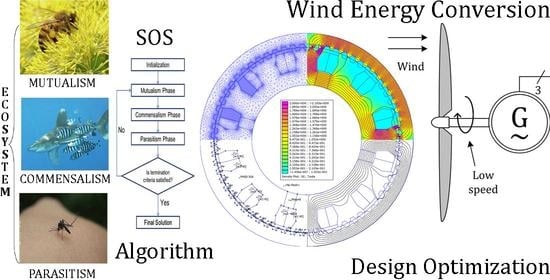
Design Optimization of Outer Rotor Toothed Doubly Salient Permanent Magnet Generator Using Symbiotic Organisms Search Algorithm
Abstract
1. Introduction
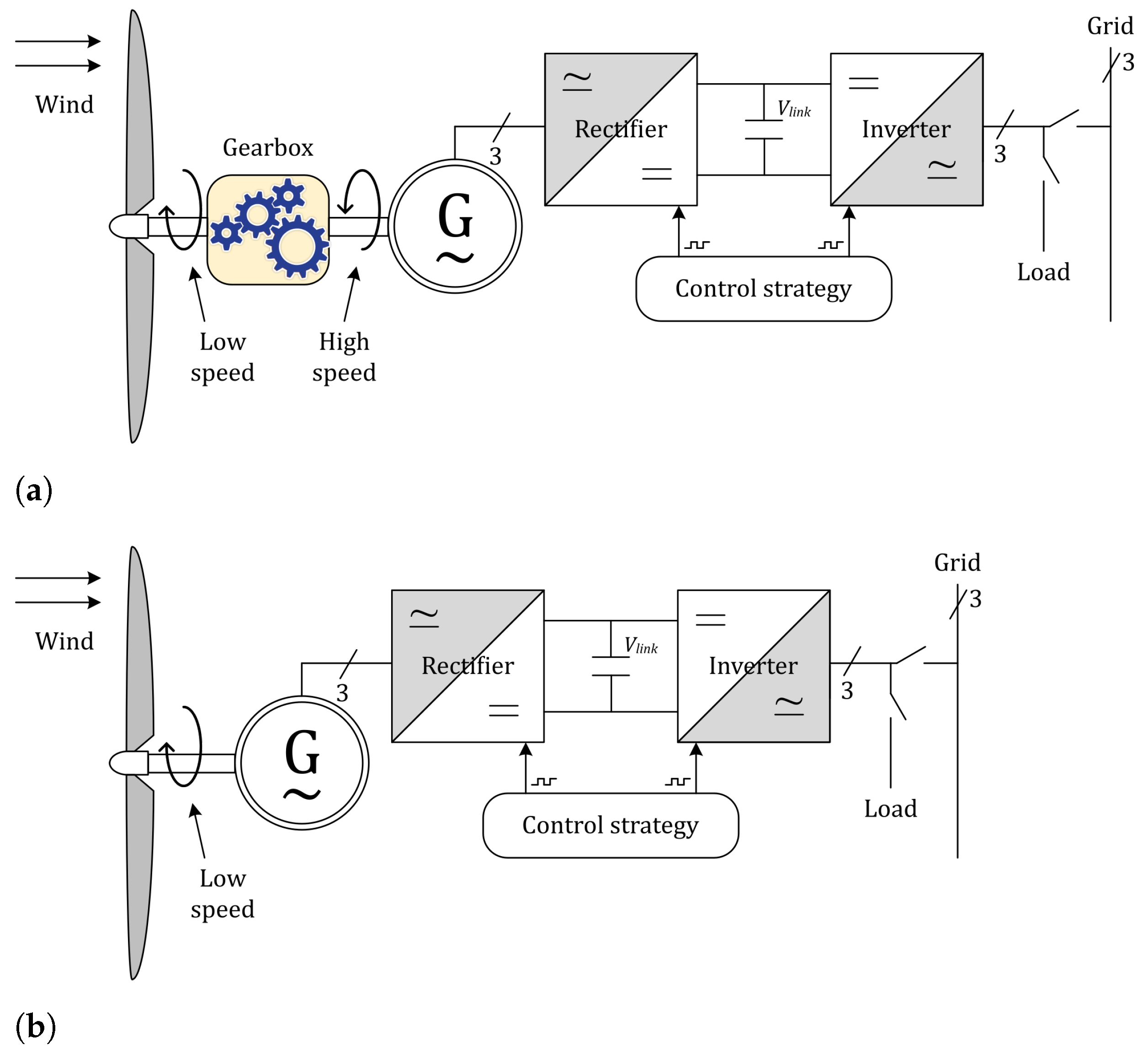
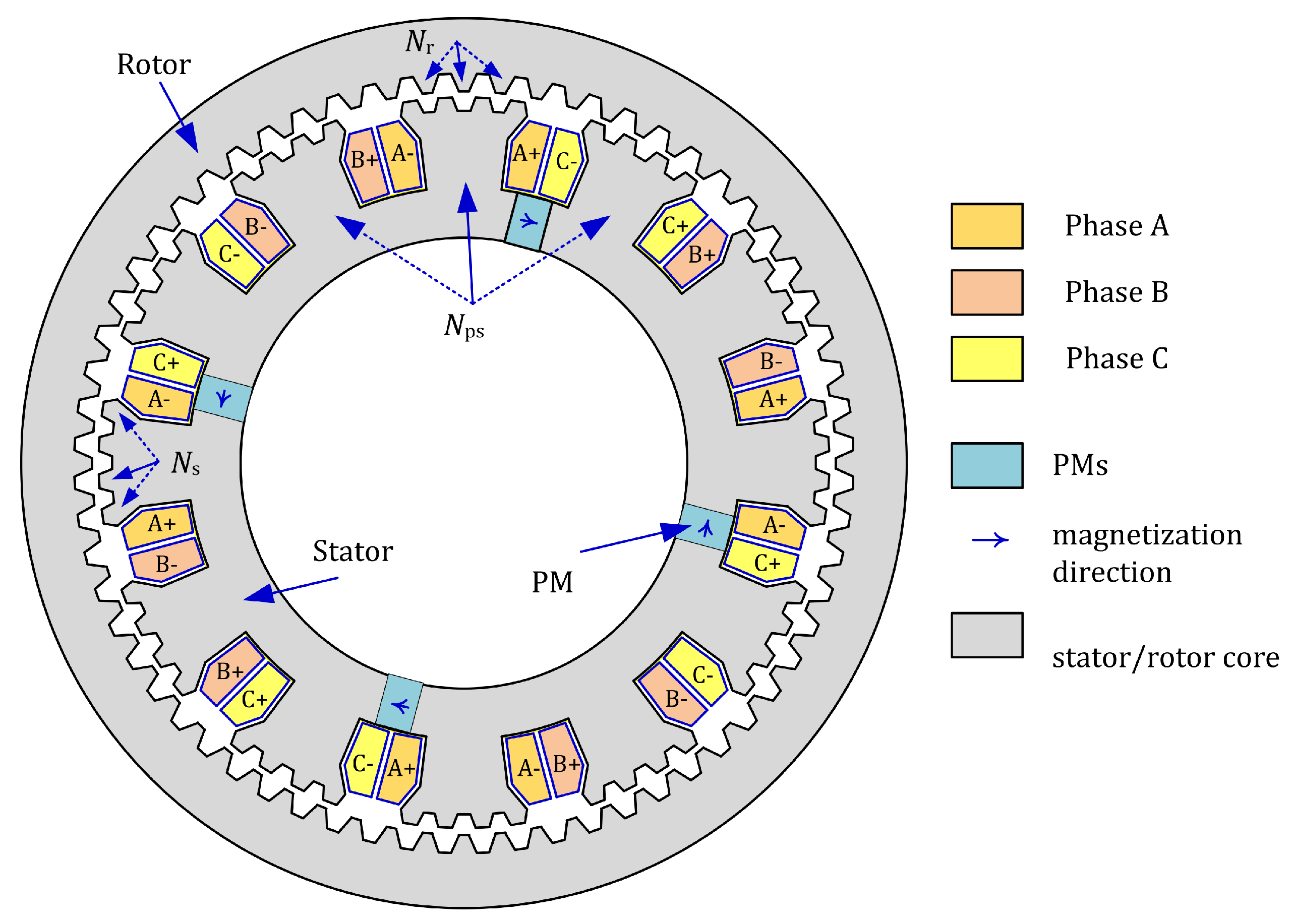
2. Toothed Poles ORDSPMG Topology Description and Operational Characteristics
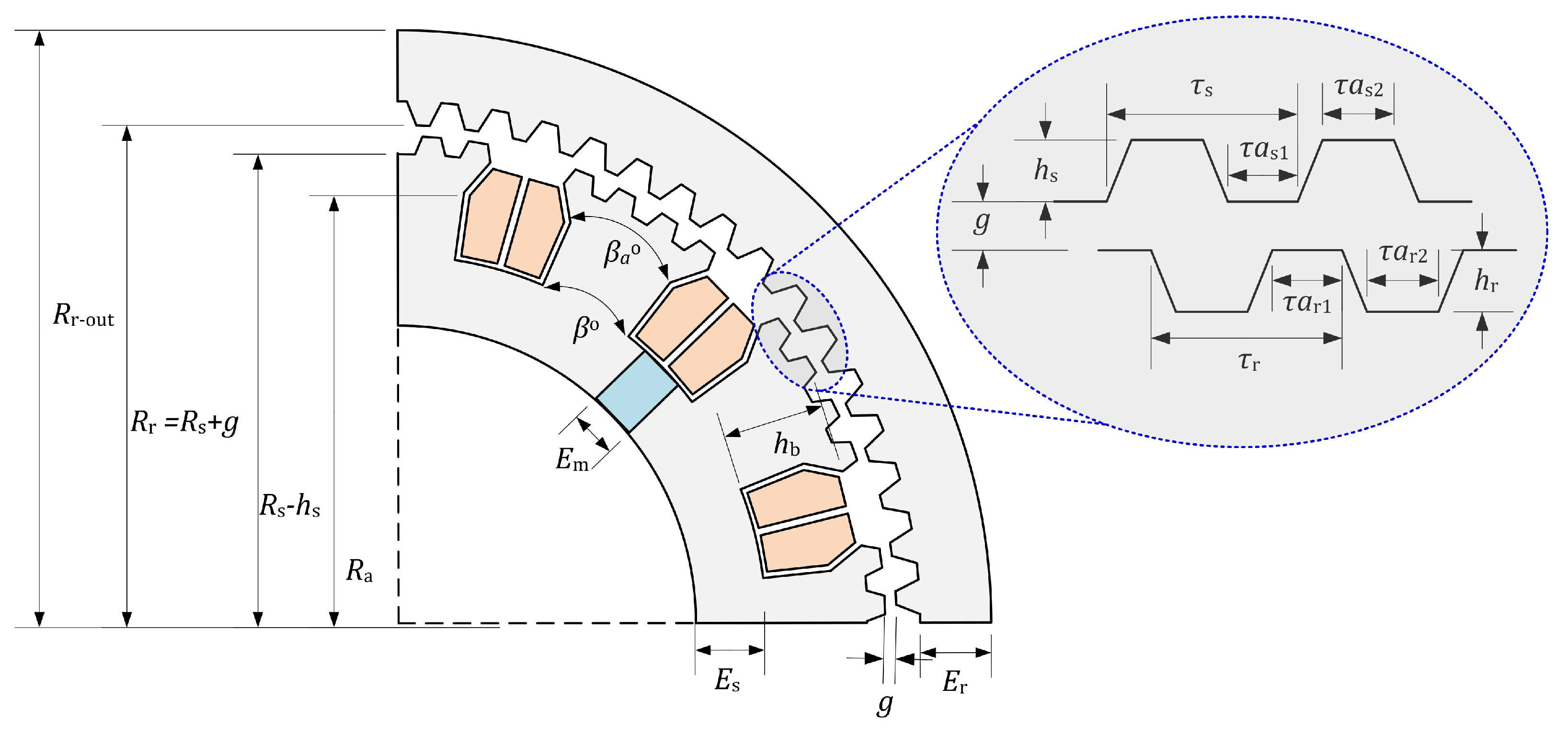
2.1. Constructional Details
- The rotor and stator teeth depth and ;
- The teeth cyclic ratios , , , and .
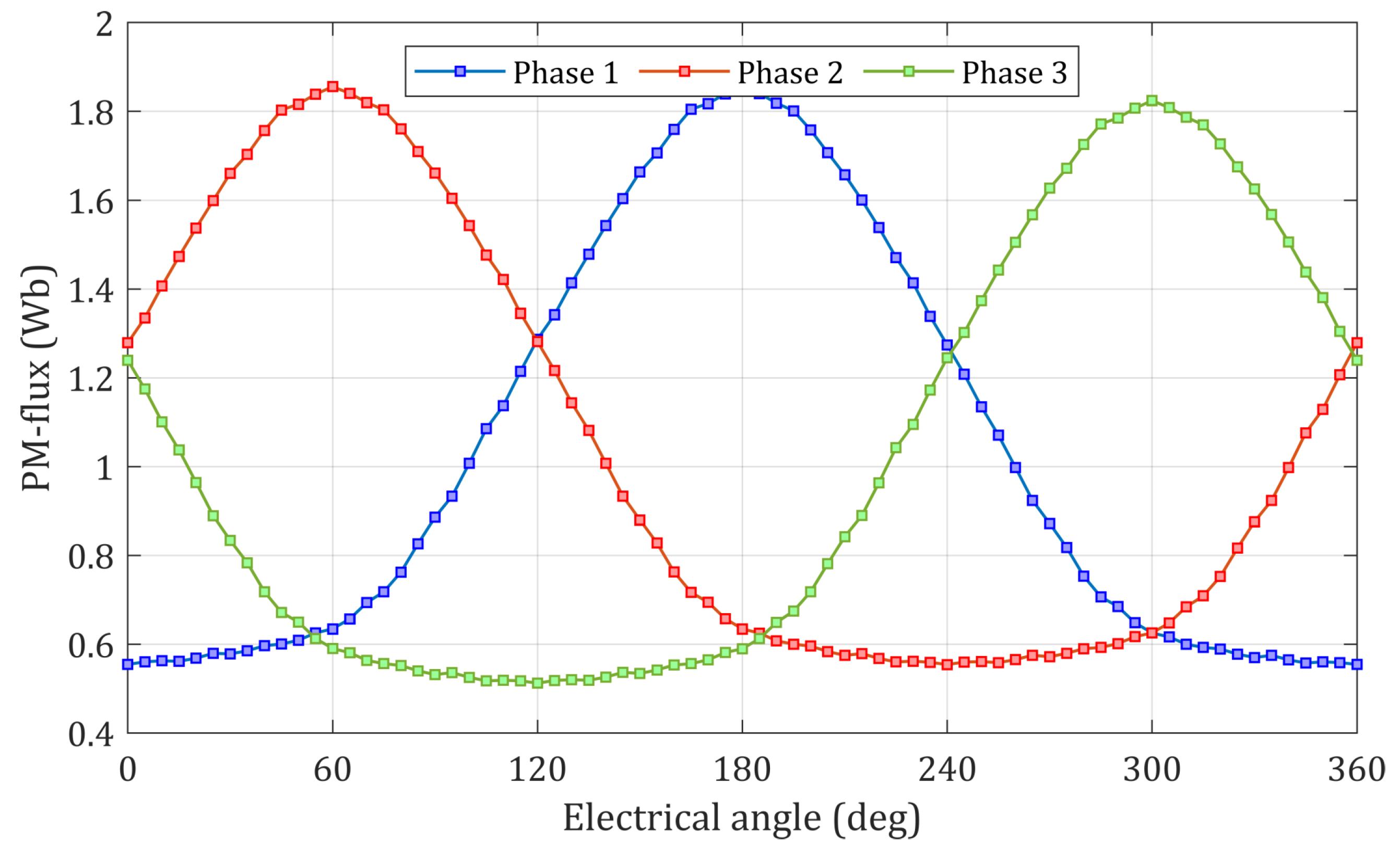
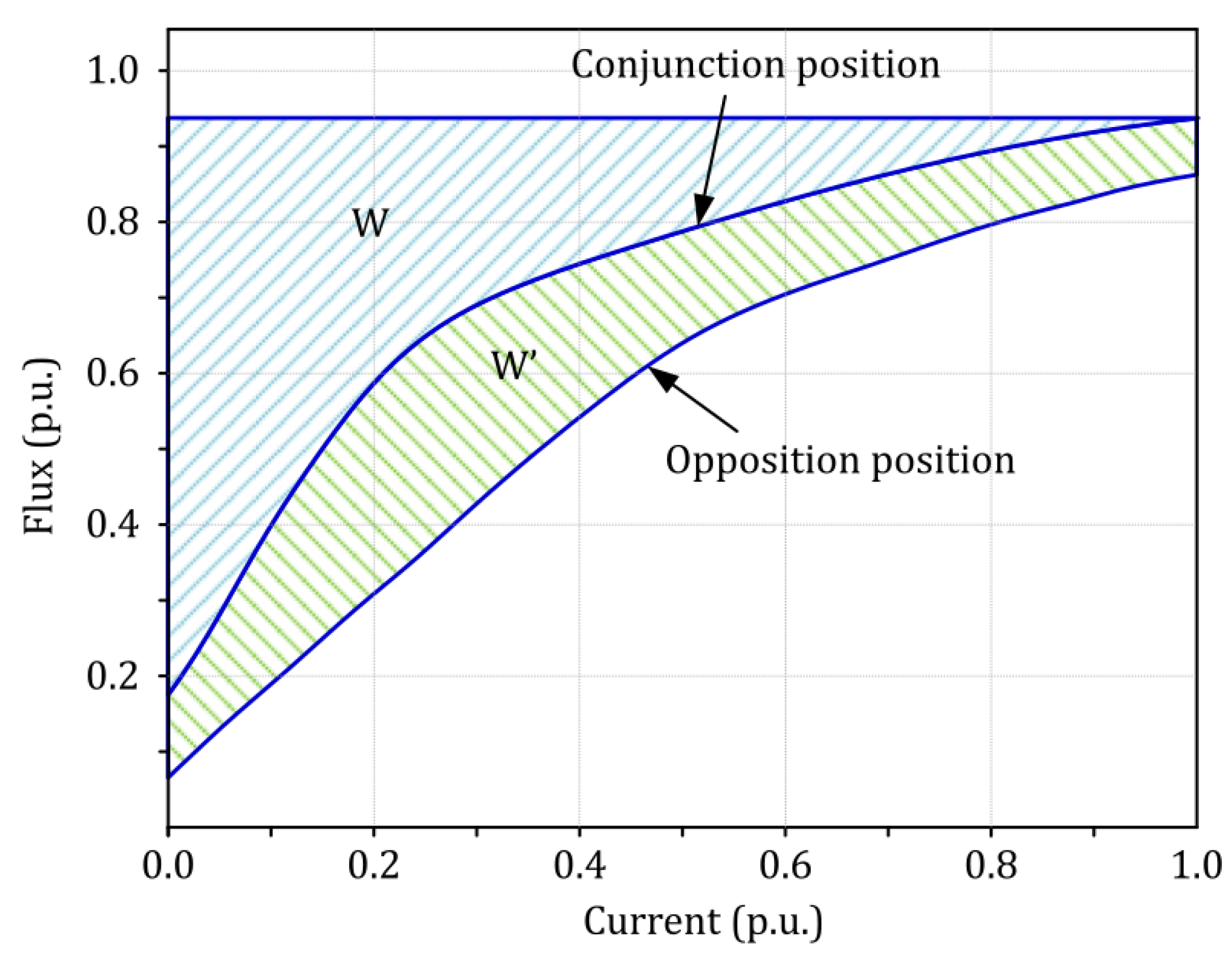
2.2. Operation Principle
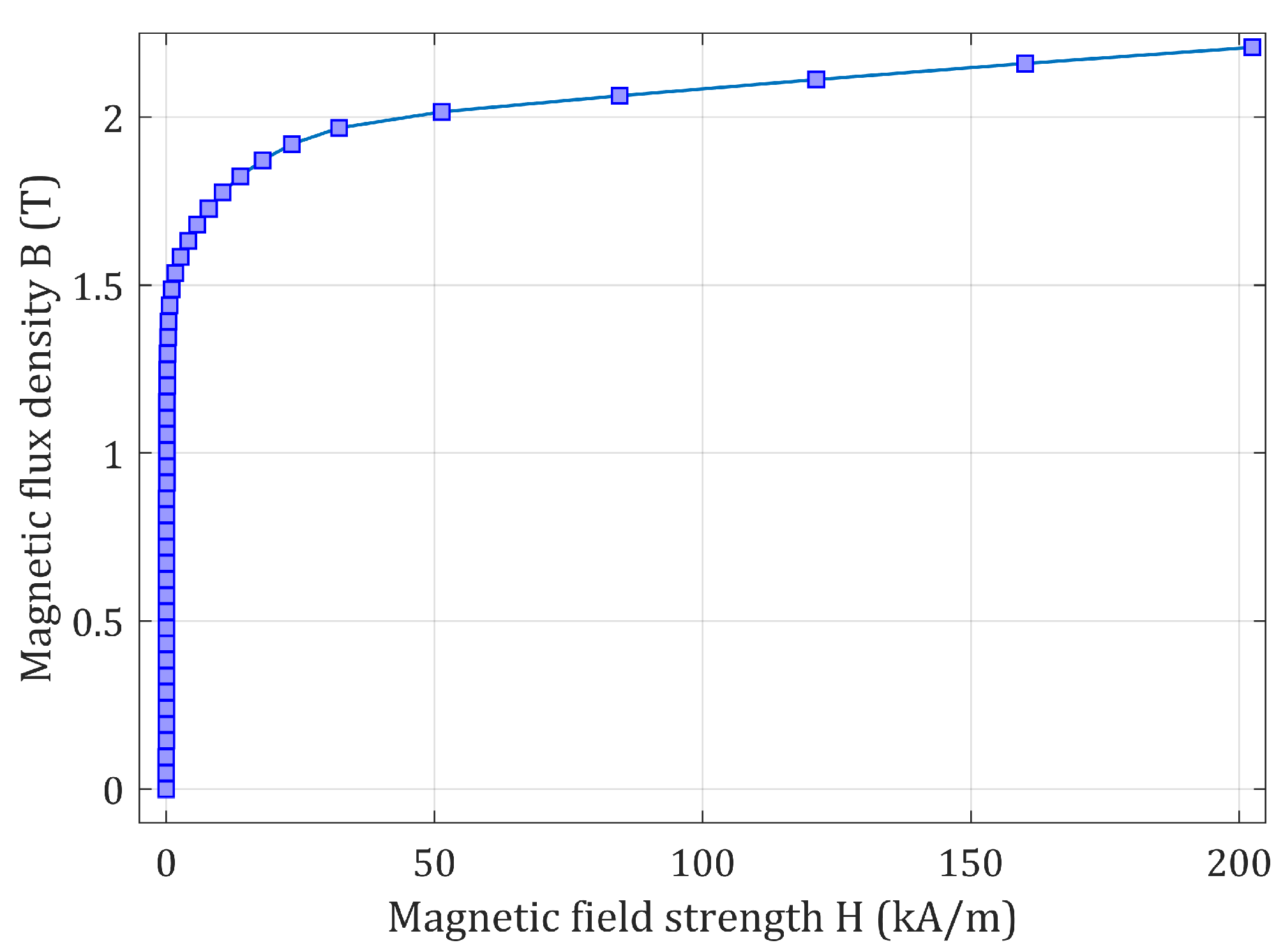
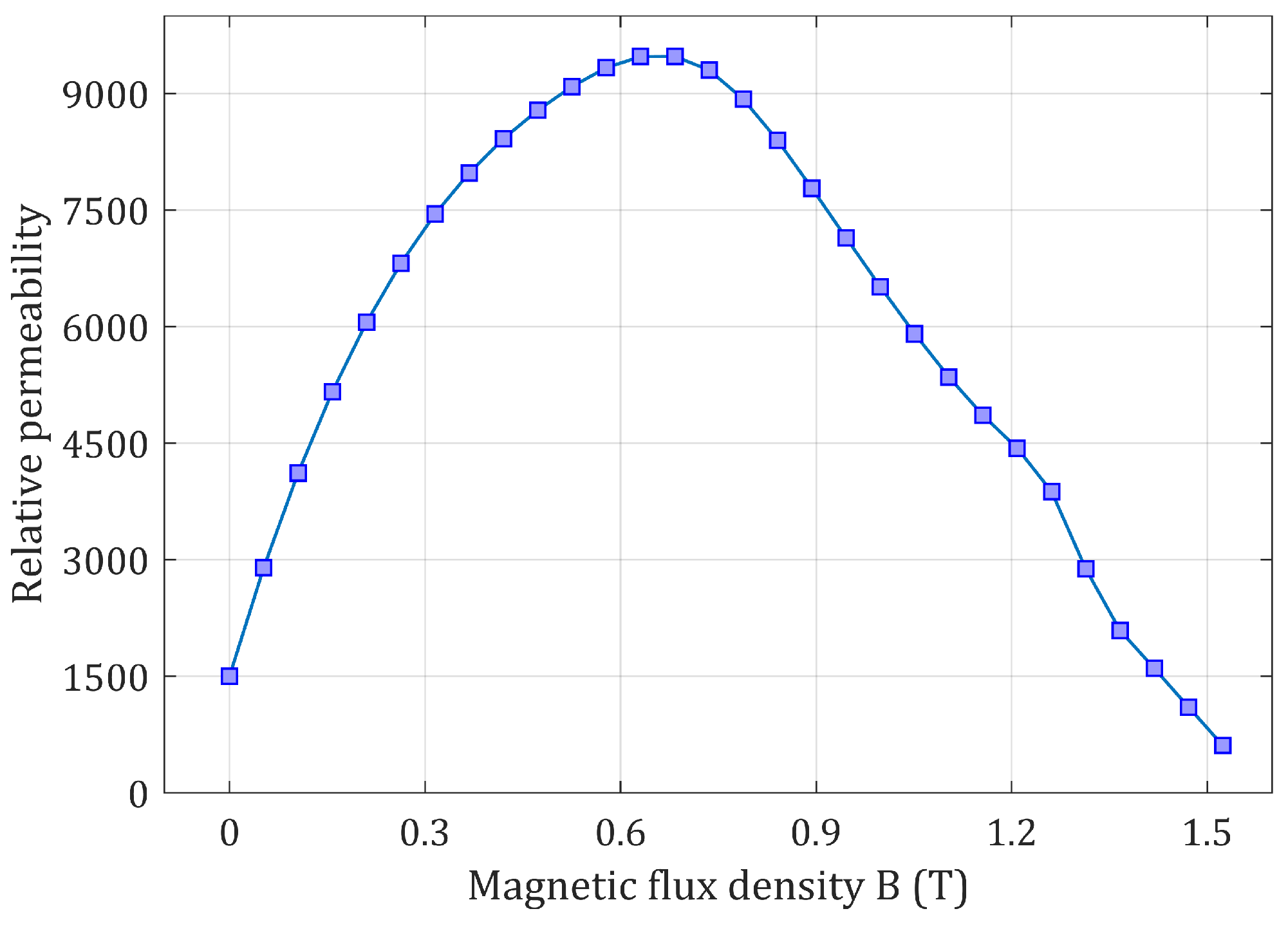
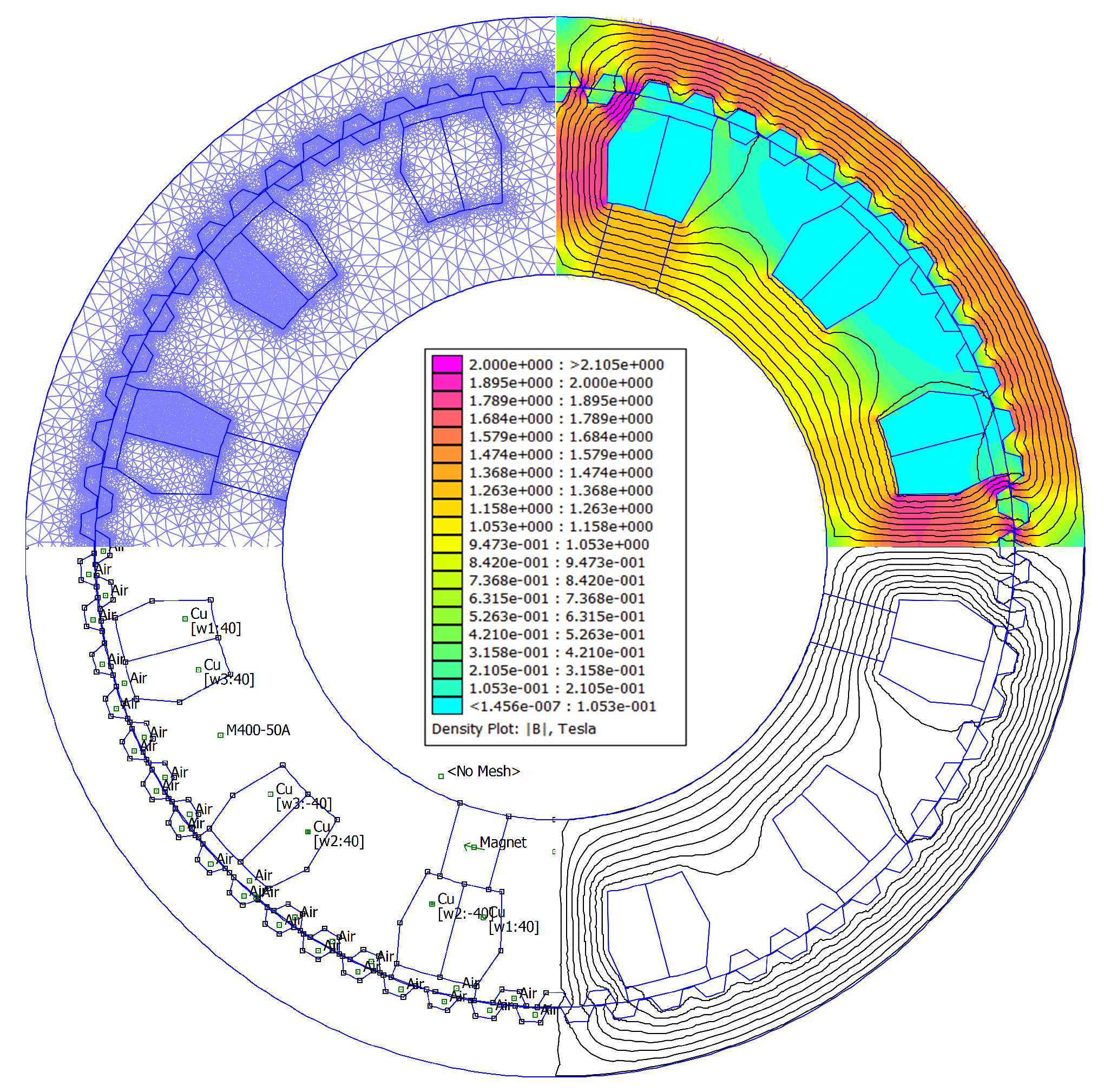
3. Analysis of Important Aspects in ORDSPMG Design
3.1. Design Model Development and Constraints
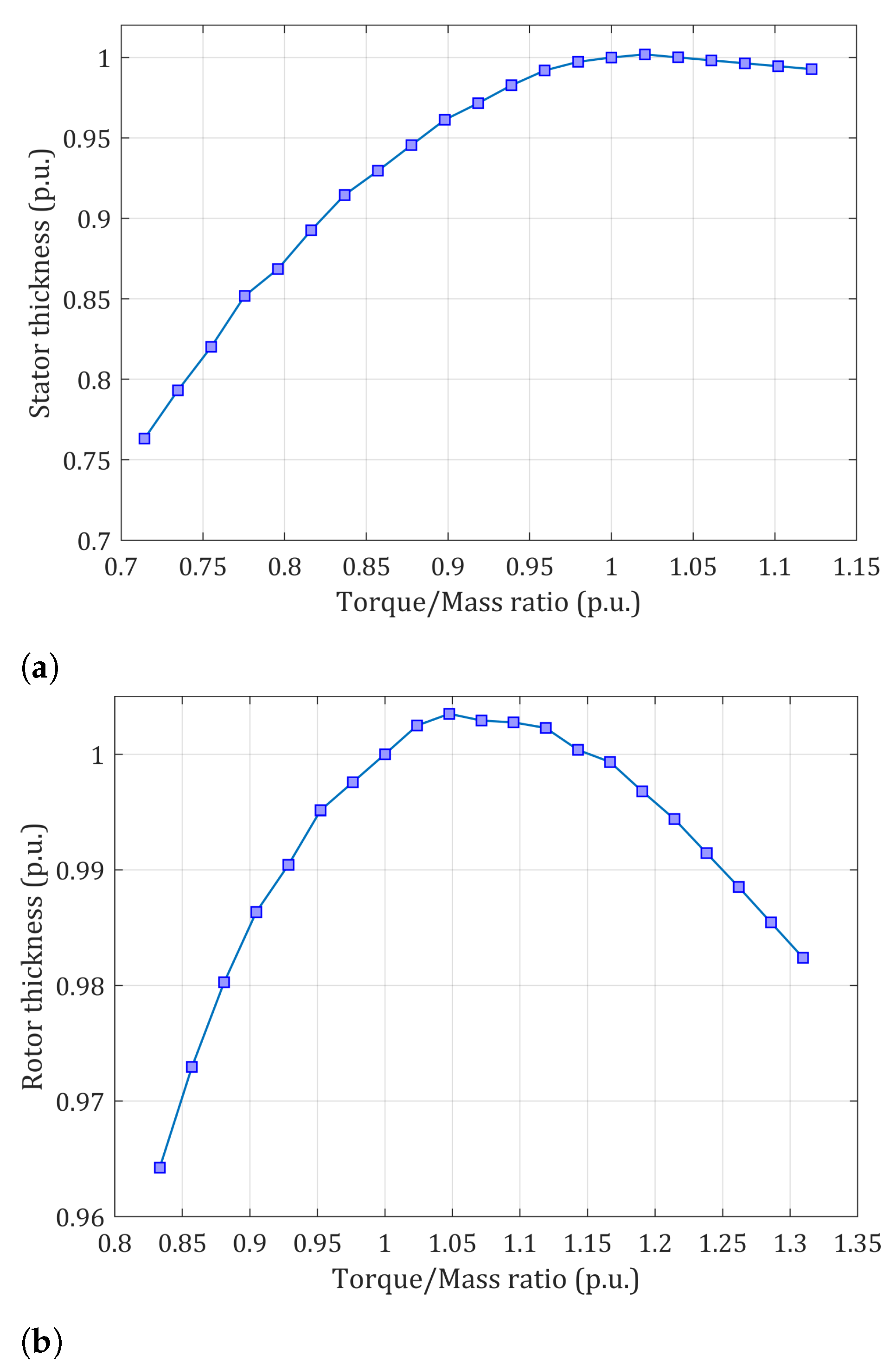
3.2. Stator and Rotor Yokes Thickness Impact
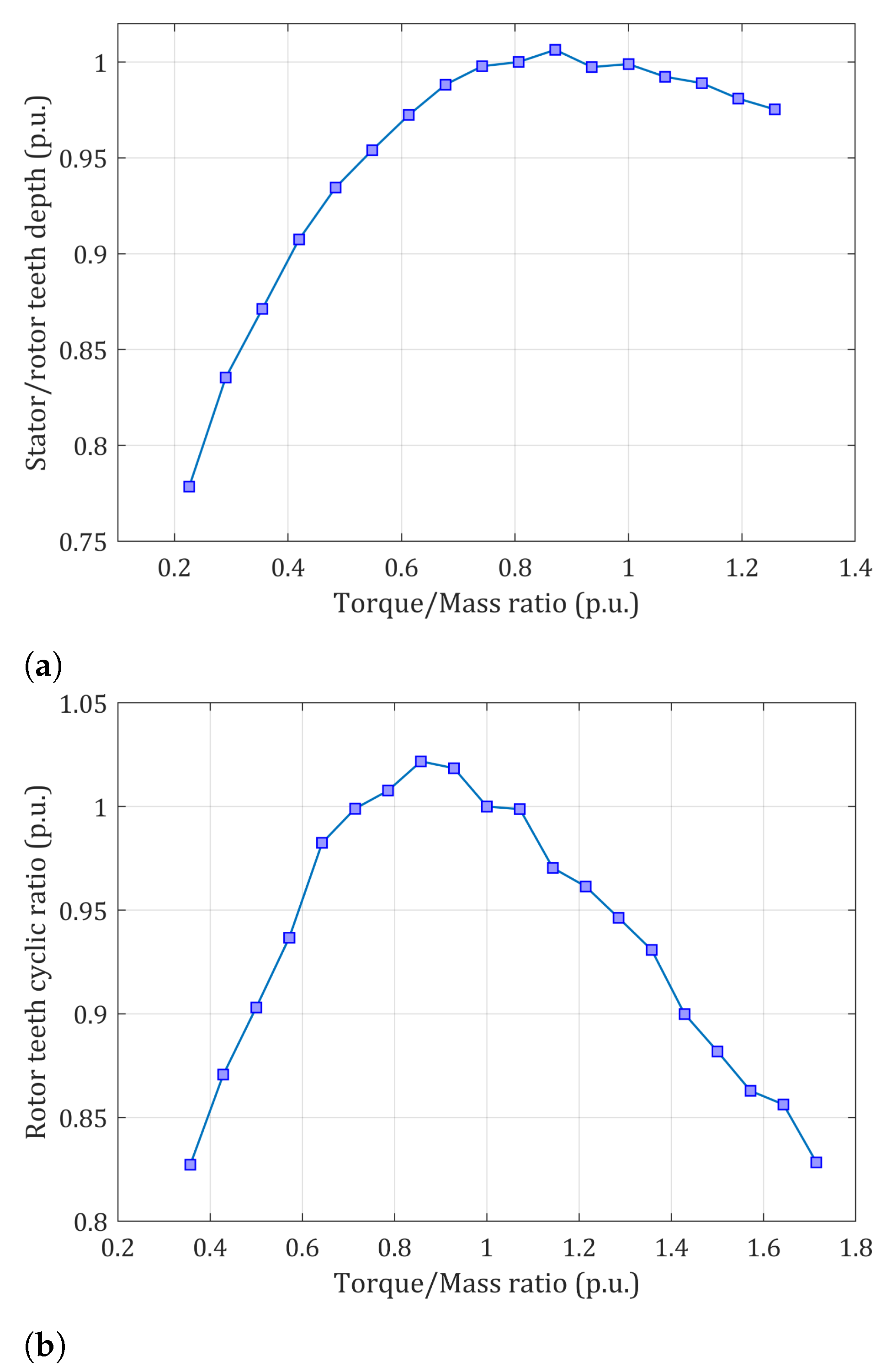
3.3. Stator and Rotor Teeth Dimensions Impact
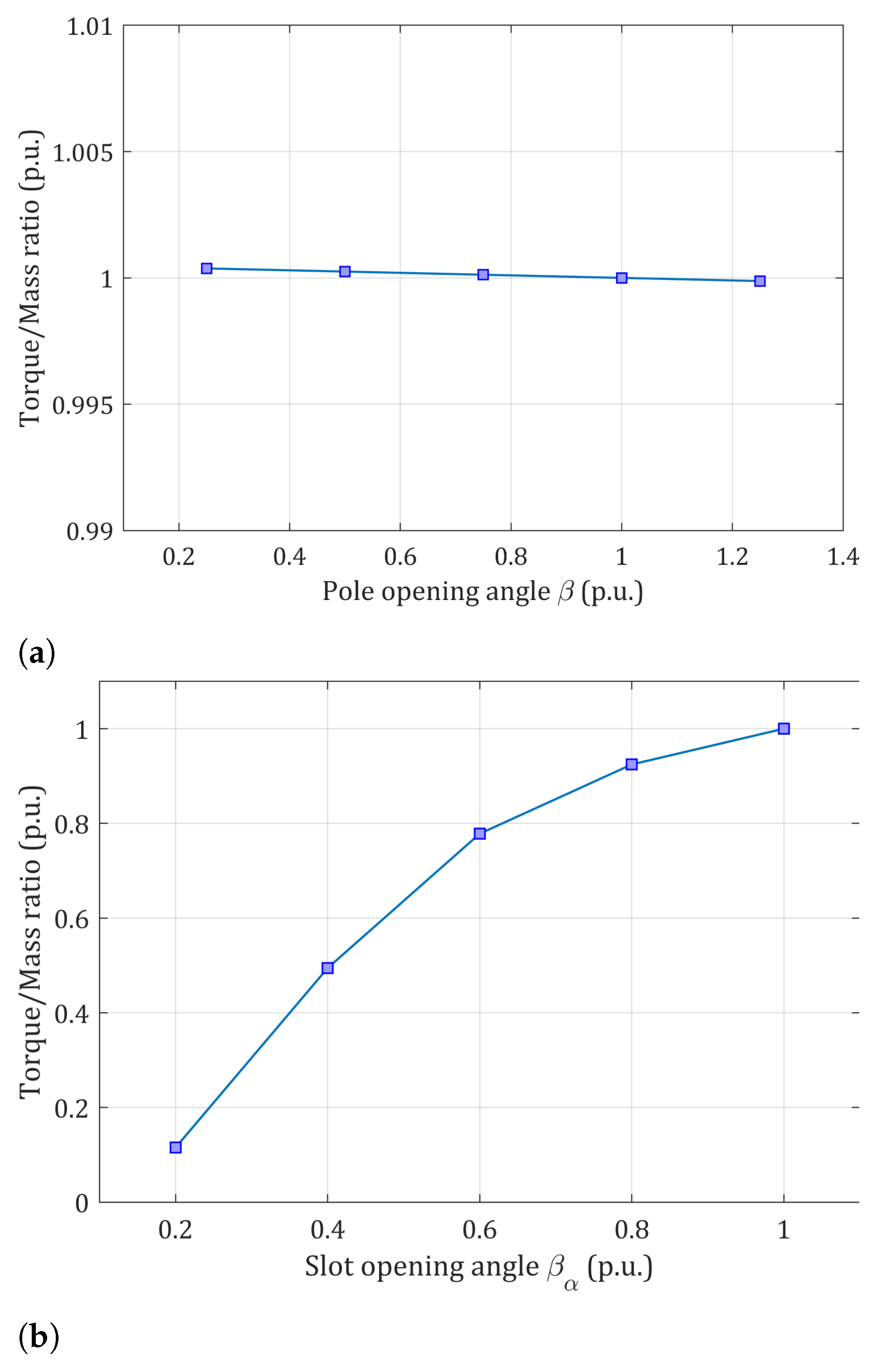
3.4. Pole and Slot Opening Angle Impact
3.5. Influence of the PM Thickness
3.6. Influence of Slot Depth
3.7. Current Density Impact
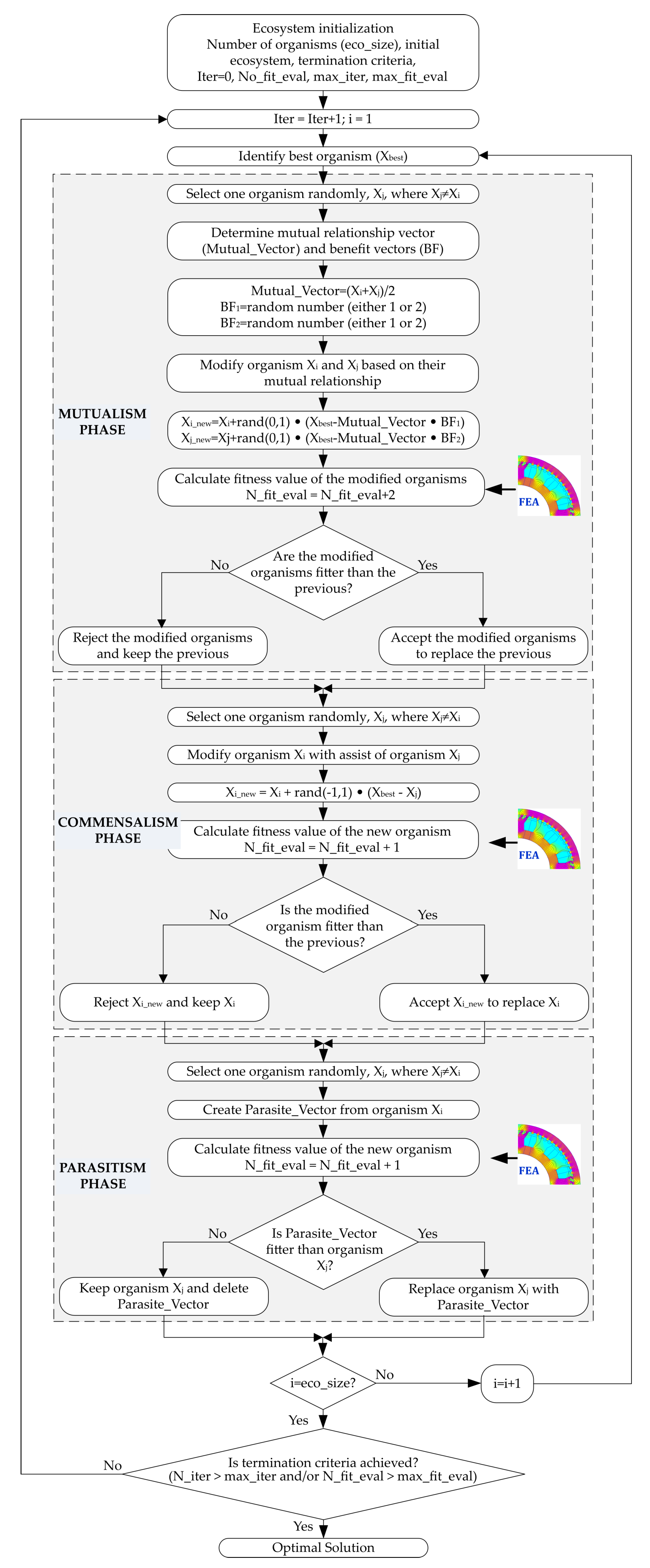
4. Symbiotic Organisms Search Algorithm Features for Problem Optimization
SOS Algorithm Principle
- Phase of mutualism: In this phase, two organisms of different species coexist in a relationship in which each finds individual advantages. Specifically, the two random organisms (let us denote them , ) interact within themselves targeting the enhancement of their chances of survival. The new candidate solutions for and are obtained from Equation (14).whereandThe vector is called the “mutuality vector” and describes the relationship between and . The term represents the organisms’ efforts to increase survival. The is a vector of random numbers, while and are the benefit factors of interaction. They are random numbers (either 1 or 2). It is noted that the interaction may provide partial of total benefit to the organism. The original solutions are replaced by all the better values. Equations (14)–(16) represent the mutuality vector, giving the relationship between and .
- Phase of comensalism: According to this symbiotic strategy, one organism () takes maximum benefit whereas the other one () remains without gaining any benefit and—at the same time—without suffering from the symbiosis. The new candidate solution of derives from Equation (17).At the above expression, the term () reflects the benefit advantage to which the organism is being profited by the organism . The organism will be updated if the new fitness values is greater than the previous one.
- Phase of parasitism: Here, the randomly selected organism acts as a parasite. It is modified by a random number. At the same time, the is created. A randomly chosen organism is treated as the parasite’s host. The and the organism fight for survival. If the fitness value of the is higher than the corresponding one of , the is damaged and the parasite takes its place in the ecosystem. Otherwise, the (having greater fitness) overcomes the and the parasite’s durability in the ecosystem deteriorates.
5. Optimization Results and Discussion
- Ecosystem organisms number: ;
- The maximum number of function evaluations: , where d = 11 is problem’s search variables number (problem dimension);
- The maximum number of iterations: .
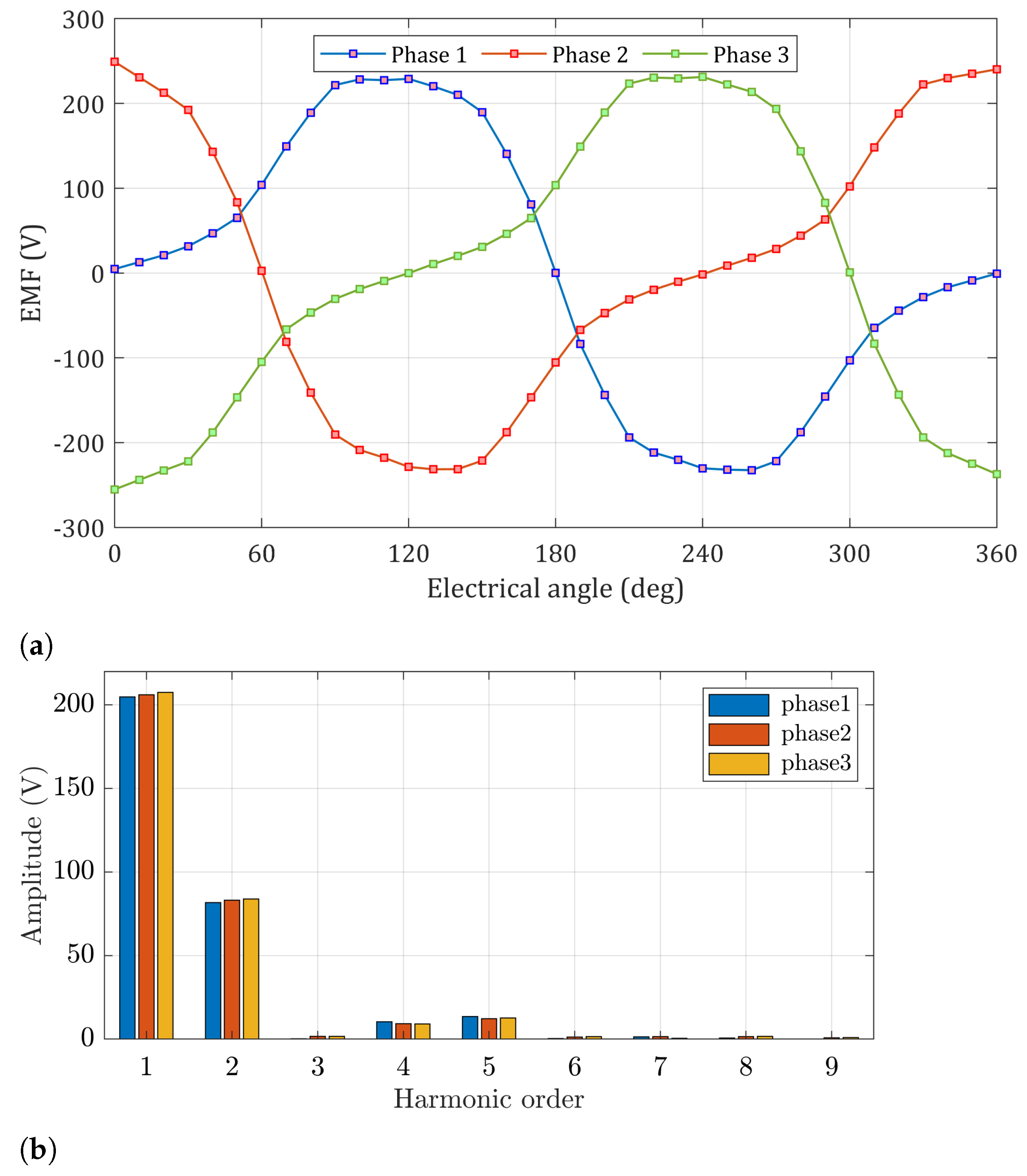
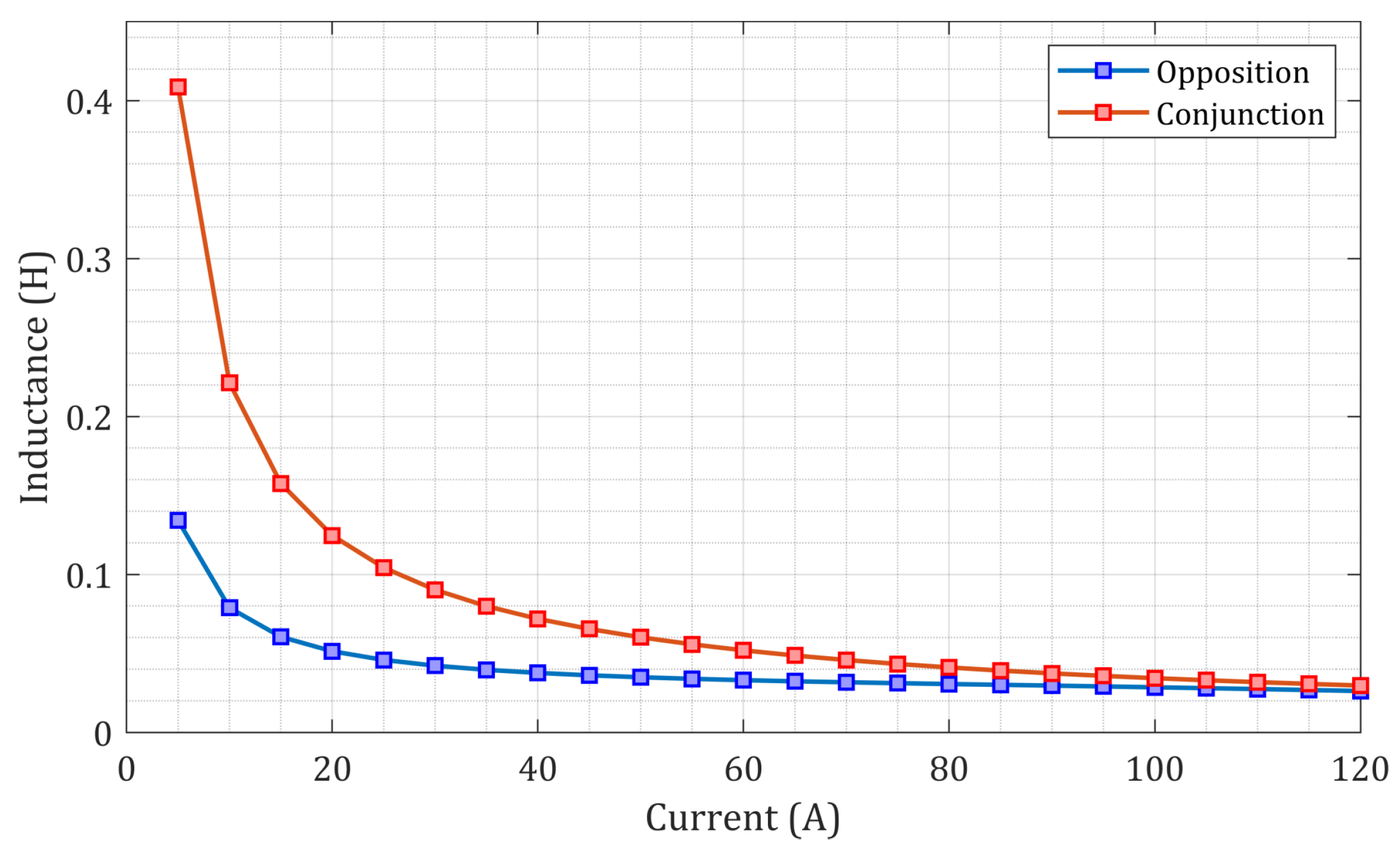
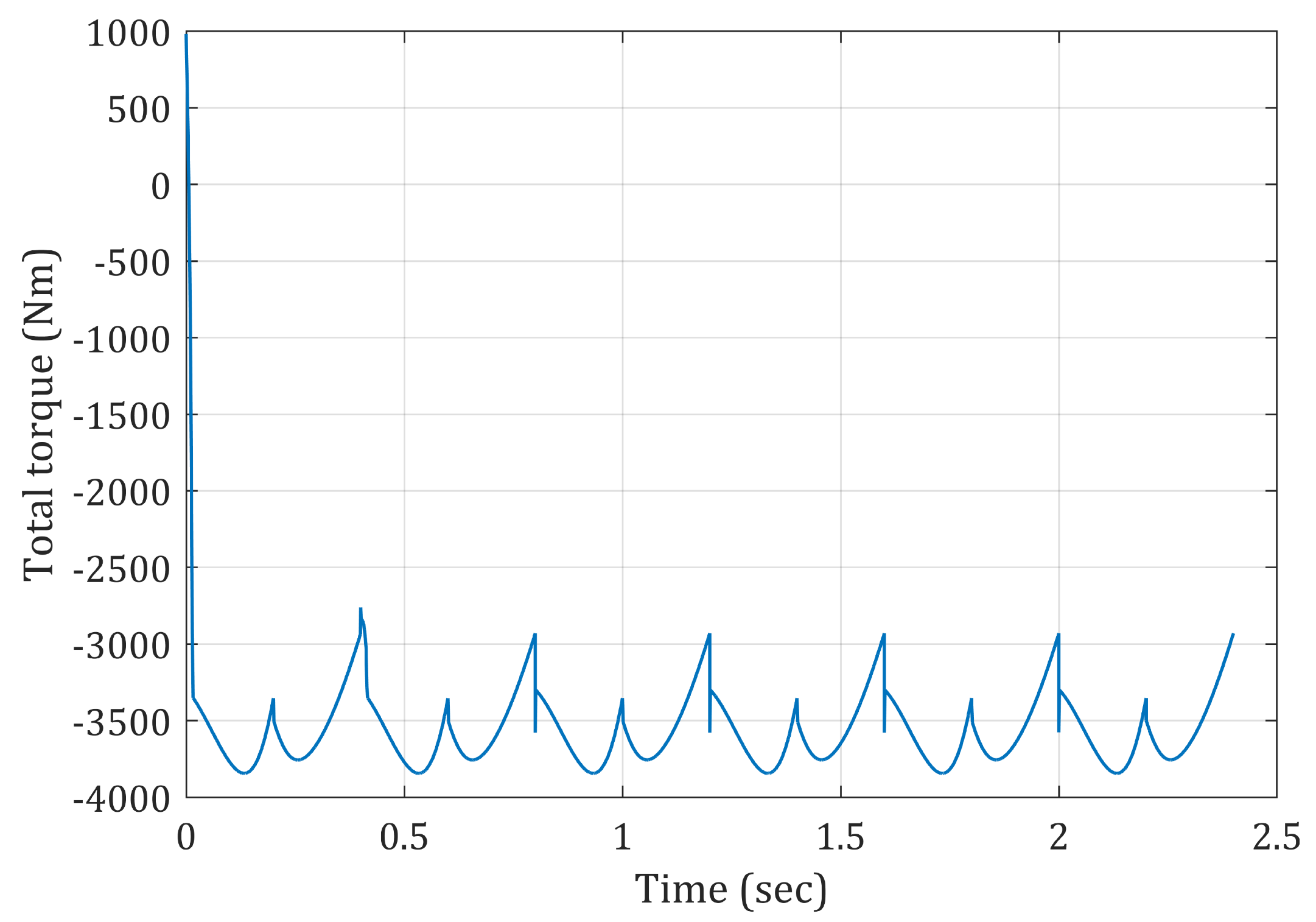
6. Analysis of the Torque, Energy Ratio and Losses
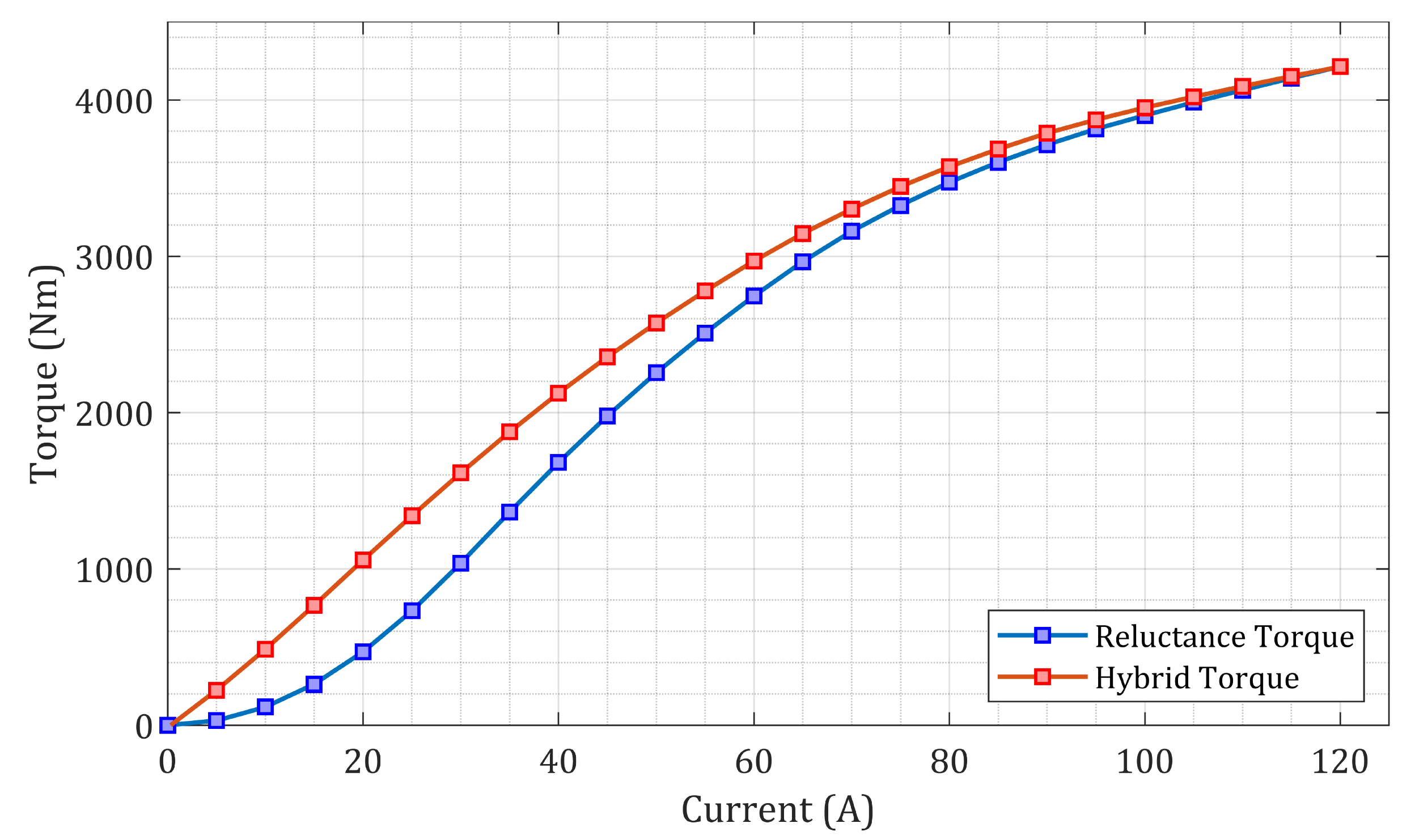
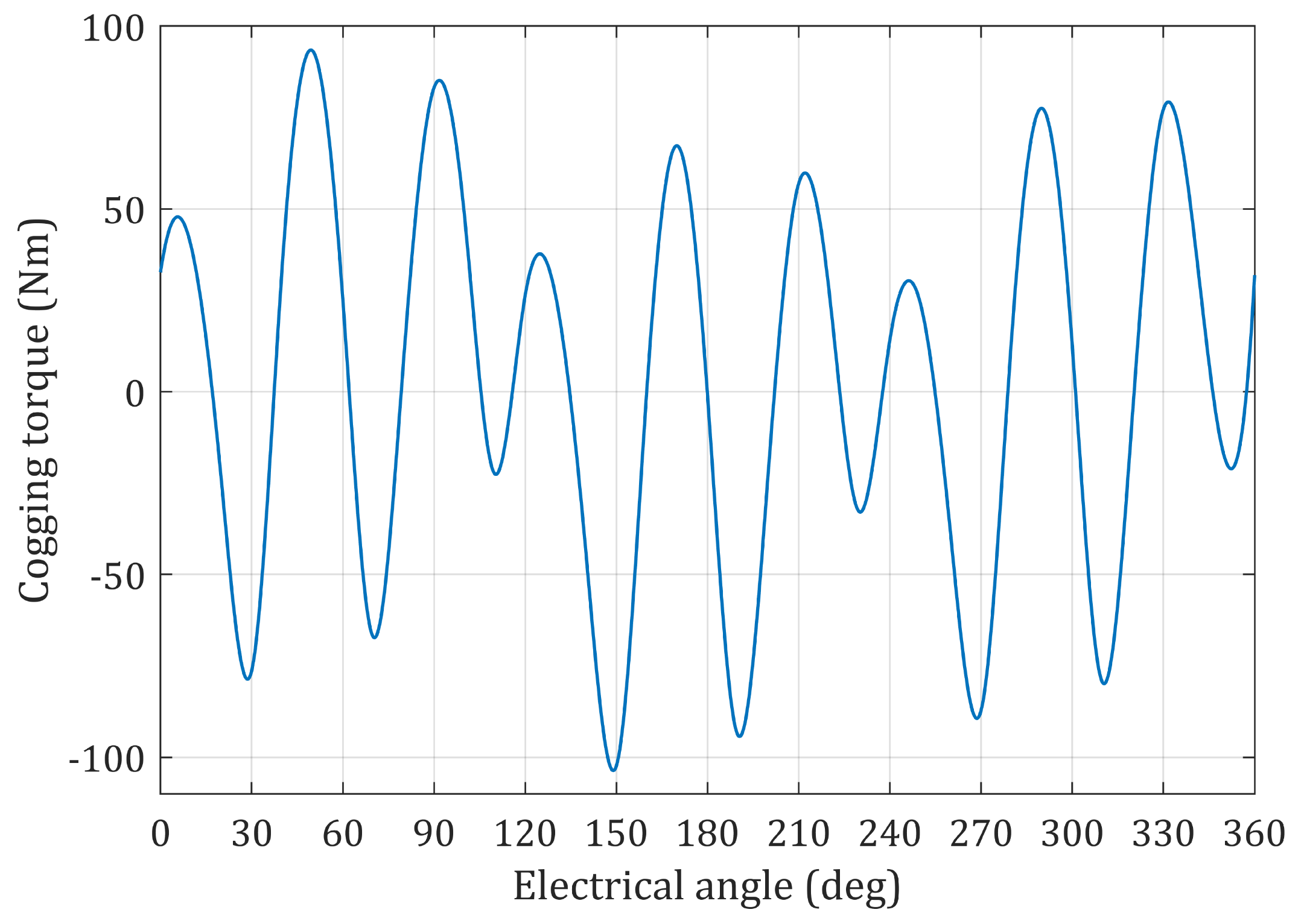
6.1. Analysis of the Steady-State Torque Including All the Components
6.2. Energy Ratio
6.3. Losses and Efficiency
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xiaojing, W.; Xinyan, Z.; Haojie, S. Mutation Assessment Model for the Potential of Clean Energy Development. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Infield, D.; Freris, L. Renewable Energy in Power Systems; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2020. [Google Scholar]
- Merabet, A.; Al-Durra, A.; Debouza, M.; Tanvir, A.; Eshaft, H. Integral sliding mode control for back-to-back converter of DFIG wind turbine system. IET J. Eng. 2020, 2020, 834–842. [Google Scholar] [CrossRef]
- Wicki, S.; Hansen, E.G. Clean energy storage technology in the making: An innovation systems perspective on flywheel energy storage. J. Clean. Prod. 2017, 162, 1118–1134. [Google Scholar] [CrossRef]
- Yao, L.; Yang, B.; Cui, H.; Zhuang, J.; YE, J.; Xue, J. Challenges and progresses of energy storage technology and its application in power systems. J. Mod. Power Syst. Clean Energy 2016, 4, 519–528. [Google Scholar] [CrossRef]
- Akuru, U.B.; Kamper, M.J. Evaluation of flux switching PM machines for medium-speed wind generator drives. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 1925–1931. [Google Scholar] [CrossRef]
- Schmidt, S.; Vath, A. Comparison of Existing Medium-Speed Drive Train Concepts with a Differential Gearbox Approach; European Wind Energy Association, EWEA: Copenhagen, Denmark, 2015; pp. 179–186. [Google Scholar]
- Akuru, U.B.; Kamper, M.J. Comparative advantage of flux switching PM machines for medium-speed wind drives. In Proceedings of the 2015 International Conference on the Domestic Use of Energy (DUE), Cape Town, South Africa, 31 March–1 April 2015; pp. 149–154. [Google Scholar] [CrossRef]
- Manne, B.; Kiran Kumar, M.; B. Akuru, U. Design and Performance Assessment of a Small-Scale Ferrite-PM Flux Reversal Wind Generator. Energies 2020, 13, 5565. [Google Scholar] [CrossRef]
- Sun, W.; Li, Q.; Sun, L.; Li, L. Development and Investigation of Novel Axial-Field Dual-Rotor Segmented Switched Reluctance Machine. IEEE Trans. Transp. Electrif. 2020, 1–12. [Google Scholar] [CrossRef]
- Chen, Y.; Ding, Y.; Zhuang, J.; Zhu, X. Multi-Objective Optimization Design and Multi-Physics Analysis a Double-Stator Permanent-Magnet Doubly Salient Machine. Energies 2018, 11, 2130. [Google Scholar] [CrossRef]
- Guerroudj, C.; Saou, R.; Charpentier, J.F.; Boulayoune, A. Optimal Design of a Novel Doubly Salient Permanent Magnet Motors for High Power Ship Propulsion. In Proceedings of the 2018 XXIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 2556–2562. [Google Scholar] [CrossRef]
- Karnavas, Y.L.; Chasiotis, I.D.; Korkas, C.D.; Amoutzidis, S.K. Modelling and multiobjective optimization analysis of a permanent magnet synchronous motor design. Int. J. Numer. Model. Electron. Netw. Devices Fields 2017, 30, e2232. [Google Scholar] [CrossRef]
- Chasiotis, I.D.; Karnavas, Y.L. A Generic Multi-Criteria Design Approach Toward High Power Density and Fault-Tolerant Low-Speed PMSM for Pod Applications. IEEE Trans. Transp. Electrif. 2019, 5, 356–370. [Google Scholar] [CrossRef]
- Dmitrievskii, V.; Prakht, V.; Kazakbaev, V. Design Optimization of a Permanent-Magnet Flux-Switching Generator for Direct-Drive Wind Turbines. Energies 2019, 12, 3636. [Google Scholar] [CrossRef]
- Liu, H.; Pu, S.; Cao, J.; Yang, X.; Wang, Z. Torque Ripple Mitigation of T-3L Inverter Fed Open-End Doubly-Salient Permanent-Magnet Motor Drives Using Current Hysteresis Control. Energies 2019, 12, 3109. [Google Scholar] [CrossRef]
- Sriwannarat, W.; Seangwong, P.; Lounthavong, V.; Khunkitti, S.; Siritaratiwat, A.; Khunkitti, P. An Improvement of Output Power in Doubly Salient Permanent Magnet Generator Using Pole Configuration Adjustment. Energies 2020, 13, 4588. [Google Scholar] [CrossRef]
- Rauch, S.E.; Johnson, L.J. Design Principles of Flux-Switch Alternators [includes discussion]. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1955, 74, 1261–1268. [Google Scholar] [CrossRef]
- Anuchin, A.; Demidova, G.L.; Hao, C.; Zharkov, A.; Bogdanov, A.; Šmídl, V. Continuous Control Set Model Predictive Control of a Switch Reluctance Drive Using Lookup Tables. Energies 2020, 13, 3317. [Google Scholar] [CrossRef]
- Chau, K.T.; Li, W.; Lee, C.H. Challenges and opportunities of electric machines for renewable energy. Prog. Electromagn. Res. 2012, 42, 45–74. [Google Scholar] [CrossRef]
- Liu, C.; Chau, K.; Jiang, J.; Jian, L. Design of a new outer-rotor permanent magnet hybrid machine for wind power generation. IEEE Trans. Magn. 2008, 44, 1494–1497. [Google Scholar]
- Alireza, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Rezzoug, A.; Zaïm, M.E.H. Non-Conventional Electrical Machines; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Guerroudj, C.; Saou, R.; Boulayoune, A.; El-hadi Zaïm, M.; Moreau, L. Performance Analysis of Vernier Slotted Doubly Salient Permanent Magnet Generator for Wind Power. Int. J. Hydrogen Energy 2017, 42, 8744–8755. [Google Scholar] [CrossRef]
- Bekhouche, L.; Saou, R.; Guerroudj, C.; Kouzou, A.; Zaïm, M.E.H. Electromagnetic Torque Ripple Minimization of Slotted Doubly-Salient-Permanent-Magnet Generator for Wind Turbine Applications. Prog. Electromagn. Res. M 2019, 83, 181–190. [Google Scholar] [CrossRef]
- Saou, R.; Zaïm, M.E.H.; Alitouche, K. Optimal Designs and Comparison of the Doubly Salient Permanent Magnet Machine and Flux-reversal Machine in Low-speed Applications. Electr. Power Components Syst. 2008, 36, 914–931. [Google Scholar] [CrossRef]
- Guerroudj, C.; Zaïm, M.E.H.; Bekhouche, L.; Saou, R.; RAMELI, A. Comparison of Outer and Inner-Rotor toothed Doubly Salient Permanent Magnet Machine. In Proceedings of the 19th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF), Nancy, France, 29–31 August 2019; pp. 1–2. [Google Scholar] [CrossRef]
- Pyrhönen, J.; Jokinen, T.; Hrabovcová, V. Design of Rotating Electrical Machines, 2nd ed.; John Wiley & Sons Ltd.: Flatbush, NY, USA, 2014. [Google Scholar]
- Harkati, N.; Moreau, L.; Zaïm, M.H.; Charpentier, J.F. Optimized design of doubly salient permanent magnet generator taking into account converter constraints. In Proceedings of the International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Marrakech, Morocco, 26–28 October 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Khazdozian, H.A.; Hadimani, R.L.; Jiles, D.C. Size reduction of permanent magnet generators for wind turbines with higher energy density permanent magnets. In Proceedings of the 2014 North American Power Symposium (NAPS), Pullman, WA, USA, 7–9 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Guerroudj, C.; Boulayoune, A.; Saou, R.; Zaïm, M.E.H.; Moreau, L. Study of Vernier effect on the EMF of a slotted DSPM generator for wind power applications. In Proceedings of the Conference Intenationale des Energies Renouvelables (CIER), Sousse, Tunisia, 21–23 December 2015. [Google Scholar]
- Boulayoune, A.; Guerroudj, C.; Saou, R.; Zaïm, M.E.H. Optimisation par Algorithme génétique et Essaim de particule d une machine a inversion de Flux dédiée à l’éolien. In Proceedings of the Conference Internationale des Energies Renouvelables (CIER), Sousse, Tunisia, 21–23 December 2015. [Google Scholar]
- Li, H.; Chen, Z. Overview of different wind generator systems and their comparisons. IET Renew. Power Gener. 2008, 2, 123–138. [Google Scholar] [CrossRef]
- Boldea, I.; Tutelea, L. Reluctance Electric Machines: Design and Control; Taylor & Francis Group: New York, NY, USA, 2018. [Google Scholar]
- Alexandrova, Y.; Semken, R.S.; Pyrhönen, J. Permanent magnet synchronous generator design solution for large direct-drive wind turbines: Thermal behavior of the LC DD-PMSG. Appl. Therm. Eng. 2014, 65, 554–563. [Google Scholar] [CrossRef]
- Lekić, Đ.; Vukosavić, S. Split ratio optimization of high torque density PM BLDC machines considering copper loss density limitation and stator slot leakage. Int. J. Electr. Power Energy Syst. 2018, 100, 231–239. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Prayogo, D. Symbiotic Organisms Search: A new metaheuristic optimization algorithm. Comput. Struct. 2014, 139, 98–112. [Google Scholar] [CrossRef]
- Prasad, D.; Mukherjee, V. A novel symbiotic organisms search algorithm for optimal power flow of power system with FACTS devices. Eng. Sci. Technol. Int. J. 2016, 19, 79–89. [Google Scholar] [CrossRef]
- Karnavas, Y.L.; Chasiotis, I.D.; Pechlivanidou, M.S.C.; Karamanis, E.K.; Kladas, A.G. Azimuth Thruster PMSM Optimization using Symbiotic Organisms Search Algorithm. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Göthenburg, Sweden, 23–26 August 2020; Volume 1, pp. 2231–2237. [Google Scholar] [CrossRef]
- Lawrenson, P.J.; Stephenson, J.M.; Blenkinsop, P.T.; Corda, J.; Fulton, N.N. Variable-speed switched reluctance motors. IEE Proc. B Electr. Power Appl. 1980, 127, 253–265. [Google Scholar] [CrossRef]
- Miller, T.J.E. Converter Volt-Ampere Requirements of the Switched Reluctance Motor Drive. IEEE Trans. Ind. Appl. 1985, IA-21, 1136–1144. [Google Scholar] [CrossRef]
- Miller, T.J.E. Switched Reluctance Motors and Their Control; Clarendon Press; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Bertotti, G. Physical interpretation of eddy current losses in ferromagnetic materials. I. Theoretical considerations. J. Appl. Phys. 1985, 57, 2110–2117. [Google Scholar] [CrossRef]




| Parameter | Value | Unit |
|---|---|---|
| Rated speed n | 50 | rpm |
| Rated power | 10 | kW |
| Rated torque | 3000 | Nm |
| Outer diameter () | 600 | mm |
| Axial length L () | 200 | mm |
| Number of turns per phase | 160 | |
| Copper fill factor | 0.5 | |
| Air-gap thickness g | 0.5 | mm |
| Parameter (Search Variable) | Lower Limit | Upper Limit |
|---|---|---|
| Rotor outer radius, | 150 mm | 300 mm |
| Stator and rotor teeth depth, , | 3 mm | 15 mm |
| Magnet thickness, | 5 mm | 35 mm |
| Stator and rotor teeth cyclic ratios, , | 0.15 | 0.50 |
| Stator and rotor teeth cyclic ratios, , | 0.15 | 0.50 |
| Coil height, | 10 mm | 70 mm |
| Slot radius, | /3 | |
| Angular pole opening, | 3 | 15 |
| Angular slot opening, | 3 | 15 |
| Rotor yoke thickness, | 15 mm | 50 mm |
| Stator yoke thickness, | 15 mm | 50 mm |
| Method | ||||
|---|---|---|---|---|
| Parameters/Quantities | Unit | GA [27] | PSO [27] | SOS (Proposed) |
| Stator yoke thickness, | mm | 37.623 | 34.298 | 40.91 |
| Rotor yoke thickness, | mm | 31.669 | 26.06 | 29.66 |
| Coil height, | mm | 53.921 | 49.56 | 52.12 |
| Angular pole opening, | 6.573 | 6.838 | 8.61 | |
| Angular slot opening, | 5.749 | 5.980 | 7.53 | |
| Slot radius, | mm | 190.41 | 202.4 | 218.53 |
| Stator teeth cyclic ratio, | 0.306 | 0.283 | 0.2596 | |
| Rotor teeth cyclic ratio, | 0.258 | 0.258 | 0.2596 | |
| Stator teeth cyclic ratio, | 0.390 | 0.500 | 0.3939 | |
| Rotor teeth cyclic ratio, | 0.323 | 0.409 | 0.3939 | |
| Magnet thickness, | mm | 20.58 | 27.133 | 27.05 |
| Stator teeth depth, | mm | 9.062 | 10.32 | 7.7039 |
| Rotor teeth depth, | mm | 9.350 | 9.196 | 7.7039 |
| Rotor inner radius, | mm | 258.97 | 265.00 | 247.846 |
| Output torque (average) | Nm | 3867.62 | 3907.80 | 3504.35 |
| Active mass M | kg | 274.49 | 251.14 | 185.44 |
| Torque density | Nm/kg | 14.09 | 15.56 | 18.89 |
| Part of the Machine | Mean Loss (W) |
|---|---|
| Stator | 151.41 |
| Rotor | 79.81 |
| PM | 0.377 |
| Total | 231.596 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerroudj, C.; Karnavas, Y.L.; Charpentier, J.-F.; Chasiotis, I.D.; Bekhouche, L.; Saou, R.; Zaïm, M.E.-H. Design Optimization of Outer Rotor Toothed Doubly Salient Permanent Magnet Generator Using Symbiotic Organisms Search Algorithm. Energies 2021, 14, 2055. https://doi.org/10.3390/en14082055
Guerroudj C, Karnavas YL, Charpentier J-F, Chasiotis ID, Bekhouche L, Saou R, Zaïm ME-H. Design Optimization of Outer Rotor Toothed Doubly Salient Permanent Magnet Generator Using Symbiotic Organisms Search Algorithm. Energies. 2021; 14(8):2055. https://doi.org/10.3390/en14082055
Chicago/Turabian StyleGuerroudj, Cherif, Yannis L. Karnavas, Jean-Frederic Charpentier, Ioannis D. Chasiotis, Lemnouer Bekhouche, Rachid Saou, and Mohammed El-Hadi Zaïm. 2021. "Design Optimization of Outer Rotor Toothed Doubly Salient Permanent Magnet Generator Using Symbiotic Organisms Search Algorithm" Energies 14, no. 8: 2055. https://doi.org/10.3390/en14082055
APA StyleGuerroudj, C., Karnavas, Y. L., Charpentier, J.-F., Chasiotis, I. D., Bekhouche, L., Saou, R., & Zaïm, M. E.-H. (2021). Design Optimization of Outer Rotor Toothed Doubly Salient Permanent Magnet Generator Using Symbiotic Organisms Search Algorithm. Energies, 14(8), 2055. https://doi.org/10.3390/en14082055