A Sizing Method for PV–Battery–Generator Systems for Off-Grid Applications Based on the LCOE
Abstract
1. Introduction
2. Materials and Methods
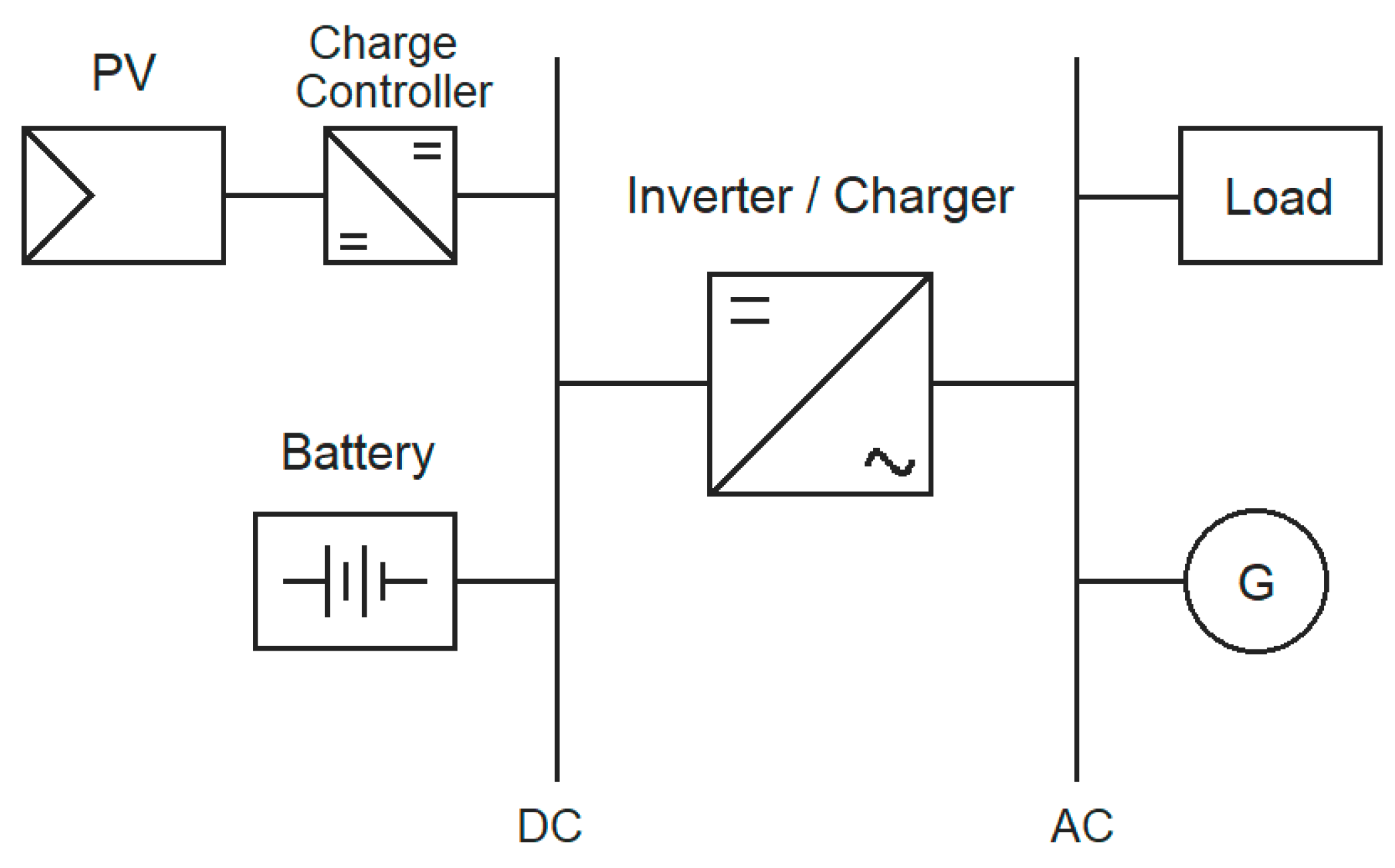
2.1. Off-Grid PV–Battery–Generator System
2.1.1. Preference of the DC-Coupled Architecture
2.1.2. Selection of the System Components
2.2. Annual Electricity Generation Estimation
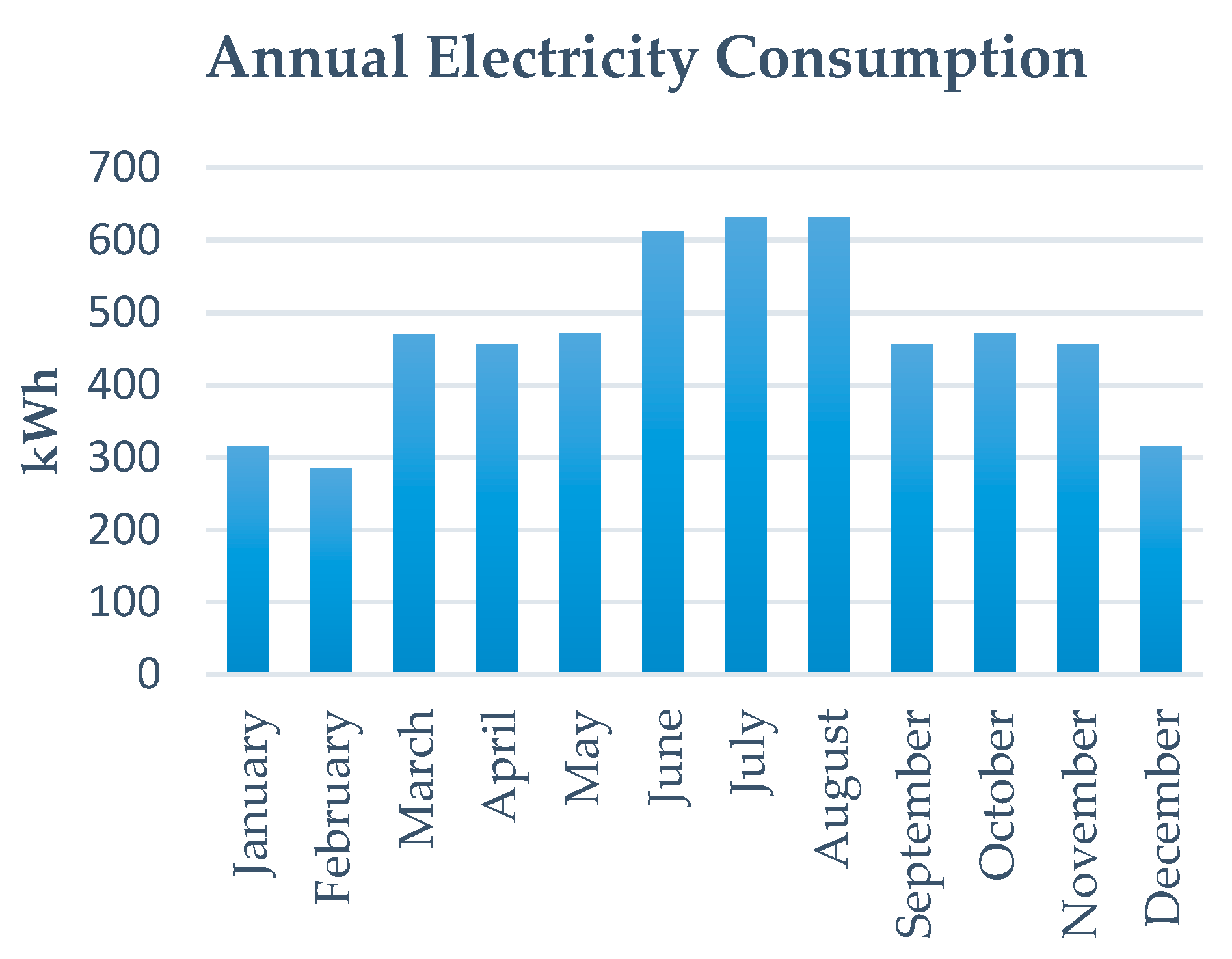
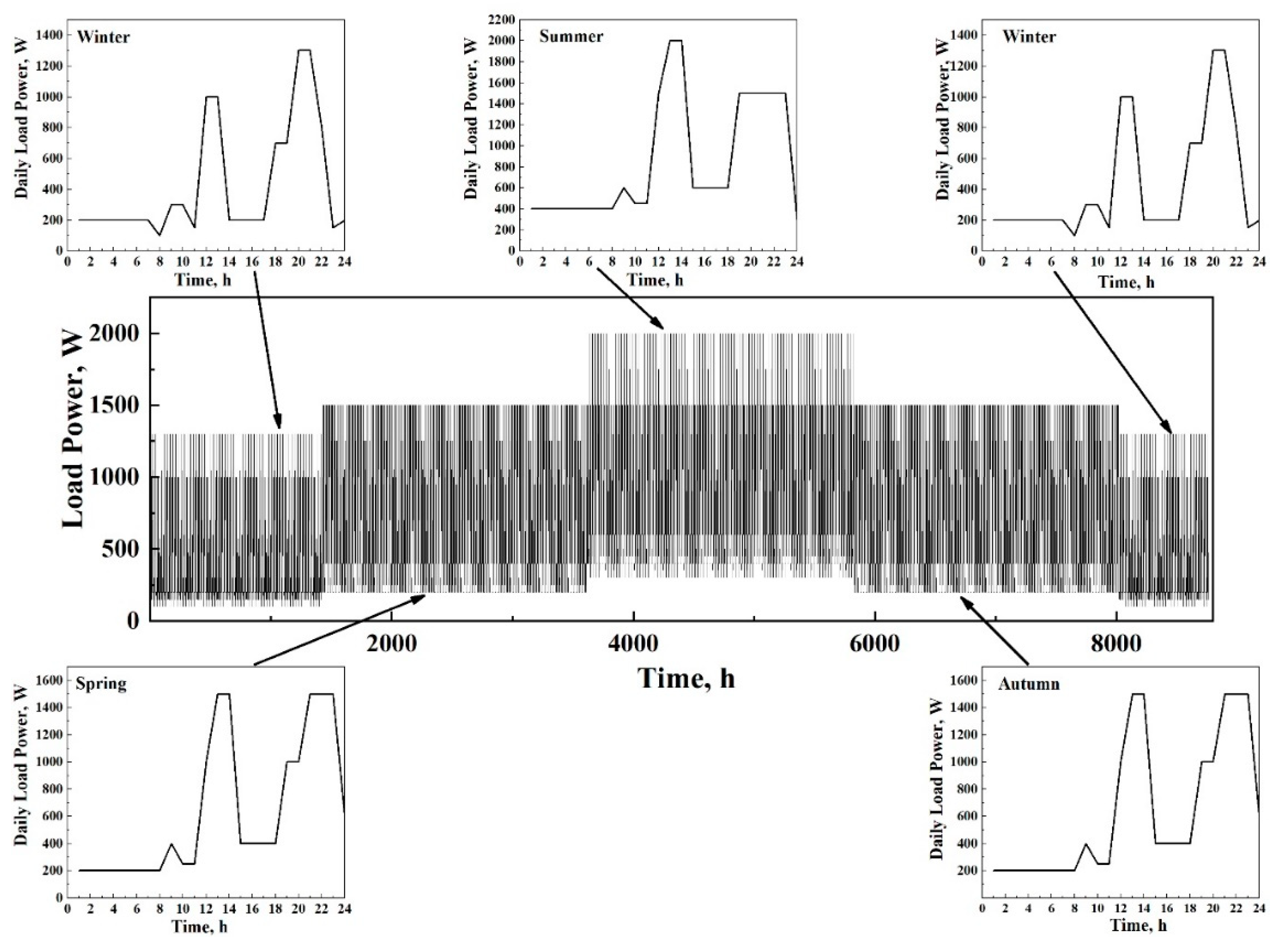
2.3. Reference Load Profile
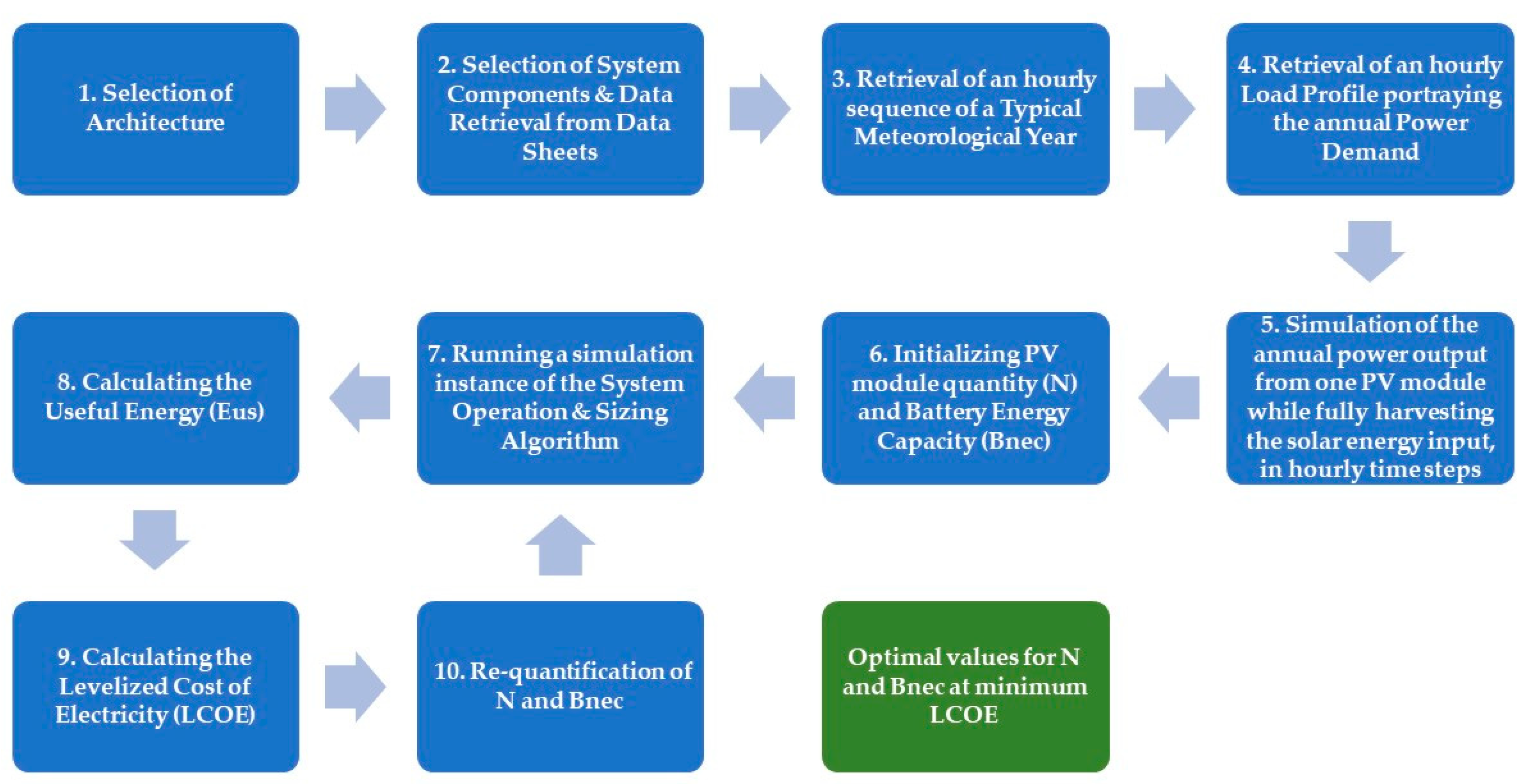
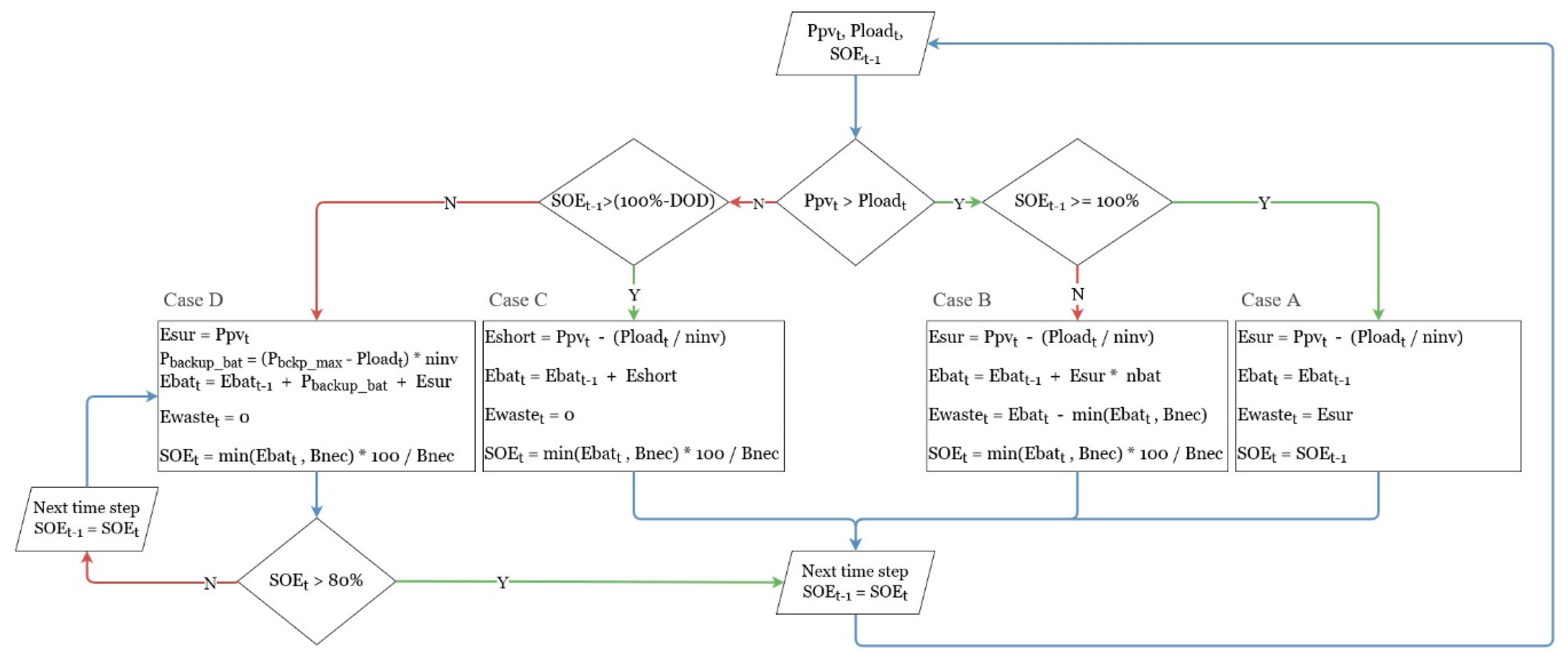
2.4. System Operation and Sizing Algorithm
- Case A.
- Surplus energy case and a fully charged battery
- Case B.
- Surplus energy case and a partially charged battery
- Case C.
- Energy shortage case
- Case D.
- Backup case
2.5. System Cost Analysis and the Levelized Cost of Electricity (LCOE)
2.5.1. Cost of Battery Replacement (Cb,r)
2.5.2. Estimations of Annual Cm, Ceb, and Ces
3. Results
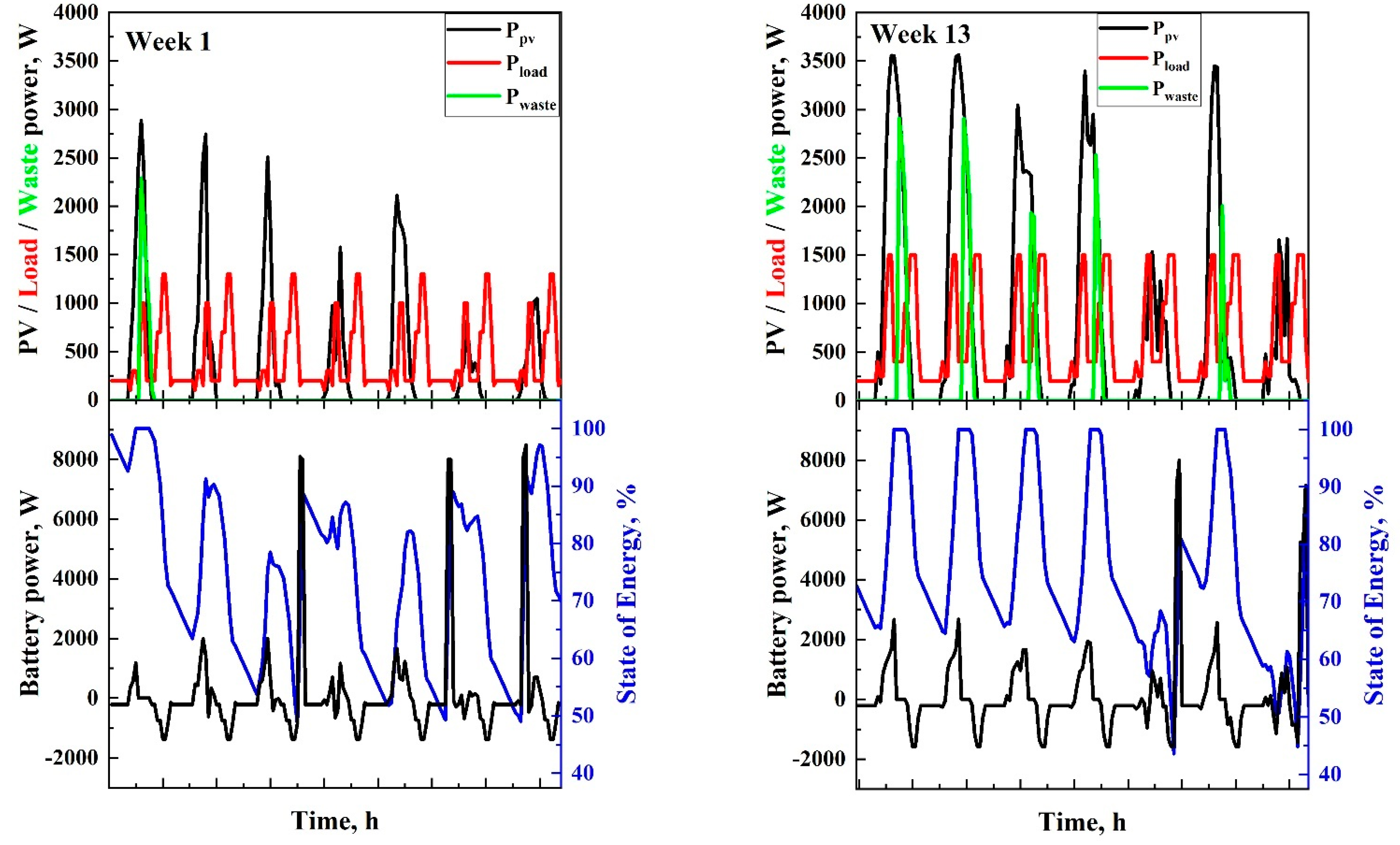
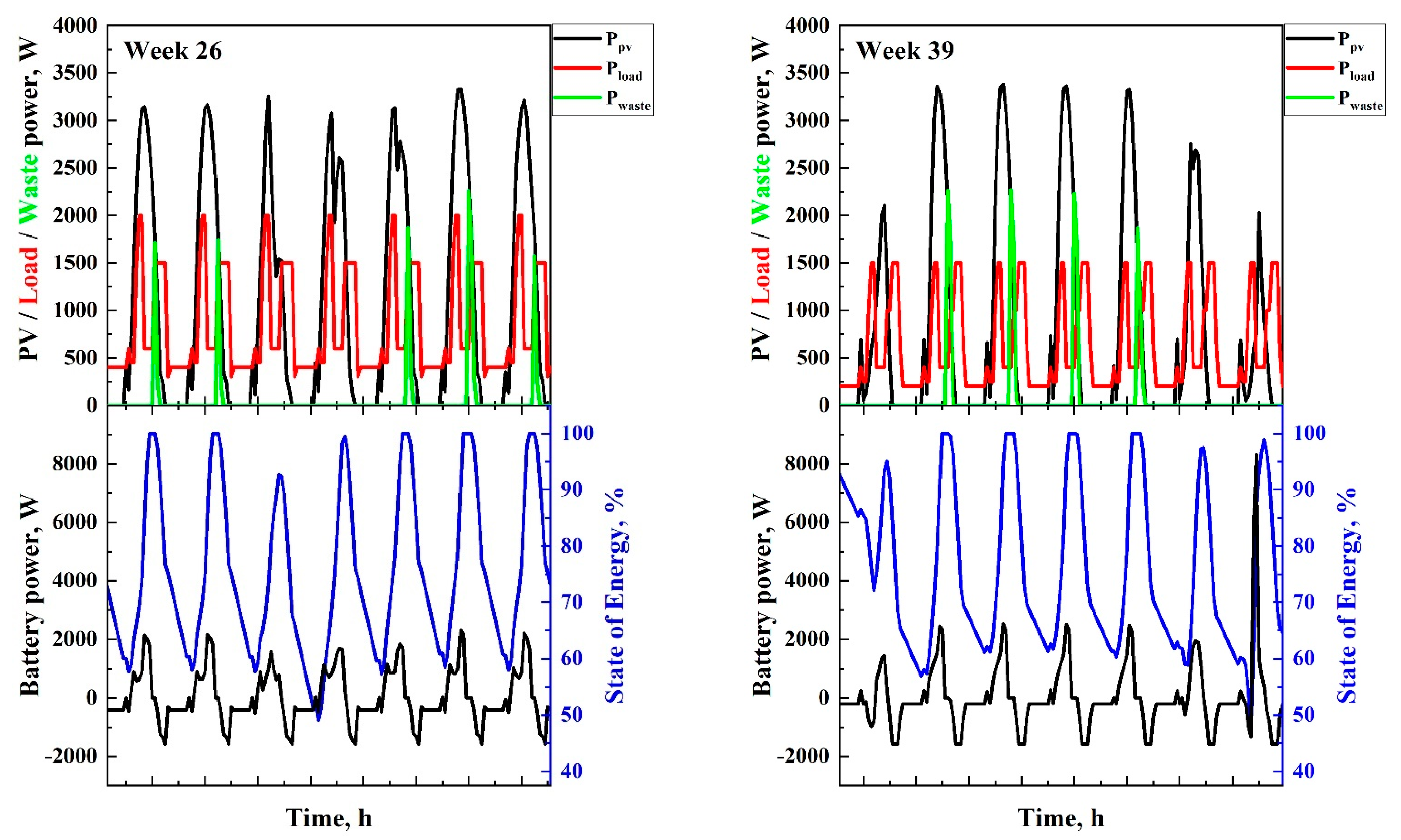
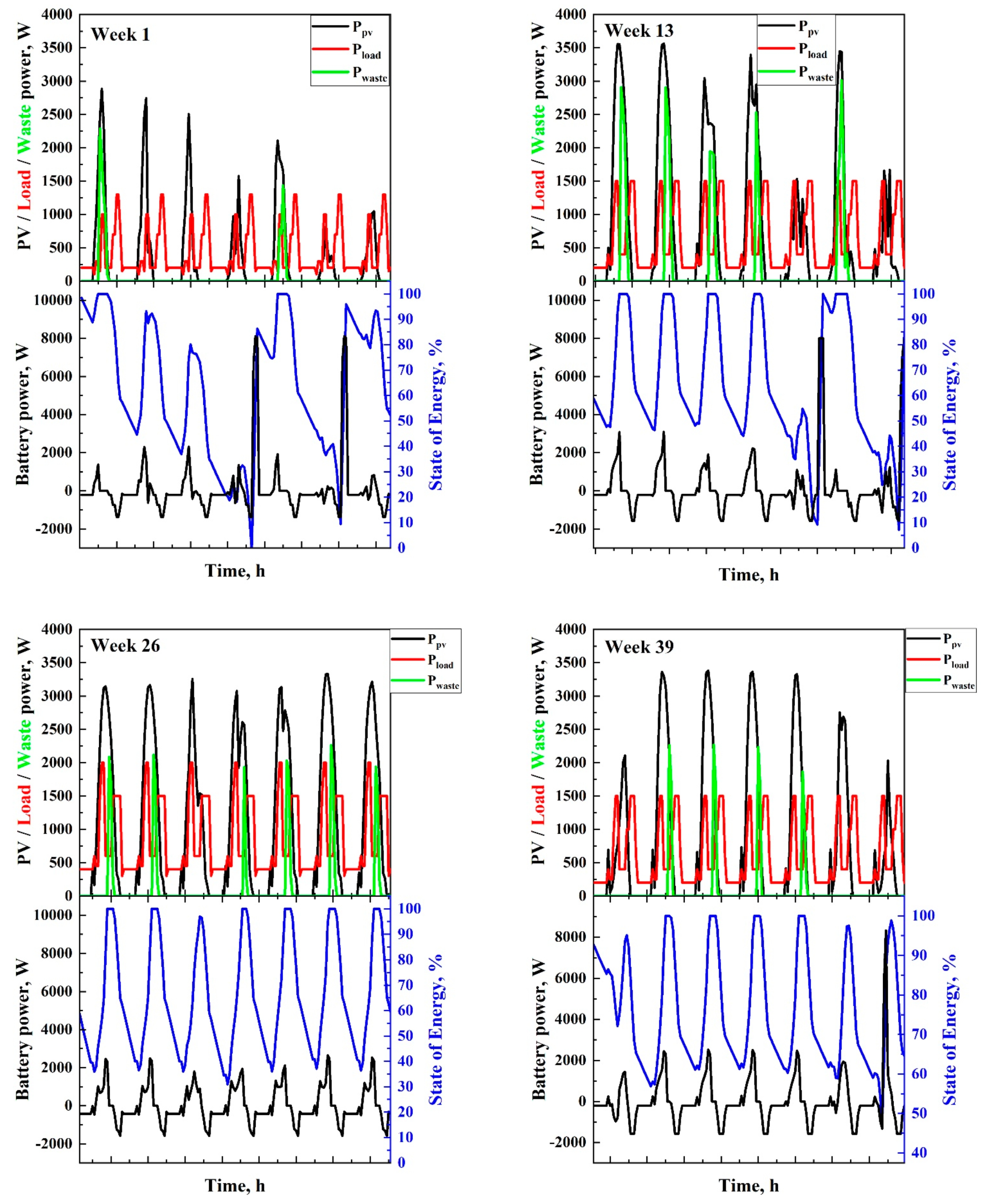
3.1. Sizing Simulations
3.2. Performance of Systems
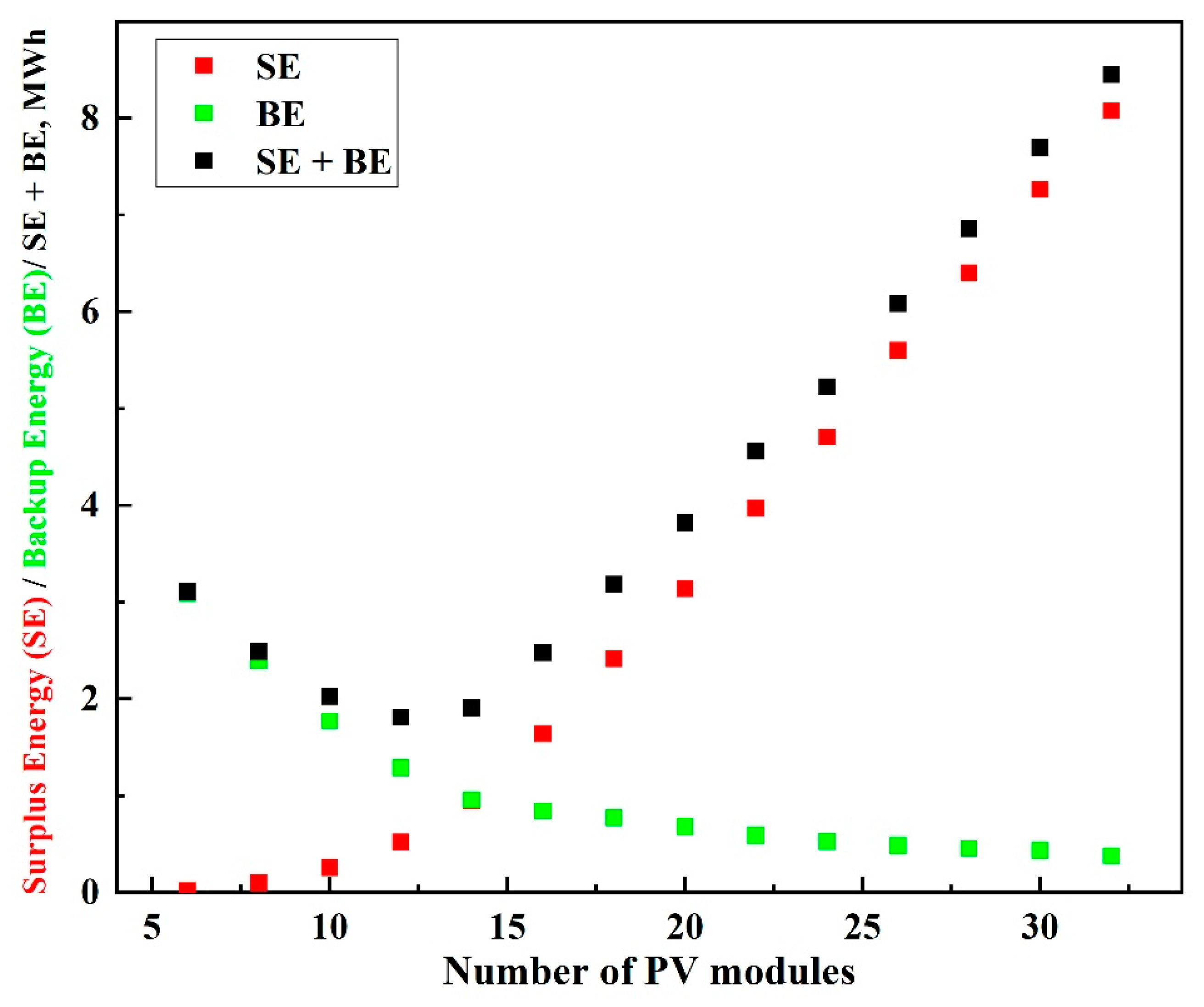
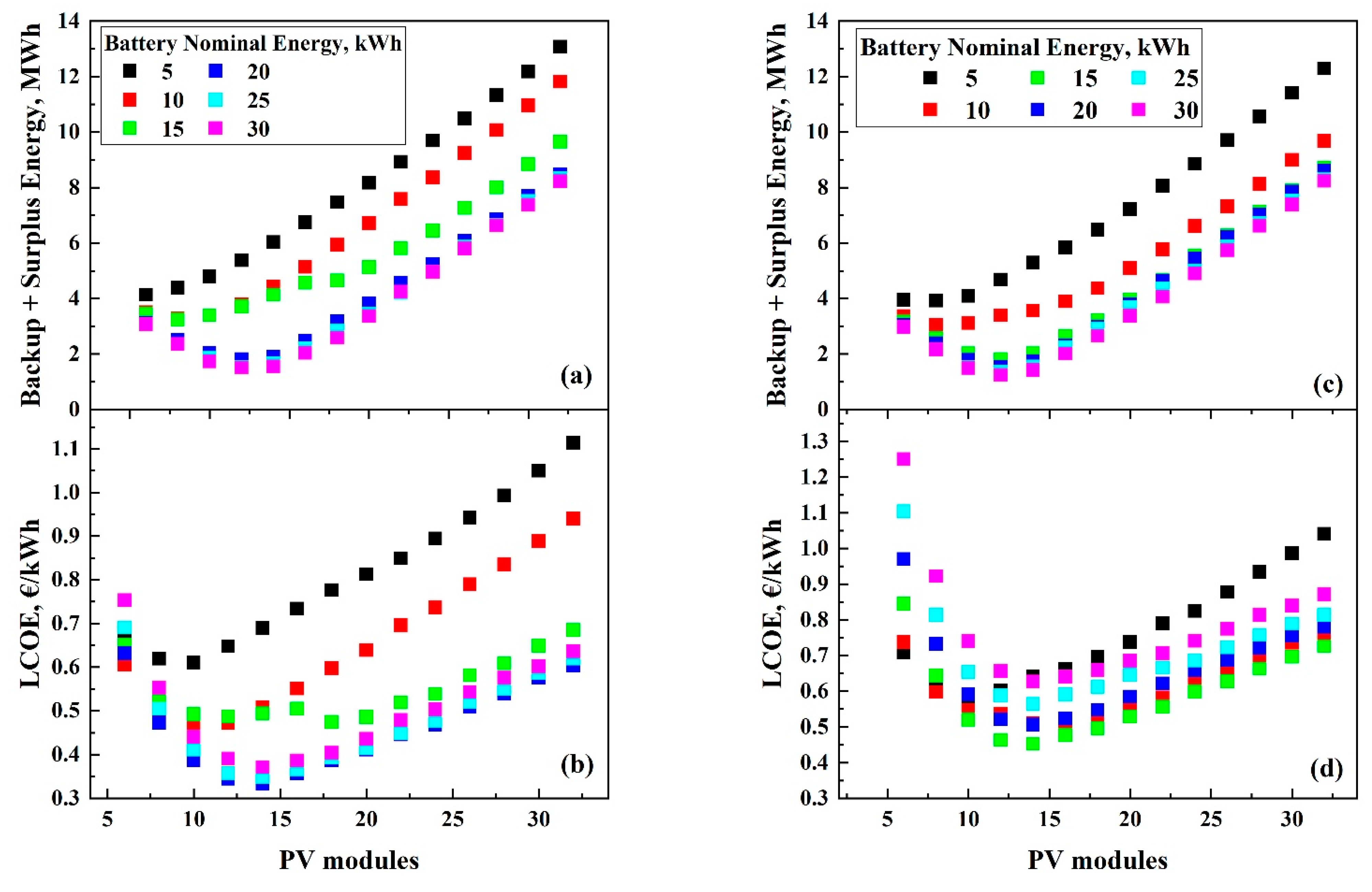
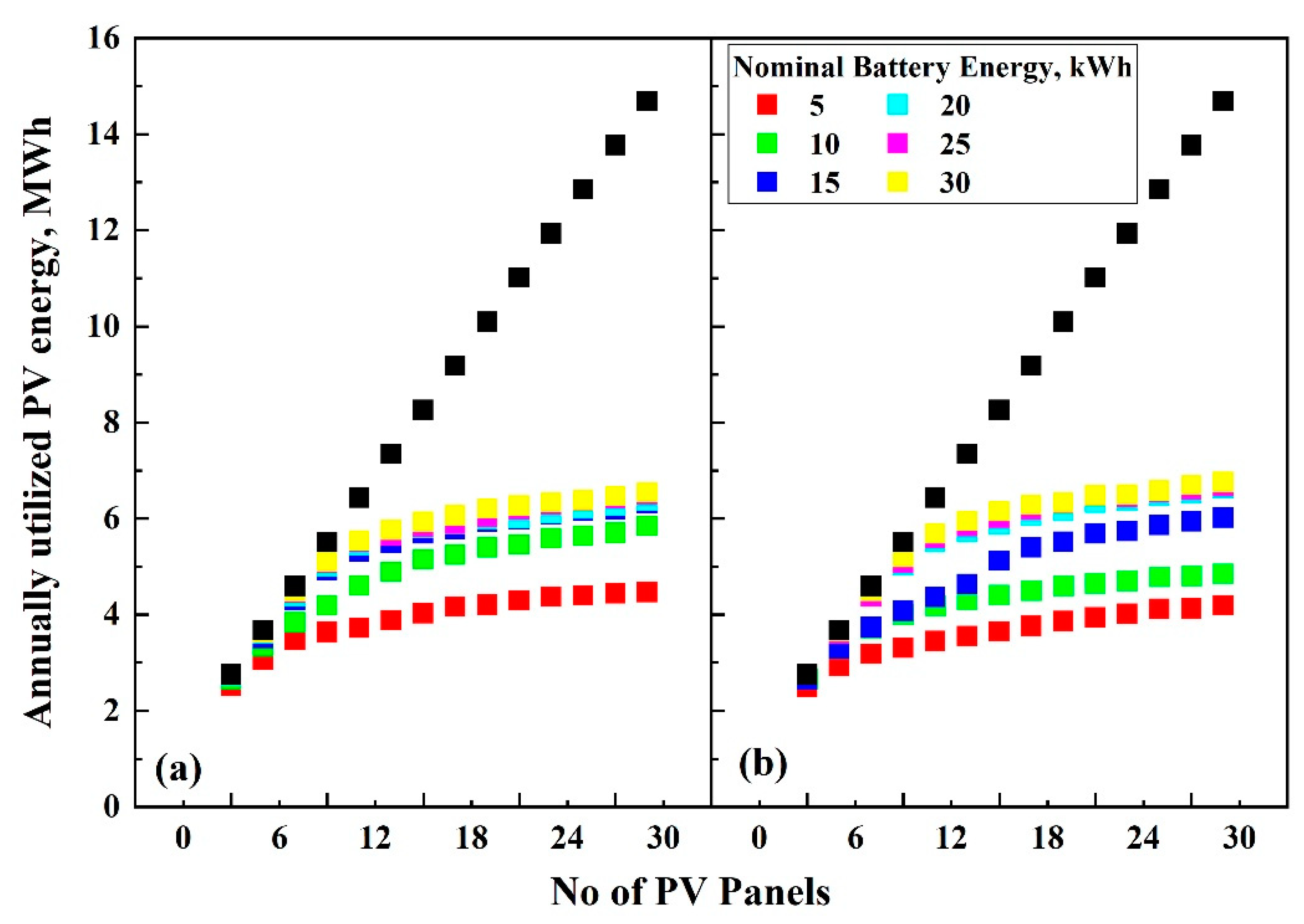
3.2.1. Maximizing the Contribution of Solar Energy
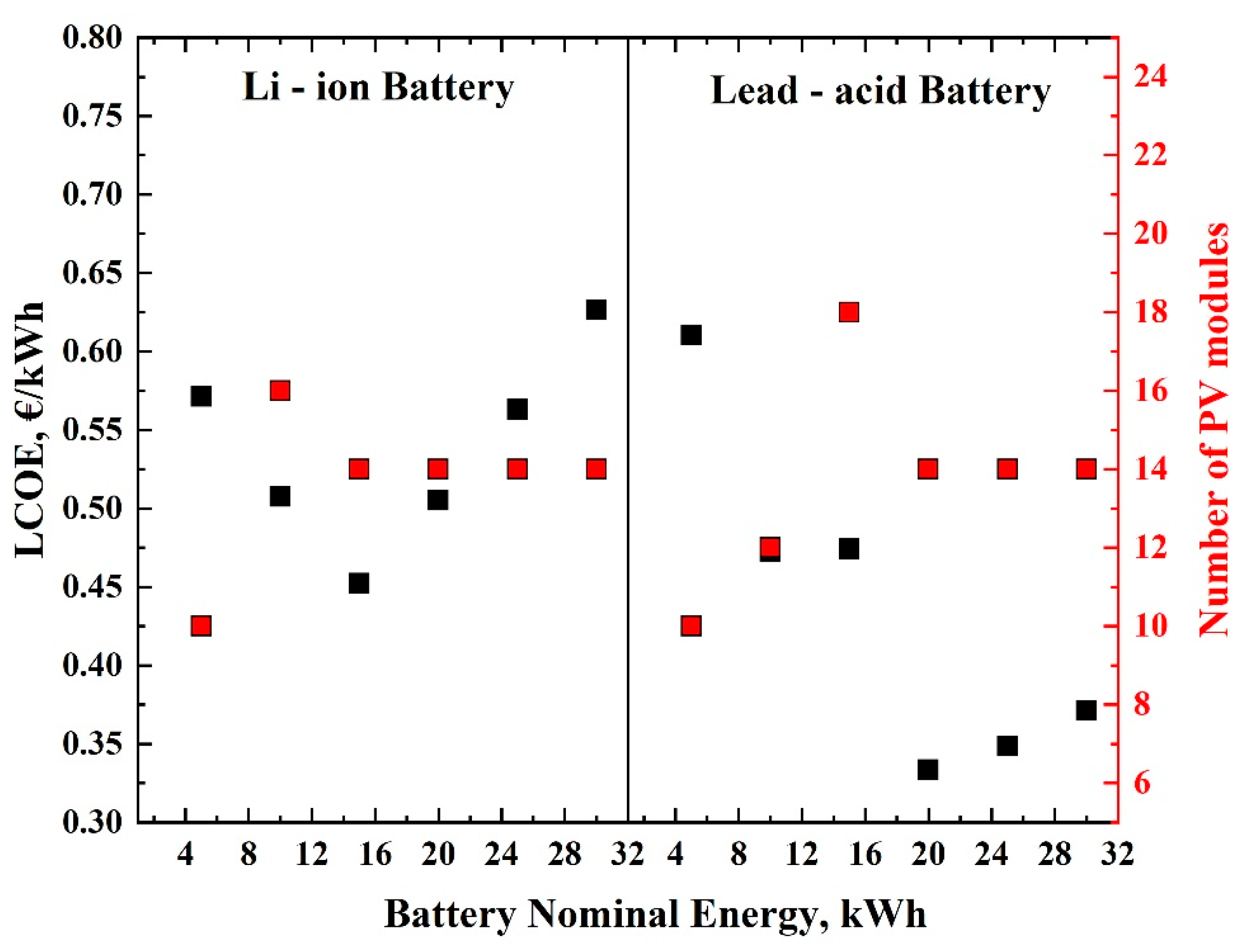
3.2.2. Minimizing the LCOE
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ALV | Average load value of diesel generator |
| AOI | Angle of incidence |
| APT | Annual operation time of diesel generator |
| BMS | Battery management system |
| Bnec | The required battery energy capacity |
| Cb,r | Discounted battery replacement cost, |
| Ceb | Annual backup energy cost |
| Ces | Cost of the discarded renewable energy |
| Cm | Annual system maintenance cost |
| Cpi | Total capital cost |
| CTU | Maximum continuous time use of diesel generator |
| DER | Distributed energy resource |
| DHI | Diffuse horizontal irradiance |
| DNI | Direct normal irradiance |
| DOD | Depth of discharge |
| Ebatt | The remaining amount of energy that is transferred to the battery at time t |
| EES | Electrical energy storage |
| Eshort | Energy shortage when the PV output cannot cover the power demand |
| Esur | Surplus energy |
| Eus | Annually utilized PV energy output |
| Ewaste | Excess solar power that remains unused |
| GHI | Global horizontal irradiance |
| I0 | Diode reverse saturation current |
| IL | Photocurrent |
| LCOE | Levelized cost of electricity |
| LPG | Liquefied petroleum gas |
| MPPT | Maximum power point tracking |
| N | The required PV module number |
| nbat | Charging efficiency of the battery |
| ninv | Inverter efficiency |
| nNsVth | Modified diode ideality factor |
| Pbackup->battery | The remaining generator output on the DC side charging the battery |
| PbackupMAX | Maximum diesel generator output |
| PERC | Passivated emitter and rear contact PV module |
| Pload | The hourly power demand for in a year. |
| Ppv | Hourly PV power output in a year |
| PVBG | Photovoltaic system with batteries and generator set |
| PVLIB | Solar simulation library for PV energy systems |
| Rs | Series resistance |
| Rsh | Shunt resistance |
| SA | Operation and sizing algorithm |
| SOE | Battery state of energy |
| SOE | Battery state of energy (SOE) available |
| STC | Standard test conditions |
| T | Atmospheric temperature |
| TC | PV cell temperature |
| TM | PV module temperature |
| TMY | Typical meteorological year |
| WS | Horizontal windspeed |
Appendix A
Appendix B
| Parameter | Description | |
|---|---|---|
| p.1 | Bnec | The minimum multiple battery nominal energy capacity, in Wh. |
| p.2 | N | The PV module number in an array. |
| p.3 | Σ(Ppv) | The sum of hourly PV power output in a year, in Wh. |
| p.4 | Σ(Pload) | The sum of the hourly power demand on the consumption side in a year, in Wh. |
| p.5 | Σ(Pbat,d) | The annual sum of energy discharging the battery, in Wh. |
| p.6 | Σ(Pbat,ch) | The annual sum of energy charging the battery, in Wh. |
| p.7 | Σ(Ewaste) | The annual sum of unused (discarded) energy, in Wh. |
| p.8 | Σ(Pbackup) | The annual sum of the generator output, in Wh. |
| p.9 | Σ(Pbackup->bat) | The annual sum of energy flowing from the generator to the battery, in Wh. |
| p.10 | Σ(Backup_Operation) | The sum of operational hours of the generator in a year. |
| p.11 | Σ(Pload)_Σ(Ppv)_ratio | The ratio of the annual PV power output to the annual power demand. |
| p.12 | Battery_Cycles | Battery_Cycles = abs(Σ(Pbat,d))/Bnec The total charge–discharge cycles of the battery for a year. |
| p.13 | Σ(Εwaste) + Σ(Pbackup) | The sum of annual discarded energy and annual energy supplied by the generator, in Wh. |
| p.14 | Eus | = Σ(Ppv) − Σ(Ewaste) Useful_Energy The utilized PV output, in Wh. |
| p.15 | Bat_Replac_Years | = NBC/Battery_Cycles Where NBC is the nominal battery cycle life stated by the battery manufacturer in the datasheet. |
| p.16 | PV_Cost(N) | = N × PV_Module_Cost The capital cost of PV panels. |
| p.17 | Battery_Cost_Lead | = (Bnec/1000) × Bat_Cost_Lead–Acid, where Bat_Cost_Lead–Acid is the battery capital cost per kWh. |
| p.18 | Battery_Cost_Lithium | = (Bnec/1000) × Bat_Cost_LiFePO4, where Bat_Cost_LiFePO4 is the battery capital cost per kWh. |
| p.19 | Power_Electr_Cost(N) | = Inverter_Cost + Monitoring_Cost + N × 50, in EUR. The capital cost for power electronics depends on the number of PV panels installed. The above function is an approximation and can usually be derived by the power electronics distributor pricelist. |
| p.20 | Mounting_Cost(N) | = N × 1_Panel_Roof_Mounting_Cost. The capital cost for PV mounting systems can vary significantly depending on site-specific individualities. Although, in this work, a simple dependency on the amount of PV panels was acceptable, a more precise cost estimation must be considered in demanding installation sites. |
| p.21 | Installation_Service_Cost(Ν) | = Electrical_Install_Cost + Mounting_Cost(N), where Electrical_Install_Cost is the service cost for the indoor electrical construction, i.e., the power electronics–battery–wiring setup. Installation_Service_Cost(Ν) is also dependent on the amount of installed PV panels since more modules generally mean more converters, batteries, cabling, and mounting stands to install. This is an empirically determined quantity and scaled to the size of the total PV installation. |
| p.22 | Electr&Install_Materials(N) | = N × 12.5 + Electrical_Install_Cost, in Euro. The material purchasing and installation cost for the electrical wiring, and construction, consisting mainly of low voltage protection and control equipment (Miniature circuit breakers (MCBs), wires, enclosure, switchboards, etc.). This is also an empirically determined quantity, scaled to the number of PV panels and dependent on the service cost for the indoor electrical construction. |
| p.23 | Σ_COST_(PV&Lead-Acid) | = [PV_Cost(N) + Battery_Cost_Lead + Power_Electr_Cost(N) + Mounting_Cost(N) + Installation_Service_Cost + Electr&Install_Materials] |
| p.24 | Σ_COST_(PV&LiFePO4) | = [PV_Cost(N) + Battery_Cost_Lithium + Power_Electr_Cost(N) + Mounting_Cost(N) + Installation_Service_Cost + Electr&Install_Materials] |
| p.25 | Σ_Bat_Repl_Cost_Lead | Accumulation of net present value battery replacement cost for lead–acid batteries. |
| p.26 | Σ_Bat_Repl_Cost_Lithium | Accumulation of net present value battery replacement cost for LiFePO4 batteries. |
| p.27 | Efuel | = Σ(Pbackup)/ngen The fuel energy required by the generator to cover the load and battery demand, in kWh per year. |
| p.28 | Ces | = Σ(Εwaste) × LCOEPVBAT/1000 The unit cost of the discarded energy, based on the estimated LCOE of a typical PV-Battery setup, approximately 0.26 EUR/kWh. |
| p.29 | Ceb | = Efuel × Cost_of_Fuel/Fuel_energy_vol Cost_of_Fuel = 1.175 EUR/L and Fuel_energy_vol = 9850 |
| p.30 | Cost_of_Energy | = [(Ces + Ceb) × ((1 + Real_Interest) ^ (Project_Years + 1) − 1)/(Real_Interest × (1 + Real_Interest) ^ Project_Years)] |
| p.31 | Total_Cost | = T + Generator_Cost + Σ_Bat_Repl_Cost + Cost_of_Energy, where T = [Σ_COST_(PV&Lead–Acid) or Σ_COST_(PV&LiFePO4)] |
| p.32 | TC_UE_ratio | = Total_Cost/ΣUseful_Energy (EUR/kWh) |
References
- REN21. Renewables 2020 Global Status Report; REN21 Secretariat: Paris, France, 2020; ISBN 978-3-948393-00-7. [Google Scholar]
- El-houari, H.; Allouhi, A.; Rehman, S.; Buker, M.S.; Kousksou, T.; Jamil, A.; El Amrani, B. Design, Simulation, and Economic Optimization of an Off-Grid Photovoltaic System for Rural Electrification. Energies 2019, 12, 4735. [Google Scholar] [CrossRef]
- Bahramara, S.; Parsa Moghaddam, M.; Haghifam, M.R. Optimal planning of hybrid renewable energy systems using HOMER: A review. Renew. Sustain. Energy Rev. 2016, 62, 609–620. [Google Scholar] [CrossRef]
- Khatib, T.; Ibrahim, I.A.; Mohamed, A. A review on sizing methodologies of photovoltaic array and storage battery in a standalone photovoltaic system. Energy Convers. Manag. 2016, 120, 430–448. [Google Scholar] [CrossRef]
- Hina Fathima, A.; Palanisamy, K. Optimization in microgrids with hybrid energy systems—A review. Renew. Sustain. Energy Rev. 2015, 45, 431–446. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J.L.; Yusta-Loyo, J.M.; Domínguez-Navarro, J.A.; Ramírez-Rosado, I.J.; Lujano, J.; Aso, I. Multi-objective optimization minimizing cost and life cycle emissions of stand-alone PV-wind-diesel systems with batteries storage. Appl. Energy 2011, 88, 4033–4041. [Google Scholar] [CrossRef]
- Maleki, A.; Askarzadeh, A. Optimal sizing of a PV/wind/diesel system with battery storage for electrification to an off-grid remote region: A case study of Rafsanjan, Iran. Sustain. Energy Technol. Assess. 2014, 7, 147–153. [Google Scholar] [CrossRef]
- Wei, Z.; Li, X.; Xu, L.; Cheng, Y. Comparative study of computational intelligence approaches for NOx reduction of coal-fired boiler. Energy 2013, 55, 683–692. [Google Scholar] [CrossRef]
- Ghafoor, A.; Munir, A. Design and economics analysis of an off-grid PV system for household electrification. Renew. Sustain. Energy Rev. 2015, 42, 496–502. [Google Scholar] [CrossRef]
- Mandelli, S.; Brivio, C.; Colombo, E.; Merlo, M. A sizing methodology based on Levelized Cost of Supplied and Lost Energy for off-grid rural electrification systems. Renew. Energy 2016, 89, 475–488. [Google Scholar] [CrossRef]
- Mandelli, S.; Brivio, C.; Colombo, E.; Merlo, M. Effect of load profile uncertainty on the optimum sizing of off-grid PV systems for rural electrification. Sustain. Energy Technol. Assess. 2016, 18, 34–47. [Google Scholar] [CrossRef]
- Shang, C.; Srinivasan, D.; Reindl, T. An improved particle swarm optimization algorithm applied to battery sizing for stand-alone hybrid power systems. Int. J. Electr. Power Energy Syst. 2016, 74, 104–117. [Google Scholar] [CrossRef]
- Rodríguez-Gallegos, C.D.; Yang, D.; Gandhi, O.; Bieri, M.; Reindl, T.; Panda, S.K. A multi-objective and robust optimization approach for sizing and placement of PV and batteries in off-grid systems fully operated by diesel generators: An Indonesian case study. Energy 2018, 160, 410–429. [Google Scholar] [CrossRef]
- Li, J. Optimal sizing of grid-connected photovoltaic battery systems for residential houses in Australia. Renew. Energy 2018, 136, 1245–1254. [Google Scholar] [CrossRef]
- Wu, J.; Wei, Z.; Liu, K.; Quan, Z.; Li, Y. Battery-Involved Energy Management for Hybrid Electric Bus Based on Expert-Assistance Deep Deterministic Policy Gradient Algorithm. IEEE Trans. Veh. Technol. 2020, 69, 12786–12796. [Google Scholar] [CrossRef]
- Wu, J.; Wei, Z.; Li, W.; Wang, Y.; Li, Y.; Sauer, D.U. Battery Thermal- and Health-Constrained Energy Management for Hybrid Electric Bus Based on Soft Actor-Critic DRL Algorithm. IEEE Trans. Ind. Inform. 2021, 17, 3751–3761. [Google Scholar] [CrossRef]
- Aldersey-Williamsa, J.; Rubert, T. Levelized cost of energy—A theoretical justification and critical assessment. Energy Policy 2019, 124, 169–179. [Google Scholar] [CrossRef]
- Lai, C.S.; McCulloch, M.D. Levelized cost of electricity for solar photovoltaic and electrical energy. Appl. Energy 2017, 190, 191–203. [Google Scholar] [CrossRef]
- Available online: https://www.energy.gov/eere/solar/crystalline-silicon-photovoltaics-research (accessed on 20 January 2021).
- Available online: https://www.nrel.gov/docs/fy20osti/77010.pdf (accessed on 20 January 2021).
- Available online: https://www.solarcall.it/home-en/download (accessed on 20 January 2021).
- Kosmadakis, I.; Elmasides, C. Towards performance enhancement of hybrid power supply systems based on renewable energy sources. Energy Procedia Elsevier 2018, 157, 977–991. [Google Scholar] [CrossRef]
- Available online: https://www.victronenergy.gr/media/pricelist/WEB_WithoutIP65_PricelistVictron2020-Q4.pdf (accessed on 20 January 2021).
- Ayeng’o, S.P.; Schirmer, T.; Kairies, K.; Axelsen, H.; Sauer, D.U. Comparison of off-grid power supply systems using lead-acid and lithium-ion batteries. Sol. Energy 2018, 162, 140–152. [Google Scholar] [CrossRef]
- Kosmadakis, I.E.; Elmasides, C.; Eleftheriou, D.; Tsagarakis, K.P. A Techno-Economic Analysis of a PV-Battery System in Greece. Energies 2019, 12, 1357. [Google Scholar] [CrossRef]
- Liu, N.; Senthil, R.A.; Zhang, X.; Pan, J.; Sun, Y.; Liu, X. A green and cost-effective process for recovery of high purity α-PbO from spent lead acid batteries. J. Clean. Prod. 2020, 267, 122107. [Google Scholar] [CrossRef]
- Available online: https://www.systems-sunlight.com/wp-content/uploads/2018/10/sunlight_res_sopzv_eu_us_2_19_6p_web_final.pdf (accessed on 20 January 2021).
- Available online: https://www.victronenergy.com/upload/documents/Datasheet-12,8-&-25,6-Volt-lithium-iron-phosphate-batteries-Smart-EN.pdf (accessed on 20 January 2021).
- Keil, P.; Schuster, S.F.; Wilhelm, J.; Travi, J.; Hauser, A.; Karl, R.C.; Jossen, A. Calendar Aging of Lithium-Ion Batteries. J. Electrochem. Soc. 2016, 163, A1872. [Google Scholar] [CrossRef]
- Li, D.; Danilov, D.L.; Xie, J.; Raijmakers, L.; Gao, L.; Yang, Y.; Notten, P.H.L. Degradation Mechanisms of C6/LiFePO4 Batteries: Experimental Analyses of Calendar Aging. Electrochim. Acta 2016, 190, 1124–1133. [Google Scholar] [CrossRef]
- Yilmaz, S.; Dincer, F. Optimal design of hybrid PV-Diesel-Battery systems for isolated lands: A case study for Kilis, Turkey. Renew. Sustain. Energy Rev. 2017, 77, 344–352. [Google Scholar] [CrossRef]
- Marqusee, J.; Jenket, D. Reliability of emergency and standby diesel generators: Impact on energy resiliency solutions. Appl. Energy 2020, 268, 114918. [Google Scholar] [CrossRef]
- Benton, K.; Yang, X.; Wang, Z. Life cycle energy assessment of a standby diesel generator set. J. Clean. Prod. 2017, 149, 265–274. [Google Scholar] [CrossRef]
- Kosmadakis, I.E.; Elmasides, C.; Koulinas, G.; Tsagarakis, K.P. Energy Unit Cost Assessment of Six Photovoltaic-Battery Configurations. Renew. Energy 2021. [Google Scholar] [CrossRef]
- Maxwell, E.L. A Quasi-Physical Model for Converting Hourly Global to Direct Normal Insolation. August 1987; (SERI/TR-215-3087); pp. 35–46. Available online: http://rredc.nrel.gov/solar/pubs/PDFs/TR-215-3087.pdf (accessed on 21 August 2018).
- Loutzenhiser, P.G.; Manz, H.; Felsmann, C.; Strachan, P.A.; Frank, T.; Maxwell, G.M. Empirical validation of models to compute solar irradiance on inclined surfaces for building energy simulation. Sol. Energy 2007, 81, 254–267. [Google Scholar] [CrossRef]
- King, D.L.; Boyson, W.E.; Kratochvil, J.A. Photovoltaic Array Performance Model. Sandia Report 2004 (SAND2004-3535). Available online: http://www.osti.gov/servlets/purl/919131-sca5ep/ (accessed on 17 August 2018).
- De Soto, W.; Klein, S.A.; Beckman, W.A. Improvement and Validation of a Model for Photovoltaic Array Performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Hongmei, T.; Mancilla-David, F.; Ellis, K.; Muljadi, E.; Jenkins, P. A Cell-to-Module-to-Array Detailed Model for Photovoltaic Panels. Sol. Energy 2012, 86, 2695–2706. [Google Scholar]
- Gray, J.L. The Physics of the Solar Cell; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2003; Chapter 3; pp. 62–112. ISBN 0-471-49196-9. [Google Scholar] [CrossRef]
- Holmgren, W.F.; Hansen, C.W.; Mikofski, M.A. pvlib python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef]
- Stein, J.S.; Holmgren, W.F.; Forbess, J.; Hansen, C.W.H. PVLIB: Open Source Photovoltaic Performance Modeling Functions for Matlab and Python. In Proceedings of the IEEE 44th Photovoltaic Specialist Conference, Portland, OR, USA, 5–10 June 2017; pp. 3425–3430. [Google Scholar]
- Andrews, R.W.; Stein, J.S.; Hansen, C.W.H.; Riley, D. Introduction to the Open Source PV LIB for Python Photovoltaic System Modelling Package. In Proceedings of the IEEE 40th Photovoltaic Specialist Conference, Denver, CO, USA, 8–13 June 2014; pp. 170–174. [Google Scholar]
- Holmgren, W.F.; Groenendyk, D.G. An Open Source Solar Power Forecasting Tool Using PVLIB-Python. In Proceedings of the IEEE 43rd Photovoltaic Specialists Conference, Portland, OR, USA, 5–10 June 2016; pp. 972–975. [Google Scholar]
- Stein, J.S. The Photovoltaic Performance Modeling Collaborative (PVPMC). In Proceedings of the 2012 38th IEEE Photovoltaic Specialists Conference, Austin, TX, USA, 3–8 June 2012; pp. 3048–3052. [Google Scholar]
- Available online: https://ec.europa.eu/jrc/en/PVGIS/tools/tmy (accessed on 17 August 2018).
- Andersen, F.M.; Baldini, M.; Hansen, L.G.; Jensen, C.L. Households’ hourly electricity consumption and peak demand in Denmark. Appl. Energy 2017, 208, 607–619. [Google Scholar] [CrossRef]
- Short, W.; Packey, D.; Holt, T. A Manual for the Economic Evaluation of Energy Efficiency and Renewable Energy Technologies. National Renewable Energy Laboratory—March 1995. Available online: https://www.nrel.gov/docs/legosti/old/5173.pdf (accessed on 20 January 2021).
- Blejer, M.I.; Eden, B. A note on the specification of the fisher equation under inflation uncertainty. Econ. Lett. 1979, 3, 249–255. [Google Scholar] [CrossRef]
- Dufo-López, R.; Cortés-Arcos, T.; Artal-Sevil, J.S.; Bernal-Agustín, J.L. Comparison of Lead-Acid and Li-Ion Batteries Lifetime Prediction Models in Stand-Alone Photovoltaic Systems. Appl. Sci. 2021, 11, 1099. [Google Scholar] [CrossRef]
- Kost, C.; Shammugam, S.; Juelch, V.; Nguyen, H.; Schlegl, T. Study: Levelized Cost of Electricity—Renewable Energy Technologies; Fraunhofer ISE: Freiburg, Germany, 2018. [Google Scholar]
- Newnham, R.H.; Baldsing, W.G.A. Benefits of partial-state-of-charge operation in remote-area power-supply systems. J. Power Sources 2002, 107, 273–279. [Google Scholar] [CrossRef]
- de Vries, H.; Nguyen, T.T.; Veld, B.O.H. Increasing the cycle life of lithium ion cells by partial state of charge cycling. Micrroelectronics Reliability 2015, 55, 2247–2253. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, J.; He, H.; Ding, G.; Cui, H.; Liu, L. Future smart battery and management: Advanced sensing from external to embedded multi-dimensional measurement. J. Power Sources 2021, 489, 229462. [Google Scholar] [CrossRef]
| Input Parameters | Sim Data A | Sim Data B | Units | Input Type | |
|---|---|---|---|---|---|
| 1 | Number of PV modules, N | 6 to 34 | 6 to 34 | Physical model assumptions | |
| 3 | Nominal PV module power, Pmpp | 310 | 310 | Wp | |
| 2 | Nominal energy capacity, Bnec | 5 to 30 | 5 to 30 | kWh | |
| 4 | Nominal battery cycle life | 500 | 2500 | Cycles (100% DOD) | |
| 5 | Calendar battery life | 5 | 10 | Years | |
| 6 | Depth of discharge | 50 | 80 | % | |
| 7 | SOEt=0 | 100 | 100 | % | |
| 8 | Inverter efficiency, ninv | 95 | 95 | % | |
| 9 | Battery charging efficiency, nbat | 85 | 98 | % | |
| 10 | Pbackup_max | 4000 | 4000 | W | |
| 11 | Number of inverters | 1 | 1 | ||
| 12 | Pload_max | 4000 | 4000 | W | |
| 13 | Battery type | Lead–acid | Lithium-ion | ||
| 14 | Generator efficiency, ngen | 80 | 80 | % | |
| 15 | Battery cost | 154 | 574 | EUR/kWh | Economic cost assumptions |
| 16 | PV module cost | 110 | 110 | EUR | |
| 17 | Inverter cost | 1600 | 1600 | EUR | |
| 18 | Monitoring and BMS cost | 250 | 500 | EUR | |
| 19 | PV mounting system cost | 50 | 50 | EUR/mod | |
| 20 | Electrical installation cost | 1000 | 1000 | EUR | |
| 21 | Generator cost | 1300 | 1300 | EUR | |
| 22 | LCOEpvbat | 0.26 | 0.26 | EUR/kWh | |
| 23 | LHV | 9.85 | 9.85 | kWh/lt | |
| 24 | Cost of fuel | 1.175 | 1.175 | EUR/lt | |
| 25 | Real interest rate | 0.06919 | 0.06919 | % | |
| 26 | Maintenance cost, Cm | 160 | 160 | EUR/year | |
| 27 | Project years | 25 | 25 | Years |
| Battery Type | N (mods) | Bnec (kWh) | Component Cost | Installation Cost (EUR) | Maintenance Cost | Operation Cost | Eus (kWh/year) | LCOE (EUR/kWh) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PV (EUR) | Battery (EUR) | PE&M * (EUR) | Generator (EUR) | Cbr (Discounted) (EUR) | Cm (EUR/year) | Ces (EUR/year) | Ceb (EUR/year) | ||||||
| Lead–Acid | 10 | 5 | 1100 | 770 | 2600 | 1300 | 3125 | 4445 | 100 | 369 | 503 | 3487.4 | 0.61 |
| 12 | 10 | 1320 | 1540 | 2700 | 1300 | 3350 | 4405 | 100 | 389 | 341 | 4409.8 | 0.48 | |
| 18 | 15 | 1980 | 2310 | 3000 | 1300 | 4025 | 4289 | 100 | 834 | 215 | 5557.0 | 0.47 | |
| 14 | 20 | 1540 | 3080 | 2800 | 1300 | 3575 | 5719 | 100 | 247 | 143 | 6021.8 | 0.34 | |
| 14 | 25 | 1540 | 3850 | 2800 | 1300 | 3575 | 7149 | 100 | 215 | 126 | 6157.9 | 0.36 | |
| 14 | 30 | 1540 | 4620 | 2800 | 1300 | 3575 | 8579 | 100 | 199 | 117 | 6226.7 | 0.38 | |
| Lithium-Ion | 10 | 5 | 1100 | 2870 | 2600 | 1300 | 3125 | 4972 | 100 | 282 | 449 | 3856.2 | 0.57 |
| 16 | 10 | 1760 | 5740 | 2900 | 1300 | 3800 | 4446 | 100 | 655 | 205 | 5306.1 | 0.51 | |
| 14 | 15 | 1540 | 8610 | 2800 | 1300 | 3575 | 6669 | 100 | 301 | 129 | 5792.4 | 0.46 | |
| 14 | 20 | 1540 | 11,480 | 2800 | 1300 | 3575 | 8892 | 100 | 265 | 107 | 5944.1 | 0.51 | |
| 14 | 25 | 1540 | 14,350 | 2800 | 1300 | 3575 | 11,115 | 100 | 241 | 92 | 6047.0 | 0.57 | |
| 14 | 30 | 1540 | 17,220 | 2800 | 1300 | 3575 | 13,338 | 100 | 227 | 82 | 6106.0 | 0.63 | |
| Battery Type | N (mods) | Bnec (kWh) | CTU (h) | APT (h/year) | ALV (kW) |
|---|---|---|---|---|---|
| Lead–Acid | 10 | 5 | 1 | 873 | 4000 |
| 12 | 10 | 2 | 571 | 4000 | |
| 18 | 15 | 2 | 360 | 4000 | |
| 14 | 20 | 3 | 239 | 4000 | |
| 14 | 25 | 3 | 211 | 4000 | |
| 14 | 30 | 4 | 196 | 4000 | |
| Lithium-Ion | 10 | 5 | 1 | 784 | 4000 |
| 16 | 10 | 3 | 343 | 4000 | |
| 14 | 15 | 4 | 216 | 4000 | |
| 14 | 20 | 5 | 180 | 4000 | |
| 14 | 25 | 5 | 158 | 4000 | |
| 14 | 30 | 6 | 137 | 4000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kosmadakis, I.E.; Elmasides, C. A Sizing Method for PV–Battery–Generator Systems for Off-Grid Applications Based on the LCOE. Energies 2021, 14, 1988. https://doi.org/10.3390/en14071988
Kosmadakis IE, Elmasides C. A Sizing Method for PV–Battery–Generator Systems for Off-Grid Applications Based on the LCOE. Energies. 2021; 14(7):1988. https://doi.org/10.3390/en14071988
Chicago/Turabian StyleKosmadakis, Ioannis E., and Costas Elmasides. 2021. "A Sizing Method for PV–Battery–Generator Systems for Off-Grid Applications Based on the LCOE" Energies 14, no. 7: 1988. https://doi.org/10.3390/en14071988
APA StyleKosmadakis, I. E., & Elmasides, C. (2021). A Sizing Method for PV–Battery–Generator Systems for Off-Grid Applications Based on the LCOE. Energies, 14(7), 1988. https://doi.org/10.3390/en14071988







