Model-Based Analysis of Flow Separation Control in a Curved Diffuser by a Vibration Wall
Abstract
1. Introduction
2. A Nonlinear Simplified Model for Flow Separation Control by a Vibration Wall
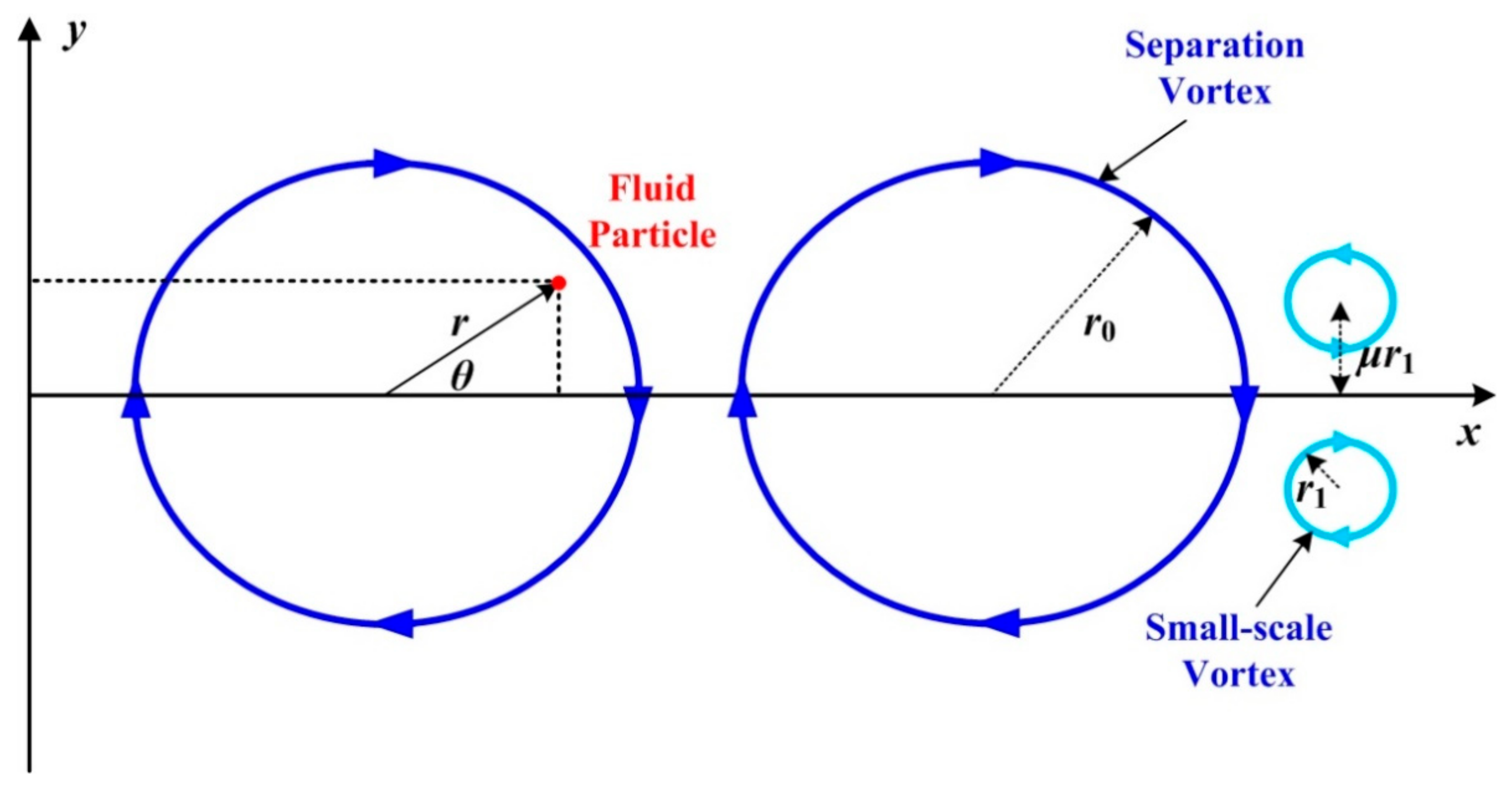
2.1. Time-Averaged Pressure Gradient Based on the Concentrated Vortex Model
2.2. Time-Averaged Dissipation Term
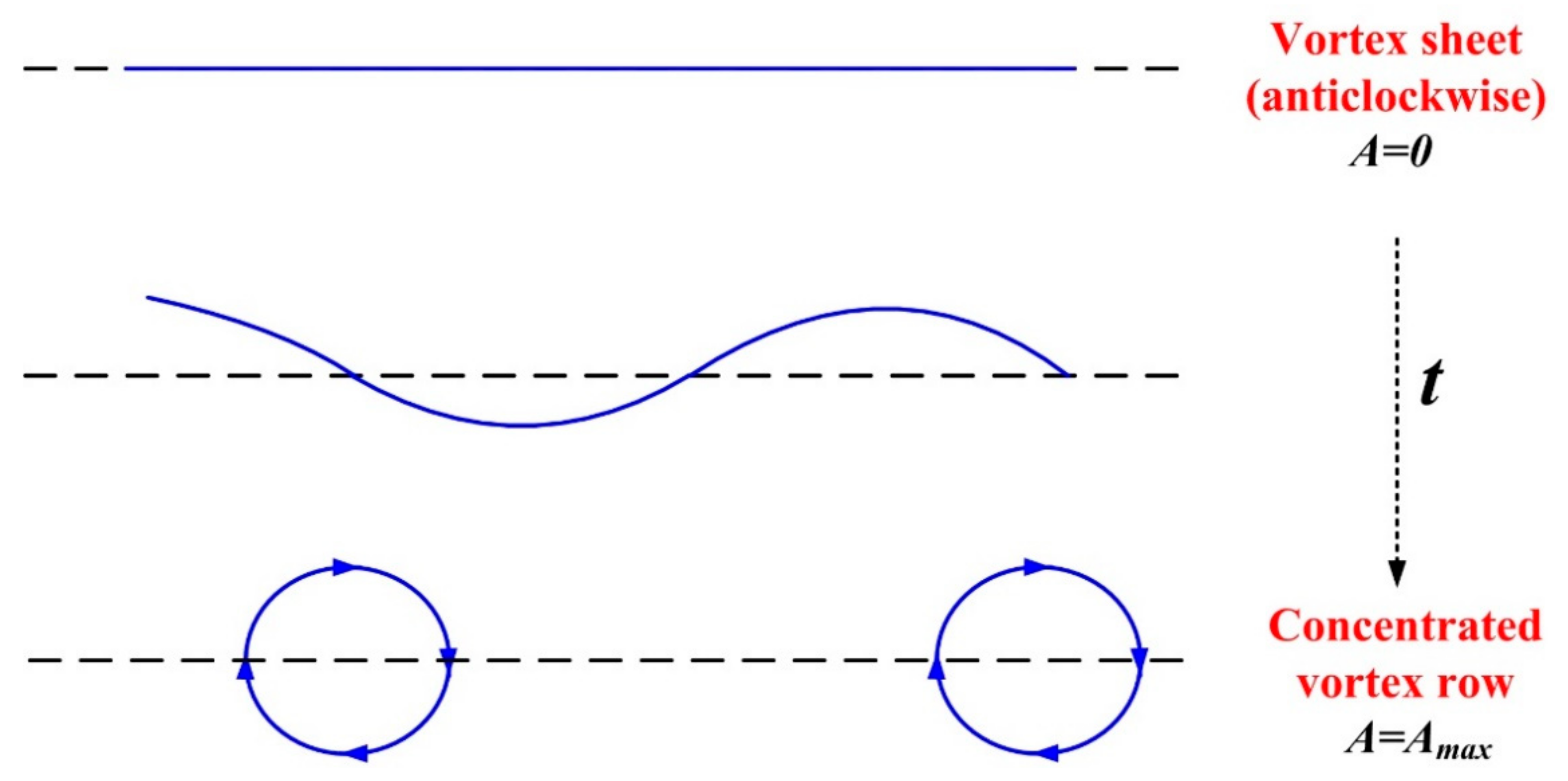
2.3. Time-Dependent Term Based on the Self-Excitation and External Excitation Model
2.4. Complete Form of the Simplified Model and Its Evaluation Index
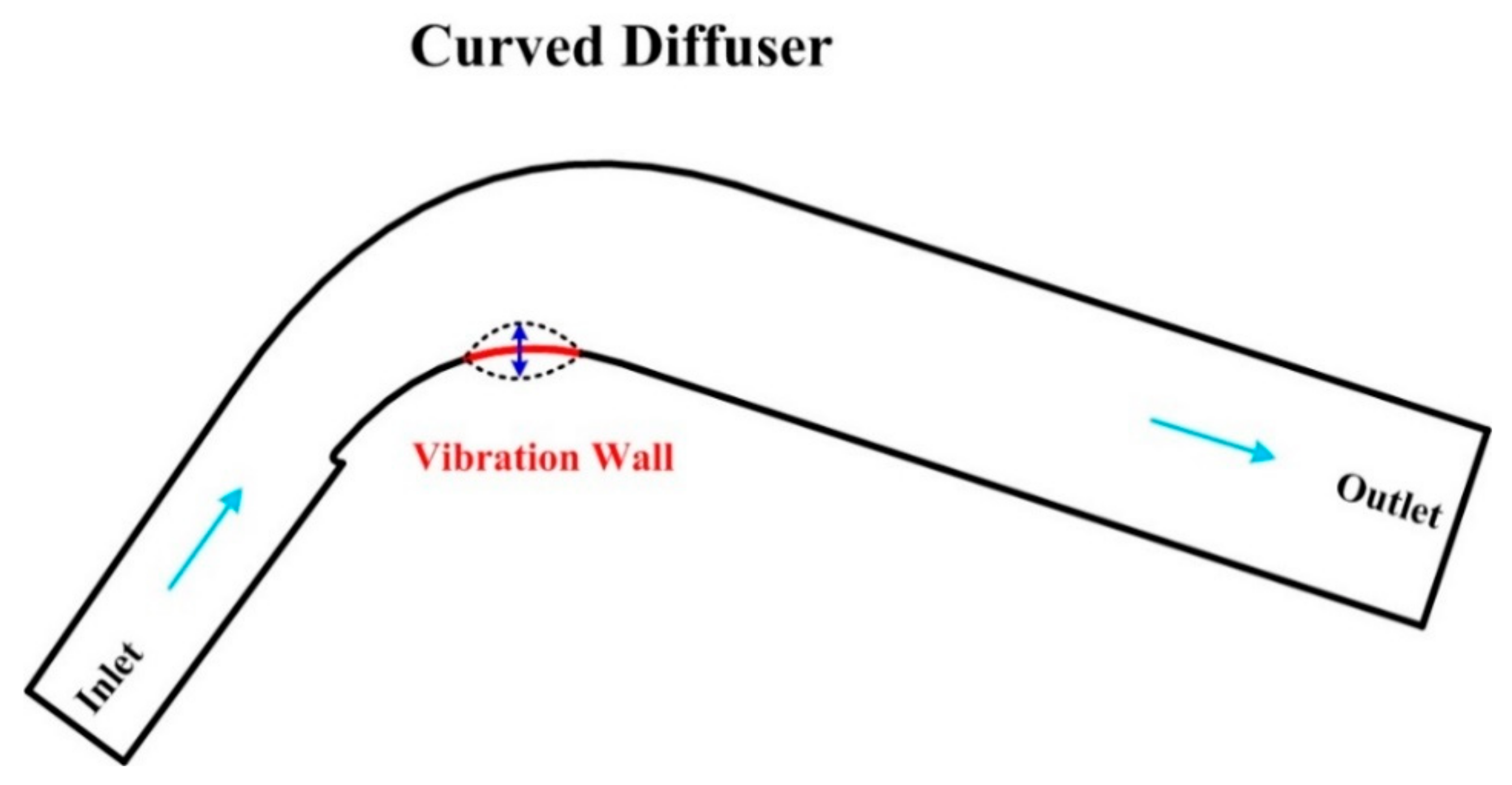
3. CFD Method of Flow Separation Control by a Vibration Wall in a Curved Diffuser
3.1. Introduction of the Numerical Method
3.2. Nondimensional Parameters of the Vibration Wall
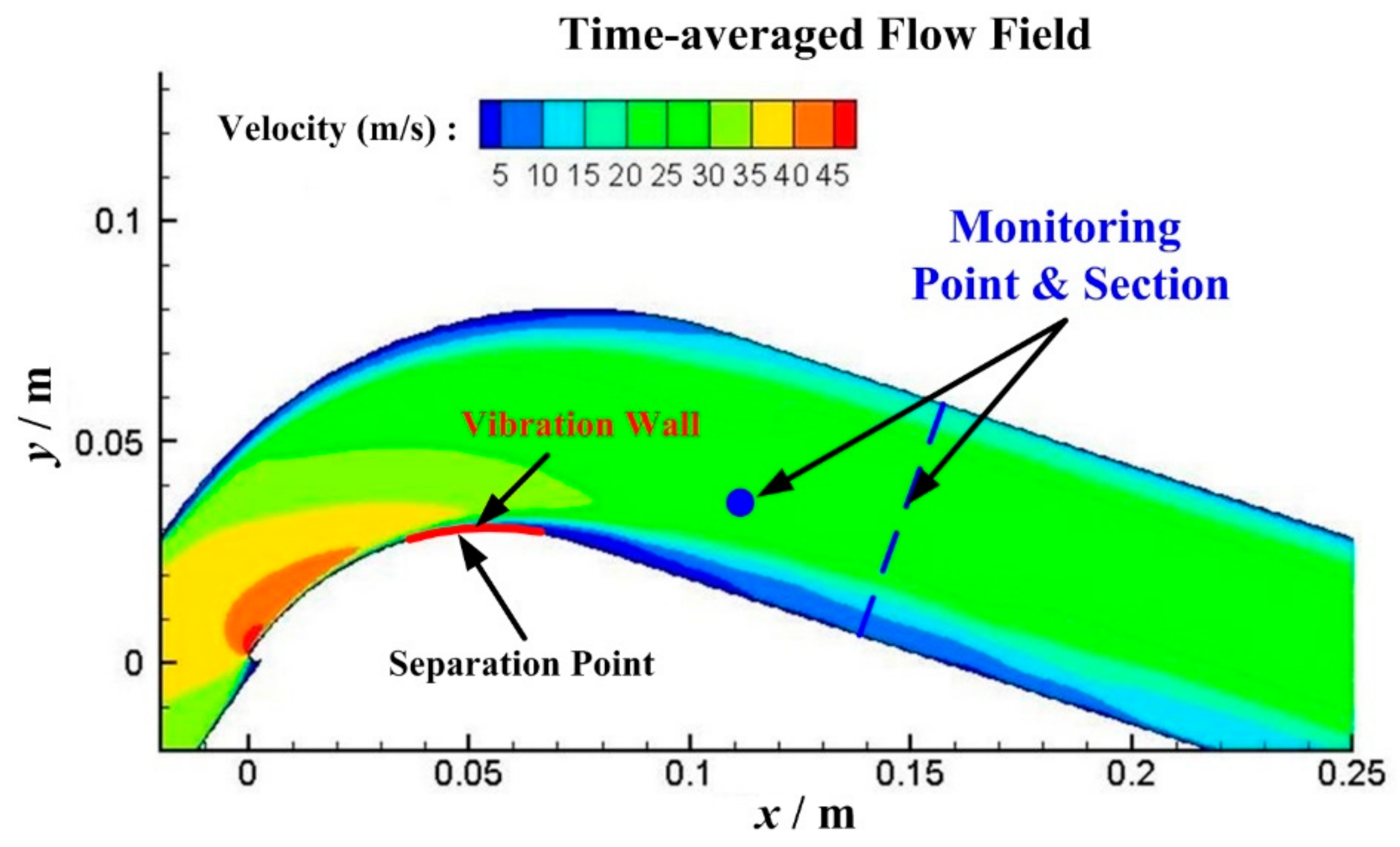
3.3. Evaluation Indexes
4. Comparison of Model-Based and CFD Results
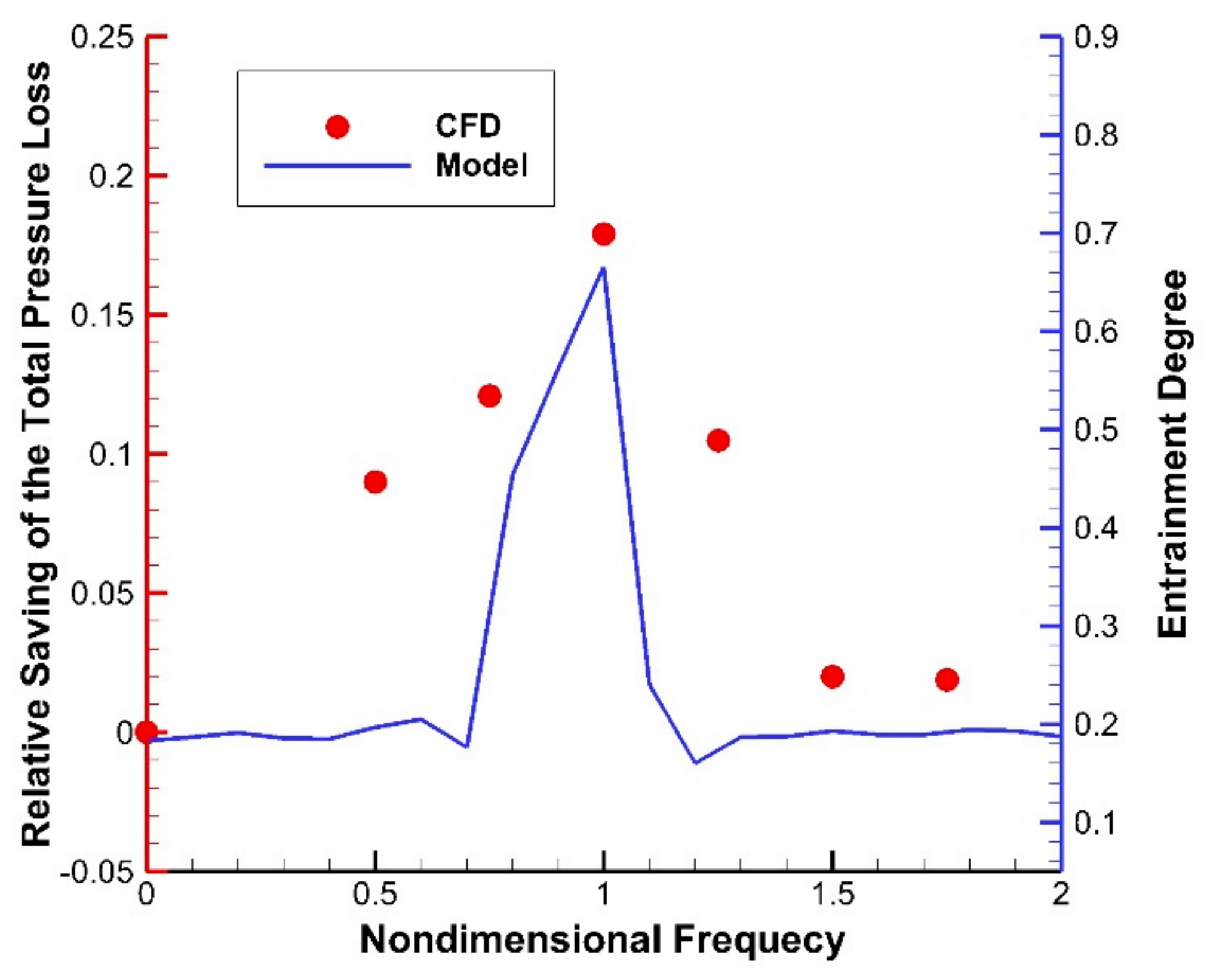
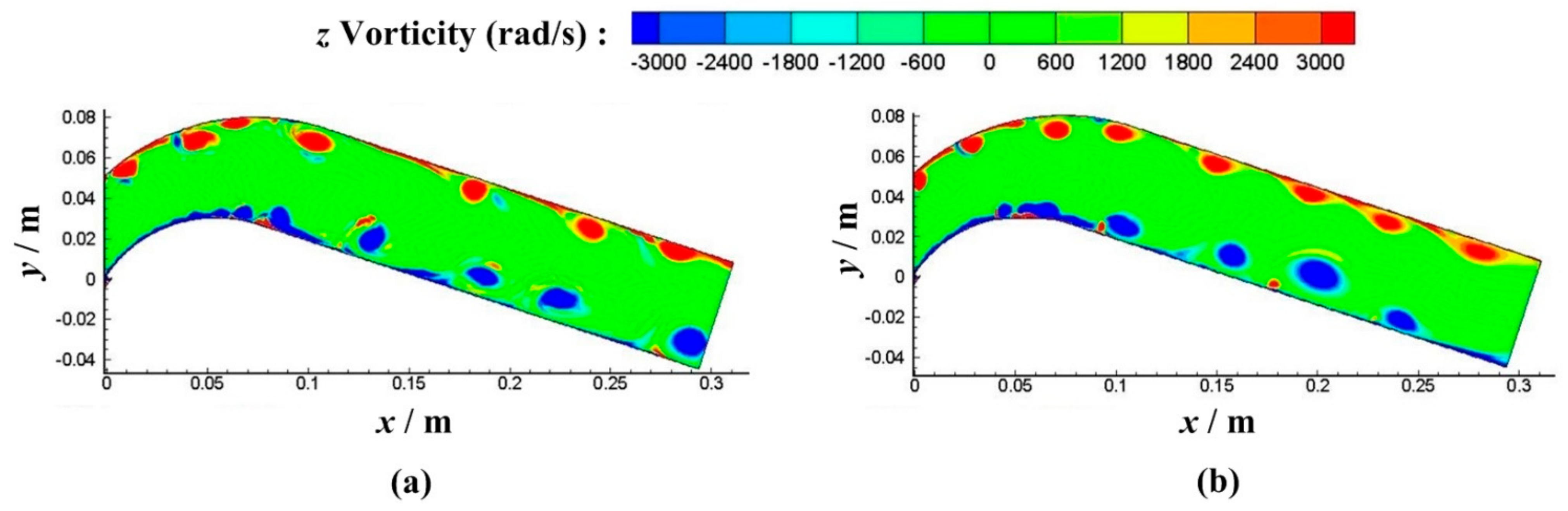
4.1. Vibration Frequency Analysis
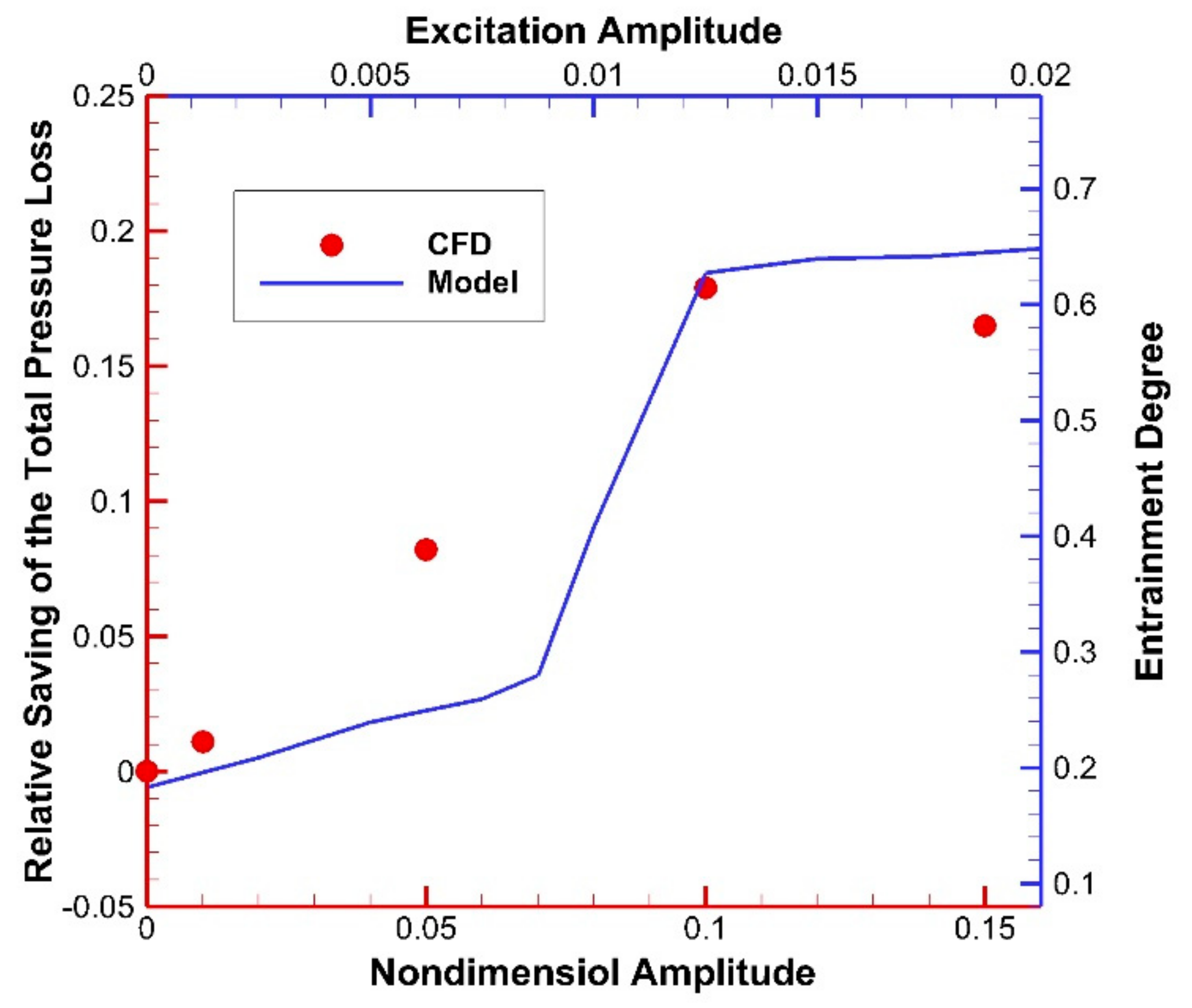
4.2. Vibration Amplitude Analysis
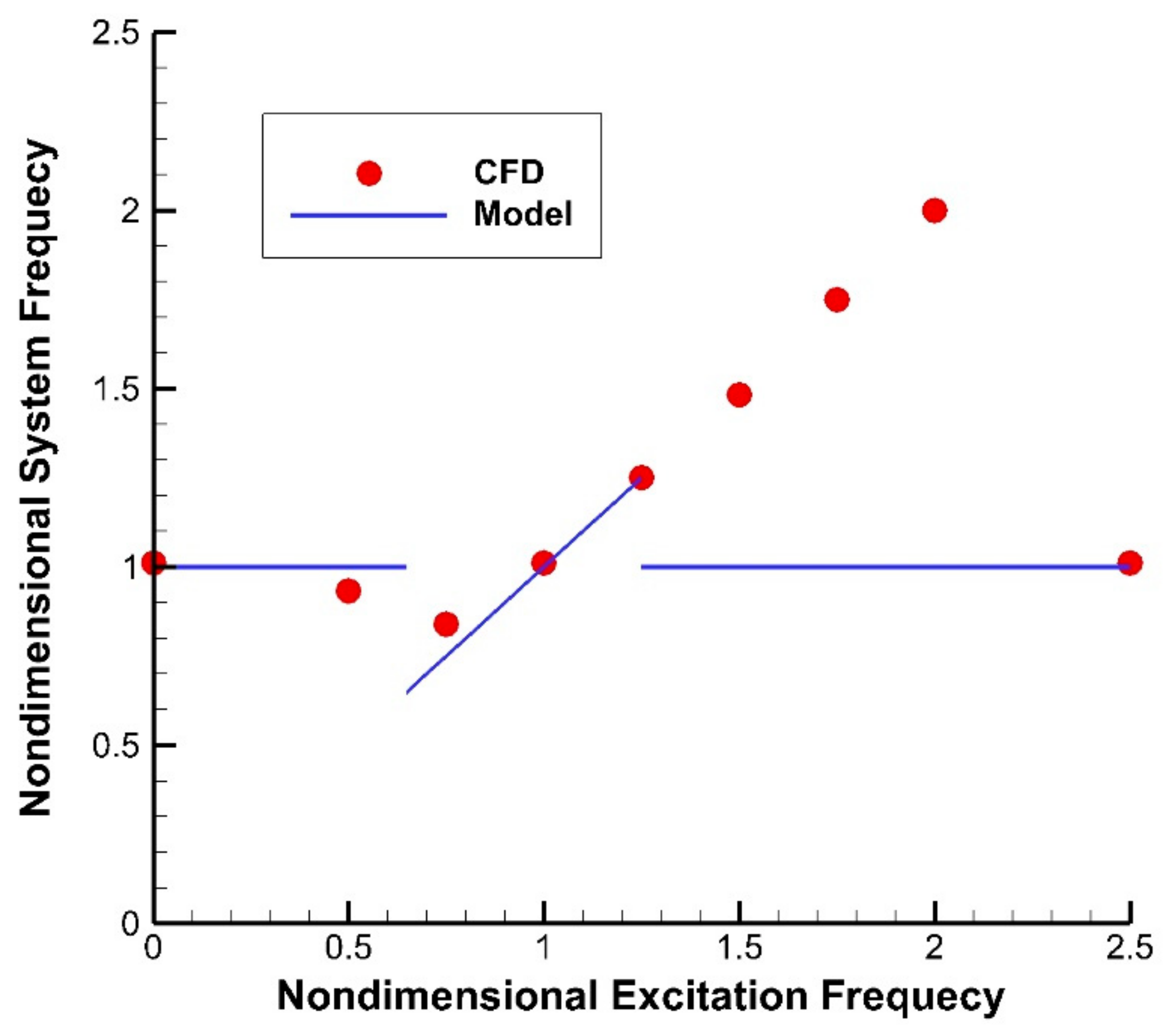
4.3. Lock-In Analysis
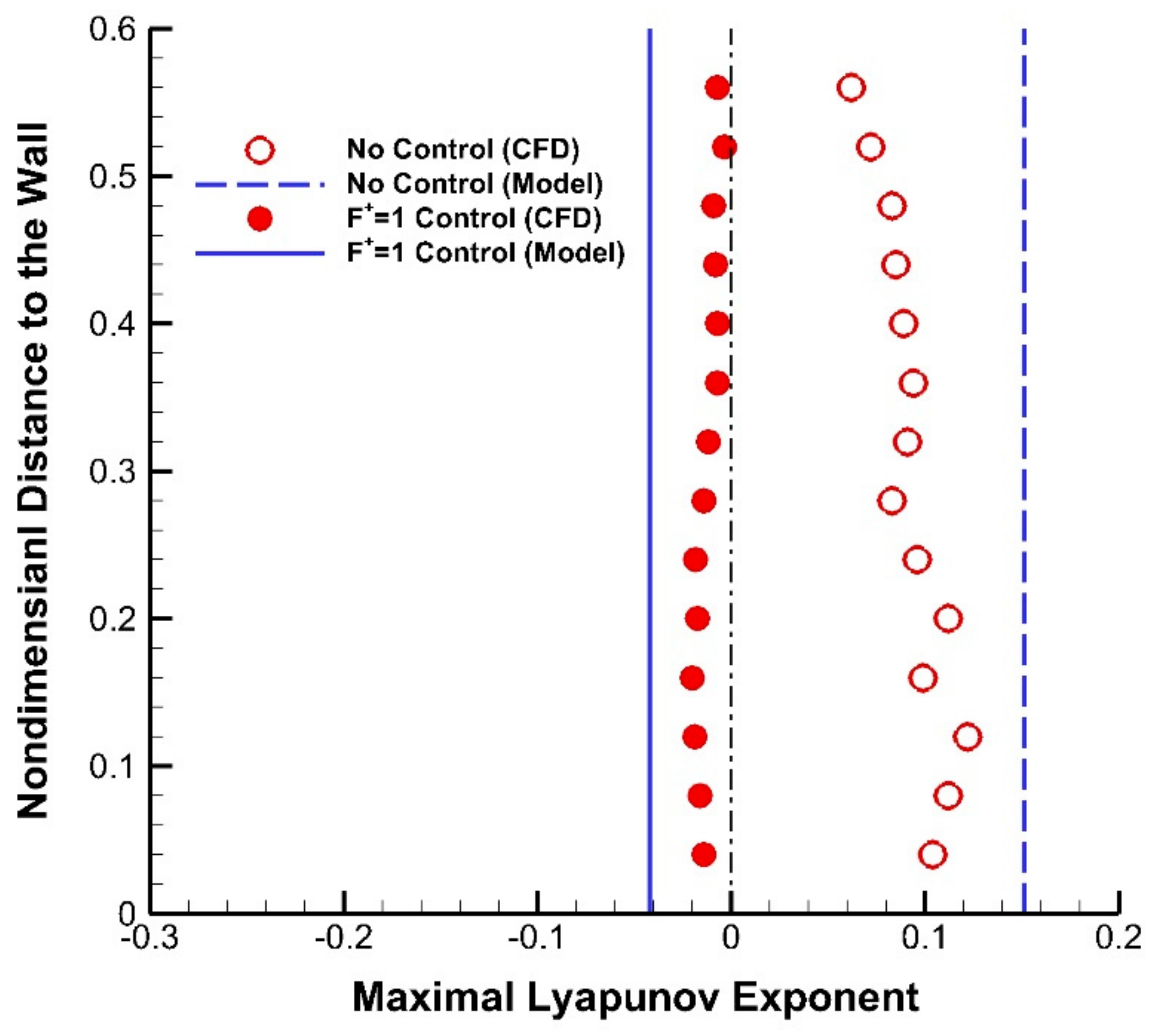
4.4. Degree of Order Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Amplitude of a K-H wave, m/s2 | |
| Amplitude of the vibration wall, m | |
| Nondimensional vibration amplitude, 1 | |
| Coefficient in Duffing equations, 1/s2 | |
| Coefficient in Duffing equations, 1/(m2s2) | |
| Damping coefficient, 1/s | |
| Nondimensional frequency of vibration walls, 1 | |
| Time-dependent term, m/s2 | |
| Dominant vortex frequency, Hz | |
| Frequency of vibration walls, Hz | |
| , | Coefficients in Oseen vortices, 1 |
| Amplitude of vibration walls, m | |
| Characteristic length, m | |
| Landau constant, m3/m2 | |
| Mass flow averaged pressure, Pa | |
| Static pressure, Pa | |
| Radius, m | |
| Vortex core radius of large-scale separation vortices, m | |
| Vortex core radius of small-scale vortices, m | |
| Time, s | |
| Mass flow averaged velocity, m/s | |
| Velocity vector, m/s | |
| y-direction Velocity, m/s | |
| Circumferential velocity, m/s | |
| , | Cartesian coordinates, m |
| Vortex strength, m2/s | |
| th Lyapunov exponent, 1 | |
| Maximal Lyapunov exponent, 1 | |
| Linear growth rate of the K-H wave, 1/s | |
| Entrainment degree, m/s | |
| Coefficient in Oseen vortices, 1 | |
| Coefficient of kinetic viscosity, m2/s | |
| Coefficient of small-scale eddy viscosity, m2/s | |
| , | Lagrange variables, m |
| Density, kg/m3 | |
| Total pressure loss coefficient, 1 | |
| Relative saving of the total pressure loss, 1 | |
| Subscripts | |
| 1 | Diffuser inlet |
| 2 | Diffuser outlet |
| c | with flow control |
| n | without flow control |
| Superscripts | |
| * | Absolute total state |
References
- Telionis, D.P. Review—Unsteady boundary layers, separated and attached. J. Fluids Eng. 1979, 101, 29–43. [Google Scholar] [CrossRef]
- Greenblatt, D.; Wygnanski, I.J. The control of flow separation by periodic excitation. Prog. Aerosp. Sci. 2000, 36, 487–545. [Google Scholar] [CrossRef]
- Nishioka, M.; Asai, M.; Yoshida, S. Control of Flow Separaion by Acoustic Excitation. AIAA J. 1987, 28, 1909–1915. [Google Scholar] [CrossRef]
- Glezer, A.; Amitay, M. Synthetic jets. Annu. Rev. Fluid Mech. 2002, 34, 503–529. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, P.; Yang, J. Parameters effect of pulsed-blowing over control surface. Aerosp. Sci. Technol. 2016, 58, 103–115. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Hajipour, M. Flow separation control over an airfoil using dual excitation of DBD plasma actuators. Aerosp. Sci. Technol. 2018, 79, 658–668. [Google Scholar] [CrossRef]
- Wu, X.H.; Wu, J.Z.; Wu, J.M. Streaming effect of wall oscillation to boundary layer separation. In Proceedings of the 29th Aerospace Sciences Meeting, Reno, NV, USA, 7–10 January 1991. [Google Scholar]
- Sinha, S.; Hyvärinen, J. Flexible-Wall Turbulence Control for Drag Reduction Streamlined and Bluff Bodies. In Proceedings of the 4th Flow Control Conference, Seattle, WA, USA, 23–26 June 2008. [Google Scholar]
- Yang, R.; Zhong, D.; Ge, N. Numerical investigation on flow control effects of dynamic hump for turbine cascade at different Reynolds number and hump oscillating frequency. Aerosp. Sci. Technol. 2019, 92, 280–288. [Google Scholar] [CrossRef]
- Kang, W.; Xu, M.; Yao, W.; Zhang, J. Lock-in mechanism of flow over a low-Reynolds-number airfoil with morphing surface. Aerosp. Sci. Technol. 2020, 97, 105647. [Google Scholar] [CrossRef]
- Zheng, X.Q.; Zhou, X.B.; Zhou, S. Investigation on a type of flow control to weaken unsteady separated flows by unsteady excitation in axial flow compressors. J. Turbomach. 2005, 127, 489–496. [Google Scholar] [CrossRef]
- Collis, S.S.; Joslin, R.D.; Seifert, A.; Theofilis, V. Issues in active flow control: Theory, control, simulation, and experiment. Prog. Aerosp. Sci. 2004, 40, 237–289. [Google Scholar] [CrossRef]
- Orszag, S.A. Accurate solution of the Orr-Sommerfeld stability equation. J. Fluid Mech. 1971, 50, 689–703. [Google Scholar] [CrossRef]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Batcheler, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Kovacic, I.; Brennan, M.J. The Duffing Equation: Nonlinear Oscillators and Their Behavior; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Stuart, J.T. On the non-linear mechanics of hydrodynamic stability. J. Fluid Mech. 1958, 4, 1–21. [Google Scholar] [CrossRef]
- Lu, W.; Huang, G.; Wang, J.; Yang, Y. Flow Separation Control in a Curved Diffuser with Rigid Traveling Wave Wall and Its Mechanism. Energies 2019, 12, 192. [Google Scholar] [CrossRef]
- Wang, J.C.; Fu, X.; Huang, G.P.; Hong, S.L.; Zou, Y.C. Application of the Proper Orthogonal Decomposition Method in Analyzing Active Separation Control with Periodic Vibration Wall. Int. J. Turbo Jet Engines 2019, 36, 175–184. [Google Scholar] [CrossRef]
- Lu, W.; Huang, G.; Zhu, J.; Fu, X.; Wang, J. A nonlinear dynamic model for unsteady separated flow control and its mechanism analysis. J. Fluid Mech. 2017, 826, 942–974. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]


| 0 | −1 | +1 |
| 0.5 | −0.82 | −0.02 |
| 1 | +0.54 | −1.01 |
| 2 | +0.33 | +0.1 |
| Types of the Duffing Equation | ||
|---|---|---|
| + | − | softening nonlinearity |
| + | + | hardening nonlinearity |
| − | + | Negative linear positive cubic stiffness nonlinearity |
| − | − | Negative linear negative cubic stiffness nonlinearity |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Fu, X.; Wang, J.; Zou, Y. Model-Based Analysis of Flow Separation Control in a Curved Diffuser by a Vibration Wall. Energies 2021, 14, 1781. https://doi.org/10.3390/en14061781
Lu W, Fu X, Wang J, Zou Y. Model-Based Analysis of Flow Separation Control in a Curved Diffuser by a Vibration Wall. Energies. 2021; 14(6):1781. https://doi.org/10.3390/en14061781
Chicago/Turabian StyleLu, Weiyu, Xin Fu, Jinchun Wang, and Yuanchi Zou. 2021. "Model-Based Analysis of Flow Separation Control in a Curved Diffuser by a Vibration Wall" Energies 14, no. 6: 1781. https://doi.org/10.3390/en14061781
APA StyleLu, W., Fu, X., Wang, J., & Zou, Y. (2021). Model-Based Analysis of Flow Separation Control in a Curved Diffuser by a Vibration Wall. Energies, 14(6), 1781. https://doi.org/10.3390/en14061781





