Flexibility Management with Virtual Batteries of Thermostatically Controlled Loads: Real-Time Control System and Potential in Spain
Abstract
1. Introduction
2. The Virtual Battery
2.1. The TCL Model
2.2. The VB Model
2.3. The VB Controller
2.3.1. Checking of TCL
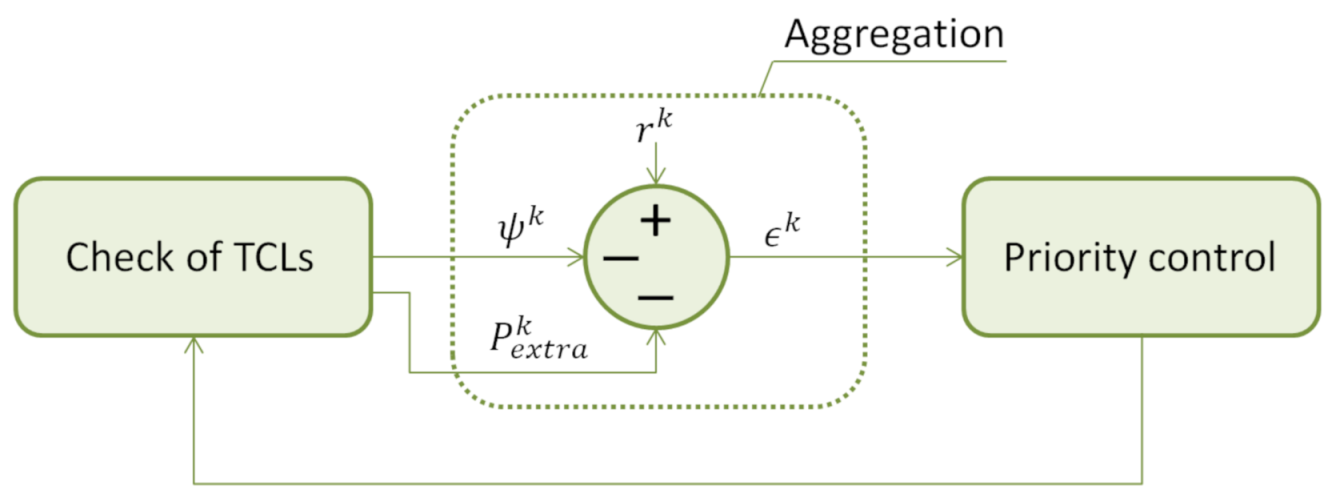
2.3.2. Aggregation
2.3.3. Priority Control
3. Residential Virtual Battery Potential in Spain
4. Results and Discussion
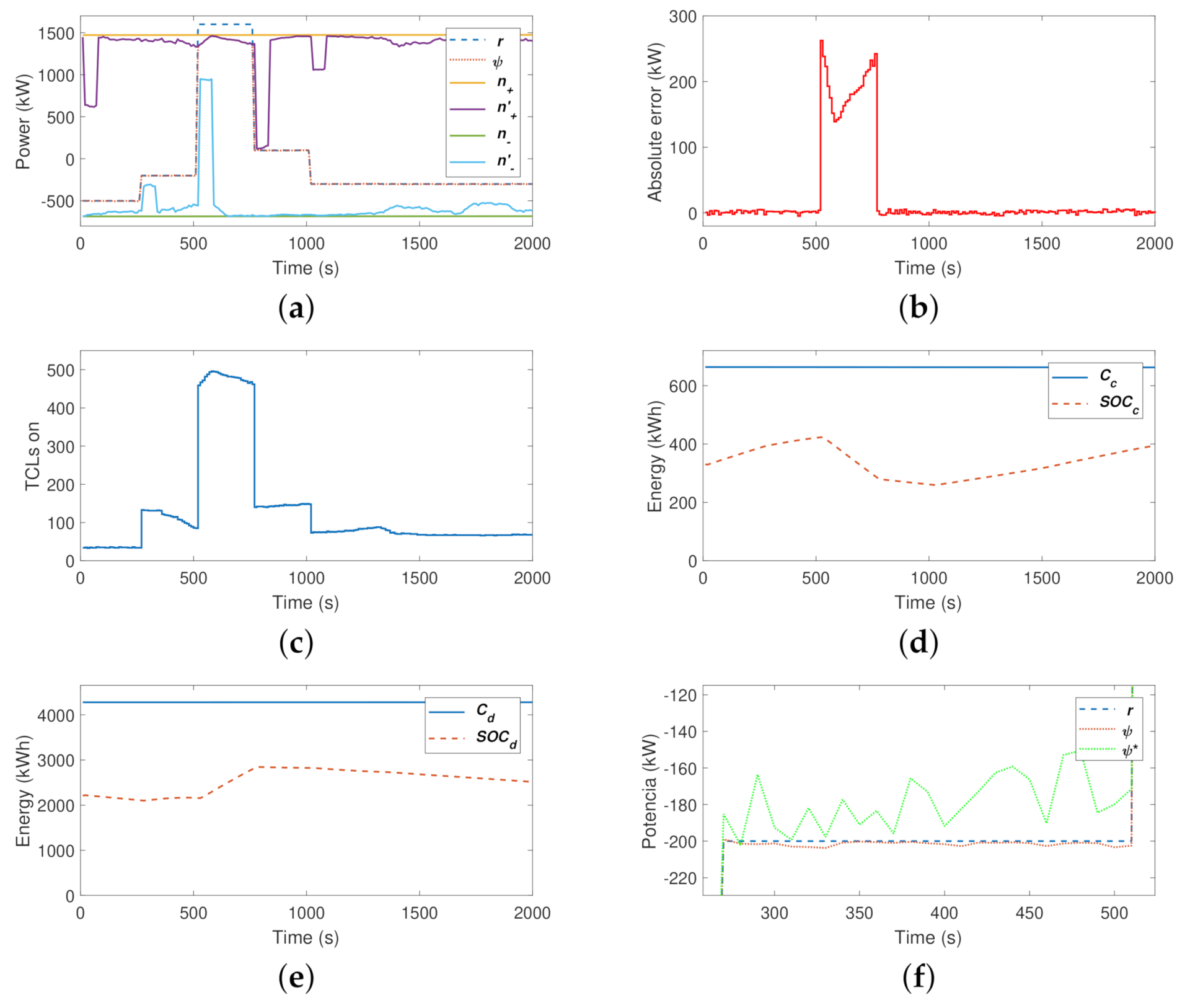
4.1. Case Study: VB Controller Operation
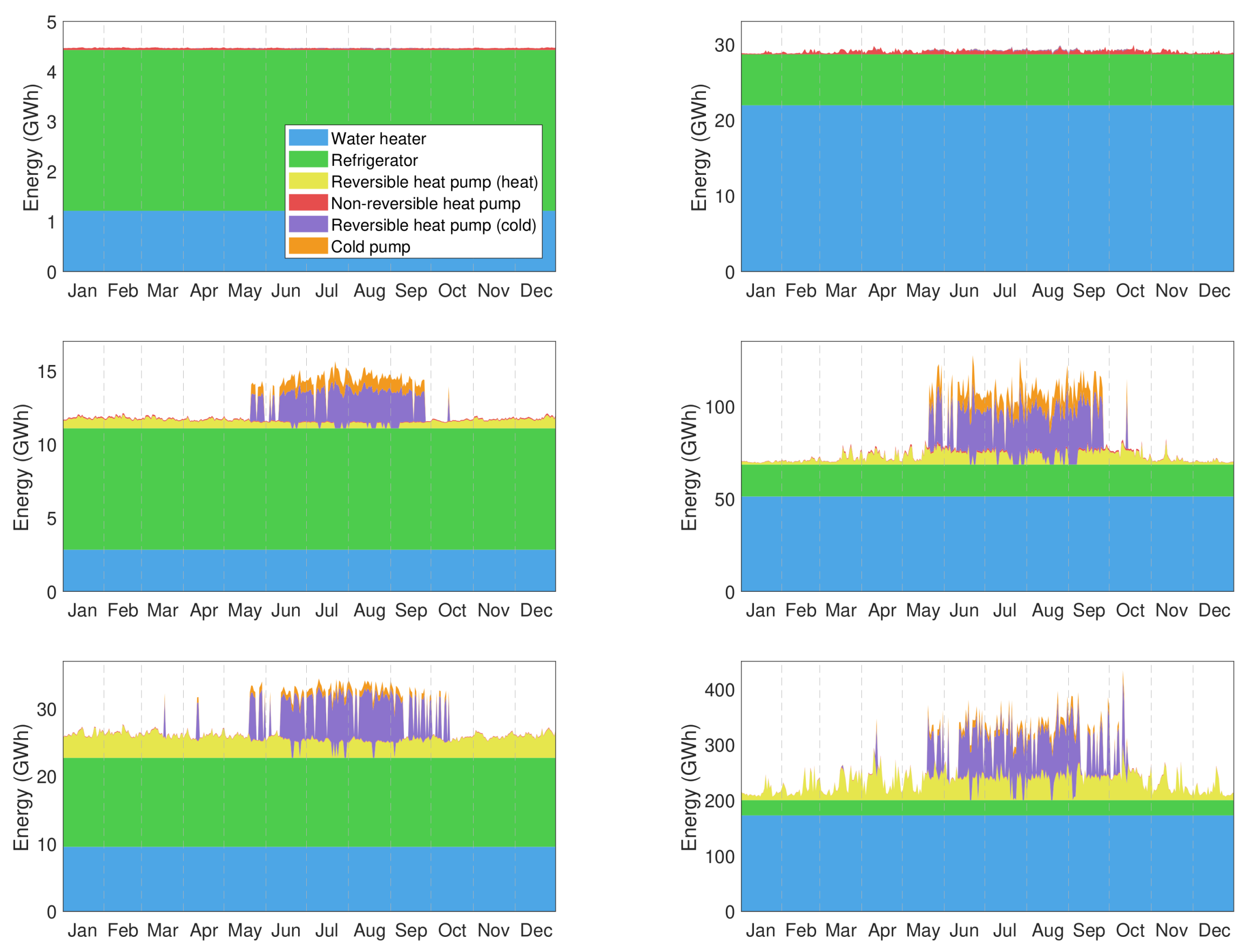
4.2. Case Study: VB Potential in Spain
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Meaning |
| Thermostatically controlled load (TCL) temperature () | |
| Forecast ambient temperature () | |
| Set point temperature () | |
| Temperature dead-band () | |
| Perturbation () | |
| Thermal resistance (/kW) | |
| Thermal capacity (kWh/) | |
| P | Nameplate power (kW) |
| Mean power (kW) | |
| Coefficient of performance | |
| Kind of device | |
| u | Status |
| Availability | |
| Full availability | |
| Time to reach bound temperature (h) | |
| Cycle elapsed time (h) | |
| Minimum cycle elapsed time (h) | |
| Set of TCLs with cardinality N | |
| / | Charging/Discharging capacity (kWh) |
| / | Charging/Discharging state of charge (kWh) |
| / | Maximum charging/discharging power (kW) |
| / | Maximum available charging/discharging power (kW) |
| Extra power (kW) | |
| r | System operator signal (kW) |
| Aggregated power (kW) | |
| Base power (kW) | |
| System deviation (kW) | |
| Regulation signal (kW) | |
| p | Power switched (kW) |
| i | Subindex denoting individual TCL |
| k | Subindex denoting time instant |
Appendix A. Control Algorithms
| Algorithm A1 Check of TCLs |
{Total availability}
{Forecast ambient temperature}
{TCL temperature}
{Cycled passed time}
|
| Algorithm A2 Aggregation |
{Capacity}
{State of charge}
{Maximum power}
{Regulation signal}
|
| Algorithm A3 Priority Control |
{Disaggregation}
|
References
- Callaway, D.S.; Hiskens, I.A. Achieving Controllability of Electric Loads. Proc. IEEE 2011, 99, 184–199. [Google Scholar] [CrossRef]
- Koch, S.; Mathieu, J.L.; Callaway, D.S. Modeling and Control of Aggregated Heterogeneous Thermostatically Controlled Loads for Ancillary Services. In Proceedings of the 17th Power Systems Computation Conference (PSCC’11), Stockholm, Sweden, 22–26 August 2011. [Google Scholar]
- Hao, H.; Sanandaji, B.M.; Poolla, K.; Vincent, T.L. A generalized battery model of a collection of Thermostatically Controlled Loads for providing ancillary service. In Proceedings of the 2013 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–4 October 2013; pp. 551–558. [Google Scholar] [CrossRef]
- Acharya, S.; El Moursi, M.S.; Al-Hinai, A. Coordinated frequency control strategy for an islanded microgrid with demand side management capability. IEEE Trans. Energy Convers. 2017, 33, 639–651. [Google Scholar] [CrossRef]
- Tindemans, S.H.; Trovato, V.; Strbac, G. Decentralized control of thermostatic loads for flexible demand response. IEEE Trans. Control Syst. Technol. 2015, 23, 1685–1700. [Google Scholar] [CrossRef]
- Wang, P.; Wu, D.; Kalsi, K. Flexibility Estimation and Control of Thermostatically Controlled Loads with Lock Time for Regulation Service. IEEE Trans. Smart Grid 2020, 11, 3221–3230. [Google Scholar] [CrossRef]
- Mathieu, J.L.; Rasmussen, T.B.; Sørensen, M.; Jòhannsson, H.; Andersson, G. Technical resource potential of non-disruptive residential demand response in Denmark. In Proceedings of the 2014 IEEE PES General Meeting, Conference Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Gils, H.C. Economic potential for future demand response in Germany—Modeling approach and case study. Appl. Energy 2016, 162, 401–415. [Google Scholar] [CrossRef]
- Trovato, V.; Sanz, I.M.; Chaudhuri, B.; Strbac, G. Advanced control of thermostatic loads for rapid frequency response in Great Britain. IEEE Trans. Power Syst. 2016, 32, 2106–2117. [Google Scholar] [CrossRef]
- Kamgarpour, M.; Vrettos, E.; Andersson, G.; Lygeros, J. Population of Thermostatically Controlled Loads for the Swiss Ancillary Service Market. In Proceedings of the COLEB 2014 Workshop Computational Optimisation of Low-Energy Buildings, Zürich, Switzeland, 6–7 March 2014; pp. 49–50. [Google Scholar]
- Hao, H.; Sanandaji, B.M.; Poolla, K.; Vincent, T.L. Potentials and economics of residential thermal loads providing regulation reserve. Energy Policy 2015, 79, 115–126. [Google Scholar] [CrossRef]
- Conte, F.; Massucco, S.; Silvestro, F.; Ciapessoni, E.; Cirio, D. Stochastic modelling of aggregated thermal loads for impact analysis of demand side frequency regulation in the case of Sardinia in 2020. Int. J. Electr. Power Energy Syst. 2017, 93, 291–307. [Google Scholar] [CrossRef]
- Instituto para la Diversificación y ahorro de la Energía. Proyecto SHEC-SPAHOUSEC. Análisis del Consumo Energético del Sector Residencial en España. Informe Final. 2011. Available online: http://www.idae.es/uploads/documentos/documentos_Informe_SPAHOUSEC_ACC_f68291a3.pdf (accessed on 19 February 2021).
- Han, S.; Han, S.; Sezaki, K. Estimation of achievable power capacity from plug-in electric vehicles for V2G frequency regulation: Case studies for market participation. IEEE Trans. Smart Grid 2011, 2, 632–641. [Google Scholar] [CrossRef]
- Liu, H.; Hu, Z.; Song, Y.; Lin, J. Decentralized vehicle-to-grid control for primary frequency regulation considering charging demands. IEEE Trans. Power Syst. 2013, 28, 3480–3489. [Google Scholar] [CrossRef]
- Kempton, W.; Udo, V.; Huber, K.; Komara, K.; Letendre, S.; Baker, S.; Brunner, D.; Pearre, N. A test of vehicle-to-grid (V2G) for energy storage and frequency regulation in the PJM system. Results Ind. Univ. Res. Partnersh. 2008, 32, 1–32. [Google Scholar]
- Hao, H.; Sanandaji, B.M.; Poolla, K.; Vincent, T.L. Aggregate Flexibility of Thermostatically Controlled Loads. IEEE Trans. Power Syst. 2015, 30, 189–198. [Google Scholar] [CrossRef]
- Nandanoori, S.P.; Chakraborty, I.; Ramachandran, T.; Kundu, S. Identification and Validation of Virtual Battery Model for Heterogeneous Devices. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM 2019), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar] [CrossRef][Green Version]
- Ding, Y.; Cui, W.; Zhang, S.; Hui, H.; Qiu, Y.; Song, Y. Multi-state operating reserve model of aggregate thermostatically-controlled-loads for power system short-term reliability evaluation. Appl. Energy 2019, 241, 46–58. [Google Scholar] [CrossRef]
- Lu, N.; Chassin, D.P.; Widergren, S.E. Modeling uncertainties in aggregated thermostatically controlled loads using a state queueing model. IEEE Trans. Power Syst. 2005, 20, 725–733. [Google Scholar] [CrossRef]
- Zhang, W.; Kalsi, K.; Fuller, J.; Elizondo, M.; Chassin, D. Aggregate model for heterogeneous thermostatically controlled loads with demand response. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Perfumo, C.; Kofman, E.; Braslavsky, J.H.; Ward, J.K. Load management: Model-based control of aggregate power for populations of thermostatically controlled loads. Energy Convers. Manag. 2012, 55, 36–48. [Google Scholar] [CrossRef]
- Kundu, S.; Sinitsyn, N.; Backhaus, S.; Hiskens, I. Modeling and control of thermostatically controlled loads. arXiv 2011, arXiv:1101.2157. [Google Scholar]
- Radaideh, A.; Vaidya, U.; Ajjarapu, V. Sequential Set-Point Control for Heterogeneous Thermostatically Controlled Loads Through an Extended Markov Chain Abstraction. IEEE Trans. Smart Grid 2019, 10, 116–127. [Google Scholar] [CrossRef]
- Mathieu, J.L.; Callaway, D.S. State estimation and control of heterogeneous thermostatically controlled loads for load following. In Proceedings of the 2012 45th Hawaii International Conference on System Sciences, Maui, HI, USA, 4–7 January 2012; pp. 2002–2011. [Google Scholar]
- Xia, M.; Song, Y.; Chen, Q. Hierarchical control of thermostatically controlled loads oriented smart buildings. Appl. Energy 2019, 254, 113493. [Google Scholar] [CrossRef]
- Liu, M.; Shi, Y. Model predictive control of aggregated heterogeneous second-order thermostatically controlled loads for ancillary services. IEEE Trans. Power Syst. 2015, 31, 1963–1971. [Google Scholar] [CrossRef]
- Liu, M.; Peeters, S.; Callaway, D.S.; Claessens, B.J. Trajectory tracking with an aggregation of domestic hot water heaters: Combining model-based and model-free control in a commercial deployment. IEEE Trans. Smart Grid 2019, 10, 5686–5695. [Google Scholar] [CrossRef]
- Khan, S.; Shahzad, M.; Habib, U.; Gawlik, W.; Palensky, P. Stochastic battery model for aggregation of thermostatically controlled loads. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 570–575. [Google Scholar] [CrossRef]
- Conte, F.; di Vergagni, M.C.; Massucco, S.; Silvestro, F.; Ciappessoni, E.; Cirio, D. Frequency Regulation by Thermostatically Controlled Loads: A Technical and Economic Analysis. In Proceedings of the 2018 IEEE Power Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Bogodorova, T.; Vanfretti, L.; Turitsyn, K. Voltage control-based ancillary service using thermostatically controlled loads. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Wang, Y.; Tang, Y.; Xu, Y.; Xu, Y. A Distributed Control Scheme of Thermostatically Controlled Loads for the Building-Microgrid Community. IEEE Trans. Sustain. Energy 2019, 11, 350–360. [Google Scholar] [CrossRef]
- Cheng, M.; Sami, S.S.; Wu, J. Benefits of using virtual energy storage system for power system frequency response. Appl. Energy 2017, 194, 376–385. [Google Scholar] [CrossRef]
- Mathieu, J.L.; Kamgarpour, M.; Lygeros, J.; Andersson, G.; Callaway, D.S. Arbitraging intraday wholesale energy market prices with aggregations of thermostatic loads. IEEE Trans. Power Syst. 2014, 30, 763–772. [Google Scholar] [CrossRef]
- Martín Crespo, A.; Saludes Rodil, S. Uso de la flexibilidad de cargas eléctricas con inercia térmica mediante una batería virtual para la regulación de red. In Proceedings of the V Congreso Smart Grids: Libro de Comunicaciones, Madrid, Spain, 13 December 2018. [Google Scholar]
- Lakshmanan, V.; Marinelli, M.; Kosek, A.M.; Nørgård, P.B.; Bindner, H.W. Impact of thermostatically controlled loads’ demand response activation on aggregated power: A field experiment. Energy 2016, 94, 705–714. [Google Scholar] [CrossRef]
- Instituto Nacional de Estadística. Número de Hogares por Provincias Según Tipo de Hogar y Número de Habitaciones de la Vivienda. Available online: http://www.ine.es/jaxi/Tabla.htm?path=/t20/p274/serie/def/p03/l0/&file=03003.px&L=0 (accessed on 19 February 2021).
- Mathieu, J.L. Modeling, Analysis, and Control of Demand Response Resources. Ph.D. Thesis, UC Berkeley, Berkeley, CA, USA, 2012. [Google Scholar]
- The Mathworks, Inc. MATLAB Version 2019b; The Mathworks, Inc.: Natick, MA, USA, 2019. [Google Scholar]
- España. Resolución de 13 de julio de 2006, de la Secretaría General de Energía, por la que se aprueba el procedimiento de operación 1.5 «Establecimiento de la reserva para la regulación frecuencia-potencia». In Boletín Oficial del Estado; Ministerio de Industria, Turismo y Comercio: Madrid, Spain, 2016; Volume 173, pp. 27473–27474. [Google Scholar]
- Smart Energy Demand Coalition. Explicit Demand Response In Europe—Mapping the Markets. 2017. Available online: https://www.smarten.eu/wp-content/uploads/2017/04/SEDC-Explicit-Demand-Response-in-Europe-Mapping-the-Markets-2017.pdf (accessed on 19 February 2021).
- España. Documento Básico HE Ahorro de Energía; Código Técnico de la Edificación: Madrid, Spain, 2017. [Google Scholar]
- European Union. Regulation (EU) 2019/943 of the European Parliament and of the Council of 5 June 2019 on the internal market for electricity. Off. J. Eur. Union 2019, L 158/154. Available online: http://data.europa.eu/eli/reg/2019/943/oj (accessed on 19 February 2021).
- European Union. Directive (EU) 2019/944 of the European Parliament and of the Council of 5 June 2019 on common rules for the internal market for electricity and amending Directive 2012/27/EU. Off. J. Eur. Union 2019, L 158/125. Available online: http://data.europa.eu/eli/dir/2019/944/oj (accessed on 19 February 2021).
- Red Eléctrica de España. Net Balancing Energy. Available online: https://www.esios.ree.es/en/analysis/762?vis=1&start_date=01-01-2019T00%3A00&end_date=31-12-2019T23%3A50&compare_start_date=01-01-2018T00%3A00&groupby=year (accessed on 19 February 2021).
- Red Eléctrica de España. Net Balancing Energy. Available online: https://www.esios.ree.es/en/analysis/762?vis=1&start_date=01-01-2019T00%3A00&end_date=31-12-2019T23%3A50&compare_start_date=01-01-2018T00%3A00&groupby=hour (accessed on 19 February 2021).
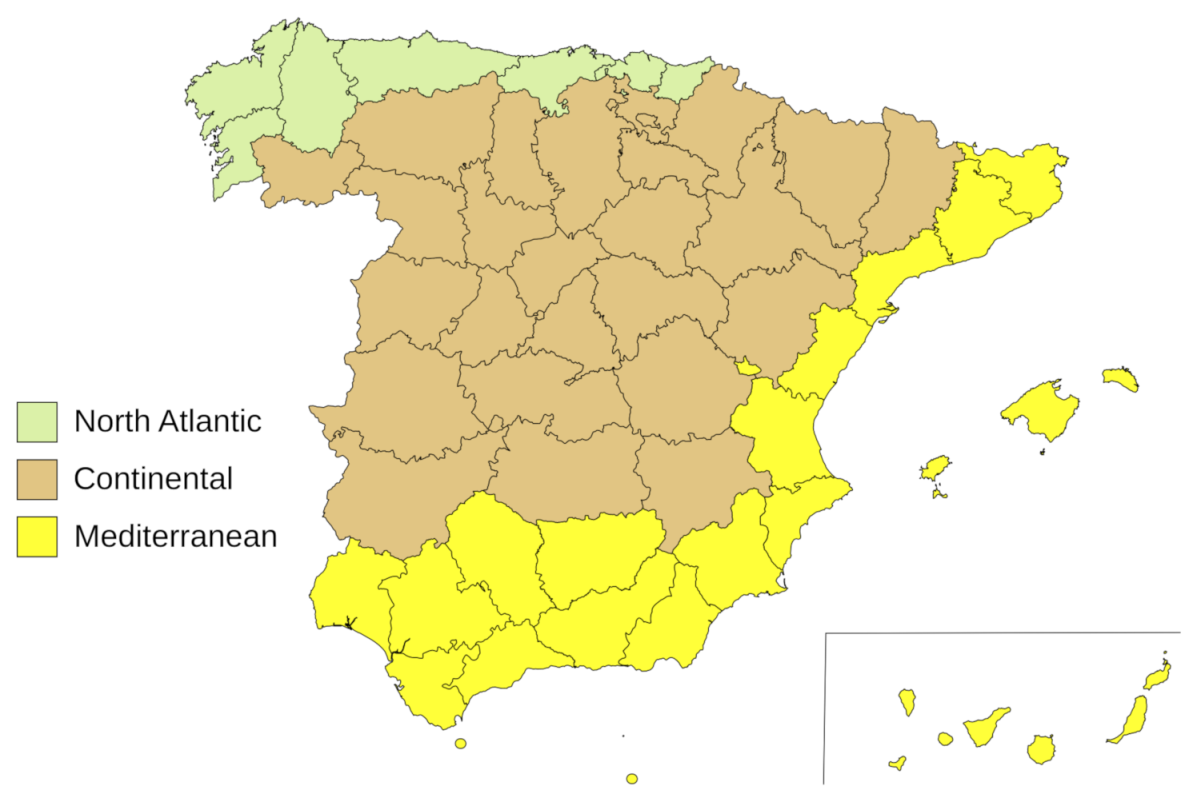
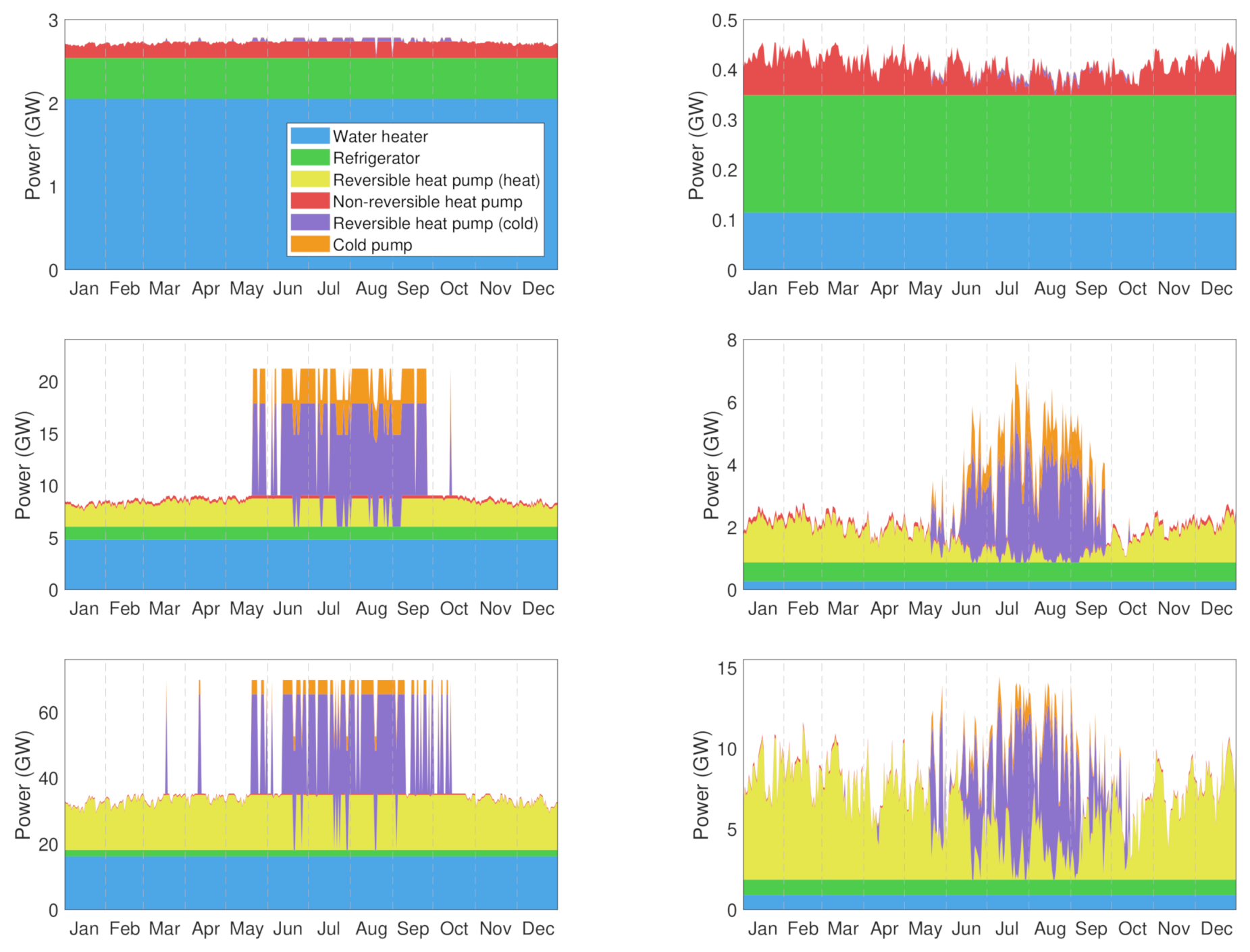
| TCL Type (%) | North Atlantic | Continental | Mediterranean |
|---|---|---|---|
| Reversible heat pump (heat) | 0.0 | 7.9 | 30.5 |
| Reversible heat pump (cold) | 0.3 | 25.9 | 55.4 |
| Non-reversible heat pump | 1.5 | 0.9 | 0.7 |
| Cold pump | 0.1 | 9.8 | 8.0 |
| Electric water heater | 19.9 | 18.1 | 38.0 |
| Refrigerator | 99.9 | 99.8 | 99.4 |
| TCL Type (#) | North Atlantic | Continental | Mediterranean |
|---|---|---|---|
| Reversible heat pump (heat) | 0 | 488,924 | 3,035,739 |
| Reversible heat pump (cold) | 7444 | 1,611,424 | 5,508,641 |
| Non-reversible heat pump | 36,527 | 56,542 | 73,960 |
| Cold pump | 1329 | 610,388 | 796,430 |
| Electric water heater | 480,534 | 1,123,051 | 3,783,823 |
| Refrigerator | 2,414,583 | 6,200,175 | 9,890,698 |
| TCL Type | (C/kW) | (kWh/C) | P (kW) | (C) | (C) | |
|---|---|---|---|---|---|---|
| Reversible heat pump (heat) | – | – | – | 15–24 | – | |
| Reversible heat pump (cold) | – | – | 4– | 18–27 | – | |
| Non-reversible heat pump | – | – | – | 15–24 | – | |
| Cold pump | – | – | 4– | 18–27 | – | |
| Electric water heater | 100–140 | – | – | 1 | 43–54 | 2–4 |
| Refrigerator | 80–100 | – | – | 2 | – | 1–2 |
| Greatest Capacities (kWh) and Maximum Powers (kW) | Value |
|---|---|
| Greatest charging capacity | 671.0 |
| Greatest discharging capacity | 4314.9 |
| Greatest maximum charging power | 1476.6 |
| Greatest maximum discharging power | 692.4 |
| Greatest Capacity (kWh) and Power (kW) | North Atlantic | Continental | Mediterranean |
|---|---|---|---|
| Greatest charging capacity/home | 1.86 | 2.52 | 3.24 |
| Greatest discharging capacity/home | 12.37 | 19.68 | 38.88 |
| Greatest maximum charging power/home | 1.13 | 2.93 | 5.29 |
| Greatest maximum discharging power/home | 0.19 | 1.18 | 1.39 |
| Charge Capacity Contribution (%) | North Atlantic | Continental | Mediterranean |
|---|---|---|---|
| Water heater | 27.23 | 23.74 | 37.11 |
| Refrigerator | 72.16 | 69.14 | 51.16 |
| Reversible heat pump (cold) | 0.02 | 2.80 | 3.12 |
| Cold pump | 0.00 | 1.06 | 0.45 |
| Reversible heat pump (heat) | 0.00 | 2.93 | 7.96 |
| Non-reversible heat pump | 0.59 | 0.34 | 0.19 |
| Discharging Capacity Contribution (%) | North Atlantic | Continental | Mediterranean |
|---|---|---|---|
| Water heater | 76.17 | 70.85 | 79.73 |
| Refrigerator | 23.34 | 23.85 | 12.71 |
| Reversible heat pump (cold) | 0.02 | 2.34 | 2.35 |
| Cold pump | 0.00 | 0.89 | 0.34 |
| Reversible heat pump (heat) | 0.00 | 1.85 | 4.76 |
| Non-reversible heat pump | 0.47 | 0.21 | 0.12 |
| Maximum Charging Power Contribution (%) | North Atlantic | Continental | Mediterranean |
|---|---|---|---|
| Water heater | 76.72 | 51.06 | 50.19 |
| Refrigerator | 18.34 | 13.41 | 6.24 |
| Reversible heat pump (cold) | 0.11 | 13.25 | 10.48 |
| Cold pump | 0.02 | 5.02 | 1.51 |
| Reversible heat pump (heat) | 0.00 | 15.47 | 30.83 |
| Non-reversible heat pump | 4.81 | 1.79 | 0.75 |
| Maximum Discharging Power Contribution (%) | North Atlantic | Continental | Mediterranean |
|---|---|---|---|
| Water heater | 29.80 | 14.61 | 17.39 |
| Refrigerator | 61.29 | 33.01 | 18.60 |
| Reversible heat pump (cold) | 0.10 | 15.11 | 10.39 |
| Cold pump | 0.02 | 5.72 | 1.50 |
| Reversible heat pump (heat) | 0.00 | 28.28 | 50.88 |
| Non-reversible heat pump | 08.79 | 3.27 | 1.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martín-Crespo, A.; Saludes-Rodil, S.; Baeyens, E. Flexibility Management with Virtual Batteries of Thermostatically Controlled Loads: Real-Time Control System and Potential in Spain. Energies 2021, 14, 1711. https://doi.org/10.3390/en14061711
Martín-Crespo A, Saludes-Rodil S, Baeyens E. Flexibility Management with Virtual Batteries of Thermostatically Controlled Loads: Real-Time Control System and Potential in Spain. Energies. 2021; 14(6):1711. https://doi.org/10.3390/en14061711
Chicago/Turabian StyleMartín-Crespo, Alejandro, Sergio Saludes-Rodil, and Enrique Baeyens. 2021. "Flexibility Management with Virtual Batteries of Thermostatically Controlled Loads: Real-Time Control System and Potential in Spain" Energies 14, no. 6: 1711. https://doi.org/10.3390/en14061711
APA StyleMartín-Crespo, A., Saludes-Rodil, S., & Baeyens, E. (2021). Flexibility Management with Virtual Batteries of Thermostatically Controlled Loads: Real-Time Control System and Potential in Spain. Energies, 14(6), 1711. https://doi.org/10.3390/en14061711






